1 Introduction

Implementation of initially curved (arch) shallow beam elements in construction of micro/nano-electro-mechanical-systems (M/NEMS) has been reported by various research groups in recent years. Specific applications including memories (Charlot et al. 2008), sensors (Southworth et al. 2010), switches (Intaraprasonk and Fan 2011), and band-pass filters (Maani Miandoab et al. 2015b; Tajaddodianfar et al. 2015b) have motivated the growing research in the field of M/NEMS with arch beam elements. Functional advantages of these systems originate from their bistability which refers to their capability to operate in two symmetric concave and convex buckled configurations at the same values of actuation parameters. Transition between these separate configurations is triggered by a precipitate motion known as the snap-through. In fact, for sufficiently curved beams, bistability occurs under the transverse load between two critical points: snap-through and release (snap-back) values (Krylov et al. 2008).

Electrostatic force, which is a popular actuation mechanism in the field of M/NEMS, enriches dynamics of the system by adding deflection-dependent nonlinearity. The beam element becomes softer as its deflection increases under the electrostatic load; while the load itself increases as a function of beam deflection. However, in a critical loading value, the structure collapses suddenly and the electrodes may stick together. This type of instability, known as the pull-in, is a characteristic of most of the electrostatically actuated M/NEMS, and is widely discussed in the literature. Zhang et al. (2014) have reviewed the extensive research performed for the study of pull-in instability in M/NEMS.

Krylov et al. (2008) and Krylov and Dick (2010) have investigated symmetric snap-through and release of the arch MEMS triggered by quasi-static or suddenly applied DC electrostatic voltages. Zhang et al. (2007) experimentally and theoretically investigated snap-through and pull-in instabilities of a bell-shaped electrostatically actuated arch. Das and Batra (2009a) continued the research on the same system by implementation of finite element numerical methods. Other research groups have investigated the snap-through motion of the arch MEMS resonators. Younis et al. (2010) and Tajaddodianfar et al. (2015b) proposed discussions on the study of the nonlinear dynamics in an arch MEMS actuated by combined static and harmonic electrostatic actuation. Later, Tajaddodianfar et al. (2014b, 2015c, 2016a) and Maani Miandoab et al. (2015b) suggested an analytical procedure for the study of nonlinear frequency response of the MEMS resonators. Recently, they (Tajaddodianfar et al. 2015a, 2016b; Maani Miandoab et al. 2014, 2015c; Alemansour et al. 2017) have studied in detail the possibility of chaotic vibrations in this type of resonators imposed by the snap-through instabilities.

Sufficiently curved beams are also possible to present symmetry breaking which refers to appearing of non-symmetric buckling modes in their transient motion between the stable configurations. Symmetric snap-through and the possibility of accompanying asymmetric configurations are well-discussed and well-established topics in structural mechanics of macro-scaled arches (Seyranian and Elishakoff 1989; Simitses 1990; Chen and Chang 2007; Plaut 2009; Camescasse et al. 2014; Plaut 2015; Amini Khoiy et al. 2016). In macro scales, these instabilities are fully parameterized by the geometry of the arch (Simitses 1990; Amini Khoiy and Amini 2016). However, in contrast to the macro-scaled arches, it has been shown that the electrostatic force affects both symmetric and asymmetric buckling behaviors of the initially curved micro-beams. Krylov et al. (2008) proposed an analytical criterion for the study of snap-through instability of the MEMS stress-free bell-shaped arches which clearly reflected the nonlinearity imposed by the deflection-dependent electrostatic load. Das and Batra (2009b) numerically investigated the snap-through and pull-in instabilities, as well as the symmetry breaking, in an electrostatically loaded shallow micro arch. Later, Krylov et al. (2011) and Tajaddodianfar et al. (2014a) studied the structural stability of a free-of-pull-in initially curved micro-beam actuated by fringing electrostatic fields. They proposed the possibility of appearing non-symmetric buckling modes based on their computational methods. Using reduced order mathematical models consisting of the first symmetric and asymmetric mode shapes, Medina et al. (2012) explored in detail the structural stability of stress-free micro-arches actuated by either deflection-independent mechanical or deflection-dependent electrostatic loads. Based on the bifurcation study of their models, they derived analytical expressions for prediction of the symmetric snap-through and asymmetric buckling of the arch, arguing that for sufficiently curved beams asymmetric instabilities are possible to occur prior to symmetric snap-through. Thus, validity of the reduced order models consisting only the first symmetric mode will be undermined for the sufficiently curved arches (Medina et al. 2012). Later, they (Medina et al. 2014b) extended their studies of symmetry breaking and snap-through to pre-stressed initially curved micro-beams. They (Medina et al. 2014a) also have recently reported experimental investigations for symmetric and asymmetric buckling of the arch micro-beams.

Various advantages, including higher natural frequencies and faster responses, motivate extensive research for scaling down the micro structures and constructing nano-scaled systems. However, many experimental observations have shown that, as the smallest dimension of the system decreases below a few microns, the conventional continuum theories fail to accurately address the nonlinear behavior of NEMS (Wang et al. 2008). For example, Namazu et al. (2000) have experimentally observed that as the thickness of silicon beams decrease below 255 nm their bending stiffness increases by a factor of four. Also, due to Fleck et al. (1994), torsion stiffness of copper wires increase by a factor of three as their diameter decrease from 170 to 12 μm. Based on such observations, in contrast to classic continuum theories, elastic properties of material vary as a function of its size. To account for these size-dependencies, non-classic continuum theories including the strain gradient (Kong et al. 2009; Mustapha and Ruan 2015), modified couple stress (Ghayesh et al. 2013; Akgöz and Civalek 2013; Farokhi et al. 2013), surface energy (Fu et al. 2010; Nejat Pishkenari et al. 2015), and nonlocal stress (Reddy 2010) theories have been developed in recent years. In the past few years, several investigations have been conducted to understand the size-dependent nature of the nano-beams statics and dynamics (Wang et al. 2011; Akgöz and Civalek 2013). It is worth noting that various strain gradient theories are reported in the literature; however, throughout this paper, when using the term “strain gradient theory”, we refer to the theory developed by Lam et al. (2003). Recently, Tajaddodianfar et al. (2015d) have proposed a strain gradient continuum model based on the Euler–Bernoulli and shallow arch assumptions for the study of size-dependent nonlinear phenomena in the initially curved nano-beams. They have shown that the snap-through and pull-in instabilities in the shallow nano-arches are size-dependent, as predicted by the strain gradient theory (Tajaddodianfar et al. 2015d). Moreover, as the nano-arch scales down the minimum initial rise parameter required for the possibility of symmetric snap-through increases (Tajaddodianfar et al. 2015d).

Benefiting from the combined functional advantages of initially curved beams and nano-scale systems motivates us to investigate, in this paper, the influence of size on the structural dynamics of initially curved shallow nano-beams. To the authors’ best knowledge, size-dependent asymmetric buckling of shallow nano-arches has not been thoroughly investigated in the literature. We aim in this paper to scrutinize the size-dependent snap-through and pull-in instabilities as well as the size-dependent symmetry breaking in the stress-free shallow nano-arches. In this regard, this paper extends the previous knowledge of the structural stability of initially curved beams to the nano-scale where the conventional continuum theories, which have been used so far e.g. by Medina et al. (2012), fail to account for size-dependencies. Additionally, this work is an extension to a previous work by Tajaddodianfar et al. (2015d) where they have limited their discussions to the presentation of the strain gradient model and the corresponding single-degree-of-freedom reduced-order model which is capable of accounting only for the symmetric instabilities. In summary, in this paper we focus on the size-dependent asymmetric structural instabilities of the shallow nano-arches.

Toward our aim, we first use the double-mode Galerkin projection method to derive the two-degree-of-freedom reduced-order strain gradient model which governs the transverse motion of the nano-arch. Using three-dimensional bifurcation diagrams, we investigate the symmetric and asymmetric buckling of the nano-arch, showing that the critical values describing the limit point snap-through, release and pull-in, as well as the symmetry breaking, are all size dependent. Later, we derive analytical expressions for description of the minimum required value for the initial curvature to facilitate the size-dependent symmetric and asymmetric buckling.

In the rest of this paper, we propose the mathematical reduced order models in Sect. 2. Then in Sect. 3 we propose our bifurcation studies on the obtained models. In Sect. 4 we propose our study of the arch’s nonlinear behaviors in its parameter space. Derivation of analytical expressions and conclusions are given in Sects. 5 and 6, respectively.

2 Mathematical modeling

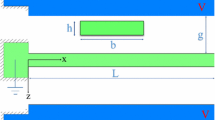
An initially curved beam of length \(L\), width \(w\) and thickness \(d\), clamped at the two ends, is considered under the static DC electrostatic load distributed over the beam length, as shown in Fig. 1. We suppose that the initial deflection of the beam is described by a function \(w_{0} (x)\), while the load-dependent deflection of it is given by a function \(w(x)\), measured from the x axis as shown in Fig. 1. Using the parameters given in Table 1, and based on the shallow arch and Euler–Bernoulli beam assumptions (\(h_{0} \ll L\), \(d \ll L\)), the equilibrium equations of the stress-free arch using the strain gradient elasticity theory are given as (Tajaddodianfar et al. 2015d):

$$\frac{\partial }{\partial x}\left[ {\tilde{E}A\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{1}{2}\left( {\frac{{dw_{0} }}{dx}} \right)^{2} } \right)} \right] = 0,$$
(1)
$$- K\left( {\frac{{\partial^{6} w}}{{\partial x^{6} }} - \frac{{\partial^{6} w_{0} }}{{\partial x^{6} }}} \right) + S\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{d^{4} w_{0} }}{{dx^{4} }}} \right) - \frac{\partial }{\partial x}\left\{ {\frac{\partial w}{\partial x}\left[ {\tilde{E}A\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{1}{2}\left( {\frac{{dw_{0} }}{dx}} \right)^{2} } \right)} \right]} \right\} = \frac{{ - \varepsilon_{0} bV^{2} }}{{2(g_{0} + w)^{2} }}$$
(2)

where:

$$K = GI\left( {2l_{0}^{2} + \frac{4}{5}l_{1}^{2} } \right)$$
(3)
$$S = \tilde{E}I + GA\left( {2l_{0}^{2} + \frac{8}{15}l_{1}^{2} + l_{2}^{2} } \right)$$
(4)

with \(\tilde{E} = E/(1 - \nu^{2} )\) and other parameters are given in Table 1. Boundary conditions are also given as:

Fig. 1
figure 1

Schematics of electrostatically actuated initially curved shallow nano-beam clamped at both ends

Full size image
Table 1 Nomenclature
Full size table
$$\begin{aligned} w(0) = w(L) = 0, \hfill \\ \left. {\frac{\partial w}{\partial x}} \right|_{x = 0} = \left. {\frac{\partial w}{\partial x}} \right|_{x = L} = 0, \hfill \\ \left. {\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right|_{x = 0} = \left. {\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right|_{x = L} = 0 \hfill \\ \end{aligned}$$
(5)

Regarding that the Eq. (1) implies constant deflection-dependent axial force along the beam, Eqs. (1) and (2) are converted to the following single equation (Tajaddodianfar et al. 2015d):

$$- K\left( {\frac{{\partial^{6} w}}{{\partial x^{6} }} - \frac{{d^{6} w_{0} }}{{dx^{6} }}} \right) + S\left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{d^{4} w_{0} }}{{dx^{4} }}} \right) - \frac{{\partial^{2} w}}{{\partial x^{2} }}\left[ {\frac{{\tilde{E}A}}{2L}\int_{0}^{L} {\left[ {\left( {\frac{\partial w}{\partial x}} \right)^{2} - \left( {\frac{{dw_{0} }}{dx}} \right)^{2} } \right]} dx} \right] = \frac{{ - \varepsilon_{0} bV^{2} }}{{2(g_{0} + w)^{2} }}$$
(6)

with the boundary conditions (5).

Using the non-dimensional quantities given in Table 2, one can convert Eq. (6) to the following dimensionless counterparts:

$$\theta_{0} \left( {\frac{{\partial^{6} \hat{w}}}{{\partial \hat{x}^{6} }} - \frac{{d^{6} \hat{w}_{0} }}{{d\hat{x}^{6} }}} \right) + \left( {\frac{{\partial^{4} \hat{w}}}{{\partial \hat{x}^{4} }} - \frac{{d^{4} \hat{w}_{0} }}{{d\hat{x}^{4} }}} \right) - \theta_{1} \frac{{\partial^{2} \hat{w}}}{{\partial \hat{x}^{2} }}\left[ {\int_{0}^{1} {\left[ {\left( {\frac{{\partial \hat{w}}}{{\partial \hat{x}}}} \right)^{2} - \left( {\frac{{d\hat{w}_{0} }}{{d\hat{x}}}} \right)^{2} } \right]} d\hat{x}} \right] = \frac{ - \beta }{{(1 + \hat{w})^{2} }}$$
(7)

with the nondimensionalized boundary conditions:

$$\begin{aligned} \hat{w}(0) = \hat{w}(1) = 0, \hfill \\ \left. {\frac{{d\hat{w}}}{{d\hat{x}}}} \right|_{x = 0} = \left. {\frac{{d\hat{w}}}{{d\hat{x}}}} \right|_{x = 1} = 0, \hfill \\ \left. {\frac{{d^{3} \hat{w}}}{{d\hat{x}^{3} }}} \right|_{x = 0} = \left. {\frac{{d^{3} \hat{w}}}{{d\hat{x}^{3} }}} \right|_{x = 1} = 0 \hfill \\ \end{aligned}$$
(8)
Table 2 Dimensionless parameters
Full size table

2.1 Reduced order model

The Galerkin decomposition is employed to convert the governing Eq. (7) to the reduced-order (RO) model which will be more convenient for the study of snap-through, pull-in and symmetry breaking in the investigated shallow nano-arch. The procedure starts with assuming the deflection of the arch to be approximated by finite-term weighted sum of base functions:

$$\hat{w}(\hat{x}) = \sum\limits_{n = 1}^{N} {q_{n} \varphi_{n} (\hat{x})}$$
(9)

where \(N\) is the number of considered base functions \(\varphi_{n} (\hat{x})\) which represent mode shapes of the shallow double clamped nano-arch satisfying the boundary conditions (8).

For a straight double clamped strain gradient beam (\(w_{0} = 0\)), the mode shapes are obtained as solutions for the following Eigen-value problem:

$$\theta_{0} \frac{{d^{6} \varphi_{n} }}{{d\hat{x}^{6} }} + \frac{{d^{4} \varphi_{n} }}{{d\hat{x}^{4} }} - k_{n} \varphi_{n} (\hat{x}) = 0,$$
(10)

with the boundary conditions (8) and with \(k_{n}\) as the n-th eigen-value. Maani Miandoab et al. (2015a) have proposed discussions on the solution of Eq. (10) for \(\varphi_{n} (\hat{x})\) and \(k_{n}\). They have shown that for very small values of \(\theta_{0}\), the solution of Eq. (10) meets those of the following Eigen-value problem which governs the mode shapes of the classical double clamped straight beam:

$$\frac{{d^{4} \varphi_{n} }}{{d\hat{x}^{4} }} - k_{n} \varphi_{n} (\hat{x}) = 0,$$
(11)

with the first two of boundary conditions (8). However, although the solution for (11) does not satisfy the 3rd of boundary conditions (8), but the difference between the solutions of (10) and (11) is negligible, provided that \(\theta_{0} \ll 1\). For instance, for a typical silicon arch with the parameters given in Table 3, \(\theta_{0} = - 4.4 \times 10^{ - 8}\) is calculated. Thus, implementation of the mode shapes of the classical straight beam instead of that of the strain gradient straight beam is justified for very small \(\theta_{0}\). Additionally, due to negligible encountered error, most researchers employ the mode shapes of straight beam for the analysis of shallow arches (Krylov et al. 2008; Krylov and Dick 2010; Younis et al. 2010). With all these discussions, we make use of the mode shapes of the classical straight double clamped beam, governed by (11), as the base functions in Eq. (9):

$$\begin{aligned} \varphi_{n} (\hat{x}) & = C_{n} \left[ {\cosh (k_{n} \hat{x}) - \cos (k_{n} \hat{x}) - \left( {\frac{{\cosh (k_{n} ) - \cos (k_{n} )}}{{\sinh (k_{n} ) - \sin (k_{n} )}}} \right)(\sinh (k_{n} \hat{x}) - \sin (k_{n} \hat{x}))} \right], \\ & \quad k_{1} = 4.7300,k_{2} = 7.8532, \ldots \\ \end{aligned}$$
(12)

with \(C_{n}\) as a normalizing coefficient which guarantees \(\mathop {\hbox{max} \{ \varphi_{n} (\hat{x})\} }\nolimits_{{\hat{x} \in [0,1]}} = 1\).

Table 3 Typical values for the material and geometrical parameters of the nano-arch
Full size table

Supposing the initial curvature of the arch to be given by the first mode shape,\(w_{0} (\hat{x}) = h\varphi_{1} (\hat{x})\), we substitute (9) in (7), multiply both sides by \(\varphi_{n} (\hat{x})\) and integrate over the arch length. Regarding the orthogonality of mode shapes, and setting \(N = 2\), we can obtain the following two degrees-of-freedom model governing the equilibrium of the strain gradient shallow arch under electrostatic actuation:

$$(b_{11} + \theta_{0} n_{11} )(q_{1} - h) + \theta_{1} s_{11}^{2} q_{1} (q_{1}^{2} - h^{2} ) + \theta_{1} s_{11} s_{22} q_{1} q_{2}^{2} + \beta \int_{0}^{1} {\frac{{\varphi_{1} }}{{(1 + q_{1} \varphi_{1} + q_{2} \varphi_{2} )^{2} }}dx} = 0,$$
(13)
$$(b_{22} + \theta_{0} n_{22} )q_{2} + \theta_{1} s_{11} s_{22} q_{2} (q_{1}^{2} - h^{2} ) + \theta_{1} q_{2}^{3} s_{22}^{2} + \beta \int_{0}^{1} {\frac{{\varphi_{2} }}{{(1 + q_{1} \varphi_{1} + q_{2} \varphi_{2} )^{2} }}dx} = 0$$
(14)

where we have:

$$\begin{aligned} b_{ij} = \int_{0}^{1} {\varphi^{\prime\prime}_{i} } \varphi^{\prime\prime}_{j} d\hat{x}, \hfill \\ s_{ij} = \int_{0}^{1} {\varphi^{\prime}_{i} \varphi^{\prime}_{j} d\hat{x}} , \hfill \\ n_{ij} = \int_{0}^{1} {\varphi_{i} \frac{{d^{6} \varphi_{j} }}{{d\hat{x}^{6} }}d\hat{x}} \hfill \\ \end{aligned}$$
(15)

Using the mode shapes given by (12), the above constants are found as: \(b_{11} = 198.463,\) \(b_{22} = 1669.859,\) \(n_{11} = - 2441.6,\) \(n_{22} = - 7692.0\), \(s_{11} = 4.878,\) and \(s_{22} = 20.218\). Note that with the assumption \(\theta_{0} \ll 1\) we can replace \(b_{11} + \theta_{0} n_{11}\) and \(b_{22} + \theta_{0} n_{22}\) by \(b_{11}\) and \(b_{22}\), respectively. Moreover, since the nonlinear integrals arising in Eqs. (13) and (14) cannot be treated analytically, we Taylor expand them about \(q_{2} = 0\) up to the first order. This yields a simpler form of the reduced order model which seems similar to what is already reported by Medina et al. (Medina et al. 2012) for the classical arch:

$$b_{11} (q_{1} - h) + \theta_{1} s_{11}^{2} q_{1} (q_{1}^{2} - h^{2} ) + \theta_{1} s_{11} s_{22} q_{1} q_{2}^{2} + \beta I_{1} (q_{1} ) = 0,$$
(16)
$$[b_{22} + \theta_{1} s_{11} s_{22} (q_{1}^{2} - h^{2} ) + \theta_{1} q_{2}^{2} s_{22}^{2} - \beta I_{2} (q_{1} )]q_{2} = 0$$
(17)

where we have:

$$\begin{aligned} I_{1} (q_{1} ) = \int_{0}^{1} {\frac{{\varphi_{1} }}{{(1 + q_{1} \varphi_{1} )^{2} }}d\hat{x},} \hfill \\ I_{2} (q_{1} ) = \int_{0}^{1} {\frac{{2\varphi_{2}^{2} }}{{(1 + q_{1} \varphi_{1} )^{3} }}d\hat{x}} , \hfill \\ \int_{0}^{1} {\frac{{\varphi_{1} \varphi_{2} }}{{(1 + q_{1} \varphi_{1} )^{3} }}d\hat{x}} = 0, \hfill \\ \int_{0}^{1} {\frac{{\varphi_{2} }}{{(1 + q_{1} \varphi_{1} )^{2} }}d\hat{x}} = 0, \hfill \\ \end{aligned}$$
(18)

Note that Eq. (16) governs the first symmetric mode shape of the arch, while Eq. (17) is associated with the second mode shape; therefore, nonzero value for \(q_{2}\) implies asymmetric behaviors of the arch. Also, knowing that the stretching parameter \(\theta_{1}\) and the voltage parameter \(\beta\) are both size-dependent, we aim to investigate the size-dependent pull-in, snap-through and symmetry breaking of the shallow nano-arch, using Eqs. (16) and (17).

3 Bifurcation analysis

3.1 Bifurcation diagrams with the classical theory

As the first step toward the analysis of size-dependent nonlinear behaviors of the investigated nano-arch, we need to analyze the bifurcation diagram of the fixed points associated with the 2-DOF model given by Eqs. (16) and (17). Since the nonlinear integrals do not have closed form solutions, the bifurcation diagrams are plotted numerically. To this aim, we first mention that \(q_{2} = 0\) is a trivial solution for Eq. (17); thus, setting \(q_{2} = 0\) in Eq. (16), prescribing values for \(q_{1}\) and solving (16) for \(\beta\), one can derive the bifurcation diagram associated with the first symmetric mode shape of the arch (see Fig. 2). Such a bifurcation diagram, which is plotted in \(q_{2} = 0\) plane, is always a solution for the 2-DOF model, and governs the symmetric nonlinear behaviors including pull-in, symmetric snap-through and symmetric release, and has been a subject of various previous studies (Krylov et al. 2008; Krylov and Dick 2010; Tajaddodianfar et al. 2015a). As the main results of these previous works, we can enumerate some of the bold points which will be used later in this paper:

Fig. 2
figure 2

Bifurcation diagram of fixed points, with the classical theory, for the typical parameters given in Table 3 and associated with four values of the initial rise parameter. Pull-in (PI), symmetric snap-though (S) and release (R), asymmetric snap-through (AS) and release (AR), as well as the stable branches of the diagram are pointed in the blue-colored diagram. These critical points have similar counterparts in other diagrams. See the text for further discussion (color figure online)

Full size image

  • The electrostatically actuated arch always experience the pull-in instability which is represented by a pull-in bifurcation point (PI) with the property \(d\beta /dq_{1} = 0\) (all curves in Fig. 2).

  • Provided that the initial elevation of the arch is larger than a critical value, \(h_{S} < h\), the arch undergoes symmetric snap-through at a bifurcation point (S) with the property \(d\beta /dq_{1} = 0\). The symmetric release, or snap-back, is also represented by a bifurcation point (R) (all curves except \(h = 0.15\) in Fig. 2).

For the study of asymmetric behaviors with \(q_{2} \ne 0\) values, we first solve Eq. (17) for the nontrivial value of \(q_{2}^{2} (q_{1} ,\beta )\) and substitute it in Eq. (16); then, with a prescribed value of \(q_{1}\), we solve the obtained equation for \(\beta\). The prescribed value for \(q_{1}\) and the obtained value for \(\beta\) is put back into Eq. (17), solving it for \(q_{2}\); a real value of which stands for the asymmetric snap-through and release. Medina et al. (2012) have already studied the symmetric and asymmetric instabilities of the shallow arch, adding to the above points that:

  • Provided that the initial elevation of the arch is larger than another critical value, \(h_{S} < h_{AS} < h\), the asymmetric equilibrium points with the property \(q_{2} \ne 0\) bifurcate from the unstable branch of the symmetric bifurcation diagram via the bifurcation points AS and AR, associated with asymmetric snap-through and asymmetric release, respectively (curves associated with \(h = 0.33\) and \(h = 0.45\) in Fig. 2).

  • For values of the initial elevation parameter larger than a third threshold value \(h_{S} < h_{AS} < h_{TS} < h\) the asymmetric bifurcation points, AS and AR, move from the unstable branch to the stable branch of the symmetric bifurcation diagram; imposing the asymmetric snap-through to take place at the loading values smaller than the corresponding loading value associated with symmetric buckling. Thus, in this case, the asymmetric points AS and AR are the critical instability points (\(h = 0.45\) curve in Fig. 2).

Figure 2, displays the equilibrium values of the voltage parameter \(\beta\) versus \(q_{1}\) and \(q_{2}\) for several values of the initial rise parameter \(h\), and for the parameter values associated with a typical shallow arch given in Table 3. Note that Fig. 2 is obtained with the classical theory which implies the material length scale parameters equal to zero.

3.2 Bifurcation diagrams with the strain gradient theory

In order to study the size-dependent nature of the described bifurcation diagrams based on the strain gradient theory, we scale the nano-arch given in Table 3 by several scaling factors. Then, for each scaled nano-arch we compute the corresponding size-dependent parameter \(\theta_{1}\) and employ it for derivation of the corresponding bifurcation diagram. We suppose three equal material length scale parameters, \(l_{0} = l_{1} = l_{2} = Cl\), taking \(Cl = 100\;{\text{nm}}\). Note that as the thickness of the nano-arch is varied by scaling, geometrical ratios \(L/d\), \(b/d\) and \(g/d\) are all preserved; thus, the classical theory, with zero length scale parameter, yields equal nondimensional parameters for all of the scaled nano-arches, and results in the same bifurcation diagram regardless of the size. However, regarding the nonzero length scale parameters, the bifurcation diagrams vary depending on the scale and size of the nano-arch. Thus, for each of the bifurcation diagrams predicted by the classical theory for the given value of the initial rise parameter \(h\), as in Fig. 2, the strain gradient theory predicts size-dependent bifurcation diagrams.

Figure 3 describes the size-dependent bifurcation diagrams associated with the classical ones shown in Fig. 2. The two-dimensional plots in Fig. 3 display the \(q_{2} = 0\) section of the three-dimensional diagram which is also shown as the inset in each figure. Figure 3a, with \(h = 0.15\), represents the case where both the classical and non-classical theories predict the pull-in as the only instability of the nano-arch. However, as the nano-arch scales down, the non-dimensional pull-in voltage decreases. For the deeper nano-arches displaying bistability, as in Fig. 3b with \(h = 0.28\), the strain gradient theory predicts reduction in symmetric pull-in and snap-through values of \(\beta\), while the corresponding value for the symmetric release increases. Thus, as the nano-arch scales down, its bistable property fades. This is more transparent in Fig. 3b for \(d/Cl = 4\) where the strain gradient theory predicts an almost zero-width bistable interval over the \(\beta\) axis; while the classical theory predicts the nano-arch to be bistable.

Fig. 3
figure 3

Two-dimensional bifurcation diagrams obtained by the classical and strain gradient theories for two separate values of d/Cl ratio. The three-dimensional counterparts are shown as the insets. The critical pull-in (PI), symmetric snap-through (S) and release (R), asymmetric snap-through (AS) and release (AR) are all shown on the classical diagram. These points have non-classical analogues. All parts are obtained for the scaled values of the parameters given in Table 3 and with a \(h = 0.15\), b \(h = 0.28\), c \(h = 0.33\) and d \(h = 0.39\)

Full size image

Figure 3c with \(h = 0.33\) illustrates the case where the classical theory predicts emerging of the symmetry breaking from the bifurcation points AS and AR. However, the strain gradient theory does not predict symmetry breaking for the scaled nano-arches in this case. This shows that the symmetry breaking behavior of the nano-arch is size-dependent, as well as the symmetric instabilities of it.

As the initial elevation of the nano-arch increases, the bifurcation points AS and AR move toward the stable branches of the bifurcation diagram, and eventually, they pass the critical points S and R, where the asymmetric instability becomes practically critical. Emerging of the bifurcation points AS and AR and their move toward the stable branches are all size-dependent. As detectable from Fig. 3d for \(h = 0.39\), while the classical theory predicts the points AS and AR to be almost coincided with the points S and R, respectively, the strain gradient theory predicts that for very small scales of the nano-arch, \(d/Cl = 4\), the symmetry breaking is still absent. Nevertheless, for larger sized nano-arch with \(d/Cl = 8\), the strain gradient theory predicts emerging of AS and AR bifurcation points which are still located on the unstable branch of the corresponding bifurcation diagram.

Plots in Fig. 3 show that, at each case, the classical and size-dependent bifurcation diagrams share two inflection points; each of which located on one of the stable and unstable branches of the bifurcation diagram. Moreover, Fig. 3d shows that the mathematical surface constructed by the asymmetric branches of the classical bifurcation diagram and its non-classical counterpart share a gradient vector which is also perpendicular to the \(q_{2}\) axis. However, our observations proposed in Fig. 3 prove that both symmetric and asymmetric behaviors of the nano-arch are size-dependent. In the next section, we analytically investigate the symmetric and asymmetric instabilities of the nano-arch, as well as the critical values \(h_{S}\), \(h_{AS}\) and \(h_{TS}\).

4 Nonlinear behaviors in parameter space

4.1 Symmetric behaviors

For the study of the symmetric and asymmetric instabilities, we refer again to the 2-DOF model given by Eqs. (16) and (17). Noticing that \(q_{2} = 0\) is always a solution contributing to the symmetric behaviors, the first-mode Eq. (16) is linearized about \(q_{2} = 0\) yielding (Medina et al. 2012):

$$b_{11} (q_{1} - h) + \theta_{1} s_{11}^{2} q_{1} (q_{1}^{2} - h^{2} ) + \beta I_{1} (q_{1} ) = 0,$$
(19)

which governs the first-mode bifurcation diagram. Solving this equation for \(\beta\) and setting \(d\beta /dq_{1} = 0\), one can derive the following equation; the roots of which contribute to the pull-in (PI) and symmetric snap-through (S) and release (R) points (Medina et al. 2012).

$$\theta_{1} s_{11}^{2} q_{1}^{2} (I^{\prime}_{1} q_{1} - 3I_{1} ) + (I^{\prime}_{1} q_{1} - I_{1} )(b_{11} - \theta_{1} s_{11}^{2} h^{2} ) - b_{11} I^{\prime}_{1} h = 0$$
(20)

where \(()^{\prime}\) denotes differentiation with respect to \(q_{1}\). One can obtain the critical pull-in and symmetric snap-through and release curves by prescribing values for \(q_{1}\) and solving Eq. (20) for \(h\). The set of \((q_{1} ,h)\) obtained in this way is fed to Eq. (19) for obtaining the corresponding critical value for \(\beta\). Note that with the size-dependent nature of parameter \(\theta_{1}\), this procedure results in various curves associated with pull-in, snap-through and release branches at each scale. Figure 4a displays the critical values of \(q_{1}\) versus \(h\) for various scales of the typical nano-arch given in Table 3. Also, Fig. 4b depicts the corresponding critical values of \(\beta\) versus \(h\).

Fig. 4
figure 4

a Critical values of \(q_{1}\) associated with pull-in (PI), symmetric snap-through (S) and release (R) instabilities versus the initial elevation parameter \(h\), obtained from Eq. (20) and shown by solid curves, together with the critical values of the asymmetric snap-through (AS) and release (AR) given by Eq. (21) and depicted by dotted curves. Results are obtained both with the classical theory and two scaled structures contributing to the strain gradient theory. b Corresponding values of \(\beta\) versus \(h\)

Full size image

Noting that Eq. (20) is quadratic in \(h\), one can find the minimum value of the initial elevation parameter, required for the possibility of symmetric snap-through and release, by solving Eq. (20) for \(h\) and differentiating it with respect to \(q_{1}\); solving \(dh/dq_{1} = 0\) and substituting the resulting value of \(q_{1}\) back into Eq. (20), one can obtain the minimum value of \(h\) required for bistability of the nano-arch, \(h_{S}\). Regarding the size-dependency of \(\theta_{1}\), we can obtain \(h_{S}\) for each value of the ratio \(d/Cl\), and depict it in Fig. 5. Note that, despite the classical theory which predicts a constant value of \(h_{S}\), the strain gradient theory predicts that \(h_{S}\) increases as the nano-structure scales down.

Fig. 5
figure 5

Normalized values of the minimum initial rise parameter required for symmetric snap-through (\(h_{S}\)), asymmetric snap-through (\(h_{AS}\)) and threshold snap-through (\(h_{TS}\)) given by the strain gradient theory versus the \(d/Cl\) ratio. Corresponding constant values given by the classical theory are shown as the inset

Full size image

4.2 Asymmetric behaviors

Since the asymmetric bifurcation points AS and AR arise on the symmetric bifurcation diagram governed by (19), these points are obtained by simultaneous solving of Eqs. (17) and (19). To this aim, \(\beta\) is found from (19) and is substituted in (17) with \(q_{2} \ne 0\). This yields the following equation governing the asymmetric critical points:

$$I_{1} (b_{22} + \theta_{1} s_{11} s_{22} (q_{1}^{2} - h^{2} )) + 2I_{2} (q_{1} - h)(b_{11} + \theta_{1} s_{11}^{2} q_{1} (q_{1} + h)) = 0$$
(21)

Prescribing values for \(q_{1}\) and solving Eq. (21) for \(h\), one can find the critical values of \(q_{1}\) versus \(h\) corresponding to the asymmetric bifurcation points AS and AR. Feeding these values back into Eq. (19) one can find the corresponding values of \(\beta\) versus \(h\). Additionally, depending on the scaling parameter, we expect size-dependent values for the critical points AS and AR. This is shown in Fig. 4a and 4b, too.

Regarding Fig. 4a, for finding the minimum value of \(h\) required for the possibility of symmetry breaking \(h_{AS}\), we solve Eq. (21) for \(h\) and equate \(dh/dq_{1} = 0\); substituting the obtained value for \(q_{1}\) back into Eq. (21) and solving it for \(h\), we find the critical value of \(h_{AS}\). Note again that, while the classical value of \(h_{AS}\) is constant at all scales, the strain gradient theory predicts that the value of \(h_{AS}\) increases by scaling down the nano-structure, as shown in Fig. 5. This is also clear in Fig. 4a and 4b.

For finding the critical value of \(h\) which brings about the AR and AS points to the stable branches of the bifurcation diagram, thus making the sufficient condition for symmetry breaking, Eqs. (20) and (21) need to be satisfied simultaneously. Based on Fig. 4a, this happens at two points where the symmetric and asymmetric critical curves intersect. One of these points with positive \(q_{1}\) represents the sufficient condition for asymmetric snap-through (TS), and the other point with negative \(q_{1}\) stands for threshold asymmetric release (TR). Figure 4a shows that the normalized value of \(h\) corresponding to TS point is slightly smaller than that contributing to TR (\(h_{TS} < h_{TR}\)). Figure 5 displays the normalized values of \(h_{TS}\) versus various values of the d/Cl ratio. Corresponding constant classical values of \(h_{S}\), \(h_{AS}\) and \(h_{TS}\) are shown as the inset in Fig. 5.

5 Analytical criteria

In this section, we aim to provide analytical expressions for prediction of the symmetric and asymmetric instabilities of the nano-arch. Referring to Fig. 4a, one can find that the critical value of \(q_{1}\) associated with the minimum initial rise parameter needed for symmetric buckling,\(h_{S}\), is close to zero. Medina et al. (2012) have shown that, for the case of an initially curved beam under deflection-independent loading provided by elastic foundation, such critical value of \(q_{1}\) always equals to zero; but, for the case of deflection-dependent loading provided by the electrostatic actuation, this critical value of \(q_{1}\) is not necessarily zero, while being small. Thus, we can make a good approximation for \(h_{S}\) by analytically solving Eq. (20) for \(h\) and evaluating it at \(q_{1} = 0\). Moreover, using Table 3 and the definition (4) with \(G = \tilde{E}/2(1 + \nu )\), the size-dependent stretching parameter \(\theta_{1}\) is given by the following expression:

$$\theta_{1} = \frac{6}{{d^{2} + 20n^{2} }}$$
(22)

where \(d\) is the non-dimensional thickness given in Table 3, and \(n = Cl/g\) which reflects size-dependency. However, using (22) and following the procedure described above, we obtain \(h_{S}\) by the following approximation:

$$\begin{aligned} h_{S} (d,n) & = \kappa_{1} (d^{2} + 20n^{2} )\left( {1 + \sqrt {1 + \frac{{\chi_{1} }}{{d^{2} + 20n^{2} }}} } \right), \\ & \quad \kappa_{1} = \frac{{I^{\prime}_{10} b_{11} }}{{12s_{11}^{2} I_{10} }},\;\chi_{1} = \frac{{24s_{11}^{2} I_{10}^{2} }}{{b_{11} I_{10}^{\prime 2} }}, \\ \end{aligned}$$
(23)

with \(I_{10}\) and \(I^{\prime}_{10}\) representing the values of \(I_{1} (q_{1} )\) and its derivative with respect to \(q_{1}\) evaluated at \(q_{1} = 0\). Equation (23) yields size-dependent values of \(h_{S}\), which are in good agreement with the numerically-obtained values given in Fig. 5. The ratio of \(h_{S} /d\) obtained from (23) for various values of \(d/Cl\) ratios is depicted in Fig. 6.

Fig. 6
figure 6

Critical values of \(h/d\) ratio for symmetric snap-through (\(h_{S} /d\) in dark color), asymmetric snap-through (\(h_{AS} /d\) in blue), and threshold snap-through (\(h_{TS} /d\) in red). The results obtained by two values of \(d/Cl\) ratio are compared with the classical results at each case (color figure online)

Full size image

We can employ the same procedure for obtaining an expression for description of the necessary condition for possibility of symmetry breaking. Solving Eq. (21) for \(h\) and evaluating the result at \(q_{1} = 0\), replacing \(\theta_{1}\) from (22) and using Table 3, we are left with the following expression for \(h_{AS}\):

$$\begin{aligned} h_{AS} (d,n) = \kappa_{2} (d^{2} + 20n^{2} )\left( { - 1 + \sqrt {1 + \frac{{\chi_{2} }}{{d^{2} + n^{2} }}} } \right), \hfill \\ \begin{array}{*{20}c} {\kappa_{2} = \frac{{b_{11} I_{20} }}{{6s_{11} s_{22} I_{10} }},} & {\chi_{2} = \frac{{6b_{22} s_{11} s_{22} I_{10}^{2} }}{{b_{11}^{2} I_{20}^{2} }}} \\ \end{array} , \hfill \\ \end{aligned}$$
(24)

where \(I_{20}\) is the value of \(I_{2} (q_{1} )\) given by (18) and evaluated at \(q_{1} = 0\). Other parameters are as before. Values of \(h_{AS}\) given by (24) are in good agreement with the numerically-obtained values displayed in Fig. 5. Also, the size-dependent values of \(h_{AS} /d\) given by (24) are depicted in Fig. 6 for various values of the \(d/Cl\) ratio.

For the threshold value of parameter \(h\), representing the sufficient condition for symmetry breaking, the analytical solution for the simultaneous Eqs. (20) and (21) is not available. Thus, for each scaled nano-arch, one can numerically solve these two concurrent equations for \(h\), and select the smaller of the two obtained results as the threshold value for asymmetric snap-through \(h_{TS}\). We have done this in Fig. 6 which illustrates the size-dependent values of \(h_{TS} /d\) for various values of the \(d/Cl\) ratio.

6 Conclusion

In this paper, we have investigated the size-dependent nature of symmetric and asymmetric nonlinear behaviors in an electrostatically actuated initially curved stress-free shallow nano-beam modeled by the strain gradient theory which is a continuum theory capable of incorporating with the size-effects. To this aim, we have derived a two-degree-of-freedom model by application of the Galerkin projection method to the partial differential equation given by the strain gradient theory. The obtained reduced-order model consists of the first symmetric and asymmetric mode shapes of the beam, and is capable to account for the beam instabilities as well as the size-dependencies.

Using the bifurcation diagrams of equilibrium points of the obtained reduced-order model, we have obtained the critical size-dependent snap-through, release and pull-in values of the DC voltage parameter. Moreover, we have obtained the minimum initial elevation parameter which is required for the possibility of symmetric or asymmetric buckling.

Our investigations show that, despite what is already proposed using the classical continuum models, the critical snap-through, release and pull-in points as well as the minimum initial elevation parameters required for the possibility of snap-through and symmetry breaking are all size-dependent. We have shown that as the nano-arch scales down, the critical values of the voltage parameter for the symmetric snap-through and pull-in decreases, while that of the symmetric release increases. Thus, the range of bistability shrinks as the nano-arch scales down, and the minimum initial elevation parameter required for the possibility of symmetric buckling increases at smaller sizes. Additionally, as the structure scales down, the possibility of symmetry breaking reduces, and the minimum initial elevation parameter required for the possibility of symmetry breaking increases. In the same way, the critical threshold value of the voltage and initial elevation parameters, which result in the initiation of asymmetric buckling prior to the symmetric snap-through, increase as the structure scales down. We have derived analytical expressions for the size-dependent critical values of initial elevation parameter required for symmetric and asymmetric buckling using the obtained reduced order model.

Results of this paper provide deep insight into the size-dependency of nonlinear dynamics in nano-scaled initially curved electrostatically actuated beams, and suggest that application of the conventional classical continuum models for the design of bistable nano-scaled NEMS can provide conservative or even inaccurate results. Further experimental investigations for validation of the obtained results are required and are left as future work.