Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

In the past years, nanostructures involving carbon have been the focus of an intense research activity which is driven to a large extent by the request for new materials with specific applications. Throughout this section, G is a simple connected graph with the vertex and edge sets V(G) and E(G), respectively. Usually, the distance between the vertices u and v of a connected graph G is denoted by d G (u,v), and it is defined as the number of edges in a minimal path connecting the vertices u and v. A topological index is a numeric quantity, derived from the structure of a graph, which is invariant under automorphisms of the graph under consideration. One of the most famous topological indices is the Wiener index , introduced by Harold Wiener, see (Wiener 1947). The Wiener index of G is the sum of distances between all unordered pairs of vertices of G,

$$ W(G)={\displaystyle {\sum}_{\left\{u,v\right\}\subseteq V(G)}{d}_G\left(u,v\right)}. $$

The Szeged index is another topological index which is defined by Ivan Gutman (Gutman 1994) as \( Sz(G)={\displaystyle {\sum}_{e=uv\in E(G)}{n}_u(e){n}_v(e)} \), where n u (e) is the number of vertices of G lying closer to u than to v and n v (e) is the number of vertices of G lying closer to v than to u. If in the definition of Szeged index, we consider the sum of contributions, then we obtain a recently defined topological index , named vertex PI index. In mathematical language, the vertex PI index of G is defined as \( P{I}_v(G)={\displaystyle {\sum}_{e=uv\in E(G)}\left[{n}_u(e)+{n}_v(e)\right]} \) (see Ashrafi et al. 2008; Ashrafi and Rezaei 2007).

Let G(V, E) be a connected bipartite graph, with the vertex set V(G) and edge set E(G). Two edges e = (x,y) and f = (u,v) of G are called codistant (briefly: e co f) if

$$ d\left(x,v\right)=d\left(x,u\right)+1=d\left(y,v\right)+1=d\left(y,u\right). $$

Let \( C(e):=\left\{f\in E(G);\kern0.5em f\kern0.5em co\kern0.5em e\right\} \) denote the set of edges in G, codistant to the edge \( e\in E(G) \). If relation co is an equivalence relation, then G is called a co-gr aph. The set C(e) is called an orthogonal cut (oc for short) of G, with respect to edge e. If G is a co-graph , then its orthogonal cuts C 1, C 2, …, C k form a partition of E(G): \( E(G)={C}_1\cup {C}_2\cup \dots \cup {C}_k,\kern0.24em {C}_i\cap {C}_j=\phi,\;i\ne j \). Observe co is a Θ relation (Djoković-Winkler ) (Djoković 1973).

We say that edges e and f of a plane graph G are in relation opposite, e op f, if they are opposite edges of an inner face of G. Note that the relation co is defined in the whole graph, while op is defined only in faces. Using the relation op, we can partition the edge set of G into opposite edge strips, ops. An ops is a quasi-orthogonal cut qoc, since ops is not transitive.

Let G be a connected graph and S 1, S 2, …, S k be the ops strips of G. Then the ops strips form a partition of E(G). The length of ops is taken as maximum. It depends on the size of the maximum fold face/ring Fmax/Rmax considered, so that any result on Omega polynomial will have this specification.

Denote by m(G,s) the number of ops of length s, and define the Omega polynomial as: \( \Omega \left(G,x\right)={\displaystyle {\sum}_sm\left(G,s\right)\;{x}^s} \) (see Diudea et al. 2008). Its first derivative (in x = 1) equals the number of edges in the graph: \( {\Omega}^{\prime}\left(G,1\right)={\displaystyle {\sum}_sm\left(G,s\right)\;.s=e=\left|E(G)\right|} \).

On Omega polynomial, the Cluj-Ilmenau index (see John et al. 2007), CI = CI(G), was defined:

$$ CI(G)=\left\{{\left[{\Omega}^{\prime}\left(G,1\right)\right]}^2-\left[{\Omega}^{\prime}\left(G,1\right)+{\Omega}^{{\prime\prime}}\left(G,1\right)\right]\right\}. $$

The formulas for calculating CI index are established on cones of various apex rings and various extensions of the cone shirt.

Recently, one-two descriptor has been defined, and it has been shown that it is a good predictor of the heat capacity at P constant (CP) and of the total surface area (TSA). In this chapter, we analyze its generalizations by replacing the value 2 by arbitrary positive-value α. The molecular descriptor is the final result of a logical and mathematical procedure which transforms chemical information encoded within a symbolic representation of a molecule into a useful number or the result of some standardized experiment (Todeschini and Consonni 2000). Molecular descriptors have been shown to be useful in modeling many physicochemical properties in numerous QSAR and QSPR studies (Trinajstić 1992), (Devillers and Balaban 1999; Karelson 2000).

One-alpha descriptor is defined as the sum of the vertex contributions in such a way that each pendant vertex contributes 1, each vertex of degree two adjacent to pendant vertex contributes α, and also each vertex of degree higher than two also contributes α. If we take \( \alpha =2 \), we get one-two descriptor. In Vukičević et al. 2010, this is the definition for 3-ethyl-hex ane by Fig. 6.1:

Fig. 6.1
figure 1

Vertex contributions of 3-ethyl- hexane

Full size image

One-alpha descriptor of graph G will be denoted by OA(G). For instance, if G is 3-ethyl-hex ane, then \( OA(G)=3+4\alpha \).

The Padmakar-Ivan (PI) index of the graph G is defined as \( PI(G)={\displaystyle {\sum}_{e=uv\in E(G)}\left[{m}_u(e)+{m}_v(e)\right]} \), where m u (e) is the number of edges of G lying closer to u than to v and m v (e) is the number of edges of G lying closer to v than to u (see Khadikar 2000; Khadikar and Karmarkar 2001). Finally, the first and second Zagreb indices of the graph G are defined as \( Z{g}_1(G)={\displaystyle {\sum}_{u\in V(G)}{ \deg}_G^2u} \) and \( Z{g}_2(G)={\displaystyle {\sum}_{e=uv\in E(G)}{ \deg}_Gu\kern0.24em { \deg}_Gv} \), respectively (see Gutman and Das 2004; Gutman and Trinajstic 1972; Khalifeh et al. 2009) for mathematical properties and chemical applications.

For a given vertex u of V(G), its eccentricity ε(u) is the largest distance between u and any other vertex v of G. The maximum eccentricity over all vertices of G is called the diameter of G and denoted by d(G), and the minimum eccentricity among the vertices of G is called radius of G and denoted by r(G). Also, u is a central vertex if \( \varepsilon\;\left(u\;\right)=r\;\left(G\;\right). \) The center of G, C(G) is defined as \( C(G)=\left\{u\in V(G)\Big|\;\varepsilon\;(u)=r(G)\right\} \). The eccentric connectivity index is a topological index that has been much used in the study of various properties of many classes of chemical compounds. This index is defined as

$$ \xi\;(G)={\displaystyle {\sum}_{\;u\in V(G)} \deg \kern0.24em (u)\;\varepsilon\;(u)} $$

where deg (u) denotes the degree of vertex u in G and ε(u) is its eccentricity . It used in a series of papers concerned with QSAR/QSPR studies. Its mathematical properties started to be studied only recently (see Ashrafi et al. 2011; Ilić and Gutman 2011 for details). The investigation of its mathematical properties started only recently, and so far, results in determining the extremal values of the invariant and the extremal graphs where those values are achieved are also in a number of explicit formulas for the eccentric connectivity index of several classes of graphs (see Fischermann et al. 2002; Gupta et al. 2002; Kumar et al. 2004; Sardana and Madan 2001; Sharma et al. 1997).

Another topological index that we attended in this paper is augmented eccentric connectivity index . This is defined as the summation of the quotients of the product of adjacent vertex degrees and eccentricity of the concerned vertex, for all vertices in the hydrogen-suppressed molecular graph . It is expressed as

$$ {}\xi (G)={\displaystyle {\sum}_{\;u\in V(G)}\frac{M(u)}{\varepsilon (u)},} $$

where M(u) denotes the product of degrees of all neighbors of vertex u (see Dureja and Madan 2007).

A chemical graph is a graph such that each vertex represents an atom of the molecule and covalent bonds between atoms are represented by edge between the corresponding vertices.

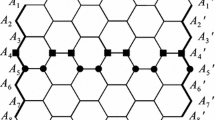
The nanocone is an important type of nanostructure involving carbon. In recent years, some researchers considered the mathematical properties of such nanostructures (Alipour and Ashrafi 2009a, b). One type of nanocones is the C4 nanocone, which is symbolized by CNC 4[n] (Fig. 6.2).

Fig. 6.2
figure 2

The nanocone CNC 4[3]

Full size image

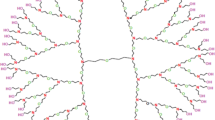
Nanostar dendrimer is a kind of nanostructure. One type of nanostar dendrimer is N-branched phenylacetylenes, and it is shown that by NSB[n], some topological indices were obtained in Yarahmadi (2010) (Yarahmadi and Fath-Tabar 2011). In Fig. 6.3, the molecular graph of NSB[1] and in Fig. 6.4 the molecular graph of NSB[2] are shown.

Fig. 6.3
figure 3

The molecular graph of NSB[1]

Full size image
Fig. 6.4
figure 4

The molecular graph of NSB[2]

Full size image

In this chapter, at first we compute the Wiener and Szeged and Cluj-Ilmenau indices of a family of cones, denoted CNC 4 [n]. Moreover, we present explicit formula for Wiener, Szeged, PI, vertex PI, the first and second Zagreb eccentric connectivity , and augmented eccentric connectivity indices of N-branched phenylacetylenes nanostar dendrimer . For terms and concepts not defined here, we refer the reader to any of several standard monographs, such as Cameron (1994) and Trinajstić (1992).

6.2 The Wiener, Szeged, and Cluj-Ilmenau Indices of CNC 4[n] Nanocones

In this section, we study on some graph invariant of CNC 4[n]. In order to compute some topological indices of CNC 4[n], firstly the number of vertices of this nanostructure is computed.

Lemma 6.2.1

The number of vertices of CNC 4[n] is computed by the formula:

$$ \left|V\Big(CN{C}_4\left[n\right]\right|=4{\left(n+1\right)}^2. $$

For computing the Wiener index of CNC 4[n], the method of Klavžar (2008) is used. In what follows, we recall some useful concepts.

Let G be a connected graph . Then edges e = xy and f = uv of G are in the Djoković-Winkler relation Θ (Djoković 1973; Winkler 1984), if

$$ d\left(x,u\right)+d\left(y,v\right)\ne d\left(x,v\right)+d\left(y,u\right). $$

The relation Θ is always reflexive and symmetric. Let Θ* be the transitive closure of Θ. Then Θ* is an equivalence relation on E(G) for any connected graph , and it partitions the edge set of G into Θ*-classes. For computing Θ*-classes, it is useful to know the following facts. Since two adjacent edges of G are in relation Θ if and only if they belong to a common triangle, all the edges of a given complete subgraph of G will be in the same Θ*-class. Also, since an edge e of an isometric cycle C of G is in relation Θ with its antipodal edge(s) on C, all the edges of an odd cycle will be in the same Θ*-class.

In what follows a powerful method, given by Klavžar (see Klavžar 2006, 2008), enabling to compute the Wiener index of a graph is presented. The canonical metric representation α of a connected graph G is defined as:

  • Let G be connected graph and F 1 ,F 2,…,F k its Θ*-classes.

  • Define quotient graph G/F i , i = 1,…,k, as follows. Its vertices are the connected components of G-F i , two vertices C and C′ being adjacent if there exist vertices x \( \in \) C and y \( \in \) C′ such that xy \( \in \) F i .

  • Define \( \alpha :G\to {\displaystyle \prod_{i=1}^kG/{F}_{\mathrm{i}}} \) with α: u → (α 1(u),..,α k (u)),

where αi(u) is a connected component of G-Fi that contains u. Let G be an arbitrary connected graph and

$$ \alpha :G\to {\displaystyle \prod_{i=1}^kG/{F}_{\mathrm{i}}} $$

the canonical metric representation of G. Let (G/F i , w i ) be natural weighted graphs; the weight of G/F i is the number of vertices in the corresponding connected component of G-F i .

Theorem 6.2.2

(Klavžar 2008) For any connected graph G, \( W(G)={\displaystyle \sum_{i=1}^kW\left(G/{F}_i,{w}_i\right).} \)

Theorem 6.2.3

The Wiener index of CNC 4[n] is computed as follows:

$$ W\left(CN{C}_4\left[n\right]\right)={\scriptscriptstyle \frac{1}{2}}\left|V\right|\;{\displaystyle {\sum}_{k=1}^n\left(k\;{\alpha}_n+k\left(k-1\right)\left)\right(\left|V\right|-k{\alpha}_n-k\left(k-1\right)\right)}, $$

where \( \left|V\right|=\left|V\right(CN{C}_4\left[n\right]\Big| \) and \( {\alpha}_n=2n+3 \).

In the following theorems, Szeged and Cluj-Ilmenau indices for CNC 4[n] are computed.

Theorem 6.2.4

The Szeged index of CNC 4[n] is computed as follows:

$$ Sz\left(CN{C}_4\left[n\right]\right)=\left(n+1\right)\left|V\right|{\;}^2+{\displaystyle {\sum}_{k=1}^n\left(n+k+1\right)\left(k{\alpha}_n-k\left(k-1\right)\right)}\left(\right|V\Big|\left(k{\alpha}_n-k\left(k-1\right)\right), $$

by notation of pervious theorem.

Theorem 6.2.5

The Cluj-Ilmenau in dex of CNC 4[n] is computed by:

$$ \begin{array}{ll}CI\left(CN{C}_{p\left(\mathrm{even}\right)}\left[n\right]\right)=& \left(1/12\right)p\left(n+1\right)\hfill \\ {}& \times \left(27p{n}^3-28{n}^2+63p{n}^2-50n+48pn+12p-24\right),\hfill \end{array} $$
$$ CI\left(CN{C}_{p\left(\mathrm{odd}\right)}\left[n\right]\right)=CI\left(CN{C}_{p\left(\mathrm{even}\right)}\left[n\right]\right)+p{\left(n+1\right)}^2. $$

Theorem 6.2.6

One-alpha descriptor of CNC 4[n] is computed as follows:

$$ OA\Big(CN{C}_4\left[n\right]=4\alpha \left({n}^2+n+1\right). $$

6.3 Topological Indices of N-Branched Phenylacetylene Nanostar Dendrimer

The nanostar dendrimer is a part of a new group of macromolecules that seem photon funnels just like artificial antennas, and also, it is a great resistant of photo bleaching. Experimental and theoretical insight is needed in order to understand the energy transfer mechanism. In recent years, some people investigated the mathematical properties of these nanostructures (Ashrafi and Mirzargar 2008; Dorosti et al. 2009; Iranamanesh and Gholami 2009; Mirzargar 2009; Yousefi-Azari et al. 2008). One type of nanostar dendrimers is N-branched phenylacetylenes (see Bharathi et al. 1995). It is shown by NSB[n] (see Fig. 6.1). In order to compute some topological indices of the nanostar dendrimer NSB[n], we first compute the number of vertices and edges of this nanostructure.

Lemma 6.3.1

The numbers of vertices and edges of dendrimer NSB[n] are given as:

$$ \left|V\left(NSB\left[n\right]\right)\right|=87\times {2}^n-38, $$
$$ \left|E\left(NSB\left[n\right]\right)\right|=99\times {2}^n-45. $$

Also for computing the Wiener index of NSB[n], we use the method of Theorem 6.2.2 (see Klavžar 2008).

Theorem 6.3.2

The Wiener index of NSB[n] is given as follows:

$$ W\left(NSB\left[n\right]\right)=27{\displaystyle \sum_{k=0}^n{2}^{n-k}\left({\alpha}_k\left|V\right|-{\alpha_k}^2-14\right)}+9\times {2}^n\left(87\times {2}^n-39\right), $$

where \( {\alpha}_{\mathrm{n}}=29\times {2}^n-19,\;\left|V\right|=\left|V\left(NSB\left[n\right]\right)\right|. \)

Theorem 6.3.3

With notation of Theorem 6.3.2, the Szeged index of NSB[n] is given by:

$$ {S}_Z\left(NSB\left[n\right]\right)=5\times {3}^2{\displaystyle \sum_{k=0}^n{2}^{n-k}\left({\alpha}_k\left|V\right|-{\alpha}_k^2-14\right)+9\times {2}^n\left(87\times {2}^n-39\right)}. $$

Theorem 6.3.4

The PI index of the dendrimer NSB[n] is obtained by:

$$ PI\left(NSB\left[n\right]\right)=9801\times {2}^{2n}-9081\times {2}^n+2106. $$

Theorem 6.3.5

The vertex PI index of the dendrimer NSB[n] is obtained as follows:

$$ P{I}_V\left(NSB\left[n\right]\right)=8613\times {2}^{2n}-7677\times {2}^n+1710. $$

Theorem 6.3.6

The first and second Zagreb indices of NBS[n] are computed as follows:

$$ {Z}_{g1}\left(NSB\left[n\right]\right)=492\times {2}^n-222,\;{Z}_{g2}\left(NSB\left[n\right]\right)=591\times {2}^n-273. $$

In the following lemma, the eccentricity of each vertex of NSB[n] is obtained, by using the eccentricity of the central vertex.

Lemma 6.3.7

Let v 0 be the central vertex and u is a vertex of NSB[n], such that d(u,v 0) = k. Then

$$ \varepsilon \left({v}_0\right)=9\;n+10, $$
$$ \varepsilon (u)=9n+k+10. $$

By Lemma 6.3.1 and 6.3.7, we can compute the eccentric connectivity index of N-branched phenylacetylenes.

Theorem 6.3.8

The eccentric connectivity index of NSB[n] is computed as follows:

$$ \xi \left(NSB\;\left[n\right]\right)=\left(945n+\frac{3015}{2}\right){2}^{n+1}-810n-1359+837{\displaystyle {\sum}_{i=1}^ni{2}^i}. $$

Finally, in the following theorem, we obtained the augmented eccentric connectivity index of NSB[n].

Theorem 6.3.9

The augmented eccentric connectivity index of NSB[n] is given by the following formula:

$$ \begin{array}{l}{}^A\xi \left(NSB\;\left[n\right]\right)={3}^2.\;{2}^2{\displaystyle {\sum}_{i=0}^n{\displaystyle {\sum}_{j=2}^9\frac{2^i}{9\;\left(n-i\right)+10+j}}}+{3}^4{\displaystyle {\sum}_{i=0}^{n-1}\frac{1}{9\;\left(n+i\right)+19}}\\ {}\kern3.36em +\frac{3^2.\;{2}^n}{18n+19}+\frac{3^2{.2}^{n+1}+{3}^3}{9n+10}.\end{array} $$