50 Years of Time Parallel Time Integration

Abstract

Time parallel time integration methods have received renewed interest over the last decade because of the advent of massively parallel computers, which is mainly due to the clock speed limit reached on today’s processors. When solving time dependent partial differential equations, the time direction is usually not used for parallelization. But when parallelization in space saturates, the time direction offers itself as a further direction for parallelization. The time direction is however special, and for evolution problems there is a causality principle: the solution later in time is affected (it is even determined) by the solution earlier in time, but not the other way round. Algorithms trying to use the time direction for parallelization must therefore be special, and take this very different property of the time dimension into account.We show in this chapter how time domain decomposition methods were invented, and give an overview of the existing techniques. Time parallel methods can be classified into four different groups: methods based on multiple shooting, methods based on domain decomposition and waveform relaxation, space-time multigrid methods and direct time parallel methods. We show for each of these techniques the main inventions over time by choosing specific publications and explaining the core ideas of the authors. This chapter is for people who want to quickly gain an overview of the exciting and rapidly developing area of research of time parallel methods.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

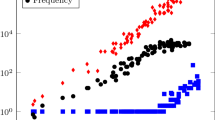
It has been precisely 50 years ago that the first visionary contribution to time parallel time integration methods was made by Nievergelt [64]. We show in Fig. 1 an overview of the many important contributions over the last 50 years to this field of research. The methods with iterative character are shown on the left, and the direct time parallel solvers on the right, and large scale parallel methods are more toward the center of the figure, whereas small scale parallel methods useful for multicore architectures are more towards the left and right borders of the plot.

Fig. 1

An overview over important contributions to time parallel methods

We also identified the four main classes of space-time parallel methods in Fig. 1 using color:

• 1. methods based on multiple shooting are shown in magenta,

• 2. methods based on domain decomposition and waveform relaxation are shown in red,

• 3. methods based on multigrid are shown in blue,

• 4. and direct time parallel methods are shown in black.

There have also been already overview papers, shown in green in Fig. 1, namely the paper by Gear [40], and the book by Burrage [12].

The development of time parallel time integration methods spans now half a century, and various methods have been invented and reinvented over this period. We give a detailed account of the major contributions by presenting seminal papers and explaining the methods invented by their authors.

2 Shooting Type Time Parallel Methods

Time parallel methods based on shooting solve evolution problems in parallel using a decomposition of the space-time domain in time, as shown in Fig. 2. An iteration is then defined, or some other procedure, which only uses solutions in the time subdomains, to obtain an approximate solution over the entire time interval (0, T).

Fig. 2

Decomposition of the space-time domain in time for multiple shooting type methods

2.1 Nievergelt 1964

Nievergelt was the first to consider a pure time decomposition for the parallel solution of evolution problems [64]. He stated precisely 50 years ago at the time of writing of this chapter, how important parallel computing was to become in the near future:

For the last 20 years, one has tried to speed up numerical computation mainly by providing ever faster computers. Today, as it appears that one is getting closer to the maximal speed of electronic components, emphasis is put on allowing operations to be performed in parallel. In the near future, much of numerical analysis will have to be recast in a more ‘parallel’ form.

As we now know, the maximal speed of electronic components was only reached 40 years later, see Fig. 3.

Fig. 3

Maximal speed of electronic components reached 40 years after the prediction of Nievergelt (taken from a talk of Bennie Mols at the VINT symposium 12.06.2013)

Nievergelt presents a method for parallelizing the numerical integration of an ordinary differential equation, a process which “by all standard methods, is entirely serial”. We consider in Nievergelt’s notation the ordinary differential equation (ODE)

$$\displaystyle{ y' = f(x,y),\quad y(a) = y_{0}, }$$

(1)

and we want to approximate its solution on the interval [a, b]. Such an approximation can be obtained using any numerical method for integrating ODEs, so-called time stepping methods, but the process is then entirely sequential. Nievergelt proposes instead to partition the interval [a, b] into subintervals $x_{0} = a < x_{1} <\ldots < x_{N} = b$, as shown in his original drawing in Fig. 4, and then introduces the following direct time parallel solver:

Fig. 4

First idea by Nievergelt to obtain a parallel algorithm for the integration of a first order ODE

• 1. Compute a rough prediction y _i ⁰ of the solution y(x _i ) at each interface (see Fig. 4), for example with one step of a numerical method with step size $H = (b - a)/N$.

• 2. For a certain number M _i of starting points $y_{i,1},\ldots,y_{i,M_{i}}$ at x _i in the neighborhood of the approximate solution y _i ⁰ (see Fig. 4), compute accurate (we assume here for simplicity exact) trajectories y _i, j (x) in parallel on the corresponding interval [x _i , x _i+1], and also y _0, 1(x) on the first interval [x ₀, x ₁] starting at y ₀.

• 3. Set Y ₁: = y _0, 1(x ₁) and compute sequentially for each $i = 1,\ldots,N - 1$ the interpolated approximation by

  • finding the interval j such that Y _i  ∈ [y _i, j , y _i, j+1],

  • determining p such that $Y _{i} = py_{i,j} + (1 - p)y_{i,j+1}$, i.e. $p = \frac{Y _{i}-y_{i,j+1}} {y_{i,j}-y_{i,j+1}}$,

  • setting the next interpolated value at x _i+1 to $Y _{i+1}:= py_{i,j}(x_{i+1}) + (1 - p)y_{i,j+1}(x_{i+1})$.

For linear ODEs, this procedure does actually produce the same result as the evaluation of the accurate trajectory on the grid, i.e. Y _i  = y(x _i ) in our case of exact local solves, there is no interpolation error, and it would in fact suffice to have only two trajectories, M _i  = 2 in each subinterval, since one can also extrapolate.

In the non-linear case, there is an additional error due to interpolation, and Nievergelt defines a class of ODEs for which this error remains under control if one uses Backward Euler for the initial guess with a coarse step H, and also Backward Euler for the accurate solver with a much finer step h, and he addresses the question on how to choose M _i and the location of the starting points y _i, j in the neighborhood. He then concludes by saying

The integration methods introduced in this paper are to be regarded as tentative examples of a much wider class of numerical procedures in which parallelism is introduced at the expense of redundancy of computation. As such, their merits lie not so much in their usefulness as numerical algorithms as in their potential as prototypes of better methods based on the same principle. It is believed that more general and improved versions of these methods will be of great importance when computers capable of executing many computations in parallel become available.

What a visionary statement again! The method proposed is inefficient compared to any standard serial integration method, but when many processors are available, one can compute the solution faster than with just one processor. This is the typical situation for time parallel time integration methods: the goal is not necessarily perfect scalability or efficiency, it is to obtain the solution faster than sequentially.

The method of Nievergelt is in fact a direct method, and we will see more such methods in Sect. 5, but it is the natural precursor of the methods based on multiple shooting we will see in this section.

2.2 Bellen and Zennaro 1989

The first to pick up the idea of Nievergelt again and to formally develop an iterative method to connect trajectories were Bellen and Zennaro in [6]:

In addition to the two types of parallelism mentioned above, we wish to isolate a third which is analogous to what Gear has more recently called parallelism across the time. Here it is more appropriately called parallelism across the steps. In fact, the algorithm we propose is a realization of this kind of parallelism. Without discussing it in detail here, we want to point out that the idea is indeed that of multiple shooting and parallelism is introduced at the cost of redundancy of computation.

Bellen and Zennaro define their method directly at the discrete level, for a recurrence relation of the form

$$\displaystyle{ y_{n+1} = F_{n+1}(y_{n}),\quad y_{0}\ \mbox{ known.} }$$

(2)

This process looks entirely sequential, one needs to know y _n in order to be able to compute y _n+1. Defining the vector of unknowns $\mathbf{y}:= (y_{0},y_{1},\ldots,y_{n},\ldots )$ however, the recurrence relation (2) can be written simultaneously over many levels in the fixed point form

$$\displaystyle{ \mathbf{y} =\boldsymbol{\phi } (\mathbf{y}), }$$

(3)

where $\boldsymbol{\phi }(\mathbf{y}) = (y_{0},F_{1}(y_{0}),F_{2}(y_{1}),\ldots,F_{n}(y_{n-1}),\ldots )$. Bellen and Zennaro propose to apply a variant of Newton’s method called Steffensen’s method to solve the fixed point equation (3). Like when applying Newton’s method and simplifying, as we will see in detail in the next subsection, this leads to an iteration of the form

$$\displaystyle{ \mathbf{y}^{k+1} =\boldsymbol{\phi } (\mathbf{y}^{k}) +\varDelta \boldsymbol{\phi } (\mathbf{y}^{k})(\mathbf{y}^{k+1} -\mathbf{ y}^{k}), }$$

(4)

where $\varDelta \boldsymbol{\phi }$ is an approximation to the differential $D\boldsymbol{\phi }$, and they choose as initial guess y _n ⁰ = y ₀. Steffensen’s method for a nonlinear scalar equation of the form f(x) = 0 is

$$\displaystyle\begin{array}{rcl} x_{k+1}& =& x_{k} - g(x_{k})^{-1}f(x_{ k}) {}\\ g(x)&:=& \frac{f(x + f(x)) - f(x)} {f(x)}, {}\\ \end{array}$$

and one can see how the function g(x) becomes a better and better approximation of the derivative f′(x) as f(x) goes to zero. As Newton’s method, Steffensen’s method converges quadratically once one is close to the solution.

Bellen and Zennaro show several results about Steffensen’s method (4) applied to the fixed point problem (3):

• 1. They observe that each iteration gives one more exact value, i.e. after one iteration, the exact value y ₁ ¹ = y ₁ is obtained, and after two iterations, the exact value y ₂ ² = y ₂ is obtained, and so on. Hence convergence of the method is guaranteed if the vector $\mathbf{y}^{k}$ is of finite length.

• 2. They prove that convergence is locally quadratic, as it holds in general for Steffensen’s method applied to non-linear problems.

• 3. The corrections at each step of the algorithm can be computed in parallel.

• 4. They also present numerically estimated speedups of 29–53 for a problem with 400 steps.

In contrast to the ad hoc interpolation approach of Nievergelt, the method of Bellen and Zennaro is a systematic parallel iterative method to solve recurrence relations.

2.3 Chartier and Philippe 1993

Chartier and Philippe return in [13] to the formalization of Bellen and Zennaro,¹ which was given at the discrete level, and formulate their parallel integration method at the continuous level for evolution problems:

Parallel algorithms for solving initial value problems for differential equations have received only marginal attention in the literature compared to the enormous work devoted to parallel algorithms for linear algebra. It is indeed generally admitted that the integration of a system of ordinary differential equations in a step-by-step process is inherently sequential.

The underlying idea is to apply a shooting method, which was originally developed for boundary value problems, see [47] and references therein, to an initial value problem, see also [48]. For a boundary value problem of the form

$$\displaystyle{ u'' = f(u),\quad u(0) = a,\quad u(1) = b, }$$

(5)

a shooting method also considers the same differential equation, but as an initial value problem,

$$\displaystyle{ u'' = f(u),\quad u(0) = a,\quad u'(0) = s, }$$

(6)

and one then tries to determine the so-called shooting parameter s, the ‘angle of the cannon to shoot with’, such that the solution passes through the point u(1) = b, which explains the name of the method. To determine the shooting parameter s, one needs to solve in general a non-linear equation, which is preferably done by Newton’s method, see for example [47].

If the original problem is however already an initial value problem,

$$\displaystyle{ u' = f(u),\quad u(0) = u^{0},\qquad x \in [0,1], }$$

(7)

then there is in no target to hit at the other end, so at first sight it seems shooting is not possible. To introduce targets, one uses the idea of multiple shooting: one splits the time interval into subintervals, for example three, $[0, \frac{1} {3}]$, $[\frac{1} {3}, \frac{2} {3}]$, $[\frac{2} {3},1]$, and then solves on each subinterval the underlying initial value problem

$$\displaystyle{\begin{array}{rclrclrcl} u_{0}' & =&f(u_{0}),\quad & u_{1}' & =&f(u_{1}),\quad & u_{2}' & =&f(u_{2}), \\ u_{0}(0)& =&U_{0}, &u_{1}(\frac{1} {3})& =&U_{1}, &u_{2}(\frac{2} {3})& =&U_{2},\end{array} }$$

together with the matching conditions

$$\displaystyle{U_{0} = u^{0},\quad U_{ 1} = u_{0}(\frac{1} {3},U_{0}),\quad U_{2} = u_{1}(\frac{2} {3},U_{1}).}$$

Since the shooting parameters U _n , n = 0, 1, 2 are not known (except for U ₀ = u ⁰), this leads to a system of non-linear equations one has to solve,

$$\displaystyle{F(\mathbf{U}):= \left (\begin{array}{c} U_{0} - u^{0} \\ U_{1} - u_{0}(\frac{1} {3},U_{0}) \\ U_{2} - u_{1}(\frac{2} {3},U_{1}) \end{array} \right ) = 0,\qquad \mathbf{U} = (U_{0},U_{1},U_{2})^{T}.}$$

If we apply Newton’s method to this system, like in the classical shooting method, to determine the shooting parameters, we obtain for k = 0, 1, 2, … the iteration

$$\displaystyle{\left (\begin{array}{c} U_{0}^{k+1} \\ U_{1}^{k+1} \\ U_{2}^{k+1} \end{array} \right ) = \left (\begin{array}{c} U_{0}^{k} \\ U_{1}^{k} \\ U_{2}^{k} \end{array} \right )-\left [\begin{array}{ccc} 1 & & \\ - \frac{\partial u_{0}} {\partial U_{0}} (\frac{1} {3},U_{0}^{k})& 1 & \\ & - \frac{\partial u_{1}} {\partial U_{1}} (\frac{2} {3},U_{1}^{k})\ \ \ &1 \\ \end{array} \right ]^{-1}\left (\begin{array}{c} U_{0}^{k} - u^{0} \\ U_{1}^{k} - u_{1}(\frac{1} {3},U_{0}^{k}) \\ U_{2}^{k} - u_{1}(\frac{2} {3},U_{1}^{k}) \end{array} \right ).}$$

Multiplying through by the Jacobian matrix, we find the recurrence relation

$$\displaystyle\begin{array}{rcl} U_{0}^{k+1}& =& u^{0}, {}\\ U_{1}^{k+1}& =& u_{ 0}(\frac{1} {3},U_{0}^{k}) + \frac{\partial u_{0}} {\partial U_{0}} (\frac{1} {3},U_{0}^{k})(U_{ 0}^{k+1} - U_{ 0}^{k}), {}\\ U_{2}^{k+1}& =& u_{ 1}(\frac{2} {3},U_{1}^{k}) + \frac{\partial u_{1}} {\partial U_{1}} (\frac{2} {3},U_{1}^{k})(U_{ 1}^{k+1} - U_{ 1}^{k}). {}\\ \end{array}$$

In the general case with N shooting intervals, solving the multiple shooting equations using Newton’s method gives thus a recurrence relation of the form

$$\displaystyle{ \begin{array}{rcl} U_{0}^{k+1} & =&u^{0}, \\ U_{n+1}^{k+1} & =&u_{n}(t_{n+1},U_{n}^{k}) + \frac{\partial u_{n}} {\partial U_{n}}(t_{n+1},U_{n}^{k})(U_{n}^{k+1} - U_{n}^{k}),\quad n = 0,1,2,\ldots N,\end{array} }$$

(8)

and we recognize the form (4) of the method by Bellen and Zennaro. Chartier and Philippe prove that (8) converges locally quadratically. They then however already indicate that the method is not necessarily effective on general problems, and restrict their analysis to dissipative right hand sides, for which they prove a global convergence result. Finally, also discrete versions of the algorithm are considered.

2.4 Saha, Stadel and Tremaine 1996

Saha, Stadel and Tremaine cite the work of Bellen and Zennaro [6] and Nievergelt [64] as sources of inspiration, but mention already the relation of their algorithm to waveform relaxation [52] in their paper on the integration of the solar system over very long time [67]:

We describe how long-term solar system orbit integration could be implemented on a parallel computer. The interesting feature of our algorithm is that each processor is assigned not to a planet or a pair of planets but to a time-interval. Thus, the 1st week, 2nd week, …, 1000th week of an orbit are computed concurrently. The problem of matching the input to the (n + 1)-st processor with the output of the n-th processor can be solved efficiently by an iterative procedure. Our work is related to the so-called waveform relaxation methods….

Consider the system of ordinary differential equations

$$\displaystyle{\dot{y} = f(y),\quad y(0) = y_{0},}$$

or equivalently the integral formulation

$$\displaystyle{y(t) = y(0) +\int _{ 0}^{t}f(y(s))ds.}$$

Approximating the integral by a quadrature formula, for example the midpoint rule, we obtain for each time t _n for y(t _n ) the approximation

$$\displaystyle{ y_{n} = y_{0} + h\sum _{m=0}^{n-1}f(\frac{1} {2}(y_{m+1} + y_{m})),\quad n = 1,\ldots,N. }$$

(9)

Collecting the approximations y _n in a vector $\mathbf{y}:= (y_{0},y_{1},\ldots,y_{N})$, the relation (9) can again be written simultaneously over many steps as a fixed point equation of the form

$$\displaystyle{ \mathbf{y} = F(\mathbf{y}), }$$

(10)

which can be solved by an iterative process. Note that the quadrature formula (9) can also be written by reusing the sums already computed at earlier steps,

$$\displaystyle{ y_{n} = y_{n-1} + hf(\frac{1} {2}(y_{n} + y_{n-1})),\quad n = 1,\ldots,N, }$$

(11)

so the important step here is not the use of the quadrature formula. The interesting step comes from the application of Saha, Stadel and Tremaine, namely a Hamiltonian problem with a small perturbation:

$$\displaystyle{\dot{p} = -\partial _{q}H,\ \dot{q} = \partial _{p}H,\quad H(p,q,t) = H^{0}(p) +\epsilon H^{1}(p,q,t).}$$

Denoting by y: = (p, q), and $f(y):= (-H_{q}(y),H_{p}(y))$, Saha, Stadel and Tremaine derive Newton’s method for the associated fixed point problem (10), as Chartier and Philippe derived (8). Rewriting (8) in their notation gives

$$\displaystyle{ Y _{n+1}^{k+1} = y_{ n}^{\epsilon }(t_{ n+1},Y _{n}^{k}) + \frac{\partial y_{n}^{\epsilon }} {\partial Y _{n}}(t_{n+1},Y _{n}^{k})(Y _{ n}^{k+1} - Y _{ n}^{k}), }$$

(12)

where the superscript ε denotes the solution of the perturbed Hamiltonian system.

The key new idea of Saha, Stadel and Tremaine is to propose an approximation of the derivative by a cheap difference for the unperturbed Hamiltonian problem,

$$\displaystyle{ Y _{n+1}^{k+1} = y_{ n}^{\epsilon }(t_{ n+1},Y _{n}^{k}) + y_{ n}^{0}(t_{ n+1},Y _{n}^{k+1}) - y_{ n}^{0}(t_{ n+1},Y _{n}^{k}). }$$

(13)

They argue that with the approximation for the Jacobian used in (13), each iteration now improves the error by a factor ε; instead of quadratic convergence for the Newton method (12), one obtains linear convergence.

They show numerical results for our solar system: using for H ⁰ Kepler’s law, which leads to a cheap integrable system, and for ε H ¹ the planetary perturbations, they obtain the results shown in Fig. 5. They also carefully verify the possible speedup with this algorithm for planetary simulations over long time. Figure 6 shows the iterations needed to converge to a relative error of 1e − 15 in the planetary orbits.

Fig. 5

Maximum error in mean anomaly M versus time, $h = 7 \frac{1} {32}$ days, compared to results from the literature, from [67]

Fig. 6

Top linear scaling, and bottom logarithmic scaling of the number of iterations to reach a relative error of 1e − 15 as a function of the number of processors (time intervals) used

2.5 Lions, Maday and Turinici 2001

Lions, Maday and Turinici invented the parareal algorithm in a short note [54], almost independently of earlier work; they only cite the paper by Chartier and Philippe [13]:

On propose dans cette Note un schéma permettant de profiter d’une architecture parallèle pour la discrétisation en temps d’une équation d’évolution aux dérivées partielles. Cette méthode, basée sur un schéma d’Euler, combine des résolutions grossières et des résolutions fines et indépendantes en temps en s’inspirant de ce qui est classique en espace. La parallélisation qui en résulte se fait dans la direction temporelle ce qui est en revanche non classique. Elle a pour principale motivation les problèmes en temps réel, d’où la terminologie proposée de ‘pararéel’.

Lions, Maday and Turinici explain their algorithms on the simple scalar model problem²

$$\displaystyle{ \dot{y} = -ay,\quad \mbox{ on $[0,T]$},\quad y(0) = y_{0}. }$$

(14)

The solution is first approximated using Backward Euler on the time grid T _n with coarse time step Δ T,

$$\displaystyle{ Y _{n+1}^{1} - Y _{ n}^{1} + a\varDelta TY _{ n+1}^{1} = 0,\quad Y _{ 0}^{1} = y_{ 0}. }$$

(15)

The approximate solution values Y _n ¹ are then used to compute on each time interval [T _n , T _n+1] exactly and in parallel the solution of

$$\displaystyle{ \dot{y}_{n}^{1} = -ay_{ n}^{1},\quad y_{ n}^{1}(T_{ n}) = Y _{n}^{1}. }$$

(16)

One then performs for k = 1, 2, … the correction iteration

• 1. Compute the jumps $S_{n}^{k}:= y_{n-1}^{k}(T_{n}) - Y _{n}^{k}$.

• 2. Propagate the jumps $\delta _{n+1}^{k} -\delta _{n}^{k} + a\varDelta T\delta _{n+1}^{k} = S_{n}^{k}$, δ ₀ ^k = 0.

• 3. Set $Y _{n}^{k+1}:= y_{n-1}^{k}(T_{n}) +\delta _{ n}^{k}$ and solve in parallel

  $$\displaystyle{\dot{y}_{n}^{k+1} = -ay_{ n}^{k+1},\quad \mbox{ on $[T_{ n},T_{n+1}]$},\quad y_{n}^{k+1}(T_{ n}) = Y _{n}^{k+1}.}$$

The authors prove the following error estimate for this algorithm ³

Proposition 1 (Lions, Maday and Turinici 2001)

The parareal scheme is of order k, i.e. there exists c _k s.t.

$$\displaystyle{\vert Y _{n}^{k} - y(T_{ n})\vert +\max _{t\in [T_{n},T_{n+1}]}\vert y_{n}^{k}(t) - y(t)\vert \leq c_{ k}\varDelta T^{k}.}$$

This result implies that with each iteration of the parareal algorithm, one obtains a numerical time stepping scheme which has a truncation error that is one order higher than before. So for a fixed iteration number k, one can obtain high order time integration methods that are naturally parallel. The authors then note that the same proposition also holds for Forward Euler. In both discretization schemes however, the stability of the higher order methods obtained with the parareal correction scheme degrades with iterations, as shown in Fig. 7 taken from the original publication [54]. The authors finally show two numerical examples: one for a heat equation where they obtain a simulated speedup of a factor 8 with 500 processors, and one for a semi-linear advection diffusion problem, where a variant of the algorithm is proposed by linearization about the previous iterate, since the parareal algorithm was only defined for linear problems. Here, the speedup obtained is 18.

Fig. 7

Stability of the parareal algorithm as function of the iteration, on the left for Backward Euler, and on the right for Forward Euler

Let us write the parareal algorithm now in modern notation, directly for the non-linear problem

$$\displaystyle{ u' = f(u),\quad u(t_{0}) = u_{0}. }$$

(17)

The algorithm is defined using two propagation operators:

• 1. G(t ₂, t ₁, u ₁) is a rough approximation to u(t ₂) with initial condition u(t ₁) = u ₁,

• 2. F(t ₂, t ₁, u ₁) is a more accurate approximation of the solution u(t ₂) with initial condition u(t ₁) = u ₁.

Starting with a coarse approximation U _n ⁰ at the time points t ₀, t ₁, t ₂, …, t _N , for example obtained using G, the parareal algorithm performs for k = 0, 1, … the correction iteration

$$\displaystyle{ U_{n+1}^{k+1} = F(t_{ n+1},t_{n},U_{n}^{k}) + G(t_{ n+1},t_{n},U_{n}^{k+1}) - G(t_{ n+1},t_{n},U_{n}^{k}). }$$

(18)

Theorem 1 (Parareal is a Multiple Shooting Method [35])

The parareal algorithm is a multiple shooting method

$$\displaystyle{ U_{n+1}^{k+1} = u_{ n}(t_{n+1},U_{n}^{k}) + \frac{\partial u_{n}} {\partial U_{n}}(t_{n+1},U_{n}^{k})(U_{ n}^{k+1} - U_{ n}^{k}), }$$

(19)

where the Jacobian has been approximated in  (18) by a difference on a coarse grid.

We thus have a very similar algorithm as the one proposed by Saha, Stadel and Tremaine [67], the only difference being that the Jacobian approximation does not come from a simpler model, but from a coarser discretization.

We now present a very general convergence result for the parareal algorithm applied to the non-linear initial value problem (17), which contains accurate estimates of the constants involved:

Theorem 2 (Convergence of Parareal [28])

Let F(t _n+1 ,t _n ,U _n ^k ) denote the exact solution at t _n+1 and G(t _n+1 ,t _n ,U _n ^k ) be a one step method with local truncation error bounded by C ₁ ΔT ^p+1 . If

$$\displaystyle{\vert G(t +\varDelta T,t,x) - G(t +\varDelta T,t,y)\vert \leq (1 + C_{2}\varDelta T)\vert x - y\vert,}$$

then the following error estimate holds for  (18) :

$$\displaystyle\begin{array}{rcl} \max _{1\leq n\leq N}\vert u(t_{n}) - U_{n}^{k}\vert & \leq & \frac{C_{1}\varDelta T^{k(p+1)}} {k!} (1 + C_{2}\varDelta T)^{N-1-k}\prod _{ j=1}^{k}(N - j)\max _{ 1\leq n\leq N}\vert u(t_{n}) - U_{n}^{0}\vert {}\end{array}$$

(20)

$$\displaystyle\begin{array}{rcl} & \leq & \frac{(C_{1}T)^{k}} {k!} e^{C_{2}(T-(k+1)\varDelta T)}\varDelta T^{pk}\max _{ 1\leq n\leq N}\vert u(t_{n}) - U_{n}^{0}\vert.{}\end{array}$$

(21)

The proof uses generating functions and is just over a page long, see [28]. One can clearly see the precise convergence mechanisms of the parareal algorithm in this result: looking in (20) on the right, the product term is initially growing, for k = 1, 2, 3 we get the products N − 1, $(N - 1)(N - 2)$, $(N - 1)(N - 2)(N - 3)$ and so on, but as soon as k = N the product contains the factor zero, and the method has converged. This is the property already pointed out by Bellen and Zennaro in [6]. Next looking in (21), we see that the method’s order increases at each iteration k by p, the order of the coarse propagator, as already shown by Lions, Maday and Turinici in their proposition for the Euler method. We have however also a precise estimate of the constant in front in (21), and this constant contracts faster than linear, since it is an algebraic power of C ₁ T divided by k! (the exponential term is not growing as the iteration k progresses). This division by k! is the typical convergence behavior found in waveform relaxation algorithms, which we will see in more detail in the next section.

3 Domain Decomposition Methods in Space-Time

Time parallel methods based on domain decomposition solve evolution problems in quite a different way in parallel from multiple shooting based methods. The decomposition of the space-time domain for such methods is shown in Fig. 8. Again an iteration is then used, which computes only solutions on the local space-time subdomains Ω _j . Since these solutions are obtained over the entire so-called time window [0, T] before accurate interface values are available from the neighboring subdomains over the entire time window, these methods are also time parallel in this sense, and they are known under the name waveform relaxation.

Fig. 8

Decomposition of the space-time domain for domain decomposition time parallel methods

3.1 Picard and Lindelöf 1893/1894

The roots of waveform relaxation type methods lie in the existence proofs of solutions for ordinary differential equations of Picard [65] and Lindelöf [53]. Like the alternating Schwarz method invented by Schwarz to prove the Dirichlet principle [70] and hence existence of solutions of Laplace’s equation on general domains, Picard invented his method of successive approximations to prove the existence of solutions of the specific class of ordinary differential equations:

Les méthodes d’approximation dont nous faisons usage sont théoriquement susceptibles de s’appliquer à toute équation, mais elles ne deviennent vraiment intéressantes pour l’étude des propriétés des fonctions définies par les équations différentielles que si l’on ne reste pas dans les généralités et si l’on envisage certaines classes d’équations.

Picard thus considers ordinary differential equations of the form

$$\displaystyle{ v'(t) = f(v(t)),\quad t \in [0,T], }$$

(22)

with given initial condition v(0). In order to analyze if a solution of such a non-linear problem exists, he proposed the nowadays called Picard iteration

$$\displaystyle{ v^{n}(t) = v(0) +\int _{ 0}^{t}f(v^{n-1}(\tau ))d\tau,\quad n = 1,2,\ldots, }$$

(23)

where v ⁰(t) is some initial guess. This transforms the problem of solving the ordinary differential equation (22) into a sequence of problems using only quadrature, which is much easier to handle. Picard proved convergence of this iteration in [65], which was sufficient to answer the existence question. It was Lindelöf a year later who gave the following convergence rate estimate in [53]:

Theorem 3 (Superlinear Convergence)

On bounded time intervals t ∈ [0,T], the iterates  (23) satisfy the superlinear error bound

$$\displaystyle{ \vert \vert v - v^{n}\vert \vert _{ \infty }\leq \frac{(CT)^{n}} {n!} \vert \vert v - v^{0}\vert \vert _{ \infty }, }$$

(24)

where C is the Lipschitz constant of the nonlinear right hand side f.

We see in the convergence estimate (24) the same term appear as in the parareal convergence estimate (21). This term is typical for the convergence of waveform relaxation methods we will see next, and thus the comment of Saha, Stadel and Tremaine in the quote at the beginning of Sect. 2.4 is justified.

3.2 Lelarasmee, Ruehli and Sangiovanni-Vincentelli 1982

The Picard iteration was not very successful as an iterative method for concrete computations,⁴ but in the circuit community, an interesting variant was developed based on a decomposition of the circuit by Lelarasmee, Ruehli and Sangiovanni-Vincentelli [52]:

The Waveform Relaxation (WR) method is an iterative method for analyzing nonlinear dynamical systems in the time domain. The method, at each iteration, decomposes the system into several dynamical subsystems, each of which is analyzed for the entire given time interval.

The motivation for this method was really the extremely rapid growth of integrated circuits, which made it difficult to simulate a new generation of circuits on the present generation computers.⁵ Lelarasmee, Ruehli and Sangiovanni-Vincentelli explain the waveform relaxation algorithm on the concrete example of a MOS ring oscillator shown in Fig. 9. The reason why this circuit is oscillating can be seen as follows: suppose the voltage at node v ₁ equals 5 V. Then this voltage is connected to the gate of the transistor to the right, which will thus open, and hence the voltage at node v ₂ will be pulled down to ground, i.e. 0 V. This is however connected to the gate of the next transistor to the right of v ₂, which will thus close, and v ₃ will be pulled up to 5 V. These 5 V will now feedback to the gate of the transistor to the left of v ₁, which will thus open, and thus v ₁, which was by assumption at 5 V, will be pulled down to ground at 0 V, and we see how the oscillation happens.

Fig. 9

Historical example of the MOS ring oscillator, for which the waveform relaxation algorithm was derived

Using the laws of Ohm and Kirchhoff, the equations for such a circuit can be written in form of a system of ordinary differential equations

$$\displaystyle{\begin{array}{rcll} \mathbf{v}'(t)& =&\mathbf{f}(\mathbf{v}(t)),\quad &0 < t < T,\\ \mathbf{v}(0)&=&\mathbf{g}, \end{array} }$$

where $\mathbf{v} = (v_{1},v_{2},v_{3})$, and $\mathbf{g}$ is the initial state of the circuit.

If the circuit is extremely large, so that it does not fit any more on one single computer, the waveform relaxation algorithm is based on the idea of decomposing the circuit into subcircuits, as shown in Fig. 10. The idea is to cut the wires with which the subcircuits are connected, and then to assume that there are small voltage sources on the wires that were cut, which feed in the voltage that was calculated at the previous iteration. This leads to the iterative method

$$\displaystyle{ \begin{array}{rcl} \partial _{t}v_{1}^{k+1} & =&f_{1}(v_{1}^{k+1},v_{2}^{k},v_{3}^{k}), \\ \partial _{t}v_{2}^{k+1} & =&f_{2}(v_{1}^{k},v_{2}^{k+1},v_{3}^{k}), \\ \partial _{t}v_{3}^{k+1} & =&f_{3}(v_{1}^{k},v_{2}^{k},v_{3}^{k+1}).\end{array} }$$

(25)

Since in the circuit simulation community signals along wires are called ‘waveforms’, this gave the algorithm the name Waveform Relaxation. We see in (25) that on the right all neighboring waveforms have been relaxed to the previous iteration, which results in a Jacobi type relaxation known in numerical linear algebra, which is entirely parallel. Naturally one could also use a Gauss-Seidel type relaxation which would then be sequential.

Fig. 10

Decomposition of the MOS ring oscillator circuit for the waveform relaxation algorithm

We show in Fig. 11 a historical numerical convergence study for the MOS ring oscillator taken from [52]. We can see that this circuit has the property that the waveform relaxation algorithm converges in a finite number of steps. This can be understood by the finite propagation speed of the information in this circuit,⁶ and we will see this again when looking at hyperbolic equations in the following section. The convergence of waveform relaxation methods depends strongly on the type of equations that are being solved, and the general convergence estimate of Lindelöf (24), also valid for waveform relaxation, is not always sharp.

Fig. 11

Historical convergence result for the MOS ring oscillator from [52]. The x axis represents time here and the y axis voltage values

3.3 Gander 1996

The waveform relaxation algorithm from the previous subsection can be naturally extended to partial differential equations, as it was shown in [24]:

Motivated by the work of Bjørhus [8], we show how one can use overlapping domain decomposition to obtain a waveform relaxation algorithm for the semi-discrete heat equation which converges at a rate independent of the mesh parameter.

The idea is best explained for the simple model problem of the one dimensional heat equation,

$$\displaystyle{ \partial _{t}u = \partial _{xx}u,\quad 0 < x < 1,\ t > 0 }$$

(26)

with given initial condition u(x, 0) = u ₀(x) and homogeneous boundary conditions. Like in the waveform relaxation algorithm, where the circuit was partitioned into subcircuits, one partitions the domain Ω = (0, 1) into overlapping subdomains, say Ω ₁ = (0, β) and Ω ₁ = (α, 1), α < β, and then performs the iteration

$$\displaystyle{ \begin{array}{rcll} \partial _{t}u_{1}^{n}& =&\partial _{xx}u_{1}^{n},\quad &0 < x <\beta,\ t > 0, \\ u_{1}^{n}(\beta,t)& =&u_{2}^{n-1}(\beta,t), \\ \partial _{t}u_{2}^{n}& =&\partial _{xx}u_{2}^{n},\quad &\alpha < x < 1,\ t > 0, \\ u_{2}^{n}(\alpha,t)& =&u_{1}^{n-1}(\alpha,t). \end{array} }$$

(27)

Since the decomposition is overlapping like in the classical overlapping Schwarz method for steady problems, and time dependent problems are solved in each iteration like in waveform relaxation, these algorithms are called Schwarz Waveform Relaxation algorithms. One can show that algorithm (27) converges linearly on unbounded time intervals, see [34], and superlinearly on bounded time intervals, see [41]. Both results can be found for nonlinear problems in [25]. The superlinear convergence rate in Schwarz waveform relaxation algorithms is faster than in classical waveform relaxation methods for circuits, since the heat kernel decay gives additional contraction. If the equation is a wave equation, then one obtains convergence in a finite number of steps, see for example [29]. Much better waveform relaxation methods can however be obtained using the new concept of optimized transmission conditions we will see next.

3.4 Gander, Halpern and Nataf 1999

It was shown in [36] that the Dirichlet transmission conditions used for the information exchange do not lead to good convergence behavior of the Schwarz waveform relaxation algorithm:

We then show that the Dirichlet conditions at the artificial interfaces inhibit the information exchange between subdomains and therefore slow down the convergence of the algorithm.

This observation holds for all types of partial differential equations, also for steady state problems [62]. The key new idea is to introduce more effective transmission conditions, which leads for the model problem (26) to the new Schwarz waveform relaxation algorithm

$$\displaystyle{ \begin{array}{rcll} \partial _{t}u_{1}^{n}& =&\partial _{xx}u_{1}^{n},\quad &0 < x <\beta,\ t > 0, \\ \mathcal{B}_{1}u_{1}^{n}(\beta,t)& =&\mathcal{B}_{1}u_{2}^{n-1}(\beta,t), \\ \partial _{t}u_{2}^{n}& =&\partial _{xx}u_{2}^{n},\quad &\alpha < x < 1,\ t > 0, \\ \mathcal{B}_{2}u_{2}^{n}(\alpha,t)& =&\mathcal{B}_{2}u_{1}^{n-1}(\alpha,t).\end{array} }$$

(28)

If one chooses $\mathcal{B}_{1} = \partial _{n_{1}} + \mbox{ DtN}_{2}$ and $\mathcal{B}_{2} = \partial _{n_{2}} + \mbox{ DtN}_{1}$, where $\partial _{n_{j}}$ denotes the normal derivative, and DtN _j denotes the Dirichlet to Neumann operator of the subdomain j, then algorithm (28) converges in two iterations, independently of the overlap: it becomes a direct solver. This can be generalized to N iterations with N subdomains, or one iteration when using an alternating sweep, and is the underlying mechanism for the good convergence of the sweeping preconditioner recently presented in [20]. Since the DtN operators are in general expensive, so-called optimized Schwarz waveform relaxation methods use local approximations; for a complete treatment of advection reaction diffusion equations see [7, 30], and for the wave equation, see [29, 37]. An overview for steady problems and references can be found in [26]. We show in Fig. 12 as an illustration for an advection reaction diffusion equation and a decomposition into eight overlapping subdomains how much faster optimized Schwarz waveform relaxation methods converge compared to classical Schwarz waveform relaxation methods. While the Dirichlet transmission conditions in the left column greatly inhibit the information exchange, the absorbing conditions (here second order Taylor conditions) lead almost magically to a very good approximation already in the very first iteration. For more information, see [7, 30]. Waveform relaxation methods should thus never be used with classical transmission conditions, also when applied to circuits; optimized transmission conditions have also been proposed and analyzed for circuits, see for example [1, 2] and references therein.

Fig. 12

Snapshots in time of the first classical Schwarz waveform relaxation iteration in the left column, and the first optimized Schwarz waveform relaxation iteration in the right column: the exact solution is shown in solid red, and the Schwarz waveform relaxation approximation in dashed blue

3.5 Recent Developments

Other domain decomposition methods for steady problems have been recently proposed and analyzed for time dependent problems: for the convergence properties of the Dirichlet-Neumann Waveform Relaxation algorithm, see [39, 58], and for the Neumann-Neumann Waveform Relaxation algorithm, see [39, 50] for a convergence analysis, and [44] for well posedness of the algorithm.

It is also naturally possible to combine the multiple shooting method and the Schwarz waveform relaxation methods, which leads to a space-time decomposition of the form shown in Fig. 13. A parareal Schwarz waveform relaxation algorithm for such decompositions was proposed in [38], see also [57] for a method which uses waveform relaxation as a solver within parareal. These methods iterate simultaneously on sets of unknowns in the space-time domain, as the space-time multigrid methods we will see next.

Fig. 13

Space-time decomposition for parareal Schwarz waveform relaxation

4 Multigrid Methods in Space-Time

The methods we have seen so far were designed to be naturally parallel: the time decomposition methods based on shooting use many processors along the time axis, the waveform relaxation methods use many processors in the space dimensions. The multigrid methods we see in this section are not naturally parallel, but their components can be executed in parallel in space-time, since they work simultaneously on the entire space-time domain, as indicated in Fig. 14.

Fig. 14

Space-time multigrid methods work simultaneously on the entire space-time domain

4.1 Hackbusch 1984

The first such method is the parabolic multigrid method developed by Hackbusch in [43]. Like other multigrid methods, the smoother can be naturally implemented in parallel in space, and in the parabolic multigrid method, the smoother operates over many time levels, so that interpolation and restriction can be performed in parallel in space-time.

In order to explain the method, we consider the parabolic PDE $u_{t} + \mathcal{L}u = f$ discretized by Backward Euler:

$$\displaystyle{ (I +\varDelta t\mathcal{L})u_{n} = u_{n-1} +\varDelta tf(t_{n}). }$$

(29)

Hackbusch makes the following comment about this equation

The conventional approach is to solve (29) time step by time step; u _n is computed from u _n−1, then u _n+1 from u _n etc. The following process will be different. Assume that u _n is already computed or given as an initial state. Simultaneously, we shall solve for u _n+1 , u _n+2 , …, u _n+k in one step of the algorithm.

In the method of Hackbusch, one starts with a standard smoother for the problem at each time step. Let A be the iteration matrix, $A:= I +\varDelta t\mathcal{L}$; then one partitions the matrix into its lower triangular, diagonal and upper triangular part, $A = L + D + U$, and uses for example as a smoother the Gauss-Seidel iteration over many time levels:

for n = 1: N

for j = 1: ν

$u_{n}^{j} = (L + D)^{-1}(-Uu_{n}\,^{j-1} + u_{n-1}^{\nu } +\varDelta tf(t_{n}))$;

end;

end;

We see that the smoothing process is sequential in time: one first has to finish the smoothing iteration at time step n − 1 in order to obtain u _n−1 ^ν, before one can start the smoothing iteration at time step n, since u _n−1 ^ν is needed on the right hand side.

After smoothing, one restricts the residual in space-time like in a classical multigrid method to a coarser grid, before applying the procedure recursively. Hackbusch first only considers coarsening in space, as shown in Fig. 15. In this case, one can prove that standard multigrid performance can be achieved for this method. If one however also coarsens in time, one does not obtain standard multigrid performance, and the method can even diverge. This is traced back by Hackbusch to errors which are smooth in space, but non smooth in time. Hackbusch illustrates the performance of the method by numerical experiments for buoyancy-driven flow with finite difference discretization.

Fig. 15

Original figure of Hackbusch about the coarsening in the parabolic multigrid method. This figure was taken from [43]

4.2 Lubich and Ostermann 1987

Lubich and Ostermann [55] used the waveform relaxation context to define a space-time multigrid method:

Multi-grid methods are known to be very efficient solvers for elliptic equations. Various approaches have also been given to extend multi-grid techniques to parabolic problems. A common feature of these approaches is that multi-grid methods are applied only after the equation has been discretized in time. In the present note we shall rather apply multi-grid (in space) directly to the evolution equation.

Their work led to the so-called Multigrid Waveform Relaxation algorithm. The easiest way to understand it is to first apply a Laplace transform to the evolution problem, assuming for simplicity a zero initial condition,

$$\displaystyle{u_{t} + L_{h}u = f\quad \Longrightarrow\quad A(s)\hat{u}:= s\hat{u} + L_{h}\hat{u} = \hat{f}.}$$

One then applies a standard multigrid method to the Laplace transformed linear system $A(s)\hat{u} = \hat{f}$. Let $A(s) = L + D + sI + U$ be again the lower triangular, diagonal and upper triangular part of the matrix A(s). A standard two grid algorithm would then start with the initial guess $\hat{u}_{0}^{0}(s)$, and perform for n = 0, 1, 2, … the steps

for j = 1: ν

$\hat{u}\,_{n}^{j}(s) = (L + D + sI)^{-1}(-U\hat{u}\,_{n}^{j-1}(s) + \hat{f} (s))$;

end;

$\hat{u}_{n+1}^{0}(s) =\hat{ u}_{n}^{\nu }(s) + PA_{c}^{-1}R(\,\hat{f}- A\hat{u}_{n}^{\nu }(s))$;

smooth again;

where R and P are standard multigrid restriction and prolongation operators for steady problems, and the coarse matrix can be defined using a Galerkin approach, A _c : = RAP.

Applying the inverse Laplace transform to this algorithm, we obtain the multigrid waveform relaxation algorithm: the smoothing step

$$\displaystyle{(sI + L + D)\hat{u}\,_{n}^{j}(s) = -U\hat{u}\,_{ n}^{j-1}(s) + \hat{f} (s)}$$

becomes in the time domain

$$\displaystyle{\partial _{t}u\,_{n}^{j} + (L + D)u\,_{ n}^{j} + Uu\,_{ n}^{j-1} = f,}$$

which is a Gauss Seidel Waveform Relaxation iteration, see Sect. 3.2. The coarse correction

$$\displaystyle{\hat{u}_{n+1}^{0}(s):=\hat{ u}_{ n}^{\nu }(s) + PA_{ c}^{-1}R(\,\hat{f}- A\hat{u}_{ n}^{\nu }(s))}$$

becomes back in the time domain

solve $v_{t} + L_{H}v = R(f - \partial _{t}u_{n}^{\nu } - L_{h}u_{n}^{\nu })$,

$u_{n+1}^{0} = u_{n}^{\nu } + Pv$.

This is a time continuous parabolic problem on a coarse spatial mesh.

Lubich and Ostermann prove for the heat equation and finite difference discretization that red-black Gauss Seidel smoothing is not as good as for the stationary problem, but still sufficient to give typical multigrid convergence, and that damped Jacobi smoothing is as good as for stationary problems. The authors show with numerical experiments that in the multigrid waveform relaxation algorithm one can use locally adaptive time steps.

4.3 Horton and Vandewalle 1995

Horton and Vandewalle are the first to try to address the problem of time coarsening in [45]:

In standard time-stepping techniques multigrid can be used as an iterative solver for the elliptic equations arising at each discrete time step. By contrast, the method presented in this paper treats the whole of the space-time problem simultaneously.

They first show that time coarsening does not lead to multigrid performance, since the entire space-time problem is very anisotropic because of the time direction. To address this issue, they explain that one could either use line smoothers, which is related to the multigrid waveform relaxation algorithm we have seen in Sect. 4.2, or the following two remedies:

• 1. Adaptive semi-coarsening in space or time depending on the anisotropy,

• 2. Prolongation operators only forward in time.

For the heat equation with finite difference discretization and Backward Euler, BDF2 and Crank-Nicolson, Horton and Vandewalle perform a detailed local Fourier mode analysis, and show that good contraction rates can be obtain for space-time multigrid V-cycles, although not quite mesh independent. F-cycles are needed to get completely mesh independent convergence rates. These results are illustrated by numerical experiments for 1d and 2d heat equations.

4.4 Emmett and Minion 2012

There are several steps in the development of the solver PFASST, which stands for Parallel Full Approximation Scheme in Space-Time. The underlying iteration is a deferred correction method [60]:

This paper investigates a variant of the parareal algorithm first outlined by Minion and Williams in 2008 that utilizes a deferred correction strategy within the parareal iterations.

We thus have to start by explaining the deferred correction method. Consider the initial value problem

$$\displaystyle{ u' = f(u),\quad u(0) = u_{0}. }$$

(30)

We can rewrite this problem in integral form

$$\displaystyle{ u(t) = u(0) +\int _{ 0}^{t}f(u(\tau ))d\tau. }$$

(31)

Let $\tilde{u}(t)$ be an approximation with error $e(t):= u(t) -\tilde{ u}(t)$. Inserting $u(t) =\tilde{ u}(t) + e(t)$ into (31), we get

$$\displaystyle{ \tilde{u}(t) + e(t) = u(0) +\int _{ 0}^{t}f(\tilde{u}(\tau ) + e(\tau ))d\tau. }$$

(32)

Defining the function $F(u):= u(0) +\int _{ 0}^{t}f(u(\tau ))d\tau - u(t)$ from Eq. (31), the residual r(t) of the approximate solution $\tilde{u}(t)$ is

$$\displaystyle{ r(t):= F(\tilde{u}) =\tilde{ u}(0) +\int _{ 0}^{t}f(\tilde{u}(\tau ))d\tau -\tilde{ u}(t), }$$

(33)

and thus from (32) the error satisfies the equation

$$\displaystyle\begin{array}{rcl} e(t)& =& u(0) +\int _{ 0}^{t}f(\tilde{u}(\tau ) + e(\tau ))d\tau -\tilde{ u}(t) {}\\ & =& r(t) +\int _{ 0}^{t}f(\tilde{u}(\tau ) + e(\tau )) - f(\tilde{u}(\tau ))d\tau, {}\\ \end{array}$$

or written as a differential equation

$$\displaystyle{ e'(t) = r'(t) + f(\tilde{u}(t) + e(t)) - f(\tilde{u}(t)). }$$

(34)

The idea of integral deferred correction is to choose a numerical method, for example Forward Euler, and to get a first approximation of the solution of (30) by computing

$$\displaystyle{\tilde{u}_{m+1} =\tilde{ u}_{m} +\varDelta tf(\tilde{u}_{m}),\quad \mbox{ for $m = 0,1,\ldots,M - 1$}.}$$

With these values, one then computes the residual defined in (33) at the points t _m , m = 0, 1, …, M using a high order quadrature formula. One then solves the error equation (34) in differential form again with the same numerical method, here Forward Euler,

$$\displaystyle{ e_{m+1} = e_{m} + r_{m+1} - r_{m} +\varDelta t(f(\tilde{u}_{m} + e_{m}) - f(\tilde{u}_{m})). }$$

(35)

Adding this correction, one obtains a new approximation $\tilde{u}_{m} + e_{m}$, for which one can show in our example of Forward Euler that the order has increased by one, i.e. it is now a second order approximation. One can continue this process and increase the order up to the order of the quadrature used.

This spectral deferred correction iteration can also be considered as an iterative method to compute the Runge-Kutta method corresponding to the quadrature rule used to approximate the integral: if we denote by $\mathbf{u}^{0}$ the initial approximation obtained by forward Euler, $\mathbf{u}^{0}:= (\tilde{u}_{0},\tilde{u}_{1},\ldots,\tilde{u}_{M})^{T}$, each integral deferred correction corresponds to one step in the non-linear fixed point iteration

$$\displaystyle{ \mathbf{u}^{k} = F(\mathbf{u}^{k-1},u_{ 0}), }$$

(36)

where u ₀ is the initial condition from (30). The classical application of integral deferred correction is to partition the time interval [0, T] into subintervals [T _j−1, T _j ], j = 1, 2, …, J, and then to start on the first subinterval [T ₀, T ₁] to compute approximations $\mathbf{u}_{1}^{k}$ by performing K steps of (36) before passing to the next time interval [T ₁, T ₂], see also Fig. 18 for an example with M = 3. The overall iteration is therefore

u _0, M ^K = u ₀;

for j = 1: J

compute $\mathbf{u}_{j}^{0}$ as Euler approximation on [T _j−1, T _j ];

for k = 1: K

$\mathbf{u}_{j}^{k} = F(\mathbf{u}_{j}^{k-1},u_{j-1,M}^{K})$;

end;

end;

We see that this is purely sequential, like a time stepping scheme: in each time subinterval, one first has to finish the K spectral deferred corrections, before one can pass to the next time subinterval. Minion proposed in [60] not to wait for each time subinterval to finish, and to replace the inner updating formula by

$$\displaystyle{ \mathbf{u}_{j}^{k} = F(\mathbf{u}_{ j}^{k-1},u_{ j-1,M}^{k}),\quad \mbox{ (note the lower case $k$ !)}, }$$

(37)

which means that one can now perform the spectral deferred corrections on many time subintervals [T _j−1, T _j ] in parallel. This is very similar to the iteration of Womble we will see Sect. 5.3. In the approach of Minion, this is however combined with a coarse correction from the parareal algorithm, so it is like using a more and more accurate fine integrator, as the iteration progresses.

The PFASST algorithm proposed in [19] is based on using the parallel deferred correction iteration above as a smoother in a multigrid full approximation scheme in space-time for non-linear problems:

The method is iterative with each iteration consisting of deferred correction sweeps performed alternately on fine and coarse space-time discretizations. The coarse grid problems are formulated using a space-time analog of the full approximation scheme popular in multigrid methods for nonlinear equations.

The method has successfully been applied to non-linear problems in [19, 75, 76], but there is so far no convergence analysis for PFASST.

4.5 Neumüller 2014

The new idea in this multigrid variant is to replace the classical point smoothers by block Jacobi smoothers. Suppose we discretize the heat equation

$$\displaystyle{u_{t} =\varDelta u + f}$$

globally in space-time by an implicit method, for example Backward Euler. Then we obtain a block triangular linear system in space-time of the form

$$\displaystyle{ \left (\begin{array}{ccccc} A_{1} & & & & \\ B_{2} & A_{2} & & & \\ & B_{3} & A_{3} & & \\ & & \ddots & \ddots & \\ & & & B_{n}&A_{n}\\ \end{array} \right )\left (\begin{array}{c} \mathbf{u}_{1} \\ \mathbf{u}_{2} \\ \mathbf{u}_{3}\\ \vdots \\ \mathbf{u}_{n} \end{array} \right ) = \left (\begin{array}{c} \mathbf{f}_{1} \\ \mathbf{f}_{2} \\ \mathbf{f}_{3}\\ \vdots \\ \mathbf{f}_{n} \end{array} \right ). }$$

(38)

The space-time multigrid method consists now of applying a few damped block Jacobi smoothing steps, inverting the diagonal blocks A _n , before restricting by standard multigrid restriction operators in space-time to a coarser grid, and recursively continuing. One can show that for the heat equation, we have (see Martin Neumüller’s PhD thesis [63]):

• The optimal damping parameter for the block Jacobi smoother is $\omega = \frac{1} {2}$.

• One always obtains good smoothing in time (semi-coarsening is always possible).

• For $\frac{\varDelta t} {\varDelta h^{2}} \geq C$, one also obtains good smoothing in space.

• One V-cycle in space suffices to invert the diagonal blocks A _n in the Jacobi smoother.

This multigrid method has excellent scaling properties for the heat equation, as it was shown in [63], from which the example in Table 1 is taken. The results are for the 3D heat equation, and computed on the Vienna Scientific Cluster VSC-2; see also [32].

Table 1 Scaling results for the space-time multigrid method with block Jacobi smoother; all simulations performed by M. Neumüller

5 Direct Solvers in Space-Time

The time parallel solvers we have seen so far were all iterative. There have been also attempts to construct direct time parallel solvers. There are both small scale parallel direct solvers and also large scale parallel direct solvers.

5.1 Miranker and Liniger 1967

The first small scale direct parallel solver was proposed by Miranker and Liniger [61], who also were very much aware of the naturally sequential nature of evolution problems:

It appears at first sight that the sequential nature of the numerical methods do not permit a parallel computation on all of the processors to be performed. We say that the front of computation is too narrow to take advantage of more than one processor…Let us consider how we might widen the computation front.

For y′ = f(x, y), Miranker and Liniger consider the predictor corrector formulas

$$\displaystyle{y_{n+1}^{p} = y_{ n}^{c} + \frac{h} {2}(f(y_{n}^{c}) - f(y_{ n-1}^{c})),\quad y_{ n+1}^{c} = y_{ n}^{c} + \frac{h} {2}(f(y_{n+1}^{p}) + f(y_{ n}^{c})).}$$

This process is entirely sequential as they illustrated with a figure, a copy of which is shown in Fig. 16 on the left. They then consider the modified predictor corrector formulas

$$\displaystyle{y_{n+1}^{p} = y_{ n-1}^{c} + 2hf(y_{ n}^{p}),\quad y_{ n}^{c} = y_{ n-1}^{c} + \frac{h} {2}(f(y_{n}^{p}) + f(y_{ n-1}^{c})).}$$

Those two formulas can now be evaluated in parallel by two processors, as illustrated in Fig. 16 on the right. Miranker and Liniger then show how one can systematically derive a general class of numerical integration methods which can be executed on 2s processors in parallel, and present a stability and convergence analysis for those methods.

Fig. 16

Symbolic representation by Miranker and Liniger of an entirely sequential predictor corrector method on the left, and a parallel one on the right

Similar parallelism can also be obtained with the block implicit one-step methods developed by Shampine and Watts in [71]. These methods use different time stepping formulas to advance several time levels at once. For an early numerical comparison for parallel block methods and parallel predictor corrector methods, see Franklin [23]. These methods are ideally suited to be used on the few cores of a multicore processor, but they do not have the potential for large scale parallelism.

5.2 Axelson and Verwer 1985

Boundary value methods for initial value problems are a bit strange. A very good early introduction is the paper by Axelson and Verwer [4]:

Hereby we concentrate on explaining the fundamentals of the method because for initial value problems the boundary value method seems to be fairly unknown […] In the forward-step approach, the numerical solution is obtained by stepping through the grid […] In this paper, we will tackle the numerical solution in a completely different way […] We will consider $\dot{y} = f(x,y)$ as a two point boundary value problem with a given value at the left endpoint and an implicitly defined value, by the equation $\dot{y} = f(x,y)$ , at the right endpoint.

It is best to understand boundary value methods by looking at a simple example.⁷ Suppose we discretize $\dot{y} = f(y)$ with the explicit midpoint rule

$$\displaystyle{y_{n+1} - y_{n-1} - 2hf(y_{n}) = 0,\quad y_{0} = y(0).}$$

Since the explicit midpoint rule is a two step method, we also need an initial approximation for y ₁. Usually, one defines y ₁ from y ₀ using a one step method, for example here by Backward Euler. In boundary value methods, one leaves y ₁ as an unknown, and uses Backward Euler at the endpoint y _N to close the system, imposing

$$\displaystyle{y_{N} - y_{N-1} - 2hf(y_{N}) = 0.}$$

For a linear problem $\dot{y} = ay$, the midpoint rule and Backward Euler to define y ₁ gives the triangular linear system

$$\displaystyle{ \left (\begin{array}{ccccc} 1 - ah& & & & \\ - 2ah& 1 & & & \\ - 1 & - 2ah& 1 & & \\ & \ddots & \ddots & \ddots & \\ & & - 1& - 2ah&1\\ \end{array} \right )\left (\begin{array}{c} y_{1} \\ y_{2} \\ y_{3}\\ \vdots \\ y_{N} \end{array} \right ) = \left (\begin{array}{c} y_{0} \\ y_{0} \\ 0\\ \vdots\\ 0 \end{array} \right ). }$$

(39)

For the boundary value method, leaving y ₁ free and using Backward Euler on the right gives the tridiagonal system

$$\displaystyle{ \left (\begin{array}{ccccc} - 2ah& 1 & & & \\ - 1 & - 2ah& 1 & & \\ & \ddots & \ddots & \ddots & \\ & & - 1& - 2ah& 1 \\ & & & - 1 &1 - ah\\ \end{array} \right )\left (\begin{array}{c} y_{1} \\ y_{2} \\ y_{3}\\ \vdots \\ y_{N} \end{array} \right ) = \left (\begin{array}{c} y_{0} \\ 0\\ 0\\ \vdots \\ 0 \end{array} \right ). }$$

(40)

The tridiagonal system can now be solved either directly by factorization, or also by iteration, thus working on all time levels simultaneously.

It is very important however to realize that boundary value methods are completely different discretizations from initial value methods. The stability properties often are the contrary when one transforms an initial value method into a boundary value method. We show in Fig. 17 numerical examples for the initial value method (39) and boundary value method (40). We see that for a decaying solution, a < 0, the initial value method is exhibiting stability problems, while the boundary value method is perfectly stable (top row of Fig. 17). For growing solutions, a > 0 it is the opposite, the initial value method gives very good approximations, while the boundary value method needs extremely fine time steps to converge (bottom row of Fig. 17). One can therefore not just transform an initial value method into a boundary value method in order to obtain a parallel solver, one has to first carefully study the properties of the new method obtained, see [10, 11] and references therein. Now if the method has good numerical properties and the resulting system can well be solved in parallel, boundary value methods can be an attractive way of solving an evolution problem in parallel, see for example [9], where a Backward Euler method is proposed to precondition the boundary value method. This is still sequential, but if one only uses subblocks of the Backward Euler method as preconditioner, by dropping the connection after, say, every 10th time step, a parallel preconditioner is obtained. Such methods are called nowadays block boundary value methods, see for example [11]. If one introduces a coarse mesh with a coarse integrator, instead of the backward Euler preconditioner, and does not use as the underlying integrator a boundary value method any more, but just a normal time stepping scheme, the approach can be related to the parareal algorithm, see for example [3].

Fig. 17

Stability comparison of initial value and boundary value methods. (a) $a = -6$, $h = 1/20$. (b) $a = -6$, $h = 1/100$. (c) a = 6, $h = 1/20$. (d) a = 6, $h = 1/2000$

5.3 Womble 1990

The method presented by Womble in [79], see also the earlier work by Saltz and Naik [68], is not really a direct method, it is using iterations, but not in the same way of the iterative methods we have seen so far:

Parabolic and hyperbolic differential equations are often solved numerically by time stepping algorithms. These algorithms have been regarded as sequential in time; that is, the solution on a time level must be known before the computation for the solution at subsequent time levels can start. While this remains true in principle, we demonstrate that it is possible for processors to perform useful work on many time levels simultaneously.

The relaxation idea is similar to the one later used by Minion in [60] as a smoother in the context of PFASST, see Sect. 4.4, but not for a deferred correction iteration. In order to explain the method, we discretize the parabolic problem

$$\displaystyle{u_{t} = \mathcal{L}u + f}$$

by an implicit time discretization and obtain at each time step a linear system of the form

$$\displaystyle{A_{n}u_{n} = f_{n} + B_{n}u_{n-1}.}$$

Such systems are often solved by iteration. If we want to use a stationary iterative method, for example Gauss-Seidel, we would partition the matrix $A_{n} = L_{n} + D_{n} + U_{n}$, its lower triangular, diagonal, and upper triangular parts. Then starting with an initial guess u _n ⁰, one solves for k = 1, 2, …, K

$$\displaystyle{ (L_{n} + D_{n})u_{n}^{k} = -U_{ n}u_{n}^{k-1} + f_{ n} + B_{n}u_{n-1}^{K}. }$$

(41)

The key idea to break the sequential nature is to modify this iteration slightly so that it can be performed in parallel over several time steps. It suffices to not wait for convergence of the previous time level, but to iterate like

$$\displaystyle{ (L_{n} + D_{n})u_{n}^{k} = -U_{ n}u_{n}^{k-1} + f_{ n} + B_{n}u_{n-1}^{k-1}, }$$

(42)

which is the same idea also used in (37). Womble obtained quite good results with this approach, and he was the first person to really demonstrate practical speedup results with this time parallel method on a 1024-processor machine. Even though it was later shown that only limited speedups are possible with this relaxation alone [16], the work of Womble made people realize that indeed time parallelization could become an important direction, and it drew a lot of attention toward time-parallel algorithms.

5.4 Worley 1991

Worley was already in his PhD thesis in 1988 very interested in theoretical limits on the best possible sequential and parallel complexity when solving PDEs. While the ultimate sequential algorithm for such a problem of size n is O(n) on a sequential machine, it is $O(\log n)$ on a parallel machine. In [80], Worley presented an additional direct time parallelization method, which when combined with multigrid waveform relaxation leads to a nearly optimal time-parallel iterative method:

The waveform relaxation multigrid algorithm is normally implemented in a fashion that is still intrinsically sequential in the time direction. But computation in the time direction only involves solving linear scalar ODEs. If the ODEs are solved using a linear multistep method with a statically determined time step, then each ODE solution corresponds to the solution of a banded lower triangular matrix equation, or, equivalently, a linear recurrence. Parallelizing linear recurrence equations has been studied extensively. In particular, if a cyclic reduction approach is used to parallelize the linear recurrence, then parallelism is introduced without increasing the order of the serial complexity.

The approach is based on earlier ideas for the parallel evaluation of recurrence relations [49] and the parallel inversion of triangular matrices [69]. Worley explains the fundamental idea as follows: suppose we want to solve the bidiagonal matrix equation

$$\displaystyle{ \left (\begin{array}{cccc} a_{11} & & & \\ a_{21} & a_{22} & & \\ & a_{32} & a_{33} & \\ & & a_{43} & a_{44} \end{array} \right )\left (\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4}\end{array} \right ) = \left (\begin{array}{c} f_{1} \\ f_{2} \\ f_{3} \\ f_{4}\end{array} \right ). }$$

(43)

Then one step of the cyclic reduction algorithm leads to a new matrix equation of half the size,

$$\displaystyle{ \left (\begin{array}{cc} a_{22} & \\ -\frac{a_{43}} {a_{33}} a_{32}\quad & a_{44} \end{array} \right )\left (\begin{array}{c} x_{2} \\ x_{4}\end{array} \right ) = \left (\begin{array}{c} f_{2} -\frac{a_{21}} {a_{11}} f_{1} \\ f_{4} -\frac{a_{43}} {a_{33}} f_{3} \end{array} \right ), }$$

(44)

i.e. we simply computed the Schur complement to eliminate variables with odd indices. For a bigger bidiagonal matrix, this process can be repeated, and we always obtain a bidiagonal matrix of half the size. Once a two by two system is obtained, one can solve directly, and then back-substitute the values obtained to recover the values of the eliminated variables. Each step of the cyclic reduction is parallel, since each combination of two equations is independent of the others. Similarly the back-substitution process is also parallel. Cyclic reduction is therefore a direct method to solve a linear forward recurrence in parallel, and the idea can be generalized to larger bandwidth using block elimination. The serial complexity of simple forward substitution in the above example is 3n, whereas the cyclic reduction serial complexity is 7n (or 5n if certain quantities are precomputed), and thus the algorithm is not of interest for sequential computations. But performed in parallel, the complexity of cyclic reduction becomes a logarithm in n, and one can thus obtain the solution substantially faster in parallel than just by forward substitution. For further theoretical considerations and numerical results in combination with multigrid waveform relaxation, see [46]. A truly optimal time-parallel algorithm, based on a preconditioner in a waveform relaxation setting using a fast Fourier transform in space to decouple the unknowns, and cyclic reduction in time can be found in [74].

5.5 Sheen, Sloan and Thomée 1999

A new way to solve evolution problems with a direct method in parallel was proposed in [72]:

These problems are completely independent, and can therefore be computed on separate processors, with no need for shared memory. In contrast, the normal step-by-step time-marching methods for parabolic problems are not easily parallelizable.

see also [15]. The idea is to Laplace transform the problem, and then to solve a sequence of steady problems at quadrature nodes used for the numerical evaluation of the inverse Laplace transform, and goes back to the solution in the frequency domain of hyperbolic problems, see for example [17]. Suppose we have the initial value problem

$$\displaystyle{u_{t} + Au = 0,\quad u(0) = u_{0},}$$

where A represents a linear operator. Applying a Laplace transform to this problem in time with complex valued Laplace transform parameter s leads to the parametrized equation

$$\displaystyle{ s\hat{u} + A\hat{u} = u_{0}, }$$

(45)

and to obtain the solution in the time domain, one has to perform the inverse Laplace transform

$$\displaystyle{ u(t) = \frac{1} {2\pi i}\int _{\varGamma }e^{st}\hat{u}(s)ds, }$$

(46)

where Γ is a suitably chosen contour in the complex plane. If the integral in (46) is approximated by a quadrature rule with quadrature nodes s _j , one only needs to compute u(s) from (45) at s = s _j , and these solutions are completely independent of one another, see the quote above, and can thus be performed in parallel. This direct time parallel solver is restricted to problems where Laplace transform can be applied, i.e. linear problems with constant coefficients in the time direction, and one needs a solver that works with complex numbers for (45). It is however a very successful and efficient time parallel solver when it can be used, see [18, 51, 73, 77].

5.6 Maday and Ronquist 2008

A new idea for a direct time parallel solver by diagonalization was proposed in [56]:

Pour briser la nature intrinsèquement séquentielle de cette résolution, on utilise l’algorithme de produit tensoriel rapide.

To explain the idea, we discretize the linear evolution problem u _t  = Lu using Backward Euler,

$$\displaystyle{\left (\begin{array}{cccc} \frac{1} {\varDelta t_{1}} - L& & & \\ - \frac{1} {\varDelta t_{2}} & \frac{1} {\varDelta t_{2}} - L& & \\ & \ddots & \ddots & \\ & & - \frac{1} {\varDelta t_{N}} & \frac{1} {\varDelta t_{N}} - L \end{array} \right )\left (\begin{array}{c} u_{1} \\ u_{2}\\ \vdots \\ u_{N} \end{array} \right ) = \left (\begin{array}{c} f_{1} + \frac{1} {\varDelta t_{1}} u_{0} \\ f_{2}\\ \vdots \\ f_{N} \end{array} \right ).}$$

Using the Kronecker symbol, this linear system can be written in compact form as

$$\displaystyle{ (B \otimes I_{x} - I_{t} \otimes L)\mathbf{u} =\mathbf{ f}, }$$

(47)

where I _x is the identity matrix of the size of the spatial unknowns, and I _t is the identity matrix of the size of the time direction unknowns, and the time stepping matrix is

$$\displaystyle{B:= \left (\begin{array}{cccc} \frac{1} {\varDelta t_{1}} & & & \\ - \frac{1} {\varDelta t_{2}} & \frac{1} {\varDelta t_{2}} & & \\ & \ddots & \ddots & \\ & & - \frac{1} {\varDelta t_{N}} & \frac{1} {\varDelta t_{N}} \end{array} \right ).}$$

If B is diagonalizable, $B = SDS^{-1}$, one can rewrite the system (47) in factored form, namely

$$\displaystyle{ (S \otimes I_{x})(\mbox{ diag}(D - L))(S^{-1} \otimes I_{ x})\mathbf{u} =\mathbf{ f}, }$$

(48)

and we can hence solve it in 3 steps:

$$\displaystyle{\begin{array}{lrcl} (a)& (S \otimes I_{x})\mathbf{g}& =&\mathbf{f}, \\ (b) & ( \frac{1} {\varDelta t_{n}} - L)\mathbf{w}^{n}& =&\mathbf{g}^{n},\quad 1 \leq n \leq N, \\ (c)\quad &(S^{-1} \otimes I_{x})\mathbf{u}& =&\mathbf{w}. \end{array} }$$

Note that the expensive step (b) requiring a solve with the system matrix L can now be done entirely in parallel for all time levels t _n . Maday and Ronquist obtain with this algorithm for the 1d heat equation close to perfect speedup. They recommend to use a geometric time mesh $\varDelta t_{k} =\rho ^{k-1}\varDelta t_{1}$, with ρ = 1. 2, since “choosing ρ much closer to 1 may lead to instabilities”. This algorithm is not defined if identical time steps are used, since it is not possible to diagonalize a Jordan block ! For a precise truncation error analysis for a geometric time grid, a round-off error analysis due to the diagonalization, and error estimates based on the trade-off between the two, see [31].

5.7 Christlieb, Macdonald and Ong 2010

The integral deferred correction methods we have already seen in Sect. 4.4 in the context of PFASST can also be used to create naturally small scale parallelism [14]:

…we discuss a class of defect correction methods which is easily adapted to create parallel time integrators for multicore architectures.

As we see in the quote, the goal is small scale parallelism for multicore architectures, as in the early predictor corrector and block methods from Sect. 5.1. The new idea introduced by Christlieb, Macdonald and Ong is to modify integral deferred correction so that pipelining becomes possible, which leads to so called RIDC (Revisionist Integral Deferred Correction) methods. As we have seen already in Sect. 4.4, the classical integral deferred correction method is working sequentially on the time point groups I ₀, I ₁, …, I _J−1 we show in Fig. 18 taken from [14], corresponding to the time intervals [T ₀, T ₁], [T ₁, T ₂], …, [T _J−1, T _J ] in Sect. 4.4. For each time point group I _j , one has to evaluate in the step (35) of integral deferred correction the quadrature formula for (33) at time t _j, m+1, using quadrature points at time t _j, 0, t _j, 1, …, t _j, M , 0 < m < M, where M = 3 in the example shown in Fig. 18. Only once all deferred correction steps on the time point group I _j are finished, one can start with the next time point group I _j+1, the method is like a sequential time stepping method.

Fig. 18

Classical application of integral deferred correction, picture taken from [14]

In order to obtain parallelism, the idea is to increase the size of the time point groups M to contain more points than the quadrature formula needs. One can then pipeline the computation, as shown in Fig. 19: the number of quadrature points is still four, but M is much larger, and thus the Euler prediction step and the correction steps of the integral deferred correction can be executed in parallel, since all the values represented by the black dots are available simultaneously to compute the next white ones, after an initial setup of this new ‘computation front’.

Fig. 19

RIDC way to compute integral deferred correction type methods in a pipelined way, figure taken from [14]

This leads to small scale parallel high order integrators which work very well on multicore architectures. When run in parallel, RIDC can give high order accuracy in a time comparable to the time of the low order integration method used, provided the startup costs are negligible.

5.8 Güttel 2012

A new direct time parallel method based on a completely overlapping decomposition of the time direction was proposed in [42]:

We introduce an overlapping time-domain decomposition method for linear initial-value problems which gives rise to an efficient solution method for parallel computers without resorting to the frequency domain. This parallel method exploits the fact that homogeneous initial-value problems can be integrated much faster than inhomogeneous problems by using an efficient Arnoldi approximation for the matrix exponential function.

This method, called ParaExp [27], is only defined for linear problems, and especially suited for the parallel time integration of hyperbolic problems, where most large scale time parallel methods have severe difficulties (for a Krylov subspace remedy, see [22, 33, 66], but reorthogonalization costs might be high). ParaExp works very well also on diffusive problems [27], as we will also illustrate with a numerical experiment. To explain the method, we consider the linear system of evolution equations

$$\displaystyle{\mathbf{u}'(t) = A\mathbf{u}(t) +\mathbf{ g}(t),\quad t \in [0,T],\quad \mathbf{u}(0) =\mathbf{ u}_{0}.}$$

The ParaExp algorithm is based on a completely overlapping decomposition, as shown in Fig. 20: the time interval [0, T] is decomposed into subintervals [0, T ₄: = T], [T ₁, T ₄], [T ₂, T ₄], and [T ₃, T ₄]. ParaExp is a direct solver, consisting of two steps: first one solves on the initial parts of the overlapping decomposition, [0, T ₁], [T ₁, T ₂], [T ₂, T ₃], and [T ₃, T ₄] the non-overlapping inhomogeneous problems (shown in solid red in Fig. 20)

$$\displaystyle{\mathbf{v}_{j}'(t) = A\mathbf{v}_{j}(t) +\mathbf{ g}(t),\quad \mathbf{v}_{j}(T_{j-1}) = {\boldsymbol 0},\quad t \in [T_{j-1},T_{j}],}$$

and then one solves the overlapping homogeneous problems (shown in dashed blue in Fig. 20)

$$\displaystyle{\mathbf{w}_{j}'(t) = A\mathbf{w}_{j}(t),\quad \mathbf{w}_{j}(T_{j-1}) =\mathbf{ v}_{j-1}(T_{j-1}),\quad t \in [T_{j-1},T]}$$

Fig. 20

Overlapping decomposition and solution strategy of ParaExp

By linearity, the solution is then simply obtained by summation,

$$\displaystyle{\mathbf{u}(t) =\mathbf{ v}_{k}(t) +\sum _{ j=1}^{k}\mathbf{w}_{ j}(t)\quad \mbox{ with $k$ such that}\quad t \in [T_{k-1},T_{k}].}$$

Like in many time parallel methods, this seems to be absurd, since the overlapping propagation of the linear homogeneous problems is redundant, and the blue dashed solution needs to be integrated over the entire time interval [0, T]! The reason why substantial parallel speedup is possible in ParaExp is that near-optimal approximations of the matrix exponential are known, and so the homogeneous problems in dashed blue become very cheap. Two approaches work very well: projection based methods, where one approximates $\mathbf{a}_{n}(t) \approx exp(tA)\mathbf{v}$ from a Krylov space built with $S:= (I - A/\sigma )^{-1}A$, and expansion based methods, which approximate $\exp (tA)\mathbf{v} \approx \sum _{j=0}^{n-1}\beta _{j}(t)p_{j}(A)\mathbf{v}$, where p _j are polynomials or rational functions. For more details, see [27].

We show in Table 2 the performance of the ParaExp algorithm applied to the wave equation from [27],

$$\displaystyle\begin{array}{rcl} \partial _{tt}u(t,x)& =& \alpha ^{2}\partial _{ xx}u(t,x) + \mbox{ hat($x$)}\sin (2\pi ft),\qquad x,t \in (0,1), {}\\ u(t,0)& =& u(t,1) = u(0,x) = u'(0,x) = 0, {}\\ \end{array}$$

where hat(x) is a hat function centered in the spatial domain. The problem is discretized with a second order centered finite difference scheme in space using $\varDelta x = \frac{1} {101}$, and RK45 is used in time with $\varDelta t_{0} =\min \{ 5 \cdot 10^{-4}/\alpha,1.5 \cdot 10^{-3}/f\}$ for the inhomogeneous solid red problems. The homogeneous dashed blue problems were solved using a Chebyshev exponential integrator, and 8 processors were used in this set of experiments. We see that the parallel efficiency of ParaExp is excellent for this hyperbolic problem, and it would be difficult for other time parallel algorithms to achieve this.

Table 2 Performance of ParaExp on a wave equation

ParaExp also works extremely well for parabolic problems. For the heat equation

$$\displaystyle\begin{array}{rcl} \partial _{t}u(t,x)& =& \alpha \partial _{xx}u(t,x) + \mbox{ hat($x$)}\sin (2\pi ft),\qquad x,t \in (0,1), {}\\ u(t,0)& =& u(t,1) = 0,\quad u(0,x) = 4x(1 - x), {}\\ \end{array}$$

we show numerical results from [27] in Table 3. The heat equation was discretized using centered finite differences in space with $\varDelta x = \frac{1} {101}$, and again an RK45 method in time was used with $\varDelta t_{0} =\min \{ 5 \cdot 10^{-4}/\alpha,1.5 \cdot 10^{-3}/f\}$ for the inhomogeneous problems, the homogeneous ones being solved also with a Chebyshev exponential integrator. For the heat equation, 4 processors were used. We see that again excellent parallel efficiency is obtained with the ParaExp algorithm. For more information and numerical results, see [27].

Table 3 Performance of ParaExp on the heat equation

6 Conclusions

The efforts to integrate evolution problems in parallel span now five decades. We have seen that historically methods have grown into four different classes of time parallel methods: shooting type methods starting with Nievergelt, domain decomposition and waveform relaxation methods starting with Lelarasmee, Ruehli and Sangiovanni-Vincentelli, space-time multigrid methods starting with Hackbusch, and direct time parallel solvers starting with Miranker and Liniger. An important area which was not addressed in this review is a systematic comparison of the performance of these methods, and a demonstration that these algorithms are really faster than classical algorithms in a given parallel computational environment. Such a result on a 512 processor machine was shown for the space-time multigrid waveform relaxation algorithm in [78], compared to space parallel multigrid waveform relaxation and standard time stepping, see also [46] for results on an even larger machine, and [5]. A very recent comparison can be found in the short note [21], where the authors show that above a certain number of processors time-parallel algorithms indeed outperform classical ones. Time parallel methods are currently a very active field of research, and many new developments extending the latest directions we have seen, like Parareal, Schwarz-, Dirichlet-Neumann and Neumann-Neumann waveform relaxation, PFASST and full space-time multigrid, and RIDC and ParaExp, are to be expected over the coming years. These will help leverage the power of new multicore and very large scale parallel computers in the near future.