A Direct Solver for Time Parallelization

Abstract

With the advent of very large scale parallel computer, having millions of processing cores, it has become important to also use the time direction for parallelization. Among the successful methods doing this are the parareal algorithm, the paraexp algorithm, PFASST and also waveform relaxation methods of Schwarz or Dirichlet-Neumann or Neumann type. We present here a mathematical analysis of a further method to parallelize in time, proposed by Maday and Ronquist in 2007. It is based on the diagonalization of the time stepping matrix. Like for many time domain parallelization methods, this seems at first not to be a very promising approach, since this matrix is essentially triangular, and for a fixed time step even a Jordan block, and thus not diagonalizable. If one however chooses different time steps, diagonalization is possible, and one has to trade of between the accuracy due to necessarily having different time steps, and numerical errors in the diagonalization process of these almost not diagonalizable matrices. We study this trade-off mathematically and propose an optimization strategy for the choice of the parameters, for a Backward Euler discretization of the heat equation in two dimensions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Using the time direction in evolution problems for parallelization is an active field of research. Most of these methods are iterative, see for example the parareal algorithm analyzed in [3], a variant that became known under the name PFASST [10], and waveform relaxation methods based on domain decomposition [4, 5], see also [1] for a method called RIDC. Direct time parallel solvers are much more rare, see for example [2]. We present here a mathematical analysis of a different direct time parallel solver, proposed in [9]. We consider as our model partial differential equation (PDE) the heat equation on a rectangular domain Ω,

$$\displaystyle{ \frac{\partial u} {\partial t} -\varDelta u = f\ \mbox{ in $\varOmega \times (0,T)$, $u = g$ on $\partial \varOmega $, and $u(\cdot,0) = u_{0}$ in $\varOmega $}. }$$

(1)

Using a Backward Euler discretization on the time mesh $0 = t_{0} < t_{1} < t_{2} <\ldots < t_{N} = T$, $k_{n} = t_{n} - t_{n-1}$, and a finite difference approximation Δ _h of Δ over a rectangular grid of size $J = J_{1}J_{2}$, we obtain the discrete problem

$$\displaystyle{ \frac{1} {k_{n}}(\mathbf{u}^{n} -\mathbf{ u}^{n-1}) -\varDelta _{ h}\mathbf{u}^{n} =\mathbf{ f}^{n}. }$$

(2)

Let I _t be the N × N identity matrix associated with the time domain and I _x be the J × J identity matrix associated with the spatial domain. Setting $\mathbf{u}:= (\mathbf{u}^{1},\ldots,\mathbf{u}^{N})$, $\mathbf{f}:= (\mathbf{f}^{1} + \frac{1} {k_{1}} \mathbf{u}_{0},\mathbf{f}^{2},\ldots,\mathbf{f}^{N})$ and using the Kronecker symbol, (2) becomes

$$\displaystyle{ (B\otimes I_{x}-I_{t}\otimes \varDelta _{h})\mathbf{u} =\mathbf{ f},\qquad B:= \left (\begin{array}{cccc} \frac{1} {k_{1}} & & & \\ - \frac{1} {k_{2}} & \frac{1} {k_{2}} & & 0 \\ 0 & \ddots & \ddots & \\ & & - \frac{1} {k_{N}} & \frac{1} {k_{N}} \end{array} \right ). }$$

(3)

If B is diagonalizable, $B = SDS^{-1}$, then (3) can be solved in 3 steps:

$$\displaystyle{ \begin{array}{lrcl} (a)& (S \otimes I_{x})\mathbf{g}& =&\mathbf{f}, \\ (b) & ( \frac{1} {k_{n}} -\varDelta _{h})\mathbf{w}^{n}& =&\mathbf{g}^{n},\quad 1 \leq n \leq N, \\ (c)\quad &(S^{-1} \otimes I_{x})\mathbf{u}& =&\mathbf{w}. \end{array} }$$

(4)

The N equations in space in step (b) can now be solved in parallel. This interesting idea comes from [9], but its application requires some care: first, B is only diagonalizable if the time steps are all different, and this leads to a larger discretization error compared to using equidistant time steps, as we will see. Second, the condition number of S increases exponentially with N, which leads to inaccurate results in step (a) and (c) because of roundoff error. We accurately estimate these two errors, and then determine for a user tolerance the maximum N and optimal time step sequence of the form $k_{n+1} = qk_{n}$, which guarantees that errors stay below the user tolerance.

2 Error Estimate for Variable Time-Steps

We start by studying for a > 0 the ordinary differential equation (ODE)

$$\displaystyle{ \frac{du} {dt} + au = 0,\quad t \in (0,T),\quad u(0) = u_{0}\quad \Longrightarrow\quad u(t) = u_{0}ae^{-aT}. }$$

(5)

For Backward Euler, $u_{n} = (1 + ak_{n})^{-1}\,u_{n-1}$ with time steps from the division $\mathcal{T} = (k_{1},\mathop{\ldots },k_{N})$ satisfying $T =\sum _{ 1}^{N}k_{n}$, we define the error propagator by

$$\displaystyle{ Err(\mathcal{T};a,T,N):=\prod \limits _{ n=1}^{N}(1 + ak_{ n})^{-1} - e^{-aT}, }$$

(6)

such that the error at time T equals $Err(\mathcal{T};a,T,N)u^{0}$. We also define the equidistant division $\overline{\mathcal{T}}:= (\overline{k},\mathop{\ldots },\overline{k})$, where $\overline{k} = T/N$.

Theorem 1 (Equidistant Partition Minimizes Error)

For any a,T and N, and any division $\mathcal{T}$ , the error propagator is positive, and for the equidistant division $\overline{\mathcal{T}}$ , the error is globally minimized.

Proof

Rewriting $Err(\mathcal{T};a,T,N) =\prod \limits _{ n=1}^{N}(1 + ak_{n})^{-1} -\prod \limits _{n=1}^{N}(e^{ak_{n}})^{-1}$, we see that the error propagator is positive, since for all positive x, e ^x > 1 + x. To minimize the error, we thus have to minimize $\varPhi (\mathcal{T} ):=\prod \limits _{ n=1}^{N}(1 + ak_{n})^{-1}$ as a function of $\mathcal{T} \in \mathbb{R}^{N}$, with N inequality constraints k _n  ≥ 0, and one equality constraint $\sum _{n=1}^{N}k_{n} = T$. We compute the derivatives

$$\displaystyle{ \frac{\partial \varPhi } {\partial k_{i}}(\mathcal{T} ) = - \frac{a} {1 + ak_{i}}\varPhi (\mathcal{T} ),\quad \frac{\partial ^{2}\varPhi } {\partial k_{i}k_{j}}(\mathcal{T} ) = \frac{(1 +\delta _{ij})a^{2}} {(1 + ak_{i})(1 + ak_{j})}\varPhi (\mathcal{T} ),}$$

and to show that Φ is convex, we evaluate for an arbitrary vector $\mathbf{x} = (x_{1},\ldots,x_{N})$

$$\displaystyle\begin{array}{rcl} \sum _{i,j=1}^{N} \frac{\partial ^{2}\varPhi } {\partial k_{i}k_{j}}(\mathcal{T} )x_{i}x_{j}& =& \big(\sum _{i\neq j} \frac{a^{2}} {(1 + ak_{i})(1 + ak_{j})}x_{i}x_{j} +\sum _{i} \frac{a^{2}} {(1 + ak_{i})^{2}}x_{i}^{2}\big)\varPhi (\mathcal{T} ) {}\\ & =& \Big(\big(\sum _{i=1}^{N} \frac{ax_{i}} {1 + ak_{i}}\big)^{2} +\sum _{ i=1}^{N}\big( \frac{ax_{i}} {1 + ak_{i}}\big)^{2}\Big)\varPhi (\mathcal{T} ) > 0. {}\\ \end{array}$$

Therefore the Kuhn Tucker theorem applies, and the only minimum is given by the existence of a Lagrange multiplier p with $\varPhi '(\mathcal{T} ) + p{\boldsymbol 1} = 0$, ${\boldsymbol 1}$ the vector of all ones, whose only solution is $\mathcal{T} = \overline{\mathcal{T}}$, $p = a(1 + a\overline{k})^{-N-1}$.

We now consider a division $\mathcal{T}_{q}$ of geometric time steps $k_{n}:= q^{n-1}k_{1}$ for $n = 1,\ldots,N$ as it was suggested in [8]. The constraint $\sum _{n=1}^{N}k_{n} =\sum _{ n=1}^{N}q^{n-1}k_{1} = T$ fixes k ₁, and using this we get

$$\displaystyle{ k_{n} = \dfrac{q^{n}} {\sum _{j=1}^{N}q^{j}}\,T. }$$

(7)

Since according to Theorem 1 the error is minimized for q = 1, one should not choose q very different from 1, and we now study the case $q = 1+\varepsilon$ asymptotically.

Theorem 2 (Asymptotic Truncation Error Estimate)

Let $u_{N}(q):=\varPhi (\mathcal{T}_{q})u_{0}$ be the approximate solution obtained with the division $\mathcal{T}_{q}$ for $q = 1+\varepsilon$ . Then, for fixed a,T and N, the difference between the geometric mesh and fixed step mesh approximations satisfies for $\varepsilon$ small

$$\displaystyle{ \begin{array}{c} u_{N}(q) - u_{N}(1) =\alpha (aT,N)u_{0}\varepsilon ^{2} + o(\varepsilon ^{2}),\ \text{with} \\ \alpha (x,N) = \dfrac{N(N^{2} - 1)} {24} \left ( \dfrac{x/N} {1 + x/N}\right )^{2}(1 + x/N)^{-N}. \end{array} }$$

(8)

Proof

Using a second order Taylor expansion, we obtain in the following two lemmas an expansion of $\varPhi (\mathcal{T}_{1+\varepsilon })$ for small $\varepsilon$.

Lemma 1

The time step k _n in (7)has for $\varepsilon$ small the expansion $k_{n} = \overline{k}(1 +\alpha _{n}\varepsilon +\beta _{n}\varepsilon ^{2} + o(\varepsilon ^{2}))$ , with $\alpha _{n} = n -\frac{N+1} {2}$ and $\beta _{n} = n(n - N - 2) + \frac{(N+1)(N+5)} {6}$ . These coefficients satisfy the relations $\sum _{n}\alpha _{n} =\sum _{n}\beta _{n} = 0$ , $\sum _{n}\alpha _{n}^{2} = \frac{N(N-1)(N+1)} {12}$ .

Lemma 2

For $\varepsilon$ small, we have the expansion

$$\displaystyle{\prod \limits _{n=1}^{N}(1 + ak_{ n}) = (1 + a\overline{k})^{N}(1 -\frac{b^{2}} {2} \sum _{n=1}^{N}\alpha _{ n}^{2}\varepsilon ^{2} + o(\varepsilon ^{2})),\mbox{ with $b = \frac{a\overline{k}} {1+a\overline{k}}$.}}$$

We can now apply Lemma 2 to obtain $\varPhi (\mathcal{T}_{1+\varepsilon }) =\varPhi (\mathcal{T}_{1})(1 + \dfrac{b^{2}} {2} \sum _{n=1}^{N}\alpha _{n}^{2}\varepsilon ^{2} + o(\varepsilon ^{2}))$, and replacing Φ in the definition of u _N concludes the proof.

3 Error Estimate for the Diagonalization of B

The matrix B is diagonalizable if and only if all time steps k _n are different. The eigenvalues are then $\frac{1} {k_{n}}$, and the eigenvectors form a basis of $\mathbb{R}^{N}$. We will see below that the matrix of eigenvectors is lower triangular. It can be chosen with unit diagonal, in which case it belongs to a special class of Toeplitz matrices:

Definition 1

A unipotent lower triangular Toeplitz matrix of size N is of the form

$$\displaystyle{ T(x_{1},\mathop{\ldots },x_{N-1}) = \left (\begin{array}{*{10}c} 1 & &\\ x_{ 1} & \ddots & &\\ \vdots & \ddots & \ \ \ddots\ \ & \\ x_{N-1} & \ \mathop{\ldots }&x_{1} & 1 \end{array} \right ). }$$

(9)

Theorem 3 (Eigendecomposition of B)

If $k_{n} = q^{n-1}k_{1}$ as in (7), then B has the eigendecomposition $B = V DV ^{-1}$ , with $D:= \mbox{ diag}( \frac{1} {k_{n}})$ , and V and its inverse are unipotent lower triangular Toeplitz matrices given by

$$\displaystyle{ V = T(p_{1},\mathop{\ldots },p_{N-1}),\quad \mbox{ with}\quad p_{n}:= \frac{1} {\prod _{j=1}^{n}(1 - q^{j})}, }$$

(10)

$$\displaystyle{ V ^{-1} = T(q_{ 1},\mathop{\ldots },q_{N-1}),\quad \mbox{ with}\quad q_{n}:= (-1)^{n}q^{\binom{n}{2}}p_{ n}. }$$

(11)

Proof

Let $\mathbf{v}^{(n)}$ be the eigenvector with eigenvalue $\frac{1} {k_{n}}$. Since B is a lower bidiagonal matrix, a simple recursive argument shows that $v_{j}^{(n)} = 0$ for j < n. One may choose $v_{n}^{(n)} = 1$, which implies that for j > n we have $v_{j}^{(n)} = (\prod _{i=1}^{n-j}(1 -\frac{k_{n+i}} {k_{n}} ))^{-1}$, and the matrix $V = (\mathbf{v}^{(1)},\ldots,\mathbf{v}^{(N)})$ is lower triangular with unit diagonal. Furthermore, if $k_{n} = q^{n-1}k_{1}$, we obtain for $j = 1,2,\ldots,N - n$ that $v_{n+j}^{(n)} = (\prod _{i=1}^{j}(1 - q^{i}))^{-1}$ which is independent of n and thus proves the Toeplitz structure in (10).

Consider now the inverse of V. First, it is easy to see that it is also unipotent Toeplitz. To establish (11) is equivalent to prove that

$$\displaystyle{ \text{for }1 \leq n \leq N - 1,\ \sum _{j=0}^{n}p_{ n-j}q_{j} = 0,\ \text{with the convention that }p_{0} = q_{0} = 1. }$$

(12)

This result can be obtained using the q−analogue of the binomial formula, see [7]:

Theorem 4 (Simplified q−Binomial Theorem)

For any q > 0, q ≠ 1, and for any $n \in \mathbb{N}$ ,

$$\displaystyle{ \sum _{j=0}^{n}(-1)^{j}q^{\frac{j(j-1)} {2} } \frac{(1 - q^{n-j+1})\cdots (1 - q^{n})} {(1 - q)\cdots (1 - q^{j})} = 0. }$$

(13)

Multiplying (13) by p _n then leads to (12).

In the steps (a) and (c) of the direct time parallel solver (4), the condition number of the eigenvector matrix S has a strong influence on the accuracy of the results. Normalizing the eigenvectors with respect to the ℓ ² norm, $S:= V \tilde{D}$, with $\tilde{D} = diag( \frac{1} {\sqrt{1+\sum _{i=1 }^{N-n }\vert p_{i } \vert ^{2}}} )$, leads to an asymptotically better condition number:

Theorem 5 (Asymptotic Condition Number Estimate)

For $q = 1+\varepsilon$ , we have

$$\displaystyle{ \mbox{ cond}_{\infty }(V ) \sim \left ((N - 1)!\varepsilon ^{N-1}\right )^{-2}, }$$

(14)

$$\displaystyle{ \mbox{ cond}_{\infty }(S) \sim \frac{N} {\phi (N)}\varepsilon ^{-(N-1)},\quad \phi (N) = \left \{\begin{array}{@{}l@{\quad }l@{}} \frac{N} {2} !(\frac{N} {2} - 1)!\quad &\mbox{ if }N\mbox{ is even}, \\ (\frac{N-1} {2} !)^{2} \quad &\mbox{ if }N\mbox{ is odd}. \end{array} \right. }$$

(15)

Proof

Note first that $\vert q_{n}\vert \sim \vert p_{n}\vert \sim (n!\,\varepsilon ^{n})^{-1}$. Therefore

$$\displaystyle{\|V \|_{\infty } = 1 + \vert p_{1}\vert + \vert p_{2}\vert +\ldots +\vert p_{N-1}\vert \sim \vert p_{N-1}\vert \sim \left ((N - 1)!\varepsilon ^{N-1}\right )^{-1}.}$$

The same holds for V ⁻¹, and gives the first result. We next define $\gamma _{n}:= \sqrt{1 +\sum _{ j=1 }^{N-n }\vert p_{j } \vert ^{2}}$, $\tilde{d}_{n}:= \frac{1} {\gamma _{n}}$, which implies $\tilde{D} = diag(\tilde{d}_{n})$. Then $\gamma _{n} \sim \vert p_{N-n}\vert$, and we obtain

$$\displaystyle{\|S\|_{\infty } =\sup _{n}\sum _{j=1}^{n}\frac{\vert p_{n-j}\vert } {\gamma _{j}} \sim \sup _{n}\sum _{j=1}^{n} \frac{\vert p_{n-j}\vert } {\vert p_{N-n}\vert } \sim \sup _{n}\sum _{j=1}^{n}\frac{(N - j)!} {(n - j)!} \varepsilon ^{N-n} \sim N.}$$

By definition $S^{-1} =\tilde{ D}^{-1}V ^{-1} =\tilde{ D}^{-1}T(q_{1},\cdots \,,q_{N-1})$, that is the line n of T(q ₁, ⋯ , q _N−1) is multiplied by γ _n . Therefore

$$\displaystyle{\begin{array}{rcl} \|S^{-1}\|_{\infty }& =&\sup _{n}\gamma _{n}\sum _{j=0}^{n-1}\vert q_{j}\vert \sim \sup _{n}\gamma _{n}\vert q_{n-1}\vert \sim \sup _{n}\gamma _{n}\vert p_{n-1}\vert \sim \sup _{n}\vert p_{N-n}\vert \vert p_{n-1}\vert \\ &\sim &\varepsilon ^{-(N-1)}\sup _{n} \frac{1} {(n-1)!(N-n)!} \sim \frac{1} {\phi (N)}\varepsilon ^{-(N-1)}. \end{array} }$$

4 Relative Error Estimates for ODEs and PDEs

We first give an error estimate for the ODE (5):

Theorem 6 (Asymptotic Roundoff Error Estimate for ODEs)

Let $\mathbf{u}$ be the exact solution of $B\mathbf{u} =\mathbf{ f}$ , and $\hat{\mathbf{u}}$ be the computed solution from the direct time parallel solver (4)applied to (5), and u denote the machine precision. Then

$$\displaystyle{ \frac{\|\mathbf{u} -\hat{\mathbf{ u}}\|_{\infty }} {\|\mathbf{u}\|_{\infty }} \lesssim \underline{ u}\,\frac{N^{2}(2N + 1)(N + aT)} {\phi (N)} \ \varepsilon ^{-(N-1)}. }$$

(16)

Proof

In the ODE case, $D = diag( \frac{1} {k_{n}} + a)$ and $\|D\|_{\infty } = 1/k_{1} + a$. Using backward error analysis [6], the computed solution satisfies the perturbed systems

$$\displaystyle{(S +\delta S_{1})\hat{\mathbf{g}} =\mathbf{ f},\quad (D +\delta D)\hat{\mathbf{w}} =\hat{\mathbf{ g}},\quad (S^{-1} +\delta S_{ 2})\hat{\mathbf{u}} =\hat{\mathbf{ w}},}$$

and since S and S ⁻¹ are triangular and D is diagonal we get (see [6])

$$\displaystyle{\|\delta S_{1}\| \leq N\underline{u}\|S\| + \mathcal{O}(\underline{u}^{2}),\quad \|\delta S_{ 2}\| \leq N\underline{u}\|S^{-1}\| + \mathcal{O}(\underline{u}^{2}),\quad \|\delta D\| \leq \underline{ u}\|D\| + \mathcal{O}(\underline{u}^{2}).}$$

Using Algorithm (4) to solve $B\mathbf{u} =\mathbf{ f}$ by decomposition is equivalent to solving $(S +\delta S_{1})(D +\delta D)(S^{-1} +\delta S_{2})\ \hat{\mathbf{u}} =\mathbf{ f}$, which is of the form

$$\displaystyle{(B +\delta B)\hat{\mathbf{u}} =\mathbf{ f},\quad \|\delta B\| \leq (2N + 1)\underline{u}\|S\|\|S^{-1}\|\|D\| + \mathcal{O}(\underline{u}^{2}).}$$

The relative error then satisfies (see [6])

$$\displaystyle{\frac{\|\mathbf{u} -\hat{\mathbf{ u}}\|} {\|\mathbf{u}\|} \leq \mbox{ cond}(B)\frac{\|\delta B\|} {\|B\|} \leq (2N + 1)\underline{u}\ \|B^{-1}\|\,\|S\|\,\|S^{-1}\|\,\|D\|.}$$

By a direct computation, we obtain for the inverse of B

$$\displaystyle{B^{-1} = k_{ 1}\left (\begin{array}{*{10}c} \ 1\ & &\\ 1 &\ q\ & & \\ 1& \vdots &\ q^{2}\ \\ \vdots & \vdots & \vdots & \ddots \\ 1&q&q^{2} & \mathop{\ldots }&\ q^{N-1} \end{array} \right ),}$$

and hence $\|B^{-1}\|_{\infty } = k_{1}(1 + q + \mathop{\ldots }q^{N-1}) \sim Nk_{1}$. Since $k_{1} \sim \overline{k} = T/N$, (16) is proved.

The error of the direct time parallel solver at time T can be estimated by

$$\displaystyle{ \frac{\vert e^{-aT}u_{0} -\hat{ u}_{N}\vert } {\vert u_{0}\vert } \leq \frac{\vert e^{-aT}u_{0} - u_{N}(1)\vert } {\vert u_{0}\vert } + \frac{\vert u_{N}(1) - u_{N}(q)\vert } {\vert u_{0}\vert } + \frac{\vert u_{N}(q) -\hat{ u}_{N}\vert } {\vert u_{0}\vert }. }$$

(17)

The first term on the right is the truncation error of the sequential method using equal time steps. The second term is due to the geometric mesh and was estimated asymptotically in Theorem 2 to be $\alpha \varepsilon ^{2}$. The last term can be estimated by $\|\mathbf{u}(q) -\hat{\mathbf{ u}}\|_{\infty }/\vert u_{0}\vert$ and thus Theorem 6, since a > 0 which implies $\vert u_{0}\vert =\|\mathbf{ u}\|_{\infty }$. Because the second term is decreasing in $\varepsilon$ and the last term is growing in $\varepsilon$, we equilibrate them asymptotically:

Theorem 7 (Optimized Geometric Time Mesh)

Suppose the time steps are geometric, $k_{n} = q^{n-1}k_{1}$ , and $q = 1+\varepsilon$ with $\varepsilon$ small. Let u be the machine precision. For $\varepsilon =\varepsilon _{0}(aT,N)$ with

$$\displaystyle{ \varepsilon _{0}(aT,N) = \left (\underline{u}\frac{N^{2}(2N + 1)(N + aT)} {\phi (N)\alpha (aT,N)} \right )^{ \frac{1} {N+1} }, }$$

(18)

where α(aT,N) is defined in (8) and ϕ(N) in (15), the error due to time parallelization is asymptotically comparable to the one produced by the geometric mesh.

Proof

This is a direct consequence of Theorem 6.

We show in Fig. 1 on the left the optimized value $\varepsilon _{0}(aT,N)$ from Theorem 7.

Fig. 1

Optimized choice $\varepsilon _{0}(aT,N)$ from Theorem 7 (left). Ratio of the additional errors due to parallelization to the truncation error of the fixed step method (17) with this choice of $\varepsilon _{0}(aT,N)$ (right)

Choosing $\varepsilon =\varepsilon _{0}(aT,N)$, the ratio between the additional errors due to parallelization to the truncation error of the fixed time step method is shown in Fig. 1 on the right.

In order to obtain a PDE error estimate for the heat equation (1), one can argue as follows: expanding the solution in eigenfunctions of the Laplacian, we can apply our results for the ODE with $a =\lambda _{\ell}$, $\lambda _{\ell}$ for ℓ = 1, 2, … the eigenvalues of the negative Laplacian. One can show for all N ≥ 1 and machine precision u small enough (single precision suffices in practice) that our error estimate (17) has its maximum for $aT < a_{T}^{{\ast}} = 2.5129$, and thus if $\lambda _{\min }$ and T are such that $\lambda _{\min }T > a_{T}^{{\ast}}$, one can read off the optimal choice $\varepsilon _{0}$ and resulting error estimate in Fig. 1 at $aT =\lambda _{\min }T$ for a given number of processors N. Similarly, if we have N processors and do not want to increase the error compared to a sequential computation by more than a given factor, we can read in Fig. 1 on the right the size of the time window T to use (knowing $a =\lambda _{\min }$), and the corresponding optimized $\varepsilon _{0}$ on the left.

5 Numerical Experiments

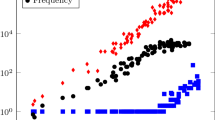
We first perform a numerical experiment for the scalar model problem (5) with a = 1, T = 1 and N = 10. We show in Fig. 2 on the left

Fig. 2

Discretization and parallelization errors, and condition number of the eigenvector matrix, together with our theoretical bounds, left for the ODE, right for the PDE

how the discretization error increases and the parallelization error decreases as a function of $\varepsilon$, together with our theoretical estimates, and also the condition number of the eigenvector matrix, and our theoretical bound. We can see that the theoretically predicted optimized $\varepsilon$ marked by a rhombus is a good estimate, and on the safe side, of the optimal choice a bit to the left, where the dashed lines meet.

We next show an experiment for the heat equation in two dimensions on the unit square, with homogeneous Dirichlet boundary conditions and an initial condition $u_{0}(x,y) =\sin (\pi x)\sin (\pi y)$. We discretize with a standard five point finite difference method in space with mesh size $h_{1} = h_{2} = \frac{1} {10}$, and a Backward Euler discretization in time on the time interval $(0, \frac{1} {5})$ using N = 30 time steps. In Fig. 2 on the right we show again the measured discretization and parallelization errors compared to our theoretical bounds. As one can see from the graph, in this example, one could solve the problem using 30 processors, and would obtain an error which is within a factor two of the sequential computation.