Note to an Undercut Limit of Involute Gearing

Abstract

An undercut of an involute tooth flank is a routine matter. Moreover there is no need to be concerned with an undercut if there is no problem with teeth strength. A problem occurs if undercutting strikes not only a root but an involute flank too. It even does not matter until an operational part of an involute is not cut off. In this case the size of decreasing of a transverse ratio coefficient ε_α is necessary to specify. This contribution deals with two approaches to the determination of start of undercut involute and performs their evaluation with possible implications. At the conclusion the contribution is highlighting to one unpublished fact.

1 Undercut Limit

An undercut limit is simply determined for the case when the end point of a linear edge of a tool L “meshes” with an involute just in its beginning on a base circle – see Fig. 1. For this situation it is easy to derive a number of teeth at the undercut limit and needed minimum addendum shifting coefficient (for achieving of the undercut limit).

Fig. 1

Undercut limit

$$ {z}_{mez}=\frac{2\cdot \cos \beta }{{ \sin}^2{\alpha}_t}\cdot \left({h}_{a0}^{*}-{c}_{a0}^{*}-x\right) $$

(1)

$$ {x}_{mez}={h}_{a0}^{*}-{c}_{a0}^{*}-z\cdot \frac{{ \sin}^2{\alpha}_t}{2\cdot \cos \beta } $$

(2)

2 Start of an Undercut Involute (the Usual Way)

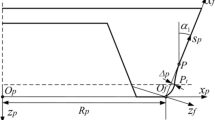
Once the end point of a linear edge of a tool L “meshes” under point N – undercutting takes place. Thereby a truncation of an involute above a base circle occurs. A guideline how to determine a diameter of a start of an undercut involute is presented in [1] and [2]. An influence of a rounded tool crest is not considered. The system of three transcendental equations is solved. This must be carried out numerically. See Fig. 2 end Eqs. (3), (4) and (5).

Fig. 2

Start of an undercut involute (the usual way)

$$ \frac{d}{d_b}-\frac{y}{0,5\cdot {d}_b}-\frac{d_L}{d_b}\cdot \cos \left({\alpha}_t+\beta +inv\kern0.5em \delta \right)=0 $$

(3)

$$ \frac{d_L}{d_b}-\frac{\beta }{ \sin \left(\beta +inv\kern0.5em \delta \right)}=0 $$

(4)

$$ \tan \left( \arccos \frac{d_b}{d_L}\right)- \arccos \frac{d_b}{d_L}-inv\kern0.5em \delta =0 $$

(5)

3 Exact Start of an Undercut Involute

Although one might expect that a rounded tool crest, which turns aside from a linear edge of a tool, will not cause further undercutting – so contrary is the case. This rounding (which is creating a tooth fillet) cuts off in addition a part of involute indeed, which has already been undercut by a linear edge of a tool. Two curves are seen on the Fig. 3. Curve k_L is manufactured by an end point of a linear edge of a tool. The second one labelled as k_p is a fillet curve which is manufactured by a rounded tool crest (an envelope of its positions). It is seen that an additional undercutting really takes place. This truncation is otherwise very small but when accurate calculations are making, it is necessary to take it into account.

Fig. 3

Two curves

Finding of a point of intersection between a curve k_p and an involute is rather difficult. The most commonly used technique is finding such a diameter (bigger than d_b) for which thicknesses on the involute s_e and on the fillet curve s_p have the same size, see Fig. 4. Only one solution exists above a base diameter. It is important to realize that a rounded tool crest will change into ellipse in transverse section in which the solving is made. A fillet curve k_p is an envelope of this ellipse discrete positions.

Fig. 4

Comparing of thicknesses

Except this method there is another method for finding of a point of intersection between a curve k_p and an involute. This method is published among others in the standard ISO 6336, part 2, Annex A [3]. Analysis there is made in polar coordinates. But potential user must be warn of quite a number of typing errors and mistakes in equations and figures.

4 Magnitude of the Difference of Undercutting Between Both Methods

Accuracy of the calculation for both methods will be shown in two examples. The standard basic profile will be used (Table 1).

Table 1 Two examples

Differences are practically insignificant. It is possible to use the first simpler method for routine tasks. Its sufficiency is verified in practice. However be aware that the slightest change of a diameter evokes a substantially greater change in a position on a meshing line. For high accurate calculations (contact stresses) it is necessary to use the second method. This method is exactly accurate. Its accuracy was proved by CAD drawing, see Fig. 5. The diameter d_L obtained by this method is 19,854637 mm.

Fig. 5

CAD verification

5 Conclusion

It would seem that the difference between both calculation methods is insignificant. And it is true in the majority of cases (Figs. 6 and 7). But for some FEM calculations it is necessary to know the absolutely precise tooth form. Also for precise geometry calculations it needs to be concern with it. Very interesting thing is that well known Eqs. (1) and (2) are thereby inaccurate ones because they are derived using the first not very precise method. As long as a designer must know the undercut limit exactly, he must calculate with an additional undercutting (although relatively small one) of an involute and thus with slightly different results.

Fig. 6

z = 10, β = 0, x = −0.2

Fig. 7

z = 20, β = 20, x = −0.6