Modeling Perspectives of Hybrid Systems and Network Systems

Abstract

This article presents two topics, i.e., well-posedness of piecewise affine systems, and model reduction of network systems. The well-posedness problem, i.e., the problem of existence and uniqueness of solutions, of hybrid systems is one of the fundamental research topics, which the first author has collaborated with Prof. Arjan van der Schaft in 1998. Some results are revisited by focusing on the class of bimodal piecewise affine systems. The latter discusses the most recent topic that both Arjan and the first author have common interest in. In particular, the clustering-based $H_\infty -$ and $H_2$-model reduction approaches of large-scale network systems, which have been independently developed by the authors, are represented in a unified way.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

I, the first author, has started with research topics on hybrid systems since I stayed in Twente University for one year from May 1998 as a visiting researcher under Professor Arjan van der Schaft. In those days, Arjan tried to publish a book entitled “An Introduction to Hybrid Dynamical Systems” with van der Schaft and Schumacher [1]. I had a lucky opportunity to read this first draft with great interest. In particular, the concept of complementarity systems and its well-posedness problem were very impressive for me, and started with the well-posedness problem of bimodal piecewise linear systems together with Arjan [2, 3]. Since then, this topic brought me various kinds of results on modeling, analysis, and control synthesis of hybrid systems including feedback well-posedness and stabilizability of piecewise affine systems [4, 5], controllability analysis of piecewise affine systems [6, 7], discrete abstraction of nonlinear systems [8], and so on. The first part of this article revisits the well-posedness issue of hybrid systems, which I look back with valuable collaboration with Arjan.

The second part focuses on more recent topic of model reduction of large-scale network systems, which recently gave common interest to Arjan and myself. Throughout the study of discrete abstraction of nonlinear systems, which produces a kind of graph structure for approximately expressing complex system behavior based on bisimilarity notation, I and my colleagues also had great interest in model reduction of large-scale network systems. We thus have developed a clustering-based approach in the framework of projective model reduction [9–12], which we call clustered model reduction. This is also a kind of structure-preserving model reduction methods. On the other hand, for the concept of the port-controlled Hamiltonian systems preserving the essential property of physical structure, proposed by Arjan and B.M. Maschke (e.g., [13, 14]), the problem of model reduction preserving such physical structure is naturally and relevantly induced. Most recently, Arian and his colleagues have solved this problem by a clustering framework, where the strict $H_2$ norm-approximation-error evaluation and an extension to the case of second-order systems are provided [15, 16]. This result is also based on the research works by H. Trentleman and his colleagues [17]. The second part of this article provides a summary on our previous results including $H_2/H_\infty$-norm-error evaluation and extensions to the case of second-order subsystems in a unified way. We hope this unified approach will provide any further common framework with the works by Arjan, Harry, and their colleagues. In addition, as an application of clustered model reduction, we present our recent result on the design of a projective state observer, which estimates the average state behavior of large-scale network systems according to the above clustered model reduction [18]. Numerical simulations on power systems show that the method is effective.

Notation We denote the set of real numbers by $\mathbb {R}$, the n-dimensional identity matrix by $I_{n}$, the ith column of $I_{n}$ by $e_{i}$, the cardinality of a set $\mathcal {I}$ by $|\mathcal {I}|$, the $l_p$-norm of a vector x by $\Vert x\Vert _{l_p}$, the Frobenius norm of a matrix M by $\Vert M\Vert _\mathrm{F}$, the $l_{2}$-induced norm of a matrix M by $\Vert M\Vert$, and the $l_{\infty }$-induced norm of a matrix $M\in \mathbb {R}^{n\times m}$ is defined by

$$\begin{aligned} \Vert M\Vert _{l_{\infty }}:=\max _{i\in \{1,\ldots ,n\}}\sum _{j=1}^{m}|M_{i,j}| \end{aligned}$$

where $M_{i,j}$ denotes the (i, j)-element of M. The positive (negative) definiteness of a matrix $M=M^T$ is denoted by $M\succ 0 (M \prec 0)$. Furthermore, we denote the block diagonal matrix having matrices $M_{1},\ldots ,M_{n}$ on its block diagonal by $\mathrm{diag}(M_{1},\ldots ,M_{N})$. Finally, the $\mathcal {H}_{\infty }$-norm and $\mathcal {H}_{2}$-norm of a stable transfer matrix G are denoted by $\Vert G(s)\Vert _{\mathcal {H}_{\infty }}$ and $\Vert G(s)\Vert _{\mathcal {H}_{2}}$, respectively.

Fig. 8.1

2-tank system with a valve

Fig. 8.2

Trajectories for the system in Fig. 8.1

8.2 Revisit: Well-Posedness of Piecewise Affine Systems

8.2.1 Motivating Example

Consider a 2-tank system in Fig. 8.1, where $x_i$ is the deviation of the water level from the equilibrium state $x_{ie}$, and $u_{i}$ is the volume of water discharged from the tap i. We assume that $u_{i}$ is an input, i.e., $u_{i}=u_{ie}$, where $u_{ie}$ is constant, and the valve at the tap is open or closed according to the rule shown in Fig. 8.1. Equations of motion of this system are given by

$$\begin{aligned} \dot{x}&= \left\{ \begin{array}{ll} \left[ \begin{array}{cc} -1 &{} 0 \\ 1 &{} -1 \end{array}\right] x &{} \text{ if } x_2\le 1\\ \left[ \begin{array}{cc} 0 &{} 0 \\ 0 &{} -1 \end{array}\right] x+ \left[ \begin{array}{c} u_{1e} \\ -u_{1e} \end{array}\right]&\text{ if } x_2> 1 \end{array} \right. \end{aligned}$$

(8.1)

where $x=[x_1,x_2]^T$. The coefficients are normalized to 1 for brevity, and the equilibrium state and input satisfy $-x_{1e}+u_{1e}=0$, $-x_{2e}+x_{1e}+u_{2e}=0$, $x_{1e}>0$, and $0<x_{2e}<1$. Although this tank system is nonlinear, we here consider the linearization of the system at the equilibrium since the solution behavior will be essentially similar to that of the original system.

Figure 8.2 shows trajectories of the system from six different initial states. There exists a sliding motion when $x(0)=[2\ \ 2]^\mathsf{T}$ and $[2\ \ 0.8]^\mathsf{T}$, where, in fact, chattering phenomena happen due to numerical simulation. Since we consider the Open/Closed motion of the valve in this case, such phenomena is not desirable. It is important to specify a condition on discontinuity of the vector field to avoid such phenomena. The next section gives a solution to this question.

8.2.2 Well-Posedness Condition

Consider the discontinuous system

$$\begin{aligned} \dot{x}=f_{I}(x) \text{ if } x\in \mathcal{X}_{I},\ \ I\in \mathcal{I}, \end{aligned}$$

(8.2)

where $x\in \mathbb {R}^n$, $\mathcal{I}=\{1,2,\ldots ,M\}$, and $\mathcal{X}_I$ is a closed subset of $\mathbb {R}^n$ satisfying

$$ \text{ int }{}\mathcal{X}_I\ne \emptyset , \ \ \bigcup _{I=1}^{M}\mathcal{X}_{I}=\mathbb {R}^{n}, \ \ \text{ int }{}\mathcal{X}_{I} \bigcap \text{ int }{}\mathcal{X}_J=\emptyset . $$

Then a solution of this system is defined as follows:

Definition 8.1

(Extended Carathéodory solution) Suppose that an initial state $x(t_0){=}x_0\in \mathbb {R}^n$ is given. Then if on $[t_0,t_1)$ for some $t_1>t_0$, x(t) satisfies

$$\begin{aligned} x(t)=x_0+\int _{t_0}^{t} f_{I(\tau )}(x(\tau ))d\tau , \end{aligned}$$

(8.3)

and there is no left accumulation point of event times, x(t) is said to be a solution of (8.2) on $[t_0,t_1)$ in the sense of Carathéodory for $x(t_0)=x_0$.

Note that this notion of solutions does not admit sliding motions and left-Zeno behavior, although the right-Zeno behavior is regarded as a solution. The system (8.2) is said to be well-posed if for every initial state $x(t_0)\in \mathbb {R}^{n}$, there exists a right unique extended Caratéodory solution of (8.2) on $[t_0,\infty )$.

The notion of smooth continuation is very important for characterizing the well-posedness property [19]. Consider a solution of $\dot{x}=f_{I}(x)$ in (8.2) with a fixed I. If for an initial state $x(t_0)=x_0$ there exists an $\varepsilon >0$ such that $x(t)\in \mathcal{X}_{I}$ for all $t\in [0,\varepsilon ]$, we say that smooth continuation is possible from $x_0$ in $\mathcal{X}_{I}$. Furthermore, we call the smooth continuation set, denoted by $\mathcal{S}_{I}$, the set of all $x_0$ from which smooth continuation is possible in $\mathcal{X}_{I}$.

Obviously $\mathcal{S}_{I}\subseteq \mathcal{X}_{I}$ holds, and the smooth continuation set $\mathcal{S}_{I}$ expresses the region of existence of solutions x(t) of the system, while the difference set $\mathcal{X}_{I}-\mathcal{S}_{I}$ expresses all the state from which there exists no solution x(t).

Then we have the following theorem [3]:

Theorem 8.2

The system (8.2) is well-posed if and only if the following two conditions:

(a):

$\bigcup _{I\in \mathcal{I}} \mathcal{S}_{I} =\mathbb {R}^n$.

(b):

For every $I_1,\ I_2\in \mathcal{I}$, there exists an $\varepsilon >0$ such that both solutions x(t) of $\dot{x}=f_{I}(x)$, $I=I_1, I_2$ are the same on $[t_0,t_0+\varepsilon )$ for every $x_0\in \mathcal{S}_{I_1}\bigcap \mathcal{S}_{I_2}$.

To derive an explicit representation of the above conditions, consider

$$\begin{aligned} \dot{x}&= \left\{ \begin{array}{ccc} A_1 x &{} \text{ if } Cx\ge 0, \\ A_2 x &{} \text{ if } Cx\le 0. \end{array} \right. \end{aligned}$$

(8.4)

Denote by $T_{1}$ and $T_{2}$ the observability matrices of $(C,A_1)$ and $(C,A_2)$, respectively, and by $m_1$ and $m_2$ their observability indexes. We also let $\mathcal{L}_{+}$ be the set of $n \times n$ lower triangular matrices with all diagonal elements positive. Then, the conditions (a) and (b) in Theorem 8.2 are reduced into the following conditions [3]:

Theorem 8.3

The system (8.4) is well-posed if and only if the following conditions hold:

(a):

$m_1=m_2$,

(b):

$T_2=M T_1$ for some $M\in \mathcal{L}_{+}$,

(c):

$(A_1-A_2)x=0$ for all $x\in \text{ Ker }T_1$.

 

The smooth continuation set for $\mathcal{X}_1:=\{ x\in \mathbb {R}^n\ |\ Cx\ge 0\}$ is given by $\mathcal{S}_{1}=\{ x\in \mathbb {R}^n\ |\ T_{1}x\succeq 0\}$, where $x\succeq 0$ expresses the lexicographic inequality, i.e., for each i, $x_j=0$ $(j=1,2,\ldots ,i-1)$ and $x_i>0$, or $x=0$. This comes from the fact that for sufficiently $\varepsilon >0$, $y(t)(:=Cx(t))=y(t_0)+\dot{y}(t_0)(t-t_0)+\ddot{y}(t_0)(t-t_0)^2+\cdots \ge 0$ holds for all $t\in [t_0,t_0+\varepsilon )$. Thus $\mathcal{S}_1\bigcup \mathcal{S}_2=\mathbb {R}^{n}$, which corresponds to condition (a) in Theorem 8.2, implies condition (b) in Theorem 8.3. Conditions (a) and (c) in Theorem 8.3 come from condition (b) in Theorem 8.2.

Note that the above conditions can be easily checked. A similar but rather complicated necessary and sufficient condition can be obtained for bimodal piecewise affine systems [4], and a sufficient condition for a multimodel piecewise affine system with external inputs to be well-posed can be also obtained [5]. In addition, the feedback well-posedness condition, which implies that the system can be made well-posed by a feedback controller, can be characterized for bimodal piecewise affine systems [4].

8.3 Clustered Model Reduction of Network Systems

In this section, we briefly summarize our clustered model reduction method for linear network systems, which belongs to a type of structured model reduction methods. In this model reduction, toward the preservation of network structure of systems, clustering of subsystems is performed according to a notion of uncontrollability of local states, called cluster reducibility. All mathematical proofs of theoretical results are omitted due to page limitation; see [9–12] for details.

8.3.1 Clustered Model Reduction Problem

We first deal with a stable linear network system denoted by

$$\begin{aligned} \varSigma :\dot{x}=Ax+Bu,\quad A\in \mathbb {R}^{n\times n},\quad B\in \mathbb {R}^{n}, \end{aligned}$$

(8.5)

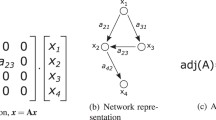
whose network structure is represented by the Boolean structure of A. For simplicity, we consider only single-input systems while a similar result can be obtained also for multi-input systems. To formulate a clustered model reduction problem for $\varSigma$ in (8.5), we introduce the following notion of network clustering:

Definition 8.4

For $\mathbb {L}:=\{1,\ldots ,L\}$, the family of an index set, $\{\mathcal {I}_{[l]}\}_{l\in \mathbb {L}}$, is called a cluster set, each of whose elements is referred to as a cluster, if each element $\mathcal {I}_{[l]}\subseteq \{1,\ldots ,n\}$ satisfies

$$ \bigcup _{l\in \mathbb {L}}\mathcal {I}_{[l]}=\{1,\ldots ,n\},\quad \mathcal {I}_{[l]}\cap \mathcal {I}_{[l^{\prime }]}=\emptyset ,\quad l\ne l^{\prime }. $$

Furthermore, an aggregation matrix compatible with $\{\mathcal {I}_{[l]}\}_{l\in \mathbb {L}}$ is defined by

$$\begin{aligned} P:=\varPi \mathrm{diag}(p_{[1]},\ldots ,p_{[L]})\in \mathbb {R}^{n\times L}, \end{aligned}$$

(8.6)

where $p_{[l]}\in \mathbb {R}^{|\mathcal {I}_{[l]}|}$ such that $\Vert p_{[l]}\Vert =1$, and the permutation matrix $\varPi$ is defined as

$$ \varPi :=[e_{\mathcal {I}_{[1]}},\ldots ,e_{\mathcal {I}_{[L]}}]\in \mathbb {R}^{n\times n},\quad e_{\mathcal {I}_{[l]}}\in \mathbb {R}^{n\times |\mathcal {I}_{[l]}|}. $$

In this definition, the aggregation matrix P clearly satisfies $P^\mathsf{T}P=I_{L}$, i.e., all column vectors of P are orthonormal. Using the aggregation matrix P in (8.6), we define the aggregated model of $\varSigma$ in (8.5) by

$$\begin{aligned} \hat{\varSigma }: \left\{ \begin{array}{cl} \dot{\xi }&{}=P^\mathsf{T}AP{\xi }+P^\mathsf{T}Bu\\ \hat{x}&{}=P\xi . \end{array} \right. \end{aligned}$$

(8.7)

Note that each state of the aggregated model $\hat{\varSigma }$ represents an approximant of the clustered states, given by $e_{\mathcal {I}_{[l]}}^{\mathsf{T}}x\in \mathbb {R}^{|\mathcal {I}_{[l]}|}$. The trajectory of each state of $\hat{\varSigma }$ aims at tracing the trajectory of a kind of centroid compatible with the clustered states of $\varSigma$. In this notation, we formulate a clustered model reduction problem as follows:

Probelm 8.5

Let a stable linear system $\varSigma$ in (8.5) be given. Given a constant $\varepsilon \ge 0$, find a stable aggregated model $\hat{\varSigma }$ in (8.7) such that

$$\begin{aligned} \Vert G(s)-\hat{G}(s)\Vert _{\mathcal {H}_{2}}\le \varepsilon \quad \mathrm{or}\quad \Vert G(s)-\hat{G}(s)\Vert _{\mathcal {H}_{\infty }}\le \varepsilon , \end{aligned}$$

(8.8)

where

$$\begin{aligned} G(s):=(sI_{n}-A)^{-1}B,\quad \hat{G}(s):=P(sI_{L}-P^{\mathsf{T}}AP)^{-1}P^{\mathsf{T}}B \end{aligned}$$

(8.9)

denote the transfer matrices of $\varSigma$ and $\hat{\varSigma }$, respectively.

In traditional model reduction methods, each state of the reduced model is usually obtained as a linear combination of all states of the original system [20]. This can be rephrased as that the projection matrix has no specific sparse structure. Note that the aggregation matrix P in (8.6) is block-diagonally structured. In this sense, our problem formulation clearly contrasts with the traditional model reduction problems.

8.3.2 Controllability Characterizations for Clustered Model Reduction

In systems and control theory, $\varSigma$ in (8.5) is said to be controllable if there exists an input function u such that the state x is moved from any initial state to any other final state in a finite time interval. One best-known characterization of controllability is the Kalman rank condition, i.e., $\varSigma$ is controllable if and only if $[B,AB,\ldots ,A^{n-1}B]$ has full row rank [20]. However, the Kalman rank condition is not necessarily useful for model reduction because it cannot capture the controllability of systems quantitatively. Such a quantitative characterization of controllability plays an important role in performing an approximation error analysis in model reduction.

In view of this, let us seek some other characterizations of controllability that have good compatibility with model reduction. One of useful controllability characterizations is given by the controllability Gramian, related to the $\mathcal {H}_{2}$-norm of linear systems. It is known that a stable linear system $\varSigma$ in (8.5) is controllable if and only if the controllability Gramian, defined as

$$\begin{aligned} M:=\displaystyle \int _{0}^{\infty }e^{At}B(e^{At}B)^\mathsf{T}dt\in \mathbb {R}^{n\times n}, \end{aligned}$$

(8.10)

is nonsingular. It will turn out below that this characterization based on the controllability Gramian can be used to evaluate the approximation error of clustered model reduction in terms of the $\mathcal {H}_{2}$-norm.

To devise a controllability characterization compatible with the $\mathcal {H}_{\infty }$-norm, we provide the following lemma that gives a particular realization of $\varSigma$, called the controller-Hessenberg form:

Lemma 8.6

For any linear system $\varSigma$ in (8.5), there exists a unitary matrix $H\in \mathbb {R}^{n\times n}$ such that $\mathfrak {A}:=H^{\mathsf{T}}AH\in \mathbb {R}^{n\times n}$ and $\mathfrak {B}:=H^{\mathsf{T}}B\in \mathbb {R}^{n}$ are in the form of

$$\begin{aligned} \mathfrak {A}=\left[ \begin{array}{ccccc} \alpha _{1,1}&{}\alpha _{1,2}&{}\cdots &{}\cdots &{}\alpha _{1,n}\\ \alpha _{2,1}&{}\alpha _{2,2}&{}\alpha _{2,3}&{}\cdots &{}\alpha _{2,n}\\ 0&{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ \vdots &{}\ddots &{}\ddots &{}\ddots &{}\vdots \\ 0&{}\cdots &{}0&{}\alpha _{n,n-1}&{}\alpha _{n,n} \end{array}\right] ,\quad \mathfrak {B}=\left[ \begin{array}{cccc}\beta _{1}\\ 0\\ 0\\ \vdots \\ 0\end{array}\right] . \end{aligned}$$

(8.11)

Furthermore, the dimension of the controllable subspace of $\varSigma$ is given by

$$\begin{aligned} \nu := \left\{ \begin{array}{cl} \displaystyle \displaystyle \min _{i\in \{1,\ldots ,n-1\}}\{i:\alpha _{i+1,i}=0\},&{}\quad \mathrm{if}\quad \textstyle {\prod _{i=1}^{n-1}\alpha _{i+1,i}}=0,\\ n,&{}\quad \mathrm{otherwise}. \end{array}\right. \end{aligned}$$

(8.12)

Note that the controller-Hessenberg form of $\varSigma$ in Lemma 8.6 has the serially cascaded structure as shown in (8.11). From this particular structure, it follows that $\varSigma$ is controllable if and only if $\alpha _{i+1,i}\ne 0$ for all $i\in \{1,\ldots ,n-1\}$. Controllability characterizations in the following lemma will be used to give a solution to Problem 8.5:

Lemma 8.7

Let a stable linear system $\varSigma$ in (8.5) be given. For the controllability Gramian M in (8.10), define $\varPhi _{\mathcal {H}_{2}}\in \mathbb {R}^{n\times n}$ such that $M=\varPhi _{\mathcal {H}_{2}}\varPhi _{\mathcal {H}_{2}}^\mathsf{T}$. Furthermore, for $\mathfrak {A}$ and $\mathfrak {B}$ with H in Lemma 8.6, define

$$\begin{aligned} \varPhi _{\mathcal {H}_{\infty }}:=H\mathrm{diag}(\gamma _{1},\ldots ,\gamma _{n})\in \mathbb {R}^{n\times n},\quad \gamma _{i}:=\left\| e_{i}^{\mathsf{T}}(sI_{n}-\mathfrak {A})^{-1}\mathfrak {B}\right\| _{\mathcal {H}_{\infty }}. \end{aligned}$$

(8.13)

Then, $\varSigma$ is controllable if and only if $\varPhi _{\mathcal {H}_{p}}$ is nonsingular, where $p=2$ or $p=\infty$.

8.3.3 Clustered Model Reduction Theory

8.3.3.1 Exact Clustered Model Reduction

In this subsection, we first consider the case where no approximation error is caused by the cluster aggregation. To do this, we introduce the following notion of the reducibility of clusters:

Definition 8.8

Let a linear system $\varSigma$ in (8.5) be given. A cluster $\mathcal {I}_{[l]}$ is said to be reducible if there exist a scalar rational function $G^{\star }_{[l]}$ and a vector $\eta _{[l]}\in \mathbb {R}^{|\mathcal {I}_{[l]}|}$ such that

$$\begin{aligned} e_{\mathcal {I}_{[l]}}^{\mathsf{T}}G(s)=\eta _{[l]}G^{\star }_{[l]}(s), \end{aligned}$$

(8.14)

where G is defined as in (8.9).

This definition of cluster reducibility represents that the states corresponding to $\mathcal {I}_{[l]}$ have the same trajectories for all input signals. The following theorem shows that the cluster reducibility can be characterized by a kind of local singularity of $\varPhi _{\mathcal {H}_{p}}$ defined in Lemma 8.7:

Theorem 8.9

Let a stable linear system $\varSigma$ in (8.5) be given. With the same notation as that in Lemma 8.7, a cluster $\mathcal {I}_{[l]}$ is reducible if and only if there exist $\phi ^{\star }_{[l]}\in \mathbb {R}^{1\times n}$ and $\eta _{[l]}\in \mathbb {R}^{|\mathcal {I}_{[l]}|}$ such that

$$\begin{aligned} e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{p}}=\eta _{[l]}\phi ^{\star }_{[l]}, \end{aligned}$$

(8.15)

where $p=2$ or $p=\infty$. In addition, if $\mathcal {I}_{[l]}$ is reducible, then $\eta _{[l]}$ coincides with a multiple of $-e_{\mathcal {I}_{[l]}}^{\mathsf{T}}A^{-1}B$. Moreover, if all clusters are reducible, then the aggregated model $\hat{\varSigma }$ in (8.7) given by $p_{[l]}=\Vert \eta _{[l]}\Vert ^{-1}\eta _{[l]}$ is stable and satisfies

$$\begin{aligned} G(s)=\hat{G}(s), \end{aligned}$$

(8.16)

where G and $\hat{G}$ are defined as in (8.9).

Theorem 8.9 shows that the cluster reducibility is characterized by linear dependence among the row vectors of $\varPhi _{\mathcal {H}_{p}}$. However, the cluster reducibility is generally restrictive for the reduction of dimensions. This is because it represents a kind of structured uncontrollability representing that the controllable subspace of $e_{\mathcal {I}_{[l]}}^{\mathsf{T}}x$ is one-dimensional.

8.3.3.2 Approximation Error Evaluation for Clustered Model Reduction

In what follows, aiming at more significant dimension reduction, we consider the case where a degree of approximation errors is caused by cluster aggregation. In this situation, even if the original system $\varSigma$ in (8.5) is stable, the aggregated model $\hat{\varSigma }$ in (8.7) is not necessarily stable. In clustered model reduction, the stability preservation is to be guaranteed on the basis of the following two facts:

Lemma 8.10

Let a stable linear system $\varSigma$ in (8.5) be given. If

$$\begin{aligned} A+A^\mathsf{T}\prec 0, \end{aligned}$$

(8.17)

then the aggregated model $\hat{\varSigma }$ in (8.7) is stable for any cluster set $\{\mathcal {I}_{[l]}\}_{l\in \mathbb {L}}$.

Lemma 8.11

Let $A\in \mathbb {R}^{n\times n}$ be such that

$$\begin{aligned} \textit{DA}+A^\mathsf{T}D\prec 0 \end{aligned}$$

(8.18)

for a diagonal matrix $D\succ 0$. Then

$$\begin{aligned} \tilde{A}+\tilde{A}^\mathsf{T}\prec 0,\quad \tilde{A}:=D^{\frac{1}{2}}\textit{AD}^{-\frac{1}{2}}, \end{aligned}$$

(8.19)

where $D^{\frac{1}{2}}\succ 0$ is a diagonal matrix whose diagonal elements are the square roots of those of D.

Lemma 8.10 shows that, if A is negative definite as in (8.17), the stability of aggregated models can be guaranteed for any choice of cluster sets. Furthermore, Lemma 8.11 shows that any stable system having a diagonal Lyapunov function as in (8.18) is diagonally similar to a system having a negative definite system matrix as in (8.19). Note that a similarity transformation (coordinate transformation) by a diagonal matrix does not break the network structure, i.e., the Boolean structure, of the original system. Thus, by combining Lemmas 8.10 and 8.11, we can theoretically guarantee the stability preservation in clustered model reduction for the class of systems having diagonal Lyapunov functions.

In the following, focusing especially on this class of stable network systems, we analyze the approximation error in clustered model reduction. To this end, we introduce a weaker notion of cluster reducibility as follows:

Definition 8.12

Let a stable linear system $\varSigma$ in (8.5) be given. With the same notation as that in Lemma 8.7, a cluster $\mathcal {I}_{[l]}$ is said to be $\theta$-reducible with respect to the $\mathcal {H}_{p}$-norm if there exists $\phi ^{\star }_{[l]}\in \mathbb {R}^{1\times n}$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{2}}-\eta _{[l]}\phi ^{\star }_{[l]}\right\| _\mathrm{F}\le \sqrt{|\mathcal {I}_{[l]}|}\ \theta ,&{}\quad p=2,\\ \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{\infty }}-\eta _{[l]}\phi ^{\star }_{[l]}\right\| _{l_{\infty }}\le \theta ,&{}\quad p=\infty \end{array} \right. \end{aligned}$$

(8.20)

for $\eta _{[l]}=-e_{\mathcal {I}_{[l]}}^{\mathsf{T}}A^{-1}B$.

In Definition 8.12, the constant $\theta \ge 0$ represents the degree of cluster reducibility. In the case of $p=2$, the scaling by $\sqrt{|\mathcal {I}_{[l]}|}$ is introduced for technical reasons. It can be easily verified by Theorem 8.9 that the $\theta$-reducibility with $\theta =0$ is equivalent to the cluster reducibility in Definition 8.8. In the following theorem, on the basis of the $\theta$-reducibility, we perform approximation error evaluation in clustered model reduction:

Theorem 8.13

Let a stable linear system $\varSigma$ in (8.5) be given and assume that (8.17) holds. Furthermore, let $\gamma >0$ be such that

$$\begin{aligned} A+A^\mathsf{T}+\gamma ^{-1}(\textit{AA}^\mathsf{T}+I_{n})\prec 0, \end{aligned}$$

(8.21)

and either $p=2$ or $p=\infty$. If all clusters are $\theta$-reducible with respect to the $\mathcal {H}_{p}$-norm, then the aggregated model $\hat{\varSigma }$ in (8.7) given by $p_{[l]}=\Vert \eta _{[l]}\Vert ^{-1}\eta _{[l]}$ is stable and satisfies

$$\begin{aligned} G(0)=\hat{G}(0),\quad \Vert G(s)-\hat{G}(s)\Vert _{\mathcal {H}_{p}}\le \gamma \sqrt{\textstyle {\sum _{l=1}^{L}}|\mathcal {I}_{[l]}|(|\mathcal {I}_{[l]}|-1)}\ \theta , \end{aligned}$$

(8.22)

where G and $\hat{G}$ are defined as in (8.9).

Theorem 8.13 shows a linear relation between the approximation error caused by cluster aggregation and the parameter $\theta$ expressing the degree of cluster reducibility. Thus, we can use $\theta$ as a criterion to regulate the approximation error of the resultant aggregated model. In this sense, Theorem 8.13 gives a strategy for reasonable cluster construction.

On the basis of the premise that $\theta \ge 0$ is given and $\varPhi _{\mathcal {H}_{p}}$ is calculated in advance, we propose an algorithm to construct a set of $\theta$-reducible clusters. Assuming that a set of $\theta$-reducible clusters $\mathcal {I}_{[1]},\ldots ,\mathcal {I}_{[l-1]}$ are already formed, we consider determining a new cluster $\mathcal {I}_{[l]}$. Let

$$ \mathcal {N}:=\{1,\ldots ,n\}\backslash \bigcup _{i=1}^{l-1}\mathcal {I}_{[i]}. $$

When constructing $\mathcal {I}_{[l]}$, we first select an index $j\in \mathcal {N}$. Then, letting either $p=2$ or $p=\infty$, we find all indices $i\in \mathcal {N}$ such that

$$\begin{aligned} \left\| \phi _{i}-\eta _{i}\eta _{j}^{-1}\phi _{j}\right\| _{l_{p}}\le \theta , \end{aligned}$$

(8.23)

where $\phi _{i}\in \mathbb {R}^{1\times n}$ denotes the ith row vector of $\varPhi _{\mathcal {H}_{p}}$ and $\eta _{i}\in \mathbb {R}$ denotes the ith entry of $\eta =-A^{-1}B$. We notice that (8.23) is a sufficient condition for (8.20) with $\phi ^{\star }_{[l]}=\eta _{j}^{-1}\phi _{j}$; thereby verifying that the new cluster $\mathcal {I}_{[l]}$ is $\theta$-reducible.

8.3.3.3 Generalization to Second-Order Networks

As giving an advanced result on clustered model reduction, we generalize the results in Sect. 8.3.3.2 to those in the case of interconnected second-order systems. More specifically, we deal with a class of interconnected second-order systems denoted by

$$\begin{aligned} \varSigma :\ddot{x}+D\dot{x}+Kx=Fu, \end{aligned}$$

(8.24)

where $D=D^{\mathsf{T}}\in \mathbb {R}^{n\times n}$ and $K=K^{\mathsf{T}}\in \mathbb {R}^{n\times n}$ are assumed to be positive definite, and $F\in \mathbb {R}^{n}$. The network structure of $\varSigma$ can be represented as the Boolean structure of K. Using the aggregation matrix P in (8.6), we define the aggregated model of $\varSigma$ in (8.24) by

$$\begin{aligned} \hat{\varSigma }: \left\{ \begin{array}{l} \ddot{\xi }+P^\mathsf{T}DP\dot{\xi }+P^\mathsf{T}KP\xi =P^\mathsf{T}Fu,\\ \hat{x}=P\xi . \end{array} \right. \end{aligned}$$

(8.25)

Note that the aggregated model $\hat{\varSigma }$ is stable for any P because $P^\mathsf{T}DP$ and $P^\mathsf{T}KP$ are also positive definite. In this notation, similarly to Problem 8.5, we address the following clustered model reduction problem for interconnected second-order systems:

Probelm 8.14

Let a stable second-order system $\varSigma$ in (8.24) be given. Given a constant $\varepsilon \ge 0$, find a stable aggregated model $\hat{\varSigma }$ in (8.25) such that (8.8) for

$$\begin{aligned} G(s):=(s^{2}I_{n}+sD+K)^{-1}F,\quad \hat{G}(s):=P(s^{2}I_{L}+sP^\mathsf{T}DP+P^\mathsf{T}KP)^{-1}P^\mathsf{T}F \end{aligned}$$

(8.26)

denoting the transfer matrices of $\varSigma$ and $\hat{\varSigma }$, respectively.

To give a solution to this problem, let us represent $\varSigma$ in (8.24) by the first-order form as

$$\begin{aligned} \varSigma :\left\{ \begin{array}{cl} \dot{X}&{}=AX+Bu, \\ x&{}=CX, \end{array} \right. \end{aligned}$$

(8.27)

where $X:=[x^{\mathsf{T}},\dot{x}^\mathsf{T}]^{\mathsf{T}}\in \mathbb {R}^{2n}$, and

$$\begin{aligned} A:=\left[ \begin{array}{cc} 0&{}I_{n}\\ -K&{}-D \end{array}\right] \in \mathbb {R}^{2n\times 2n},\quad B:=\left[ \begin{array}{cc} 0\\ F \end{array}\right] \in \mathbb {R}^{2n},\quad C:=\left[ \begin{array}{cc} I_{n}&0 \end{array}\right] \in \mathbb {R}^{n\times 2n}. \end{aligned}$$

On the basis of this representation, as a generalization of Definition 8.12, we define the notion of $\theta$-reducibility for second-order systems as follows:

Definition 8.15

Let a stable second-order system $\varSigma$ in (8.24) be given. For $p=2$ or $p=\infty$, define $\varPhi _{\mathcal {H}_{p}}\in \mathbb {R}^{2n\times 2n}$ similarly to those in Lemma 8.7. A cluster $\mathcal {I}_{[l]}$ is said to be $\theta$-reducible with respect to the $\mathcal {H}_{p}$-norm if there exist $\phi ^{\star }_{[l]}\in \mathbb {R}^{1\times 2n}$ and $\psi ^{\star }_{[l]}\in \mathbb {R}^{1\times 2n}$ such that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \max \left\{ \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{2}}^{(1)}-\eta _{[l]}\phi ^{\star }_{[l]}\right\| _\mathrm{F}, \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{2}}^{(2)}-\eta _{[l]}\psi ^{\star }_{[l]}\right\| _\mathrm{F}\right\} \le \sqrt{|\mathcal {I}_{[l]}|}\theta ,&{}\quad p=2\\ \displaystyle \max \left\{ \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{\infty }}^{(1)}-\eta _{[l]}\phi ^{\star }_{[l]}\right\| _{l_{\infty }}, \left\| e_{\mathcal {I}_{[l]}}^{\mathsf{T}}\varPhi _{\mathcal {H}_{\infty }}^{(2)}-\eta _{[l]}\psi ^{\star }_{[l]}\right\| _{l_{\infty }}\right\} \le \theta ,&{}\quad p=\infty \end{array} \right. \end{aligned}$$

for $\eta _{[l]}=-e_{\mathcal {I}_{[l]}}^{\mathsf{T}}K^{-1}F$, where $\varPhi _{\mathcal {H}_{p}}^{(1)}\in \mathbb {R}^{n\times 2n}$ and $\varPhi _{\mathcal {H}_{p}}^{(2)}\in \mathbb {R}^{n\times 2n}$ denote the upper and lower half components of $\varPhi _{\mathcal {H}_{p}}$, respectively.

In Definition 8.15, $\varPhi _{\mathcal {H}_{p}}^{(1)}$ and $\varPhi _{\mathcal {H}_{p}}^{(2)}$ correspond to the controllability Gramians with respect to the position and velocity of states. Then, Theorem 8.13 can be generalized to second-order systems as follows:

Theorem 8.16

Let a stable second-order system $\varSigma$ in (8.24) be given. If all clusters are $\theta$-reducible for the $\mathcal {H}_{p}$-norm, then the aggregated model $\hat{\varSigma }$ in (8.25) given by $p_{[l]}=\Vert \eta _{[l]}\Vert ^{-1}\eta _{[l]}$ is stable and satisfies (8.22) for (8.26) with

$$ \gamma :=\sqrt{2}\left\| P^{\mathsf{T}}\Bigl (s^{2}I_{L}+sP^\mathsf{T}DP+P^\mathsf{T}KP\Bigr )^{-1}\left[ P^\mathsf{T}K\ \ P^\mathsf{T}D\right] - \Bigl [I_{n}\ \ 0\Bigr ]\right\| _{\mathcal {H}_{\infty }}. $$

Similarly to Theorem 8.13, we can derive an approximation error bound for clustered model reduction of second-order systems. In Theorem 8.16, even though the value of $\gamma$ is not computable a priori, i.e., before determining the aggregation matrix P, the parameter $\theta$ can be used to regulate the approximation error of the resultant aggregated model.

8.3.4 Application to Average State Observer

Based on the results of Sect. 8.3.3, this section presents a design method of reduced-order observers for average state estimation of large-scale network systems, which we called here a projective state observer. This has been developed by the authors and their colleagues [18]. It is remarked that the physical meaning of the average state variable of the original systems can be preserved in the obtained reduced-order observer by using a block-diagonal structured projection matrix.

Consider also a stable linear system $\varSigma$ of (8.5) as a large-scale network system, where the measurement output $y\in \mathbb {R}^{m_y}$ is given by $y=Cx$, and $u\in \mathbb {R}^{m_u}$ (i.e., $B\in \mathbb {R}^{n\times m_u}$). Motivated by a reduced-order model of $\varSigma$ given by $\hat{\varSigma }$ of (8.7), we consider the following observer, called here a projective state observer:

$$\begin{aligned} {O}: \left\{ \begin{array}{cl} \dot{\hat{x}}&{}= P^\mathsf{T}\textit{AP}\hat{x}+P^\mathsf{T}Bu+H(y-\textit{CP} \hat{x}) \\ {z}&{}=\hat{x}. \end{array} \right. \end{aligned}$$

(8.28)

Then the projective state observer problem is to find P and H such that the estimation error $Px-\hat{x}(=:e)$ is within the specified precision. The dynamics of the error system is given by

$$\begin{aligned} \left. \begin{array}{cl} \left[ \begin{array}{c}\dot{e} \\ \dot{x} \end{array}\right] &{}= \left[ \begin{array}{cc} P^\mathsf{T}\textit{AP} - \textit{HCP}&{} (P^\mathsf{T}A-\textit{HC})(I_n-{\textit{PP}}^\mathsf{T}) \\ 0 &{} A \end{array} \right] \left[ \begin{array}{c} e \\ x \end{array} \right] + \left[ \begin{array}{c} 0 \\ B \end{array} \right] u. \end{array}\right. \end{aligned}$$

(8.29)

Thus the estimation error depends on the external input u and the initial state $x_0$ as well as the initial estimation error $e_0$, which is denoted by $e(t)=e(t;e_0,x_0,u)$. Since the dynamics of the error system is linear, we can independently consider $e(t;e_0,0,0)$, $e(t;0,x_0,0)$, and e(t; 0, 0, u). For simplicity of explanation, we only consider here the case of e(t; 0, 0, u). See [18] for further details. In this case, owing to the cascaded structure of the error dynamics, the estimation error with for an impulse input u is characterized by

$$\begin{aligned} \Vert e(t;0,0,u)\Vert _{\mathcal{L}_{2}} \le \Vert \varGamma (s)\Vert _{\mathcal{H}_{\infty }} \Vert (I- {P} {P}^\mathsf{T})(sI-A)^{-1}B \Vert _{\mathcal{H}_2} \end{aligned}$$

(8.30)

where $\varGamma (s)$ is given by a certain system that includes P and H. Thus for a given $\varepsilon >0$, we first consider to determine P such that $\Vert (I-{\textit{PP}}^\mathsf{T})(sI-A)^{-1}B\Vert _{\mathcal{H}_2} \le \rho$, which can be solved by the clustered model reduction, and then for a given P, determine H in solving a kind of $\mathcal{H}_{\infty }$ state feedback control problem with $\Vert \varGamma (s)\Vert _{\mathcal{H}_{\infty }}\le \varepsilon /\rho$.

Figure 8.3 shows a network of 54 power generators based on the IEEE 118 bus system, where each generator has two-dimensional system, and its reduced-order network model of 9 dimension obtained according to the above model reduction procedure. We also show the average behavior of the state variable (i.e., angular velocity $\omega _i$) of the original system with solid lines and the corresponding state behavior of the projective state observer with dotted lines in Fig. 8.4. We can see that both trajectories are almost the same and the proposed observer works effectively.

Fig. 8.3

Power network based on IEEE 118 bus system

Fig. 8.4

Simulation result of a projective state observer

8.4 Conclusion

This article discussed two topics, i.e., one the revisit of the well-posedness issue of hybrid systems, and the other is the clustered model reduction of large-scale network systems. The former treats how to characterize an essential structure of mathematical models including switching phenomena in a proper way, while the latter deals with how to extract a strongly controllable network system from a large-scale network system. In this sense, their research directions are very similar, and the beginning of them was the first author’s stay at Twente University under Arjan’s host.