Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Radio-frequency circuit (RF) design is a laborious strained and iterative cumbersome task that mainly relies on the experience of the skilled designers. The literature offers a plethora of papers dealing with techniques, approaches, and algorithms aimed at assisting the designer in such a cumbersome task, see for instance [22, 47].

Mathematical approaches have been used for alleviating the sizing task of such circuits, and it has already been proven that classical approaches are powerless vis-a-vis these NP-hard optimization problems [23].

Metaheuristics bid interesting and arguably efficient tools for overcoming impotence of the classical techniques. This can be briefly explained by the fact that due to the stochastic aspect of metaheuristics, ‘efficient’ sweeping of large dimension search spaces can be insured. Furthermore, metaheuristics allow dealing with many objective problems as well as constrained ones [15, 51, 52, 57].

Evolutionary metaheuristics have been used to deal with the optimal design of RF circuits, as well as analog circuits, and a large number of algorithms have been tested [2, 19, 24, 25, 29, 32, 40–44, 47, 50, 53, 54].

Swarm intelligence techniques (SI) have also been used, such as particle swarm optimization techniques (PSO) [20, 21, 38, 55, 56], ant colony optimization techniques (ACO) [3, 5], and bacterial foraging techniques (BFO) [10, 31]. SI metaheuristics are nowadays largely adopted for the resolution of similar optimization problems. Actually, it has been shown that when compared to notorious optimization algorithms, mainly genetic algorithms (GA) [26, 33] and simulated annealing (SA) [35], SI techniques can be much interesting to be used because they can be more robust, faster, and require much less tuning of control parameters, see for instance [48].

Very recently, an evolutionary algorithm’s enhanced version has been proposed, and it is called the backtracking search optimization technique (BSA or BSOA), and it has been shown via mathematical test functions and few engineering problems that BSA offers superior qualities [11].

Thus, in this work, we have put BSA to the test. It was used for the optimal sizing of low-noise amplifiers (LNAs), namely an UMTS LNA and a multistandard LNA.

BSA performances were checked with those obtained using conventional PSO algorithm and also with published results (for the same circuits) using ACO and BA-ACO techniques [42] as it is highlighted in the following sections.

The rest of this chapter is structured as follows. In Sect. 14.2, we offer a brief introduction to the considered RF circuits. In Sect. 14.3, the BSA technique is detailed, and a concise overview of the PSO technique is recalled. Section 14.4 presents the BSA obtained results, which provides a comparison with performances from the other techniques. ADS simulation techniques are also given in this section. Finally, Sect. 14.5 concludes this chapter and discusses the reached results.

2 Low-Noise Amplifiers

Despite the tremendous efforts on RF circuit design automation, this realm remains very challenging. This is due to the complexity of the domain and its high interaction and dependency on other disciplines, as depicted in Fig. 14.1 [45].

Fig. 14.1
figure 1

Pictorial illustration of some disciplines involved in the RF design process

Full size image

It is to be stressed that one among the most different tasks in this design is the handling of various tradeoffs, known by the famous hexagon introduced in [45], see Fig. 14.2.

Fig. 14.2
figure 2

RF design tradeoffs

Full size image

The most important block of a front-end receiver is arguably the low-noise amplifier, which principal role consists in amplifying the weak RF input signal fed from the external antenna with a sufficient gain, while adding as less noise as possible, hence its name [1].

Advances in CMOS technology have resulted in deep submicron transistors with high transit frequencies. Such advances have already been investigated for the design of CMOS RF circuits, particularly LNAs [39].

In this work, we deal with two CMOS LNAs, namely a wideband LNA and a multistandard LNA. Both architectures are chosen for comparison reasons with an already published paper [4] regarding performance optimization, as it is detailed in Sect. 14.4.

  • A multistandard LNA

The CMOS transistor level schematic of the LNA is shown in Fig. 14.3. It is intended for multistandard applications in the frequency range 1.5–2.5 GHz [8].

Fig. 14.3
figure 3

A multistandard CMOS LNA

Full size image

In short, this LNA encompasses a cascade architecture for reducing the Miller effect and uses the reverse isolation. M 3, R 2, and R 1 for the biasing circuitry of the input transistor; L 2, C 1, and C 2 allow the input matching.

  • An UMTS dedicated LNA

Figure 14.4 presents a CMOS LNA, in which topology was optimized in order to be dedicated for UMTS applications. R 1, R 2, and M 3 form the bias circuitry. M2 forms the isolation stage between the input and the output of the circuit. L L , R L , and C L form the circuit’s output impedance.

Fig. 14.4
figure 4

An UMTS CMOS LNA

Full size image

In Sect. 14.4, we will deal with the optimal sizing of these circuits. Most important performances of such LNAs are considered, i.e., the voltage gain and the noise figure. It is to be noted that the voltage gain is handled via the scattering parameter ‘S21’ [8]. Corresponding expression (generated using a symbolic analyzer [18]), as well as expressions of the noise figure and the input/output matching conditions, is not provided. We refer the reader to [8] for details regarding these issues.

3 PSO and BSA Metaheuristics

As introduced in Sect. 14.1, metaheuristics exhibit a wide spectrum of advantages when compared to the conventional mathematical optimization techniques. Metaheuristics are intrinsically stochastic techniques. They ensure random exploration of the parameter search space, allowing converging to the neighborhood of the global optimum within a reasonable computing time. According to [49], the name ‘metaheuristics’ was attributed to nature-inspired algorithms by Fred Glover [28].

Genetic algorithms [26, 33], which are parts of the evolutionary algorithms, are the oldest most known metaheuristics. A large number of variants of GA were proposed since the introduction of the basic GA (see for instance [15, 51]).

More recently, a new discipline was proposed, so-called swarm intelligence (SI). SI is an artificial reproduction of the collective behavior of individuals that is based on a decentralized control and self-organization [6].

A large number of such systems were studied by swarm intelligence, such as schools of fishes, flocks of birds, colonies of ants, and groups of bacteria, to name few processes [7, 9, 27, 34, 46]. Nowadays, particle swarm optimization may be the most known and the most used technique, particularly in the analog and RF circuits and systems designs, see for instance [13, 20, 21, 37, 48, 55].

More recently, a new improved variant of GA was proposed, and it is called backtracking search optimization technique (BSA) [11]. It offers some interesting features, mainly its robustness (vis-a-vis GA), its rapidity, and the low number of control parameters.

BSA is being used in the fields of analog and RF designs, see for instance [14, 16, 17, 30, 36]. BSA will be used for optimizing performances of both LNAs given in Sect. 14.2.

Presently, PSO is, as introduced above, largely used in design fields; it will also be considered for comparison reasons with BSA.

Furthermore, obtained results are also compared to the ones published in [3], using ant colony optimization (ACO) and backtrack ACO (BA-ACO) techniques.

  • PSO technique is inspired from the observation of social behavior of animals, particularly birds and fish. It is a population-based approach that has the particularity that the decision within the group is not centralized [12, 34]. In short, PSO algorithm can be presented as follows.

    The group, which is formed of potential solutions called particles, moves (flies) within the hyper search space seeking for the best location of food (the fitness value).

    Movements of the group are guided by two factors: the particle velocity and the particle position, with respect to Eqs. (14.1) and (14.2).

    $$ \begin{array}{*{20}c} {\mathop {v_{i} }\limits^{ \to } (t + 1) = } \\ \end{array} \left| {\begin{array}{*{20}l} {\omega \mathop {v_{i} }\limits^{ \to } (t)} \hfill \\ { + C_{1} {\text{rand}}(0,1)(\mathop {x_{{P{\text{best}}i}} }\limits^{{\mathop{\longrightarrow}\limits{{}}}} (t) - \mathop {x_{i} }\limits^{ \to } (t))} \hfill \\ { + C_{2} {\text{rand}}(0,1)(\mathop {x_{{G{\text{best}}i}} }\limits^{{\mathop{\longrightarrow}\limits{{}}}} (t) - \mathop {x_{i} }\limits^{ \to } (t))} \hfill \\ \end{array} } \right. $$
    (14.1)
    $$ \begin{array}{*{20}c} {\mathop {x_{i} }\limits^{ \to } (t + 1) = } \\ \end{array} \mathop {x_{i} }\limits^{ \to } (t) + \mathop {v_{i} }\limits^{ \to } (t) $$
    (14.2)

    \( \mathop {x_{{P{\text{best}}i}} }\limits^{{\mathop{\longrightarrow}\limits{{}}}} \) is the best position of particle i reached so far; \( \mathop {x_{{G{\text{best}}i}} }\limits^{{\mathop{\longrightarrow}\limits{{}}}} \) is the best position reached by particle i’s neighborhood.

    \( \omega \), C 1rand(0, 1), C 2rand(0, 1) are weighting coefficients. \( \omega \) controls the diversification feature of the algorithm, and it is known as the inertia weight. It is a critical parameter that acts on the balance between diversification and intensification. Thus, a large value of \( \omega \) makes the algorithm unnecessarily slow. On the other hand, small values of \( \omega \) promote the local search ability. C 1 and C 2 control the intensification feature of the algorithm. They are known as the cognitive parameter and the social parameter, respectively.

    PSO algorithm is given in Fig. 14.5.

    Fig. 14.5
    figure 5

    Basic flowchart of PSO

    Full size image

    As shown above, PSO algorithm is simple to be implemented and is computationally inexpensive. Thus, it does not require large memory space and is rapid, as well. These facts are on the basis of its popularity.

  • BSA (or BSOA) is a new population-based global minimizer evolutionary algorithm for real-valued numerical optimization problems [11]. BSA offers some enhancements over the evolutionary algorithms, mainly the reduction in sensitivity to control parameters and improvement in convergence performances.

    Classic genetic operators, namely selection, crossover, and mutation, are used in BSA, but in a novel way.

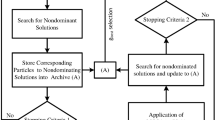
    BSA encompasses five main processes: (i) initialization, (ii) selection ①, (iii) mutation, (iv) crossover, and (v) selection ②. BSA structure is simple, which confers low computational cost, rapidity, and necessitates low memory space. Moreover, the power of BSA can be summarized through its control process of the search directions within the parameters’ hyperspace.

    BSA algorithm is given in Fig. 14.6.

    Fig. 14.6
    figure 6

    BSA algorithm

    Full size image

    • Initialization: The population P = (p ij )(N,M) is initialized via a uniform stochastic selection of particles values within the hypervolume search space, as shown by expression (14.3):

      $$ \begin{aligned} & p_{ij} = p_{j\hbox{min} } + {\text{rand}}(0,1)(p_{{j{\text{Max}}}} - p_{j\hbox{min} } ) \\ & (i,j) \in \left\{ {1, \ldots ,N} \right\}x\left\{ {1, \ldots ,M} \right\} \\ \end{aligned} $$
      (14.3)

      BSA takes benefits from previous experiences of the particles; thus, it uses a memory where the best position of each particle visited so far is memorized. The corresponding matrix noted P best  = (p bestij )(N,M) is initialized in the same way as matrix P:

      $$ \begin{aligned} & p_{{{\text{best}}ij}} = p_{j\hbox{min} } + {\text{rand}}(0,1)(p_{{j{\text{Max}}}} - p_{{j{ \hbox{min} }}} ) \\ & (i,j) \in \left\{ {1, \ldots ,N} \right\}x\left\{ {1, \ldots ,M} \right\} \\ \end{aligned} $$
      (14.4)

    • Selection ① consists of the update of theP best matrix,

    • The Mutation process operates as follows. A mutant MUTANT = (mutant ij )(N,M) is generated as shown in Eq. (14.5).

      $$ \begin{aligned} & {\text{mutant}}_{ij} = p_{ij} + {\mathcal{F}} \left( {p{\text{best}}_{ij} - p_{ij} } \right) \\ & (i,j) \in \left\{ {1, \ldots ,N} \right\}x\left\{ {1, \ldots ,M} \right\} \\ \end{aligned} $$
      (14.5)

      \( {\mathcal{F}}\) is a normally distributed factor that is used to control the search path, i.e., the direction.

    • Crossover: It consists in generating a uniformly distributed integer valued matrix MAP = (map ij )(N,M). MAP elements values are controlled via a strategy that defines the number of particle components that mutate. This is performed via the ‘dimension-rate’ coefficient. Matrix MAP is used for determining the matrix P components to be handled: the offspring matrix.

    • Selection ② consists of the update of the trial population via P best matrix.

4 Experimental Results and Comparisons

In this section, we will first deal with the application of the BSA technique to some mathematic test functions and give comparison results with the ones obtained by means of PSO regarding the robustness and the algorithm execution time. Then, we will consider the case of both LNAs introduced in Sect. 14.2. It is to be noted that a Core™2 Duo Processor T5800 (2 M Cache, 2.00 GHz, 4.00 Go) PC was used for that purpose.

  • Test functions

Five test functions were considered: DeJong’s, Eason 2D, Griewank, Parabola, and Rosenbrock.

The corresponding expressions are given by (14.6)–(14.10), respectively. Figure 14.7 shows a plot of these functions.

Fig. 14.7
figure 7

Plots of the five considered functions (n = 2). (x* is the minimum of f). a DeJong’s x * = (0, 0), f(x *) = 0. b Eason 2D x * = (π, π), f(x *) = −1. c Griewank x * = (0, 0), f(x *) = 0. d Parabola x * = (0, 0), f(x *) = 0. e Rosenbrock x * = (1), f(x *) = 0

Full size image

Both algorithms, i.e., PSO and BSA, were run 100 times. The algorithms’ parameters are given in Table 14.1.

$$ \begin{aligned} & f(x) = \sum\limits_{i = 1}^{n} {ix_{i}^{4} } \\ & - 5.12 \le x_{i} \le 5.12 \\ \end{aligned} $$
(14.6)
$$ \begin{aligned} & f(x) = - \cos (x_{1} )\cos (x_{2} )e^{{( - (x_{2} - \pi )^{2} - (x_{2} - \pi )^{2} )}} \\ & - 5 \le x_{1} \le 5, - 5 \le x_{2} \le 5 \\ \end{aligned} $$
(14.7)
$$ \begin{aligned} & f(x) = \frac{1}{4000}\sum\limits_{i = 1}^{n} {x_{i}^{2} } - \prod\limits_{i = 1}^{n} {\cos \left( {\frac{{x_{i} }}{{\sqrt i }}} \right)} + 1 \\ & 5.12 \le x_{i} \le 5.12 \\ \end{aligned} $$
(14.8)
$$ \begin{aligned} & f(x) = \sum\limits_{i = 1}^{n} {x_{i}^{2} } \\ & - 5.12 \le x_{i} \le 5.12 \\ \end{aligned} $$
(14.9)
$$ \begin{aligned} & f(x) = \sum\limits_{i = 1}^{n - 1} {\left[ {100(x_{i + 1} - x_{i}^{2} )^{2} + (x_{i} - 1)^{2} } \right]} \\ & - 2.048 \le x_{i} \le 2.048 \\ \end{aligned} $$
(14.10)
Table 14.1 PSO and BSA algorithms’ parameters
Full size table

Figure 14.8 gives a whisker boxplot relative to the 100 executions of both algorithms.

Fig. 14.8
figure 8

Boxplot of the 100 executions results for both PSO and BSA applied to the five test functions. a DeJong’s. b Eason 2D. c Griewank. d Parabola. e Rosenbrock

Full size image

Table 14.2 gives the mean execution time of both algorithms with respect to the five considered functions.

Table 14.2 Mean execution time for PSO and BSA (sec.)
Full size table

  • LNAs

PSO and BSA algorithms were used for optimally sizing both LNAs presented in Sect. 14.2. The same conditions observed above were considered. Tables 14.3 and 14.4 give the circuits’ optimized parameters. Moreover, simulations were performed using ADS software to check the viability of these results. Obtained performances are given in Tables 14.5 and 14.6. In addition, these tables present the results published in [4] obtained by application of ACO and BA-ACO techniques. The mean execution times for both problems are given in Table 14.7. Robustness results are shown in Figs. 14.9 and 14.10.

Table 14.3 Multistandard LNA’s optimal parameters’ values
Full size table
Table 14.4 UMTS LNA’s optimal parameters’ values
Full size table
Table 14.5 UMTS LNA’s optimal performances
Full size table
Table 14.6 Multistandard LNA’s optimal performances
Full size table
Table 14.7 Mean execution time per run
Full size table
Fig. 14.9
figure 9

Boxplot for the 100 executions runs for the UMTS LNA using PSO and BSA

Full size image
Fig. 14.10
figure 10

Boxplot for the 100 executions runs for the multistandard LNA using PSO and BSA

Full size image

Simulation results obtained using the ‘a priori’ optimal parameters for both circuits are depicted in Figs. 14.11, 14.12, 14.13, 14.14, 14.15, 14.16, 14.17, 14.18, 14.19, 14.20, 14.21, 14.22, 14.23, 14.24, 14.25, and 14.26.

Fig. 14.11
figure 11

ADS simulation results of S21 of the UMTS LNA, using PSO results

Full size image
Fig. 14.12
figure 12

ADS simulation results of S11 of the UMTS LNA, using PSO results

Full size image
Fig. 14.13
figure 13

ADS simulation results of the noise figure of the UMTS LNA, using PSO results

Full size image
Fig. 14.14
figure 14

ADS simulation results of S22 of the UMTS LNA, using PSO results

Full size image
Fig. 14.15
figure 15

ADS simulation results of S21 of the UMTS LNA, using BSA results

Full size image
Fig. 14.16
figure 16

ADS simulation results of S11 of the UMTS LNA, using BSA results

Full size image
Fig. 14.17
figure 17

ADS simulation results of the noise figure of the UMTS LNA, using BSA results

Full size image
Fig. 14.18
figure 18

ADS simulation results of S22 of the UMTS LNA, using BSA results

Full size image
Fig. 14.19
figure 19

ADS simulation results of S21 of the multistandard LNA, using PSO results

Full size image
Fig. 14.20
figure 20

ADS simulation results of the noise figure of the multistandard LNA, using PSO results

Full size image
Fig. 14.21
figure 21

ADS simulation results of S11 of the multistandard LNA, using PSO results

Full size image
Fig. 14.22
figure 22

ADS simulation results of S22 of the multistandard LNA, using PSO results

Full size image
Fig. 14.23
figure 23

ADS simulation results of S21 of the multistandard LNA, using BSA results

Full size image
Fig. 14.24
figure 24

ADS simulation results of the noise figure of the multistandard LNA, using BSA results

Full size image
Fig. 14.25
figure 25

ADS simulation results of S11 of the multistandard LNA, using BSA results

Full size image
Fig. 14.26
figure 26

ADS simulation results of S22 of the multistandard LNA, using BSA results

Full size image

5 Discussion and Conclusion

This chapter investigated the application of BSA, the very recently proposed EA technique, on the resolution of RF sizing problems. For comparison reasons, PSO technique was also applied for optimizing these circuits (namely two LNAs). Furthermore, obtained performances were also compared with the already published results dealing with the same circuits but using ACO and BA-ACO, and also the application to the resolution of some test functions.

The obtained results show that BSA outperforms the other optimization techniques in terms of computing time. However, it has been noted that PSO is relatively more robust. Nonetheless, the rapidity of BSA and its good performances make this algorithm a good and interesting technique to be considered within a computer-aided design approach/tool.