1 Introduction

Advances in VLSI technology nowadays allow the realization of complex integrated electronic circuits and systems [1]. Analog components are important part of integrated systems either in terms of elements and area in mixed-signal systems or as vital parts in digital systems [1, 2]. Despite their importance, design automation for analog circuits still lags behind that of digital circuits. As a matter of fact optimal design of analog component is often a bottleneck in the design flow. Analog synthesis is complicated because it does not only consist of topology and layout synthesis but also of component sizing [3]. The sizing procedure is often a slow, tedious and iterative manual process which relies on designer intuition and experience [4]. Optimizing the sizes of the analog components automatically is an important issue towards being able to rapidly design true high performance circuits [2, 4].

Common approaches are generally either fixed topology ones or/and statistic-based techniques (see for instance [5–8]). They generally start with finding a “good” DC operating point, which is provided by the analog ‘expert’ designer. Then a simulation based tuning procedure takes place. However these statistic-based approaches are time consuming and do not guarantee the convergence to the global optimum solution [9].

Some heuristic-based mathematical approaches were also used, such as local search (LS) [10], simulated annealing (SA) [11–14], tabu search (TS) [15, 16], scatter search (SS) [17], genetic algorithms (GA) [11, 18–20] etc. However these techniques do not offer general solution strategies that can be applied to problem formulations where different types of variables, objectives and constraint functions are used (linear/non linear objective and constraint functions, posynomial/signomial objective function, etc.). In addition, their efficiency is also highly dependent on the algorithm parameters, the dimension of the solution space, the convexity of the solution space, and the number of variables.

Actually, most of the circuit design optimization problems simultaneously require different types of variables, objective and constraint functions in their formulation. Therefore, the abovementioned optimization procedures are generally not adequate or not flexible enough.

In order to overcome drawbacks of these optimization procedures, a new set of nature inspired heuristic optimization algorithms were proposed. These techniques are resourceful, efficient and easy to use. These algorithms are part of Swarm Intelligence. They focus on animal behavior and insect conduct in order to develop some metaheuristics which can mimic their problem solution abilities, namely Ant Colony (AC) [21], Artificial Bee Colony (ABC) [22], Wasp Nets [22] and Particle Swarm Optimization (PSO) [23, 24].

This work deals with optimal analog circuit sizing using the PSO technique. In Sect. 2, we deal with the general formulation of the analog constrained optimization problem. In Sect. 3, we focus on the PSO heuristic for both mono and multiobjective problems. In Sect. 4, two application examples are given. The first application is a mono-objective problem that deals with optimizing the sizing of a low noise amplifier to meet fixed specifications. The second application is a multiobjective problem that consists of generating the trade off surface (Pareto front) linking two conflicting performances of a current conveyor. Conclusion remarks are given in Sect. 5.

2 The constrained problem formulation

Typically, an analog circuit designer formulates the requirements for the design of analog block in terms of bounds on performance functions. Analytical equations that predict these performance functions are then expressed in terms of device model parameters [25]. Next, these model parameters are replaced by their symbolic expressions at the design variables level. For instance, a simple MOSFET amplifier is depicted in Fig. 1. Expression 1 gives its voltage transfer function V0/Vin:

$$ \begin{aligned} {\frac{{V_{0} }}{{V_{in} }}} = & - {\frac{{g_{mM1} (\vec{x})}}{{(C_{gsM2} (\vec{x}) + C_{gsM3} (\vec{x}))s + (g_{0M1} (\vec{x}) + g_{0M2} (\vec{x}) + g_{mM2} (\vec{x}))}}} \\ = & - {\frac{{\sqrt {{\frac{{K_{P} I_{0} W_{1} }}{{L_{1} }}}} L_{1} L_{2} }}{{\lambda_{N} I_{0} L_{2} + \lambda_{P} I_{0} L_{1} + 2\sqrt {{\frac{{K_{P} I_{0} W_{2} }}{{L_{2} }}}} L_{1} L_{2} + {\frac{2}{3}}C_{ox} L_{1} L_{2} (L_{2} W_{2} + L_{3} W_{3} )}}} \\ \end{aligned} $$
(1)

where gmMi, g0Mi, CgsMi, are transconductance, conductance and grid to source capacitance of the corresponding MOS transistor, respectively. I0 is the bias current. W i and L i are width and length of the MOSFET’s channel, respectively. C ox , λ N , λ P , K N and K P are technology parameters. The variable vector \( \vec{x} \) represents bias voltages, bias currents and device sizes.

Fig. 1
figure 1

A MOSFET amplifier

Full size image

Optimal sizing of the circuit consists in finding variable set \( \vec{x} = \left\{ {L_{1} ,W_{1} ,L_{2} ,W_{2} , \ldots } \right\} \) that optimizes performance function(s) and meets imposed specifications, such as maximizing the amplifier’s bandwidth while satisfying (V 0 /V in ) dB >G aindB . G aindB is the gain low boundary that depends on the application.

Besides additional constraints have to be satisfied, such as voltage range constraints (MOS saturation conditions…), size ranges (minimum sizing allowed by the technology…), etc.

Thus, a general optimization problem can be defined in the following format:

$$ \begin{array}{*{20}c} {\left| {\begin{array}{*{20}c} {Minimize\,f(\overrightarrow {x} );} \hfill & {f(\overrightarrow {x} ) \in R} \hfill \\ {such\,that:} \hfill & {} \hfill \\ {\overrightarrow {g} (\overrightarrow {x} ) \le 0;} \hfill & {\overrightarrow {g} (\overrightarrow {x} ) \in R\mathop {}\limits^{m} } \hfill \\ {and\;\overrightarrow {h} (\overrightarrow {x} ) = 0;} \hfill & {\vec{h}(\overrightarrow {x} ) \in R\mathop {}\limits^{n} } \hfill \\ \end{array} } \right.} \hfill \\ {\left| {where\;x_{Li} \le x_{i} \le x_{Ui} } \right.,\quad i \in \left[ {1,p} \right]} \hfill \\ \end{array} $$
(2)

m inequality constraints to satisfy; n equality constraints to assure; p parameters to manage; and \( \vec{x}_{L} \) and \( \vec{x}_{U} \) are lower and upper boundaries vectors of the parameters.

Actually, circuit optimization problems involve more than one objective. For instance, for the MOSFET amplifier, more than one objective function (OF) may be optimized, such as gain, noise figure, slewrate, bandwidth, etc. Consequently expression 2 should be modified as:

$$ \begin{array}{*{20}c} {\left| {\begin{array}{*{20}c} {Minimize\,\vec{f}(\overrightarrow {x} );} \hfill & {\vec{f}(\overrightarrow {x} ) \in R\mathop {}\limits^{k} } \hfill \\ {subject\,to:} \hfill & {} \hfill \\ {\overrightarrow {g} (\overrightarrow {x} ) \le 0;} \hfill & {\overrightarrow {g} (\overrightarrow {x} ) \in R\mathop {}\limits^{m} } \hfill \\ {and\,\overrightarrow {h} (\overrightarrow {x} ) = 0;} \hfill & {\overrightarrow {h} (\overrightarrow {x} ) \in R\mathop {}\limits^{n} } \hfill \\ \end{array} } \right.} \hfill \\ {\left| {where\,x_{Li} \le x_{i} \le x_{Ui} ,\quad i \in \left[ {1,p} \right]} \right.} \hfill \\ \end{array} $$
(3)

where k number of objectives (≥2); m inequality constraints to satisfy; n equality constraints to assure; and p parameters to manage.

The flowchart depicted in Fig. 2 summarizes main steps of the sizing approach.

Fig. 2
figure 2

Pictorial view of a design optimization approach

Full size image

The goal of optimization is usually to minimize an objective function; the problem for maximizing \( \vec{f}(\overrightarrow {x} ) \) can be transformed to minimizing \( - \vec{f}(\overrightarrow {x} ) \). This goal is reached when the variables are located in the set of optimal solutions.

As it was introduced in section I, there exist many papers and books dealing with mathematical optimization methods and studying in particular their convergence properties (see for example [9, 11, 26]). These optimizing methods can be classified into two categories: deterministic methods and stochastic methods, known as heuristics.

Deterministic methods, such as simplex [27], branch and bound [28], goal programming [29], dynamic programming [30]… are effective only for problems of small size. They are not efficient when dealing with NP-hard and multi-criterion problems. In addition, it was proven that these optimization techniques impose several limitations due to their inherent solution mechanisms and their tight dependence on the algorithm parameters. Besides they rely on the type of objective, the type of constraint functions, the number of variables and the size and the structure of the solution space. Moreover, they do not offer general solution strategies.

Most of the optimization problems require different types of variables, objective and constraint functions simultaneously in their formulation. Therefore, classical optimization procedures are generally not adequate. Heuristics are necessary to solve large size problems and/or with many criteria [31]. They can be ‘easily’ modified and adapted to suit specific problem requirements, as it is illustrated in Fig. 3 [22]. Even though they don’t guarantee to find in an exact way the optimal solution(s), they give ‘good’ approximation of it (them) within an acceptable computing time. Heuristics can be divided into two classes: on the one hand, there are algorithms which are specific to a given problem and, on the other hand, there are generic algorithms, i.e., metaheuristics. Metaheuristics are classified into two categories: local search techniques, such as simulated annealing, tabu search … and global search ones, like evolutionary techniques, swarm intelligence techniques …

Fig. 3
figure 3

A pictorial comparison of classical and modern heuristic optimization strategies (taken from [22])

Full size image

AC, ABC, PSO are swarm intelligence techniques, they form a subset of metaheuristics. Metaheuristics are inspired from nature and were proposed by researchers to overcome drawbacks of the aforementioned methods. In the following we focus on the use of the Particle Swarm Optimization technique for the optimal design of both mono-objective and multiobjective optimization problems [24], (http://www.particleswarm.info/).

3 The particle swarm optimization

The Particle Swarm Optimization (PSO) is a metaheuristic inspired from nature. This technique mimics some animal’s problem solution abilities, such as bird flocking or fish schooling. Interactions between animals contribute to the collective intelligence of the swarm. This approach was proposed in 1995 by Kennedy and Eberhart [23].

In PSO, multiple candidate solutions coexist and cooperate with each other simultaneously. Each solution, called a particle, ‘flies’ within the problem search space looking for the optimal position to land [22]. A particle, as time passes through its quest, adjusts its position according to its own ‘experience’ as well as the experience of its neighboring particles. Each particle remembers its best position and is informed of the best position reached by the swarm in the global version of the algorithm, or by the particle’s neighborhood in the local version of the algorithm.

PSO system combines local search method (through self experience) with global search methods (through neighboring experience) [22]. It is becoming popular due to the fact that the algorithm is relatively straightforward and is easy to be implemented [24]. Additionally there is plenty of source codes of PSO available in public domain (see for example http://www.swarmintelligence.org/codes.php).

When compared to the other well known heuristics, such as GA (NSGA II for multiobjective problems) and SA, PSO presents the advantage of the rapid convergence to the promising regions. On the other hand, PSO can be trapped into a local minimum. This phenomenon highly relies on the global search constituent. We refer the reader to [24] for further details on such characteristics.

3.1 Mono-objective PSO

PSO has been proposed for solving mono-objective problems and has been successfully used for both continuous non linear and discrete mono-objective optimization. In short, the approach consists of the following [24].

The algorithm starts with a random initialization of a swarm of particles in the multi-dimensional search space, where a particle represents a potential solution of the problem being solved. Each particle is modeled by its position in the search space and its velocity. At each time step, all particles adjust their positions and velocities, i.e., directions in which particles need to move in order to improve their current position, thus their trajectories.

This is done according to their best locations and the location of the best particle of the swarm in the global version of the algorithm, or of the neighbors in the local version. Figure 4 illustrates this principle.

Fig. 4
figure 4

Principle of the movement of a particle

Full size image

Changes to the position of the particles within the search space are based on the social-psychological tendency of individuals to emulate the success of other individuals [32]. Thus each particle tends to be influenced by the success of any other particle it is connected to.

Expressions of a particle position at time step t and its velocity are as follows [22, 33]:

$$ \vec{v}_{i} (t) = \underbrace {{\omega \vec{v}_{i} (t - 1)}}_{Inertia} + \underbrace {{c_{1} r_{1} (\vec{x}_{pbesti} - \vec{x}_{i} (t))}}_{Personal\;Influence} + \underbrace {{c_{2} r_{2} (\vec{x}_{leaderi} - \vec{x}_{i} (t))}}_{Social\;Influence} $$
(4)
$$ \vec{x}_{i} (t) = \vec{x}_{i} (t - 1) + \vec{v}_{i} (t) $$
(5)

where x pbesti is the best personal position of a given particle, x leaderi refers to the best position reached by the particle’s neighborhood, ω is an inertia weight that controls the diversification feature of the algorithm, c 1 and c 2 control the attitude of the particle of searching around its best location and the influence of the swarm on the particle’s behavior, respectively (c 1 and c 2 control the intensification feature of the algorithm). r 1 and r 2 are random values uniformly sampled in [0,1] for each dimension.

Figure 5 illustrates the flowchart of the mono-objective PSO. N is the swarm’s size. Pi = [p i,1, p i,2,…, p i,N] denotes the best location reached by the ith particle at time t. Xi = [x i,1, x i,2,…,x i,N] is the ith particle position and g = [g 1, g 2,…, g N ] represents the best location reached by the entire swarm.

Fig. 5
figure 5

Flowchart of the mono-objective PSO

Full size image

An application example of performance maximization in terms of voltage gain of a Low Noise Amplifier is given in section IV.

3.2 Multiobjective PSO

As it was introduced in section II, multiobjective optimization is a common task in circuit design. Commonly designers transform the multiobjective problem into a mono-objective one using the aggregation approach [34]. The latter requires the designer to select values of weights for each objective. The so obtained mono-objective function can be written as:

$$ F(\vec{x}) = \sum\limits_{i = 1}^{k} {\omega_{i} f_{i} (\vec{x})} $$
(6)

ω i , i ∈ [1, k], are weighting coefficients

For instance, in [35] a normalization method was used to guide the choice of the weighting coefficients. Yet, this approach is not suitable in most problems since it is not able to detect solutions when the solution space is not convex. Furthermore, it was shown in [36] that varying the weighting coefficients ω i cannot allow sweeping the entire Pareto front and cannot also ensure a homogeneous distribution of the design over the Pareto front. Besides, obtained solutions may be very sensitive to a small variation of these coefficients [36].

Even though some approaches, such as geometric programming, have overcome this main drawback by converting the non convex problem into a convex one [37], using the weighting approach, only a unique “optimal” point can be obtained. This solution depends on the choice of the weighting coefficients.

On the other hand, a multiobjective approach (MO) can be stated as finding vectors \( \vec{x} = (x_{1} ,x_{2} , \ldots ,x_{n} ) \) that satisfy the constraints and optimize the vector function \( \vec{f}(\vec{x}) \) [38]. However, the objective functions may be in conflict. Thus, the goal of the MO algorithm is to provide a set of Pareto optimal solutions of the aforementioned problem [26, 38–40]. It is to be noticed that a solution \( \vec{x} \) of a MO problem is said Pareto optimal if and only if there does not exist another solution \( \vec{y} \) such that \( \vec{f}(\vec{y}) \) dominates \( \vec{f}(\vec{x}) \), i.e., no component of \( \vec{f}(\vec{x}) \) is smaller than the corresponding component of \( \vec{f}(\vec{y}) \) and at least one component is greater [41]. Without loss of generality, we consider the minimization case. Figure 6 depicts the multiobjective approach.

Fig. 6
figure 6

Illustration of a general multiobjective optimization problem

Full size image

PSO was adapted to be able to deal with multiobjective optimization problems. The idea consists of the use of an external memory: an archive, in which each particle deposits its ‘flight’ experience at each running cycle. More precisely, the aim of the archive is to store all the non-dominated solutions found during the optimization process. At the end of the execution, all the positions stored in the archive give us an approximation of the theoretical Pareto Front.

Algorithm 1 Archive’s update
Full size table

In order to avoid excessive growing of this memory, its size is fixed. This implies to define some rules for the update of the archive. Algorithm 1 depicts the pseudo-code of these rules.

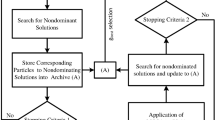
The crowding distance of the ith element of the archive estimates the size of the largest cuboid enclosing the point i without including any other point in the archive. The idea is to maximize the crowding distance of the particles in order to obtain a Pareto front as uniformly spread as possible. In Fig. 7, the crowding distance of the ith solution of the archive (black spots) is the average side length of the cuboid shown by the dashed box. The flowchart presented in Fig. 8 depicts the MO-PSO [41, 42].

Fig. 7
figure 7

Crowding distance

Full size image
Fig. 8
figure 8

Flowchart of a MO-PSO

Full size image

In the following section we give two application examples where mono-objective and multiobjective PSO are considered.

4 Application examples

4.1 A mono-objective problem:

The problem consists of optimally sizing a common source low noise amplifier (LNA) with an inductive degeneration [43] presented at Fig. 9, for the UMTS standard.

Fig. 9
figure 9

A CMOS LNA with biasing network

Full size image

The problem is defined in the following way.

4.1.1 Constraints

  • Ensure input and output matching of the LNA to guarantee a maximum power transfer from the antenna to the LNA then to the pre-amplifier. This leads to the equality constraints 7 and 8:

    $$ Ls = {\frac{{RsC_{gs} }}{{g_{m} }}} $$
    (7)
    $$ Lg = {\frac{1}{{\omega_{0}^{2} C_{gs} }}} - L_{S} $$
    (8)

    where Cgs and gm are the grid to source capacitance and the transconductance of the MOS transistor M1, respectively. ω 0 is the pulsation of the UMTS standard, ω 0 = 2πf 0, with f 0  = 2.14 GHz.

  • Linearity, which is highly dependent on the saturation of the MOS transistors. Thus inequalities 9 and 10 must be satisfied. These conditions were determined by fixing the 1 dB compression point value (CP1=0 dBm).

    $$ V_{DS1\min } > V_{DSsat1} $$
    (9)
    $$ V_{DS2\min } > V_{DSsat2} $$
    (10)

    where V DSimin and V DSsati are the minimum drain to source voltages and the saturation voltages of transistors M1 and M2, respectively.

  • Noise Figure: the reduced NF expression proposed in [44] was used. The constraint is:

    $$ NF < (NF_{\max } = 1dB) $$
    (11)

  • Transit frequency: f T must be five times higher than the UMTS frequency.

4.1.2 Objective function

  • Gain: its symbolic expression was computed using the small-signal equivalent circuit and the objective function is that the gain has to present its maximum value at the UMTS frequency. The gain’s expression is not given due to its large number of terms.

This optimizing problem was solved using mono-objective PSO technique. The algorithm was programmed using C++ software. Notice that, boundaries of parameters were imposed by the used technology. PSO algorithm parameters are given in Table 1 [33]. Optimal obtained parameters are presented in Table 2. We notice that 25 runs were performed, and the average computing time equals 1.57 s.Footnote 1 Simulation conditions and reached performances, obtained using ADS software (Agilent Advanced Design System), are given in Tables 3 and 4, respectively.

Table 1 Parameters of the mono-objective algorithm
Full size table
Table 2 Optimal parameters’ values
Full size table
Table 3 Simulation conditions
Full size table
Table 4 Reached performances (Gain at umts frequency)
Full size table

ADS simulation results are depicted in the following figures; they show the good agreement between ADS and expected results. Figure 10(a) and (b) prove that input and output matching are insured (50 Ω). Figure 11 shows the LNA performs a compression point CP1 of −2 dBm. Figure 12(a) and (b) illustrate LNA noise figure and voltage gain that equal 0.91 dB, and 13.35 dB, respectively.

Fig. 10
figure 10

Input (a) and output (b) matching (scattering parameters S(1,1) and S(2,2))

Full size image
Fig. 11
figure 11

The LNA compression point (CP1)

Full size image
Fig. 12
figure 12

The noise figure (a) and the voltage gain (b)

Full size image

4.2 A multiobjective problem

The problem consists of optimizing performances of a second generation current conveyor (CCII) [45, 46] regarding to its main influencing performances. The aim consists of maximizing the conveyor high current cutoff frequency and minimizing its parasitic X-port resistance [47]. Figure 13 illustrates the conventional positive second generation current conveyor.

4.2.1 Constraints

  • Transistor saturation conditions: all the CCII transistors must operate in the saturation mode. Saturation constraints of each MOSFET were determined. For instance, expression 12 gives constraints on M2 and M8 transistors:

    $$ {\frac{{V_{DD} }}{2}} - V_{TN} - \sqrt {{\frac{{I_{0} }}{{K_{P} {{W_{2} } \mathord{\left/ {\vphantom {{W_{2} } {L_{2} }}} \right. \kern-\nulldelimiterspace} {L_{2} }}}}}} \ge \sqrt {{\frac{{I_{0} }}{{K_{N} {{W_{8} } \mathord{\left/ {\vphantom {{W_{8} } {L_{8} }}} \right. \kern-\nulldelimiterspace} {L_{8} }}}}}} $$
    (12)

    where I 0 is the bias current, W i /L i are the aspect ratio of the ith MOS transistor. K N , K P and V TN are technology parameters. V DD is the DC voltage power supply.

Fig. 13
figure 13

The second generation current conveyor

Full size image

4.2.2 Objective functions

  • R X : the value of the X-port input parasitic resistance has to be minimized.

  • f chi : the high current cut off frequency has to be maximized.

Symbolic expressions of these functions are not given due to their large number of terms.

Table 5 gives PSO algorithm parameters. PSO optimal parameter values and simulation conditions are shown in Tables 6 and 7, respectively, where LN, WN, LP and WP refer to length and width of NMOS and PMOS transistors, respectively. The average time taken for 25 runs, under the same conditions as in the mono-objective case, equals 2.32 s Fig. 14 shows both the parameter space and the solution space (Pareto front) and the correspondence between each parameter value and its solution. Notice that additional degrees of freedom are given to the designer to choose his ‘optimal’ parameter vector within the set of the non-dominated solutions. For instance, an additional criterion can be the occupied area. Figure 15 illustrates the solution space (RX vs. f chi ) for different values of the bias current I0. Finally, Figs 16, 17, 18, 19 show SPICE simulation results performed for two particular solutions, i.e., edges of the Pareto boarder (solutions giving the maximum f chi and the minimum RX, respectively). These results are in good agreement with the expected theoretical ones. Table 8 summarizes and compares reached performances.

Table 5 Parameters of the multiobjective algorithm
Full size table
Table 6 Optimal parameters’ values
Full size table
Table 7 Simulation conditions
Full size table
Fig. 14
figure 14

Illustration of the correspondence between parameter and solution spaces

Full size image
Fig. 15
figure 15

Pareto fronts obtained for various values of the bias current I0

Full size image
Fig. 16
figure 16

SPICE simulation results for RX: solution giving maximum f chi

Full size image
Fig. 17
figure 17

SPICE simulation results for RX: solution giving minimum RX

Full size image
Fig. 18
figure 18

SPICE simulation results for f chi : solution giving maximum f chi

Full size image
Fig. 19
figure 19

SPICE simulation results for f chi : solution giving minimum RX

Full size image
Table 8 Reached performances (points located at the pareto front edges)
Full size table

Finally, it is to be highlighted that this CCII was optimized in [48], but using a weighting approach. The unique ‘optimal’ solution given in [48] belongs to the Pareto front and it corresponds to its high boundary. Besides, and for comparison reasons, NSGA II algorithm (http://www.mathworks.com/matlabcentral/fileexchange/10351) was used to generate the Pareto front (R X , f chi ). Figure 20 presents fronts obtained using PSO and NSGA II, for I0 = 100μA. Results obtained using PSO are much better than those of NSGA II. This is mainly due to the fact that PSO handles constraints better than its counterpart.

Fig. 20
figure 20

PSO front versus NSGA II front

Full size image

5 Conclusion

This paper details the particle swarm optimization (PSO) technique for the optimal design of analog circuits. Reached results can be summarized as follows:

  • We show the practical applicability of PSO to optimize performances of analog circuits and its suitability for solving both a mono-objective optimization problem and a multiobjective one. Two applications were presented. The first deals with maximizing the voltage gain of a low noise amplifier: a mono-objective optimization problem. The second is a bi-objective one. It consists in computing the Pareto tradeoff surface in the space solutions: parasitic input resistance vs. high current cutoff frequency.

  • According to the simulation results, severe parameter tuning is not required. Indeed, PSO only requires less than 10,000 iterations for obtaining “optimal” solutions, even for large-scale systems.

Our current work focuses on integrating PSO approach in an automated design flow.