On the Use of the Multiple Scale Harmonic Balance Method for Nonlinear Energy Sinks Controlled Systems

Abstract

The Multiple Scale Harmonic Balance Method (MSHBM) is discussed here for several paradigmatic systems (primary structures) equipped with a Nonlinear Energy Sink (NES). This is a small-mass oscillator with essentially nonlinear stiffness, used for passive control purpose. The method permits to overcome the difficulties inherent to standard perturbation methods, which occur as a consequence of the nonlinearizable nature of the NES equation. It combines the Multiple Scale Method and the Harmonic Balance Method to furnish Amplitude Modulation Equations ruling the slow asymptotic dynamics of the augmented system. The MSHBM is illustrated here for a general, internally non-resonant, multi d.o.f. structure equipped with a NES and under multiple concurrent actions, namely steady wind inducing Hopf bifurcation , and 1:1 and 1:3 resonant harmonic forces. The relevant Amplitude Modulation Equations are specialized for simpler cases, where the single contributions of each external action is considered separately. The effect of the NES on the dynamics of the system is discussed for each case and numerical results are displayed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Nonlinear Energy Sinks (NES) are strongly nonlinear oscillators, typically equipped with a small mass, a linear damper and an essentially nonlinear spring, attached to a primary structure to be controlled. Their main goal is to induce irreversible transfer of vibrational energy from the primary structure to themselves, and to dissipate it as a passive control device. A comprehensive report on the characteristics and uses on NES is found in [1, 2].

The one-way energy convey from the primary structure to the NES, referred as Target Energy Transfer (TET), and investigated in the literature in analytical, numerical and experimental sense [3–7], as well as the capacity (in theory) of the NES of oscillating at any frequencies, giving rise of large band tuning with the structure to be controlled, are consequences of the essentially nonlinear nature of the NES and its lacking of linear stiffness. Moreover, the presence of small mass is responsible of (almost) singularity in the equations, inducing relaxation oscillations , typically referred as Weakly Modulated Response (WMR) and Strongly Modulated Response (SMR) [8, 9].

Recently, these kind of devices have received great attention in the literature, being used in many applications. In [10, 11], a NES was applied to a main linear oscillator harmonically excited by a 1:1 resonant force. In [12, 13], multiple parallel NESs were considered to dissipate first-mode oscillations of a linear structure under impulse as well as harmonic forcing. In [14] non-smooth NES was considered to control a two-d.o.f. system. In [15], NES was used to suppress aeroelastic instabilities on a rigid wing, modeled as a two-d.o.f. section-model, under steady wind. In [16] a single NES is used to control oscillations of a long-span bridge prone to coupled flutter.

To analytically study the slow-flow dynamics of systems with NES, the researchers generally make use of two steps: (a) the complexification-averaging procedure by Manevitch [17], referred as CX-A, recently extended also to non-polynomial nonlinearity [18] and piece-wise systems [14], and, subsequently, (b) the Multiple Scale Method (MSM, [19]). In fact, due to the non-linearizable nature of the equations of NES, it was stated in [20], where a grounded NES was studied, that “for this type of problem the standard analytical techniques from nonlinear dynamics (such as the method of multiple-scales, and the standard method of averaging), are not directly applicable, and an alternative approach must be followed”; accordingly, the complexification method was employed. Dealing with the same problem, three different methods were used in [21], namely, the method of harmonic balance, a combination of a shooting method and Floquet theory, and direct time integration, but not the MSM. In the same paper, the authors used an adapted version of the method of averaging, and defined their theoretical analysis as “limited”.

For all these reasons, the authors of this paper, in a series of work [22–24] investigated the possibility of implementing a nonstandard version of the MSM, for general systems equipped with NES, under specific external actions. In particular, in [22], they used the Multiple Scale Harmonic Balance Method (MSHBM), to get Amplitude Modulation Equations (AME) for a multi d.o.f. system under 1:1 resonant external force. The main advantage of the algorithm is that the initial complexification procedure is avoided, dealing directly with variables having clear physical meanings. In [23], the same algorithm was specialized for a system undergoing a Hopf bifurcation due to steady wind. In [24] the MSHBM was extended to infinite dimensional systems, in direct approach, to deal with an internally nonresonant string under a harmonic force considered resonant to a certain mode.

In this paper, the MSHBM is illustrated for a general discrete system under simultaneous external actions. The scope of the paper is multifold: (a) to collect old results by the authors in a more systematic and exhaustive manner; (b) to present new results concerning subharmonic excitations, not analyzed in the past; (c) to open the way to further investigations relevant to the interaction among simultaneous excitations, here accounted for in formulation, but not addressed in the numerical results, yet. To this ends, a general, nonlinear, multi-d.o.f. system under effect of steady wind, which induces a Hopf bifurcation, concurrently acting with external 1:1 and 1:3 resonant harmonic excitation, is considered. A NES is attached to it, in order to control amplitude of vibrations, and the MSHBM is applied to the equations of motion, to get the AME ruling the dominant dynamics of the system. Then, numerical results are extracted for simpler cases, when one single component of excitation is applied in turn, with the aim of analyze the effect on the dynamics of the principal structure and to check the reliability of the algorithm. However, a complete unfolding of the dynamics of the proposed examples, as well as a deep analysis of the possible beneficial effect of the NES, are not fulfilled herein, since they are out of the aim of this paper.

The paper is organized as follows: in Sect. 2, the algorithm is applied to a general system; in Section 3, some examples are discussed: in Sect. 3.1 a one d.o.f. system under 1:1 resonant force is studied; in Sect. 3.2 the effect of a NES on the dynamics of a one d.o.f. system under 1:3 subharmonic resonance is discussed; in Sect. 3.3 results on a two-d.o.f. system under steady wind are analyzed; in Sect. 3.4 a N-d.o.f. internally nonresonant string with NES and under harmonic excitation is considered; in Sect. 4 some conclusions are drawn.

2 The Multiple Scale Harmonic Balance Method

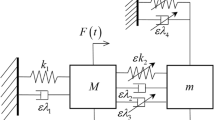
A nonlinear multi-d.o.f. mechanical systems, which is close to a Hopf bifurcation caused by aerodynamic forces , and under both 1:1 and 1:3 resonant harmonic excitations, is considered herein. The aerodynamic forces, due to the steady wind of (non-dimensional) speed $\mu$ which blows orthogonally to the plane of the structure, are assumed to be described by the quasi-steady theory. The main system is equipped with an essentially nonlinear oscillator with small mass and linear damper, behaving as a Nonlinear Energy Sink (NES), attached at a selected point (see Fig. 1). The relevant nondimensional equations of motion for the whole system read:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {x}}&+\mathbf {C}(\mu )\dot{\mathbf {x}}+\mathbf {K}(\sigma ,\mu )\mathbf {x}+\xi (\mathbf {r}^T\dot{\mathbf {x}}-\dot{y})\mathbf {r}+\kappa (\mathbf {r}^T\mathbf {x}-y)^3\mathbf {r}\nonumber \\&+\mathbf {n}(\mathbf {x},\mathbf {x},\mathbf {x})=\eta _1\mathbf {f}_1\cos (\omega t)+\eta _3\mathbf {f}_3\cos (3\omega t)\end{aligned}$$

(1)

$$\begin{aligned} m\ddot{y}&-\xi (\mathbf {r}^T\dot{\mathbf {x}}-\dot{y}) -\kappa (\mathbf {r}^T\mathbf {x}-y)^3=0 \end{aligned}$$

(2)

where: $\mathbf {x}=\mathbf {x}(t)$ is the time-depending N-dimensional column matrix of the displacements of the main structure; $\mathbf {M}$ is the mass matrix; $\mathbf {C}(\mu )$ is the (non-proportional) damping matrix and $\mathbf {K}(\sigma ,\mu )$ is the stiffness matrix; $\mathbf {C}$ depends on $\mu$ while $\mathbf {K}$ depends on $\mu$ and (linearly) by a structural parameter $\sigma$; both $\mu$ and $\sigma$ act as bifurcation parameters; $\mathbf {n}$ is the column of the (cubic) geometric nonlinearities, $\mathbf {f}_1$ is a unitary vector ($||\mathbf {f}_1||=1$) providing the shape of the component of the external force, of amplitude $\eta _1$, which is modulated by the frequency $\omega$; in analogy, $\mathbf {f}_3$ is the unitary vector ($||\mathbf {f}_3||=1$) describing the component of the external force modulated by frequency $3\omega$ and with amplitude $\eta _3$; $y=y(t)$ is the time-depending displacement of the added oscillator, m its mass, $\xi$ its damping-ratio and $\kappa$ the coefficient of its essentially nonlinear (cubic) spring; $\mathbf {r}$ is the influence coefficient column; finally, the dot represents time-differentiation. It is assumed that, when $\mu$ is equal to a critical value, the wind triggers a Hopf bifurcation and the dynamics of the (homogeneous) system with NES disengaged evolves on a critical mode; moreover, when $\sigma =0$, the external excitation $\mathbf {f}_1$ is 1:1 resonant with the same critical mode of the main structure, and $\mathbf {f}_3$ is 1:3 resonant with the same mode as well, whereas no other resonance combinations are possible; $\sigma$ acts as a detuning parameter.

Fig. 1

Sketch of a multi-d.o.f. system equipped with a NES

It is convenient to introduce the relative displacement between main structure and NES, $z\mathrel {\mathop :}=\mathbf {r}^T\mathbf {x}-y$, so that the (1) and (2) become:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {x}}&+\mathbf {C}(\mu )\dot{\mathbf {x}}+\mathbf {K}(\sigma ,\mu )\mathbf {x}+\xi \dot{z}\mathbf {r}+\kappa z^3\mathbf {r}\nonumber \\&+\mathbf {n}(\mathbf {x},\mathbf {x},\mathbf {x})=\eta _1\mathbf {f}_1\cos (\omega t)+\eta _3\mathbf {f}_3\cos (3\omega t)\end{aligned}$$

(3)

$$\begin{aligned} m(&\mathbf {r}^T\ddot{\mathbf {x}}-\ddot{z})-\xi \dot{z} -\kappa z^3 =0 \end{aligned}$$

(4)

The dependent variables are rescaled through a nondimensional small parameter $\varepsilon >0$, as $(\mathbf {x},z)\mathrel {\mathop :}=\varepsilon ^{1/2}( \tilde{\mathbf {x}},\tilde{z})$, consistently with the presence of cubic nonlinearity; the bifurcation parameter $\mu$ is expressed as $\mu =\mu _0+\varepsilon \mu _1$, where $\mu _0$ is its critical value, to be still evaluated, and $\varepsilon \mu _1$ is the small deviation from it. The structural parameter $\sigma$ is rescaled as $\sigma =\varepsilon \tilde{\sigma }$. The 1:1 external force is rescaled as $\eta _1=\varepsilon ^{3/2}\tilde{\eta }_1$, while the 1:3 force component is rescaled as $\eta _3=\varepsilon ^{1/2}\tilde{\eta }_1$. The parameters of the NES are also rescaled, since both its mass and damping are assumed small: $(m,\xi )\mathrel {\mathop :}=\varepsilon ( \tilde{m},\tilde{\xi })$. The rescaling and series expansion of $\mathbf {C}(\mu )$ and $\mathbf {K}(\sigma ,\mu )$ lead to the following equations, after omission of tilde and division by $\varepsilon ^{1/2}$:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {x}}\,+\,&(\mathbf {C}_0+\varepsilon \mu _1\mathbf {C}_1)\dot{\mathbf {x}}+(\mathbf {K}_0+\varepsilon \mu _1\mathbf {K}_{\mu }+\varepsilon \sigma \mathbf {K}_{\sigma })\mathbf {x}\nonumber \\&+\varepsilon \xi \dot{z}\mathbf {r}+\varepsilon \kappa z^3\mathbf {r}+\varepsilon \mathbf {n}(\mathbf {x},\mathbf {x},\mathbf {x})\nonumber \\&=\varepsilon \eta _1\mathbf {f}_1\cos (\omega t)+\eta _3\mathbf {f}_3\cos (3\omega t)\end{aligned}$$

(5)

$$\begin{aligned} \varepsilon m&(\mathbf {r}^T\ddot{\mathbf {x}}-\ddot{z})-\varepsilon \xi \dot{z} -\varepsilon \kappa z^3=0 \end{aligned}$$

(6)

where $\mathbf {C}_0\mathrel {\mathop :}=\mathbf {C}(\mu _0),\mathbf {K}_0\mathrel {\mathop :}=\mathbf {K}(0,\mu _0)$, $\mathbf {C}_1\mathrel {\mathop :}=\partial \mathbf {C}(\mu _0)/\partial \mu ,\;\mathbf {K}_{\mu }\mathrel {\mathop :}=\partial \mathbf {K}(0,\mu _0)/\partial \mu$, and $\mathbf {K}_{\sigma }\mathrel {\mathop :}=\partial \mathbf {K}(0,\mu _0)/\partial \sigma$.

According to the Multiple Scale Method, independent time scales $t_0:=t$, $t_1:=\varepsilon t$, $t_2=\varepsilon ^2t,\ldots$ are introduced and, consistently, the derivatives expressed as $\frac{d}{dt}=d_0+\varepsilon d_1+\varepsilon ^2 d_2+\ldots$ and $\frac{d^2}{dt^2}=d_0^2+2\varepsilon d_0 d_1+\varepsilon ^2(d_1^2+2d_0d_1)+\ldots$. Moreover, the dependent variables are expanded in series as:

$$\begin{aligned} \begin{Bmatrix} \mathbf {x}\\ z \end{Bmatrix}=\begin{Bmatrix} \mathbf {x}_0\\ z_0 \end{Bmatrix}+\varepsilon \begin{Bmatrix} \mathbf {x}_1\\ z_1 \end{Bmatrix}+\varepsilon ^2\begin{Bmatrix} \mathbf {x}_2\\ z_2 \end{Bmatrix}+\ldots \end{aligned}$$

(7)

Substituting in (5) and (6) and collecting terms of the same order in $\varepsilon$, lead to the following perturbation equations:

$$\begin{aligned} \text {order }\varepsilon ^0: & {} \nonumber \\ \mathbf {M}&d_0^2\mathbf {x}_0+\mathbf {C}_0d_0\mathbf {x}_0+ \mathbf {K}_0\mathbf {x}_0=\eta _3\mathbf {f}_3\cos (3\omega t_0)\end{aligned}$$

(8)

$$\begin{aligned} \text {order }\varepsilon ^1: & {} \nonumber \\ \mathbf {M}&d_0^2\mathbf {x}_1+\mathbf {C}_0d_0\mathbf {x}_1+\mathbf {K}_0 \mathbf {x}_1=-2\mathbf {M}d_0d_1\mathbf {x}_0-\mathbf {C}_0d_1\mathbf {x}_0\nonumber \\&-\mu _1\mathbf {C}_1d_0\mathbf {x}_0-\mu _1\mathbf {K}_{\mu }\mathbf {x}_0-\sigma \mathbf {K}_{\sigma }\mathbf {x}_0-\xi d_0z_0\mathbf {r}\nonumber \\&-\kappa z_0^3\mathbf {r}-\mathbf {n}(\mathbf {x}_0,\mathbf {x}_0,\mathbf {x}_0)+\eta _1\mathbf {f}_1\cos (\omega t_0)\end{aligned}$$

(9)

$$\begin{aligned} m(&\mathbf {r}^Td_0^2\mathbf {x}_0-d_0^2z_0)-\xi d_0 z_0 -\kappa z_0^3 =0\end{aligned}$$

(10)

$$\begin{aligned} \text {order }\varepsilon ^2: & {} \nonumber \\ \mathbf {M}&d_0^2\mathbf {x}_2+\mathbf {C}_0d_0\mathbf {x}_2+\mathbf {K}_0 \mathbf {x}_2=-\mathbf {M}(d_1^2\mathbf {x}_0\nonumber \\&+2 d_0d_2\mathbf {x}_0+2d_0d_1\mathbf {x}_1)-\mathbf {C}_0 (d_2\mathbf {x}_0+d_1\mathbf {x}_1)\nonumber \\&-\mu _1\mathbf {C}_1(d_0\mathbf {x}_1+d_1\mathbf {x}_0)-\sigma \mathbf {K}_{\sigma }\mathbf {x}_1-\mu _1\mathbf {K}_{\mu }\mathbf {x}_1\nonumber \\&-\xi (d_0z_1+d_1z_0)\mathbf {r}-3\kappa z_0^2z_1\mathbf {r}-3\mathbf {n}(\mathbf {x}_1,\mathbf {x}_0,\mathbf {x}_0)\end{aligned}$$

(11)

$$\begin{aligned} m(&\mathbf {r}^Td_0^2\mathbf {x}_1-d_0^2 z_1)-\xi d_0 z_1 -3\kappa z_0^2z_1=\nonumber \\&2m(d_0d_1z_0-\mathbf {r}^Td_0d_1\mathbf {x}_0)+\xi d_1z_0 \end{aligned}$$

(12)

It should be noted that, because of the vanishingly small values of the mass and damping, as well as of the lack of linear stiffness, no equation of motion relevant to NES appears in the generator problem (order $\varepsilon ^0$), which therefore describes the linear dynamics of the main structure alone (as if NES were disengaged).

First, the homogeneous version of (8) is considered, in order to evaluate the critical condition due to the wind and the complementary function. It is assumed that, at the specific critical value $\mu _0$, the system experiences a Hopf bifurcation, this entailing that the relevant eigenvalue problems

$$\begin{aligned} (\lambda ^2\mathbf {M}+\lambda \mathbf {C}_0+\mathbf {K}_0)\mathbf {u}&=\mathbf {0}\nonumber \\ (\bar{\lambda }^2\mathbf {M}^T+\bar{\lambda }\mathbf {C}^T_0+\mathbf {K}^T_0)\mathbf {v}&=\mathbf {0} \end{aligned}$$

(13)

have a solution $\lambda _{1,2}=\pm i\omega$, with the associated right ($\mathbf {u}$ and $\bar{\mathbf {u}}$) and left ($\mathbf {v}$ and $\bar{\mathbf {v}}$) eigenvectors (the overbar denoting the complex conjugate and i the imaginary unit), whereas all the other eigenvalues have negative real parts and are far from the imaginary axis.

Then, a particular solution of (8) is sought: the external forces are assumed to be 1:1 and 1:3 resonant with the same critical mode $\mathbf {u}$ of the main system (13 $_1$), and this entails that the remaining non-resonant modes bring a higher-order contribution to the overall response. Therefore, only the contribution related to the resonant mode is retained in the solution of (8), i.e.:

$$\begin{aligned} \mathbf {x}_0(t_0,t_1,\ldots )= A(t_1,\ldots )\mathbf {u}e^{i\omega t_0} +\eta _3 \mathbf {w}_0 e^{3i\omega t_0}+cc \end{aligned}$$

(14)

where: $A(t_1,\ldots )$ is a complex modal amplitude, whose modulation on the slower time-scales must be evaluated; cc stands for complex conjugate and $\mathbf {w}_0\mathrel {\mathop :}=\frac{1}{2}[\mathbf {K}_0+3i\omega \mathbf {C}_0-9\omega ^2 \mathbf {M}]^{-1}\mathbf {f}_3$.

The $\varepsilon$-order perturbation equations (9) and (10) are now addressed, and the NES (10) considered first. Since its (steady) solution cannot be expressed by elementary (nor Jacobi) functions, the Harmonic Balance Method is used, letting:

$$\begin{aligned} z_0(t_0,t_1,t_2)=\sum _k B_{0k}(t_1,t_2)e^{i k \omega t_0} +cc \end{aligned}$$

(15)

where $B_{0k}$ are complex amplitudes. In this paper, just the terms relevant to the values $k=1,3$ are retained in (15), coherently with the idea of obtaining an approximated solution, which contains at least the same frequency components of the generating solution (14). Consequently, balancing the frequencies $\omega$ and $3\omega$ in (10), the following nonlinear, complex, algebraic equations are obtained:

$$\begin{aligned} m\omega ^2&(-B_{01}+u A)+i\xi \omega B_{01}+3\kappa (B_{01}^2\bar{B}_{01}+B_{03}\bar{B}_{01}^2\nonumber \\ +\,&2B_{01}B_{03}\bar{B}_{03})=0 \end{aligned}$$

(16)

$$\begin{aligned} m\omega ^2&(-9B_{03}+9\eta _3w_0)+3i\xi \omega B_{03}+\kappa (B_{01}^3+3B_{03}^2\bar{B}_{03}\nonumber \\ +\,&6B_{03}B_{01}\bar{B}_{01})=0 \end{aligned}$$

(17)

where $u\mathrel {\mathop :}=\mathbf {r}^T\mathbf {u}$ and $w_0\mathrel {\mathop :}=\mathbf {r}^T\mathbf {w}_0$.

Equations (16) and (17) provide, at the first order of perturbation, an algebraic constrain between the (active) resonant amplitude A of oscillation of the main structure and the (passive) amplitudes of the NES elongation, $B_{01}$ and $B_{03}$; it, therefore, describes a manifold in the state-space, on which the asymptotic dynamics takes place (at the first perturbation order).

Equation (9) is then considered, in which $z_0$ is assumed as in (15). By requiring that the resonant forcing term is orthogonal to the null space of the adjoint operator (solvability condition), the following equation must hold

$$\begin{aligned} \mathbf {v}^H[&(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u}) d_1 A+(i\omega \mathbf {C}_1\mathbf {u}+\mathbf {K}_{\mu }\mathbf {u})\mu _1 A \nonumber \\&+\sigma \mathbf {K}_{\sigma }\mathbf {u}A+i\omega \xi \mathbf {r}B_{01}\nonumber \\&+3\kappa \mathbf {r}(B_{01}^2\bar{B}_{01}+B_{03}\bar{B}_{01}^2+2B_{01}B_{03}\bar{B}_{03})\nonumber \\&+3A^2\bar{A}\mathbf {n}(\bar{\mathbf {u}},\mathbf {u},\mathbf {u})\nonumber \\&+3\eta _3\bar{A}^2\mathbf {n}(\mathbf {w}_0,\bar{\mathbf {u}},\bar{\mathbf {u}})+6\eta _3^2A\mathbf {n}(\mathbf {w}_0,\bar{\mathbf {w}}_0,\mathbf {u})]=0 \end{aligned}$$

(18)

producing the following differential equation:

$$\begin{aligned} c_1d_1A&=(\mu _1c_2+\sigma c_3+\eta _3^2c_8 )A+\xi c_4B_{01}\nonumber \\&+\kappa c_5(B_{01}^2\bar{B}_{01}+B_{03}\bar{B}_{01}^2+2B_{01}B_{03}\bar{B}_{03})\nonumber \\&+c_6A^2\bar{A}+\eta _3c_7\bar{A}^2+\eta _1 c_9 \end{aligned}$$

(19)

where the expression of the complex coefficients $c_i$ is given in Appendix A. It is worth noticing that, when $B_{01}=B_{03}=\eta _3=0$ is put into (19), this reduces to the normal form equation for the Hopf bifurcation of the principal system. This entails that the NES modifies both the bifurcation point and the limit cycle, thus bringing potential benefits to the mechanical behavior of the original system.

If one decided to stop the perturbation analysis at this step, (19) and (16), (17) should be considered together. In this case, since the NES provides an algebraic constraint, its (complex) amplitudes $B_{01}$ and $B_{03}$ would be passive variables, whereas the dynamic evolution of the (active) amplitude A of the main system would be completely restrained onto the manifold (16), (17). To overcome this tight limitation, a further perturbation step must be accomplished.

The non-diverging solution of (9) can now be evaluated, after tacking into account (19): it contains terms of frequency $\omega$, $3\omega$, $5\omega$, $7\omega$ and $9\omega$. However, still driven by the idea of obtaining and approximated solution, just the terms of frequency $\omega$ and $3\omega$ are retained in it, which turns out to be:

$$\begin{aligned} \mathbf {x}_1(t_0,&\,t_1, t_2)=[(\mu _1\mathbf {w}_1+\sigma \mathbf {w}_2+\eta _3^2\mathbf {w}_3)A+\xi \mathbf {w}_4B_{01}\nonumber \\&+\kappa \mathbf {w}_5(B_{01}^2\bar{B}_{01}+B_{03}\bar{B}_{01}^2+2B_{01}B_{03}\bar{B}_{03})\nonumber \\&+\mathbf {w}_6A^2\bar{A}+\eta _3\mathbf {w}_7\bar{A}^2+\eta _1\mathbf {w}_8]e^{i\omega t_0}\nonumber \\&+[\eta _3\mu _1\mathbf {w}_9+\eta _3\sigma \mathbf {w}_{10}+\xi \mathbf {w}_{11}B_{03}\nonumber \\&+\kappa \mathbf {w}_{12}(B_{01}^3+3B_{03}^2\bar{B}_{03}+6B_{03}B_{01}\bar{B}_{01})\nonumber \\&+\mathbf {w}_{13}A^3+\eta _3\mathbf {w}_{14}A\bar{A}+\eta _3^3\mathbf {w}_{15}]e^{3i\omega t_0}+cc \end{aligned}$$

(20)

where $\mathbf {w}_j$, $(j=1,\ldots ,15)$ are defined in Appendix A.

Equation (12) is finally considered: a new harmonic balance is carried out, assuming the following expression for $z_1$:

$$\begin{aligned} z_1(t_0,t_1,t_2)=\sum _k B_{1k}(t_1,t_2)e^{i k \omega t_0} +cc \end{aligned}$$

(21)

Substituting (14), (15), (20) and (21) in (12) and balancing the $\omega$- and $3\omega$-frequency terms, the following equations are obtained:

$$\begin{aligned} -\,\omega ^2m&[(\mu _1w_1+\sigma w_2+\eta _3^3w_3)A+\xi w_4B_{01}+\kappa w_5(B_{01}^2\bar{B}_{01}\nonumber \\ +\,&B_{03}\bar{B}_{01}^2+2B_{01}B_{03}\bar{B}_{03})+w_6A^2\bar{A}+\eta _3w_3\bar{A}^2\nonumber \\ +\,&\eta _1w_8-B_{11}]-i\omega \xi B_{11}-3\kappa (B_{01}^2\bar{B}_{11}+2 B_{01}\bar{B}_{03}B_{13}\nonumber \\ +\,&2 B_{01}B_{03}\bar{B}_{13}+B_{13}\bar{B}^2_{01}+2B_{01}\bar{B}_{01}B_{11}+2B_{11}\bar{B}_{03}B_{03}\nonumber \\ +\,&2B_{03}\bar{B}_{01}\bar{B}_{11})-2im\omega (d_1B_{01}-u d_1A)\nonumber \\ -\,&i\omega \xi d_1B_{01}=0\end{aligned}$$

(22)

$$\begin{aligned} -9\omega ^2m&[\eta _3\mu _1w_9+\eta _3\sigma w_10+\xi B_{03}w_{11}+\kappa w_{12}(B_{01}^3\nonumber \\ +\,&3B_{03}^2\bar{B}_{03}+6B_{03}B_{01}\bar{B}_{01})+w_{13}A^3+\eta _3w_{14}A\bar{A}\nonumber \\ +\,&\eta _3^3w_{15}-B_{13}]-3i\omega \xi B_{13}-3\kappa (B_{01}^2B_{11}+B_{03}^2\bar{B}_{13}\nonumber \\ +\,&2 B_{01}B_{03}\bar{B}_{11} +2 B_{01}B_{13}\bar{B}_{01}+2 B_{03}B_{13}\bar{B}_{03}\nonumber \\ +\,&2B_{03}B_{11}\bar{B}_{01})-6i\omega md_1B_{03}-3i\omega \xi d_1B_{03}=0 \end{aligned}$$

(23)

where $w_j\mathrel {\mathop :}=\mathbf {r}^T\mathbf {w}_j$, $j=1,\ldots ,15$. Equations (16) and (22), and (17) and (23), can be reconstituted, respectively, using the definitions $B_1\mathrel {\mathop :}= B_{01}+\varepsilon B_{11}$ and $B_3\mathrel {\mathop :}= B_{03}+\varepsilon B_{13}$; coming back to the true time, they become:

$$\begin{aligned} -\,\omega ^2m&[(u+\mu _1w_1+\sigma w_2+\eta _3^3w_3)A+\kappa w_5(B_{1}^2\bar{B}_{1}\nonumber \\ +\,&B_{3}\bar{B}_{1}^2+2B_{1}B_{3}\bar{B}_{3})+w_6A^2\bar{A}+\eta _3w_3\bar{A}^2\nonumber \\ +\,&\eta _1w_8-(1-\xi w_4)B_{1}]-i\omega \xi B_{1}-3\kappa (B_{1}^2\bar{B}_{1}\nonumber \\ +\,&2 B_{1}\bar{B}_{3}B_{3}+B_{3}\bar{B}^2_{1})-2im\omega (\dot{B}_{1}-u \dot{A})\nonumber \\ -\,&i\omega \xi \dot{B}_{1}=0\end{aligned}$$

(24)

$$\begin{aligned} -\,9\omega ^2m&[\eta _3(w_0+\mu _1w_9+\sigma w_{10})+\kappa w_{12}(B_{1}^3\nonumber \\ +\,&3B_{3}^2\bar{B}_{3}+6B_{3}B_{1}\bar{B}_{1})+w_{13}A^3+\eta _3w_{14}A\bar{A}\nonumber \\ +\,&\eta _3^3w_{15}-(1-\xi w_{11})B_{3}]-3i\omega \xi B_{3}\nonumber \\ -\,&\kappa (B_{1}^3+3B_{3}^2\bar{B}_{3}+6B_{3}B_{1}\bar{B}_{1})\nonumber \\ -\,&3i\xi \omega B_{3}-6i\omega m\dot{B}_{3}-3i\omega \xi \dot{B}_{3}=0 \end{aligned}$$

(25)

It appears that (24) and (25) describe the dynamics of the amplitudes $B_1$ and $B_3$, differently from (16) and (17). The key-terms containing $\dot{B}_1$and $\dot{B}_3$ come out only at the second-order, since they are affected by small coefficients $\xi$ and m, thus revealing the nature of singular perturbation . In contrast, the term proportional to $\dot{A}$, which also appears at this order, does not add any qualitative new contributions, being ruled by (19).

If the perturbation procedure is truncated at order $\varepsilon$ for the main system equation, the solvability condition (19) can be written in terms of the true time:

$$\begin{aligned} c_1\dot{A}&=(\mu _1c_2+\sigma c_3+\eta _3^2c_8 )A+\xi c_4B_{1}\nonumber \\&+\kappa c_5(B_{1}^2\bar{B}_{1}+B_{3}\bar{B}_{1}^2+2B_{1}B_{3}\bar{B}_{3})\nonumber \\&+c_6A^2\bar{A}+\eta _3c_7\bar{A}^2+\eta _1 c_9 \end{aligned}$$

(26)

Therefore, the prevalent dynamics of the primary system coupled with NES is described by (26), (24), (25), in terms of the complex variables A, $B_1$ and $B_3$. To get the real form of the system, either the polar or the Cartesian transformations can be applied to the equations: the first one is $A(t)\mathrel {\mathop :}=\frac{1}{2}a(t)e^{i\alpha (t)}$ and $B_k(t)\mathrel {\mathop :}=\frac{1}{2}b_k(t)e^{i\beta _k(t)}$, for $k=1,3$; the second one is $A(t)\mathrel {\mathop :}=\frac{1}{2}(p_1(t)+iq_1(t))$, $B_1(t)\mathrel {\mathop :}=\frac{1}{2}(p_2(t)+iq_2(t))$ and $B_3(t)\mathrel {\mathop :}=\frac{1}{2}(p_3(t)+iq_3(t))$. The substitution of one of the two kinds of transformations in the equations and the separation of real and imaginary parts provides the six real ordinary differential equations in the six real variables ($a(t),\alpha (t),b_1(t),\beta _1(t),b_3(t),\beta _3(t)$ in the polar case, $p_1(t),q_1(t),p_2(t),q_2(t),p_3(t),q_3(t)$ in the Cartesian case). Equilibrium points of the system represent periodic oscillations in the displacements $\mathbf {x},z$.

3 Sample Systems and Numerical Results

Sample systems are analyzed here, (a) to investigate the mechanical effects of the attached NES on the dynamics of the main system; (b) to check the reliability of the MSHBM via comparison with direct numerical integrations of the equations of motion.

3.1 One d.o.f. Main System Under 1:1 External Force

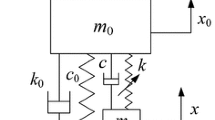
A sample system, already studied in [2, 11, 22], is considered here. The main system consists of a one d.o.f. linear undamped system, with attached NES, a sketch of which is shown in Fig. 2. The nondimensional equations of motion are:

$$\begin{aligned}&\ddot{x}+(\omega ^2+\sigma )x-\xi (\dot{y}-\dot{x})-\kappa (y-x)^3=\eta _1 \cos \omega t\end{aligned}$$

(27)

$$\begin{aligned} m&\ddot{y}+\xi (\dot{y}-\dot{x})+\kappa (y-x)^3=0 \end{aligned}$$

(28)

that, for $z\mathrel {\mathop :}=x-y$, become:

$$\begin{aligned}&\ddot{x}+(\omega ^2+\sigma )x-\xi \dot{z}-\kappa z^3=\eta _1 \cos \omega t\end{aligned}$$

(29)

$$\begin{aligned} m&(\ddot{z}-\dot{x})+\xi \dot{z}+\kappa z^3=0 \end{aligned}$$

(30)

Therefore, comparing (29) and (30) with (3) and (4), it results $N=1$ and:

$$\begin{aligned} \mathbf {x}&=x,\quad \mathbf {M}=1,\quad \mathbf {C}=0,\quad \mathbf {K}_0=\omega ^2,\quad \mathbf {K}_\mu =0,\nonumber \\ \mathbf {K}_\sigma&=1,\quad \mathbf {n}(\mathbf {x},\mathbf {x},\mathbf {x})=0,\quad \mathbf {f}_1=1,\quad \mathbf {f}_3=0 \end{aligned}$$

(31)

Fig. 2

Principal linear undamped oscillator under 1:1 resonant harmonic force with NES

Since the external excitation has just the component of frequency $\omega$, the generating solution does not contain the component of frequency $3\omega$, and so is it for the terms $z_0$ and $z_1$ ($B_{03}=B_{13}=0$), leading just to the balance of the frequency $\omega$. The nonlinear manifold, (16), becomes:

$$\begin{aligned} m\omega ^2(-B_{01}+ A)+i\xi \omega B_{01}+3\kappa B_{01}^2\bar{B}_{01}=0 \end{aligned}$$

(32)

which can be easily written in real form in terms of the (real) amplitudes a and $b_1$:

$$\begin{aligned} \left( \frac{3\kappa b_1^2}{8m\omega }+\frac{\omega b_1}{2}\right) ^2+\left( \frac{\xi b_1}{2m}\right) ^2-\frac{\omega ^2 a^2}{4}=0 \end{aligned}$$

(33)

The set of numerical values considered in [2, 11] is used for this example: $m=0.05$, $\xi =0.01$, $\kappa =0.067$, $\omega =1$.

The Amplitude Modulation Equations (26), (24) read:

$$\begin{aligned} \dot{A}&=\frac{i\sigma }{2\omega }A-\frac{\xi }{2}B_1-\frac{3i\kappa }{2\omega }B_1^2\bar{B}-\frac{i \eta _1}{4\omega }\end{aligned}$$

(34)

$$\begin{aligned} 2im&\omega \dot{A}-(2im\omega +\xi )\dot{B}_1=m\omega ^2A\nonumber \\&+(i\xi \omega -m\omega ^2)B_1+3\kappa B_1^2\bar{B}_1 \end{aligned}$$

(35)

In polar form, they become:

$$\begin{aligned} \dot{a}\,=\,&\frac{3 k b_1^3 \sin (\alpha -\beta _1)}{8 \omega }-\frac{1}{2} \xi b_1 \cos (\alpha -\beta _1)-\frac{\eta _1 \sin \alpha }{2 \omega }\end{aligned}$$

(36)

$$\begin{aligned} a\dot{\alpha }&=\frac{a \sigma }{2 \omega }+\frac{3 b_1^3 k \cos (\alpha -\beta _1 )}{8 \omega }+\frac{1}{2} b_1 \xi \sin (\alpha -\beta _1)\nonumber \\&-\frac{\eta _1 \cos \alpha }{2 \omega }\end{aligned}$$

(37)

$$\begin{aligned} m\dot{a}&\sin (\alpha -\beta _1 )+ ma\dot{\alpha } \cos (\alpha -\beta _1 ) +\frac{\xi }{2 \omega } \dot{b}_1-mb \dot{\beta }_1=\nonumber \\&- \frac{m\omega }{2} a\cos (\alpha -\beta _1 )-\frac{3 b_1^3 k}{8\omega }+\frac{m\omega }{2}b_1\end{aligned}$$

(38)

$$\begin{aligned} m\dot{a}&\cos (\alpha -\beta _1 ) - ma\dot{\alpha }\sin (\alpha -\beta _1 )- m \dot{b}_1 \nonumber \\&- \frac{\xi }{2\omega } b_1 \dot{\beta }_1= \frac{\xi }{2} b_1+ \frac{m\omega }{2} a\sin (\alpha -\beta _1 ) \end{aligned}$$

(39)

When the NES is disengaged, since the main system is linear, the amplitudes of the periodic solutions in x become

$$\begin{aligned} a_e\,=\,&\frac{\eta _1}{\sigma }\end{aligned}$$

(40)

$$\begin{aligned} \tan \alpha _e\,=\,&\frac{a_e\sigma }{2\omega } \end{aligned}$$

(41)

which are always stable. They are the equilibrium points of (36), (37),when $b=0$. Due to the lack of damping in the main system, the amplitude tends to infinite when $\sigma$ goes to zero.

When the NES is considered engaged, the branches of equilibrium points of the dynamical system (36)–(39), which represent periodic oscillations in the original variables x and z, are shown in Fig. 3, for $\eta _1=0.075$. The figure is obtained via the software AUTO [25]. It can be observed that multiple solutions exist in some intervals of $\sigma$. In particular, the three equilibrium points relevant for $\sigma =-0.3$ are marked by colored points, and only the green one is stable, while the yellow and red ones are unstable; black boxes represent secondary Hopf bifurcation points.

Fig. 3

Amplitudes a and b when NES is engaged, when $m=0.05$, $\xi =0.01$, $\kappa =0.067$, $\omega =1$ and $\eta _1=0.075$. The filled squares indicate Hopf bifurcation points. The colored points are equilibria referred to following figures. Continuous line stable; dashed line unstable

The same three equilibrium points are also shown in Fig. 4, superimposed to the nonlinear manifold. Strongly modulated responses (SMR) are detected by numerical integration of the system (36)–(39). They represent quasi-periodic relaxation oscillations in the variables a and b, typically describing cycles around the two folds of the nonlinear manifold shown in Fig. 4. They are triggered in dependence of the position of the equilibrium points. In particular, a Poincaré section is shown (magenta points). For initial conditions close to the stable equilibrium point, a trajectory asymptotically falling on it is also found (black line). The corresponding time evolutions of the (reconstituted) displacement x(t) is shown in Fig. 5, in good agreement with the solutions obtained by numerical integration of the original (27), (28).

Fig. 4

Nonlinear manifold (blue line), three equilibrium points (red, green and yellow points), Poincaré map of the SMR response (magenta points), and transitional motion (black line) falling to the equilibrium point, when $\sigma =-0.3$, $f=0.075$, $m=0.05$, $\xi =0.01$, $\kappa =0.067$, $\omega =1$

Fig. 5

SMR for example 1, when $\sigma =-0.3$, $\eta _1=0.075$, $m=0.05$, $\xi =0.01$, $\kappa =0.067$, $\omega =1$; x(t) as numerical integration of the original (27), (28) (red dashed line) and as reconstituted response from (36)–(39) (blue continuous line)

A discussion on the use of the higher harmonics ($3\omega ,\ldots$) for this example and the evaluation of their negligible contribution is given in [22].

3.2 One d.o.f. Main System Under 1:3 External Force

A second example is considered here concerning an external force in 1:3 subharmonic resonance . The relevant results are believed to be new, and deserve further investigation.

The principal system is of a one d.o.f. nonlinear damped system, with attached NES, as shown in Fig. 6. The nondimensional equations of motion are:

$$\begin{aligned} \ddot{x}&+2\zeta \omega \dot{x}+\omega ^2(1-\sigma )x+\kappa _c x^3\nonumber \\&+\kappa (x-y)^3+\xi (\dot{x}-\dot{y})=\eta _3\cos (3\omega t)\nonumber \\ m\ddot{y}&-\kappa (x-y)^3-\xi (\dot{x}-\dot{y})=0 \end{aligned}$$

(42)

that, for $z\mathrel {\mathop :}=x-y$, become:

$$\begin{aligned} \ddot{x}&+2\zeta \omega \dot{x}+\omega ^2(1-\sigma )x+\kappa _c x^3\nonumber \\&+\kappa z^3+\xi \dot{z}= \eta _3 \cos (3\omega t)\nonumber \\ m&(\ddot{z}-\ddot{x})+\kappa z^3+\xi \dot{z}=0 \end{aligned}$$

(43)

Therefore, comparing (43) with (3) and (4), it results $N=1$ and:

$$\begin{aligned} \mathbf {x}&=x,\quad \mathbf {M}=1,\quad \mathbf {C}=2\zeta \omega ,\quad \mathbf {K}_0=\omega ^2,\quad \mathbf {K}_\mu =0,\nonumber \\ \mathbf {K}_\sigma&=-1,\quad \mathbf {n}(\mathbf {x},\mathbf {x},\mathbf {x})=\kappa _c x^3,\quad \mathbf {f}_1=0,\quad \mathbf {f}_3=1 \end{aligned}$$

(44)

Fig. 6

Principal nonlinear oscillator under 1:3 resonant harmonic force with NES

Here the generating solution of the principal structure contains both the components of frequency $\omega$ and $3\omega$, therefore the balance of both those frequencies in the NES equation is carried out in this case. The polar form of the three Amplitude Modulation Equations (26), (24), (25) reads:

$$\begin{aligned} \dot{a}=\mathscr {F}_1&(a,b_1,b_3,\alpha ,\beta _1,\beta _3)\end{aligned}$$

(45)

$$\begin{aligned} a\dot{\alpha }=\mathscr {F}_2&(a,b_1,b_3,\alpha ,\beta _1,\beta _3)\end{aligned}$$

(46)

$$\begin{aligned} m\omega \dot{a}\sin (&\alpha -\beta _1)+m\omega \dot{\alpha }\cos (\alpha -\beta _1)+\frac{\xi }{2}\dot{b}_1\nonumber \\&-m\omega b_1\dot{\beta }_1=\mathscr {F}_3(a,b_1,b_3,\alpha ,\beta _1,\beta _3)\end{aligned}$$

(47)

$$\begin{aligned} m\omega \dot{a}\cos (&\alpha -\beta _1)-m\omega \dot{\alpha }\sin (\alpha -\beta _1)-\frac{\xi }{2}b\dot{\beta }_1\nonumber \\&-m\omega \dot{b}_1=\mathscr {F}_4(a,b_1,b_3,\alpha ,\beta _1,\beta _3)\end{aligned}$$

(48)

$$\begin{aligned} \frac{\xi }{2}\dot{b}_3-3m&\omega b_3\dot{\beta }_3=\mathscr {F}_5(a,b_1,b_3,\alpha ,\beta _1,\beta _3)\end{aligned}$$

(49)

$$\begin{aligned} \frac{\xi }{2}b\dot{\beta }_3+3&m\omega \dot{b}_3=\mathscr {F}_6(a,b_1,b_3,\alpha ,\beta _1,\beta _3) \end{aligned}$$

(50)

where $\mathscr {F}_j$, $j=1,\ldots ,6$, are reported in Appendix A.

If the NES were disengaged, just (45) and (46) would be retained, being $b_k\equiv \beta _k\equiv 0$, and the steady state response of the system, describing periodic oscillations for x(t), is described by the solution of the system $\mathscr {F}_1=\mathscr {F}_2=0$ (see [19]). In particular the steady state response is governed by the equation

$$\begin{aligned} (\zeta \omega )^2+\Bigl (\Bigl (-\frac{\sigma \omega }{2}+\frac{3\kappa _c \eta _3^2}{64\omega ^5}\Bigr )+\frac{3\kappa _c}{8\omega }a^2\Bigr )^2=\Bigl (\frac{3\kappa _c\eta _ 3a}{32\omega ^3}\Bigr )^2 \end{aligned}$$

(51)

which, besides $a=0$ existing everywhere, defines the non-trivial response for the subharmonic resonance condition, which exists in the range

$$\begin{aligned} \sigma \ge \frac{21\eta _3^3\kappa _c}{256\omega ^6}+\frac{256\zeta ^2\omega ^6}{3\eta _3^2\kappa _c} \end{aligned}$$

(52)

The frequency-response plot of the subharmonic response is shown in Fig. 7 in black line, for $\eta _3=0.3, \zeta =0.01,\omega =1,\kappa _c=-5$. It is superimposed to the corresponding one, which is obtained when NES is engaged (red line) for $m=0.05, \xi =0.01,\kappa =1$. In particular, the NES reduces the amplitude of the subharmonic response and its domain of existence; furthermore, in comparison with the case with NES disengaged, it is found that the basin of attraction of the subharmonic response in presence of NES is noticeably reduced in favor of the trivial solution. Moreover, relaxation oscillations are found by means of numerical integrations of (45)–(50). Their phase plot is shown in Fig. 8 (red line) as superimposed to the nonlinear manifold (gray points), which is a surface in the $(b_1,b_3,a)$ space. The relaxation oscillations here described have maximum amplitudes smaller than the corresponding (periodic) oscillations which occur when the NES is disengaged (see Fig. 9).

Fig. 7

Frequency-response curve in correspondence of the 1:3 resonance for the system with NES disengaged (black line) and with NES engaged (red line), for $\eta _3=0.3$. Continuous line stable; dashed line unstable

Fig. 8

Nonlinear manifold (gray points) and relaxation oscillations (red line) for $\sigma =-0.5,\eta _3=0.3$

Fig. 9

Time-evolution of the primary system with NES disengaged in subharmonic resonance (black line) and with NES engaged (red line), for $\eta _3=0.3$ and $\sigma =-0.5$

3.3 A Two d.o.f. Airfoil

A sample system, already considered in [15, 23], is used to investigate the mechanics of a primary structure subjected to steady wind . It is constituted by a two d.o.f. rigid airfoil engaged to a NES and subjected to the (non-dimensional) steady wind $\mu$, and is sketched in Fig. 10. The (non-dimensional) Lagrangian parameters are x and $\varphi$, representing the plunge and the pitch, respectively. The two nonlinear springs, extensional and rotational respectively, have both linear and cubic coefficients. The position of the NES with respect to the center of mass of the airfoil is described by the (non-dimensional) parameter $\delta$: if it is positive, then the NES is windward, otherwise, if $\delta$ is negative, the NES is leeward. The non-dimensional equations of motion are

Fig. 10

Rigid airfoil with NES under steady wind

$$\begin{aligned} \ddot{x}&+n_{12}\ddot{\varphi }+\mu g_{11}\dot{x}+\Omega ^2 x+\mu ^2g_{11}\varphi -\xi (\dot{y}-\dot{x}+\dot{\alpha }\delta )\nonumber \\&-\kappa (y-x+\alpha \delta )^3+n_1x^3=0\nonumber \\ n_{12}&\ddot{x}+n_{22}\ddot{\varphi }+\mu g_{21}\dot{\varphi }+k_{21}x+(n_{22}-\mu ^2g_{21})\varphi \nonumber \\&+\xi (\dot{y}-\dot{x}+\dot{\alpha }\delta )\delta +\kappa (y-x+\alpha \delta )^3\delta +n_2\varphi ^3=0\nonumber \\ m&\ddot{y}+\xi (\dot{y}-\dot{x}+\dot{\alpha }\delta )+\kappa (y-x+\alpha \delta )^3=0 \end{aligned}$$

(53)

The comparison between (53) and (1) allows one to identify $N=2$ and the relevant matrices and columns as

$$\begin{aligned} \mathbf {x}&=\begin{Bmatrix} x\\ \varphi \end{Bmatrix},\; \mathbf {M}=\begin{bmatrix} 1&n_{12}\\ n_{12}&n_{22} \end{bmatrix},\; \mathbf {C}(\mu )=\mu \begin{bmatrix} g_{11}&0\\ g_{21}&0 \end{bmatrix},\nonumber \\ \mathbf {K}(\mu )&=\begin{bmatrix} \Omega ^2&\mu ^2g_{11}\\ k_{21}&n_{22}-\mu ^2g_{21} \end{bmatrix},\; \mathbf {r}=\begin{Bmatrix} 1\\ -\delta \end{Bmatrix},\;\mathbf {n}=\begin{Bmatrix} n_1x^3\\ n_2\varphi ^3 \end{Bmatrix} \end{aligned}$$

(54)

The following numerical values are chosen, corresponding to those used in [15]: $n_{12}=n_{21}=0.2$, $n_{22}=0.25$, $g_{11}=0.2$, $g_{21}=-0.08$, $\Omega =0.5$, $k_{21}=0$, $n_1=n_2=1$, $m=0.02$, $\xi =0.008$. For the specified values, the critical wind turns out to be $\mu _0=0.8704$, the corresponding critical frequency $\omega =0.8704$ (imaginary part of the eigenvalue) and the right and left eigenvectors $\mathbf {u}=\{0,\, 1 \}^T$ and $\mathbf {v}=\{-0.6521-0.5635i,\, 0.5217+ 2.7486 i \}^T$, respectively. The relevant Amplitude Modulation Equations are not reported in their explicit form for the sake of brevity.

Fig. 11

Equilibrium branches of the slow flow on the plane $(\mu _1,a)$: a $\kappa =10$, $\delta =0.75$; b $\kappa =10$, $\delta =-0.75$. Red line without NES; black line with NES; dots numerical integrations of the originating equations; continuous line stable; dashed line unstable; black square secondary Hopf point

In Fig. 11 the equilibrium branches of the AME, corresponding to periodic motions in the variables $x,\varphi ,z$, are shown for (a) windward NES ($\delta =0.75$) and (b) leeward NES ($\delta =-0.75$). The red line describes the branch when the NES is disengaged, and the dots represent results of the numerical integration of the original equations (53), which are in good agreement. It can be seen that, when the NES is disengaged, a super-critical Hopf bifurcation occurs at $\mu _1=0$ and stable periodic motions are triggered for increasing values of $\mu _1$, whose amplitudes are represented by the red line. The NES shifts forward the position of the bifurcation points, but it also makes the bifurcation sub-critical. Indeed two turning points occur, as well as two secondary Hopf bifurcation points which trigger stable periodic motions in a, corresponding to quasi-periodic motions in x, $\varphi$ and z (the amplitude of the limit cycles are shown in the pictures). In case of windward NES (Fig. 11a), next to the second turning point, the amplitude of the branch is larger than that without NES. It means that, in this case, the NES gives a harmful contribution to the dynamics of the system. On the other hand, in case of leeward NES (Fig. 11b), the branch of the amplitude is always underneath the one corresponding to the case without NES. Therefore, for leeward NES, the effective reduction of the amplitude of oscillations is accomplished. These results are in agreement with [2]. The two vertical dashed-dotted green lines in Fig. 11 represent the values of $\mu _1$ for which the phase portraits of Fig. 12 are produced ($\mu _1=0.05$ and $\mu _1=0.07$, respectively). In particular, from Fig. 12a it is evident how the stable equilibrium point (black circle), which lies on the manifold, asymptotically attracts the dynamic evolution of the system; as a correspondence, periodic oscillations in the variables $(x,\varphi ,z)$ are produced. On the other hand, in Fig. 12b, realized for a value of $\mu _1$ between the two secondary Hopf bifurcations, the equilibrium points are unstable, and a limit cycle in (b, a) is obtained. It corresponds to quasi-periodic oscillations in $(x,\varphi ,z)$, which are in good agreement with the relevant results of the numerical integrations of the originating equations (53).

Fig. 12

Phase portrait on the plane (b, a): a $\kappa =10$, $\mu _1=0.05$, $\delta =0.75$; b $\kappa =10$, $\mu _1=0.07$, $\delta =-0.75$. Red line manifold; blue line trajectory; black circle stable equilibrium point; black cross unstable equilibrium point

3.4 Nonlinear Elastic String

A nonlinear extensible elastic string PQ is considered (see Fig. 13 and [24] for details on this case study). The string is restrained at P, while a concentrated mass $m_Q$ and a vertical elastic spring of linear stiffness $k_Q$ are applied at Q. The string is supposed of initial length $\ell$ and prestress tensile force $\bar{N}$. An external, distributed, harmonically time-dependent, force $p(x)\cos (\Omega t)$ is supposed to be applied to the string (x being the abscissa measured in the prestressed configuration and t the time). The mass per unit length of the string is $\rho$ and its longitudinal stiffness EA. A NES characterized by a mass m, cubic stiffness coefficient k and linear damping coefficient c, is linked to the string at point C, corresponding to the abscissa $x_C$. Denoting by v(x, t) the in-plane transverse displacement of a generic point of the string and by y(t) the displacement of the NES, the nonlinear equations of motion, up to the cubic order, read (see [19, 26] for the equations of motion of the string, obtained after the classic condensation procedure of the longitudinal displacement and valid under the hypothesis of large ratio between the celerity of longitudinal vs. transverse waves)

$$\begin{aligned} \bar{N}&v''(x,t)+\frac{EA}{\ell }v''(x,t)\left[ \int _0^{\ell }\!\!\frac{v'^2(x,t)}{2}dx\right] -\rho \ddot{v}(x,t)\nonumber \\&+p(x)\cos (\Omega t)-\left[ k(v(x,t)-y(t))^3\right. \nonumber \\&\left. +\,c(\dot{v}(x,t)-\dot{y}(t))\right] \delta (x-x_C)=0\nonumber \\ m&\ddot{y}(t)-\left[ k(v(x_C,t)-y(t))^3\right. \nonumber \\&\left. +\,c\,(\dot{v}(x_C,t)-\dot{y}(t))\right] =0 \end{aligned}$$

(55)

where $\delta (x)$ is the Dirac delta , the dot indicates time-derivative and the prime space-derivative.

Fig. 13

Internally nonresonant elastic string equipped with a NES

The geometric boundary condition at P states that $v(0,t)=0$, while the mechanical boundary condition, to be applied at Q, reads

$$\begin{aligned} \bar{N}&v'(\ell ,t)+\frac{EA}{\ell }v'(\ell ,t)\left[ \int _0^{\ell }\!\!\frac{v'^2(x,t)}{2}dx\right] \nonumber \\&= -k_Q v(\ell ,t)-m_Q\ddot{v}(\ell ,t) \end{aligned}$$

(56)

In nondimensional form, the partial differential problem becomes:

$$\begin{aligned} \ddot{v}&+\zeta \dot{v}-v''-\eta v''\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] \nonumber \\&+\left[ \kappa z^3+\xi \dot{z}\right] \delta (x-x_C)=p\cos (\Omega t)\nonumber \\ m&(\ddot{z} -\ddot{v}_C)+\kappa z ^3+\xi \dot{z} =0 \end{aligned}$$

(57)

and the relevant boundary conditions are:

$$\begin{aligned} v&(0,t)=0\nonumber \\ v'&(1,t)+\eta v'(1,t)\left[ \int _0^{1}\!\!\frac{v'^2}{2}dx\right] \nonumber \\&= -k_Q v(1,t)-m_Q \ddot{v}(1,t) \end{aligned}$$

(58)

where $v_C(t)\mathrel {\mathop :}=v(x_C,t)$, $\eta =EA/\bar{N}$ and $z(t)\mathrel {\mathop :}=v(x_C,t)-y(t)$, and an external linear damping is introduced through the coefficient $\zeta$.

The application of a Galerkin projection of (57)–(58), using as trial functions the first N eigenfunctions $\varphi _j(x)=\sin (\omega _j x)$ ($j=1,\ldots ,N$) of the homogeneous linearized problem when NES is disengaged ($\omega _j$ are the natural frequencies of the string), allows one to obtain a discrete, approximate, version of the equations of motion, which read as (3) and (4). In particular, indicating with $x_j(t)$ the unknown modal amplitudes ($v(x,t)=\sum _{j=1}^Nx_j(t)\varphi _j(x)$), the relevant matrices and columns read:

$$\begin{aligned} \mathbf {x}&=\{x_h\},\; \mathbf {M}=\{m_{hk}\},\; \mathbf {C}=\{c_{hk}\},\nonumber \\ \mathbf {K}&=\{k_{hk}\},\; \mathbf {r}=\{r_{h}\},\;\mathbf {n}=\{n_{h}\} \end{aligned}$$

(59)

where

$$\begin{aligned} m_{hk}={\left\{ \begin{array}{ll} 1\\ 0 \end{array}\right. },\, c_{hk}={\left\{ \begin{array}{ll} 2\xi _h\omega _h\\ 0 \end{array}\right. },\, k_{hk}={\left\{ \begin{array}{ll} \omega _h^2&{}h=k\\ 0&{}h\ne k \end{array}\right. } \end{aligned}$$

(60)

and

$$\begin{aligned} \mathbf {r}&=\{\varphi _h(x_C)\},\quad \mathbf {n}=\Bigl \{n_hx_h\sum _{j=1}^Nj^2x_j^2\Bigr \},\nonumber \\ \mathbf {f}_1&=\{p_h\},\quad \mathbf {f}_3=\{0\} \end{aligned}$$

(61)

with $n_h$ elastic coefficients, $\xi _h$ modal damping factors and $p_h$ modal forces, $h,k=1,\ldots ,N$.

Actually, the MSHBM was extended in [24] for infinite dimensional systems, i.e. directly working on partial differential equations as (57) with b.c. (58). Being the results in very good agreement with those obtained for a Galerkin projection with large N, here pictures relevant to the direct case of [24] are shown, obtained when $\eta =2.825$, $m_Q=0.3167$ and $k_Q=3.9\times 10^{-3}$, the external force is assumed as uniform ($p(x)\equiv p$) with frequency $\Omega =\omega _2(1+\sigma )$ close to the 1:1 resonance with the second mode of the string (here the detuning is directly applied to the forcing frequency and not considered as a modification of the stiffness) and the external damping coefficient of the string is $\zeta =1.557\%$. The (nondimensional) parameters of the NES are $m=0.05$, $\kappa =400$, $\xi =0.01$. Moreover, the first four (nondimensional) natural frequencies of the string are $\omega _1=1.208$, $\omega _2=3.831$, $\omega _3=6.722$, $\omega _4=9.738$. The NES is supposed to be applied at about the antinode of the resonant mode, i.e. $x_C=0.4$. In the generating solution, the contribution of the resonant mode is retained only, so that it contains just the term of frequency $\omega =\omega _2$; the harmonic balance is then applied exclusively in correspondence of the frequency $\omega$. The relevant Amplitude Modulation Equations are not shown here for the sake of brevity.

Amplitude of periodic motions of both the string and NES, for force amplitude value $\eta _1=0.007$, are shown in Fig. 14 in terms of frequency detuning $\sigma$. In particular, in Fig. 14a, the frequency-response curve obtained for disengaged NES (black curve) is superimposed to the corresponding curve obtained when NES is engaged (red line). In Fig. 14b, the amplitude of oscillation b of the NES is shown. Blue points represent Hopf bifurcations. It is evident the beneficial effect of the NES, whose presence reduces the peak of the string amplitude of oscillations a.

Fig. 14

Frequency-response curves of the string (a) and NES (b), for $\eta _1=0.007$. Red line response with NES at the antinode; black line response with NES disengaged. Blue points indicate Hopf bifurcations. Continuous line stable; dashed line unstable

In Fig. 15a, b, the WMR (for $\sigma =0.064$) and SMR (for $\sigma =0.070$) are superimposed to the invariant manifold, respectively. The first one develops itself close to the fold of the invariant manifold, while the second one describes relaxation oscillations around it.

Fig. 15

Weakly modulated response ($\sigma =0.064$, blue line (a)) and strongly modulated response ($\sigma =0.070$, black line (b)) with NES at the antinode, for $\eta _1=0.007$; red line invariant manifold. Continuous line stable; dashed line unstable

In Fig. 16, the periodic time-evolutions of the vertical displacement of the mid-span of the string ($v_m\mathrel {\mathop :}=v(1/2,t)$)is shown for $\sigma =0.02$. They are superimposed to the corresponding evolutions (dotted line) obtained by time-integration of the approximated system of ODE, which is drawn after the Galerkin projection of (57), (58) on a basis constituted by the 8 first natural modes of the string. They show a very good agreement.

Fig. 16

Periodic time-evolution of the string mid-span, for $p=0.007$ and $\sigma =0.02$. Continuous line reconstituted functions from MSHBM; dotted line reconstituted functions from a discrete Galerkin model

4 Conclusions

In this paper, a general, nonlinear, multi-d.o.f. system, equipped with an essentially nonlinear oscillator with small mass, NES, is considered. Aim of the NES is to passively control the amplitude of vibrations of the primary system, which here is excited by concurrent effect of steady wind, inducing a Hopf bifurcation, and both 1:1 and 1:3 resonant harmonic forces; no internal resonances are allowed. The MSHBM is applied in order to obtain the Amplitude Modulation Equations, which turn out to be singular perturbed equations. Numerical results are shown for different case studies, in order to detect the single effect of the excitations and how the NES modifies the predominant dynamics of the principal system. The outcomes guarantee good agreement with the response as obtained by numerical integrations of the equations of motion; moreover they assure good reliability of the MSHBM (a) to detect the predominant dynamics of the system and (b) to be used as valid tool for optimization purposes in the choice of the parameters and position of the NES.

Appendix A: Coefficients of the Equations

The index H indicates the Hermitian (transpose and complex conjugate). The expression of the coefficients of (19) are:

$$\begin{aligned} c_1&= 2i\omega \mathbf {v}^H\mathbf {M}\mathbf {u}+\mathbf {v}^H\mathbf {C}\mathbf {u},\quad c_2=-i\omega \mathbf {v}^H\mathbf {C}_1\mathbf {u}-\mathbf {v}^H\mathbf {K}_\mu \mathbf {u},\nonumber \\ c_3&= -\mathbf {v}^H\mathbf {K}_\sigma \mathbf {u},\quad c_4 = -i\omega \mathbf {v}^H\mathbf {r},\quad c_5=-3\mathbf {v}^H\mathbf {r},\nonumber \\ c_6&= -3\mathbf {v}^H\mathbf {n}(\mathbf {u},\mathbf {u},\bar{\mathbf {u}}),\quad c_7=-3\mathbf {v}^H\mathbf {n}(\mathbf {w}_0,\bar{\mathbf {u}},\bar{\mathbf {u}}),\nonumber \\ c_8&= -6\mathbf {v}^H\mathbf {n}(\mathbf {u},\mathbf {w}_0,\bar{\mathbf {w}}_0),\quad c_9=\frac{1}{2}\mathbf {v}^H\mathbf {f}_1 \end{aligned}$$

(62)

In (20) the column matrices $\mathbf {w}_j$ ($j=1,\ldots ,8$) are the solutions of the following singular algebraic problems:

$$\begin{aligned} \mathbf {w}_1:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_1=-i\omega \Bigl (\mathbf {C}_1\mathbf {u}\nonumber \\&-\frac{1}{c_1}(\mathbf {v}^H\mathbf {C}_1\mathbf {u})(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\nonumber \\&-\Bigl (\mathbf {K}_\mu \mathbf {u}-\frac{1}{c_1}(\mathbf {v}^H\mathbf {K}_\mu \mathbf {u})(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(63)

$$\begin{aligned} \mathbf {w}_2:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_2=-\Bigl (\mathbf {K}_\sigma \mathbf {u}\nonumber \\&-\frac{1}{c_1}(\mathbf {v}^H\mathbf {K}_\sigma \mathbf {u})(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(64)

$$\begin{aligned} \mathbf {w}_3:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_3=-6\Bigl (\mathbf {n}(\mathbf {u},\mathbf {w}_0,\bar{\mathbf {w}}_0)\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {n}(\mathbf {u},\mathbf {w}_0,\bar{\mathbf {w}}_0)(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(65)

$$\begin{aligned} \mathbf {w}_4:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_4=-i\omega \Bigl (\mathbf {r}\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {r}(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(66)

$$\begin{aligned} \mathbf {w}_5:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_5=-3 \Bigl (\mathbf {r}\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {r}(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(67)

$$\begin{aligned} \mathbf {w}_6:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_6=-6\Bigl (\mathbf {n}(\mathbf {u},\mathbf {u},\bar{\mathbf {u}})\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {n}(\mathbf {u},\mathbf {u},\bar{\mathbf {u}})(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(68)

$$\begin{aligned} \mathbf {w}_7:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_7=-6\Bigl (\mathbf {n}(\mathbf {w}_0,\bar{\mathbf {u}},\bar{\mathbf {u}})\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {n}(\mathbf {w}_0,\bar{\mathbf {u}},\bar{\mathbf {u}})(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr )\end{aligned}$$

(69)

$$\begin{aligned} \mathbf {w}_8:\qquad (\mathbf {K}_0&+i\omega \mathbf {C}_0-\omega ^2\mathbf {M})\mathbf {w}_8=-\frac{1}{2} \Bigl (\mathbf {f}_1\nonumber \\&-\frac{1}{c_1}\mathbf {v}^H\mathbf {f}_1(2i\omega \mathbf {M}\mathbf {u}+\mathbf {C}_0\mathbf {u})\Bigr ) \end{aligned}$$

(70)

The solution is made unique by the normalization condition $\mathbf {w}_j^T\mathbf {u}=0$.

Moreover $\mathbf {w}_j$ ($j=9,\ldots ,15$) are the solutions of the following non-singular algebraic problems, in which, however, compatibility is satisfied.

$$\begin{aligned} \mathbf {w}_9:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_9=-3i\mathbf {C}_1\mathbf {w}_0-\mathbf {K}_\mu \mathbf {w}_0\end{aligned}$$

(71)

$$\begin{aligned} \mathbf {w}_{10}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{10}=-\mathbf {K}_\sigma \mathbf {w}_0\end{aligned}$$

(72)

$$\begin{aligned} \mathbf {w}_{11}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{11}=-3i\omega \mathbf {r}\end{aligned}$$

(73)

$$\begin{aligned} \mathbf {w}_{12}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{12}=-\mathbf {r}\end{aligned}$$

(74)

$$\begin{aligned} \mathbf {w}_{13}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{13}=-\mathbf {n}(\mathbf {u},\mathbf {u},\mathbf {u})\end{aligned}$$

(75)

$$\begin{aligned} \mathbf {w}_{14}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{14}=-6\mathbf {n}(\mathbf {w}_0,\mathbf {u},\bar{\mathbf {u}})\end{aligned}$$

(76)

$$\begin{aligned} \mathbf {w}_{15}:\qquad (\mathbf {K}_0&+3i\omega \mathbf {C}_0-9\omega ^2\mathbf {M})\mathbf {w}_{15}=-3\mathbf {n}(\mathbf {w}_0,\mathbf {w}_0,\bar{\mathbf {w}}_0) \end{aligned}$$

(77)

In (45)–(50), the expressions of the right hand side terms are:

$$\begin{aligned} \mathscr {F}_1&=-\zeta \omega a-\frac{3}{32\omega ^3}\eta _3\kappa _c a^2\sin (3\alpha )-\frac{1}{2}\xi b_1\cos (\alpha -\beta _1)\nonumber \\&+\frac{3}{8\omega }\kappa b_1^3\sin (\alpha -\beta _1)+\frac{3}{8\omega }\kappa b_1^2b_3\sin (\alpha +2\beta _1-\beta _3)\nonumber \\&+\frac{3}{4\omega }\kappa b_1b_3^2\sin (\alpha -\beta _1)\end{aligned}$$

(78)

$$\begin{aligned} \mathscr {F}_2&=\frac{3}{64\omega ^5}\eta _3^2\kappa _c a-\frac{\sigma \omega }{2}a-\frac{3}{32\omega ^3}\eta _3\kappa _c a^2\cos (3\alpha )+\frac{3}{8\omega }\kappa _c a^3\nonumber \\&+\frac{1}{2}\xi b_1\sin (\alpha -\beta _1)+\frac{3}{8\omega }\kappa b_1^3\cos (\alpha -\beta _1)\nonumber \\&+\frac{3}{8\omega }\kappa b_1^2b_3\cos (\alpha +2\beta _1-\beta _3)+\frac{3}{4\omega }\kappa b_1b_3^2\cos (\alpha -\beta _1)\end{aligned}$$

(79)

$$\begin{aligned} \mathscr {F}_3&=-\frac{1}{2}m\omega ^2 a\cos (\alpha -\beta _1)+\frac{1}{2}m\omega ^2 b_1\nonumber \\&-\frac{3}{8}\kappa b_1^2b_3\cos (3\beta _1-\beta _3)-\frac{3}{4}\kappa b_1b_3^2\end{aligned}$$

(80)

$$\begin{aligned} \mathscr {F}_4&=\frac{1}{2}m\omega ^2 a\sin (\alpha -\beta _1)+\frac{1}{2}\xi \omega b_1-\frac{3}{8}\kappa b_1^2b_3\sin (3\beta _1-\beta _3)\end{aligned}$$

(81)

$$\begin{aligned} \mathscr {F}_5&=\frac{9}{8}\eta _3 m\cos (\beta _3)-\frac{9}{64}\eta _3 m\sigma \cos (\beta _3)+\frac{27}{32}\eta _3m\zeta \sin (\beta _3)\nonumber \\&+\frac{27}{4096\omega ^6}\eta _3^3m\kappa _c\cos (\beta _3)+\frac{27}{128\omega ^2}\eta _3m\kappa _c a^2\cos (\beta _3)\nonumber \\&-\frac{9}{64}\kappa _c ma^3\cos (3\alpha -\beta _3)-\frac{1}{8}\kappa b_1^3\cos (3\beta _1-\beta _3)\nonumber \\&-\frac{9}{64}\kappa m b_1^3\cos (3\beta _1-\beta _3)+\frac{9}{2}m\omega ^2b_3\nonumber \\&-\frac{3}{4}\Bigl (1+\frac{9}{8}\mu _1\Bigr )\kappa b_1^2b_3-\frac{3}{8}\Bigl (1+\frac{9}{8}\mu _1\Bigr )\kappa b_3^3\end{aligned}$$

(82)

$$\begin{aligned} \mathscr {F}_6&=\frac{27}{32}\eta _3 m \zeta \cos (\beta _3)-\frac{9}{8}\Bigl (1-\frac{1}{8}\sigma \Bigr )\eta _3 m\sin (\beta _3)\nonumber \\&-\frac{27}{4096\omega ^6}\eta _3^3\kappa _c m\sin (\beta _3)-\frac{27}{128\omega ^2}\eta _3\kappa _c ma^2\sin (\beta _3)\nonumber \\&-\frac{9}{64}\kappa _c m a^3\sin (3\alpha -\beta _3)-\frac{1}{8}\Bigl (1+\frac{9}{8}m\Bigr )\kappa b_1^3\sin (3\beta _1-\beta _3)\nonumber \\&-\frac{3}{2}\Bigl (1+\frac{9}{8}m\Bigr )\xi \omega b_3 \end{aligned}$$

(83)