Keywords

1 Introduction

After the discovery of carbon nanotubes (CNTs) by Iijima [1], numerous opportunities and possibilities have been opened to produce an entire generation of new materials and structures that possesses unique physical properties [2]. Study of the CNTs is one of the most promising domains in the area of physics, mechanics, chemistry, and material science [3]. The application of CNTs lies within a wide range, including nanocomposites, nanodevices, and nanoelectronics [4–9]. The studies indicate that CNTs possess significant material properties that distinguish them from any known material. For example, the elastic modulus of CNTs is reported to be more than 1 TPa. In addition, they are also particularly flexible in bending and can undergo large elastic deformation without breaking [10]. The investigation of the behavior of CNTs are mainly divided into two groups of computational and experimental approaches. Molecular dynamics and continuum mechanics approaches (e.g. the finite element method (FEM)) have been the most common computational techniques to investigate the behavior of CNTs [11]. Due to numerous applications of CNTs in mechanical aspects, the investigation of their buckling behavior is crucially important. The following paragraph summarizes several related studies where the buckling behavior of CNTs was investigated.

In 2003, Pantano et al. [12] presented a nonlinear structural mechanics based approach for simulating the deformation of single- and multi-walled carbon nanaotubes (MWCNTs). They applied shell finite elements for the modeling the individual tubes, where a particular pairing of elastic properties and mechanical thickness of the tube wall was identified to enable successful modeling based on the shell theory. They also simulated the effects of van der Waals forces with special interaction elements. They validated their molecular dynamics simulations with high resolution micrographs available in literature [13]. They also investigated the mechanics of wrinkling of MWCNTs, demonstrating the role of the multi-walled shell structure and interwall van der Waals interactions in governing buckling and post-buckling behavior. Later in 2010, Guo and Zhang [14] investigated the bending stiffness of SWCNTs by using the molecular mechanics model and the deformation mapping technique. They proposed an analytical expression for the bending stiffness of SWCNTs. They finally showed that the bending stiffness of a SWCNT is approximately proportional to the cube of its radius.. The effect of defects on the buckling behavior of CNTs was investigated by Ghavamian and Öchsner [15]. Their study was based on the FEM. In detail, they modeled two basic CNTs in their perfect form. Then the buckling behavior of CNTs was evaluated by comparing their critical loads obtained from the simulation and analytical calculations. They concluded that the existence of any curvature in the structure of nanotubes decreases their buckling strength.

The main objective of the actual work is to continue and broaden the previous studies and investigate the buckling behavior of CNTs in the case of different bending angles.

2 Methodology

2.1 Geometric Definition

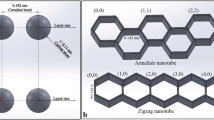
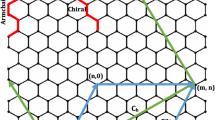
CNTs are some kind of hollow cylinder shaped structure based on the major similarity between a CNT and graphene atomic configuration, as illustrated in Fig. 1. Having the diameters ranging from 1 to 50 nm and length over 10 µm, these nanostructures can be imagined by rolling a graphene sheet into a cylinder. The geometry of a CNT is defined by the chiral vector \(\vec{C}_{h}\) and the chiral angle \(\theta\). The chiral vector is presented by two unit vectors \(\vec{a}_{1}\) and \(\vec{a}_{2}\) and two integers \(m\) and \(n\) as it is presented by the following equation [16]:

Fig. 1
figure 1

Side view of the (10,10) CNT as a space-frame structure

Full size image
$$\vec{C}_{h} =m \vec{a}_{1} + n\vec{a}_{2} ,$$
(1)

The structure of CNTs is defined based on the chiral vector or angle by which the sheet is rolled into a cylinder, in three different configurations including zigzag, armchair and chiral. In the case of (\(\theta = 0^{\circ}\)) or (\(m = 0\)) the zigzag CNT is constructed. An armchair CNT is obtained if, in terms of chiral vector (\(m = n\)) or in terms of chiral angle (\(\theta = 30^{\circ}\)), and finally a chiral CNT is shaped if (\(0^{\circ} < \theta < 30^{\circ}\)) or (\(m \ne n \ne 0\)) [16].

Based on the following equation, the diameter of the CNT can be calculated:

$$d_{\text{CNT}} = a_{0} \sqrt {m^{2} + mn + n^{2} } /\pi ,$$
(2)

where \(a_{0} = \sqrt 3 b\) and \(b = 0.142\) nm is the length of the C–C bond [16].

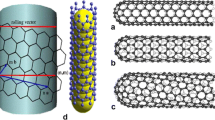
Our modeling method follows the idea first suggested in [17] where the theory of classical structural mechanics was extended into the modeling of carbon nanotubes: In a CNT, carbon atoms are bonded together by covalent bonds which have their characteristic lengths and angles in a three-dimensional space. Then, it was suggested that CNTs, when subjected to loading, act as space-frame configurations. Therefore, the bonds between carbon atoms are considered as connecting load-carrying generalized beam members, while the carbon atoms behave as joints of the members. This idea is illustrated in Fig. 1.

In this paper, the models of armchair and zigzag SWCNTs were simulated by the CoNTub software [18]. Defining the chirality and the length of the tubes, the spatial coordinates of the C-atoms and the corresponding connectivities (i.e. the primary bonds between two nearest-neighboring atoms) were calculated. Then the gathered data was transferred to a commercial finite element package, where C–C bonds were modeled as circular beam elements [19]. Afterwards, the FE analyses were conducted and buckling behavior of different zigzag and armchair CNTs was evaluated.

The phenomenon of buckling is in its simplest form a specific kind of elastic instability in a slender structure that occurs under certain compressive loads. In the basic theory of elasticity, the critical buckling load of a straight elastic beam is presented in Eq. 3 [20]:

$$P_{\text{cr}} = \frac{{n^{2} \pi^{2} EI}}{{(KL)^{2} }}$$
(3)

In the above equation, \(n\) represents as the buckling mode and \(I\) is the structure’s second moment of area. As the classical structure of CNTs is mostly presented by a hollow cylinder, Eq. 4 can be used to obtain analytical results for straight CNTs as:

$$I = {{\pi \left[ {\left( {d + t} \right)^{4} - \left( {d - t} \right)^{4} } \right]} \mathord{\left/ {\vphantom {{\pi \left[ {\left( {d + t} \right)^{4} - \left( {d - t} \right)^{4} } \right]} {64}}} \right. \kern-0pt} {64}}$$
(4)

In which \(t\) is the thickness of the tube’s shell and \(d\) represents the diameter of the pertaining tube [17]. It should be noted that different assumptions for the shell thickness t can be found in literature, see for example [21, 22]. We assign here the same value as in [21, 22] where the thickness of a single-walled carbon nanotube was assumed to be the same as the interlayer spacing of graphite (0.34 nm).

2.2 Material Parameters and Boundary Conditions

In this study, the buckling behavior of numerous types of SWCNTs under cantilevered boundary conditions is investigated, in which one end is fully fixed and the other end is completely free. Figure 2 illustrates an armchair CNT under cantilevered boundary condition. The models of CNTs were simulated from straight CNTs to curved CNTs with 45° bending angle.

Fig. 2
figure 2

Armchair CNT with cantilevered boundary conditions and different forms from 0° to 45° bending angle

Full size image

In order to define the properties of the equivalent beam elements for the CNT bonds, the same values for the equivalent beam elements are assumed as in the approach proposed in [2, 17, 22]. These effective material and geometrical properties were obtained in the mentioned references based on a molecular mechanics approach.

3 Results and Discussion

The buckling properties of different zigzag and armchair SWCNTs were investigated and the effect of bending angle was taken into consideration. Their critical loads (to be more precise, the first positive buckling mode since this is in practical applications the most critical one) of CNTs were obtained analytically and computationally, applying an FE approach. Afterwards, both methods were compared in the case of the straight CNTs in order to have some kind of validation of the FE approach. For the FE method, zigzag and armchair CNTs with lengths of 15 and 15.4 nm, respectively, were simulated by a commercial finite element package (MSC. Marc). Then, as illustrated in Fig. 3, by introducing arbitrary compressive point loads to one of the CNT’s end, the buckling behavior of the CNTs was investigated for cantilevered boundary condition with different curvatures from 0° to 45° bending angle (one end fixed and the other end free). Finally, the computations yielded the critical buckling loads of the CNTs. Two different boundary conditions were considered at the free end. For the first case the applied load was perpendicular to the end surface, i.e. there is an angle between the X-axis and the line of action, and for the second case the applied load was in direction to the X-axis as shown in Fig. 3. The CNTs were assumed to be hollow cylinders, so that by using Eq. 3 their critical loads were evaluated as an analytical solution. In this equation we considered K = 2 for the cantilevered case.

Fig. 3
figure 3

(10,10) zigzag CNT’s first mode under buckling load in original and buckled shape with a the first case and b the second case of cantilevered boundary conditions

Full size image

The simulated CNTs and their characteristics are presented in Table 1.

Table 1 Characteristic of simulated CNTs
Full size table

The relative difference between the analytical solution and FEM result is defined by the following equation:

$${\text{Relative difference in }} \% = \left| {\frac{{{\text{FEM result}} - {\text{analytical solution}}}}{\text{analytical solution}}} \right| \times 100$$
(5)

This difference is listed in Table 1 for each CNT. Based on the results, it can be concluded that the computational solutions are in good agreement with the analytical calculations. It was revealed that the critical buckling load of both straight armchair and zigzag CNTs increases by increasing the chiral number as shown in Fig. 4.

Fig. 4
figure 4

(10,10) zigzag CNT’s first mode under buckling load in original and buckled shape with a the first case and b the second case of cantilevered boundary conditions

Full size image

Having a closer look on the results, it can be also concluded that the buckling strength of armchair and zigzag CNTs decreases by increasing the bending angle for both cases of boundary condition, as illustrated in Fig. 5. However, it should be noted that this trend is more obvious for the CNTs with higher chirality, as the decrease of critical buckling load for both armchair and zigzag CNTs with lower chirality is almost negligible. It is also indicated that the gradual decrease for the first case of boundary condition is more significant comparing to the second case at higher curvatures.

Fig. 5
figure 5figure 5

Change in critical buckling load (\(P_{\text{cr}}\)) with a armchair and b zigzag CNTs for the first case and with c armchair and d zigzag CNTs for the second case

Full size image

4 Conclusions

In this research, several SWCNTs (zigzag and armchair) were simulated by an FE approach and their buckling behavior was investigated through performing several computational tests with cantilevered boundary condition and different variable bending angles. Towards achieving the most accurate results the buckling behavior of these CNTs were evaluated analytically and computationally and were compared together. It was concluded that the critical buckling load of both straight armchair and zigzag CNTs increases by increasing the chiral number. It was also shown that the buckling strength of armchair and zigzag CNTs with higher chirality decreases by introducing bending angles for both cases of boundary condition. Nevertheless, the change of increasing the bending angle on the critical buckling load of armchair and zigzag CNTs with lower number of chirality is almost negligible. The finding of this study may have useful effects on further investigations of armchair and zigzag CNTs.