Influence of Bending Angle on Mechanical Performance of SWCNTs and DWCNTs Based on Molecular Mechanics: FE Approach

Abstract

Purpose

Material properties of CNTs are frequently not validated due to experimental limitations. Because of the experimental limitations, authors considered a simulation-based technique created on molecular mechanics concept for incorporating mechanical characteristics of single-walled and double-walled carbon nanotubes.

Method

Authors performed a tensile analysis on SWCNTs (armchair, zigzag and chiral) and DWCNTs (chiral–chiral, zigzag–zigzag, and armchair–armchair) to predict Young’s modulus, stress and ultimate strength of tubes. Authors considered the vdW (van der Waals) in the middle of two nanotubes in DWCNTs prototypes. Here, in analysis, novelty is various bending angles ranging from 0$^\circ$ to 90$^\circ$ considered by authors.

Results

Authors considered the vdW in between the two tubes which is a more accurate method to evaluate the mechanical properties of DWCNTs. So, authors considered with and without vdW in between two tubes and compared. Authors also observed that when vdW is considered between two tubes, then Young’s modulus of DWCNTs is higher than the without vdW.

Conclusion

It is clearly observed that when bending angle increased, the Young’s modulus of SWCNTs of all three types of tubes decreased.

Introduction

Iijima [1] was first who discovered carbon nanotubes (CNTs) in 1991 by rolling the graphene sheet. From that time, many technologies are used to synthesize and manufacture CNTs for development. Carbon nanotubes have been shown to have unique thermal, electrical, and mechanical properties in several studies [2]. CNTs are sketchily categorized into three groups, according to the total number of nanotubes, they are categorized as SWCNTs, DWCNTs and MWCNTs namely as single, double, and multi-walled carbon nanotube. But if classified according to the chirality, then there are three types of CNTs listed as chiral $\left(\left(m,n\right),n\ne m\right)$, zigzag $\left(\left(m,n\right),n=m\right)$, and armchair $\left(\left(m,n\right),m=0\right)$. Because of their unique electrical properties, CNTs are frequently utilized in MEMS and NEMS, namely micro- and nano-electromechanical systems. The armchair and zigzag CNTs structure have similar properties to conductor and semiconductor based on the various studies carried out by many researchers [3].

Therefore, it is very important for many researchers to enumerate the mechanical properties of CNTs. Furthermore, the study of mechanical properties of CNTs requires the use of number of high-precision instruments. As a result, many researchers employ the molecular dynamics (MD) simulation method or the continuum mechanics-based FE technique (FEA). Using a bulk system based on numerical mechanics, MD simulation may be used to calculate numerous physical parameters of CNTs at the nanoscale. These models are based on a potential energy model that simulates atom-to-atom interactions; also, the number of atoms in the system has a significant impact on the computation cost and numerical analysis findings [4]. FEM involves the usage of element types to show an atomic model. To depict atom bonding connections, the beam and spring elements are frequently utilized. However, applying a potential energy version to such a binding connection is difficult, and the number of degrees of freedom (DOF) available for expressing atom performance is limited. The mechanical characteristics of SWCNTs and DWCNTs are analyzed using a molecular mechanics (MM)-based FE technique and a FE model is proposed.

CNTs was investigated in a variety of domains, including molecular dynamics, material science, and others. Furthermore, understanding the mechanical properties of CNTs based on continuum mechanics is required.

Smalley [5], who earned the Nobel Prize in chemistry in 1996 for discovering the soccer-ball-shaped C60 fullerene molecule, has claimed that continuum elasticity can be used to depict them when the diameter of nanomaterials is less than a few atoms.

Ru [6] applied to evaluate flexible bending of ropes-based single-walled carbon nanotubes under high pressure using a new dynamic honeycomb structure (SWCNT). The critical pressure is given as a purpose of thickness to radius ratio and Young's modulus using a simple formula. They have a high level of agreement with studies that have been published. Ru [7] constructed an anisotropic flexible shell prototype used for small-radius SWCNTs.

Gradient technique is also utilized to analyze distortion and fracture processes at the nano- and microscales, where A.C. Eringen’s non-local concept is utilized widely. It describes the gradient technique of E.C. Aifantis as employed to plastic and elastic distortions, with a focus by nanocrystalline polycrystals and ultra-fine grain (UFG), as well as a comparison to the non-local concept [8, 9].

Aifantis and Askes [10] concentrated at a broad class of gradient flexibility concepts in which higher-order terms are Laplacian of the lower-order terms. Keeping the number of additional constitutive parameters to a minimal is one of the tasks of creating gradient flexibility concepts. The eradication of individualities in dynamics and statics, new numerical results indicates the size-dependent mechanical reaction calculated by gradient flexibility.

A dynamic study of a flexible gradient-related polymeric fiber exposed to a periodic stimulation was investigated by Xu et al. [11]. For the strain and displacement fields of the fiber, analytic results in the type of Fourier series are supplied. It is defined as size effects since it is based on a dimensionless scale factor such as the length ratio to diameter.

To represent the dynamical behaviors of CNTs, Aifantis and Askes [12] used non-local flexibility and gradient flexibility within the structure of traditional improved Timoshenko beam theory or Euler Bernoulli. There was qualitative understanding through the projections of similar molecular dynamics models, but the molecular dynamics outcomes were notably different from those produced using traditional flexibility estimates. Likewise, they examined the relationship among gradient elasticity and classical solutions. Similarly, they changed the detail that will agree to this principle to be applied using the Aifantis [13] and Ru [6, 7] methodologies.

The free vibrations of a double-walled carbon nanotube (DWCNT) were explored by Xu et al. [14]. Van der Waals forces interact between the inner and outer carbon nanotubes, which are treated as two independent elastic beams. Their findings suggest that a DWNT has a unique invariable frequency that is unaffected by diverse boundary condition combinations. The resonance frequency of DWNTs of various lengths is discussed. Furthermore, the proposed simulation calculates a new coaxial–noncoaxial vibrational mode in DWNT inner and outer tubes with fixed-simple supports. He also used gradient elasticity with internal inertia to investigate the free transverse vibration of a DWNT. Internal inertia and scale’s influence on vibration behaviors were investigated. The results show that the proposed strain gradient–internal inertia generalized elasticity model's internal length and time parameters have no effect on the bottom level coaxial–noncoaxial vibration modes [15].

Belytschko et al. [16] used molecular mechanics simulations to investigate the fracture of carbon nanotubes. The fracture behaviors are discovered to be almost independent of the separation energy and to be predominantly dependent on the interatomic potential inflection point. A zigzag nanotube's fracture strain is estimated to be 10–15 percent, which matches experimental data rather well. The fracture strengths of chiral and armchair nanotubes have been calculated to be in the range of 65–93 GPa. In the experiments, carbon nanotube breakage is predicted to be brittle.

Using a molecular mechanics-based finite element approach, Meo and Rossi [17] tested the tensile strength of zigzag and armchair single-walled CNTs with nonlinear spring elements. The maximal strain and stress were compared quantitatively to the results of other simulated studies. The tensile fracture behaviors of single-walled CNTs were anticipated by Rossi and Meo [18], who also gave the fracture stress and strain. Giannopoulos et al. [19] used beam and spring link elements to simulate single-walled CNTs and defined the interatomic interactions of atoms in terms of bonding forces using the elastic strain energy of the beam, as recommended by classical structural mechanics. They also used structural mechanics to predict the Young’s modulus and shear modulus of carbon nanotubes based on their thickness and diameter. The finite element approach has been applied to atomic models of CNTs, which are considered single structures based on classical structural mechanics. Fan et al. [20] studied the Young’s and shear modulus of MWCNTs by changing the CNTs diameter.

Molecular mechanics and classical plate theory are found to be in good agreement when using this thickness in free vibration investigations of clamped cases, which removes the impact of dangling bonds, using the atomistic-continuum approach [21, 22]. Yan et al. [23] investigated longitudinal and torsional free vibration of single-walled boron nitride nanotubes.

Authors considered all three forms of CNTs—chiral, zigzag, and armchair, along with incorporating a novel aspect in their study: varied bending angles ranging from 0° to 90°. As the chirality, tube length, and bending angle change, the Young’s modulus of SWCNTs changes. Authors used the vdW between the two tubes to analyze the mechanical properties of DWCNTs, which is a more accurate method.

Carbon Nanotube Structure

Carbon nanotubes are tubes made from graphene sheets that have been rolled into tubes. The rolling direction of graphene sheets determines the chirality of CNTs. This roll direction is determined by a “chiral vector,” which can be written as a unit translational vector. Ch can be written as follows:

$${\text{Ch}} = na_{1} + \, ma_{2} ,\quad (n \ge m)$$

(1)

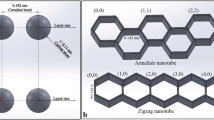
The basic vectors a₁ and a₂ are used in this example. The translation, which is the decisive factor of the structure around the circumference, is represented by the index’s “n” and “m.” The translation lattice indices (n, m), as well as the base vectors a₁ and a₂, are shown in Fig. 1. The type of CNTs [24] is defined by the chiral vector (Ch) and the chiral angle (θ).

Fig. 1

Nanotube parameters on a 2D graphene sheet

Chirality can be categorized [25] into three types: armchair, zigzag, or chiral. Figure 2 depicts these. CNTs have an armchair structure if $n$ and $m$ are identical in Eq. (1). If n and m are known, Eq. (2) can be used to calculate the diameter of the CNT.

$$D_{n} = \frac{{a_{{\text{c - c}}} \sqrt {3\left( {n^{2} + m^{2} + nm} \right)} }}{\pi }$$

(2)

Fig. 2

The chirality of carbon nanotube structures

Here, a_C–C is 0.142 nm; this is the initial bond length of C–C in a honeycomb lattice.

The chiral structure such as chiral, zigzag, and armchair, features a chiral angle (θ). This has a range of 0° ≤ θ ≤ 30° and applying in Eq. (3).

$$\theta_{{{\text{ch}}}} = \sin^{ - 1} \left( {\frac{\sqrt 3 m}{{2\sqrt {n^{2} + nm + m^{2} } }}} \right) = \tan^{ - 1} \left( {\frac{\sqrt 3 m}{{2n + m}}} \right)$$

(3)

The chiral vector $({C}_{h})$ and translation vector $(T)$ of a graphene sheet are defined as the ideal rectangular cutting region and can be calculated using Eq. (4).

$$T = \left( {\frac{2m + n}{W}} \right)a_{1} + \left( { - \frac{2m + n}{W}} \right)a_{2} ,$$

(4)

where W is defined as the greatest common divisor of 2m + n and 2n + m.

Using Eq. 5, the original graphene sheet coordinates $\left({x}^{^{\prime}}-{y}^{^{\prime}}\right)$ were translated to a new x–y–z coordinate system for CNTs in this study. The cylindrical coordinate value along the ${y}^{^{\prime}}$-axis can be obtained using the T vector. The radius of the CNTs is denoted by R.

$$\left( {x,y,z} \right) = \left( {R \cos \left( {\frac{{x^{\prime}}}{R}} \right),R \sin \left( {\frac{{x^{\prime}}}{R}} \right),y^{\prime}} \right)$$

(5)

The chiral index variation $\left(m,n\right)$ shows the various types of CNTs. Basic types of the CNTs such as zigzag $\left(m,0\right), \mathrm{i}.\mathrm{e}., n=0$, armchair $\left(m,m\right),\mathrm{ i}.\mathrm{e}., n=m$ and chiral $\left(m,n\right), \mathrm{i}.\mathrm{e}., n\ne m$. Figure 2 depicts the various forms of nanotubes [26,27,28]. Figure 2 depicts three types of CNTs such as zigzag, armchair and chiral structures; however, the current work focuses on armchair, zigzag and chiral CNT structures.

Molecular Mechanics Theory

The Morse potential energy model used in this study employs finite element analysis to discover atomic behaviors on a single link nonlinear bond stretch (Carbon–Carbon) and nonlinear bond angle (Carbon–Carbon–Carbon). As the gap among two carbon atoms grows apart, the attraction force increases and decreases, while the Carbon–Carbon bond is detached as the attractiveness force approaches to zero. The nonlinear property of the honeycomb lattice in tension on bond angle bending was considered. Except for bonding stretching and bond angle bending, all Morse potential energy factors were ignored in this analysis because they had no effect on tension [16,17,18, 28,29,30].

With an attached mass, study the modes of vibration of single-walled and double-walled carbon nanotubes [31]. Investigated by Luo et al. [32], the free vibration characteristics of an axisymmetric nanostructure subjected to uniformly distributed radial stresses.

Patel and Joshi [33,34,35] looked at the vibrational analysis of a DWCNTs that was simulated with spring elements and zeptogram masses. Ardeshana et al. [36,37,38] study of DWCNCs for resonance-based applications is discussed.

Linear Behaviors of Carbon–Carbon and Carbon–Carbon–Carbon

In general, Eq. (6) can be used to express total potential energy. Total potential energy is made up of bond stretching, bond angle bending, dihedral angle torsion, van der Waals, out-of-plane torsion, and electrostatic potential energy elements. The interatomic interactions of the atoms are seen in Fig. 3. Uniaxial tensile study was used in this investigation, which only considered bond angle bending and bond stretch; other energies are assumed to have just a minor influence [16,17,18, 28,29,30].

$$U_{{{\text{Total}}}} = \sum U_{{\text{r}}} + \sum U_{\theta } + \sum U_{\emptyset } + \sum U_{{\text{w}}} + \sum U_{{{\text{vdw}}}} + \sum U_{{{\text{electrostatic}}}}$$

(6)

Fig. 3

In molecular mechanics, interatomic contact [44]

Bond stretch and bond angle bending energy expressions are transformed to a Harmonic function that is simple. Equation 7 represents the Harmonic function that is simple form of global potential energy.

$$U\left( t \right) = \frac{1}{2}kx^{2} \left( t \right) = \frac{1}{2}kA^{2} \cos^{2} \left( {\omega t - \varphi } \right)$$

(7)

We used Eq. (7) to derive energy terms for stretching, bending, and torsion based on molecular mechanics principle. We thought that axial, bending, and torsional stiffness, as well as the force constant, were in a balanced condition. Equations (8–10) [39] can be used to explain the increment function in terms of atom bond distance, bond stretching, bond angle, and bond torsion.

$$U_{{\text{r}}} = \frac{1}{2}k_{{\text{r}}} \left( {r - r_{0} } \right)^{2} = \frac{1}{2}k_{{\text{r}}} \left( {\Delta r} \right)^{2}$$

(8)

$$U_{{\text{r}}} = \frac{1}{2}k_{\theta } \left( {\theta - \theta_{0} } \right)^{2} = \frac{1}{2}k_{\theta } \left( {\Delta \theta } \right)^{2}$$

(9)

$$U_{{\text{r}}} = U_{\emptyset } + U_{{\text{w}}} = \frac{1}{2}k_{\tau } \left( {\Delta \emptyset } \right)^{2} .$$

(10)

Equations (11–13) can be used to calculate the axial flexible strain energy $\left({U}_{\mathrm{A}}\right)$, bending elastic strain energy $\left({U}_{\mathrm{M}}\right)$, and torsional elastic strain energy $\left({U}_{\mathrm{T}}\right)$ of a homogenous beam. L is the beam’s length, which is the same as the length of the bond $\left({a}_{\mathrm{c}-\mathrm{c}}\right)$ of Carbon–Carbon described in Sect. 2, and A is the beam element's cross-section area.

$$U_{{\text{A}}} = \frac{1}{2}\mathop \int \limits_{0}^{L} \frac{{F^{2} }}{EA}dL = \frac{1}{2}\frac{{F^{2} L}}{EA} = \frac{1}{2}\frac{EA}{L}\left( {\Delta L} \right)^{2} , \quad {\text{where}} \;\frac{EA}{L} = K_{{\text{r}}}$$

(11)

$$U_{{\text{M}}} = \frac{1}{2}\mathop \int \limits_{0}^{L} \frac{{M^{2} }}{EI}dL = \frac{2EI}{L}\alpha^{2} = \frac{1}{2}\frac{EI}{L}\left( {2\alpha } \right)^{2} , \quad {\text{where}}\; \frac{EI}{L} = K_{\theta } ,$$

(12)

$$U_{{\text{T}}} = \frac{1}{2}\mathop \int \limits_{0}^{L} \frac{{T^{2} }}{GJ}dL = \frac{1}{2}\frac{{T^{2} L}}{GJ} = \frac{1}{2}\frac{GJ}{L}\left( {\Delta \beta } \right)^{2} , \quad {\text{where}}\; \frac{GJ}{L} = K_{\tau } .$$

(13)

The constant of molecular mechanics [24] (${k}_{\mathrm{r}}=938 \mathrm{kcal} {\mathrm{mol}}^{-1}{\mathrm{A}}^{-2}$, ${k}_{\theta }=126 {\text{kcal mol}}^{-1}/{\mathrm{rad}}^{2 }$, ${k}_{\tau }=40 {\text{kcal mol}}^{-1}/{\mathrm{rad}}^{2}$) was derived from published experiment results for graphite sheets in this investigation. It is founded on the concept that the structural qualities ${k}_{\mathrm{r}}=6.53\times {10}^{-7} \mathrm{N}/\mathrm{nm}$, ${k}_{\theta }=8.79\times {10}^{-10} \mathrm{N}/{\mathrm{rad}}^{2} \; \mathrm{and} \; {k}_{\tau }=2.79\times {10}^{-10} \mathrm{N}/{\mathrm{rad}}^{2}$ of a beam element's stiffness are identical when it comes to the atoms’ bonding force. Beam elements have elastic characteristics are: $d=0.147 \mathrm{nm}$, $J=4.58\times {10}^{-5}\mathrm{N}/{\mathrm{nm}}^{4}$, $G=8.70 \times {10}^{-7}\mathrm{N}/{\mathrm{nm}}^{2}$, $E=5.486\times {10}^{-6 }\mathrm{N}/{\mathrm{nm}}^{2}$. Equation (14) was used to calculate the beam elements properties such as diameter, shear modulus and Young’s modulus. Elastic properties were applied to the finite element model for the investigation.

$$d = 4\sqrt {\frac{{k_{\theta } }}{{k_{\tau } }}} ,\quad E = \frac{{k_{\tau }^{2} L}}{{4\pi k_{\theta } }}\quad {\text{and}}\quad G = \frac{{k_{r}^{2} k_{\tau } L}}{{8\pi k_{\theta }^{2} }}.$$

(14)

Carbon–Carbon and Carbon–Carbon–Carbon Nonlinear Performance

Through a molecular mechanics-based FE technique, the steric potential energy equation described in Carbon–Carbon and Carbon–Carbon–Carbon have linear behaviors section was used to calculate the nonlinear performance of Carbon–Carbon and Carbon–Carbon–Carbon bond. The different notations for distinguishing linearity and nonlinearity are shown in Eq. (15).

$${\psi _{{\rm{Total}}}} = \sum {\psi _{\rm{r}}} + \sum {\psi _\theta } + \sum {\psi _\emptyset } + \sum {\psi _{\rm{w}}} + \sum {\psi _{{\rm{vdw}}}} + \sum {\psi _{{\rm{electrostatic}}}}.$$

(15)

The bonding energy correlation of Carbon–Carbon–Carbon or Carbon–Carbon was studied using a Potential energy model of Morse. The model is based on Meo and Rossi’s [17] suggested molecular mechanics theory. The general Potential energy model of Morse is represented by Eq. (16). Equation (16) is changed to characterize the bond angle functions that increase for Carbon–Carbon–Carbon and bond length functions that increase for Carbon–Carbon, that are presented in Eqs. (17–18) [17, 18, 27].

$$\psi \left( r \right) = D_{e} \left( {e^{{ - 2a\left( {r - r_{0} } \right)}} - 2e^{{ - a\left( {r - r_{0} } \right)}} } \right),$$

(16)

$$\psi \left( r \right) = D_{e} \left( {\left[ {1 - e^{{ - \beta \left( {r - r_{0} } \right)}} } \right]^{2} - 1} \right),$$

(17)

$$\psi \left( \theta \right) = \frac{1}{2}k_{\theta } \left( {\theta - \theta_{0} } \right)^{2} \left[ {1 + k_{{{\text{sextic}}}} \left( {\theta - \theta_{0} } \right)^{4} } \right].$$

(18)

Equations (17–18) are used to transform into Eqs. (19–20), respectively. These equations can be employed in a variety of situations to compute bonding force based on the bond length for Carbon–Carbon–Carbon and the moment based on the bond angle for Carbon–Carbon–Carbon. Starting bond angle and length for Carbon–Carbon and Carbon–Carbon–Carbon were adjusted to ${r}_{0}=0.139 \mathrm{nm}$ and ${\theta }_{0}=2.094 \mathrm{rad}$, individually, for Carbon–Carbon and Carbon–Carbon–Carbon. The following were the other parameters: ${D}_{e}=6.03105{e}^{-10}\mathrm{N} \mathrm{nm}, \beta =26.25 {\mathrm{nm}}^{-1}, {k}_{\mathrm{sextic}}=0.754 {\mathrm{rad}}^{-4}\mathrm{and} {k}_{\theta }=0.9{e}^{-9}\mathrm{N} \mathrm{nm}/{\mathrm{rad}}^{-2}$ [17, 18, 27].

$$F\left( {r - r_{0} } \right) = 2\beta D_{e} \left( {1 - e^{{ - \beta \left( {r - r_{0} } \right)}} } \right)e^{{ - \beta \left( {r - r_{0} } \right)}} ,$$

(19)

$$M\left( {\theta - \theta_{0} } \right) = k_{\theta } \left( {\theta - \theta_{0} } \right)\left[ {1 + 3k_{{{\text{sextic}}}} \left( {\theta - \theta_{0} } \right)^{4} } \right].$$

(20)

Uniaxial tensile analysis was carried out in this study under the assumption that vdW, electrostatic forces, out-of-plane torsion and dihedral angle torsion had no influence [17, 18, 27, 39, 40].

The bond stretch force and bond angle moment for the Carbon–Carbon and Carbon–Carbon–Carbon bonds were estimated using a FE model, as shown in Fig. 4. The findings of the FE investigation are matched with Eqs. (19–20).

Fig. 4

Single bonding notion in FE modeling [44]

The force–strain curve generated by means of FE technique and results of the analytical solution were both uniform. The moment curvature curve was also approximately consistent according to the bond angle of Carbon–Carbon–Carbon. This means that by analyzing the behavior of a single bond (Carbon–Carbon or Carbon–Carbon–Carbon), the entire CNTs structure is dependent on the Morse potential energy model.

Modeling of SWCNTs and DWCNTs

For SWCNTs and DWCNTs, FE models were created. The nodal coordinates for the FE models were obtained by transforming the graphene sheet's coordinates to tubular coordinates for the CNTs applying Eq. (5). An edge effect, according to WenXing et al. [41], influenced the experimental results when the aspect ratio was smaller than 10. The aspect ratio (L_CNT/D_n) of the CNTs’ diameter (D_n) and total length (L_CNT) was set to 12 or greater. Aspect ratios of 14–15 were used to produce CNTs FE models. The commercial mesh generating application Ansys APDL 14.5 was used to generate a CNT FE model with beam components (BEAM188); Fig. 5 displays a graphic representation of the model. FE models for MWCNTs and SWCNTs with chirality were generated using this method.

Fig. 5

Hexagonal structure of a CNT (modeled in FE software)

To develop FE models intended for the architectures of SWCNTs and DWCNTs with varied chirality, we utilized the commercial finite element code of ANSYS APDL 14.5 to use a molecular mechanics-based FE approach to execute a uniaxial tensile study. Uniaxial tensile analysis was performed on SWCNTs having chiral, zigzag, and armchair type chirality. For the armchair, zigzag, and chiral of DWCNTs structures, uniaxial tensile tests are carried out. Fixed boundary condition set to the node on one side of CNT and on other side of force displacement is applied for the analysis purpose. The boundary conditions and loading condition of SWCNTs (a) Armchair (7,0), (b) Chiral (5,3) and (c) Zigzag (4,4) are shown in Fig. 6.

Fig. 6

Modeling with finite elements of different SWCNTs configurations with loading and boundary condition a Armchair (7,0), b Chiral (5,3), and c Zigzag (4,4)

vdW Interaction for DWCNTs

To create the vdW connections between two different nanotube walls, the 6–12 Lennard–Jones potentials are used [42, 43]. The corresponding energy is calculated as follows:

$$V_{{{\text{LJ}}}} = 4\varepsilon \left[ {\left( {\frac{\sigma }{r}} \right)^{12} - \left( {\frac{\sigma }{r}} \right)^{6} } \right].$$

(21)

$\epsilon$ and $\sigma$ are the Lennard–Jones factors. Atomic distance is denoted by r. The spring element is used to replicate the interface between dissimilar walls of MWCNTs. Stiffness of spring elements is derived by differentiating Eq. (21) with reference to r as given below. In Ansys APDL 14.5, COMBINE 14 elements is used to generate a Van der Waals interaction between two CNTs.

Spring elements in the structural system are supposed to imitate the Van der Waals forces caused by non-covalent contacts. Differentiating Eq. (21) yields the force operating on such a spring element, which is equal to

$$F_{{{\text{LJ}}}} = \frac{dV\left( r \right)}{{dr}} = 4\frac{\varepsilon }{r}\left[ { - 12\left( {\frac{\sigma }{r}} \right)^{12} + 6\left( {\frac{\sigma }{r}} \right)^{6} } \right]$$

(22)

Finally, the structural model uses the parameters in Eqs. (11–13) and (22) to characterize molecular behavior. The values in Eq. (11–13) are enough to describe the physical model of SWCNTs (which have only beam element (covalent bonds)). In the case of MWCNTs, the vdW linkages between Caron–Carbon atoms in separate homocentric tubes must also be considered, hence Eq. (22) is also employed. Authors considered the two cases: one is with vdW and second is without vdW, for the prediction of the mechanical properties of DWCNTs. Figure 7 shows the boundary and loading condition of DWCNTs for without and with van der Waals condition. For simple interpretation of the model in ANSYS 14.5, authors colored the inner tube blue, the outer tube green, and van der Waals (vdW) yellow. Authors also considered various bending angles stating from $0^\circ \mathrm{to} 90^\circ$ as shown in Fig. 8.

Fig. 7

Finite element model of Different configurations of DWCNT a Armchair ((7,0) and (11,0)), b Chiral ((5,3) and (8,4)) and c Zigzag ((4,4) and (6,6)) with loading and boundary condition, without and with van der Waals

Fig. 8

Methodology used for making the various tubes and various bending angle

Validation of the Model

The Young’s modulus and ultimate strength results simulated by FEM proximity have been identified, as shown in Table 1. However, the current model is validated for different bending angle (0$^\circ$, 22.5$^\circ$, 45$^\circ$ 67.5$^\circ$ to 90$^\circ$) of SWCNT using FEA technique.

Table 1 Comparison of Young’s modulus and ultimate strength between Doh and Lee [44] and present model for different types of SWCNT

Results and Discussion

The linear elasticity of a material or structure is indicated by the Young's modulus, which is the relationship between stress and strain. In the context of mechanical engineering, the elastic quality of the material is represented by this modulus. Young’s modulus was analyzed in respect of CNT diameter in current work from the mechanical engineer’s perspective through the uniaxial tensile analysis of chiral, zigzag and armchair varieties of SWCNTs. SWCNTs and DWCNTs would prevent permanent deformation owing to yielding if they acted (i.e., unloading and loading) in this straight zone. Aspect ratio and geometric influences have been shown to alter Young's modulus in the literature [41, 43]. Tube length and diameter are geometric shapes which influence the mechanical performance of SWCNTs, according to many numerical studies. In SWCNTs, DWCNTs and MWCNTs, as the diameter of the nanotube increases, the Young's modulus increases as well [20].

The total reaction forces are (${F}_{\mathrm{total}}$) acquired by FE analysis and the total CNTs area (${A}_{0}$) are used to apply Young’s modulus determined from Eq. (23) to the elastic region using Hooke’s law. The area of SWCNT and DWCNT are calculated using the formulas from Eq. (24) and Eq. (25), respectively. ${D}_{0}$ is the outer diameter and ${D}_{i}$ inner diameters of DWCNTs, separately, and $t=0.34 \mathrm{nm}$. The beginning size of CNTs is denoted by ${L}_{0}$, while its displacement is denoted by $\Delta L$. Young’s modulus of DWCNT changes due to the change in diameter of DWCNT are verified by this technique.

$$E = \frac{\sigma }{\varepsilon } = \left( {\frac{{F_{{{\text{total}}}} /A_{0} }}{{\Delta L/L_{0} }}} \right),$$

(23)

$$A_{{{\text{swcnt}}}} = D_{{{\text{cnt}}}} \times \pi \times t,$$

(24)

$$A_{{{\text{dwcnt}}}} = \frac{{\pi \times \left[ {\left( {D_{0} + t} \right)^{2} - \left( {D_{i} - t} \right)^{2} } \right]}}{4}$$

(25)

Authors considered the three SWCNTs tube such as Armchair {(4,4) and (5,5)}, Zigzag {(7,0) and (9,0)} and Chiral {(5,3) and (6,4)}. Authors took the tube length and diameter of the tubes such that the ${L}_{\mathrm{cnt}}/D$ ratio is in between 14 and 15. Table 2 shows that the number of atoms and number of bonds are used to make the molecular model of above stated SWCNTs tubes in the ANSYS 14.5. Moreover, diameter, length and ${L}_{\mathrm{cnt}}/D$ ratio are also included in the Table 2.

Table 2 Structure matters for SWCNTs and DWCNTs

Authors cared about the three DWCNTs tube such as Armchair {(4,4) and (6,6)}, Zigzag {(7,0) and (11,0)} and Chiral {(5,3) and (8,4)}. Authors took the tube length and diameter of the tubes such that the ${L}_{\mathrm{cnt}}/D$ ratio is in between 11.5 and 12.5 for comparison. Table 2 shows that the number of atoms, number of bonds and vdW are used to make the molecular model of above-listed DWCNTs tubes in the ANSYS 14.5. Moreover, inner, and outer diameter, length and ${L}_{\mathrm{cnt}}/D$ ratio are also incorporated in the Table 2.

Effect of Bending Angle on Young’s Modulus

Authors reflected the above-listed SWCNTs and DWCNTs tubes as shown in Table 2 for incorporating the mechanical properties of tubes. Authors also considered the various bending angle of the tubes such as 0$^\circ$–90$^\circ$ for the analysis objective. Figure 8 shows the methodology used to make FEA model for analysis purposed in ANSYS14.5. At first, authors selected the different graphene sheet as per the requirements (length and width), then rolled such that it becomes the tube as per the selection of the sheets and in last that tube is bending as per the required bending angle.

The effect of bending angle on SWCNT (armchair) tube is shown in Fig. 9. Result shows that when bending angle is increased the Young’s modulus of SWCNT is decreased. Moreover, after bending angle 45$^\circ$, Young’s modulus of (4,4) tube is drastically reduced. But in (5,5) Young’s modulus is gradually decreased when bending angle is increased. Same trend is observed in both tube in between 45$^\circ$ and 90$^\circ$ bending angle.

Fig. 9

Young’s modulus of SWCNTs (Armchair) tube with different bending angle

The effect of bending angle on the SWCNT (Zigzag) tube is shown in Fig. 10. Result shows that when bending angle is near to 22.5$^\circ$ the Young’s modulus of (7,0) reduced considerably. When bending angle is increased from 0$^\circ$ to 90$^\circ$, both tubes have different trend.

Fig. 10

Young’s modulus of SWCNTs (Zigzag) tube with different bending angle

Figure 11 shows the effect of bending angle on Young’s modulus of SWCNT (chiral) tube. The trend of both tubes is different initially when bending angle is in between 0$^\circ$ and 45$^\circ$, after 45$^\circ$ bending angle, Young’s modulus is gradually decreased.

Fig. 11

Young’s modulus of SWCNTs (Chiral) tube with different bending angle

Figure 12 shows the effect of bending angle on DWCNT (zigzag) tube with and without vdW in between two tubes. The result shows that with vdW Young’s modulus is higher than the without vdW. Here, author observed that in with vdW, Young’s modulus of DWCNT (Zigzag) tube is higher compared to without vdW when bending angle is increased. Author also observed that in with vdW condition Young’s modulus is increased when bending angle is increased and touches 67.5$^\circ$, and then it is reduced drastically when bending angle touches 90$^\circ$. In without vdW, Young’s modulus of DWCNT (Zigzag) tube is decreased when bending angle is increased. In with vdW condition, Young’s modulus of DWCNT (zigzag) tube is highest when bending angle is 67.5$^\circ$.

Fig. 12

Young’s modulus of DWCNTs (Zigzag) tube with different bending angle and with and without vdW

Figure 13 shows the effect of bending angle on DWCNT (Armchair) tube with and with vdW in between two tubes. Result shows that with vdW have higher Young’s modulus compared to the without vdW. The trend remains same in both the tube with and without vdW. Young’s modulus in both the tube with and without vdW is considerably reduced when the bending angle touches 22.5$^\circ$.

Fig. 13

Young’s modulus of DWCNTs (Armchair) with different bending angle and with and without vdW

Figure 14 shows the effect of bending angle on DWCNT (Chiral) tube with and with vdW in between two tubes. Here, the tube has diffident trend when author compared. Here, author observed that Young’s modulus of without vdW tube is first decreased when bending angle reaches 45$^\circ$ and then it is increased when bending angle touches 90$^\circ$. In with vdW, Young’s modulus of the tube is increased when bending angle is increased.

Fig. 14

Young’s modulus of DWCNTs (Chiral) with different bending angle and with and without vdW

Effect of Length Variation on Young’s Modulus

Here, authors compared the three tube such as Armchair (5,5), Zigzag (9,0) and Chiral (7,3) for the bending angle 45. Authors took the various tubes length stating from 20 Å to 100 Å for the comparison. Table 3 demonstrates the number of nodes and elements used for the various tubes for various length and diameter.

Table 3 Structure matters for DWCNTs

Figure 15 shows the effect of length variation on Young’s modulus of Armchair (5,5), Zigzag (9,0) and Chiral (7,3). Authors considered bending angle as 45$^\circ$ for the comparison. Here, authors observed that in all three tubes have different trend. Results shows that when length is increased, Young’s modulus of zigzag (9,0) is decreased till the 80 Å length, then Young’s modulus is increased when length is 100 Å. For the armchair (5,5), Young’s modulus is increased when length of tube is 60 Å and then, Young’s modulus is decreased when length of tube is 100 Å.

Fig. 15

Young’s modulus of SWCNTs (Armchair, Zigzag, Chiral) with 45$^\circ$ bending angle and various length (in Armstrong)

Conclusion

In this study, author used the molecular mechanics-based FE technique for prediction of mechanical properties of SWCNTs and DWCNTs by applying the uniaxial tensile displacement. Authors considered all three types of CNTs such as chiral, zigzag and armchair. Because of its complex structure, many researchers do not include chiral CNTs in their studies. Authors also included the various bending angle starting from 0° to 90° which is novel part in this study. Young’s modulus of each SWCNTs is changed as the chirality changes, tube length change and bending angle change. Authors also compared the results with previous reported research. Authors observed that when bending angle increased, the Young’s modulus of SWCNTs of all three types of tubes decreased. Authors considered the vdW in between the two tubes which is a more accurate method to evaluate the mechanical properties of DWCNTs. So, authors considered with and without vdW in between two tubes and compared. Authors also observed that when vdW is considered between two tubes, then Young’s modulus of DWCNTs is higher than the without vdW. The effect of bending angle on the DWCNTs is different in different chirality. Authors predicted that the consequences of this study will assist some guidelines for the CNT-based nano-composite where SWCNTs and DWCNTs can be used for increasing the mechanical characteristics of nano-composite.