Keywords

2.1 Selected Uniaxial Models of the Isotropic Linear Viscoelastic Materials

Creep phenomena at elevated temperature are usually treated as nonlinear creep phenomenon problems. There exists broad literature in the field of nonlinear creep, for example, creep anisotropy Findley et al. [4], survey on constitutive models of nonlinear creep Skrzypek [13], Betten [2], interaction creep and plasticity Krempl [6], coupling of creep and damage Skrzypek [14], Skrzypek and Ganczarski [15], creep fatigue damage Murakami [7], and nonconventional creep models of anisotropic material Altenbach [1] and others.

At the beginning, we confine to the commonly used uniaxial isotropic linear viscoelastic models for which a general differential equation models may be written as

$$\begin{aligned} p_0\sigma + p_1\dot{\sigma } + p_2\ddot{\sigma } + \cdots p_a\frac{\partial ^a\sigma }{\partial t^a} = q_0\varepsilon + q_1\dot{\varepsilon } + \cdots p_b\frac{\partial ^b\varepsilon }{\partial t^b} \end{aligned}$$
(2.1)

where \(p_0,p_1,\ldots ,q_0,q_1,\ldots \) denote material constants, and constitutive equation is a linear function of the stress \(\sigma \), strain \(\varepsilon \), and their time derivatives \(\dot{\sigma },\ddot{\sigma }\), etc., and \(\dot{\varepsilon },\ddot{\varepsilon }\), etc. In such a case by the use of the Laplace transformation \(\mathcal{L}\left\{ f(t)\right\} =\widehat{f}(s)=\int \limits _{0}^{\infty }\mathrm{e}^{-st}\mathrm{d}t\), a linear viscoelastic problem can be reduced to associated fictitious elastic problem in terms of the transformed variable \(s,\widehat{\sigma }_{ij}({{\varvec{x}}},s)\), then the viscoelastic problem \(\sigma _{ij}({{\varvec{x}}},t)\) is obtained by the inverse Laplace transformation. Symbol \(\{~\}\) stands here for function argument of the Laplace transformation and should not be confused with the Voigt vector notation.

Fig. 2.1
figure 1

Maxwell’s material: a mechanical model, b creep curve under constant loading

Full size image

2.1.1 Maxwell Model

The uniaxial Maxwell model (M) consists of a linear elastic spring \(\varepsilon ^\mathrm{H}=\sigma /E\) and a linear viscous dashpot element \(\dot{\varepsilon }^{\eta }=\sigma /\eta \) connected in a series, Fig. 2.1. Differentiation of the first formula with time yields \(\dot{\varepsilon }^\mathrm{H}=\dot{\sigma }/E\). When the additive decomposition of the strain or the stain rate \(\dot{\varepsilon }=\dot{\varepsilon }^\mathrm{H}+\dot{\varepsilon }^{\eta }\) is used, we arrive at equation of the Maxwell model, hence

$$\begin{aligned} \dot{\varepsilon } = \frac{\dot{\sigma }}{E} + \frac{\sigma }{\eta } \qquad \text{ or } \qquad \sigma + \frac{\eta }{E}\dot{\sigma } = \eta \dot{\varepsilon } \end{aligned}$$
(2.2)

When the integration of above equation at constant stress \(\sigma =\sigma _1=\mathrm{const}\quad (\dot{\sigma }=0)\) and initial condition \(\varepsilon (0)=\sigma _1/E\) is performed, we arrive at the creep function given as, see Fig. 2.1b

$$\begin{aligned} \varepsilon = \sigma _1 \left( \dfrac{1}{E} + \dfrac{1}{\eta }t\right) \end{aligned}$$
(2.3)

or

$$\begin{aligned} \varepsilon = \sigma _1 J^\mathrm{M}(t), \qquad J^\mathrm{M}(t) = \frac{1}{E} + \frac{t}{\eta } \end{aligned}$$
(2.4)

The time function \(J^\mathrm{M}(t)\) is the creep compliance function of the Maxwell model.

2.1.2 Voigt–Kelvin Model

The Voigt–Kelvin model (V–K) consists of a linear spring element and a linear dashpot element which are connected in parallel as shown in Fig. 2.2a. Adopting the additive separation of stress into two parts applied to the spring \(\sigma ^\mathrm{H}=E\varepsilon \) and to the dashpot \(\sigma ^{\eta }=\eta \dot{\varepsilon }\) with \(\varepsilon =\varepsilon ^\mathrm{H}=\varepsilon ^{\eta }\), the differential equation of the V–K model takes the form

$$\begin{aligned} \dot{\varepsilon } + \frac{E}{\eta }\varepsilon = \frac{\sigma }{\eta } \end{aligned}$$
(2.5)
Fig. 2.2
figure 2

Voigt–Kelvin model: a mechanical scheme, b creep strain at constant stress input

Full size image

If a constant stress \(\sigma =\sigma _1=\mathrm{const}\quad (\dot{\sigma }=0)\) is applied to the V–K model, we arrive at nonhomogeneous differential equation

$$\begin{aligned} \dot{\varepsilon } + \frac{E}{\eta }\varepsilon = \frac{\sigma _1}{\eta } \end{aligned}$$
(2.6)

The homogeneous equation of (2.6) is an equation of separate variables

$$\begin{aligned} \frac{\dot{\varepsilon }}{\varepsilon } = - \frac{E}{\eta } \end{aligned}$$
(2.7)

the general integral of which is given by

$$\begin{aligned} \varepsilon = C\exp \left( - \frac{E}{\eta }t\right) \end{aligned}$$
(2.8)

When variation of integration constant \(C(t)\) with initial condition \(\varepsilon (0)=0\) is done we arrive at the solution of (2.6)

$$\begin{aligned} \varepsilon = \frac{\sigma _1}{E} \left[ 1 - \exp \left( - \dfrac{E}{\eta }t\right) \right] \end{aligned}$$
(2.9)

or

$$\begin{aligned} \varepsilon = \sigma _1 J^\mathrm{VK}(t), \qquad J^\mathrm{VK}(t) = \frac{1}{E} \left[ 1 - \exp \left( - \dfrac{E}{\eta }t\right) \right] \end{aligned}$$
(2.10)

Function \(J^\mathrm{VK}(t)\) is the creep compliance function of the V–K model. Note that V–K model does not account for instantaneous elasticity, hence \(J^\mathrm{VK}(0)=0\), see Fig. 2.2b.

When the more general case of a time function \(\sigma (t)\) is applied and variation of constant \(C(t)\) is done in (2.8) we arrive at the differential equation for \(C(t)\)

$$\begin{aligned} \dot{C}(t)=\frac{1}{\eta }\exp {\left( \frac{E}{\eta }t\right) }\sigma (t) \end{aligned}$$
(2.11)

the general integral of which is expressed in form

$$\begin{aligned} C(t)=C_1+\frac{1}{\eta }\int \limits _{0}^{t}\exp \left( {\frac{E}{\eta }\xi }\right) \sigma (\xi )\mathrm{d}\xi \end{aligned}$$
(2.12)

Substitution of (2.12) to (2.8) with the initial condition \(\varepsilon (0)=0\) yields \(C_1=0\), such that the following general solution for \(\varepsilon (t)\) holds

$$\begin{aligned} \begin{array}{l} \varepsilon (t) = \dfrac{1}{\eta }\mathrm{exp}\left( -\dfrac{E}{\eta }t\right) \int \limits _{0}^{t}\mathrm{exp}\left( \dfrac{E}{\eta }\xi \right) \sigma (\xi )\mathrm{d}\xi \\ \qquad = \frac{1}{\eta } \int \limits _{0}^{t}\mathrm{exp}\left[ -{\dfrac{E}{\eta }(t-\xi )}\right] \sigma (\xi )\mathrm{d}\xi \end{array} \end{aligned}$$
(2.13)

When integration by parts is applied to (2.13), we arrive at so-called integral representation of the V–K model

$$\begin{aligned} \varepsilon (t) = \frac{\sigma (t)}{E} - \frac{1}{E}\int \limits _{0}^{t} \exp \left[ -\frac{E}{\eta }(t-\xi )\right] \dot{\sigma }(\xi )\mathrm{d}\xi \end{aligned}$$
(2.14)

in which it is clearly seen that the creep function \(J^\mathrm{VK}(t)\) has two terms: independent of time \(J_0=1/E\) and dependent on time \(\varphi (t)=\frac{1}{E}\mathrm{exp}\left[ -\frac{E}{\eta }(t-\xi )\right] \).

Analogous solution may be reached by use of the Laplace transform method (2.48). In order to do this the nonhomogeneous V–K equation (2.5) is multiplied both-side by \(\mathrm{e}^{-st}\) and integrated with respect to variable \(t\) in range from 0 to \(\infty \)

$$\begin{aligned} \int \limits _{0}^{\infty }\dot{\varepsilon }(t)\mathrm{e}^{-st}\mathrm{d}t + \frac{E}{\eta }\int \limits _{0}^{\infty }\varepsilon (t)\mathrm{e}^{-st}\mathrm{d}t=\int \limits _{0}^{\infty }\frac{\sigma (t)}{\eta } \mathrm{e}^{-st}\mathrm{d}t \end{aligned}$$
(2.15)

Consequently, the algebraic equation of the transformed variable \(s\) is obtained

$$\begin{aligned} s\widehat{\varepsilon }(s) - \varepsilon (0) + \frac{E}{\eta }\widehat{\varepsilon }(s) = \frac{\widehat{\sigma }(s)}{\eta } \end{aligned}$$
(2.16)

When the initial condition \(\varepsilon (0)=0\) is used, the solution of (2.16) with respect of transformed variable \(\widehat{\varepsilon }(s)\) is given as the following

$$\begin{aligned} \widehat{\varepsilon }(s) = \frac{1}{s + \frac{E}{\eta }}\widehat{\sigma }(s) \end{aligned}$$
(2.17)

Applying next the inverse Laplace transform and taking advantage of property that multiplication of two transforms in fictitious domain of variable \(s\) corresponds to the convolution of two functions in real time space \(t\), we arrive at the solution of linear viscoelastic problem

$$\begin{aligned} \varepsilon (t)=\frac{1}{\eta }\int \limits _{0}^{t}\exp \left[ - \frac{E}{\eta }(t-\xi )\right] \sigma (\xi )\mathrm{d}\xi \end{aligned}$$
(2.18)

identical to (2.13).

2.1.3 Standard Model

The Maxwell and the Voigt–Kelvin two-element uniaxial models described in the Sects. 2.1.1 and 2.1.2 are very simple, although they exhibit strong limitations. The linear creep function at constant stress input corresponding to the Maxwell model does not confirm experiments, whereas the Voigt–Kelvin model is not capable to capture the instantaneous elastic strain effect. Trying to overcome the above objections, the commonly used three-parameter standard model is composed of two parts, a spring element (\(E\)) and the V–K unit (\(E_1,\eta \)) connected in a series as shown in Fig. 2.3a.

Fig. 2.3
figure 3

The standard model: a mechanical scheme, b creep at constant stress input with instantaneous elastic strain built-in

Full size image

The differential equation of the standard model can be derived in an analogous way as for the Maxwell and the Voigt–Kelvin simple models, such that after necessary rearrangement used, the following is obtained

$$\begin{aligned} \frac{\eta E}{E_1+E}\dot{\varepsilon } + \frac{E_1E}{E_1+E}\varepsilon = \sigma + \frac{\eta }{E_1+E}\dot{\sigma } \end{aligned}$$
(2.19)

The simple creep function, when the standard model is subjected to a step function \(\sigma =\sigma _1=\mathrm{const}\quad (\dot{\sigma }=0)\) and integrated with the initial condition \(\varepsilon (0)=\sigma _1/E\) used, takes one of two equivalent forms

$$\begin{aligned} \varepsilon = \frac{\sigma _1}{E} \left[ \left( 1 + \frac{E}{E_1}\right) - \frac{E}{E_1} \exp \left( - \frac{E_1}{\eta }t\right) \right] \end{aligned}$$
(2.20)

or

$$\begin{aligned} \varepsilon = \sigma _1 J^\mathrm{s}(t), \qquad J^\mathrm{s}(t) = \frac{1}{E} \left[ \left( 1 + \frac{E}{E_1}\right) - \frac{E}{E_1} \exp \left( - \frac{E_1}{\eta }t\right) \right] \end{aligned}$$
(2.21)

if the time-dependent creep compliance function characterizing the standard model \(J^\mathrm{s}(t)\) is used. Note the horizontal asymptote of \(\varepsilon (t)\) curve as shown in Fig. 2.3b with the new definition used: \(1/H=1/E+1/E_1\).

2.1.4 Burgers Model

Although the standard model is free from aforementioned inconvenience of the Maxwell and the Voigt–Kelvin models, it still exhibits a horizontal asymptote (strain stabilization) when \(t\rightarrow \infty \), which usually is not true; since according to experimental findings, the creep strain shows rather the infinite increase with time. In order to control such behaviors, a more complex four-parameter Burgers model which consists of two simple units, the Maxwell unit (\(E_1,\eta _1\)), and the Voigt–Kelvin unit (\(E_2,\eta _2\)) coupled in a series can be used, as presented in Fig. 2.4a. The differential constitutive equation of Burgers’ model may be written in the format

$$\begin{aligned} \frac{\eta _1\eta _2}{E_2}\ddot{\varepsilon } + \eta _1\dot{\varepsilon } = \frac{\eta _1\eta _2}{E_1E_2}\ddot{\sigma } + \left( \frac{\eta _1}{E_1} + \frac{\eta _1}{E_2} + \frac{\eta _2}{E_2}\right) \dot{\sigma } + \sigma \end{aligned}$$
(2.22)

Note that the above equation is the second-order linear differential equation with respect to strain and stress but of constant coefficients being functions of four parameters \(E_1,E_2,\eta _1\) and \(\eta _2\). It means that all strain and stress functions and their time derivatives are the linear functions, whereas the coefficients in Eq. (2.22) are constants: two Young’s modules \(E_1,E_2\) and two viscosity parameters \(\eta _1,\eta _2\).

When the Burgers model is loaded by a step stress input applied at \(t=0\) the integration of Eq. (2.22), with two initial conditions \(\varepsilon (0)=\sigma _1/E\), \(\dot{\varepsilon }(0)=\sigma _1/\eta _1+\sigma _1/\eta _2\) used, leads to one of equivalent relationships

$$\begin{aligned} \varepsilon = \frac{\sigma _1}{E_1} \left\{ 1 + \frac{E_1}{\eta _1}t + \frac{E_1}{E_2} \left[ 1 - \exp \left( -\frac{E_2}{\eta _2}t\right) \right] \right\} \end{aligned}$$
(2.23)

or

$$\begin{aligned} \varepsilon = \sigma _1 J^\mathrm{B}(t), \qquad J^\mathrm{B}(t) = \frac{1}{E_1}\left\{ 1 + \frac{E_1}{\eta _1}t + \frac{E_1}{E_2} \left[ 1 - \exp \left( - \frac{E_2}{\eta _2}t\right) \right] \right\} \end{aligned}$$
(2.24)

where the creep compliance function characterizing the Burgers model compliance function \(J^\mathrm{B}(t)\) is applied.

Fig. 2.4
figure 4

The Burgers model: a the mechanical scheme, b the simple creep curve at constant stress input applied at \(t=0\)

Full size image

Note that the creep curve described by the Burgers model exhibits a skewed asymptote which corresponds to the unlimited strain increase with decreasing strain rate, which better fits the experimental findings, see Fig. 2.4b.

2.1.5 Creep Compliance and Relaxation Behavior of the Selected Linear Viscoelastic Models

More complex models of linear viscoelastic materials consisting of one Hooke’s element and \(n\) Voigt–Kelvin’s units coupled in a series or one Hooke’s element and \(n\) Maxwell’s units coupled in parallel are analyzed by Betten [2].

Consider now stress relaxation of simple uniaxial linear viscoelastic models discussed in Sects. 2.1.1–2.1.4, subject to a constant strain \(\varepsilon _1\) at \(t=0\), from the initial stress level \(\sigma _1=E\varepsilon _1\).

In case of the Maxwell model, the stress relaxation from the initial level \(\sigma _1\) at \(t=0\) to \(t\rightarrow \infty \) is described as follows

$$\begin{aligned} \sigma (t) = \sigma _1 \exp \left( - \frac{Et}{\eta }\right) \end{aligned}$$
(2.25)

Note that the rate of stress decrease changes from the initial \(\dot{\sigma }(0)=-\sigma _1E/\eta \) to zero, \(\dot{\sigma }(\infty )=0\). The so-called relaxation time \(t_\mathrm{r}=\eta /E\) corresponds to the fictitious case if the stress decreases continuously at the initial rate and finally it would reach zero at \(t=t_\mathrm{r}\).

The Voigt–Kelvin model does not exhibit stress relaxation effect. In this singular case application of the constant strain input, \(\varepsilon =\varepsilon _1\) at \(t=0\) can be achieved only by an infinite initial stress response \({\sigma }(0)\rightarrow \infty \), such that the following holds

$$\begin{aligned} \sigma (t) = \eta \varepsilon _1\delta (t) + E\varepsilon _1 \mathrm{H}(t) \end{aligned}$$
(2.26)

where the term containing the Heaviside unit function \(\mathrm{H}(t)\) describing the constant stress in the spring, followed by the infinite stress input in dashpot described by the \(\delta \)-Dirac function, appears.

The standard model is free from the above singularity and if it is subject to a constant strain at \(t=0\), the stress continuously decreases from the initial level \(E\varepsilon _1(t=0)\) to the asymptotically approached value \(H\varepsilon _1(t\rightarrow \infty )\) such that stress relaxation function of the standard model is written as

$$\begin{aligned} \sigma (t) = E\varepsilon _1 \left[ \frac{H}{E} + \left( 1 - \frac{H}{E}\right) \exp \left( -\frac{t}{n}\right) \right] \end{aligned}$$
(2.27)

where the definitions hold: \(\dfrac{1}{H}=\dfrac{1}{E}+\dfrac{1}{E_1}\) and \(n=\dfrac{\eta }{E+E_1}\).

Table 2.1 Properties of Maxwell, Voigt–Kelvin, standard and Burgers viscoelastic units, after Skrzypek [13]
Full size table

If the Burgers model is subject to a constant strain \(\varepsilon =\varepsilon _1\) at \(t=0\), a continuous stress relaxation is described by the combination of two exponential functions \(\exp (-r_1 t)\) and \(\exp (-r_2 t)\) (cf. Table 2.1), where after Findley et al. [4] the new definitions are used

$$\begin{aligned} \begin{array}{lll} p_1 = \dfrac{\eta _1}{E_1} + \dfrac{\eta _1}{E_2} + \dfrac{\eta _2}{E_2} &{} \quad p_2 = \dfrac{\eta _1\eta _2}{E_1 E_2} &{} \quad q_1 = \eta _1 \\ q_2 = \dfrac{\eta _1\eta _2}{E_2} &{} \quad r_{1,2} = \dfrac{p_1\mp A}{2p_2} &{} \quad A = \sqrt{p_1^2 - 4p_2} \end{array} \end{aligned}$$
(2.28)

2.2 The Uniaxial Boltzmann Superposition Principle of the Isotropic Linear Viscoelastic Materials

2.2.1 Bending of a Beam Subject to Stationary Load

Summarizing the results of previous subsection, response of the arbitrary linear viscoelastic material at step stress input \(\sigma =\sigma _1=\mathrm{const}\) can be written as follows

$$\begin{aligned} \varepsilon (x,t) = \varepsilon ^\mathrm{e}(x) \textit{EJ}(t) \end{aligned}$$
(2.29)

In other words, strain at the arbitrary material point, being a function of the space \(x\) and time \(t\) variables, can be presented as a product of the instantaneous elastic strain \(\varepsilon ^\mathrm{e}(x)\) depending on \(x\) only and the creep compliance function \(J(t)\) specifically chosen for given material model dependent on time \(t\) only. In the light of comments presented in Sect. 2.1.5, Eq. (2.29) does not apply to the Voigt–Kelvin model in a straightforward manner. The V–K model does not comprise the initial elastic strain.

In particular, a deflection of beam made of the linear viscoelastic material \(w^\mathrm{ve}(x,t)\) at constant loading can be presented as the product of the elastic deflection \(w^\mathrm{e}(x)\) and the dimensionless creep compliance function \(\textit{EJ}(t)\) as follows

$$\begin{aligned} w^\mathrm{ve} \left( x,t\right) = w^\mathrm{e} \left( x\right) \textit{EJ}\left( t\right) \end{aligned}$$
(2.30)

For creep compliance functions shown in Table 2.1, we arrive at

$$\begin{aligned} \begin{array}{l} w^\mathrm{M} \left( x,t\right) = w^\mathrm{e} \left( x\right) \left( 1 + \dfrac{E}{\eta }t\right) \\ w^\mathrm{VK} \left( x,t\right) = w^\mathrm{e} \left( x\right) \left[ 1 - \exp \left( - \dfrac{E}{\eta }t\right) \right] \\ w^\mathrm{s} \left( x,t\right) = w^\mathrm{e} \left( x\right) \left[ 1 + \dfrac{E}{E_1} - \dfrac{E}{E_1} \exp \left( - \dfrac{E_1}{\eta }t\right) \right] \\ w^\mathrm{B} \left( x,t\right) = w^\mathrm{e} \left( x\right) \left\{ 1 + \dfrac{E_1}{\eta _1}t + \dfrac{E_1}{E_2} \left[ 1 - \exp \left( - \dfrac{E_2}{\eta _2}t\right) \right] \right\} \end{array} \end{aligned}$$
(2.31)

The aforementioned relationships hold for all linear viscoelastic models discussed even though V–K model does not exhibit instantaneous response. This comment holds for all linear viscoelastic models that do not have free elastic spring.

2.2.2 Bending with Tension of a Beam Subject to Nonstationary Load

Consider a prismatic beam of doubly symmetric cross-section subject to the axial force and the bending moment being both functions of coordinate \(x\) and time \(t\): \(N=N(x,t)\), \(M=M(x,t)\). Assume also that both external forces \(N\) and \(M\) can be expressed as products of function dependent of \(x\) co-ordinate \(N=N(x)\) or \(M(x)\) and one common time function \(f(t)\): \(N(x,t)=N(x)f(t)\) and \(M(x,t)=M(x)f(t)\). Supposing for simplicity that viscoelastic deformation fulfils the Bernoulli hypothesis of straight and normal segments \(\varepsilon (x,z,t)=\lambda (x,t)+z\kappa (x,t)\), it is possible to separate Eq. (2.29) into the viscoelastic axial elongation \(\lambda ^\mathrm{ve}\) and the viscoelastic curvature \(\kappa ^\mathrm{ve}\)

$$\begin{aligned} \begin{array}{l} \lambda ^\mathrm{ve}\left( x,t\right) = \dfrac{N\left( x\right) }{A} \int \limits _{0}^{t}J(t - \xi )\dfrac{\partial f(\xi )}{\partial \xi } \mathrm{d}\xi \\ \kappa ^\mathrm{ve}\left( x,t\right) = \dfrac{M\left( x\right) }{I} \int \limits _{0}^{t}J(t - \xi )\dfrac{\partial f(\xi )}{\partial \xi } \mathrm{d}\xi \end{array} \end{aligned}$$
(2.32)

In a particular case, if both generalized forces are applied instantaneously at \(t=0\): \(N(x,t)=N(x)\mathrm{H}(t)\) and \(M(x,t)=M(x)\mathrm{H}(t)\), remembering that \(\delta \)- Dirac function is defined as \(\delta (t)=\dot{\mathrm{H}}(t)\) and applying (see Byron and Fuller [3])

$$\begin{aligned} \int \limits _{0}^{t} J(t - \xi )\delta (\xi )\mathrm{d}\xi = \int \limits _{0}^{t} J(\xi )\delta (t - \xi )\mathrm{d}\xi = J(t) \end{aligned}$$
(2.33)

we finally obtain equations for viscoelastic elongation \(\lambda ^\mathrm{ve}(x,t)\) and curvature \(\kappa ^\mathrm{ve}(x,t)\) in a form

$$\begin{aligned} \begin{array}{l} \lambda ^\mathrm{ve} \left( x,t\right) = \dfrac{N\left( x\right) }{EA} J\left( t\right) \\ \kappa ^\mathrm{ve} \left( x,t\right) = - w''\left( x,t\right) = \dfrac{M\left( x\right) }{\textit{EI}} J\left( t\right) \end{array} \end{aligned}$$
(2.34)

Hence, the axial elongation of the linear viscoelastic beam \(\lambda ^\mathrm{ve}\) is a product of instantaneous (elastic) elongation and the creep compliance function. Analogously, the curvature of the linear viscoelastic beam \(\kappa ^\mathrm{ve}\) is a product of instantaneous curvature and creep compliance function \(J(t)\). For simplicity, the conventional beam theory is adopted here.

2.2.3 Integral Representation of Creep and Relaxation Functions in Case of Arbitrary Loading History

A general differential equation of uniaxial linear viscoelastic models can be written as follows:

$$\begin{aligned} p_0 \sigma + p_1 \dot{\sigma } + p_2 \ddot{\sigma } + \cdots = q_0 \varepsilon + q_1 \dot{\varepsilon } + q_2 \ddot{\varepsilon } + \cdots \end{aligned}$$
(2.35)

where the constant \(p_i,q_i\) are coefficients of the linear arbitrary order differential constitutive equation, see Eq. (2.1). Order of Eq. (2.35) is equal to number of viscous elements (dashpots) appearing in the mechanical model. A compact operator format can be used instead of Eq. (2.35)

$$\begin{aligned} \mathrm{P}\sigma (t) = \mathrm{Q}\varepsilon (t) \end{aligned}$$
(2.36)

where \(\mathrm{P}\) and \(\mathrm{Q}\) stand for linear differential operators with respect to time acting on stress \(\sigma (t)\) and strain \(\varepsilon (t)\), respectively

$$\begin{aligned} \begin{array}{l} \mathrm{P} = p_0 + p_1 \dfrac{\partial }{\partial t} + p_2 \dfrac{\partial ^2}{\partial t^2} + \cdots \\ \mathrm{Q} = q_0 + q_1 \dfrac{\partial }{\partial t} + q_2 \dfrac{\partial ^2}{\partial t^2} + \cdots \end{array} \end{aligned}$$
(2.37)

It is clear that the linear elastic (Hooke’s) material is a particular case of linear viscoelastic material in equation of which all time derivatives disappear, whereas \(q_0/p_0=E\).

Note that differential operators \(\mathrm{P}\) and \(\mathrm{Q}\) are linear with respect to all derivatives, hence the operator format of Eq. (2.36) can formally be treated as an algebraic equation as follows

$$\begin{aligned} \begin{array}{ll} \dfrac{\sigma (t)}{\varepsilon (t)} = \mathrm{E}_\mathrm{ve}(t)&\qquad \mathrm{E}_\mathrm{ve}(t) = \dfrac{\mathrm{Q}(t)}{\mathrm{P}(t)} \end{array} \end{aligned}$$
(2.38)

The rational operator \(\mathrm{E}_\mathrm{ve}(t)\) used in Eq. (2.38) plays a role of the time-dependent stiffness operator. As a consequence by contrast to elasticity a fraction \(\sigma (t)/\varepsilon (t)\) is not constant but depends on time. Hence, Eq. (2.38) should be read in a symbolic way as follows

$$\begin{aligned} \frac{\mathrm{Q}(t)}{\mathrm{P}(t)} \nearrow \!\!\!\!\!\!\searrow \frac{\sigma (t)}{\varepsilon (t)} \end{aligned}$$
(2.39)

Class of the linear viscoelastic materials is a subclass of the nonlinear viscoelastic materials ; however, the Boltzmann superposition principle holds for the linear viscoelastic materials only. The superposition principle states that resultant response of the system \(\varepsilon (t)\) under the “sum” of causes is equal to the “sum” of responses corresponding to causes acting separately. In particular if stress \(\sigma _1\) is applied at time \(\xi _1\) and, then, stress \(\sigma _2\) is applied at time \(\xi _2\), the resultant strain \(\varepsilon (t)\) at any time \(t>\xi _2\) is represented as the sum of the strains resulting from both stresses considered as though each were acting separately

$$\begin{aligned} \varepsilon \left[ \sigma _1 \left( t - \xi _1\right) + \sigma _2 \left( t - \xi _2\right) \right] = \varepsilon \left[ \sigma _1 \left( t - \xi _1\right) \right] + \varepsilon \left[ \sigma _2 \left( t - \xi _2\right) \right] \end{aligned}$$
(2.40)

In case of arbitrary loading history, stress \(\sigma (t)\) can be approximated by a sum of \(n\) stress inputs \({\varDelta }\sigma _i\), hence from the Boltzmann principle the strain output holds

$$\begin{aligned} \varepsilon (t) = \sum \limits _{i=1}^{n} \varepsilon _i (t - \xi _i) = \sum \limits _{i=1}^{n} J(t - \xi _i) {{\varDelta }}\sigma _i \end{aligned}$$
(2.41)

If the time step tends to zero, we arrive at the integral form of uniaxial creep strain for the linear viscoelastic material

$$\begin{aligned} \varepsilon (t) = \int \limits _{0}^{t}\!\!J(t - \xi ) \frac{\partial \sigma (\xi )}{\partial \xi } \mathrm{d}\xi = \int \limits _{0}^{t}\!\!J(t - \xi ) \dot{\sigma }(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.42)

If the analogous reasoning is applied to the arbitrary strain history (kinematic control), we arrive at the integral form of the uniaxial stress relaxation for the linear viscoelastic material

$$\begin{aligned} \sigma (t) = \int \limits _{0}^{t}\!\!E(t - \xi ) \frac{\partial \varepsilon (\xi )}{\partial \xi } \mathrm{d}\xi = \int \limits _{0}^{t}\!\!E(t - \xi ) \dot{\varepsilon }(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.43)

In above integral equations, \(J(t-\xi )\) and \(E(t-\xi )\) denote the creep function and the relaxation function of the material considered, respectively. In practical applications, the alternative forms to (2.42) or (2.43) are more convenient

$$\begin{aligned} \varepsilon (t) = J_0\sigma (t) + \int \limits _{0}^{t}\!\!\varphi (t - \xi ) \dot{\sigma }(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.44)

or

$$\begin{aligned} \sigma (t) = E_0\varepsilon (t) - \int \limits _{0}^{t}\!\!\psi (t - \xi ) \dot{\varepsilon }(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.45)

where separation of the instantaneous and time-dependent outputs are distinguished. The general integral forms (2.42) or (2.43) do not comprise explicitly initial conditions, whereas in the forms (2.44) or (2.45) \(J_0\) or \(E_0\) denote initial value of creep or relaxation functions (at \(t=0\)) whereas time functions \(\varphi (t-\xi )\) or \(\psi (t-\xi )\) denote time-dependent parts of creep or relaxation functions. Note that in Eqs. (2.44) and (2.45) symbol \(\xi \) denotes time when the stress or the strain inputs are imposed, whereas \(t\) denotes the observation time when strain response \(\varepsilon (t)\) or stress response \(\sigma (t)\) are measured. This approach can be identified as the linear hereditary model where kernel function depends on time interval \(t-\xi \) by contrast to the nonlinear hereditary models where kernel functions depend on \(t,\xi \) separately, cf. Rabotnov [11].

2.3 Multiaxial Isotropic Linear Viscoelastic Materials

In what follows, we briefly summarize the fundamentals of the linear viscoelasticity in case of material isotropy. This will serve as the starting point for further extension of isotropic to anisotropic linear viscoelastic equations. Such extension will further be used as convenient tool for analysis of anisotropic viscoelastic composites.

2.3.1 Differential Representation Under a Multiaxial Stress State

In case of isotropic linear viscoelastic materials under the multiaxial states of stress and strain, it is convenient to separate volumetric effect from the shape change effect. Similar to elasticity, such separation is possible only in case of material isotropy (see Sect. 1.4.8).

Direct extension of linear isotropic viscoelastic constitutive equations (2.36) and (2.37) to the multiaxial states takes the form

$$\begin{aligned} \begin{array}{l} \mathrm{P}_1 s_{ij} \left( t\right) = \mathrm{Q}_1 e_{ij}\left( t\right) \\ \mathrm{P}_2 \sigma _{kk} \left( t\right) = \mathrm{Q}_2 \varepsilon _{kk}\left( t\right) \end{array} \end{aligned}$$
(2.46)

where \(\mathrm{P}_1,\mathrm{Q}_1,\mathrm{P}_2\), and \(\mathrm{Q}_2\) are the linear differential operators applicable to the separable shape change and the volume change effects. In the explicit format, equations (2.46) can be rewritten as

$$\begin{aligned} \begin{array}{l} \left( p'_0 + p'_1 \dfrac{\partial }{\partial t} + p'_2 \dfrac{\partial ^2}{\partial t^2} + \cdots + p'_a \dfrac{\partial ^a}{\partial t^a}\right) s_{ij} \left( t\right) = \\ \qquad \left( q'_0 + q'_1 \dfrac{\partial }{\partial t} + q'_2 \dfrac{\partial ^2}{\partial t^2} + \cdots + q'_b \dfrac{\partial ^b}{\partial t^b}\right) e_{ij} \left( t\right) \\ \left( p''_0 + p''_1 \dfrac{\partial }{\partial t} + p''_2 \dfrac{\partial ^2}{\partial t^2} + \cdots + p''_a \dfrac{\partial ^a}{\partial t^a}\right) \sigma _{kk} \left( t\right) =\\ \qquad \left( q''_0 + q''_1 \dfrac{\partial }{\partial t} + q''_2 \dfrac{\partial ^2}{\partial t^2} + \cdots + q''_b \dfrac{\partial ^b}{\partial t^b}\right) \varepsilon _{kk} \left( t\right) \end{array} \end{aligned}$$
(2.47)

For the purpose of further consideration, it is convenient to transform differential equations (2.47) expressed in terms of physical time \(t\), \(f\left( t\right) \) to the equivalent algebraic equations expressed in terms of transformed variables \(s\), \(\widehat{f}\left( s\right) \) according to the Laplace integral transform

$$\begin{aligned} \mathcal{L}\left\{ f\left( t\right) \right\} = \widehat{f}\left( s\right) = \int \limits _{0}^{\infty } \mathrm{e}^{-st}f\left( t\right) \mathrm{d}t \end{aligned}$$
(2.48)

The use of above transformation allows to replace the real initial differential problem of the linear viscoelastic material (differential equation and appropriate initial conditions) by the equivalent elastic algebraic equation of a fictitious elastic material.

In the next step, when the fictitious algebraic problem is solved in elementary way, application of the inverse Laplace transform allows to return to the original viscoelastic problem. Described procedure leads to the solution faster than the straightforward integration of a differential equation due to the Laplace transform pairs known from literature.

Basic properties of the Laplace transform commonly used in theory of viscoelasticity can be found among others in, e.g., Nowacki [8], Pipkin [9], Findley et al. [4]. Exemplary Laplace transforms for selected elementary functions \(f(t)\) are shown in Table 2.2.

Table 2.2 Laplace transforms of frequently used functions
Full size table

By use of the Laplace transformation equations of transformed isotropic linear viscoelasticity (2.46) can be expressed in terms of the transformed variable \(s\) as follows

$$\begin{aligned} \begin{array}{l} \widehat{\mathrm{P}}_1 \widehat{s}_{ij} \left( s\right) = \widehat{\mathrm{Q}}_1 \widehat{e}_{ij} \left( s\right) \\ \widehat{\mathrm{P}}_2 \widehat{\sigma }_{kk} \left( s\right) = \widehat{\mathrm{Q}}_2 \widehat{\varepsilon }_{kk}\left( s\right) \end{array} \end{aligned}$$
(2.49)

or

$$\begin{aligned} \begin{array}{l} \left( p'_0 + p'_1 s + p'_2 s^2 + \cdots + p'_a s^a\right) \widehat{s}_{ij} \left( s\right) = \\ \qquad \left( q'_0 + q'_1 s + q'_2 s^2 + \cdots + q'_b s^b\right) \widehat{e}_{ij} \left( s\right) \\ \left( p''_0 + p''_1 s + p''_2 s^2 + \cdots + p''_a s^a\right) \widehat{\sigma }_{kk} \left( s\right) = \\ \qquad \left( q''_0 + q''_1 s + q''_2 s^2 + \cdots + q''_b s^b\right) \widehat{\varepsilon }_{kk} \left( s\right) \end{array} \end{aligned}$$
(2.50)

Based on the analogy between Eq. (2.49) that describe transformed viscoelastic problem and linear isotropic elastic equations

$$\begin{aligned} s_{ij} = 2G e_{ij}, \qquad \sigma _{kk} = 3K \varepsilon _{kk} \end{aligned}$$
(2.51)

it is possible to find out the generalized modules of viscoelasticity \(\mathrm{G}_\mathrm{ve}(t)\) and \(\mathrm{K}_\mathrm{ve}(t)\) as

$$\begin{aligned} \mathrm{G}_\mathrm{ve} \left( t\right) = \frac{\mathrm{Q}_1}{2\mathrm{P}_1} \qquad \mathrm{K}_\mathrm{ve} \left( t\right) = \frac{\mathrm{Q}_2}{3\mathrm{P}_2} \end{aligned}$$
(2.52)

which are time-dependent functions of \(t\). Additionally, if the definitions of Young’s modulus \(E\) and Poisson’s ratio \(\nu \) known from the elasticity are used

$$\begin{aligned} E = \frac{9\textit{KG}}{3K + G}, \qquad \nu = \frac{3K - 2G}{6K + 2G} \end{aligned}$$
(2.53)

substitution of (2.52) to (2.53) furnishes the generalized Young’s modulus \(\mathrm{E}_\mathrm{ve}(t)\) commonly called relaxation modulus and generalized Poisson’s ratio \(\nu _\mathrm{ve}(t)\) of isotropic linear viscoelasticity that can be expressed in terms of time-dependent operators (2.46)

$$\begin{aligned} \begin{array}{l} \mathrm{E}_\mathrm{ve} \left( t\right) = \dfrac{3\frac{\mathrm{Q}_1}{\mathrm{P}_1}\frac{\mathrm{Q}_2}{\mathrm{P}_2}}{\frac{\mathrm{Q}_1}{\mathrm{P}_1} + 2\frac{\mathrm{Q}_2}{\mathrm{P}_2}} = \dfrac{3\mathrm{Q}_1 \mathrm{Q}_2}{\mathrm{P}_2 \mathrm{Q}_1 + 2\mathrm{P}_1 \mathrm{Q}_2} \\ \nu _\mathrm{ve} \left( t\right) = \dfrac{\frac{\mathrm{Q}_2}{\mathrm{P}_2} - \frac{\mathrm{Q}_1}{\mathrm{P}_1}}{2\frac{\mathrm{Q}_2}{\mathrm{P}_2} + \frac{\mathrm{Q}_1}{\mathrm{P}_1}} = \dfrac{\mathrm{P}_1 \mathrm{Q}_2 - \mathrm{P}_2 \mathrm{Q}_1}{\mathrm{P}_2 \mathrm{Q}_1 + 2\mathrm{P}_1 \mathrm{Q}_2} \end{array} \end{aligned}$$
(2.54)

By contrast to elasticity, the above modules are time-dependent differential operators but not material constants.

Table 2.3 Differential operators for seclected simple linear viscoelastic models (after Findley et al. [4])
Full size table

The deviatoric \(\mathrm{P}_1,\mathrm{Q}_1\) and the volumetric \(\mathrm{P}_2,\mathrm{Q}_2\) differential operators and the corresponding transformed operators \(\widehat{\mathrm{P}}_1\), \(\widehat{\mathrm{Q}}_1\) and \(\widehat{\mathrm{P}}_2,\widehat{\mathrm{Q}}_2\) for selected isotropic linear viscoelastic models are given in Table 2.3. When the additional assumption of hydrostatic pressure independence of the elastic response is used it is necessary to consequently apply \(\mathrm{P}_2=1,\mathrm{Q}_2=3K\). Note that the above Eqs. (2.52) and (2.54) refer to isotropic linear viscoelastic material for which number of independent generalized modules equals 2, namely \(\mathrm{G}_\mathrm{ve}(t)\) and \(\mathrm{K}_\mathrm{ve}(t)\) or equivalently \(\mathrm{E}_\mathrm{ve}(t)\) and \(\nu _\mathrm{ve}(t)\). In particular case of isotropic elasticity, the above creep modules reduce to two constants \(\mathrm{G}_\mathrm{ve}(t)=G\) and \(\mathrm{K}_\mathrm{ve}(t)=K\) or equivalently \(\mathrm{E}_\mathrm{ve}(t)=E\) and \(\nu _\mathrm{ve}(t)=\nu \).

2.3.2 Integral Representation Under a Multiaxial Stress State

As mentioned above, in case of isotropic viscoelastic materials number of the material time functions is equal to two. Hence, it is possible to separate effects of shape change from the volume change. In such a way, we arrive at the integral form of the constitutive equations of isotropic linear viscoelastic material that generalize the analogous uniaxial equation (2.43) for multiaxial states

$$\begin{aligned} \begin{array}{ll} s_{ij} \left( t\right) &{}= 2\int \limits _{0}^{t} \mathrm{G}_\mathrm{ve} \left( t - \xi \right) \dfrac{\partial e_{ij} \left( \xi \right) }{\partial \xi } \mathrm{d}\xi \\ \sigma _{kk} \left( t\right) &{}= 3\int \limits _{0}^{t} \mathrm{K}_\mathrm{ve} \left( t - \xi \right) \dfrac{\partial \varepsilon _{kk} \left( \xi \right) }{\partial \xi } \mathrm{d}\xi \end{array} \end{aligned}$$
(2.55)

In a particular case, if the volume change is pure elastic , Eq. (2.55) take the simplified form

$$\begin{aligned} \begin{array}{l} s_{ij} \left( t\right) = 2\int \limits _{0}^{t} \mathrm{G}_\mathrm{ve} \left( t - \xi \right) \dfrac{\partial e_{ij} \left( \xi \right) }{\partial \xi } \mathrm{d}\xi \\ \sigma _{kk} = 3K \varepsilon _{kk} \end{array} \end{aligned}$$
(2.56)

2.4 Elastic-Viscoelastic Correspondence Principle for the Case of Isotropic Materials

Consider at the beginning, a particular case of isotropic linear viscoelastic behavior for which separation of the volume change from the shape change holds in a similar fashion as in case of isotropic elastic behavior, see Sect. 1.4.8. Remember however that in a more general case of the anisotropic behavior, linear elastic, and linear viscoelastic, this separation is not possible, see Sect. 1.8.

Analogy between the transformed equations of linear isotropic viscoelastic materials (2.49) and conventional equations of isotropic elasticity (2.51) leads to the searching of the solutions of viscoelasticity on basis of a priori known coupled elastic problems. This analogy is known as the elastic-viscoelastic correspondence principle, see Findley et al. [4].

Let us summarize a complete set of equations of linear isotropic viscoelasticity, see Skrzypek [13]

  • the equilibrium equations

    $$\begin{aligned} \dfrac{\partial \sigma _{ij}\left( {{\varvec{x}}},t\right) }{\partial x_i} + b_j \left( t\right) = 0 \end{aligned}$$
    (2.57)

  • the constitutive equations formed either in the format of differential operator representation (2.46)

    $$\begin{aligned} \begin{array}{l} \mathrm{P}_1 s_{ij}\left( {{\varvec{x}}},t\right) = \mathrm{Q}_1 e_{ij}\left( {{\varvec{x}}},t\right) \\ \mathrm{P}_2 \sigma _{kk}\left( {{\varvec{x}}},t\right) = \mathrm{Q}_2 \varepsilon _{kk}\left( {{\varvec{x}}},t\right) \end{array} \end{aligned}$$
    (2.58)

    or in the integral representation (2.55)

    $$\begin{aligned} \begin{array}{l} s_{ij}\left( {{\varvec{x}}},t\right) = 2\int \limits _{0}^{t} \mathrm{G}_\mathrm{ev}\left( t - \xi \right) \dot{e}_{ij}\left( {{\varvec{x}}}, \xi \right) \mathrm{d}\xi \\ \sigma _{kk}\left( {{\varvec{x}}},t\right) = 3\int \limits _{0}^{t} \mathrm{K}_\mathrm{ev}\left( t - \xi \right) \dot{\varepsilon }_{kk} \left( {{\varvec{x}}},\xi \right) \mathrm{d}\xi \end{array} \end{aligned}$$
    (2.59)

  • the linearized geometric equations

    $$\begin{aligned} \varepsilon _{ij}\left( {{\varvec{x}}},t\right) = \frac{1}{2} \left[ \frac{\partial u_i \left( {{\varvec{x}}},t\right) }{\partial x_j} + \frac{\partial u_j \left( {{\varvec{x}}},t\right) }{\partial x_i}\right] \end{aligned}$$
    (2.60)

  • the boundary conditions under assumption that boundary between domains of force \({\varGamma }_P\) and displacement \({\varGamma }_U\) remain unchanged

    $$\begin{aligned} \begin{array}{lll} P_i \left( {{\varvec{x}}},t\right) = \sigma _{ij} \left( {{\varvec{x}}},t\right) n_j &{} \mathrm{na} &{} {\varGamma }_P \\ U_i \left( {{\varvec{x}}},t\right) = u_i \left( {{\varvec{x}}},t\right) &{} \mathrm{na} &{} {\varGamma }_U \end{array} \end{aligned}$$
    (2.61)

For simplicity independence of the viscoelastic modules, \(\mathrm{G}_\mathrm{ve}\), \(\mathrm{K}_\mathrm{ve}\) from the spatial coordinates holds. In other words, material homogeneity is assumed. In a particular case of composite materials although that material is inhomogeneous at microlevel a homogenization technique allows to reduce such problem to homogeneous at the RUC level of the representative unit cell, see Chap. 3.

When the Laplace transformation of the above set of Eqs. (2.57)–(2.61) is done we arrive at the fictitious coupled elastic problem

$$\begin{aligned} \begin{array}{l} \dfrac{\partial \widehat{\sigma }_{ij}\left( {{\varvec{x}}}, s\right) }{\partial x_i} + \widehat{b}_j \left( {{\varvec{x}}}, s\right) = 0 \\ \widehat{s}_{ij}\left( {{\varvec{x}}},s\right) = 2s\widehat{\mathrm{G}} \widehat{e}_{ij}\left( {{\varvec{x}}},s\right) = \dfrac{\widehat{\mathrm{Q}}_1}{\widehat{\mathrm{P}}_1} \widehat{e}_{ij}\left( {{\varvec{x}}},s\right) \\ \widehat{\sigma }_{kk}\left( {{\varvec{x}}},s\right) = 3s\widehat{\mathrm{K}} \widehat{\varepsilon }_{kk}\left( s\right) = \dfrac{\widehat{\mathrm{Q}}_2}{\widehat{\mathrm{P}}_2}\widehat{\varepsilon }_{kk} \left( {{\varvec{x}}},s\right) \\ \widehat{\varepsilon }_{ij}\left( {{\varvec{x}}},s\right) = \dfrac{1}{2} \left[ \dfrac{\partial \widehat{u}_i\left( {{\varvec{x}}},s\right) }{\partial x_j} +\dfrac{\partial \widehat{u}_j \left( {{\varvec{x}}}, s\right) }{\partial x_i}\right] \\ \widehat{P}_i \left( {{\varvec{x}}},s\right) = \widehat{\sigma }_{ji} \left( {{\varvec{x}}},s\right) n_j \quad \mathrm{at} \quad {\varGamma }_P \\ \widehat{U}_i \left( {{\varvec{x}}},s\right) = \widehat{u}_i \left( {{\varvec{x}}},s\right) \quad \quad \mathrm{at} \quad {\varGamma }_U \end{array} \end{aligned}$$
(2.62)

in which the body forces \(\widehat{b}_j\left( {{\varvec{x}}},s\right) \), external forces \(\widehat{P}_i\left( {{\varvec{x}}},s\right) \), displacements \(\widehat{U}_i\left( {{\varvec{x}}},s\right) \) as well as fictitious elastic constants \(\widehat{\mathrm{G}}\left( s\right) \) and \(\widehat{\mathrm{K}}\left( s\right) \) are functions of the transformed variable \(s\).

Finally, the analogy between viscoelastic and coupled elastic problems can be formulated. Namely if a solution of coupled fictitious elastic problem is known (2.62) \(\widehat{\sigma }_{ij}\left( {{\varvec{x}}},s\right) \) and \(\widehat{u}_i\left( {{\varvec{x}}},s\right) \), the solution of corresponding linear viscoelastic problem (2.57)–(2.61) can be obtained on the way of the inverse Laplace transformations \(\sigma _{ij}\left( {{\varvec{x}}},t\right) \) and \(u_i\left( {{\varvec{x}}},t\right) \). Simultaneously, following relations must hold

$$\begin{aligned} \widehat{\mathrm{G}}_\mathrm{ve} = \frac{\widehat{\mathrm{Q}}_1 \left( s\right) }{2s\widehat{\mathrm{P}}_1 \left( s\right) } \qquad \widehat{\mathrm{K}}_\mathrm{ve} = \frac{\widehat{\mathrm{Q}}_2 \left( s\right) }{3s\widehat{\mathrm{P}}_2 \left( s\right) } \end{aligned}$$
(2.63)

The correspondence principle can be applied only to the boundary problems where the interface between the boundary \({\varGamma }_P\) (where the external forces are prescribed) and the boundary \({\varGamma }_U\) (where the surface displacements are given) is independent of time, see Findley et al. [4]. The above limitation does not hold in case of some material forming processes, for instance rolling, where the interface between boundaries \({\varGamma }_P\) and \({\varGamma }_U\) varies with time.

An example of elastic-viscoelastic correspondence principle applied to multiaxial stress and strain states the thick walled tube made of the isotropic standard material subject to internal pressure \(p(t)=p\mathrm{H}(t)\) applied instantaneously at \(t=0\) is considered after Findley et al. [4]. Taking advantage of the correspondence principle and recalling Lamé’s solution for coupled elastic problem

$$\begin{aligned} u^\mathrm{e} = \frac{pa^2}{b^2 - a^2} \frac{1 + \nu }{E} \left( \frac{b^2}{r} + \frac{1 - \nu }{1 + \nu } r\right) \end{aligned}$$
(2.64)

substitution of (2.54) for \(E,\nu \) in (2.64) gives

$$\begin{aligned} \begin{array}{lll} \dfrac{1+\nu }{E} &{} \longrightarrow &{} \dfrac{\widehat{\mathrm{P}}_1}{\widehat{\mathrm{Q}}_1} \\ \dfrac{1+\nu }{1-\nu } &{} \longrightarrow &{} \dfrac{2\widehat{\mathrm{P}}_2 \widehat{\mathrm{Q}}_1 + \widehat{\mathrm{P}}_1 \widehat{\mathrm{Q}}_2}{3\widehat{\mathrm{P}}_1\widehat{\mathrm{Q}}_2} \end{array} \end{aligned}$$
(2.65)

In this way, a fictitious coupled elastic problem in term of \(s\)

$$\begin{aligned} \widehat{u}(s) = \frac{\widehat{p}(s)a^2}{b^2 - a^2} \frac{\widehat{\mathrm{P}}_1}{\widehat{\mathrm{Q}}_1} \left( \frac{b^2}{r} + \frac{2\widehat{\mathrm{P}}_2 \widehat{\mathrm{Q}}_1 + \widehat{\mathrm{P}}_1 \widehat{\mathrm{Q}}_2}{3\widehat{\mathrm{P}}_1 \widehat{\mathrm{Q}}_2} r\right) \end{aligned}$$
(2.66)

is find out. Applying transformed operators \(\widehat{\mathrm{P}}_1,\widehat{\mathrm{P}}_2, \widehat{\mathrm{Q}}_1\), and \(\widehat{\mathrm{Q}}_2\) of standard model (see Table 2.3) under additional assumption that shape change creep deformation is accompanied by the elastic hydrostatic deformation \(\widehat{\mathrm{P}}_2=1\), \(\widehat{\mathrm{Q}}_2=3K\), we find a solution of the fictitious coupled elastic problem

$$\begin{aligned} \widehat{u}(s) = \frac{pa^2}{b^2 - a^2} \left( \frac{A}{\frac{E_1'}{\eta '}} + \frac{B}{s}\right) \end{aligned}$$
(2.67)

where \(A\) and \(B\) are functions of radial coordinate \(r\) exclusively

$$\begin{aligned} A = - \frac{1}{E'} \left( \frac{b^2}{r} + \frac{r}{3}\right) , \qquad B = \frac{E_1' + E'}{E_1'E'}\left( \frac{b^2}{r} + \frac{r}{3}\right) + \frac{2r}{9K} \end{aligned}$$
(2.68)

Finally, the solution of the real linear viscoelastic problem is achieved by use of the inverse Laplace transform of (2.67) in the following format

$$\begin{aligned} \begin{array}{l} u(t) = \dfrac{pa^2}{b^2 - a^2} \left\{ \dfrac{1}{E'}\left( \dfrac{b^2}{r} + \dfrac{r}{3}\right) + \dfrac{2r}{9K} + \dfrac{1}{E_1'} \left( \dfrac{b^2}{r} + \dfrac{r}{3}\right) \right. \\ \qquad \, \left. \times \left[ 1 - \exp \left( -\dfrac{E_1'}{\eta '} t \right) \right] \right\} \end{array} \end{aligned}$$
(2.69)

2.5 Integral Representation of the Linear Viscoelastic Equations of Anisotropic Materials

The elastic-viscoelastic correspondence principle applied for isotropic material presented in previous Sect. 2.4, was based on mathematically convenient separation of the volumetric and the shape change effects from total viscoelastic deformation. However, in case of any class of material anisotropy such separation does not occur. Hence for sake of generality, we change formulation of the correspondence principle to the uniform fashion that does not employ the above separation. For convenience, the vector-matrix notation will be used.

In a general case of anisotropic linear viscoelastic material , the integral form of constitutive equations is furnished as (see Shu and Onat [12])

$$\begin{aligned} \varepsilon _{ij} \left( t\right) = \int \limits _{0}^{t} \ ^\mathrm{ve}\!J_{ijkl} \left( t - \xi \right) \dot{\sigma }_{kl} \left( \xi \right) \mathrm{d}\xi \end{aligned}$$
(2.70)

or

$$\begin{aligned} \sigma _{ij}(t) = \int \limits _{0}^{t} \ ^\mathrm{ve}\!E_{ijkl}(t - \xi ) \dot{\varepsilon }_{kl}(\xi )\mathrm{d}\xi \end{aligned}$$
(2.71)

where \(^\mathrm{ve}\!J_{ijkl}(t-\xi )\) defines the fourth-rank tensor of creep functions ; whereas, \(^\mathrm{ve}\!E_{ijkl}(t - \xi )\) is the fourth-rank tensor of relaxation functions which characterize viscoelastic properties of anisotropic material. Assuming the symmetry conditions: \(^\mathrm{ve}\!\!J_{ijkl}=^\mathrm{ve}\!\!J_{klij}=^\mathrm{ve}\!\!J_{jikl}=^\mathrm{ve}\!\!J_{ijlk}\), or \(^\mathrm{ve} E_{ijkl}=^\mathrm{ve}\!\!E_{klij}=^\mathrm{ve}\!\!E_{jikl}=^\mathrm{ve}\!\!E_{ijlk}\), both tensors of viscoelastic anisotropy have 21 independent functions. Both constitutive tensor functions \(^\mathrm{ve}\!J_{ijkl}\) or \(^\mathrm{ve}\!E_{ijkl}\) depend on current time \(t\) (integration limit).

When the vector-matrix notation is used, the general constitutive equation of anisotropic linear viscoelastic material defined by Eqs. (2.70) and (2.71) takes equivalent integral form

$$\begin{aligned} \left\{ \varvec{\varepsilon }(t)\right\} = \int \limits _{0}^{t} [^\mathrm{ve}\mathrm{J}(t - \xi )] \frac{\partial }{\partial \xi }\left\{ \varvec{\sigma }(\xi )\right\} \mathrm{d}\xi \end{aligned}$$
(2.72)

or

$$\begin{aligned} \left\{ \varvec{\sigma }(t)\right\} = \int \limits _{0}^{t} [^\mathrm{ve}\mathrm{E}(t - \xi )] \frac{\partial }{\partial \xi }\left\{ \varvec{\varepsilon }(\xi )\right\} \mathrm{d}\xi \end{aligned}$$
(2.73)

When nonabbreviated notation is used introducing matrix of creep compliance functions \(^\mathrm{ve}J_{ij}(t-\xi )\), we arrive at the following constitutive integral equations of anisotropic linear material

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon _{xx}(t) \\ \varepsilon _{yy}(t) \\ \varepsilon _{zz}(t) \\ \gamma _{yz}(t) \\ \gamma _{zx}(t) \\ \gamma _{xy}(t) \end{array}\right\} = \int \limits _{0}^{t} \left[ \begin{array}{ccc|ccc} ^\mathrm{ve}\!J_{11} &{} ^\mathrm{ve}\!J_{12} &{} ^\mathrm{ve}\!J_{13} &{} ^\mathrm{ve}\!J_{14} &{} ^\mathrm{ve}\!J_{15} &{} ^\mathrm{ve}\!J_{16} \\ ^\mathrm{ve}\!J_{21} &{} ^\mathrm{ve}\!J_{22} &{} ^\mathrm{ve}\!J_{23} &{} ^\mathrm{ve}\!J_{24} &{} ^\mathrm{ve}\!J_{25} &{} ^\mathrm{ve}\!J_{26} \\ ^\mathrm{ve}\!J_{31} &{} ^\mathrm{ve}\!J_{32} &{} ^\mathrm{ve}\!J_{33} &{} ^\mathrm{ve}\!J_{34} &{} ^\mathrm{ve}\!J_{35} &{} ^\mathrm{ve}\!J_{36} \\ \hline ^\mathrm{ve}\!J_{41} &{} ^\mathrm{ve}\!J_{42} &{} ^\mathrm{ve}\!J_{43} &{} ^\mathrm{ve}\!J_{44} &{} ^\mathrm{ve}\!J_{45} &{} ^\mathrm{ve}\!J_{46} \\ ^\mathrm{ve}\!J_{51} &{} ^\mathrm{ve}\!J_{52} &{} ^\mathrm{ve}\!J_{53} &{} ^\mathrm{ve}\!J_{54} &{} ^\mathrm{ve}\!J_{55} &{} ^\mathrm{ve}\!J_{56} \\ ^\mathrm{ve}\!J_{61} &{} ^\mathrm{ve}\!J_{62} &{} ^\mathrm{ve}\!J_{63} &{} ^\mathrm{ve}\!J_{64} &{} ^\mathrm{ve}\!J_{65} &{} ^\mathrm{ve}\!J_{66} \end{array}\right] \left\{ \begin{array}{l} \dot{\sigma }_{xx}(\xi ) \\ \dot{\sigma }_{yy}(\xi ) \\ \dot{\sigma }_{zz}(\xi ) \\ \dot{\tau }_{yz}(\xi ) \\ \dot{\tau }_{zx}(\xi ) \\ \dot{\tau }_{xy}(\xi ) \end{array}\right\} \mathrm{d}\xi \end{aligned}$$
(2.74)

where \([^\mathrm{ve}J]_{ij}=[J(t-\xi )]_{ij}\) is the creep compliance matrix. For Eq. (2.73) the inverse relation holds

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{xx}(t) \\ \sigma _{yy}(t) \\ \sigma _{zz}(t) \\ \tau _{yz}(t) \\ \tau _{zx}(t) \\ \tau _{xy}(t) \end{array}\right\} = \int \limits _{0}^{t} \left[ \begin{array}{ccc|ccc} ^\mathrm{ve}\!E_{11} &{} ^\mathrm{ve}\!E_{12} &{} ^\mathrm{ve}\!E_{13} &{} ^\mathrm{ve}\!E_{14} &{} ^\mathrm{ve}\!E_{15} &{} ^\mathrm{ve}\!E_{16} \\ ^\mathrm{ve}\!E_{21} &{} ^\mathrm{ve}\!E_{22} &{} ^\mathrm{ve}\!E_{23} &{} ^\mathrm{ve}\!E_{24} &{} ^\mathrm{ve}\!E_{25} &{} ^\mathrm{ve}\!E_{26} \\ ^\mathrm{ve}\!E_{31} &{} ^\mathrm{ve}\!E_{32} &{} ^\mathrm{ve}\!E_{33} &{} ^\mathrm{ve}\!E_{34} &{} ^\mathrm{ve}\!E_{35} &{} ^\mathrm{ve}\!E_{36} \\ \hline ^\mathrm{ve}\!E_{41} &{} ^\mathrm{ve}\!E_{42} &{} ^\mathrm{ve}\!E_{43} &{} ^\mathrm{ve}\!E_{44} &{} ^\mathrm{ve}\!E_{45} &{} ^\mathrm{ve}\!E_{46} \\ ^\mathrm{ve}\!E_{51} &{} ^\mathrm{ve}\!E_{52} &{} ^\mathrm{ve}\!E_{53} &{} ^\mathrm{ve}\!E_{54} &{} ^\mathrm{ve}\!E_{55} &{} ^\mathrm{ve}\!E_{56} \\ ^\mathrm{ve}\!E_{61} &{} ^\mathrm{ve}\!E_{62} &{} ^\mathrm{ve}\!E_{63} &{} ^\mathrm{ve}\!E_{64} &{} ^\mathrm{ve}\!E_{65} &{} ^\mathrm{ve}\!E_{66} \end{array}\right] \left\{ \begin{array}{l} \dot{\varepsilon }_{xx}(\xi ) \\ \dot{\varepsilon }_{yy}(\xi ) \\ \dot{\varepsilon }_{zz}(\xi ) \\ \dot{\gamma }_{yz}(\xi ) \\ \dot{\gamma }_{zx}(\xi ) \\ \dot{\gamma }_{xy}(\xi ) \end{array}\right\} \mathrm{d}\xi \quad \end{aligned}$$
(2.75)

In particular case of orthotropic linear viscoelastic material , Eqs. (2.74) and (2.75) reduce to narrower forms

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon _{11}(t) \\ \varepsilon _{22}(t) \\ \varepsilon _{33}(t) \\ \gamma _{23}(t) \\ \gamma _{31}(t) \\ \gamma _{12}(t) \end{array}\right\} = \int \limits _{0}^{t} \left[ \begin{array}{ccc|ccc} ^\mathrm{ve}\!J_{11} &{} ^\mathrm{ve}\!J_{12} &{} ^\mathrm{ve}\!J_{13} &{} &{} &{} \\ ^\mathrm{ve}\!J_{21} &{} ^\mathrm{ve}\!J_{22} &{} ^\mathrm{ve}\!J_{23} &{} &{} &{} \\ ^\mathrm{ve}\!J_{31} &{} ^\mathrm{ve}\!J_{32} &{} ^\mathrm{ve}\!J_{33} &{} &{} &{} \\ \hline &{} &{} &{} ^\mathrm{ve}\!J_{44} &{} &{} \\ &{} &{} &{} &{} ^\mathrm{ve}\!J_{55} &{} \\ &{} &{} &{} &{} &{} ^\mathrm{ve}\!J_{66} \end{array}\right] \left\{ \begin{array}{l} \dot{\sigma }_{11}(\xi ) \\ \dot{\sigma }_{22}(\xi ) \\ \dot{\sigma }_{33}(\xi ) \\ \dot{\tau }_{23}(\xi ) \\ \dot{\tau }_{31}(\xi ) \\ \dot{\tau }_{12}(\xi ) \end{array}\right\} \mathrm{d}\xi \end{aligned}$$
(2.76)

or

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{11}(t) \\ \sigma _{22}(t) \\ \sigma _{33}(t) \\ \tau _{23}(t) \\ \tau _{31}(t) \\ \tau _{12}(t) \end{array}\right\} = \int \limits _{0}^{t} \left[ \begin{array}{ccc|ccc} ^\mathrm{ve}\!E_{11} &{} ^\mathrm{ve}\!E_{12} &{} ^\mathrm{ve}\!E_{13} &{} &{} &{} \\ ^\mathrm{ve}\!E_{21} &{} ^\mathrm{ve}\!E_{22} &{} ^\mathrm{ve}\!E_{23} &{} &{} &{} \\ ^\mathrm{ve}\!E_{31} &{} ^\mathrm{ve}\!E_{32} &{} ^\mathrm{ve}\!E_{33} &{} &{} &{} \\ \hline &{} &{} &{} ^\mathrm{ve}\!E_{44} &{} &{} \\ &{} &{} &{} &{} ^\mathrm{ve}\!E_{55} &{} \\ &{} &{} &{} &{} &{} ^\mathrm{ve}\!E_{66} \end{array}\right] \left\{ \begin{array}{l} \dot{\varepsilon }_{11}(\xi ) \\ \dot{\varepsilon }_{22}(\xi ) \\ \dot{\varepsilon }_{33}(\xi ) \\ \dot{\gamma }_{23}(\xi ) \\ \dot{\gamma }_{31}(\xi ) \\ \dot{\gamma }_{12}(\xi ) \end{array}\right\} \mathrm{d}\xi \quad \end{aligned}$$
(2.77)

being extension of equations of orthotropic linear elasticity (1.103). Note that both stresses and strains are functions of time \(^\mathrm{ve}\sigma _{ij}=^\mathrm{ve}\sigma _{ij}(t)\), \(^\mathrm{ve}\varepsilon _{ij}=^\mathrm{ve}\varepsilon _{ij}(t)\), in similar fashion as elements of creep compliance \(^\mathrm{ve}\!J_{ij}=^\mathrm{ve}\!J_{ij}(t-\xi )\) and relaxation \(^\mathrm{ve}\!E_{ij}=^\mathrm{ve}\!E_{ij}(t-\xi )\) matrices.

Applying the Laplace transform to Eqs. (2.74) and (2.75), we arrive at the associated fictitious elastic constitutive equations in the transformed domain

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{\varepsilon }_{xx}(s) \\ \widehat{\varepsilon }_{yy}(s) \\ \widehat{\varepsilon }_{zz}(s) \\ \widehat{\gamma }_{yz}(s) \\ \widehat{\gamma }_{zx}(s) \\ \widehat{\gamma }_{xy}(s) \end{array}\right\} = s \left[ \begin{array}{ccc|ccc} \widehat{J}^{}_{11} &{} \widehat{J}_{12} &{} \widehat{J}_{13} &{} \widehat{J}_{14} &{} \widehat{J}_{15} &{} \widehat{J}_{16} \\ \widehat{J}_{21} &{} \widehat{J}_{22} &{} \widehat{J}_{23} &{} \widehat{J}_{24} &{} \widehat{J}_{25} &{} \widehat{J}_{26} \\ \widehat{J}_{31} &{} \widehat{J}_{32} &{} \widehat{J}_{33} &{} \widehat{J}_{34} &{} \widehat{J}_{35} &{} \widehat{J}_{36} \\ \hline \widehat{J}_{41} &{} \widehat{J}_{42} &{} \widehat{J}_{43} &{} \widehat{J}_{44} &{} \widehat{J}_{45} &{} {\widehat{J}_{46}} \\ \widehat{J}_{51} &{} \widehat{J}_{52} &{} \widehat{J}_{53} &{} \widehat{J}_{54} &{} \widehat{J}_{55} &{} \widehat{J}_{56} \\ \widehat{J}_{61} &{} \widehat{J}_{62} &{} \widehat{J}_{63} &{} \widehat{J}_{64} &{} \widehat{J}_{65} &{} \widehat{J}_{66} \end{array}\right] \left\{ \begin{array}{l} \widehat{\sigma }_{xx}(s) \\ \widehat{\sigma }_{yy}(s) \\ \widehat{\sigma }_{zz}(s) \\ \widehat{\tau }_{yz}(s) \\ \widehat{\tau }_{zx}(s) \\ \widehat{\tau }_{xy}(s) \end{array}\right\} \end{aligned}$$
(2.78)

or

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{\sigma }_{xx}(s) \\ \widehat{\sigma }_{yy}(s) \\ \widehat{\sigma }_{zz}(s) \\ \widehat{\tau }_{yz}(s) \\ \widehat{\tau }_{zx}(s) \\ \widehat{\tau }_{xy}(s) \end{array}\right\} = s \left[ \begin{array}{ccc|ccc} \widehat{E}^{}_{11} &{} \widehat{E}_{12} &{} \widehat{E}_{13} &{} \widehat{E}_{14} &{} \widehat{E}_{15} &{} \widehat{E}_{16} \\ \widehat{E}_{21} &{} \widehat{E}_{22} &{} \widehat{E}_{23} &{} \widehat{E}_{24} &{} \widehat{E}_{25} &{} \widehat{E}_{26} \\ \widehat{E}_{31} &{} \widehat{E}_{32} &{} \widehat{E}_{33} &{} \widehat{E}_{34} &{} \widehat{E}_{35} &{} \widehat{E}_{36} \\ \hline \widehat{E}_{41} &{} \widehat{E}_{42} &{} \widehat{E}_{43} &{} \widehat{E}_{44} &{} \widehat{E}_{45} &{} {\widehat{E}_{46}} \\ \widehat{E}_{51} &{} \widehat{E}_{52} &{} \widehat{E}_{53} &{} \widehat{E}_{54} &{} \widehat{E}_{55} &{} \widehat{E}_{56} \\ \widehat{E}_{61} &{} \widehat{E}_{62} &{} \widehat{E}_{63} &{} \widehat{E}_{64} &{} \widehat{E}_{65} &{} \widehat{E}_{66} \end{array}\right] \left\{ \begin{array}{l} \widehat{\varepsilon }_{xx}(s) \\ \widehat{\varepsilon }_{yy}(s) \\ \widehat{\varepsilon }_{zz}(s) \\ \widehat{\gamma }_{yz}(s) \\ \widehat{\gamma }_{zx}(s) \\ \widehat{\gamma }_{xy}(s) \end{array}\right\} \end{aligned}$$
(2.79)

2.6 Application of the Anisotropic Correspondence Principle to the Case of Orthotropic Composite Materials

For a purpose of engineering application, for instance to some composite materials in which at least one of phases exhibits viscoelastic behavior, it is sufficient to assume the narrower case of orthotropic linear viscoelastic equations (2.76) and (2.77). When the Laplace transformation is applied to the integral constitutive equations of the orthotropic linear viscoelastic material (2.76) and (2.77), we arrive at the associated fictitious orthotropic elastic equations in terms of \(s\)

$$\begin{aligned} \left\{ \widehat{\varvec{\sigma }}(s)\right\} = s [\widehat{\mathrm{E}}(s)] \left\{ \widehat{\varvec{\varepsilon }}(s)\right\} \end{aligned}$$
(2.80)

or

$$\begin{aligned} \left\{ \widehat{\varvec{\varepsilon }}(s)\right\} = s [\widehat{\mathrm{J}}(s)] \left\{ \widehat{\varvec{\sigma }}(s)\right\} \end{aligned}$$
(2.81)

When the vector-matrix notation is applied the corresponding formulas can be written in an expanded fashion

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{\sigma }_{11}(s) \\ \widehat{\sigma }_{22}(s) \\ \widehat{\sigma }_{33}(s) \\ \widehat{\tau }_{23}(s) \\ \widehat{\tau }_{31}(s) \\ \widehat{\tau }_{12}(s) \end{array} \right\} = s \left[ \begin{array}{ccc|ccc} \widehat{E}^{}_{11} &{} \widehat{E}_{12} &{} \widehat{E}_{13} &{} 0 &{} 0 &{} 0 \\ \widehat{E}_{21} &{} \widehat{E}_{22} &{} \widehat{E}_{23} &{} 0 &{} 0 &{} 0 \\ \widehat{E}_{31} &{} \widehat{E}_{32} &{} \widehat{E}_{33} &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} \widehat{E}^{}_{44} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \widehat{E}_{55} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \widehat{E}_{66} \end{array} \right] \left\{ \begin{array}{l} \widehat{\varepsilon }_{11}(s) \\ \widehat{\varepsilon }_{22}(s) \\ \widehat{\varepsilon }_{33}(s) \\ \widehat{\gamma }_{23}(s) \\ \widehat{\gamma }_{31}(s) \\ \widehat{\gamma }_{12}(s) \end{array} \right\} \end{aligned}$$
(2.82)

or

$$\begin{aligned} \left\{ \begin{array}{l} \widehat{\varepsilon }_{11}(s) \\ \widehat{\varepsilon }_{22}(s) \\ \widehat{\varepsilon }_{33}(s) \\ \widehat{\gamma }_{23}(s) \\ \widehat{\gamma }_{31}(s) \\ \widehat{\gamma }_{12}(s)\end{array}\right\} = s \left[ \begin{array}{ccc|ccc} \widehat{J}^{}_{11} &{} \widehat{J}_{12} &{} \widehat{J}_{13} &{} 0 &{} 0 &{} 0 \\ \widehat{J}_{21} &{} \widehat{J}_{22} &{} \widehat{J}_{23} &{} 0 &{} 0 &{} 0 \\ \widehat{J}_{31} &{} \widehat{J}_{32} &{} \widehat{J}_{33} &{} 0 &{} 0 &{} 0 \\ \hline 0 &{} 0 &{} 0 &{} \widehat{J}^{}_{44} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \widehat{J}_{55} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \widehat{J}_{66} \end{array} \right] \left\{ \begin{array}{l} \widehat{\sigma }_{11}(s) \\ \widehat{\sigma }_{22}(s) \\ \widehat{\sigma }_{33}(s) \\ \widehat{\tau }_{23}(s) \\ \widehat{\tau }_{31}(s) \\ \widehat{\tau }_{12}(s) \end{array} \right\} \end{aligned}$$
(2.83)

The above equations generalize constitutive equations of isotropic viscoelastic material (2.62)\(_{2,3}\) to the case of material orthotropy, where \(\widehat{E}_{ij}=\widehat{E}_{ij}(s)\) and \(\widehat{J}_{ij}=\widehat{J}_{ij}(s)\) stand for the orthotropic relaxation function matrix and the creep compliance matrix, respectively. Solution of the problem of viscoelastic orthotropy can be obtained on the way of the Laplace inverse transform applied to the transformed variables \(\widehat{\sigma }_{ij}(s)\), \(\widehat{\varepsilon }_{ij}(s)\), which are retransformed to physical variables \(\sigma _{ij}(t)\), \(\varepsilon _{ij}(t)\).

It should be emphasized that in case of anisotropic linear viscoelastic materials, similar to anisotropic elastic materials, it is not possible to separate the constitutive equations into the volumetric change and the shape change uncoupled equations since anisotropy results in full coupling between the volume and the shape viscoelastic deformation.

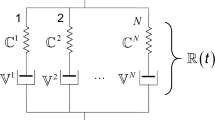
In case of composite materials, the properties of which exhibit the linear viscoelastic features, a generalization of commonly used homogenization techniques (see Chap. 3) to viscoelastic work-regime can be proposed (cf. Haasemann and Ulbricht [5]). The frequently applied concept of the representative unit cell (RUC) originally developed for elastic composites can also be adapted to nonelastic behavior of composites (matrix and/or fiber). To this end, the class of linear viscoelastic material occurs to be very convenient when use of the correspondence principle which enables to transform the real viscoelastic (time-dependent) problem to a fictitious elastic (time-independent) problem in the domain of new variable \(s\) (see Table 2.4).

Constitutive equation of viscoelastic material can be formulated twice: at the level of subcell (\(\beta \gamma \)) where components are described by different viscoelastic equations (matrix, fibers, particles) and at the level of RUC where different properties of material are homogenized in a particular way to yield mean or effective viscoelastic response.

The above described stages of description are briefly presented as follows: at level of subcell the local constitutive equations of linear viscoelasticity hold

$$\begin{aligned} ^\mathrm{ve}\varepsilon _{ij}^{(\beta \gamma )}(t) = \int \limits _{0}^{t} {^\mathrm{ve}J}_{ijkl}^{(\beta \gamma )}(t-\xi ) {^\mathrm{ve}\dot{\sigma }}_{kl}^{(\beta \gamma )}(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.84)

or

$$\begin{aligned} {^\mathrm{ve}\sigma }_{ij}^{(\beta \gamma )}(t) = \int \limits _{0}^{t} {^\mathrm{ve}E}_{ijkl}^{(\beta \gamma )}(t-\xi ) {^\mathrm{ve}\dot{\varepsilon }}_{kl}^{(\beta \gamma )}(\xi ) \mathrm{d}\xi \end{aligned}$$
(2.85)

where the local variables, microstress , and microstrain are combined by local constitutive time-dependent fourth-rank tensors (the creep compliance tensor or the relaxation tensor) for the homogeneous constituent material. In a formal fashion when a homogenization inside the RUC is used, we arrive at

$$\begin{aligned} ^\mathrm{ve}\overline{\varepsilon }_{ij}(t) = \int \limits _{0}^{t} {^\mathrm{ve}\overline{J}}_{ijkl}(t-\xi ) ^\mathrm{ve}\overline{\dot{\sigma }}_{kl}(\xi )\mathrm{d}\xi \end{aligned}$$
(2.86)

or

$$\begin{aligned} ^\mathrm{ve}\overline{\sigma }_{ij}(t) = \int \limits _{0}^{t} {^\mathrm{ve}\overline{E}}_{ijkl}(t-\xi ) ^\mathrm{ve}\overline{\dot{\varepsilon }}_{kl}(\xi )\mathrm{d}\xi \end{aligned}$$
(2.87)

Mean or effective fourth-rank tensors of creep compliance \(^\mathrm{ve}\overline{J}_{ijkl}\) or relaxation \(^\mathrm{ve}\overline{E}_{ijkl}\) are defined at the level of RUC in terms of the corresponding local tensors \({^\mathrm{ve}\overline{J}}_{ijkl}^{(\beta \gamma )}\) or \({^\mathrm{ve}\overline{E}}_{ijkl}^{(\beta \gamma )}\) at the level of subcell by the use of a homogenization procedure in an analogous way as for the elastic composite (3.58). Homogenization of the viscoelastic properties of the composite material is not a trivial problem and is seldom met in literature, cf. e.g., Haasemann and Ulbricht [5].

Application of correspondence principle occurs to be very useful since it makes possible to convert time-dependent heterogeneous viscoelastic problem to associated time-independent elastic problem for which homogenization tools can directly be applied. In particular when elastic-viscoelastic analogy is applied for anisotropic composites at the level of RUC, the application of the Laplace transform allows to reduce integral equation of real material (2.86) or (2.87) to coupled set of equations of a fictitious elastic problem in space of the transformed variable \(s\)

$$\begin{aligned} ^\mathrm{e}\widehat{\overline{\varepsilon }}_{ij}(s) = s\widehat{\overline{E}}_{ijkl}^{-1}(s) ^\mathrm{e}\widehat{\overline{\sigma }}_{kl}(s) \end{aligned}$$
(2.88)

or

$$\begin{aligned} ^\mathrm{e}\widehat{\overline{\sigma }}_{ij}(s) = s\widehat{\overline{E}}_{ijkl}(s) ^\mathrm{e}\widehat{\overline{\varepsilon }}_{kl}(s) \end{aligned}$$
(2.89)

Finally, solution of the anisotropic linear viscoelastic problem can be obtained by the use of inverse Laplace transformation from the transformed domain \(^\mathrm{e}\widehat{\overline{\varepsilon }}_{ij}(s), ^\mathrm{e}\widehat{\overline{\sigma }}_{ij}(s)\) to the physical domain \(^\mathrm{ve}\overline{\varepsilon }_{ij}(t), ^\mathrm{ve}\overline{\sigma }_{ij}(t)\). When absolute notation is used we get (see Haasemann and Ulbricht [5])

$$\begin{aligned} \begin{array}{l} {}^{\mathrm{ve}}\overline{{\sigma }}(t) = {}^\mathrm{ve}\overline{\mathbb {E}}(t): {}^{\mathrm{ve}}\!\overline{{\varepsilon }}(t=0) + \int \limits _{0}^{t} \ {}^{\mathrm{ve}}\overline{\mathbb {E}}(t-\xi ): {}^{\mathrm{ve}}\,\overline{\dot{{\varepsilon }}}(\xi )\mathrm{d}\xi \\ \qquad = {}^{\mathrm{ve}}\overline{\mathbb {E}}(t): {}^{\mathrm{ve}}\,\overline{{\varepsilon }}(t=0) + [^{\mathrm{ve}}\overline{\mathbb {E}}: {}^{\mathrm{ve}}\,\overline{\dot{{\varepsilon }}}](t) \end{array} \end{aligned}$$
(2.90)

Recall definition of the Laplace transform of the function \(f(t)\) \((t>0)\) into the function of transformed variable \(\widehat{f}(s)\)

$$\begin{aligned} \mathcal{L}\left\{ f(t)\right\} = \widehat{f}(s) \mathop {=}\limits ^\mathrm{def} \int \limits _{0}^{\infty } f(t)e^{-st}\mathrm{d}t \end{aligned}$$
(2.91)

and definition of the convolution of two functions

$$\begin{aligned} f(t) \mathop {=}\limits ^\mathrm{def} \int \limits _{0}^{t} f_1(t-\xi )f_2(\xi )\mathrm{d}\xi \equiv f_1(t)*f_2(t) \end{aligned}$$
(2.92)

Applying the Laplace transform (2.91) to the convolution integral (2.92), we arrive at the convolution theorem (see Findley et al. [4])

$$\begin{aligned} \mathcal{L}\left\{ \int \limits _{0}^{t}f_1(t-\xi )f_2(\xi )\mathrm{d}\xi \right\} = \mathcal{L}\left\{ f_1(t)*f_2(t)\right\} = \widehat{f}_1(s)\widehat{f}_2(s) \end{aligned}$$
(2.93)

Taking next the Laplace transform of the integral form of constitutive equation of the anisotropic linear viscoelasticity (2.90), we arrive at the equivalent transformed algebraic equation of anisotropic linear elasticity according to scheme

$$\begin{aligned} ^\mathrm{ve}\overline{{\sigma }}(t) = ^\mathrm{ve}\!\overline{\mathbb {E}}(t): ^\mathrm{ve}\!\overline{{\varepsilon }}(t=0) +^\mathrm{ve}\!\overline{\mathbb {E}}(t): ^\mathrm{ve}\!\overline{\dot{{\varepsilon }}}(t) \mathop {\longrightarrow }\limits ^\mathcal{L} \widehat{\overline{{\sigma }}}(s) = s\widehat{\overline{\mathbb {E}}}(s): \widehat{\overline{{\varepsilon }}}(s) \end{aligned}$$
(2.94)

defined by function of the transformed variable \(s\). The transformed matrix of anisotropic fictitious elasticity \(s\widehat{\overline{\mathbb {E}}}(s)\) is built at the level of RUC of considered composite. The above matrix is obtained by the homogenization of the transformed isotropic local matrices \(s\widehat{\overline{\mathbb {E}}}^{(\beta \gamma )}(s)\) at the level of composite microstructure (subcells).

The procedure described above is sketched by the following scheme shown in Table 2.4. The homogenization procedures for the anisotropic elastic composites are well recognized (for details see next chapter). By contrast, there is no unique and direct homogenization procedure to yield the effective creep compliance \({^\mathrm{ve}J}_{ijkl}^{(\beta \gamma )}(t)\) and relaxation \({^\mathrm{ve}E}_{ijkl}^{(\beta \gamma )}(t)\) tensors (e.g., Haasemann and Ulbricht [5]). Hence to overcome this deficiency, the suggested scheme is as follows: first apply the Laplace transform at the level of subcell in order to eliminate physical time (left path in Table 2.4), second use a homogenization method in order to reach the RUC level for fictitious elastic RUC of composite material and finally apply the inverse Laplace transform to arrive at the physical viscoelastic RUC level (right back path in Table 2.4).

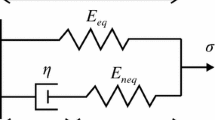
Table 2.4 Elastic-viscoelastic homogenization method based on the representative unit cell (RUC) applied to the associated elastic material by correspondence principle
Full size table

Usually for sake of simplicity of further applications, the transversely isotropic effective relaxation matrix \(s\widehat{\overline{\mathbb {E}}}(s)\) at the level of RUC is sufficient, whereas at the microlevel (subcell) the isotropic matrices for the constituents (f) fiber and (m) composite matrix \(s\widehat{\overline{\mathbb {E}}}^\mathrm{(f)}(s)\) and \(s\widehat{\overline{\mathbb {E}}}^\mathrm{(m)}(s)\) are usually accepted (see also (2.82)). Elastic-viscoelastic correspondence principle as applied to orthotropic viscoelastic and viscoplastic materials is applied by Haasemann and Ulbricht [5]. In case of unidirectionally reinforced composite considered by Haasemann and Ulbricht [5] (see Fig. 2.5), both fiber and matrix materials were described as isotropic linear viscoelastic (see Table 2.5); whereas at macroscale, the sane composite material obeyed the transverse isotropy symmetry. The Laplace–Carson transform

$$\begin{aligned} \mathcal{L}_\mathrm{C}\left\{ f\left( t\right) \right\} = \widehat{f}_\mathrm{C}\left( s\right) = s \int \limits _{0}^{\infty } \mathrm{e}^{-st}f\left( t\right) \mathrm{d}t \end{aligned}$$
(2.95)

was used in order to transform equations of transversely isotropic linear viscoelastic material in \(t\) domain into corresponding equations of fictitious linear elastic material in domain of transformed variable \(s\), in which conventional homogenization techniques of elastic composites were applicable (for details see Chap. 3).

Fig. 2.5
figure 5

Beam model and RUC of unidirectional composite according to Haasemann and Ulbricht [5]

Full size image
Table 2.5 Viscoelastic properties of fiber and matrix material following Haasemann and Ulbricht [5]
Full size table