Effective behavior of viscoelastic composites: comparison of Laplace–Carson and time-domain mean-field approach

Abstract

The paper focuses on deriving the macroscale viscoelastic constitutive laws using asymptotic expansion method. Both the differential and integral form of the linear viscoelastic constitutive relation of the phases is used in deriving the effective incremental potential and effective constitutive relation, respectively. The integral form is handled by considering the correspondence principle and the Laplace–Carson (LC) transform. A closed-form expression for the effective viscoelastic properties in LC domain is obtained by means of the asymptotic homogenization method (AHM). In addition, AHM coupled with finite element simulation of a representative volume element with periodic boundary conditions is used (AHM + FE). The last step in both approaches is the numerical inversion to the time domain. Solution in time domain is obtained with numerical Laplace inversion algorithms. In case of the differential form, using variational approach, the effective incremental potential in time domain is directly obtained using mean-field method. Different homogenization approaches are exemplified for evaluation of the effective relaxation behavior of composite (viscoelastic matrix reinforced by unidirectional elastic fibers), and they are compared. In the approaches based on LC transform, effective modulus and Poisson’s ratio agree well with each other for any property contrast and fiber volume fraction. However, in case of relatively low property contrast, mean field overpredicts as compared to LC approaches in the fiber direction, whereas at relatively higher property contrast, it is vice versa. The difference increases at higher volume fractions due to synergistic effect of the error due to geometrical assumptions involved in the localization tensor and interaction effects of the fiber inclusions. A good agreement in all directions is observed among the three schemes at intermediate volume fractions and property contrast. This study serves as benchmark for further theoretical improvements and experimental investigations.

1 Introduction

Viscoelastic homogenization of fiber-reinforced polymer composites is vital in development of virtual process chain of hybrid composites [1, 2]. Computational analysis of viscoelastic composite parts considering the details such as shape of reinforcement and its distribution would require very fine mesh considering all the heterogeneities of the microstructure, thus leading to a high computational costs and time. This issue is overcome for periodic composite materials by asymptotic expansion method. An asymptotic series approximation is applied to the field quantities such as displacement, strain and stress, assuming the existence of distinct scales associated with the composite macroscale behavior. After separation of the local field quantities, these are solved usually for periodic microstructure geometry with assistance of a full-field method such as finite element method (FEM) and fast Fourier transform [3]. Several contributions in asymptotic homogenization method (AHM) have been devoted to the development of its theoretical basis (see, e.g., [4,5,6]). Other method such as mean-field homogenization (MFH) using Eshelby’s solution [7] can be used to estimate the overall material properties for periodic composites without solving for all the field variables.

Analytical homogenization of a linear viscoelastic composite with isotropic phases and simple microstructures is widely addressed with the methodology of the correspondence principle [8, 9]. The correspondence principle utilizes an integral form of the constitutive equations of each phase. The Laplace–Carson (LC) transformation [10,11,12] converts the time-domain viscoelastic model of the phases to a linear elastic type in the Laplace–Carson domain, thereby facilitating for a direct use of analytical solution of elastic homogenization problem of the periodic composites or it can be coupled with full-field solution. An inversion of the LC transform is then performed to obtain the effective behavior in the time domain. Alternatively, homogenization in time domain evolved in the past two decades uses differential form of the constitutive equation for solving the viscoelastic homogenization problem [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The incremental variational principle-based MFH framework (IVMFH) is chosen in this study for homogenizing the viscoelastic problems as proposed by Lahellec and Suquet [13, 14, 24]. In this method, the local field statistical information is implicitly considered in the homogenization scheme via the second-order moments.

The aim of this work is to derive the effective viscoelastic behavior of composite materials by means of LC transforms and time-domain IVMFH approach in a uniform framework of asymptotic expansion. The major novelty in this manuscript lies in the comparison and contrast among these approaches. The difference in the solutions for different volume fraction and property contrast is highlighted. It is represented for effective modulus and Poisson’s ratio as a function of the direction and time for relaxation tests considering generalized Maxwell behavior of the viscoelastic phases. In the current article, a two-scale homogenization framework for periodic composites consisting of generalized standard materials is defined using the asymptotic expansion method. Microstructure of unidirectional (UD) infinitely long fiber-reinforced polymer (LFRP) composites with a periodic hexagonal arrangement of fibers is considered.

The article is organized as follows: Both the integral and differential form of the constitutive relation of the linear viscoelasticity is introduced in Sect. 2. The asymptotic expansion method is then elaborated in Sect. 3 for defining the two-scale homogenization problem. The differential form of the constitutive relation of the viscoelastic composite is homogenized in time domain using an incremental potential. Variational method is used to obtain the effective incremental potential for the composite based on the Eshelby’s solution as described in Sect. 4. The integral form of the constitutive relation is homogenized using correspondence principle. Since the considered microstructure consists of aligned fibers in a hexagonal pattern, a closed-form expression of the effective viscoelastic properties in the Laplace–Carson domain can be obtained by means of the asymptotic homogenization method (AHM). This approach is introduced as a reference for the comparisons. In addition, we present a third estimate of the effective relaxation stiffness which combines the referenced approach and finite elements simulations (AHM + FE). Finally, a numerical method for the inversion to the time domain is performed. The above is elaborated in Sect. 5. Effective modulus and Poisson’s ratio obtained from all the three methods are compared as a function of direction and time for relaxation test in UD LFRP composites. Sections 7 and 8 highlight the results and conclusions, respectively. The stepwise procedure for implementing the IVMFH scheme is described in Appendix for completeness.

1.1 Nomenclature

A symbolic tensor notation is used throughout the text. The scalars quantities are denoted by light-face-type Latin and Greek characters, e.g., a, b, φ, ψ. The first-order tensors are denoted by bold lowercase and uppercase Latin characters, e.g., x, y, u, U. The second-order tensors are denoted by bold uppercase and lowercase Greek characters, e.g., I, Σ, E, σ, ε. The fourth-order tensors are denoted by blackboard bold uppercase Latin characters, e.g., ${\mathbb{C}}{,}\;{\mathbb{V}}$. A linear map of a fourth-order tensor on a second-order tensor is denoted as ${\mathbb{C}}\left[ {\varvec{\varepsilon}} \right]$. The scalar product between second-order tensors is denoted as for, e.g., σ·ε = σ_ijε_ij. The Frobenius norm of the second-order tensor is denoted as for, e.g., ║ε║. The second- and fourth-order symmetric identity tensors are denoted by I and ${\mathbb{I}}^{{\text{s}}}$, respectively. The fourth-order orthogonal projection tensors are denoted and defined as ${\mathbb{P}}_{1} = \frac{1}{3}\left( {{\varvec{I}} \otimes {\varvec{I}}} \right)$ and ${\mathbb{P}}_{2} = {\mathbb{I}}^{{\text{s}}} - {\mathbb{P}}_{1}$ corresponding to the spherical and deviator. The elastic stiffness tensor and viscosity tensor, represented as ${\mathbb{C}}$ and ${\mathbb{V}}$, respectively, are positive definite fourth-order tensor with minor and major symmetries. The fourth-order symmetric elastic stiffness tensor ${\mathbb{C}}^{\alpha }$ for α-Maxwell branch can be defined using the projection tensors as ${\mathbb{C}}^{\alpha } = g^{\alpha }\left( {3K{\mathbb{P}}_{1} + 2G{\mathbb{P}}_{2} } \right)$, where K and G are the instantaneous bulk and shear modulus, respectively. The spatial average of the field quantities over a domain is indicated by angular brackets for e.g., $\left\langle {\varvec{\varepsilon}} \right\rangle$. All the time-dependent quantities at the current time step and previous time step are represented by t and t_n, respectively.

2 Problem definition

2.1 Constitutive behavior of linear viscoelastic phases in the composite

The constitutive behavior of linear viscoelastic materials in a small strain framework is modeled by two different approaches: hereditary approach (integral form) [10] and internal variables approach (differential form) [28]. The hereditary approach of obtaining constitutive equations in linear viscoelasticity is based on the Boltzmann superposition principle which is given as

$${\varvec{\sigma}}\left( t \right) = \int\limits_{0}^{t} {{\mathbb{R}}\left( {t - t^{\prime}} \right)\left[ {\dot{\varvec{\varepsilon }}\left( {t^{\prime}} \right)} \right]{\kern 1pt} {\text{d}}t^{\prime}}$$

(1)

where σ(t) is the stress tensor as a function of time, $\dot{\varvec{\varepsilon }}\left( t \right)$ is the strain rate, ${\mathbb{R}}\left( t \right)$ is a fourth-order tensor which represents the relaxation of stiffness. The thermodynamic constraints on the nature of relaxation function are described in [29], and generalized Maxwell model as shown in Fig. 1 fulfills them.

Fig. 1

Generalized Maxwell element for modeling linear viscoelastic behavior. The elastic stiffness tensor is indicated as ${\mathbb{C}}^{\alpha }$, and the viscosity tensor is ${\mathbb{V}}^{\alpha }$ for αth Maxwell element

The stiffness relaxation tensor is composed of bulk and shear term for isotropic materials. In this study, it is assumed that only the shear modulus participates in relaxation of the stiffness. Therefore, relaxation of the shear modulus for a generalized Maxwell model can be equivalently modeled by Prony’s series, and it is given as

$$G\left( t \right) = G_{{\text{o}}} \left( {1 - \sum\limits_{\alpha = 1}^{N} {g_{\alpha } } \left( {1 - \exp \left( { - \frac{t}{{\tau_{\alpha } }}} \right)} \right)} \right)$$

(2)

where $g^{\alpha } = \frac{{G^{\alpha } }}{{G_{{\text{o}}} }}$ is the Prony weights and τ^α is the relaxation time. The instantaneous shear modulus is indicated by G_o, and the shear modulus in α-Maxwell branch is G_α. The relaxation time can be calculated as $\tau^{\alpha } = \eta^{\alpha } /G^{\alpha }$. The shear viscosity $\eta^{\alpha }$ is the scalar part of the viscosity tensor ${\mathbb{V}}^{\alpha } = 3\left(+\infty\right) {\mathbb{P}}_{1}+2\eta^{\alpha } {\mathbb{P}}_{2}$ in α-Maxwell branch (Fig. 1). The current stress is then determined by the superposition of history of stress variables in each branch of Maxwell model.

Alternatively, in the internal variable approach, the stress history is recorded through the inelastic strains. In this setting, the constitutive mechanical behavior of the material can be framed under the generalized standard material framework. Thereby, a convex free energy function ψ and a dissipation function φ can be defined for evaluation of stress and internal variables.

$$\begin{gathered} \psi \left( {{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) = \sum\limits_{\alpha = 1}^{N} {\psi^{\alpha } \left( {{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right)} = \sum\limits_{\alpha = 1}^{N} {\frac{1}{2}\left( {{\varvec{\varepsilon}} - \varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } \right) \cdot {\mathbb{C}}^{\alpha } \left[ {{\varvec{\varepsilon}} - \varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } \right]} \hfill \\ \varphi \left( {\varvec{\dot{\varepsilon} }^{\prime}}_{{\text{v}}} \right) = \sum\limits_{\alpha = 1}^{N} {\varphi^{\alpha } \left( \varvec{\dot{\varepsilon}}^{\prime}_{\text{v}} \right)} = \sum\limits_{\alpha = 1}^{N} {\frac{1}{2}\left( {2\eta^{\alpha } {{\varvec{\dot{\varepsilon}}^{\prime}}_{{\text{v}}}^{\alpha } \cdot \varvec{\dot{\varepsilon} }^{\prime}}_{{\text{v}}}^{\alpha } } \right)} \hfill \\ \frac{\partial \psi }{{\partial \varvec{\varepsilon}^{\prime}}_{{\text{v}}} }\left( {{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) + \frac{\partial \varphi }{{\partial \varvec{\dot{\varepsilon}}^{\prime}}_{{\text{v}}} }\left( {\varvec{\dot{\varepsilon} }^{\prime}}_{{\text{v}}} \right) = {\varvec{\it 0}} \hfill \\ {\varvec{\sigma}} = \frac{\partial \psi }{{\partial {\varvec{\varepsilon}}}}\left( {{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) \hfill \\ \end{gathered}$$

(3)

where ε is the total strain. The total thermodynamic potentials ψ and φ are sum of the thermodynamic potentials ψ^α and φ^α defined for α^th Maxwell branch. This is due to the parallel arrangement of the Maxwell branches in the generalized model. The internal strain tensor is symmetric and traceless as indicated by ${\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha }$ due to the assumptions made on the relaxation behavior. The Biot’s equations as given in Eq. (3)₃ are used for calculating the evolution of ${\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha }$ in each Maxwell’s branch and subsequently determine the current state of stress in the homogenous phase using Eq. (3)₄.

3 Two-scale asymptotic expansion of a linear viscoelastic composite problem

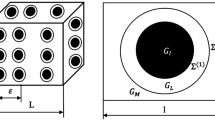
Consider a macroscopic heterogeneous body X of volume V with boundaries ∂X consisting of linear viscoelastic phases (indicated as γ) which is periodically distributed in the geometrical space. The geometrical body of the periodic microstructure is defined in domain Y of volume V_Y with boundary ∂Y and consists of cylindrical fibers oriented along x₁-axis and reinforced in the matrix domain (Fig. 2). It is assumed that interface of the fiber and matrix is under perfect contact conditions i.e., traction and displacement are continuous. The characteristic length of the heterogeneous body and the periodic body is indicated by L and l, respectively. A geometrical characteristic parameter is indicated by ϵ = l/L. The position vector of the macroscopic body (global variable) and the periodic microstructure (local variable) is indicated by x and y, respectively. These vectors are related by y = x/ϵ. The following rule of calculus holds for scale separation

$$\frac{\partial \left( \cdot \right)}{{\partial {\varvec{x}}}} = \frac{\partial \left( \cdot \right)}{{\partial {\varvec{x}}}} + \frac{1}{ \in }\frac{\partial \left( \cdot \right)}{{\partial {\varvec{y}}}}$$

(4)

Fig. 2

Schematic of the two-scale homogenization problem

The properties of the phases, the free energy function and the dissipation potential depend on y ∈ Y as the phases are defined in the Y-domain, which results in

$$\begin{gathered} {\mathbb{R}} \to {\mathbb{R}}\left( {{\varvec{y}},t} \right) \hfill \\ \psi \to \psi \left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) \hfill \\ \varphi \to \varphi \left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) \hfill \\ \end{gathered}$$

(5)

The phase averaging operator on the Y-domain yields the macroscopic quantity which is indicated as, for, e.g., $\Phi \left( {\varvec{x}} \right) \equiv \left\langle {\varphi \left( {{\varvec{x}},{\varvec{y}}} \right)} \right\rangle_{Y} = \frac{1}{{V_{Y} }}\int\limits_{V} {\varphi \left( {{\varvec{x}},{\varvec{y}}} \right){\text{d}}V_{Y} }$. The mathematical statement of viscoelastic heterogeneous problem ignoring inertial terms of the balance of linear momentum with the prescribed boundary conditions is given as

$$\begin{gathered} \begin{array}{*{20}c} \begin{gathered} {\text{div }}{\varvec{\sigma}}^{ \in } \left( {{\varvec{x}},t} \right)+\varvec{ f} = {\mathbf{0}}{\text{ for }}{\varvec{x}} \in X, \, t \in \left[ {0,T} \right] \hfill \\ {\varvec{\varepsilon}}^{ \in } \left( {{\varvec{x}},t} \right) = \nabla^{{\text{s}}} {\varvec{u}}^{ \in } \hfill \\ {\varvec{u}}^{ \in } \left( {{\varvec{x}},t} \right) = {\varvec{U}}\left( {{\varvec{x}},t} \right)\quad {\text{on }}\partial X \hfill \\ {\varvec{\sigma}}^{ \in } {\varvec{n}} = {\varvec{T}}\left( {{\varvec{x}},t} \right)\quad {\text{on }}\partial X \hfill \\ \end{gathered} \\ {} \\ \end{array} \hfill \\ {\text{Initial Conditions}} \hfill \\ {\varvec{U}}\left( {{\varvec{x}},0} \right) = \varvec {\it 0} \hfill \\ {\varvec{T}}\left( {{\varvec{x}},0} \right) = \varvec {\it 0} \hfill \\ \end{gathered}$$

(6)

where n is the outward unit normal vector normal to the surface ∂X, $\nabla^{{\text{s}}}$ is the symmetrized gradient operator and T and U are the tractions and displacement boundary conditions defined on ∂X of the macroscale body. The integral form of the constitutive relation for linear viscoelasticity to solve the problem is given as

$${\varvec{\sigma}}^{ \in } \left( {{\varvec{x}},t} \right) = \int\limits_{0}^{t} {{\mathbb{R}}\left( {{\varvec{y}},t - t^{\prime}} \right)\left[ {\dot{\varvec{\varepsilon }}^{ \in } \left( {t^{\prime}} \right)} \right]{\kern 1pt} {\text{d}}t^{\prime}}$$

(7)

The differential form of the constitutive relation is

$$\begin{gathered} {\varvec{\sigma}}^{ \in } \left( {{\varvec{x}}^{ \in } ,t} \right) = \frac{{\partial \psi^{ \in } }}{{\partial {\varvec{\varepsilon}}^{ \in } }}\left( {{\varvec{y}},{\varvec{\varepsilon}}^{ \in } ,\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{ \in } \right) \hfill \\ \frac{{\partial \psi^{ \in } }}{{\partial \varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{ \in } }\left( {{\varvec{y}},{\varvec{\varepsilon}}^{ \in } ,\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{ \in } \right) + \frac{{\partial \varphi^{ \in } }}{{\partial {\varvec{\dot{\varepsilon }}^{\prime}}_{{\text{v}}}^{ \in } }}\left( {{\varvec{y}},{\varvec{\dot{\varepsilon}}}^{\prime}}_{{\text{v}}}^{ \in } \right) = \varvec {\it 0} \hfill \\ \end{gathered}$$

(8)

Applying the asymptotic expansion on all the field variables and by Korn–Poincare inequality, microscopic balance equations are obtained which are satisfied together with macroscopic balance of linear momentum [30]. Considering ϵ⁻¹ terms and if the field variables have to remain bounded in the limit as ϵ → 0, one could obtain the microscopic balance equations as:

$$\begin{gathered} \in^{ - 1} :\;\;{\text{div }}{\varvec{\sigma}}^{0} \left( {{\varvec{x}},{\varvec{y}},t} \right) = \varvec {\it 0} {\text{ for }}{\varvec{y}} \in Y, \, t \in \left[ {0,T} \right] \hfill \\ \quad \quad {\varvec{u}}^{0} \left( {{\varvec{x}},t} \right) = {\varvec{U}}\left( {{\varvec{x}},t} \right) \hfill \\ \end{gathered}$$

(9)

Applying phase averaging operator on ϵ.⁰ terms leads to the macroscopic balance of linear momentum together with the boundary conditions, which is given as

$$\begin{gathered} \in^{0} :\;\;\;{\text{div }}\varvec{\it{\Sigma}}\left( {{\varvec{x}},t} \right) + {\varvec{f}} = {\varvec{\it 0}}{\text{ for }}{\varvec{x}} \in \Omega , \, t \in \left[ {0,T} \right] \hfill \\ \quad \quad {\varvec{E}}\left( {{\varvec{x}},t} \right) = \nabla_{x}^{{\text{s}}} {\varvec{U}}\left( {{\varvec{x}},t} \right) \hfill \\ \quad \quad \varvec{\it{\Sigma}} \varvec{n} = {\varvec{T}}\left( {{\varvec{x}},t} \right) \hfill \\ \end{gathered}$$

(10)

where $\left\langle {{\varvec{\sigma}}^{0} \left( {{\varvec{x}},{\varvec{y}},t} \right)} \right\rangle_{Y} = \varvec{\it \Sigma}\left( {{\varvec{x}},t} \right)$ is the macroscopic stress and $\left\langle {{\varvec{\varepsilon}}^{0} \left( {{\varvec{x}},{\varvec{y}},t} \right)} \right\rangle_{Y} = \varvec{ E}\left( {{\varvec{x}},t} \right)$ is the macroscopic strain. The integral form of the constitutive relation in the local domain for linear viscoelasticity is given as

$${\varvec{\sigma}}^{0} \left( {{\varvec{x}},{\varvec{y}},t} \right) = \int\limits_{0}^{t} {{\mathbb{R}}\left( {{\varvec{y}},t - t^{\prime}} \right)\left[ {\dot{\varvec{\varepsilon }}^{0} \left( {{\varvec{x}},{\varvec{y}},t^{\prime}} \right)} \right]{\kern 1pt} {\text{d}}t^{\prime}}$$

(11)

The differentiable form of the constitutive relation using internal variables in the local Y-domain is given as

$$\begin{gathered} {\varvec{\sigma}}^{0} \left( {{\varvec{x}},{\varvec{y}},t} \right) = \frac{{\partial \psi^{0} }}{{\partial {\varvec{\varepsilon}}^{0} }}\left( {{\varvec{y}},{\varvec{\varepsilon}}^{0} ,\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{0} \right) \hfill \\ \frac{{\partial \psi^{0} }}{{\partial \varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{0} }\left( {{\varvec{y}},{\varvec{\varepsilon}}^{0} ,\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{0} \right) + \frac{{\partial \varphi^{0} }}{{\partial \varvec{\dot{\varepsilon }}^{\prime}}_{{\text{v}}}^{0} }\left( {{\varvec{y}},\varvec{\dot{\varepsilon }}^{\prime}}_{{\text{v}}}^{0} \right) = \varvec {\it 0} \hfill \\ \end{gathered}$$

(12)

The macroscopic stress using integral and differentiable form of the constitutive relations is then given as

$$\begin{gathered} \varvec{\it\Sigma }\left( {\varvec{x},t} \right) = \left\langle {\int\limits_{0}^{t} {\rm{\mathbb{R}}\left( {\varvec{\it y},\it t - t^{\prime}} \right)\left[ {\varvec{\dot{\varepsilon }}^{0} \left( {\varvec{\it x},\varvec{\it y},\it {t}^{\prime}} \right)} \right]{\kern 1pt} {\text{d}}\it t^{\prime}} } \right\rangle_{Y} = \int\limits_{0}^{t} {\rm{\bar{\mathbb{R}}}\left( {\it t - t^{\prime}} \right)\left[ {\varvec{\dot{{\it E}}}\left( {\varvec{\it x},\it t^{\prime}} \right)} \right]{\kern 1pt} {\text{d}}\it t^{\prime}} \hfill \\ \varvec{\it \Sigma }\left( {\varvec{x},t} \right) = \left\langle {\frac{{\partial \psi^{0} \left( {\varvec{y},\varvec{\varepsilon }^{0} ,\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{0} \right)}}{{\partial \varvec{\varepsilon }^{0} }}} \right\rangle_{Y} = \frac{{\partial \bar{\psi }}}{{\partial \varvec{E}}} \hfill \\ \end{gathered}$$

(13)

where $\bar{\mathbb{R}}\left( t \right)$ is the effective stiffness relaxation tensor.

The objective is to obtain:

• Effective relaxation of the stiffness tensor for the integral form using LC transform.

• Effective Helmholtz free energy function in time domain using a variational method for the incremental form of the differential relations. In this conjunction, mean-field methods based on Eshelby’s solution will be used.

In the next sections, the superscript “0” is ignored for all the local field quantities. The position vector x ∈ X in all the local field quantities is omitted as they are being solved for a fixed position in the macroscopic domain.

4 Effective incremental potential by variational method (IVMFH)

4.1 Incremental potential of the local problem

Each γ-phase in the local Y-domain is indicated with an indicator function $I^{\gamma } \left( {{\varvec{y}},Y} \right)$ given as

$$I^{\gamma } \left( {{\varvec{y}},Y} \right) = \left\{ {\begin{array}{*{20}c} 1 & {{\varvec{y}} \in Y} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.$$

and occupies a volume fraction c^γ. The thermodynamic potentials for each phase in the microstructure are then given as

$$\begin{gathered} \psi \left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) = \sum\limits_{\alpha = 1}^{N} {\underbrace {{\psi^{\alpha } I^{\gamma } \left( {{\varvec{y}},Y} \right)}}_{{\psi^{{\gamma_{\alpha } }} }}} \hfill \\ \varphi \left( {{\varvec{y}},\varvec{\dot{\varepsilon }}^{\prime}_{{\text{v}}} } \right) = \sum\limits_{\alpha = 1}^{N} {\underbrace {{\varphi^{\alpha } I^{\gamma } \left( {{\varvec{y}},Y} \right)}}_{{\varphi^{{\gamma_{\alpha } }} }}} \hfill \\ \end{gathered}$$

(14)

where the thermodynamic potentials $\psi^{{\gamma_{\alpha } }}$ and $\varphi^{{\gamma_{\alpha } }}$ correspond to α-Maxwell branch in γ-phase. Equation (12) is discretized using the implicit Euler scheme in the time domain for a desired time duration of [0, T] with a time step of Δt = t – t_n. The local problem with field variables σ(y, t), ε(y, t) and $\varvec{\varepsilon}^{\prime}_{{\text{v}}} \left( {{\varvec{y}},t} \right)$ is solved by assuming that the field variables at t_n are known. The incremental potential $\hat{\psi }$ for each phase is then defined as

$$\hat{\psi }\left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) = \sum\limits_{\alpha = 1}^{N} {\underbrace {{\left( {\psi^{\alpha } \left( {{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right) + \Delta t\varphi^{\alpha } \left( {\frac{{\varvec{\varepsilon}^{\prime}_{{\text{v}}} - \varvec{\varepsilon}^{\prime}_{{\text{v n}}} }}{\Delta t}} \right)} \right)I^{\gamma } \left( {{\varvec{y}},Y} \right)}}_{{\hat{\psi }^{{\gamma_{\alpha } }} }}}$$

(15)

where the incremental potential $\hat{\psi }^{{\gamma_{\alpha } }}$ corresponds to α-Maxwell branch in γ-phase. Minimizing Eq. (15) with respect to the internal variable of the phase would lead to its evolution equation. The variational problem is defined by a condensed incremental potential $\psi_{\Delta }$.

$$\psi_{\Delta } \left( {{\varvec{y}},{\varvec{\varepsilon}}} \right) = \mathop {\inf }\limits_{{\varvec{\varepsilon}^{\prime}_{{\text{v}}} }} \hat{\psi }\left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon}^{\prime}_{{\text{v}}} } \right)$$

(16)

The effective condensed incremental potential $\overline{\psi }_{\Delta }$ can be obtained by phase averaging over the Y-domain [13], which is then given as

$$\overline{\psi }_{\Delta } \left( {\varvec{E}} \right) = \left\langle {\mathop {\inf }\limits_{{\varvec{\varepsilon}}} \psi_{\Delta } \left( {{\varvec{y}},{\varvec{\varepsilon}}} \right)} \right\rangle_{Y} = \mathop {\inf }\limits_{{\left\langle {\varvec{\varepsilon}} \right\rangle \varvec{ = E}}} \left\langle {\psi_{\Delta } \left( {\varvec{\varepsilon}} \right)} \right\rangle$$

(17)

The effective stress at t can be computed from the effective incremental potential [13], which is given as

$${\varvec{\it \Sigma}}= \frac{{\partial \overline{\psi }_{\Delta } }}{{\partial {\varvec{E}}}}$$

(18)

4.2 Variational method for homogenization of the local problem

The effective condensed incremental potential of the linear viscoelastic homogenization problem is obtained by variational method [31]. The idea is to add and subtract to $\hat{\psi }$ with a piecewise uniform reference potential $\psi_{{\text{o}}}$ of similar form. The reference potential of the phase is chosen as

$$ \begin{gathered} \psi_{{\text{o}}} \left( {{\varvec{y}},{\varvec{\varepsilon}},\varvec{\varepsilon^{\prime}}_{{\text{v}}} } \right) = \sum\limits_{\alpha = 1}^{N} {\underbrace {{\psi_{{\text{o}}}^{\alpha } \left( {{\varvec{\varepsilon}},\varvec{\varepsilon^{\prime}}_{{\text{v}}} } \right)I^{\gamma } \left( {{\varvec{y}},Y} \right)}}_{{\psi_{{\text{o}}}^{{\gamma_{\alpha } }} }}} \hfill \\ = \sum\limits_{\alpha = 1}^{N} {\frac{1}{2}\left( {\left( {{\varvec{\varepsilon}} - \varvec{\varepsilon^{\prime}}_{{\text{v}}}^{\alpha } } \right) \cdot {\mathbb{C}}^{\alpha } \left[ {{\varvec{\varepsilon}} - \varvec{\varepsilon^{\prime}}_{{\text{v}}}^{\alpha } } \right] + \frac{{2\eta_{{\text{o}}}^{\alpha } }}{\Delta t}\left( {\varvec{\varepsilon^{\prime}}_{{\text{v}}}^{\alpha } - \varvec{\varepsilon^{\prime}}_{{\text{ov n}}}^{\alpha } } \right) \cdot \left( {\varvec{\varepsilon^{\prime}}_{{\text{v}}}^{\alpha } - \varvec{\varepsilon^{\prime}}_{{\text{ov n}}}^{\alpha } } \right)} \right)} I^{\gamma } \left( {{\varvec{y}},Y} \right) \hfill \\ \end{gathered} $$

(19)

where $\eta_{{\text{o}}}^{\alpha }$ and ${\varvec{\varepsilon}^{\prime}}_{\text{ov n}}^{\alpha}$ are the artificial viscosity and effective internal variable, respectively. In this conceptualized problem, these parameters are not known and it is always determined at the current time t as described in the following. The difference or error function $\hat{\psi } - \psi_{{\text{o}}}$ can be estimated by the variational principles.

The effective condensed incremental potential [13] in terms of ψ_o is given as

$$\overline{\psi }_{\Delta } \left( {\varvec{E}} \right) = \mathop {\inf }\limits_{{\varvec{E}}} \left( {\left\langle {\mathop {\inf }\limits_{{\varvec{\varepsilon}^{\prime}_{{\text{v}}} }} \left( {\psi_{{\text{o}}} + \Delta \psi } \right)} \right\rangle } \right) \approx \mathop {\inf }\limits_{{\varvec{E}}} \left( {\left\langle {\mathop {\inf }\limits_{{\varvec{\varepsilon}^{\prime}_{{\text{v}}} }} \psi_{{\text{o}}} } \right\rangle + \left\langle {\mathop {{\text{stat}}}\limits_{{\varvec{\varepsilon}^{\prime}_{{\text{v}}} }} \, \Delta \psi } \right\rangle } \right)$$

(20)

Assuming a linear relation between the artificial and actual viscosity $\eta_{{\text{o}}}^{\alpha } = \theta^{\alpha } \eta^{\alpha }$, a close estimate of Δψ can be obtained by considering the stationarity condition [24, 32, 33], which yields

$$\mathop {{\text{stat}}}\limits_{{{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} }} \Delta \psi \left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} } \right) = \mathop {{\text{stat}}}\limits_{{{{{\varvec{\varepsilon}}^{\prime}}}_{{\text{v}}} }} \sum\limits_{{\alpha = 1}}^{N} {\frac{1}{2}\left( {\frac{{2\eta^{\alpha } }}{{\Delta t}}\left( {{{{\varvec{\varepsilon}}^{\prime}}}_{{\text{v}}}^{\alpha } - {{{\varvec{\varepsilon}}^{\prime}}}_{{{\text{v n}}}}^{\alpha } } \right) \cdot \left( {{{{\varvec{\varepsilon}}^{\prime}}}_{{\text{v}}}^{\alpha } - {{{\varvec{\varepsilon}}^{\prime}}}_{{{\text{v n}}}}^{\alpha } } \right) - \frac{{2\eta_{{\text{o}}}^{\alpha } }}{{\Delta t}}\left( {{{{\varvec{\varepsilon}}^{\prime}}}_{{\text{v}}}^{\alpha } - {{{\varvec{\varepsilon}}^{\prime}}}_{{{\text{ov n}}}}^{\alpha } } \right) \cdot \left( {{{{\varvec{\varepsilon}}^{\prime}}}_{{\text{v}}}^{\alpha } - {{{\varvec{\varepsilon}}^{\prime}}}_{{{\text{ov n}}}}^{\alpha } } \right)} \right)} I^{\gamma } \left( {\varvec{y},Y } \right)$$

(21)

The solution of Eq. (21) for α^th Maxwell branch in γ-phase is

$${\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } \left( {\varvec{y}} \right) = \frac{{{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}}^{\alpha } \left( {\varvec{y}} \right) - \theta^{\alpha } {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } }}{{1 - \theta^{\alpha } }}$$

(22)

Substituting Eq. (22) in Eq. (20) yields

$$\overline{\psi }_{\Delta } \left( {\varvec{E}} \right) \approx \mathop {\inf }\limits_{{\varvec{E}}} \left( {\left\langle {\mathop {\inf }\limits_{{{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} }} \psi_{{\text{o}}} } \right\rangle } \right) + \sum\limits_{\gamma = 1}^{n} {c^{\gamma } \left\langle {\sum\limits_{\alpha = 1}^{N} {\left( {\frac{{\eta^{\alpha } \theta^{\alpha } }}{{\Delta t\left( {\theta^{\alpha } - 1} \right)}}\left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}}^{\alpha } - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right) \cdot \left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}}^{\alpha } - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right)} \right)} } \right\rangle^{\gamma } }$$

(23)

Equation (23) is optimized with respect to $\theta^{\alpha }$ and ${\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha }$ to calculate the pair of unknowns for α-Maxwell branch in γ-phase, which is given as [24]

$$\begin{gathered} \theta^{\alpha } = 1 - \sqrt {\frac{{\left\langle {\left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}}^{\alpha } - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right) \cdot \left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}} - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right)} \right\rangle^{\gamma } }}{{\left\langle {\left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right) \cdot \left( {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } - {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } } \right)} \right\rangle^{\gamma } }}} \hfill \\ {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } = \frac{1}{{\theta^{\alpha } }}\left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}}^{\alpha } } \right\rangle^{\gamma } - \left( {1 - \frac{1}{{\theta^{\alpha } }}} \right)\left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } } \right\rangle^{\gamma } \hfill \\ \end{gathered}$$

(24)

The effective internal variable ${\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha }$ in Eq. (19) is independent of y. It considers the local fluctuations of the internal strain in the phases via its second moment, which in turn is again uniform. The field solution of the current internal strain ${\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha } \left( {\varvec{y}} \right)$ for α-Maxwell branch in γ-phase is obtained by solving the infimum problem of ψ_o in Eq. (23) using Eq. (19).

$${\varvec{\varepsilon}^{\prime}}_{\text{v}}^{\alpha} \left( {\varvec{y}} \right) = \left( {\frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\mathbb{P}}_{2} + {\mathbb{C}}^{\alpha } } \right)^{ - 1} \left[ {{\mathbb{P}}_{2} {\mathbb{C}}^{\alpha } \left[ {{\varvec{\varepsilon}}\left( {\varvec{y}} \right)} \right] + \frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\varvec{\varepsilon}^{\prime}}_{{\text{ov}}\,n}^{\alpha} }\right]$$

(25)

Substituting Eq. (25) in $\psi_{{\text{o}}}^{{\gamma_{\alpha } }}$ of Eq. (19) and after mathematical simplifications (see [34]), the expression for γ-phase yields as

$$ \psi_{{\Delta_{{\text{o}}} }}^{\gamma } = \mathop {\inf }\limits_{{\varvec{\varepsilon^{\prime}}_{{\text{v}}} }} \psi_{{\text{o}}}^{\gamma } = \frac{1}{2}{\varvec{\varepsilon}} \cdot {\mathbb{C}}_{{\text{o}}}^{\gamma } \left[ {\varvec{\varepsilon}} \right] + {\varvec{\beta}}_{{\text{o}}}^{\gamma } \cdot {\varvec{\varepsilon}} + h_{{\text{o}}}^{\gamma } $$

(26)

Equation (26) has the form of a thermoelastic energy function. In other words, it leads to a virtual thermoelastic homogenization problem for which already the solution is known. The virtual thermoelastic constant ${\mathbb{C}}_{{\text{o}}}^{\gamma }$ refers to elastic stiffness, ${\varvec{\beta}}_{{\text{o}}}^{\gamma }$ refers to thermal stress and $h_{{\text{o}}}^{\gamma }$ is a scalar constant which are uniform in γ-phase and are given

$$\begin{gathered} {\mathbb{C}}_{{\text{o}}}^{\gamma } = \sum\limits_{\alpha = 1}^{N} {{\mathbb{C}}^{\alpha } - {\mathbb{C}}^{\alpha } {\mathbb{P}}_{2} \left( {\frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\mathbb{P}}_{2} + {\mathbb{C}}^{\alpha } } \right)^{ - 1} {\mathbb{P}}_{2} {\mathbb{C}}^{\alpha } } \hfill \\ {\varvec{\beta}}_{{\text{o}}}^{\gamma } = \sum\limits_{\alpha = 1}^{N} { - {\mathbb{C}}^{\alpha } \left( {\frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\mathbb{P}}_{2} + {\mathbb{C}}^{\alpha } } \right)^{ - 1} \frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}\left[ {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha } \right]} \hfill \\ h_{{\text{o}}}^{\gamma } = \sum\limits_{\alpha = 1}^{N} {\frac{{\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\varvec{\varepsilon}^\prime}_{\text{ov n}}^{\alpha} \cdot \left( {\frac{{2\eta^{\alpha } \theta^{\alpha } }}{\Delta t}{\mathbb{P}}_{2} + {\mathbb{C}}^{\alpha } } \right)^{ - 1} {\mathbb{C}}^{\alpha } \left[ {\varvec{\varepsilon}^\prime}_{\text{ov n}}^{\alpha} \right]} \hfill \\ \end{gathered}$$

(27)

Thus, the thermoelastic constants for γ-phase in a virtual linear thermoelastic problem are defined. The terms involved in the right-hand side of Eq. (27) correspond to α-Maxwell branch of γ-phase. The effective energy of the virtual thermoelastic composite problem after minimizing $\psi_{{\Delta_{{\text{o}}} }}^{\gamma }$ with the macroscopic strain is given as

$$\overline{\psi }_{{\text{o}}} = \mathop {{\text{inf}}}\limits_{{\varvec{E}}} \left( {\sum\limits_{\gamma } {c^{\gamma } \left\langle {\psi_{{\Delta_{{\text{o}}} }}^{\gamma } \left( {\varvec{\varepsilon}} \right)} \right\rangle_{Y}^{\gamma } } } \right)$$

(28)

The effective stress at t is then given as

$${\varvec{\it \Sigma}}= \frac{{\partial \overline{\psi }_{\Delta } \left( {\varvec{E}} \right)}}{{\partial {\varvec{E}}}} = \frac{{\partial \overline{\psi }_{o} \left( {\varvec{E}} \right)}}{{\partial {\varvec{E}}}}$$

(29)

The stress in the actual viscoelastic composite problem is concurrent with the virtual linear thermoelastic problem as observed from Eq. (29). This is because the contribution of the second term in Eq. (23) is nullified with utility of the stationarity conditions of $\theta^{\alpha } ,\,\;{\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{\alpha }$ and ${\varvec{\varepsilon}^{\prime}}_{{\text{v}}}^{\alpha }$. In this study, the virtual thermoelastic homogenization problem is solved using Hashin–Shtrikman lower-bound solution (HSLB). Implementation of this scheme is described in Appendix A.1.

5 Expression for effective properties of LFRP composites in LC space

5.1 Asymptotic homogenization method (AHM)

The effective stiffness tensor $\overline{\mathbb{C}}$ for two-phase UD LFRP composite with hexagonal arrangement of fibers is obtained in [35,36,37] for an elastic framework. In [38, 39], the authors have further extended the methodology to the viscoelastic case by means of the correspondence principle and the Laplace–Carson transform. They transform the integral form of the viscoelastic homogenization problem as indicated in Eq. (11) into an elastic homogenization problem and calculate the effective coefficients $\overline{\mathbb{R}}\left( t \right)$ for LFRP composites with isotropic components.

So, based on this methodology, the effective relaxation properties in the Laplace–Carson space (s) denoted by $\overline{\mathbb{R}}\left( s \right)$(indicated as $\overline{R}\left( s \right)$ in Voigt notation) are given as follows:

$$\overline{R}\left( s \right) = \left( {\begin{array}{*{20}c} {\overline{n}\left( s \right)} & {\overline{l}\left( s \right)} & {\overline{l}\left( s \right)} & {} & {} & {} \\ {} & {\overline{k}\left( s \right) + \overline{m}^{\prime}\left( s \right)} & {\overline{k}\left( s \right) - \overline{m}^{\prime}\left( s \right)} & {} & {} & {} \\ {} & {} & {\overline{k}^{\prime}\left( s \right) + \overline{m}^{\prime}\left( s \right)} & {} & {} & {} \\ {} & {} & {} & {\overline{m}\left( s \right)} & {} & {} \\ {} & {{\text{SYM}}} & {} & {} & {\overline{p}\left( s \right)} & {} \\ {} & {} & {} & {} & {} & {\overline{p}\left( s \right)} \\ \end{array} } \right)$$

(30)

where

$$\begin{gathered} \overline{k}\left( s \right) = \left\langle {k\left( s \right)} \right\rangle - V_{2} \left( {k_{1} \left( s \right) - k_{2} \left( s \right)} \right)^{2} K_{\alpha } \left( {a,s} \right)/m_{1} \left( s \right), \hfill \\ \overline{l}\left( s \right) = \left\langle {l\left( s \right)} \right\rangle - V_{2} \left( {k_{1} \left( s \right) - k_{2} \left( s \right)} \right)\left( {l_{1} \left( s \right) - l_{2} \left( s \right)} \right)K_{\alpha } \left( {a,s} \right)/m_{1} \left( s \right), \hfill \\ \overline{n}\left( s \right) = \left\langle {n\left( s \right)} \right\rangle - V_{2} \left( {l_{1} \left( s \right) - l_{2} \left( s \right)} \right)^{2} K_{\alpha } \left( {a,s} \right)/m_{1} \left( s \right), \hfill \\ \overline{p}\left( s \right) = p_{1} \left( s \right) - 2V_{2} p_{1} \left( s \right)P_{\alpha } \left( s \right), \hfill \\ \overline{m}\left( s \right) = \overline{m}^{\prime}\left( s \right) = m_{1} \left( s \right) - V_{2} \left( {m_{1} \left( s \right) - m_{2} \left( s \right)} \right)M^{\prime}_{\alpha } \left( s \right) \hfill \\ \end{gathered}$$

(31)

In Eq. (31), indexes 1 and 2 indicate properties of matrix (m) and fibers (f), respectively. The term k is the plane-strain bulk modulus, m is the rigidity modulus for shearing in any transverse direction, n is the modulus for longitudinal uniaxial straining, l is the associated cross-modulus, and p is the rigidity modulus for shearing in the longitudinal direction. The functions $K_{\alpha } \left( {a,s} \right),P_{\alpha } \left( {a,s} \right)$ and $M^{\prime}_{\alpha } (s)$ which involve the order of accuracy α are given in [39]. Here, $\overline{m}\left( s \right) = \overline{m}^{\prime}\left( s \right)$ for hexagonal array cell where the symmetry is hexagonal with five independent effective constants. $\overline{m}^{\prime}\left( s \right)$ is different of $\overline{m}\left( s \right)$ only for square array which is not valid for the present study. In this case, the symmetry corresponds to tetragonal symmetry with six independent effective constants.

In the above expression, a = 3 to obtain the effective relaxation stiffness for a hexagonal distribution of fibers. The corresponding lattice sums for a hexagonal array are S₆ = 5.8630316, S₁₂ = 6.00096399, T₅ = 5.6568027, T₁₁ = 6.0301854, S₄ = S₈ = T₇ = 0. The infinite system of Eqs. (30–31) is used such that it is truncated for obtaining an n × n order system. It is interesting to note that the effective properties are monotonic functions of order n of the solution of the system. In general, the numerical results converge well to the exact solutions when an adequate order in the solution of the system is chosen as n increases. The truncation order for solving the system increases as the parameters and the fiber volume fraction are high. In the numerical examples, the solutions are given for n = 1, because this order of n achieves the required accuracy for the used parameters. An analysis of different truncation order of the system is carried out in [37].

5.2 Computational approach (AHM + FE)

As shown in Sect. 5.1 , local problems obtained during the asymptotic homogenization process present an analytical solution in LC space for the hexagonal arrangement of fibers. Thus, the information available at the microscale is encoded into the so-called effective coefficients (see Eq. (30)). However, the analytical solution of such problems is limited to few composite structures. This limitation is overcome by coupling the local problem with the numerical approaches based on FEM for computing the effective properties of the composite. In this section, the methodology described in [40, 41] is used for this purpose.

Assuming a ${\varvec{y}}$-constant expression for the relaxation modulus ${\mathbb{R}}$ in each phase of the periodic cell, $Y$ is given in LC space as

$${\mathbb{R}}({\varvec{y}},s) = \left\{ {\begin{array}{*{20}c} {{\mathbb{R}}^{{\text{f}}} (s),{\text{ if }}{\varvec{y}} \in Y_{1} ,} \\ {{\mathbb{R}}^{{\text{m}}} (s),{\text{ if }}{\varvec{y}} \in Y_{2} .} \\ \end{array} } \right.$$

(32)

Thus, the local problems can be rewritten as,

$$\begin{gathered} {\text{div}}_{y} {\mathbb{R}}^{\text{f}} \left( s \right)\left[ {{\varvec{\varepsilon}}^{\left( y \right)} \left( {{\varvec{\chi}}^{{\text{f}}} \left( {{\varvec{y}},s} \right)} \right)} \right] = \varvec {\it 0}\quad \quad \quad \quad \quad \quad \quad {\text{ in }} Y_{1} \times [0, + \infty ), \hfill \\ {\text{div}}_{y} {\mathbb{R}}^{\text{m}} \left( s \right)\left[ {{\varvec{\varepsilon}}^{\left( y \right)} \left( {{\varvec{\chi}}^{{\text{m}}} \left( {{\varvec{y}},s} \right)} \right)} \right] = \varvec {\it 0}\quad \quad \quad \quad \quad \quad \quad {\text{in}} \, Y_{2} \times \left[ 0 \right.,\left. { + \infty } \right), \hfill \\ \chi^{{\text{f}}} \left( {{\varvec{y}},s} \right) = \chi^{{\text{m}}} \left( {{\varvec{y}},s} \right)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{ on }} \Gamma_{Y} \times \left[ 0 \right.,\left. { + \infty } \right), \hfill \\ \left( {{\mathbb{R}}^{\text{f}} \left( s \right)\left[ {{\varvec{\varepsilon}}^{\left( y \right)} \left( {{\varvec{\chi}}^{{\text{f}}} \left( {{\varvec{y}},s} \right)} \right)} \right]} \right)n^{\left( y \right)} - \left( {{\mathbb{R}}^{\text{m}} \left( s \right)\left[ {{\varvec{\varepsilon}}^{\left( y \right)} \left( {{\varvec{\chi}}^{{\text{m}}} \left( {{\varvec{y}},s} \right)} \right)} \right]} \right)n^{\left( y \right)} \hfill \\ = \left( {{\mathbb{R}}^{\text{f}} \left( s \right) - {\mathbb{R}}^{\text{m}} \left( s \right)} \right)n^{\left( y \right)} \quad \quad \quad \quad \quad \quad \quad \quad \quad \;{\text{ on}} \, \Gamma_{Y} \times \left[ 0 \right.,\left. { + \infty } \right). \hfill \\ {\text{Initial condition in}}\, Y \times \{ 0\} , \hfill \\ \chi \left( {{\varvec{y}},s} \right) = 0. \hfill \\ \end{gathered}$$

(33)

The stress jump conditions arising in the local problems led to the interface loads (see Eq. (33)₅). The latter occur as a consequence of the discontinuities of the relaxation coefficients between the matrix and the fibers, and they represent the driving force to obtain nontrivial solutions of the six elastic-type local problems [42, 43].

At this point, it is possible to solve numerically the set of problems given in Eq. (33) in the Laplace–Carson space and then to compute the effective viscoelastic properties by using the expression,

$$\overline{\mathbb{R}}\left( s \right) = \left\langle {{\mathbb{R}}\left( s \right) + {\mathbb{R}}\left( s \right)\left[ {{\varvec{\varepsilon}}^{\left( y \right)} \left( {{\varvec{\chi}}\left( {{\varvec{y}},s} \right)} \right)} \right]} \right\rangle_{y}$$

(34)

For this purpose, commercially available FEM software COMSOL Multiphysics® and LiveLink™ for MATLAB® scripting is used for implementation.

5.3 Inversion procedure

The inversion of the effective coefficients given in Eqs. (31) and (34) to the original time domain is performed by employing the MATLAB’s function INVLAP [44, 45] and referred here to as Valsa’s method. The algorithm can transform functions of complex variable $s^{\alpha }$, where $\alpha$ is a real exponent. It also transforms functions which contain rational, irrational and transcendent expressions, and can solve fractional problems. As a drawback, it presents problems close to zero; however, the particular case at $t = 0{\text{ s}}$ is obtained from the elastic problem (instant elastic response).

It is worth mentioning that the original version of the INVLAP’s script is conceived for the inversion of Laplace transform and focuses on to invert a symbolic expression in a time interval. Here, the code is adapted to perform the inversion of the Laplace–Carson transform. Furthermore, we are able to integrate it with all the stages of the procedure allowing to invert a discrete space of solution points (see [40, 41]).

The corresponding steps are summarized as follows:

• (a) Discretize the time interval $t = \left[ {t_{1} ,t_{2} ,...,t_{N} } \right]$.

• (b) For each $t_{i}$, obtain the components $s_{j} : = \alpha_{j} /t_{i}$ and $B_{j} = \beta_{j} /t_{i}$ for $j = 1,...,(ns + nd + 1)$, where $ns$ and $nd$ are implicit parameters and $\alpha$ and $\beta$ are defined in Valsa’s method.

• (c) Calculate $\overline{\mathbb{R}}\left( {s_{j} } \right)$ for $j = 1,...,(ns + nd + 1)$.

• (d) Determine the effective coefficients in the time domain

  $$\overline{\mathbb{R}}\left( t \right) = \sum\limits_{j = 1}^{ns + nd + 1} {{\text{Re}} \left[ {B_{j} \overline{\mathbb{R}}\left( {p_{j} } \right)/p_{j} } \right]} \;\;\;\;{\text{for }}i = 1,...,N,$$

where “Re” indicates the real part of a complex variable.

The methodology is fully illustrated in the flowchart given in Fig. 2 of [41]. It is worth noticing that the parameter $\alpha_{j}$ for $j = 2,...,(ns + nd + 1)$ is defined as a complex number within the Valsa’s method [44, 45]. Therefore, the FEM-based numerical approach must be able to handled complex stiffness. Additionally, we have preserved the implicit parameters values suggested by the authors, that is, $a = 6, \, ns = 20, \, nd = 19$, and the results showed a suitable stability and accuracy.

The contributions of each of the numerical computing platforms are discussed as follows,

5.3.1 LiveLink™ for MATLAB®

This tool allows us to integrate COMSOL Multiphysics® with MATLAB® scripting. The main codes are stored in a MATLAB script.

5.3.2 MATLAB®

MATLAB plays the central role in the scheme. Specifically, the whole process is embedded into a MATLAB script and the flow of the

algorithm is controlled from this platform. For instance, we launch COMSOL Multiphysics®, perform the calculations and retrieve the results by using instructions from the MATLAB script.

5.3.3 COMSOL Multiphysics®

The main task of this platform is to solve, for every value $s_{j}$, the set of elastic local problems given in Eq. (33) in Laplace–Carson domain, by means of finite element three-dimensional simulations, and to calculate the effective relaxation modulus $\overline{\mathbb{R}}\left( s \right)$ using Eq. (34). Notice that the corresponding parameters and the properties of the materials are updated at each iteration.

In relation to the COMSOL model, we use the Structural Mechanics Module which offers tools and functionalities adapted to the analysis of the mechanical behavior of solid structures. Here, we define the geometry of the periodic cell, introduce the parameters and implement the six elastic-type local problems of Eq. (33). In addition, for each problem, the periodic boundary conditions on the outer boundary, the continuity of the local displacement Eq. (33)₃ and the stress jump Eq. (33)_4–5 are enforced. The uniqueness of the solution of the local problem is guaranteed by fixing the value of ${\varvec{\chi}}\left( {{\varvec{y}},s} \right)$ at one point of the reference periodic cell [42, 46]. Moreover, quadratic Lagrange elements are used on the finite element mesh and the resulting sparse linear system is solved using the direct solver MUMPS.

6 Material parameters

A three-term generalized Maxwell model is used to depict the viscoelastic behavior of the matrix phase. The instantaneous elastic properties for a novel polymer matrix material, unsaturated polyester–polyurethane hybrid (UPPH) [47, 48], are indicated in Table 1. The assumed Prony coefficients and the relaxation time for the shear modulus in generalized Maxwell model are indicated in Table 1. The effective stiffness relaxation tensor $\overline{\mathbb{R}}\left( t \right)$ of UD LFRP composite is obtained using IVMFH, AHM and AHM + FE. Six independent unit macroscopic strain loads which are constant with the time are applied. The macroscopic stress data are obtained for every current time step and each load case, and these components are assembled to obtain $\overline{\mathbb{R}}\left( t \right)$.

Table 1 Properties of the UPPH matrix [47] (with assumed viscoelastic properties) and elastic glass fibers

7 Results and discussion

7.1 Run-time comparison between AHM + FE and IVMFH

The average run time per number of the time steps is defined as normalized run time, and it is compared for different homogenization methods. It ranges between 0.1 and 0.4 s for IVMFH, whereas it ranges between 300 and 600 s for AHM + FE. Normalized run time for AHM + FE depends on volume fraction of the fibers after an optimal choice of mesh, whereas for IVMFH it depends on the load case, contrast in material properties and volume fraction of fibers. The convergence criteria in IVMFH are set such that the relative error between the two iterations for the unknown set of variables X (see A.1) is less than 1e-8. The convergence is attained typically in an average of 5–10 iterations with maximum iterations observed for the case of shear loading perpendicular to the fiber plane and hence the maximum normalized run time. The iterative algorithm in IVMFH always converged to a solution. It is worth mentioning that AHM being an approach based on closed-form expressions, it provides the effective properties instantly for simple UD FRP microstructures and is therefore not considered in the run-time comparisons.

Figure 3 shows the comparison of the normalized run time required to compute the effective properties for given load case for a simulation time of 20 s with a time step size of 0.05 s. The error bar in the plot indicates deviations in normalized run time for various volume fractions of fibers. The normalized run time is plotted for different shear modulus contrasts, μ = 24.4 and μ = 10. It can be observed that IVMFH provides effective field quantities relatively faster as compared to AHM + FE for simple UD FRP microstructure. The reason stems from the time taken for solving the linear homogenization problems. At each time step, a linear thermoelastic and elastic homogenization problem is being solved by IVMFH and AHM + FE, respectively. Figure 4 shows the time comparison for solving a typical elastic homogenization problem. It can be clearly observed that AHM + FE consumes more time relative to elastic MFH schemes. This limitation in AHM + FE arises because the forward-back passage between the time domain and the Laplace–Carson domain. In fact, in order to invert the effective coefficients, we needed to calculate ns + nd + 1 = 40 points in the Laplace–Carson space to determine one point in the time domain (see subsection Inversion Procedure). Since the IVMFH operates incrementally with current and past internal variable, this would be advantageous for computational purposes such as development of virtual process chain in composite processing [1].

Fig. 3

Comparison of normalized run time between time-domain IVMFH and AHM + FE

Fig. 4

Comparison of run time between MFH and AHM + FE for an elastic homogenization problem

7.2 Directional and time-dependent effective modulus and poisson’s ratio

In case of the linear elasticity, the directional dependent elastic modulus and Poisson’s ratio can be graphically plotted [49]. These graphical plots assist in the direct visual assessment on the nature of the anisotropic behavior of composite and facilitate visual comparisons with the different MFH models and AHM solutions as a function of the load direction and a normal to it. Additionally, these also assist in justifying the homogenization scheme by corresponding with the experimental data made on composite samples with fibers oriented relative to the direction of load [50]. This is extended here to additionally depict the effective behavior of the composite as a function of time. The expression is rewritten as

$$\begin{gathered} \overline{R} \left( {{\varvec{d}},t} \right) = \left( {\left( {{\varvec{d}} \otimes {\varvec{d}}} \right) \cdot \left( {\overline{\mathbb{R}}\left( t \right)} \right)^{ - 1} \left[ {{\varvec{d}} \otimes {\varvec{d}}} \right]} \right)^{ - 1} \hfill \\ \overline{\nu }\left( {{\varvec{d}},{\varvec{n}},t} \right) = - \overline{R} \left( {{\varvec{d}},t} \right)\left( {\left( {{\varvec{d}} \otimes {\varvec{d}}} \right) \cdot \left( {\overline{\mathbb{R}}\left( t \right)} \right)^{ - 1} \left[ {{\varvec{n}} \otimes {\varvec{n}}} \right]} \right) \hfill \\ \end{gathered}$$

(35)

where $\overline{R}$ is the effective modulus of the composite in the loading direction d and $\overline{\nu }$ is the effective Poisson’s ratio along the normal direction n such that n·d = 0. It is to be noted that the modulus is indicative of relaxation effect only in the direction of load. However, in the plane perpendicular to the loading direction,creep effects of Poisson’s ratio is observed which is by virtue of the definition and the assumption involved. This may not be equal to the ratio of strains for e.g. when a creep test is performed on a viscoelastic material.

The relaxation in effective modulus of composite is shown in the polar contour plots as a function of the loading direction and the time. In similar line, evolution of the Poisson’s ratio is plotted as a function of normal direction and time for loading direction along the basis vectors. The polar contour plots indicate the evolution of the effective modulus and Poisson’s ratio along the radial axis, whereas the direction vector is indicated by theta-axis computed in y₁, y₂ and y₃ plane. The time is indicated in contour. The outer periphery of the modulus contour plot depicts the instantaneous modulus, whereas the long-term modulus at t = 20 s is indicated at the inner boundary of the plot. The upper half of the region from [0, π] of the polar contour plot indicates the results obtained from the IVMFH. The lower half region of the contour plot indicates results based on AHM. The first quarter region of the lower half from [π, 1.5π] indicates the results obtained using AHM + FE, whereas the second quarter from [1.5π, 2π] indicates the results from AHM. The error percentage reported in the study for IVMFH solution is evaluated relative to AHM-based solution.

Figure 5 shows the contour plot of the relaxation of the effective modulus $\overline{R}\left( t \right)$ of UD LFRP for glass fibers (shear modulus contrast μ = 24.4). The mean-field solutions obtained using the variational method coupled to HSLB scheme are compared with solutions obtained using AHM and AHM + FE. A good agreement among the three different homogenization scheme is observed for the relaxation in the modulus in all the planes.

Fig. 5

a–c Polar contour plot of $\overline{R}\left( {{\varvec{d}},t} \right)$(radial units in GPa) and d–f $\overline{\nu }\left( {{\varvec{d}},t} \right)$ in LFRP. The upper half of the polar plot indicates for IVMFH, and the lower left quarter indicates for AHM + FE and the lower right quarter indicates for AHM (μ = 24.4, c^f = 0.25)

In case of the effective Poisson’s ratio $\overline{\nu }\left( t \right)$, it is observed from Fig. 5d–f that along the fiber direction, the $\overline{\nu }\left( t \right)$ always decreases with time, whereas on other directions it creeps with time. At certain critical n as observed from y₂- and y₃-stretch, $\overline{\nu }$ does not vary with time. A good agreement among the three different homogenization scheme is observed for $\overline{\nu }$.

7.3 Effect of contrast in shear modulus and fiber volume fraction

The elastic property contrast and the volume fraction of fibers vary in the polymer composite depending upon its application. In view of this fact and the assumptions used in this study, the contrast in shear modulus and the volume fraction of fibers are varied to understand the comparisons of the mean-field solution with asymptotic homogenization approach. Figures 6–9 show the effect of the contrast in shear modulus (μ) and volume fraction (c^f) on the solution of the effective behavior of the composite. The contrast in the shear modulus is varied to μ = 10 and 40 with a constant volume fraction of 0.1 and 0.3. The AHM-based solutions compare well in all the cases. However at c^f = 0.1, a noticeable error of about + 7% and -13% at instantaneous $\overline{R}\left( t \right)$ is observed between IVMFH and AHM-based solution, particularly in the fiber direction for μ = 10 and 40, respectively, as observed in Figs. 6c and 7c. The cause of this deviations is attributed to the assumption that the fiber is modeled as a needle-shaped inclusion in the polarization tensor (see HSLB scheme in Appendix). At higher volume fractions, the deviations caused due to interaction among the fiber reinforcements synergistically cause an increase in the error percent. Hence, in case of c^f = 0.3, the deviation increases to + 11% and -15% for μ = 10 and 40, respectively (Figs. 8c and 9c). Additionally, deviation at instantaneous $\overline{R}\left( t \right)$ perpendicular to the fiber plane is observed to be + 6.5% and 9% for μ = 10 and 40, respectively (Figs. 8a and 9a).

Fig. 6

a–c Polar contour plot of $\overline{R}\left( {{\varvec{d}},t} \right)$(radial units in GPa) and d–f $\overline{\nu }\left( {{\varvec{d}},t} \right)$ in LFRP. The upper half of the polar plot indicates for IVMFH and the lower left quarter indicates for AHM + FE and the lower right quarter indicates for AHM (μ = 10, c^f = 0.1)

Fig. 7

a–c Polar contour plot of $\overline{R}\left( {{\varvec{d}},t} \right)$(radial units in GPa) and d–f $\overline{\nu }\left( {{\varvec{d}},t} \right)$ in LFRP. The upper half of the polar plot indicates for IVMFH and the lower left quarter indicates for AHM + FE and the lower right quarter indicates for AHM (μ = 40, c^f = 0.1)

Fig. 8

a–c Polar contour plot of $\overline{R}\left( {{\varvec{d}},t} \right)$(radial units in GPa) and d–f $\overline{\nu }\left( {{\varvec{d}},t} \right)$ in LFRP. The upper half of the polar plot indicates for IVMFH and the lower left quarter indicates for AHM + FE and the lower right quarter indicates for AHM (μ = 10, c^f = 0.3)

Fig. 9

a–c Polar contour plot of $\overline{R}\left( {{\varvec{d}},t} \right)$(radial units in GPa) and d–f $\overline{\nu }\left( {{\varvec{d}},t} \right)$ in LFRP. The upper half of the polar plot indicates for IVMFH and the lower left quarter indicates for AHM + FE and the lower right quarter indicates for AHM (μ = 40, c^f = 0.3)

Similarly, at c^f = 0.1, deviations in instantaneous $\overline{\nu }\left( t \right)$ on the plane normal to y₁-stretch are observed and it is about + 5% and -7% for μ = 10 and 40, respectively (Figs. 6d and 7d). Additionally, deviation in instantaneous $\overline{\nu }\left( t \right)$ on plane normal to y₃-stretch is observed to be + 7% for μ = 40 (Fig. 7f). At c^f = 0.3, deviations in $\overline{\nu }\left( t \right)$ on plane normal to y₁-stretch increase and it is about + 17% and + 24% for μ = 10 and 40, respectively (Figs. 8d and 9d). Additionally, significant deviation in instantaneous on plane normal to y₃-stretch is observed to be + 13% at μ = 10 (Fig. 8f).

UDFRP composites are found to be useful in several commercial applications, and the c^f can go up to 0.75 depending upon the application [51]. The components of $\overline{\mathbb{R}}\left( t \right)$ are obtained as a function of c^f to understand the deviations arising due to volume fraction of fibers. In this study, the properties given in Table 1 are used. The components of the $\overline{\mathbb{R}}\left( t \right)$ (at t = 20 s) in the direction of the fiber $\overline{R}_{11}$ and in the fiber plane $\overline{R}_{33}$ are plotted for all the three methods (AHM, AHM + FE and IVMFH). Additional solution from FE-based time-domain homogenization is added in the plot which acts as reference solution. The methodology of FE-based homogenization has been adopted following Ref. [27]. Figure 10 shows that the difference between AHM and AHM + FE increases with the volume fraction. However, the magnitude of the difference remains to be less than 5% for $\overline{R}_{11}$ and $\overline{R}_{33}$. Also, the difference in the stiffness along the fiber direction is less than 5% in case of IVMFH and AHM. However, for $\overline{R}_{33}$ the difference increases exponentially with volume fraction of fibers. This gap could be possibly explained due to superimposed effects of underlying assumptions of needle-shaped inclusion in defining the polarization tensor and strong interaction effects between the fibers at higher volume fractions. The comparison of all the solutions with reference to FE-based homogenization indicated that AHM/AHM + FE yielded accurate solution within acceptable deviations. Further, it is noticed that the application of IVMH is observed to be useful in designing of composites with c^f= 0.25—0.3 for the selected property contrast.

Fig. 10

Components of relaxed stiffness tensor at t = 20 s as a function of volume fraction obtained through AHM, AHM + FE, IVMFH and FE

8 Summary and conclusions

An asymptotic expansion is applied for defining the two-scale viscoelastic homogenization problem to homogenize UD LFRP composite with hexagonal arrangement of elastic fibers in a linear viscoelastic matrix. The effective viscoelastic properties of the composite are obtained in both integral and differential form. The effective constitutive behavior of the viscoelastic composite in the differential form is obtained directly in the time domain using IVMFH. On the other hand, schemes AHM and AHM + FE handled the integral form by performing the computations in the LC space and then applying a numerical inversion algorithm to retrieve the solutions in the time domain. The solutions obtained from three different approaches are plotted in terms of effective modulus and effective Poisson’s ratio for relaxation test, thereby indicating the efficacy of the methods. AHM and AHM + FE agree well with each other for any property contrast and fiber volume fraction. However, in case of relatively low property contrast IVMFH overpredicts effective relaxation behavior as compared to AHM-based solutions in the fiber direction due to the assumption of needle-shaped geometry of fiber. Similarly, the effective Poisson’s ratio is also overpredicted in the fiber plane by IVMFH as compared to AHM-based solution. However, at relatively higher property contrast, IVMFH underpredicts compared to AHM-based solution. The error percentage increases at higher volume fraction due to superimposed effect of interaction among the inclusions along with the geometrical assumptions. However, IVMFH provides the effective behavior relatively faster compared with AHM + FE. It is found to be applicable for composites used in real application with  c^f = 0.25–0.3 for, e.g., composites found in automotive applications. It operates incrementally and also can provide fluctuation of the local field quantities, thereby making it relatively advantageous, suitable for extending this scheme for real complex microstructures and implementing in computational framework for polymer composite process chain simulations.

Appendices

Appendix

Implementation of IVMFH approach

Figure 

Fig. 11

Flowchart for implementation of the incremental variational-based MFH to compute Σ at current time step t

11 shows the flowchart of the incremental approach to compute the effective response of the composite as described in Sect. 4.2. The core aspect of the algorithm lies in finding the unknown pair of quantities $\left( {\theta^{{\gamma_{\alpha } }} ,\,\;{\varvec{\varepsilon}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} } \right)$ for all N—Maxwell branches using Eq. (24). These are assembled in a column vector X for γ-phase. This vector of unknowns is given as an input to a function specified in the form F(X) = 0 (Fig. 11), which is given as

$${\mathbf{F}}\underbrace {{\left( \begin{gathered} \theta^{{\gamma_{\alpha = 1} }} \\ \vdots \\ \theta^{{\gamma_{\alpha = N} }} \\ {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha = 1} }} \\ \vdots \\ {\varvec{\varepsilon}^{\prime}}_{{{\text{ov }}n}}^{{\gamma_{\alpha = N} }} \\ \end{gathered} \right)}}_{{\left( {\varvec{X}} \right)}} = \left( {\begin{array}{*{20}c} {1 - \sqrt {\frac{{\left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}} \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{v n}}} } \right\rangle^{{\gamma_{\alpha } }} - 2 \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} \cdot \left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v n}}} } \right\rangle^{{\gamma_{\alpha } }} + {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} }}{{\left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{v}}} } \right\rangle^{{\gamma_{\alpha } }} - 2 \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} \cdot \left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} } \right\rangle^{{\gamma_{\alpha } }} + {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} \cdot {\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} }}} - \,\theta^{{\gamma_{\alpha } }} } \\ {\frac{1}{{\theta^{{\gamma_{\alpha } }} }}\left\langle {{\varvec{{\varepsilon}}^{\prime}}_{{\text{v n}}} } \right\rangle^{{\gamma_{\alpha } }} + \left( {1 - \frac{1}{{\theta^{{\gamma_{\alpha } }} }}} \right)\left\langle {{\varvec{\varepsilon}^{\prime}}_{{\text{v}}} } \right\rangle^{{\gamma_{\alpha } }} - \;{\varvec{\varepsilon}^{\prime}}_{{\text{ov n}}}^{{\gamma_{\alpha } }} } \\ \end{array} } \right) = \underbrace {{\left( \begin{gathered} 0 \hfill \\ \vdots \hfill \\ 0 \hfill \\ \varvec{\it{0}} \hfill \\ \vdots \hfill \\ {\varvec{\it{0}}} \hfill \\ \end{gathered} \right)}}_{{\left( {\mathbf{0}} \right)}}$$

(A.1)

The function is assembled with the pair of unknowns for all N-Maxwell branches using expanded form of Eq. (24). The flowchart also indicates the dependencies of the quantities involved in the computations. The steps for determining the effective response of the composite are summarized as follows:

The first and second moments of the internal strain ($\left\langle {\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right\rangle^{\gamma }$ and $\left\langle {\varvec{\varepsilon}^{\prime}_{{\text{v}}} \cdot \varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right\rangle^{\gamma }$, respectively) at past time t_n are known for γ-phase. Here, the initial conditions are assumed that $\left\langle {\varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right\rangle^{\gamma } = \it {\varvec{0}}$ and $\left\langle {\varvec{\varepsilon}^{\prime}_{{\text{v}}} \cdot \varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right\rangle^{\gamma } = 0$.

The nonlinear set of equations involved in F(X) is solved for all Maxwell branches. The unknown vector X at t is initialized at ith iteration to the solution vector X_n available at t_n to achieve a faster convergence. However, at t = 0 it is assumed that the shear viscosity in the actual problem and virtual thermoelastic problem is same, and the effective internal variable in the virtual problem is zero. Hence, the pair of unknowns for α-Maxwell element in γ-phase is initialized as $\theta^{{\gamma_{\alpha } }} = 1,\,\;{\varvec{\varepsilon}}_{{{\text{ov }}n}}^{{\gamma_{\alpha } }} = \it \varvec{0}$. Based on this, all the thermoelastic constants for the virtual thermoelastic problem are evaluated using Eq. (27) before entering a Jacobian-free optimization loop:

The first and second moments of the total strain ($\left\langle {\varvec{\varepsilon}} \right\rangle^{\gamma }$ and $\left\langle {{\varvec{\varepsilon}^{\prime}} \cdot {\varvec{\varepsilon}^{\prime}}} \right\rangle^{\gamma } ,$ respectively) in the virtual thermoelastic problem are evaluated using an appropriate elastic MFH scheme such as HSLB or DI method for the considered composite microstructure. These moments depend on the thermoelastic constants which in turn depend on unknown vector X.

Based on step 2.1, the first and second moment of the internal strain for the α-Maxwell element in γ-phase ($\left\langle {\varvec{\varepsilon}^{\prime}_{{\text{v}}} } \right\rangle^{{\gamma_{\alpha } }}$ and $\left\langle {\varvec{\varepsilon}^{\prime}_{{\text{v}}} \cdot \varvec{\varepsilon}^{\prime}}_{{\text{v}}} \right\rangle^{{\gamma_{\alpha } }}$, respectively) is evaluated using local field solution in Eq. (25). These quantities also depend on unknown vector X via $\left\langle {\varvec{\varepsilon}} \right\rangle^{\gamma }$ and $\left\langle {\varvec{\varepsilon}^{\prime} \cdot \varvec{\varepsilon}^{\prime}} \right\rangle^{\gamma }$.

The residual for F(X) is computed. If the residual vector is approximately zero, store the first and second moments of the internal strain and go to step 3, else return to step 2.1. The Jacobian of the F(X) is approximated numerically using finite difference.

The macroscopic stress Σ at t can be obtained by the using the converged solution vector X obtained at i + 1 iteration of the optimization loop via Eqs. (25) and (29) (Fig. 11). If t ≤ T, return to step 1 else the time loop stops.

This scheme is implemented in MATLAB using trust-region-dogleg algorithm available in fsolve function. All the tensor calculations are done in the normalized Voigt notation.

Evaluation of first and second moments of total strain

The first and second moment of the internal strain deviator as required in Eq. (24)₁ depends on the first and second moment of the total strain by use of Eq. (25). These are expressed [52] as

$$\begin{gathered} \left\langle {\varvec{\varepsilon}} \right\rangle^{\gamma } = {\mathbb{A}}^{\gamma } \left[ {\varvec{E}} \right] + {\varvec{a}}^{\gamma } \hfill \\ \left\langle {\varvec{\varepsilon}^{\prime} \cdot \varvec{\varepsilon}^{\prime}} \right\rangle^{\gamma } = \left( {\frac{1}{{c^{\gamma } }}\frac{{\partial \overline{\psi }_{{\text{o}}} \left( {K^{\gamma } ,G^{\gamma } } \right)}}{{\partial G^{\gamma } }}} \right) = \frac{1}{{c^{\gamma } }}\frac{{\overline{\psi }_{{\text{o}}} \left( {K^{\gamma } ,G^{\gamma } + \delta G^{\gamma } } \right) - \overline{\psi }_{{\text{o}}} \left( {K^{\gamma } ,G^{\gamma } - \delta G^{\gamma } } \right)}}{{{2}\left( {\delta G^{\gamma } } \right)}} \hfill \\ \end{gathered}$$

(A.2)

where δG^γ is variation in the shear modulus, ${\mathbb{A}}^{\gamma }$ is the strain localization tensor and a^γ is the thermal strain localization tensor of γ-phase. It is sufficient to define ${\mathbb{A}}^{\gamma }$ for homogenizing a two-phase thermoelastic composite problem (see Eq. (A.5)).

Mean-field solution of a linear thermoelastic homogenization problem

Consider a two-phase linear thermoelastic composite (identified as phase γ = 1 and 2, labeled as “m” and “f,” respectively) defined with the thermoelastic energy function of the local constituents as

$$\psi_{{\text{o}}} = \frac{1}{2}\left( {{\varvec{\varepsilon}} - {\varvec{\varepsilon}}_{\theta } } \right) \cdot {\mathbb{C}}\left[ {{\varvec{\varepsilon}} - {\varvec{\varepsilon}}_{\theta } } \right] = \frac{1}{2}{\varvec{\varepsilon}} \cdot {\mathbb{C}}\left[ {\varvec{\varepsilon}} \right] + {\varvec{\beta}} \cdot {\varvec{\varepsilon}} + h$$

(A.3)

where the local terms ε_θ is the thermal strain and β is the thermal stress. Consider the composite constitutes of fiber stiffness surrounded by the matrix stiffness, i.e., ${\mathbb{C}}^{{\text{f}}}$ and ${\mathbb{C}}^{{\text{m}}}$, respectively, with the thermal stresses β^f and β^m. The effective thermoelastic energy function and effective stress are given as

$$\begin{gathered} \overline{\psi }_{{\text{o}}} = \frac{1}{2}\varvec{\it E} \cdot \overline{\mathbb{C}}\left[ \varvec{\it E} \right] + \varvec{\it B} \cdot \varvec{\it E} + \overline{h} \hfill \\{\varvec{\it \Sigma}}= \frac{{\partial \overline{\psi }_{{\text{o}}} }}{{\partial {\varvec{E}}}} = \overline{\mathbb{C}}\left[ {\varvec{E}} \right] + \varvec{\it B} \hfill \\ \overline{\mathbb{C}} = {\mathbb{C}}^{{\text{m}}} + c^{{\text{f}}} \delta {\mathbb{C}}{\mathbb{A}}^{{\text{f}}} \hfill \\ \varvec{\rm B} = \left\langle {\varvec{\beta}} \right\rangle + c^{{\text{f}}} \delta {\mathbb{C}}\,\left[ {{\varvec{a}}^{{\text{f}}} } \right] \hfill \\ \overline{h} = \left\langle h \right\rangle + c^{{\text{f}}} \delta {\varvec{\beta}} \cdot {\varvec{a}}^{{\text{f}}} \hfill \\ \end{gathered}$$

(A.4)

where B is the effective thermal stress, $\delta {\mathbb{C}} = {\mathbb{C}}^{{\text{f}}} - {\mathbb{C}}^{{\text{m}}}$, δβ = β^f–β^m and ${\mathbb{A}}^{{\text{f}}}$ is the strain localization tensor for the fiber phase. In two-phase composite problem, the following two identities are applicable, i.e., $\left\langle {\mathbb{A}} \right\rangle = {\mathbb{I}}^{{\text{s}}}$ and $\left\langle {\varvec{a}} \right\rangle = \it {\varvec{0}}$. In this problem, it is sufficient to define ${\mathbb{A}}^{{\text{f}}}$ as the thermal strain localization tensor a^f can be expressed in terms of ${\mathbb{A}}^{{\text{f}}}$ [53] as

$${\varvec{a}}^{{\text{f}}} = \left( {{\mathbb{A}}^{{\text{f}}} - {\mathbb{I}}^{{\text{s}}} } \right)\delta {\mathbb{C}}^{ - 1} \left[ {\delta {\varvec{\beta}}} \right]$$

(A.5)

The strain localization tensor for the fiber phase ${\mathbb{A}}^{\text{f}}$ is defined by HSLB elastic homogenization scheme.

4.1 Hashin–Shtrikman lower bound (HSLB)

A closer estimate of effective elastic stiffness tensor can be obtained using a variational principle [54] that yields in estimating the upper and lower bounds of the effective stiffness of composite by the choice of reference medium. If the comparison material corresponds to the matrix material or the compliant medium, it estimates the lower bound of the effective stiffness. The strain localization tensor corresponding to the lower bound is given as

$$\begin{gathered} {\mathbb{A}}_{{{\text{HSLB}}}}^{{\text{f}}} = \left( {c^{{\text{m}}} \left( {{\mathbb{A}}^{{{\text{SIP}}}} } \right)^{ - 1} + c^{{\text{f}}} {\mathbb{I}}^{{\text{s}}} } \right)^{ - 1} \hfill \\ {\mathbb{A}}^{{{\text{SIP}}}} = \left( {{\mathbb{I}}^{{\text{s}}} + {\mathbb{P}}_{{\text{o}}} \left( {\delta {\mathbb{C}}} \right)^{ - 1} } \right)^{ - 1} \hfill \\ \end{gathered}$$

(A.6)

where the strain localization tensor ${\mathbb{A}}^{{{\text{SIP}}}}$ corresponds to a single inclusion problem and $\delta {\mathbb{C}} = {\mathbb{C}}^{\text{f}} - {\mathbb{C}}_{{\text{o}}}$ with ${\mathbb{C}}_{{\text{o}}} = {\mathbb{C}}^{{\text{m}}}$ for HSLB. The Hill’s polarization tensor, ${\mathbb{P}}_{{\text{o}}}$, is a function of the elastic properties of the comparison material, i.e., the matrix material in case of HSLB and the geometrical shape of the inhomogeneity [55]. In case of UD FRP composites, the geometrical shape of the fiber is modeled as a needle-shaped inclusion rather than actually being a cylinder of higher aspect ratio [50].