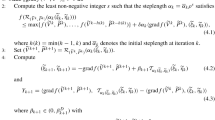Palindromic Eigenvalue Problems in Applications

Abstract

We list a number of practical applications of linear and quadratic palindromic eigenvalue problems. This chapter focuses on two applications which are discussed in detail. These are the vibration analysis of rail tracks and the regularization of the solvent equation. Special purpose algorithms are introduced and numerical examples are presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this chapter we discuss applications of palindromic eigenvalue problems (PEPs), a special structure of eigenvalue problems that is also introduced in Chaps. 2 and 12. Let us recall that a polynomial eigenvalue problem $P(\lambda )x =\sum _{ i=0}^{k}\lambda ^{i}A_{i}x = 0$ with real or complex n × n matrices A _i and with the property $A_{i} = A_{k-i+1}^{\top }$ for all i = 0: k is called palindromic (or, more precisely, ⊤-palindromic, but we will omit the “⊤” for simplicity). Most prevalent in applications are the linear and the quadratic case, which are of the form

$$\displaystyle{ \mathit{Ax} = (-\lambda )A^{\top }x,\quad \text{and}\quad (\lambda ^{2}A^{\top } +\lambda B + A)x = 0,\quad \text{with}\quad B = B^{\top }. }$$

(3.1)

It is easy to see (e.g., by transposing (3.1) and dividing by λ ^k) that the spectrum of a palindromic eigenvalue problem has a reciprocal pairing, that is the eigenvalues come in pairs (λ, 1∕λ). Such a pair reduces to a singleton whenever $\lambda = 1/\lambda$, that is for λ = ±1. Note that in case of real matrices A _i the reciprocal pairing is in addition to the complex conjugate pairing. So, in the real case the eigenvalues come in quadruples $(\lambda,\overline{\lambda },1/\lambda,1/\overline{\lambda })$, which reduces to a reciprocal pair for real nonunimodular eigenvalues (that is $\lambda \in \mathbb{R}$, λ ≠ ± 1), to a complex conjugate pair for unimodular nonreal eigenvalues (that is | λ |  = 1, λ ≠ ± 1) and to a singleton for λ = ±1. In many applications the absence or presence of unimodular eigenvalues is an important property.

With the basics out of the way let us now turn to applications. A rich source of palindromic eigenvalue problems is the area of numerical systems and control theory, an area that belongs to the core interests of Volker Mehrmann. A list of PEPs in this area can be found in [29] and the references therein. The linear-quadratic optimal control problem was already mentioned in Chap. 2: this control problem gives rise to a structured linear eigenvalue problem which is equivalent to a palindromic one via the Cayley transformation. Another application is the optimal H _∞ control problem that, when solved with the so-called γ-iteration method, gives rise to two linear even eigenvalue problems in every iteration of that method. In both of these cases the invariant subspace corresponding to the stable eigenvalues inside the unit circle has to be computed. A third problem from systems theory is the test for passivity of a linear dynamical system that may be implemented by finding out whether a certain palindromic pencil has unimodular eigenvalues or not [7].

Other applications of palindromic eigenvalue problems that we only mention in passing include the simulation of surface acoustic wave (SAW) filters [36, 37], and the computation of the Crawford number of a Hermitian pencil [16] (where the latter is actually a ∗-palindromic eigenvalue problem, obtained by replacing A _i ^⊤ by A _i ^∗ in the definition).

In the remainder of this chapter we will focus on two applications in more detail. First is the simulation of rail track vibrations in Sect. 3.2. This is the application that started the whole field of palindromic eigenvalue problems. We show the derivation of the eigenvalue problem, briefly review algorithms for general polynomial palindromic eigenvalue problems and then discuss a special purpose algorithm exploiting the sparse block structure of the matrices arising in the rail problem.

Second we discuss the regularization of the solvent equation which itself has applications in parameter estimation, see Sect. 3.3. This problem is not a palindromic eigenvalue problem in itself, but the algorithm we describe for its solution requires the repeated solution of many PEPs.

We will use the following notation. $\Re$ and $\Im$ denote real and imaginary part, respectively. We use I _n (or just I) for the identity matrix of order n. We denote by $\overline{A}$, A ^⊤, and A ^∗ the conjugate, the transpose, and the conjugate transpose of a matrix A, respectively. The symbol ρ(A) denotes the spectral radius of a matrix. For a vector x we denote by $\|x\|$ its standard Euclidean norm. For a matrix A, $\|A\|_{2}:= (\rho (A^{{\ast}}A))^{1/2}$ denotes the spectral norm, whereas $\|A\|_{F}:= (\sum _{i,j}\vert a_{\mathit{ij}}\vert ^{2})^{1/2}$ denotes the Frobenius norm. We define for each $m,n \in \mathbb{N}$ the operator $\mathrm{vec}(\cdot ): \mathbb{C}^{m,n} \rightarrow \mathbb{C}^{\mathit{mn}}$ that stacks the columns of the matrix in its argument, i.e., for $A = [a_{1},\ldots,a_{n}]$

$$\displaystyle{ \mathrm{vec}(M):= [a_{1}^{\top },a_{ 2}^{\top },\ldots,a_{ n}^{\top }]^{\top }. }$$

It is well-known that $\mathrm{vec}(\mathit{AXB}) = (B^{\top }\otimes A)\mathrm{vec}(X)$ for each triple of matrices A, X, B of compatible size, where ⊗ denotes the Kronecker product, e.g., [18].

2 Rail Track Vibration

With new Inter-City Express trains crossing Europe at speeds up to 300 kph, the study of the resonance phenomena of the track under high frequent excitation forces becomes an important issue. Research in this area does not only contribute to the safety of the operations of high-speed trains, but also to the design of new train bridges. As shown by Wu and Yang [35], and by Markine, de Man, Jovanovic and Esveld [27], an accurate numerical estimation to the resonance frequencies of the rail plays an important role in the dynamic response of the vehicle-rail-bridge interaction system under different train speeds as well as the design of an optimal embedded rail structures. However, in 2004 the classical finite element packages failed to deliver even a single correct digit for the resonance frequencies.

As reported by Ipsen [20], this problem was posed by the Berlin-based company SFE GmbH to researchers at TU Berlin. So, Hilliges, Mehl and Mehrmann [17] first studied the resonances of railroad tracks excited by high-speed trains in a joint project with this company. Apart from the provided theoretical background for the research of the vibration of rail tracks the outcome was two-fold: (a) the traditionally used method to resolve algebraic constraints was found to be ill-conditioned and was replaced by a well-conditioned alternative, and (b) the arising quadratic eigenvalue problem was observed to have the reciprocal eigenvalue pairing. A search for a structure of the matrix coefficients that corresponds to the eigenvalue pairing finally resulted in the palindromic form (3.1). Then, searching for a structure preserving numerical algorithm for palindromic quadratic eigenvalue problems (PQEPs), D.S. Mackey, N. Mackey, Mehl and Mehrmann [26] proposed a structure preserving linearization with good condition numbers. It linearizes the PQEP (1) to a linear PEP of the form

$$\displaystyle{ \left (\lambda \left [\begin{array}{cc} A^{\top } &A^{\top } \\ B - A&A^{\top } \end{array} \right ] + \left [\begin{array}{cc} A&B - A^{\top } \\ A& A \end{array} \right ]\right )\left [\begin{array}{c} x\\ \lambda x \end{array} \right ] = 0. }$$

(3.2)

In the same paper [26] a first structure-preserving numerical algorithm for the linear PEP is presented: in a Jacobi-like manner the matrix A is iteratively reduced to anti-triangular form by unitary congruence transformations. The eigenvalues are then given as ratios of the anti-diagonal elements. Later, more algorithms for linear PEPs (QR-like, URV-like, or based on the “ignore structure at first, then regain it” paradigm) were developed by a student of Mehrmann [31] and Kressner, Watkins, Schröder [21]. These algorithms typically perform well for small and dense linear palindromic EVPs. An algorithm for large sparse linear palindromic EVPs is discussed in [29]. From the fast train model, D.S. Mackey, N. Mackey, Mehl and Mehrmann [24, 25] first derived the palindromic polynomial eigenvalue problems (PPEP) and systematically studied the relationship between PQEP/PPEP and a special class of “good linearizations for good vibrations” (loosely from the casual subtitle of [24]). Based on these theoretical developments of the PQEP/PPEP [17, 24–26], Chu, Hwang, Lin and Wu [8], as well as, Guo and Lin [15] further proposed structure-preserving doubling algorithms (SDAs) from two different approaches for solving the PQEP which are described in the following.

In conclusion, a great deal of progress has been achieved since the first works in 2004. Ironically, the mentioned well-conditioned resolution of algebraic constraint in that first paper [17] alone (i.e., without preserving the palindromic structure) was enough to solve the eigenvalue problem to an accuracy sufficient in industry. Still, the story of the palindromic eigenvalue problem is a good example of an academic industrial cooperation where (opposite to the usual view of knowledge transfer from academia into industry) a question from industry sparked a whole new, still growing and flourishing research topic in academia. Moreover, the good experience led to further joint projects with the same company [28].

2.1 Modeling

To model the rail track vibration problem, we consider the rail as a 3D isotropic elastic solid with the following assumptions: (i) the rail sections between consecutive sleeper bays are identical; (ii) the distance between consecutive wheels is the same; and (iii) the wheel loads are equal. Based on the virtual work principle, we model the rail by a 3D finite element discretization with linear isoparametric tetrahedron elements (see Fig. 3.1) which produces an infinite-dimensional ODE system for the fast train:

Fig. 3.1

Finite element rail models. Left: consisting of three coupled shells, used in industry. Right: tetrahedral, used in [8]

$$\displaystyle{ \tilde{M}\ddot{u} +\tilde{ D}\dot{u} +\tilde{ K}u =\tilde{ F}, }$$

(3.3)

where $\tilde{M},\ \tilde{K}$ and $\tilde{D}$ are block tridiagonal matrices, representing mass, stiffness and damping matrices of (3.3), respectively. The external excitation force $\tilde{F}$ is assumed to be periodic with frequency ω > 0. In practice, we consider $\tilde{D}$ is a linear combination of $\tilde{M}$ and $\tilde{K}$ of the form $\tilde{D} = c_{1}\tilde{M} + c_{2}\tilde{K}$ with c ₁, c ₂ > 0. Furthermore, we assume that the displacements of two boundary cross sections of the modeled rail have a ratio λ. Under these assumptions, the vibration analysis of rail tracks induces two real symmetric matrices M and K given by

$$\displaystyle{ M = \left [\begin{array}{*{10}c} M_{0} & M_{1}^{\top }&0& \cdots & M_{1} \\ M_{1} & \ddots & \ddots & & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & & \ddots & \ddots &M_{1}^{\top } \\ M_{1}^{\top }& \cdots &0&M_{1} & M_{0} \end{array} \right ]_{m\times m},\quad K = \left [\begin{array}{*{10}c} K_{0} & K_{1}^{\top }&0& \cdots & K_{1} \\ K_{1} & \ddots & \ddots & & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & & \ddots & \ddots &K_{1}^{\top } \\ K_{1}^{\top }& \cdots &0&K_{1} & K_{0} \end{array} \right ]_{m\times m}, }$$

(3.4)

where each block in M and K is of the size q × q. Let M _t be the block tridiagonal part of M, and M _c be the m × m matrix with M ₁ on the upper-right corner and zero blocks else where. Then we can write $M = M_{t} + M_{c} + M_{c}^{\top }$. Correspondingly, we have $K = K_{t} + K_{c} + K_{c}^{\top }$ and $D = D_{t} + D_{c} + D_{c}^{\top }$, where $K_{t},K_{c},D_{t},D_{c}$ are defined analogously.

Letting $u = \mathit{xe}^{\iota \omega t}$ in the spectral model (3.3), where $\iota$ denotes the imaginary unit, leads to a PQEP of the form [8, 15]:

$$\displaystyle{ P(\lambda )x = (\lambda ^{2}A^{\top } +\lambda B + A)x = 0, }$$

(3.5)

where

with n = mq.

The PQEP problem in (3.5) is typically badly scaled and some numerical difficulties need to be addressed: (i) the problem size n can be 30,000–100,000 (typically, m is 50–100, and q is 700–1,000); (ii) it is needed to compute all finite, nonzero eigenvalues and associated eigenvectors for all frequencies ω between 100 and 5,000 Hz; (iii) many of eigenvalues are zero and infinity; (iv) the range of eigenvalues | λ | is typically in $[10^{-20},\ 10^{20}]$ (see Fig. 3.2).

Fig. 3.2

Typical distribution of eigenvalues

To solve the PQEP in (3.5), one may use an initial deflating procedure for zero and infinite eigenvalues to obtain a deflated q × q dense PQEP [17]

$$\displaystyle{ P_{d}(\lambda )x_{d} \equiv (\lambda ^{2}A_{ d}^{\top } +\lambda B_{ d} + A_{d})x_{d} = 0. }$$

(3.6)

On the other hand, one can solve the original block-banded PQEP (3.5) directly.

2.2 SDA for General PQEPs

To solve (3.6) we rewrite P _d (λ) in (3.6) as

$$\displaystyle\begin{array}{rcl} P_{d}(\lambda ) =\lambda ^{2}A_{ d}^{\top } +\lambda B_{ d} + A_{d} = (\lambda A_{d}^{\top } + X_{ d})X_{d}^{-1}(\lambda X_{ d} + A_{d})& &{}\end{array}$$

(3.7)

assuming that X _d is non-singular. It follows that P _d (λ) can be factorized as (3.7) for some non-singular X _d if and only if X _d satisfies the nonlinear matrix equation (NME)

$$\displaystyle{ X_{d} + A_{d}^{\top }X_{ d}^{-1}A_{ d} = B_{d}. }$$

(3.8)

As shown in [25], there are many solutions to the NME (3.8). Each of them enable to facilitate the factorization of P _d (λ). Assume that there are no eigenvalues on the unit circle. Then, by (3.7) we can partition the spectrum into $\varLambda _{s} \oplus \varLambda _{s}^{-1}$ with Λ _s containing the stable eigenvalues (inside the unit circle). We call a solution X _d, s of (3.8) a stabilizing solution if the spectrum of $X_{d,s}^{-1}A_{d}$ is the same as that of Λ _s . The structure-preserving algorithm (SDA) in [15] can then be applied to solve the NME (3.8) and subsequently the PQEP (3.6).

Algorithm 1 (SDA_CHLW)

Let $A_{0} = A_{d},\;B_{0} = B_{d},\;P_{0} \equiv 0$ .

For k = 0,1,…, compute

$$\displaystyle\begin{array}{rcl} & & A_{k+1} = A_{k}(B_{k} - P_{k})^{-1}A_{ k}, {}\\ & & B_{k+1} = B_{k} - A_{k}^{\top }(B_{ k} - P_{k})^{-1}A_{ k}, {}\\ & & P_{k+1} = P_{k} + A_{k}(B_{k} - P_{k})^{-1}A_{ k}^{\top }, {}\\ \end{array}$$

if no break down occurs.

For the convergence of Algorithm 1, we have the following theorem.

Theorem 1 ([8])

Let X _d,s and $\hat{X}_{d,s}$ be the stabilizing solutions of NME  (3.8) and the dual NME $\hat{X}_{d} + A_{d}\hat{X}_{d}^{-1}A_{d}^{\top } = B_{d}$ . Then the sequences $\left \{A_{k}\right \},\ \left \{B_{k}\right \},\ \left \{P_{k}\right \}$ generated by Algorithm  1 satisfy

• (i) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert B_{k} - X_{d,s}\right \Vert } \leq \rho (X_{d,s}^{-1}A_{d})^{2}$ ,

• (ii) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert A_{k}\right \Vert } \leq \rho (X_{d,s}^{-1}A_{d}),$

• (iii) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert B_{k} - P_{k} -\hat{ X}_{d,s}\right \Vert } \leq \rho (X_{d,s}^{-1}A_{d})^{2}.$

provided that all the required inverses of B _k − P _k exist.

2.3 SDA for Block-Banded PQEPs

We now apply the solvent approach directly to the original block-banded PQEP (3.5). To this end, as in (3.7), we first factorize the PQEP (3.5) into

$$\displaystyle\begin{array}{rcl} P(\lambda ) =\lambda ^{2}A^{\top } +\lambda B + A = (\lambda A^{\top } + X)X^{-1}(\lambda X + A)& &{}\end{array}$$

(3.9)

and then solve the nonlinear matrix equation (NME)

$$\displaystyle{ X + A^{\top }X^{-1}A = B. }$$

(3.10)

There are two advantages of the solvent approach in (3.9) over the deflation approach in (3.6) [2, 26]. First, the deflation procedure is used for the sake of efficiency, which involves the inverses of two potentially ill-conditioned matrices. Second, in the deflation approach, the eigenvalues of the smaller PQEP range in modulus from $\varepsilon$ to $\varepsilon ^{-1}$, where $\varepsilon$ is close to 0, while in the solvent approach the eigenvalues of λ X + A range in modulus from $\varepsilon$ to 1.

The success of the solvent approach depends on the existence of a stabilizing solution of (3.10) and an efficient method for its computation.

From the classic Poincaré-Bendixson Theorem we obtain the following result.

Theorem 2 ([15])

Let $K_{t},K_{c},M_{t},M_{c}$ be given as in (3.4) , and set $D_{t} = c_{1}M_{t} + c_{2}K_{t}$ , $D_{c} = c_{1}M_{c} + c_{2}K_{c}$ with $c_{1},c_{2} > 0$ . Then the PQEP  (3.5) has no eigenvalues on the unit circle.

Based on a deep result on linear operators [10] one can prove the following existence theorem.

Theorem 3 ([15])

Under the assumptions in Theorem  2 , the NME  (3.10) has a unique stabilizing solution, and the solution is complex symmetric. Moreover, the dual equation of ( 3.10)

$$\displaystyle{ \hat{X} + A\hat{X}^{-1}A^{\top } = B }$$

(3.11)

also has a unique stabilizing solution and the solution is complex symmetric.

The SDA as in Algorithm 1 with A ₀ = A, B ₀ = B,  P ₀ = 0 can then be applied to solve the NME (3.10) and the dual NME (3.11). In order to distinguish it from Algorithm 1, we call this procedure as Algorithm 2.

Algorithm 2 (SDA)

Let $A_{0} = A,\;B_{0} = B,\;P_{0} \equiv 0$ .

For k = 0,1,…, compute A _k+1 , B _k+1 and P _k+1 as in Algorithm  1.

In contrast to Theorem 1, the following theorem shows that the Algorithm 2 is well-defined and no break down occurs (i.e., B _k − P _k is always invertible). Moreover, B _k and B _k − P _k converge quadratically to the unique stabilizing solutions of NME as well as the dual NME, respectively.

Theorem 4 ([15])

Let X _s and $\hat{X}_{s}$ be the stabilizing solutions of NME  (3.10) and the dual NME (3.11) , respectively. Then

• (i) The sequences $\left \{A_{k}\right \},\ \left \{B_{k}\right \},\ \left \{P_{k}\right \}$ generated by Algorithm  2 are well-defined.

• (ii) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert B_{k} - X_{s}\right \Vert } \leq \rho (X_{s}^{-1}A)^{2}$ ,

• (iii) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert A_{k}\right \Vert } \leq \rho (X_{s}^{-1}A),$

• (iv) $\mathop{\limsup }\limits_{k \rightarrow \infty }\root{2^{k}}\of{\left \Vert B_{k} - P_{k} -\hat{ X}_{s}\right \Vert } \leq \rho (X_{s}^{-1}A)^{2}.$

where $\|\cdot \|$ is any matrix norm.

At the first sight, Algorithm 2 (the solvent approach applied to the original PQEP (3.5)) would be very expensive. However, the complexity of Algorithm 2 can be reduced drastically by using the special structure of the matrix A as in (3.5). Let $B_{k} = B - R_{k}$. Then by induction it is easily seen that the matrices in the sequences $\left \{A_{k}\right \},\ \left \{R_{k}\right \},\ \left \{P_{k}\right \}$ have the special forms

$$\displaystyle{ A_{k} = \left [\begin{array}{ccc} & &E_{k} \\ &0& \\ 0 & & \end{array} \right ],\quad R_{k} = \left [\ \ \begin{array}{c@{}c@{}c@{}c} 0&& & \\ &\ddots & &\\ & &0 & \\ && &F_{k} \end{array} \right ],\quad P_{k} = \left [\begin{array}{c@{}c@{}c@{}c} G_{k}& && \\ &0&& \\ & &\ddots &\\ & & &0 \end{array} \right ] }$$

(3.12)

where the q × q matrices E _k , F _k and G _k can be determined by the following simplified algorithm in which

$$\displaystyle\begin{array}{rcl} B = \left [\begin{array}{c@{}c@{}c@{}c} H_{0}&H_{1}^{\top }& & \\ H_{1}& \ddots & \ddots & \\ & \ddots & \ddots &H_{1}^{\top } \\ & &H_{1}& H_{0} \end{array} \right ]_{m\times m}& &{}\end{array}$$

(3.13)

is given in (3.5) with $H_{0} = K_{0} +\iota \omega M_{0}$,$\quad H_{1} = K_{1} +\iota \omega D_{1} -\omega ^{2}M_{1}$.

Algorithm 3 (SDA_GL; a sparse version of Algorithm 2)

Let $E_{0} = H_{1},\;F_{0} = 0,\;G_{0} = 0$ . For k = 0,1,…, compute

$$\displaystyle{ \left [\begin{array}{cc} S_{k,1} & T_{k,1} \\ S_{k,2} & T_{k,2}\\ \vdots & \vdots \\ S_{k,m}&T_{k,m} \end{array} \right ] = \left (B -\left [\begin{array}{ccccc} G_{k}& && & \\ &0&& & \\ & &\ddots & &\\ & & &0 & \\ & && &F_{k} \end{array} \right ]\right )^{-1}\left [\begin{array}{cc} E_{k}& 0 \\ 0 & \vdots\\ \vdots & 0 \\ 0 &E_{k}^{\top } \end{array} \right ], }$$

(3.14)

where all matrix blocks on the left side of ( 3.14 ) are q × q.

Then compute

$$\displaystyle{ E_{k+1} = E_{k}S_{k,m},\quad F_{k+1} = F_{k} + E_{k}^{\top }S_{ k,1},\quad G_{k+1} = G_{k} + E_{k}T_{k,m}. }$$

(3.15)

Note that the linear systems in (3.14) can be solved by the Sherman–Morrison–Woodbury formula. The details can be found in [15].

After the solvent X _s is computed, we can compute all eigenpairs. Let B = U ^H R be the QR-factorization in a sparse way. Multiplying U to A and X _s from the left, respectively, we have

$$\displaystyle{ UA = \left [\begin{array}{*{10}c} 0_{n-q}&\tilde{H}_{1}^{\top } \\ 0 & \varPhi _{1} \end{array} \right ],\ UX_{s} = \left [\begin{array}{*{10}c} X_{1} & X_{2} \\ 0 & \varPhi _{2} \end{array} \right ], }$$

(3.16)

where $X_{1} = R(1: n - q,1: n - q)$ and $X_{2}(1: n - 3q,1: q) = 0$. In view of the factorization of $P(\lambda ) = (\lambda A^{\top } + X_{s})X_{s}^{-1}(\lambda X_{s} + A)$, the nonzero stable eigenpairs (λ _s , z _s ) of P(λ) are those of λ X _s + A and can be computed by the generalized eigenvalue problem

$$\displaystyle{ \varPhi _{1}z_{s,2} = -\lambda _{s}\varPhi _{2}z_{s,2}, }$$

(3.17)

and set

$$\displaystyle{ z_{s,1} = -X_{1}^{-1}(X_{ 2}z_{s,2}+\lambda _{s}^{-1}\tilde{H}_{ 1}^{\top }z_{ s,2}),\ z_{s} = \left [\begin{array}{*{10}c} z_{s,1} \\ z_{s,2} \end{array} \right ], }$$

(3.18)

for s = 1, ⋯ , q.

We now compute all left eigenvectors of $\lambda \varPhi _{2} +\varPhi _{1}$ by

$$\displaystyle{ y_{s}^{\top }\varPhi _{ 1} = -\lambda _{s}y_{s}^{\top }\varPhi _{ 2}, }$$

(3.19)

for s = 1, ⋯ , q. The finite unstable eigenpairs $\left (\lambda _{u},z_{u}\right )$ of P(λ) satisfy

$$\displaystyle{ P(\lambda _{u})z_{u} \equiv P(1/\lambda _{s})z_{u} = \frac{1} {\lambda _{s}^{2}}\left (A^{\top } +\lambda _{ s}X_{s}\right )X_{s}^{-1}\left (X_{ s} +\lambda _{s}A\right )z_{u} = 0. }$$

(3.20)

From (3.16) and (3.19), it follows that

$$\displaystyle{ (A^{\top }+\lambda _{ s}X_{s})U^{\top }\left [\begin{array}{c} 0\\ y_{ s}\end{array} \right ] = \left (\left [\begin{array}{cc} 0 & 0 \\ \tilde{H}_{1} & \varPhi _{1}^{\top } \end{array} \right ] + \left [\begin{array}{cc} \lambda _{s}X_{1}^{\top }& 0 \\ \lambda _{s}X_{2}^{\top }&\lambda _{s}\varPhi _{2}^{\top } \end{array} \right ]\right )\left [\begin{array}{c} 0\\ y_{s}\end{array} \right ] = 0. }$$

(3.21)

From (3.20) the eigenvector z _u corresponding to $\lambda _{u} =\lambda _{ s}^{-1}$ can be found by solving the linear system

$$\displaystyle{ \left (X_{s} +\lambda _{s}A\right )z_{u} = X_{s}\left (U^{\top }\left [\begin{array}{c} 0\\ y_{ s}\end{array} \right ]\right ) = \left [\begin{array}{c} 0 \\ \varPhi _{2}^{\top }y_{s} \end{array} \right ]. }$$

(3.22)

Premultiplying (3.22) by U, the finite unstable eigenpairs $\left (\lambda _{u},z_{u}\right )$ of P(λ) can be computed by

$$\displaystyle{ \left [\begin{array}{c} \zeta _{u,1} \\ \zeta _{u,2} \end{array} \right ] = U\left [\begin{array}{c} 0\\ \varPhi _{2 }^{\top }y_{s} \end{array} \right ],\quad z_{u,2} = \left (\varPhi _{2} +\lambda _{s}\varPhi _{1}\right )^{-1}\zeta _{ u,2}, }$$

(3.23)

$$\displaystyle{ z_{u,1} = X_{1}^{-1}\left [\zeta _{ u,1} -\left (X_{2} +\lambda _{s}\tilde{H}_{1}^{\top }\right )z_{ u,2}\right ],\quad z_{u} = \left [\begin{array}{c} z_{u,1} \\ z_{u,2} \end{array} \right ], }$$

(3.24)

for u = 1, ⋯ , q. The total computational cost for eigenpairs of P(λ) is $\frac{154} {3} \mathit{mq}^{2}$ flops which is the same as the initial deflation procedure.

We quote some numerical results from [15] with (q, m) = (705, 51). The matrices M and K are given by (3.4) and we take $D = 0.8M + 0.2K$. To measure the accuracy of an approximate eigenpair (λ, z) for P(λ) we use the relative residual

$$\displaystyle{ \text{RRes} = \frac{\|\lambda ^{2}A^{\top }z +\lambda Bz + Az\|_{2}} {(\vert \lambda \vert ^{2}\|A\|_{F} + \vert \lambda \vert \|B\|_{F} +\| A\|_{F})\|z\|_{2}}. }$$

(3.25)

In Table 3.1 we give $\|F_{k+1} - F_{k}\|_{2}/\|F_{k}\|_{2}$ for (q, m) = (705, 51), and for ω = 100, 1, 000, 3, 000, 5, 000, respectively, computed by Algorithm 3. The convergence behavior of F _k is roughly the same as indicated by Theorem 4.

Table 3.1 $\|F_{k+1} - F_{k}\|_{2}/\|F_{k}\|_{2}$ for different ω values with (q, m) = (705, 51)

To demonstrate the accuracy of Algorithm 3, in Fig. 3.3, we plot the relative residuals (3.25) of approximate eigenpairs computed by Algorithm 3 (SDA_GL) and those of the other existing methods SA_HLQ [8] as well as Algorithm 1 (SDA_CHLW) [19] for ω = 1, 000 and (q, m) = (705, 51).

Fig. 3.3

Relative residuals of eigenpairs with (q, m) = (705, 51)

In Fig. 3.3, we see that Algorithm 3 (SDA_GL) has significantly better accuracy for stable eigenpairs. This is because that SA_HLQ [8] and Algorithm 1 (SDA_CHLW) [19] are structure-preserving methods only applied for the deflated PQEP (3.7). The deflation procedure possibly involves the inverses of two potentially ill-conditioned matrices so that SA_HLQ [8] and SDA_CHLW may lose the accuracy of eigenpairs when we transform the approximate deflated eigenpairs to the ones of the original PQEP (3.5).

We efficiently and accurately solve a PQEP arising from the finite element model for fast trains by using the SDA_GL (Algorithm 3) in the solvent approach. Theoretical issues involved in the solvent approach are settled satisfactorily. The SDA_GL has quadratic convergence and exploits the sparsity of the PQEP.

3 Regularization of the Solvent Equation

Here we consider the nonlinear matrix equation

$$\displaystyle{ X + A^{\top }X^{-1}A = B, }$$

(3.26)

where $A,B \in \mathbb{R}^{n,n}$ with B > 0 (i.e., B is Hermitian and positive definite). Note that this is the solvent equation we already saw in (3.8). Here, we are interested in making sure that there is a solution $X \in \mathbb{R}^{n,n}$, X > 0. It is known (e.g., [9]) that such a solution exists if and only if the matrix Laurent polynomial

$$\displaystyle{ Q(\lambda ) =\lambda A^{\top } + B +\lambda ^{-1}A }$$

is regular (i.e., the matrix Q(λ) is non-singular for at least one value of $\lambda \in \mathbb{C}$) and Q(λ) ≥ 0 (i.e., Q(λ) is Hermitian and positive semi-definite) for each complex value λ on the unit circle. Moreover, a stabilizing solution X (i.e., one with ρ(X ⁻¹ A) < 1; as it is needed in applications) exists if and only if Q(λ) > 0 for each unimodular λ. Assuming positive definiteness of Q(λ) for at least one such λ, the last condition is equivalent to stating that Q has no generalized eigenvalues on the unit circle.

In practice, often the coefficients A and B are affected by errors, e.g., because they come out of data measurements, or their determination involves some form of linearization, truncation, or other such simplifications. Then it may well be the case that the original intended matrix equation admits a solution, whereas the perturbed one – which is available in practice – does not.

In this section we present a method to compute perturbations $\tilde{A} = A + E$, $\tilde{B} = B + F$, with $\|E\|$ and $\|F\|$ small, such that Eq. (3.26) (with A, B replaced by $\tilde{A},\tilde{B}$) is solvable. This is achieved by removing all generalized eigenvalues of $\tilde{Q}(\lambda ) =\lambda \tilde{ A}^{\top } +\tilde{ B} +\lambda ^{-1}\tilde{A}$ from the unit circle. The presented method is described in [6] (with an application in parameter estimation, see below) and is based upon similar methods in [3, 7, 12, 32–34] (used there to enforce passivity, dissipativity, or negative imaginariness of an LTI control system). Other related methods that aim to move certain eigenvalues to or from certain regions by perturbing the matrix coefficients in an eigenvalue problem include [13, 14] (where pseudo-spectral methods are used) and [1, 5] by Mehrmann et. al.

We note that λ Q is a palindromic matrix polynomial, and that $Q(\lambda ^{-1}) = Q(\lambda )^{\top }$. Thus the eigenvalues of Q come in reciprocal pairs. As a consequence unimodular eigenvalues cannot just leave the unit circle under small perturbations of A and B. For this to happen two of them have to move together, merge, and then split off into the complex plane. Suppose that Q has ℓ unimodular eigenvalues $\lambda _{j} = e^{\imath \omega _{j}}$ with normalized eigenvectors v _j , $\|v_{j}\| = 1$, $j = 1,2,\ldots,\ell$.

The method to compute E and F is iterative. In a single iteration the unimodular eigenvalues shall be moved to $e^{\imath \tilde{\omega }_{j}}$, $j = 1,2,\ldots,\ell$ on the unit circle. We assume that “the $\tilde{\omega }_{j}$ are closer together than the ω _j ” and that $\vert \tilde{\omega }_{j} -\omega _{j}\vert$ is small for all j. More on how to chose $\tilde{\omega }_{j}$ will be discussed later.

In order to relate the change of the unimodular eigenvalues to small perturbations of A and B, we use the following first-order perturbation result.

Theorem 5 ([6])

Let $A,B \in \mathbb{R}^{n,n}$ with B = B ^⊤ and let $Q(\lambda ) =\lambda A^{\top } + B +\lambda ^{-1}A$ have a simple unimodular generalized eigenvalue $\lambda _{j} = e^{\imath \omega _{j}}$ , with eigenvector v _j . Let $\sigma _{j}:= -2\mathfrak{I}(\lambda _{j}v_{j}^{{\ast}}A^{\top }v_{j})$ . Furthermore, let $\tilde{Q}(\lambda ):=\lambda (A + E)^{\top } + B + F +\lambda ^{-1}(A + E)$ be a sufficiently small perturbation of Q(λ), with F = F ^⊤ . Then σ _j ≠ 0 and $\tilde{Q}$ has a generalized eigenvalue $\tilde{\lambda }_{j} = e^{\imath \tilde{\omega }_{j}}$ such that

$$\displaystyle{ \sigma _{j}(\tilde{\omega }_{j} -\omega _{j}) = -\mathfrak{R}(2e^{\imath \omega _{j} }v_{j}^{{\ast}}E^{\top }v_{ j} + v_{j}^{{\ast}}Fv_{ j}) +\hat{\varPhi } (E,F). }$$

(3.27)

for some function $\hat{\varPhi }(E,F)$ with $\hat{\varPhi }(E,F) = o(\|E,F\|)$ .

Usually such perturbation results are used to find out where eigenvalues move when the matrices are perturbed. We will use it the other way round: we know where we want the eigenvalues to move to and use the result to find linear constraints to the perturbation matrices.

Moreover, we wish to allow only perturbations in the special form

$$\displaystyle{ (E,F) =\sum _{ i=1}^{m}(E_{ i},F_{i})\delta _{i} }$$

(3.28)

for some $\delta _{i} \in \mathbb{R}$, where $(E_{i},F_{i}) \in \mathbb{R}^{n,n} \times \mathbb{R}^{n,n}$, with $F_{i} = F_{i}^{\top }$ for each $i = 1,2,\ldots,m$, is a given basis of allowed modifications to the pair (A, B).

For instance, if n = 2, a natural choice for this perturbation basis is

$$\displaystyle{ \left (\left [\begin{matrix}\scriptstyle 1&\scriptstyle 0 \\ \scriptstyle 0&\scriptstyle 0\end{matrix}\right ],0\right ),\left (\left [\begin{matrix}\scriptstyle 0&\scriptstyle 0 \\ \scriptstyle 0&\scriptstyle 1\end{matrix}\right ],0\right ),\left (\left [\begin{matrix}\scriptstyle 0&\scriptstyle 1 \\ \scriptstyle 0&\scriptstyle 0\end{matrix}\right ],0\right ),\left (\left [\begin{matrix}\scriptstyle 0&\scriptstyle 0 \\ \scriptstyle 1&\scriptstyle 0\end{matrix}\right ],0\right ),\left (0,\left [\begin{matrix}\scriptstyle 1&\scriptstyle 0 \\ \scriptstyle 0&\scriptstyle 0\end{matrix}\right ]\right ),\left (0,\left [\begin{matrix}\scriptstyle 0&\scriptstyle 0 \\ \scriptstyle 0&\scriptstyle 1\end{matrix}\right ]\right ),\left (0,\left [\begin{matrix}\scriptstyle 0&\scriptstyle 1 \\ \scriptstyle 1&\scriptstyle 0\end{matrix}\right ]\right ). }$$

(3.29)

This choice gives all possible perturbations on the entries of each matrix that preserve the symmetry of B. However, if necessary we can enforce some properties of E and F like being symmetric, Toeplitz, circular, or having a certain sparsity structure by choosing $(E_{i},F_{i})_{i=1}^{m}$ suitably.

Using the vec-operator, we can rewrite (3.27) as

$$\displaystyle\begin{array}{rcl} \sigma _{j}(\tilde{\omega }_{j} -\omega _{j})& \approx & -\mathfrak{R}([2e^{\imath \omega _{i} },1] \otimes v_{j}^{\top }\otimes v_{ j}^{{\ast}})\left [\begin{array}{*{10}c} \mathrm{vec}(E^{\top }) \\ \mathrm{vec}(F) \end{array} \right ],{}\\ \end{array}$$

and (3.28) as

$$\displaystyle{ \left [\begin{array}{*{10}c} \mathrm{vec}(E^{\top }) \\ \mathrm{vec}(F) \end{array} \right ] = \left [\begin{array}{*{10}c} \mathrm{vec}(E_{1}^{\top })&\cdots &\mathrm{vec}(E_{m}^{\top }) \\ \mathrm{vec}(F_{1}) &\cdots & \mathrm{vec}(F_{m}) \end{array} \right ]\left [\begin{array}{*{10}c} \delta _{1}\\ \vdots\\ \delta _{m} \end{array} \right ]. }$$

Together we obtain a system of ℓ linear equations in m unknowns

$$\displaystyle{ \mathcal{A}\delta = \mathcal{B}, }$$

(3.30)

where $\delta = [\delta _{1},\ldots,\delta _{m}]^{\top }$ and

$$\displaystyle{ \mathcal{A} = \left [\begin{array}{*{10}c} -\mathfrak{R}([2e^{\imath \omega _{1}},1] \otimes v_{ 1}^{\top }\otimes v_{ 1}^{{\ast}})\\ \vdots \\ -\mathfrak{R}([2e^{\imath \omega _{\ell}},1] \otimes v_{\ell}^{\top }\otimes v_{\ell}^{{\ast}}) \end{array} \right ]\left [\begin{array}{*{10}c} \mathrm{vec}(E_{1}^{\top })&\cdots &\mathrm{vec}(E_{m}^{\top }) \\ \mathrm{vec}(F_{1}) &\cdots & \mathrm{vec}(F_{m}) \end{array} \right ],\ \mathcal{B} = \left [\begin{array}{*{10}c} \sigma _{1}(\tilde{\omega }_{1} -\omega _{1})\\ \vdots \\ \sigma _{\ell}(\tilde{\omega }_{\ell} -\omega _{\ell}) \end{array} \right ]. }$$

So, any sufficiently small perturbation (3.28) satisfying (3.30) moves the unimodular eigenvalues approximately to the wanted positions. We are interested in the smallest such perturbation. To this end we assume that the system (3.30) is under-determined, m > ℓ, but of full rank. Hence, we can use a simple QR factorization to compute its minimum-norm solution, given by $\delta = \mathit{QR}^{-T}\mathcal{B}$, where $\mathcal{A}^{\top } = \mathit{QR}$ denotes a thin QR factorization. Note that for the system to be solved efficiently it is sufficient that ℓ is small and the matrix product $\mathcal{A}$ is efficiently formed (e.g., using the sparsity of E _i , F _i ); m, on the other hand, may be large.

Using several steps of this procedure, the unimodular eigenvalues are made to coalesce into pairs in sufficiently small steps and then leave the circle. To sum up, our regularization algorithm is as follows.

Algorithm 4

Input: $A,B = B^{\top }\in \mathbb{R}^{n,n}$ such that $Q(\lambda ) =\lambda A^{\top } + B +\lambda ^{-1}A$ is regular, $\{E_{i},F_{i}\}_{i=1}^{m}$

Output: $\tilde{A},\tilde{B} =\tilde{ B}^{\top }\in \mathbb{R}^{n,n}$ such that $\tilde{Q}(\lambda ) =\lambda \tilde{ A}^{\top } +\tilde{ B} +\lambda ^{-1}\tilde{A}$ has no unimodular eigenvalues.

• 1. Set $\tilde{A} = A,\tilde{B} = B$

• 2. Compute the unimodular generalized eigenvalues $\lambda _{j} = e^{\imath \omega _{j}}$ of $\tilde{Q}(\lambda )$ , $j = 1,2,\ldots,\ell$ and the associated eigenvectors v _j . If there is none, terminate the algorithm. Also compute $\sigma _{j} = -2\mathfrak{I}(\lambda _{j}v_{j}^{{\ast}}\tilde{A}^{\top }v_{j})$ .

• 3. Determine suitable locations for the perturbed generalized eigenvalues $\tilde{\omega }_{j}$ .

• 4. Assemble the system ( 3.30 ) and compute its minimum-norm solution δ.

• 5. Set $\tilde{A} =\tilde{ A} +\sum _{ i=1}^{m}\delta _{i}E_{i}$ , $\tilde{B} =\tilde{ B} +\sum _{ i=1}^{m}\delta _{i}F_{i}$ and repeat from step 2.

A few remarks are in order. Although the perturbation in every single iteration is minimized, this does not imply that the accumulated perturbation is also minimal. In numerical experiments the norm of the accumulated perturbation decreased and finally seemed to converged when more and more steps of Algorithm 4 were used that each move the unimodular eigenvalues by a smaller and smaller distance, see Fig. 3.4 (top right plot) below. Second, there is nothing to prevent non-unimodular eigenvalues from entering the unit circle in the course of the iterations. This is not a problem since they are moved off again in the following few iterations. Finally, step 2 consists of solving a quadratic palindromic eigenvalue problem where the eigenvalues on the unit circle are wanted. For general eigenvalues methods it is difficult to decide whether a computed eigenvalue is really on or just close by the unit circle. Here, structured methods that compute the eigenvalues in pairs can show their strengths.

Fig. 3.4

Top left: Spectral plot (i.e., eigenvalues of $Q(e^{\imath \omega })$ on the y-axis plotted over $\omega \in [-\pi,\pi ]$) for (3.31); top right: dependence of size of cumulative perturbation and of number of needed iterations on τ; bottom row: Spectral plot after 1, 3, and 6 iterations using τ = 0. 2

3.1 An Example and Spectral Plots

In order to get a better insight of what is happening and to explain how to choose the $\tilde{\omega }_{j}$ it is best to look at an example. We start from the matrices [6]

$$\displaystyle{ A = \left [\begin{array}{*{10}c} 1&0& 0 & 0\\ 0 &1 & 1 & 0 \\ 0&1&-1& 0\\ 0 &0 & 0 &-1 \end{array} \right ],\quad B = \left [\begin{array}{*{10}c} 3&2&1&0\\ 2 &3 &2 &1 \\ 1&2&3&2\\ 0 &1 &2 &3 \end{array} \right ]. }$$

(3.31)

The top left plot of Fig. 3.4 shows the eigenvalues of the Hermitian matrix $Q(e^{\imath \omega })$ for these A, B on the y-axis as they vary with ω ∈ [−π, π]. Obviously the plot is 2π-periodic and symmetric (because $Q(e^{\imath \omega }) = Q(e^{\imath (\omega +2\pi )}) = (Q(e^{-\imath \omega }))^{\top }$). For instance, one sees from the graph that all the lines lie above the x-axis for $\omega =\pi /2$, so $Q(e^{\imath \pi /2})$ is positive definite. Instead, for ω = 0 (and in fact for most values of ω) there is a matrix eigenvalue below the imaginary axis, thus $Q(e^{\imath 0})$ is not positive definite. There are four points in which the lines cross the x-axis and these correspond to the values of ω for which $Q(e^{\imath \omega })$ is singular, i.e., for which $e^{\imath \omega }$ is a generalized eigenvalue of Q on the unit circle. We label them ω ₁, ω ₂, ω ₃, ω ₄ starting from left.

Notice that in our example the lines corresponding to different matrix eigenvalues come very close to each other, but never cross. This is not an error in the graph, but an instance of a peculiar phenomenon known as eigenvalue avoidance, see, e.g., [22, p. 140] or [4].

Recall that the overall goal is to find a perturbation that renders Q(λ) positive definite on the whole unit circle. This perturbation will have to move up the two bumps that extend below the x-axis. For this to happen the two central intersections ω ₂ and ω ₃ have to move towards each other, until they coalesce and then disappear (i.e., the curve does not cross the x-axis anymore). The other two intersections ω ₁ and ω ₄ moved towards the borders of the graph, coalesce at ω = π and then disappear as well. In particular, we see that the intersections ω _i in which the slope of the line crossing the x-axis is positive (i = 1, 3) need to be moved to the left, and the ω _i for which it is negative (i = 2, 4) need to be moved to the right.

Moreover, the sign of the slope with which the line crosses the x-axis is known in the literature as sign characteristic of the unimodular generalized eigenvalue [11], and it is well known that only two close-by generalized eigenvalues with opposite sign characteristics can move off the unit circle through small perturbations.

These slopes are easily computable, in fact the are given by σ _j in Theorem 5. In order to obtain the $\tilde{\omega }_{j}$ that are moved “to the correct direction” and that are not too far away from the ω _j , we use $\tilde{\omega }_{j} =\omega _{j} -\tau \mathrm{ sign}(\sigma _{j})$, where τ is a step size parameter. Other choices are discussed in [7].

For our example, Algorithm 4 with a step size of τ = 0. 2 needs 6 iterations. The spectral plots for the intermediate polynomials $\tilde{Q}(\lambda )$ after 1, 3, and 6 iterations are shown in the lower row of Fig. 3.4. One can see that the topmost eigenvalue curves are almost unchanged, while the bottom ones are modified slightly at each iteration, and these modifications have the overall effect of slowly pushing them upwards. After six iterations, the resulting palindromic Laurent matrix polynomial Q(λ) is positive definite on the whole unit circle (as shown in the bottom-right graph), and thus it has no more unimodular generalized eigenvalues. The resulting matrices returned by the algorithm are

$$\displaystyle{ \tilde{A} \approx \left [\begin{array}{*{10}c} 0.816 &0.183& 0.0379 &-0.0565\\ 0.183 &0.915 & 0.775 & 0.152 \\ 0.0379 &0.775&-0.647& -0.173\\ -0.0565 &0.152 &-0.173 & -0.922 \end{array} \right ],\quad \tilde{B} \approx \left [\begin{array}{*{10}c} 3.16 &1.67&0.956&0.0913\\ 1.67 &3.28 & 1.62 & 1.13 \\ 0.956 &1.62& 3.41 & 1.55\\ 0.0913 &1.13 & 1.55 & 3.13 \end{array} \right ]. }$$

The relative magnitude of the obtained perturbation is

$$\displaystyle{ \frac{\|[\tilde{A} - A,\tilde{B} - B]\|_{F}} {\|[A,B]\|_{F}} = 0.157. }$$

Such a large value is not unexpected, since the plot in Fig. 3.4 extends significantly below the real axis, thus quite a large perturbation is needed.

The step size τ plays a role here. With a smaller value of τ, one expects the resulting perturbation to be smaller, since the approximated first-order eigenvalue locations are interpolated more finely; on the other hand, the number of needed steps should increase as well. This expectation is supported by the top right plot in Fig. 3.4 where we report the resulting values for different choices of τ in this example.

Note that a naive way to move all eigenvalue curves above the x-axis is to add a multiple of the identity matrix to B. This results in an upwards-shift of all eigenvalue curves. In this example the minimum eigenvalue occurs for ω = 0 and is − 0. 675 (correct to the digits shown) which amounts to a relative perturbation in $\|[A,B]\|_{F}$ of 0. 161. So, the perturbation found by Algorithm 4 is better in the sense that (i) it is smaller and (ii) it perturbs the upper eigenvalue curves less.

3.2 Parameter Estimation

The application for enforcing solvability of (3.26) treated in [6] is the parameter estimation for econometric time series models. In particular, the vector autoregressive model with moving average; in short VARMA(1,1) model [23] is considered. Given the parameters $\varPhi,\varTheta \in \mathbb{R}^{d,d}$, $c \in \mathbb{R}^{d}$ and randomly drawn noise vectors $\hat{u}_{t} \in \mathbb{R}^{d}$ (independent and identically distributed, for instance, Gaussian), this stochastic process produces a vector sequence $(\hat{x}_{t})_{t=1,2,\ldots }$ in $\mathbb{R}^{d}$ by

$$\displaystyle{ \hat{x}_{t} =\varPhi \hat{ x}_{t-1} + c +\hat{ u}_{t} -\varTheta \hat{ u}_{t-1},\quad t = 2,3,\ldots. }$$

The task is to recover (i.e., estimate) the parameters Φ, Θ, and c from an observed finite subsequence $(\hat{x}_{t})_{t=1,\ldots,N}$. In [6] such an estimator is described, that only uses (approximations of) the mean $\mu:=\lim _{t\rightarrow \infty }\mathbb{E}(x_{t})$ and the autocorrelation matrices $M_{k}:= \mathit{lim}_{t\rightarrow \infty }\mathbb{E}((x_{t+k}-\mu )(x_{t}-\mu )^{\top })$. Here, $\mathbb{E}$ denotes the expected value and x _t is the random variable that $\hat{x}_{t}$ is an instance of. Using μ and M _k the parameters can be obtained as [30]

$$\displaystyle{ \varPhi = M_{k+1}M_{k}^{-1}\text{ for any }k \geq 1;\quad c = (I-\varPhi )\mu;\quad \varTheta = -\mathit{AX}^{-1}, }$$

(3.32)

where X solves the solvent equation (3.26) for $A:= M_{1}^{\top }- M_{0}\varPhi ^{\top }$ and $B:= M_{0} -\varPhi M_{1}^{\top }- M_{1}\varPhi ^{\top } +\varPhi M_{0}\varPhi ^{\top }$. Note that X is guaranteed to exist since it can be interpreted as the covariance matrix of u (the random variable that $\hat{u}_{t}$ are instances of).

Since μ and M _k are unknown, the estimator approximates them by the finite-sample moments

$$\displaystyle{ \hat{\mu }:= \frac{1} {N}\sum _{t=1}^{N}\hat{x}_{ t},\quad \hat{M}_{k}:= \frac{1} {N - k}\sum _{t=1}^{N-k}(\hat{x}_{ t+k}-\hat{\mu })(\hat{x}_{t}-\hat{\mu })^{\top }, }$$

(3.33)

(which converge to the true values for N → ∞) and then replace μ and M _k by $\hat{\mu }$ and $\hat{M}_{k}$, respectively, in (3.32) giving rise to approximations $\hat{A},\hat{B},\hat{X},\hat{\varTheta },\hat{\varPhi },\hat{c}$. Unfortunately, the finite-sample moments (3.33) converge rather slowly to the true asymptotic ones, i.e., substantial deviations are not unlikely. Therefore, one may encounter the situation described above, where the solvent equation (3.26) for $\hat{A},\hat{B}$ admits no solution that satisfies all the required assumptions. The regularization technique presented above can then be used to obtain solutions in cases in which the estimator would fail otherwise; the robustness of the resulting method is greatly increased.

4 Conclusion

We saw that the palindromic eigenvalue problem has numerous applications ranging from control theory via vibration analysis to parameter estimation. Often the stable deflating subspace is wanted, but other times just the question whether unimodular eigenvalues exist is of interest.

The rail track vibration problem was discussed and an efficient algorithm for its solution presented. Another presented algorithm aims to remove the unimodular eigenvalues via small perturbations, a task that is useful for passivation and parameter estimation.