Horizontal Axis Hydroturbine Shroud Airfoil Optimization

Abstract

The present work concerns the optimization of the shroud of an horizontal axis hydro turbine (HAHT). The main aim is to improve the hydro-turbine efficiency by designing a new shroud airfoil through an optimization process that maximize, as objective function, the power coefficient. The optimization process is carried out by MATLAB  on the supercomputing infrastructure SCoPE of the University of Naples, “Federico II”. Results are obtained with CFD calculations, namely by STARCCM+ for an axisymmetric model, taking advantage of the symmetry of the problem, to minimize the computational time; in addition the HAHT is simulated with an actuator disk that gave reliable results in good agreement with previous works, developed with different software, and with experimental results. The original airfoil was designed for high-lift regimes, so it already gave excellent performance in these kind of applications. For that reason, is not expected a very high increase of the power coefficient. Nevertheless the optimization process results into a power coefficient increase of 4.5 %, with respect to the original airfoil.

1 Introduction

One of the most promising fields in energy production from renewable sources is related to the intensive exploitation of marine and river currents [5]. The marine current resource has a major advantage over other renewable energy resources in that it is essentially non-intermittent and predictable over long time periods. Having a density of approximately $830$ times that of air, water allows for greater kinetic energy extraction over that of wind at similar flow speeds and rotor size. Given a suitable site of concentrated flow and high speed velocities, ocean currents can offer up to four times the energy density of a good wind site, and $30$ times the energy density of a solar plant in the Sahara Desert [17]. Ocean currents are consistent, and their strength and directional frequency can be predicted. Flow speed velocities in ocean currents vary little from average flow velocities, and the source availability differentiates it from other renewable technologies. Many configurations have been proposed so far to extract amounts of energy from water currents.

This paper is related to the optimization of an innovative system configuration for clean energy applications whose concept has been already tested on a preliminary prototype model at the University of Naples. The research activities, upon which the present work is based, directly follows the preliminary testing phase oriented to explore the feasibility of plants based on such concept [6]. The original system configuration consists of a submerged floating body linked to the seabed by means of a tether. Electrical generators and auxiliary systems are housed within the hulls of the floating bodies. Two turbines are installed on a support structure exposed to the flow. The system under development is suitable for applications in sea and rivers. According to what has been observed at this stage of development, it possesses also the desirable characteristics of constructive simplicity and ease of operation. This is the basic concept of what we call here “GEM system” (Generatore Elettrico Marino, Marine Electrical Generator) or “Ocean’s kite” configuration, and starting from such patented concept a scale model has been realized and tested (see Figs. 15.1 and 15.2).

Fig. 15.1

A CAD image of GEM hydro-turbine

Fig. 15.2

A picture of GEM hydro-turbine full-scale prototype installed in Venice’s lagoon. The prototype has been sponsored by a consortium of Venetian companies and by the Veneto regional authority (source http://www.adag.unina.it)

The proposed configuration, due to a relatively safe and easy self-orienting behavior, is a good candidate to solve some problems involved with oscillating and reversing streams. An additional major advantage of this configuration is related to the possibility of avoiding the use of expensive submarine foundations on the seabed. The use of diffuser augmented turbines is intended to reduce the dimensions of actuator disks for a given rated power and to increase the rotational speed, respect of a rotor with higher diameter, reducing the torque. To extract energy from the wind, a thrust force $T$ directed downstream must be generated. On a horizontal axis turbine the thrust is obtained by rotating blades, which create a pressure drop across the rotor disk. The extracted power is the product of the airflow through the disk ($\mathrm{m}^{3}/\mathrm{s}$) and the pressure drop across the disk. Increasing the thrust increases the pressure drop but decreases the airflow through the disk. An optimum exists for the power coefficient $C_p$, which is the ratio between the extracted power and the available power. This optimum for a bare turbine (without a diffuser) is known as the Betz limit [24],

$$\begin{aligned} C_{P_{max}} = \frac{16}{27} \, . \end{aligned}$$

(15.1)

However, if a mechanism is used to increase the airflow through the rotor disk, the Betz limit can be exceeded. According to [13], a ring vortex of the appropriate sign around the rotor plane would induce (by the Biot-Savart law) a velocity vector to increase the mass flow through the disk. This effect can be obtained by placing a diffuser around the rotor. If the cross-section of the diffuser is shaped as an aerofoil, the generated lift will give the circulation of a ring vortex. The more lift that can be achieved, the more the air will be sucked through the disk. The amount of lift is limited by separation of the boundary layer on the diffuser wall, so the geometry of the diffuser plays an important role in the overall performance of the shrouded wind turbine (see Fig. 15.3 on the following page). The radial distribution of the axial flow is also important in order to ensure a uniform speed-up factor.

Conversely, Van Bussel [25] asserts that, with a simple momentum theory, developed along the lines of momentum theory for bare turbines, power augmentation is proportional to the mass flow increase generated at the nozzle of the diffuser augmented turbine. Such mass flow augmentation can be achieved through two basic principles: increase in the diffuser exit/inlet ratio and/or by decreasing the negative back pressure at the exit. The power increase could results in a misleading overcoming of the Betz limit. As shown by Van Bussel this is due to an incorrect choice of the reference area. In this case the suitable reference area should be the shroud exit area. From this momentum theory, it can be seen that the achievable power is comparable with the power of a normal Horizontal Axis Wind Turbine (HAWT) having a diameter equal to the exit diameter of the diffuser. But from this momentum model it can also be seen that larger performances are possible when a substantial low back pressure level can be achieved at the diffuser exit. As shown by Tognaccini in [24] the power augmentation is proportional to the thrust exerted by the flow on the diffuser. The shroud design criteria were based on the maximization of this thrust. An high lift airfoil has been opportunely chosen, and the working angle of attack has been numerically estimated by Scherillo et al. [18]. The experimental results achieved in that work, both in the wind tunnel and in the towing tank, show a remarkable increase of the thrust for the shrouded configurations. Besides, according to the theory, the power increases remarkably with the diffuser. The power coefficient of the shrouded configuration, computed referring to the turbine area is almost $0.8$, and shows an increase of about twice compared to the bare turbine, that has a $C_P = 0.4$. Referred the power coefficient of the shrouded configuration to the diffuser exit area, the $C_P$ increase is about $7\,\%$.

Fig. 15.3

Lift force on the shroud airfoil and pitch angle $\theta$

The main target of this work is to exploit this limit with the use of an optimization process for the shape of the airfoil on which is based the annular diffuser. In Sect. 15.2 the numerical methodology is described, in Sect. 15.3 the results are summarized, then in Sect. 15.4 the conclusions and future works are highlighted.

2 Method

Both in aircraft design and in turbine design, the choice of airfoils is critical because it affects overall project performance. Often, an ad hoc designed airfoil is used. The aim of this section is to apply numerical optimization concepts to the airfoil design problem. One of the most important ingredients in numerical optimization is the choice of design variables and the parametrization of the system by using these variables. In general, an airfoil is given by its coordinates, typically a set of $150$–$200$ points for panel codes; evidently, it is not suitable to use directly the airfoil’s coordinates as design variables, because, even if it is the easier method to implement, there is a large number of design variables to represent 2D or 3D geometries, and displacement of a single mesh point can lead to unsmooth shapes and cause the flow solver to become ill-conditioned, as observed in [4, 27].

In order to reduce the number of parameters to take into account necessary to describe the airfoil’s shape, but without geometrical information loss, several mathematical formulations have been proposed in literature as Bezier [12], PARSEC [21, 22] and Legendre polynomials as suggested by Hicks and Van der Plaats in [14, 15]. The latter one has been chosen among the others because of its capability of describing only limited change in the airfoil shape by summing polynomials on the original airfoil coordinates. A Legendre polynomial is a function that satisfies the Legendre’s differential equation whose expression is shown in Eq. 15.2:

$$\begin{aligned} \frac{\mathrm {d} }{\mathrm {d} x}\left[ (1-x^2)\frac{\mathrm {d} }{\mathrm {d} x}P(x) \right] +n(n+1)P(x) \end{aligned}$$

(15.2)

The ordinary differential equation is quite frequent in mathematics and physics since it allows to solve Laplace’s equation in spherical coordinates and several partial derivative differential equation. Legendre’s differential equation can be solved trough standard methods applying power series so that converging solutions are obtained if $|x|<1$. Converging solutions are obtained also if $x = \pm 1$ and $n$ is a natural integer (i.e. $n = 0,1,2,\dots$). In such cases the solutions according to $n$ form a polynomial succession called Legendre’s polynomials succession. The generic Legendre’s polynomial $P_n(x)$ of $n$ degree can be expressed trough the following Eq. 15.3:

$$\begin{aligned} P_n(x) = \left( 2^nn! \right) ^{-1}\frac{\mathrm {d}^n }{\mathrm {d} x^n} \left[ \left( x^2-1 \right) ^n \right] \end{aligned}$$

(15.3)

Several artifices have been adopted in order to use Legendre’s polynomials for the optimization process according to [14]. Airfoil thickness distributions are given by summing a perturbation on the original geometry as shown in Eq. 15.4

$$\begin{aligned} y(x)_{new} = y(x)_{old} + \varDelta y(x)_{(up/low)} \end{aligned}$$

(15.4)

where $y(x)_{old}$ represents the original airfoil $y$ coordinate and $\varDelta y$ the perturbation term for the upper and lower surfaces ordinates. This term is evaluated according to Eqs. 15.5 and 15.6

$$\begin{aligned} \varDelta y(x)_{up} = \left( 1-x \right) ^3&\Bigl [\sqrt{a_1x}+a_2 \left( P_2+1 \right) +a_3 \left( P_3-1 \right) \nonumber \\&\quad +\, a_4 \left( P_4+1 \right) +a_5 \left( P_5-1 \right) +a_6 \left( P_6+1 \right) \Bigr ] \end{aligned}$$

(15.5)

$$\begin{aligned} \varDelta y(x)_{low} = \left( 1-x \right) ^3&\Big [\sqrt{b_1x}+b_2 \left( P_2+1 \right) +b_3 \left( P_3-1 \right) \nonumber \\&\quad +\, b_4 \left( P_4+1 \right) +b_5 \left( P_5-1 \right) +b_6 \left( P_6+1 \right) \Bigr ] \end{aligned}$$

(15.6)

where and $P_{2}, \dots , P_{6}$, are Legendre polynomials given by Eq. 15.7 and shown in Fig. 15.4. The coefficients $a_{1} , \dots , a_{6}$ and $b_{1} , \dots , b_{6}$ are the design variables perturbed by the optimization program to achieve optimum design. The square root term in Eqs. 15.5 and 15.6 allows a blunt leading edge and assures matching of upper-surface and lower-surface derivatives of all orders at the leading edge. The term $(1-x)^3$ allows to optimize the airfoil in a chosen chord range. This term could be removed by specify that whole the airfoil wants be optimized.

$$\begin{aligned} P_{2}&= 2\left( x/c \right) -1 \nonumber \\ P_{3}&= 6\left( x/c \right) ^{2} - 6\left( x/c \right) +1 \nonumber \\ P_{4}&= 20\left( x/c \right) ^{3} - 30\left( x/c \right) ^{2} + 12\left( x/c \right) -1 \\ P_{5}&= 70\left( x/c \right) ^{4} - 140\left( x/c \right) ^{3} + 90\left( x/c \right) ^{2} - 20\left( x/c \right) +1 \nonumber \\ P_{6}&= 252\left( x/c \right) ^{5}- 630\left( x/c \right) ^{4} + 560\left( x/c \right) ^{3} - 210\left( x/c \right) ^{2} + 30\left( x/c \right) -1 \nonumber \end{aligned}$$

(15.7)

Fig. 15.4

Legendre polynomials

During years, a lot of optimization methods have been proposed and developed, often starting from theoretical concepts and logics very far each from each other. In general it is very difficult to state which method is the best because each one has several advantages and, at same time, disadvantages; just referring to a particular application, or problem, it is possible to operate this choice. Genetic algorithms (GA) is a heuristic search method derived from natural selection and evolution. At the start of a GA optimization, a set of decision variable solutions are encoded as members of a population. There are multiple ways to encode elements of solutions including binary, value, and tree encodings. Crossover and mutation, operators based on reproduction, are used to create the next generation of the population. One of advantages of GA is that multiple areas of the search space are explored to find a global minimum. Through the use of the crossover operator, GA are particularly strong at combining the best features from different solutions to find one global solution. Through observation of these crossover combinations, the user gains insight about how parts of the simulation interact. The non-dominated Sorting Genetic Algorithm [1] is a Multiple Objective Optimization (MOO) algorithm and is an instance of an Evolutionary Algorithm from the field of Evolutionary Computation [8]. NSGA is an extension of the Genetic Algorithm for multiple objective function optimization. There are two versions of the algorithm, the classical NSGA and the updated and currently canonical form NSGA-II [9]. The objective of the NSGA algorithm is to improve the adaptive fit of a population of candidate solutions to a Pareto front constrained by a set of objective functions. The algorithm uses an evolutionary process with surrogates for evolutionary operators including selection, genetic crossover, and genetic mutation. The population is sorted into a hierarchy of sub-populations based on the ordering of Pareto dominance. Similarity between members of each sub-group is evaluated on the Pareto front, and the resulting groups and similarity measures are used to promote a diverse front of non-dominated solutions. NSGA-II [8, 9] is an improved version of NSGA which alleviates main criticisms of the NSGA approach. NSGA-II is here used in its single objective functionality. Parametrization and optimization setup for this numerical optimization will be now presented in detail.

Fig. 15.5

Base airfoil used for the shroud

The base airfoil selected for the optimization process is a high-lift airfoil for low Reynolds number (see Fig. 15.5 [19]). It is a quite suitable airfoil for a shroud that maximize the hydroturbine power coefficient [11, 16]. In this type of problem, a suitable method of reconstruction is that based on Legendre polynomials, because, as explained before, it performs geometric reconstruction by applying small perturbation on the original geometrical coordinates of the airfoil. Three cases have been analysed, with different abscissa variation ranges in percent of the chord; for each of them variation on 90 % of chord length are imposed: $BC = \pm 0.01,\;\pm 0.05$ and $\pm 0.10$. No geometric and aerodynamic constraints are setted in these analysis. Concerning numerical optimization, the chosen method is NSGA-II [20], executed by use of MATLAB. A single-objective optimization was performed, the aim of which is maximize the hydro-turbine power coefficient.

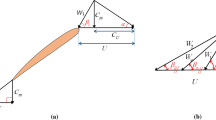
The population size of the algorithm was setted to 40, while the generation limit is 20. Three analysis are carried out, by changing the airfoil pitch angle, that is defined as the angle between the turbine axis and the chord of the airfoil, as explained in Fig. 15.3. Starting from a pitch angle of $26^{\circ }$ (that is the best angle in this analysis conditions for the base airfoil, as proved by [26]) a variation of $\pm 3^{\circ }$ was provided for the optimization process.

Finally three pitch angles are implemented: $\theta = 23,\;26,\;29^{\circ }$; considering the fact that the airfoil resulting from the optimization process could work better with different pitch angle. Moreover, an airfoil with good performance in a range of $\pm 3$ deg can have good performance also in off-design conditions.

The analysis solver is STAR-CCM+, and, to carry out the analysis, the axisymmetric model was chosen. As a matter of fact, this model is the less computationally expensive one, but results are consistent with previous thesis works [26] and exhibit the same ratio between shrouded and non-shrouded configuration (slightly more than 2) as measured experimentally in [18]. Hence it is the most suitable model to carry out a very expensive calculation as an optimization analysis. The logic diagram of the optimization algorithm used is shown in Fig. 15.6.

Fig. 15.6

Numerical optimization routine

The analysis was performed with the parameters illustrated in Table 15.1. The Turbulent Viscosity Ratio (TVR) has the default value present in STAR-CCM+ [3] simulation set-up, and it represents the sole parameter that characterizes the turbulence using the Spalart-Allmaras model [23].

Table 15.1 Axisymmetric model: physics data of the simulation

In Table 15.2 mesh parameters are shown. Base size is setted to have the same chord order of magnitude. Prism layer thickness is calculated by XFOIL software [10], and the other prism layer parameters are such as to have a $y^{+}$ value in the first laminar sublayer less than one. Figure 15.7 shows the mesh around the airfoil with the prism layer mesh. Physical boundary conditions are setted as shown in Table 15.3.

The pressure difference in the fan interface is setted as a constant value to simulate the nominal condition of the hydroturbine, as done in previous simulations based on different CFD solver [26].

Table 15.2 Axisymmetric model: mesh characteristics, general parameters

Fig. 15.7

Axisymmetric model: mesh around the airfoil

Table 15.3 Axisymmetric model: physical description of the boundaries

3 Results

Most of the analysis has been executed on the supercomputing infrastructure SCoPE, in the University of Naples Federico II. This infrastructure consists of a grid of computer, where is possible to use hundreds of parallel processors. Further details about SCoPE can be found in [7], while concerning the programming language, it can be consulted in [2].

Table 15.4 Axisymmetric model: physical quantities for the original diffuser airfoil Selig 1223

The objective function of the analysis is the turbine power coefficient, defined, in the hypothesis of actuator disk, by the Eq. 15.8, and evaluated with respect to the diffuser exit area, defined in the Eq. 15.9 [26], where the exit area is a function of the airfoil pitch angle. This latter value is the most important to evaluate the real advantage of the shrouded configuration with respect to a not-shrouded HAHT with an area equal to the exit area of the shroud [25].

$$\begin{aligned} C_P = C_T \left( \frac{V_d}{V_\infty } \right) , \end{aligned}$$

(15.8)

$$\begin{aligned} C_{P_{exit}} = C_P \left( \frac{A_d}{A_{exit}} \right) , \end{aligned}$$

(15.9)

where the subscript $d$ stands for disk, $C_T$ is the disk thrust coefficient, $V_\infty$ is the free-stream or inlet velocity, $A_{exit}$ is the shroud exit area. In Table 15.4 the pressure and velocity values, evaluated as surface average on the actuator disk interface, are indicated. The power coefficients are also specified, respectively, the reference $C_{P_{ref}}$ of the not-shrouded case, and the $C_P$ for shrouded configuration evaluated using both the actuator disk and shroud exit area (see Eqs. 15.8 and 15.9) for the original diffuser airfoil Selig 1223 at three different pitch angles. The pitch angle of the prototype installed in Venice lagoon is $26^{\circ }$ because of the greater extracted power for a given pressure drop across the actuator disk. The power coefficient values suggest that using a shroud implies an increasing in power generated of $99\,\%$, if evaluated with respect to the throat area, but of only $13\,\%$, with respect to the outlet area. By using the shroud there is a little zone of separation flow, and not a complete stall of the airfoil, despite the high pitch angle. This is due to two factors:

• the presence of the actuator disk (or of the turbine, in the real case), deviates upwards the streamlines, reducing the effective angle of attack of the airfoil (see Fig. 15.8 in which the velocity field around the original airfoil for a pitch angle $\theta$ equal to $26^{\circ }$ is shown). Without actuator disk, there would be a complete separation of the flow behind the disk along the diffuser surface.

• The gap between shroud and actuator disk generates a channel that energizes the flow and avoids separation. By reducing the gap, the actuator disk interacts with the shroud boundary layer, the velocity profile is altered, and the separation of the flow occurs, as proven in [26].

Fig. 15.8

Axisymmetric model: velocity field around the original airfoil for a pitch angle $\theta = 26^{\circ }$. The streamlines are indicated by the continuos solid lines. Actuator disk is located at the throat

In this section the optimization results are shown, for each of the three boundary conditions analysed: $BC = \pm 0.02,\;\pm 0.05$ and $\pm 0.10$. The values of the power coefficient with respect to the generations show a tendency of the $C_P$ to compact the region with elevate values, by increasing the generations, because of the automatized procedure that avoid replication of bad performing airfoil or bad reconstructed ones (the CAD modeler within STARCCM+ is not always capable of correctly reconstruct the parametrized shape produced by Legendre polynomials). The genetic algorithm used for the optimization process, namely the NSGA-II, has been employed with the characteristics summarized in table Table 15.5.

Table 15.5 Genetic algorithm characteristics

Table 15.6 Summary table with power coefficients

Fig. 15.9

$BC=\pm 0.02$: variation of the power coefficient, $\theta =26^{\circ }$

This trend is evident in all of the cases, thanks to the generations limit imposed in the optimization process. The most interesting case is the one with boundary condition amounting to 2 % of the airfoil chord for which after 10 generations the algorithm stabilizes the population’s objective function range (see Fig. 15.9).

In Table 15.6 are summarized the results of the optimization process. The choice of the Selig 1223 as starting airfoil derives from its own already excellent performance. Thus, the optimization process, conducted for different diffuser pitch angle and boundary coefficient for Legendre polynomials to be added on the original shape (see Figs. 15.10, 15.11 and 15.12), returns as best solution the one characterized by a pitch angle equal to $26^{\circ }$ and the minimum modification of the airfoil shape, i.e. limiting it to the $\pm 0.02$ % of the airfoil chord. The maximum improvement with respect to the initial condition is obtained for a pitch angle of $29^{\circ }$ and modification of the airfoil shape fixed to the $\pm 0.05$ % of the airfoil chord (Fig. 15.12).

It is important to remarks that all the results refer to an axisymmetric model with an actuator disk modelling the turbine. This means that all the power coefficient should be scaled for taking in consideration the difference between actuator disk and real turbine. From previous experimental tests [18] and forthcoming numerical simulations of the authors, is has been observed that this scaling factor is about $2/3$, having finally that from a bare turbine maximum power coefficient of about $0.41$, with the old diffuser shape based on Selig 1223 airfoil grows up to about $0.46$, and it reaches with the optimized diffuser shape the value of $0.48$.

Fig. 15.10

Optimized airfoils, $\theta =23^{\circ }$: — Original airfoil, $\cdots \;\pm 0.02$, $-\;-\;\pm 0.05$, $-\,\cdot \,-\;\pm 0.10$

Fig. 15.11

Optimized airfoils, $\theta =26^{\circ }$: — Original airfoil, $\cdots \;\pm 0.02$, $-\;-\;\pm 0.05$, $-\,\cdot \,-\;\pm 0.10$

Concerning the computational time the following considerations could be done. It should be divided into two phases: the meshing and simulation. The meshing phase is performed in serial mode, having the STARCCM+ 7.06 version here used a not very reliable management of parallel meshing tools, expected to be improved in a future version. It takes about 7.5 min, while the simulation phase for a parallel run on 16 cpus lasts about 3.5 min. Since the number of evaluations for the objective functions is 800 with a serial use of the NSGA-II code the total optimization time is about 6 days for a single angle of pitch and a single boundary condition relative to Legendre polynomials. This computational time is abruptly reduced by virtue of the JobCollection utility available on the SCoPE distributed grid computing resource: it is an object with the main purpose of allowing the execution of collective operations on sets of independent jobs, being just a logical container, in which both not yet submitted and already submitted jobs can be inserted in. A job collection is somehow orthogonal with respect to a job cluster being a set of dependent jobs (e.g. all jobs spawned by the same father process). The parallel use of the NSGA-II code leads to a total optimization time of only 3.7 h. Further reduction in the computational time could be obtained by means of a different meshing technique as suggested in Sect. 15.4.

4 Conclusions and Future Works

The main objective of this work has been the optimization process of an airfoil shape for the shroud of a horizontal axis hydro turbine that that would increase the power extracted from marine currents. To achieve the target, an optimization routine has been developed: starting from the input base airfoil, a geometry parametrization method is chosen, in this case Lagrange polynomial, and a numerical optimization method as NSGA evaluates the objective function, namely the $C_P$, with a CFD solver giving in output, through an automated process, a new airfoil that improves the objective function. The base airfoil is designed for high-lift regimes, so it gives excellent performance in these kind of applications. For that reason, was not expected a very high increase of the power coefficient. The airfoil obtained as a result of the optimization process shows a higher power coefficient of 4.5 %. This result is quite in agreement with the expectations, so it is a satisfying result. The CFD analysis, in axisymmetric flow field and actuator disk hypothesis, gave reliable results, in agreement with previous works, developed with different software, and with experimental results. Future works will aim to reduce computational time in optimization process, and to enhance the general robustness of the developed numerical code in order to increase its versatility and use in more complex contexts. In particular, by virtue of the use of the overlapping grid tool, recently incorporated in the STARCCM+ distribution, it is possible to design a single grid for more than one diffuser position and or orientation, so that a multi-objective optimization (considering the power coefficient at several pitch angle as objective functions) could be implemented saving the time consuming fraction related to mesh generation.

Fig. 15.12

Optimized airfoils, $\theta =29^{\circ }$: — Original airfoil, $\cdots \;\pm 0.02$, $-\;-\;\pm 0.05$, $-\,\cdot \,-\;\pm 0.10$

In addiction, further analysis on curved plate would be performed, following the preliminary promising results of Reinecke [17] for an even more efficient diffuser shape, not more constrained to a classical airfoil shape, exploiting the expansion ratio and simplifying the manufacturing process. At the end of this process two candidates would be ready for testing and then prototyping a new diffuser solution for GEM.