Robust Output Feedback Stabilization of a Magnetic Levitation System Using Higher Order Sliding Mode Control Strategy

Abstract

This work studies the problem of robust output feedback stabilization of a Magnetic Levitation System using Higher Order Sliding Mode Control (HOSMC) strategy. The traditional (first order) sliding mode control (SMC) design tool provides for a systematic approach to solving the problem of stabilization and maintaining a predefined (user specified) consistent performance of a minimum-phase nonlinear system in the face of modeling imprecision and parametric uncertainties. Recently reported variants of SMC commonly known as Higher Order Sliding Mode Control schemes have gained substantial attention since these provide for a better transient performance together with robustness properties. In this work, we focus on design of an output feedback controller that robustly stabilizes a Magnetic Levitation System with an added objective of achieving an improvement in the transient performance. The proposed control scheme incorporates a higher-order sliding mode controller (HOSMC) to solve the robust semi-global stabilization problem in presence of a class of somewhat unknown disturbances and parametric uncertainties. The state feedback control design is extended to output feedback by including a high gain observer that estimates the unmeasured states. It is shown that by suitable choice of observer gains, the output feedback controller recovers the performance of state feedback and achieves semi-global stabilization over a domain of interest. A detailed analysis of the closed-loop system is given highlighting the various factors that lead to improvement in transient performance, robustness properties and elimination of chattering. Simulation results are included and a performance comparison is given for the traditional SMC and HOSMC designs employing the first and second order sliding modes in the controller structure.

1 Introduction

Output feedback control schemes have long been considered as the preferred and useful design tools for stabilization of control systems. This work focuses on design of an output feedback controller that robustly stabilizes a minimum-phase nonlinear system with an added objective of achieving an improvement in the transient performance. The proposed control scheme incorporates a Higher-Order Sliding Mode Controller (HOSMC) together with a High-Gain Observer (HGO) (Hassan 2008; Atassi and Hassan 1999) to solve the robust output feedback stabilization problem. It is usually required that the controller be able to stabilize the system over a large set of initial conditions, and assure robustness and asymptotic error convergence in presence of somewhat unknown disturbances and parametric uncertainties. Sliding Model Control (SMC) scheme is regarded as one of the most significant control design tools that addresses these requirements effectively (Guldner and Utkin 1999; Edwards and Spurgeon 1998). The variants of SMC, known as Higher Order Sliding Mode Controllers (Pukdeboon 2012; Levant 2001) provide for an improved error convergence, better robustness properties and elimination of chattering in control designs for minimum phase nonlinear systems (Rhif and Zohra 2012; Rhif 2012; Pridor Gitizadeh et al. 2000; Levant 2010).

We consider the problem of robust feedback stabilization of a Magnetic Levitation System, which is widely regarded as a benchmark system for testing various control techniques (Milica Naumovic and Boban 2008; Levine and Ponsart 1996). The system’s mathematical model results in a set of coupled nonlinear differential equations which require special treatment (Woodson and Melcher 1968). Furthermore, such systems usually require use of a high gain feedback for achieving the task of stabilization and tracking of the system’s output to some desired references, making the control synthesis relatively difficult.

The novelty of this work lies in the application of an HOSMC based Output Feedback Controller which uses an HGO for estimation of system states. This provides us with the leverage of the robust control and control of the convergence speed of the system states. The rest of the chapter is organized as follows: we start with a mathematical description of the magnetic levitation system and formulate the stabilization problem for this system. The following section summarizes some previous work related to the same problem. In Sect. 3, we present control design, first utilizing a first-order SMC, and then incorporating a second-order and third-order SMC structures. In the later part of this section, we extend the state feedback design to output feedback using an HGO. We present performance analysis and simulation results of the proposed control designs in Sect. 4. Finally, Sect. 5 draws the conclusions.

1.1 The Magnetic Levitation System

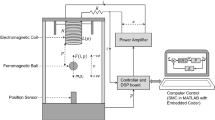
We undertake the problem of robust feedback stabilization of a benchmark nonlinear Magnetic Levitation System. A schematic of the system is shown in Fig. 1, where a ferromagnetic ball is required to be precisely levitated using a current controlled electromagnet with position feedback from an optical sensor.

Fig. 1

A 3D view of magnetic levitation system

The system is described by the following nonlinear differential equations:

$$\begin{aligned} \dot{x}= f(x) + g(x)u \end{aligned}$$

(1)

where

$$\begin{aligned} x = \left[ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right] , f(x) = \left[ \begin{array}{c} x_2 \\ g - \frac{k}{m} x_2 - \frac{L_o a x^2_3}{2m(a+x_1)^2} \\ \frac{1}{L(x_1)} \left[ -Rx_3 + \frac{L_o a x_2 x_3}{(a+x_1)^2}\right] \\ \end{array} \right] , g(x) = \left[ \begin{array}{c} 0 \\ 0 \\ \frac{1}{L(x_1)} \\ \end{array} \right] \end{aligned}$$

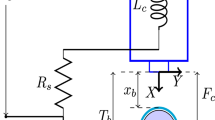
where the states are $x_1= y$ (position), $x_2= \dot{y}$ (velocity), $x_3= i$ (current) and $u = v$ (control input). Other parameters include m as the ball mass, y the measured position, $g$ being the gravitational acceleration coefficient, k as the viscous friction coefficient, $L_1$, $L_0$, a are positive constants referred to as the inductance parameters of electromagnet and R is the overall equivalent resistance of the current path. The term $L(x_1)$ and the steady state current value, with $r$ as the desired reference (height) are given as:

$$\begin{aligned} L(x_1)= L_1 + \frac{L_o}{1+\frac{x_1}{a}}; \quad I_{ss} = \frac{2mg (a+r)^2}{L_o a} \end{aligned}$$

(2)

The control objective is to regulate the system output to the desired height while also stabilizing the closed-loop system in the presence of parametric uncertainties. The complex dynamical model of the system along with the requirement of robustness under physical uncertainties make the control design task even more challenging.

2 Previous Work

Many researchers, in the past few decades have considered this problem using various nonlinear control design techniques e.g. Back-stepping, Feedback Linearization, and Extended Kalman Filter. This section presents a review of their work.

The Back-stepping method Mahmoud (2003), and Wai and Lee (2008), provides a nonlinear design tool for recursive design of control law based on Lyapunov theory. Researchers of these works have used back-stepping technique together with an adaptive observer to design controller for stabilization of the magnetic levitation system. Stabilization of the closed-loop system is achieved by incorporating a Lyapunov function whose derivative is rendered negative definite by the control law to achieve stability. In the proposed adaptive control method, a filter mechanism is incorporated with the back-stepping controller to cope with the problem of the finite escape time terms occurring due to repeated differentiations in back-stepping design procedure. Moreover, the observer is designed in such a way to cater for system uncertainties, to solve the trouble of chattering phenomena caused by the sign function in back-stepping and adaptive controller law. The results show that the parameter estimation error converges only locally using Lyapunov methods and to ensure stability of the overall closed-loop system the Lyapunov function is extended with a term penalizing the estimation error. This work shows that the stability was not global because the parameter estimation for control coefficients show to be only locally convergent.

Trumper et al. (1997) used feedback linearization technique to design a suitable controller that stabilizes the system at a desired operating point. The researcher suggests that for applications where large excursions or disturbance forces are not anticipated, a simple linear controller based on a linearized plant model may suffice. This model is derived by writing the states and inputs in terms of operating point, the operating points of the state variables are chosen and evaluating Jacobians at the operating point to get the linearized second-order magnetic suspension system. A major setback of this method is that the model is valid only for small perturbations about the operating point and as the system moves away, quality of this approximation decreases and the performance degrades. The proposed method shows remarkable performance for the single DOF system described described in this work, however only locally since it uses a linearized (i.e. requires accurate) plant model and any modeling errors in actuator input lead to sustained oscillations.

Another way to approach the problem is described by Levis (2003), by designing an ideal LQR controller and then extending the design towards robust control using the Lyapunov redesign method. The system is first represented in a simpler form using a transform and the feedback loop is completed by a standard LQR controller, designed by solving the Riccati equation, without taking uncertainties into account. Using Lyapunov analysis it is shown that the controller is able to stabilize the system but the result is only local as certain limits have to be put on the current input and no variations from the nominal model are allowed. To cater this, a robust controller is designed based on lyapunov redesign by adding an extra term to the linear controller to overcome matched disturbances. An upper bound on the disturbance term is taken and using the augmented controller a Lyapunov analysis is performed. The control input is taken to render the Lyapunov function negative definite using on a smooth switching controller based on Lyapunov redesign. The controller gain is taken greater than the bound on overall system subject to disturbances, to ensure the convergence of steady state error to zero. A comparison with the linear controller depicts that the later strategy is able to handle small parametric variations while resulting in semi-global asymptotic stability of the closed-loop system.

Henley John (2007) proposed a stabilizing controller structure based on feedback linearization in an Extended Kalman Filter (EKF) framework for a single-axis magnetic levitation device. For implementation of the controller, a discrete Extended Kalman Filter provides the system states’ estimates. The EKF is based on the standard predict-correct format where the current state estimate and covariance are propagated forward until the next measurement occurs. Then, the Kalman Gain is computed and the state estimate and covariance are updated using appropriate initial conditions on object velocity and input current. The process noise and the sensor noise is taken as a zero mean Gaussian white-noise. The key feature of this method is that the Kalman Filter gain is chosen such that it minimizes the state estimation error. Then using the standard feedback linearizing method a state feedback controller, based on estimated states form the EKF, is used to stabilize the system using the pole placement method. Although this controller formulation is near optimal, it is robust enough that parameter changes and un-modeled plant dynamics do not effect the results.

3 Control Design

This section presents the development of robust stabilizing control for the problem under consideration, by utilizing a first-order SMC initially, and then incorporating a second-order and third-order SMC structures. In the later part of this section, we extend the SMC and HOSMC based state feedback design to output feedback using an HGO.

In order to proceed with systematic control design, we first transform the system into strict feedback normal form by using a suitable state transformation of the form

$$\begin{aligned} z = T(x) \end{aligned}$$

(3)

in which T is such that T is invertible; i.e. it must have an inverse map $T^{-1}(.)$ such that $x = T^{-1}(z)$ for all $z \in T(D)$, where D is the domain of T. From (Hassan 2002), the system (1) can be represented in feedback linearizable form if and only if there is a domain $D_o \subset D$ such that:

• 1. For the system  (1), the matrix $G(x) = [g(x) \;\;ad_{f}g(x) \;\;ad^{2}_{f}g(x)]$ is full rank for all $x \in D_o$

• 2. The distribution $D =$ span$g(x),ad_{f}g(x)$ is involutive in $D_o$

It can be verified that $G(x) = [g(x) \;\;ad_{f}g(x) \;\;ad^{2}_{f}g(x)]$ has rank 3, and the vector represented as $D =$ span{$g(x),\,ad_f g(x)$} is involutive, because $[g,\;ad_f g]$ becomes a null vector and distribution D has rank 2. The foregoing calculation is valid in the domain {$D = a + x_1 > 0$ and $x_3 > 0$}. The system has relative degree 3 (equivalent to the rank of G(x)), hence it is full-state linearizable. Therefore, T(x) can be written as follows:

$$\begin{aligned} T(x)= \left[ \begin{array}{c} h(x) \\ L_f h(x) \\ L^{2}_{f} h(x) \\ \end{array} \right] = \left[ \begin{array}{c} x_1 \\ x_2 \\ g- \frac{k}{m} x_2 - {\frac{L_o a {x}^2_3}{2m (a+x_1)^2}} \\ \end{array} \right] \end{aligned}$$

(4)

Using  (4) above, system  (1) can now be re-written as:

$$\begin{aligned} \dot{z_1}&= z_2 \nonumber \\ \dot{z_2}&= z_3 \\ \dot{z_3}&= - \frac{k}{m} z_3 + {\frac{L_o L_1 a x_2 {x}^2_3}{m L(x_1) (a+x_1)^3}} + {\frac{L_o a R{x}^2_3}{m L(x_1) (a+x_1)^2}} - {\frac{L_o a x_3}{m L(x_1) (a+x_1)^2}} u \nonumber \end{aligned}$$

(5)

The nominal system parameter values are given in Table 1.

Table 1 Nominal system parameters

3.1 First Order Sliding Mode Control

We start with development of first-order sliding mode controller for System (5). The task is to design a feedback control law to stabilize the system at a desired reference.

Fig. 2

A typical trajectory of sliding mode control

The controller is designed such that firstly the system trajectories reach a boundary/manifold (surface) near origin in finite time to ensure a semi-global bounded solution and once the trajectory reaches the manifold, it cannot leave it. This phase is called “reaching phase” as shown in Fig. 2.

Consider the system represented as

$$\begin{aligned} \dot{z} = f(z) + g(z)u \end{aligned}$$

(6)

To start with, we define a Sliding manifold (s) in terms of the system dynamics i.e.

$$\begin{aligned} s=z_3+a_2 z_2+a_1(z_1-r)=0 \end{aligned}$$

(7)

where r is the desired reference (height). The Control Law for the SMC is based on the constraint

$$\begin{aligned} s \equiv 0 \end{aligned}$$

(8)

The first task is to design the controller in such a way to bring the trajectory to this manifold $s\equiv 0$ in finite time. The variable $s$ satisfies the equation

$$\begin{aligned} \dot{s}=a_1 z_2 + a_2 z_3 + f(z) + g(z)u \end{aligned}$$

(9)

let $f$ and $g$ satisfy the inequality

$$\begin{aligned} \Bigg | \frac{(a_1 z_2 + a_2 z_3) + f(z)}{g(z)}\Bigg | \le \rho (z) \;\;\; \forall z\in \mathfrak {R}^n \end{aligned}$$

(10)

for some known function $\rho (z)$.

To guarantee that the trajectory reaches the manifold we take an energy Lyapunov function

$$\begin{aligned} V=\frac{1}{2} s^2 \Rightarrow \dot{V}=s\dot{s}<0 \end{aligned}$$

(11)

as the Lyapunov function candidate for the system. We get

$$\begin{aligned} \dot{V}=s\dot{s}=s(a_2z_3+a_1 z_2 +f(z)) + g(z)su \end{aligned}$$

(12)

We take control input to be composed of two parts, i.e.

$$\begin{aligned} u=u_{eq} + \nu \end{aligned}$$

(13)

where $u_{eq}$ is taken to cancel all nonlinear part from the above equation and $\nu$ is based on the switching controller to make the controller negative definite inside the boundary layer, i.e.

$$\begin{aligned} u_{eq} = \frac{1}{g(z)} (-f(z)-a_2z_3-a_1 z_2) \end{aligned}$$

(14)

and the nonlinear functions are defined as

$$\begin{aligned} \frac{1}{g(z)}&=\frac{m L(x_1) (a+x_1)^2}{L_o a x_3} \end{aligned}$$

(15)

$$\begin{aligned} f(z)&=-\frac{k}{m} z_3 + {\frac{L_o L_1 a x_2 {x}^2_3}{m L(x_1) (a+x_1)^3}} +{\frac{L_o a R{x}^2_3}{m L(x_1) (a+x_1)^2}} \end{aligned}$$

(16)

We take

$$\begin{aligned} \nu =-\gamma sat{\bigg (\frac{s}{\epsilon }\bigg )} \end{aligned}$$

(17)

where $\gamma$ is a positive class $K$ function such that $\gamma \ge \rho (z) + \beta _o, \beta _o > 0$, and sat is the nonlinear saturation function. Under nominal system parameters the gain $\gamma$ is chosen by using

$$\begin{aligned} \Bigg | \frac{(a_1 z_2 + a_2 z_3) + f(z)}{g(z)}\Bigg |&\le \frac{((z_2 + z_3)m - kz_3) L(x_1)(a+x_1)^3 + L_o a{x}^2_3 (x_2 L_1 + R(a+x_1)) }{m L_o a x_3 L(x_1)(a+x_1)} \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned} \qquad sat{\bigg (\frac{s}{\epsilon }\bigg )}= {\left\{ \begin{array}{ll} {\textit{s}ign}(s) &{} \quad \mathrm{if }\; |s| > 1\\ \bigg (\frac{s}{\epsilon }\bigg ) &{} \quad \mathrm{if }\; |s| \le 1 \end{array}\right. } \end{aligned}$$

(19)

$$\begin{aligned} sign(s)= {\left\{ \begin{array}{ll} 1 &{} \quad \mathrm{if }\; |s| > 0\\ 0 &{} \quad \mathrm{if }\; |s| = 0 \\ -1 &{} \quad \mathrm{if }\; |s| < 0 \end{array}\right. } \end{aligned}$$

(20)

Using the parametric values given in Table. 1 results in $\rho (z) \le 6.27$. With this controller, the Lyapunov function becomes

$$\begin{aligned} \dot{V}\le g(z)|s|\rho (z) - g(z)s(\rho +\beta _o) sat\bigg (\frac{s}{\epsilon }\bigg ) \le -g(z)\beta _o |s| \le -g_o \beta _o |s| \;\;\;\;\; ;|g(z)|\le g_o \end{aligned}$$

where $g_o > 0$. Therefore, under the influence of the controller the trajectory reaches the sliding manifold $(s=0)$ in finite time and once on the manifold it cannot leave it as $\dot{V}$ is negative definite. This motion is called the reaching phase followed by a sliding phase during which the motion is confined to the manifold. This control law $\nu =-\gamma sat{\big (\frac{s}{\epsilon }\big )}$ is called the continuous sliding mode control where $\epsilon$ is the maximum bound of the sliding manifold on either side of origin in the sliding phase.

To check the controller robustness in presence of parametric uncertainties, outside and inside the boundary layer, we define the system parameters within a range i.e. $0.009<L_o \le 0.01, 0.01<L_1 \le 0.02, 0.1<m \le 0.11, 0.9<R \le 1.1$. Under these conditions, let $\hat{f}(z)$ and $\hat{g}(z)$ be the nominal models of $f(z)$ and $g(z)$, respectively. Taking

$$\begin{aligned} u= - \frac{[(a_1 z_2 + a_2 z_3) + \hat{f}(z)]}{\hat{g}(z)} + \nu \end{aligned}$$

results in

$$\begin{aligned} \dot{s}= a_1 (z_2 + z_3) + \Bigg [ 1- \frac{g(z)}{\hat{g}(z)}\Bigg ] + f(z) - \frac{g(z)}{\hat{g}(z)} \hat{f}(z) + g(z)\nu = \delta (z) + g(z)\nu \end{aligned}$$

where $\delta$ is the perturbation term which satisfies the inequality

$$\begin{aligned} \Bigg |\frac{\delta (z)}{g(z)}\Bigg | \le \rho (z) \end{aligned}$$

(21)

we can take

$$\begin{aligned} \nu =-\gamma sat{\bigg (\frac{s}{\epsilon }\bigg )} \end{aligned}$$

(22)

where $\gamma \ge \rho (z) + \beta _o, \beta _o > 0$. Since $\rho$ is an upper bound on the perturbation term, it is likely to be smaller than an upper bound on the whole function.

$$\begin{aligned} \Bigg | \frac{(a_1 z_2 + a_2 z_3) + \hat{f}(z)}{\hat{g}(z)}\Bigg |&\le \frac{((z_2 + z_3)\hat{m} - kz_3) \hat{L}(x_1)(a+x_1)^3 + \hat{L}_o a{x}^2_3 (x_2 \hat{L}_1 + \hat{R}(a+x_1)) }{\hat{m} \hat{L}_o a x_3 \hat{L}(x_1)(a+x_1)} \nonumber \\ \end{aligned}$$

(23)

Taking the parametric values as the upper bound on limits, we get $\rho (z) \le 7.27$. To analyze the performance of this continuous sliding mode controller in the reaching phase, we take a Lyapunov function $V=\frac{1}{2} s^2$ whose derivative satisfies the inequality

$$\begin{aligned} \dot{V}\le -g_o \beta _o |s| \end{aligned}$$

when $|s|\ge \epsilon$ outside the boundary layer {$|s|\le \epsilon$}. So until reaching the boundary layer in finite time, $|s(t)|$ will be strictly decreasing and remains inside this set afterwards. Inside the boundary layer, we have

$$\begin{aligned} z_2 = -a_1 (z_1 -r) - z_3 + s \end{aligned}$$

where $|s|\le \epsilon$. The derivative of $V_1 =\frac{1}{2} z^{2}_1$ satisfies

$$\begin{aligned} \dot{V}_1 = -a_1 (z^{2}_1 -z_1r) - z_1 z_3 + z_1 s \le -a_1 z^{2}_1 - z_1 z_3 + z_1 \epsilon \le -(1-\theta )a_1 z^{2}_1 \;\;\;\; \forall z_1\ge \frac{\epsilon }{a_1 \theta } \end{aligned}$$

where $0< \theta <1$ . Thus the trajectory reaches the set $\Omega _\epsilon =$ {$|z_1| \le \frac{\epsilon }{a_1 \theta }, |s|\le \epsilon$} in finite time. So we get ultimate boundedness with an ultimate bound that can be reduced by decreasing $\epsilon$. Inside the boundary layer $|s|\le \epsilon$ the control reduces to the linear feedback law $u=- \gamma {\big (\frac{s}{\epsilon }\big )}$ and the closed loop system can be stabilized by suitable choice of gain $\gamma$, to be large enough to overcome the bound $\rho$. Inside the boundary layer, the closed loop system given as

$$\begin{aligned} \dot{z_1}&= z_2 \\ \dot{z_2}&= z_3 \\ \dot{z_3}&= f(z) - g(z) {\big (\gamma \frac{s}{\epsilon }\big )} \end{aligned}$$

has a unique equilibrium point at $(\bar{x}_1,0,I_{ss})$, where $\bar{x}_1$ satisfies the equation

$$\begin{aligned} \dot{z_3} = - k m z_3 L_o a \epsilon + R L_o a \epsilon {x}^2_3 + L_o a \gamma s I_{ss} - k m z_3 \epsilon L_1 (a+\bar{x}_1) \end{aligned}$$

and for small $\epsilon$ can be approximated by

$$\begin{aligned} \bar{x}_1 \approx \frac{L_o a }{k L_1} \Bigg ( I_{ss} + \frac{\gamma s}{\epsilon }\Bigg ) \end{aligned}$$

introducing a change of variables to shift to origin results in,

$$\begin{aligned} y_1&= z_1 - \bar{z}_1 \;\;\;\;\; \dot{y}_1 = y_2 \\ y_2&= z_2 \;\;\;\;\;\;\;\;\;\;\;\;\; \dot{y}_2 = y_3 \\ y_3&= z_3 \;\;\;\;\;\;\;\;\;\;\;\;\; \\ \dot{y}_3&= - \frac{k}{m} y_3 +{\frac{L_o a R{x}^2_3}{m L(\bar{x}_1) (a+ \bar{x}_1)^2}} + {\frac{L_o a \gamma x_3 (z_3+ a_2 z_2 + a_1(z_1-r))}{m \epsilon L(\bar{x}_1) (a+\bar{x}_1)^2}} \\&\approx - \Big ( \frac{k}{m} y_3 - \frac{L_o a I_{ss} \gamma }{m\epsilon L_1 (a+y_1 + \bar{z}_1)^2} \Big ) {y}^2_3 - \sigma (y_1) \end{aligned}$$

where

$$\begin{aligned} \sigma (y_1) = - \frac{I_{ss} L_o a \gamma y_1 x_3}{m \epsilon L_1(a+y_1 + \bar{z}_1)^2} \end{aligned}$$

Consider the Lyapunov function

$$\begin{aligned} \tilde{V} = \int \limits ^{y_1}_{o} \sigma (s)d(s) - \frac{1}{2} y^{2}_3 \end{aligned}$$

where $\tilde{V}$ is positive definite ($|\tilde{V}|$ is radially unbounded) for $y_3 > \frac{L_o a I_{ss} \gamma z_3}{m L_1 \epsilon }$ and its derivative satisfies

$$\begin{aligned} \dot{\tilde{V}} = \sigma (y_1) + y_3\dot{y_3} \le \frac{L_o a I_{ss} \gamma }{m L_1 \epsilon } y^{2}_3 < 0 \end{aligned}$$

Using LaSalle’s Invariance Principle we can show that the equilibrium point $(\bar{x}_1,0,I_{ss})$ is asymptotically stable and attracts every trajectory in $\Omega _\epsilon$. For better accuracy, we choose $\epsilon$ as small as possible, however we should keep in mind that choosing too small a value may result in chattering. With a suitable choice of $\epsilon$ close to zero, the controller achieves ultimate boundedness as all trajectories starting off the manifold $|s| \le \epsilon$ reach it in finite time and stay there onwards. By suitable choice of $\epsilon \rightarrow 0$ and a high enough controller gain $\gamma$ the proposed controller yields semi-global asymptotic stabilization.

3.2 Higher Order Sliding Control

We now focus our attention to development of stabilizing controllers for the system under consideration that use Higher Order Sliding Modes. This approach has gained substantial attention recently due to its ability to yield in better transient performance, superior robustness properties and removal of chattering when compared to a first-order SMC. The formulation of controller (Korovin and Emeryanov 1996) is as follows:

Consider an uncertain single-input nonlinear system

$$\begin{aligned} \dot{x}=f(x,t,u), \;\;\;\; s=s(t,x) \;\;\;\;\; t \ge 0 \end{aligned}$$

(24)

with $x \in X \subseteq \mathfrak {R}^n$ as the state vector, $u \in U \subset \mathfrak {R}$ being the control input and the time varying non-linear function $f(x,t,u):[0,+\infty ) \times \mathfrak {R}^{n} \times U \rightarrow \mathfrak {R}^n$ is a sufficiently smooth uncertain vector field and $s(x,t):[0,+\infty ) \rightarrow \mathfrak {R}$ is the function as defined in (7). The relative degree r of the system is defined such that u explicitly appears in only the rth derivative of s and $\frac{d}{du} s^r \ne 0$ at the given point. The task is to achieve the constraint $s\equiv 0$ in finite time and stay there using a discontinuous feedback control. Since $s,\dot{s}, \ddot{s},\ldots ,s^{r-1}$ are continuous functions, the corresponding motion corresponds to an r-sliding mode (Levant 2001).

The term Higher Order Sliding Mode specifies a movement on the discontinuity set of the dynamic system in Filippov’s sense (i.e. it consists of Filippov’s trajectories of the discontinuous dynamic system) (Levant 1999). The controller Sliding Order indicates the dynamic smoothness degree in the vicinity of the mode i.e. it is a number of total continuous derivatives of the manifold $(s)$ (including $s^0$) in the vicinity of sliding mode. Therefore the $r$th order sliding mode is determined by the following equalities:

$$\begin{aligned} s=\dot{s} =\ddot{s} = \cdots s^{r-1}=0 \;\;\;\; ; \;\;0<K_m \le \frac{\partial }{\partial u}s^r \le K_M \end{aligned}$$

(25)

for some positive constants $K_m$ and $K_M$. This forms an r-dimensional condition on the state of the dynamic system and any motion satisfying  (25) is called an r-sliding mode with respect to the essential constraint $s \equiv 0$ (Fridman and Levant 2002).

3.2.1 Two Sliding Controller

We start with defining the sliding variable $s$ as the regulated output of the system (5). The second order sliding mode approach provides for the finite time stabilization of the output $s$ and its time derivative $\dot{s}$ by characterizing a discontinuous control input $(u)$ for the system (Perruquetti 2010).

Considering $y_1 = s$, it can been shown that, the second order sliding mode problem is equivalent to the finite time stabilization problem for the following uncertain second order system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \; \dot{y_1} &{} = y_2 \\ \; \dot{y_2} &{} = \varphi (t,y) + \gamma (t,y)u \end{array}\right. } \end{aligned}$$

(26)

where it is considered that only the information about sign of $y_2$ is available (Fridman and Levant 2002). The nominal functions $\varphi (t,y)$ and $\gamma (t,y)$ are defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \; |\varphi (t,y)| < \Phi \;\;\;\; ; \Phi > 0 &{} \\ \; 0 < \Gamma _{m} < \gamma < \Gamma _{M} < 1 &{} \end{array}\right. } \end{aligned}$$

(27)

$\forall y \in Y \subseteq \mathfrak {R}^{2}$, such that the system  (26) is bounded and stable.

3.2.2 Twisting Algorithm

The Twisting Algorithm is the basic 2-sliding controller (Punta 2006). This algorithm features the twisting of sliding trajectory infinite times around the origin of the 2-sliding plane $y_1 O y_2$. The method is called ‘Twisting Controller’ because the trajectories perform an infinite number of rotations while converging to the origin along with the vibration magnitudes decays along the axes and the rotation times decreasing in geometric progression (Levant 1999).

The controller, based on the constraint $(s=\dot{s}=0)$, is able to stabilize the dynamic system while achieving semi-global asymptotic output regulation. The control algorithm is defined by the following control law (Floquet and Barbot 2007) in which the condition on $|u|$ provides for $|u|\le 1$:

$$\begin{aligned} \dot{u}(t)= {\left\{ \begin{array}{ll} -u &{} \;\;\;\; ; |u| > 1\\ -V_m sign(y_1) &{} \;\;\;\; ; (y_1)(y_2) < 0 \;\; \mathrm{and} \;\; |u| \le 1 \\ -V_M sign(y_1) &{} \;\;\;\; ; (y_1)(y_2) > 0 \;\; \mathrm{and} \;\; |u| \le 1 \end{array}\right. } \end{aligned}$$

(28)

The corresponding sufficient conditions to ensure the elimination of reaching phase and finite time convergence to the sliding manifold are:

$$\begin{aligned} {\left\{ \begin{array}{ll} \; V_M > V_m \;\;\;\;\;\;\;\;\;\; ; V_m > 4\frac{\Gamma _m}{s_o} &{} \\ \; V_M > \frac{2\Phi +V_M}{\Gamma _M} \;\;\;\; ; V_m > \frac{\Phi }{\Gamma _M} &{} \end{array}\right. } \end{aligned}$$

(29)

where $s_o$ is the max allowed value for manifold s. The results for the controller are discussed in Analysis and Results section and it is shown that this controller results in much better transient phase response as compared to the First Order SMC but due to large relative degree of the system chattering is not completely removed when used to control the nonlinear system.

3.2.3 Three Sliding Controller

For the Magnetic Levitation System with relative degree $\rho =3$, the 2-sliding controller described above does not completely eliminate chattering. As mentioned in Levant (2010), Korovin and Emeryanov (1996), the main drawbacks of the previously described methods are that when the relative degree $\rho$ of the control variable $s$ is higher than one, the control methods, to completely remove chattering, generally require the knowledge of up to $(\rho -1)$ derivatives of $s$. For systems with $\rho =3$, the usually unavailable quantities $\dot{s}$ and $\ddot{s}$ need to be measured or estimated using an observer (e.g. High-Gain Observer, sliding differentiator) for controller design that completely removes chattering. The 2-sliding controller when applied to a higher relative degree system does not eliminate chattering.

For systems with relative degree higher than 2, the recommended practice is to use a 3-sliding controller (3rd order SMC) to completely eliminate chattering under the constraints described in  (29) (Levant 2010). The 3-sliding controller is designed as follows:

Let p be a positive number. Denoting

$$\begin{aligned} J_{1,r}&= |s|^{(r-1)/r} \\ J_{i,r}&= \Big (|s|^{p/r} + |\dot{s}|^{p/(r-1)} + \cdots + |s^{(i-1)}|^{p/(r-i+1)} \Big )^{(r-i)/p} , \;\;\; i=1,\ldots ,r-1 \\ J_{r-1,r}&= \Big ( |s|^{p/r} + |\dot{s}|^{p/(r-1)} + \cdots + |s^{(r-2)}|^{p/2} \Big )^{1/p} \\ \psi _{0,r}&= s \\ \psi _{1,r}&= \dot{s} + \beta _1 J_{1,r} sign(s) \\ \psi _{i,r}&= s^{(i)} + \beta _i J_{i,r} sign(\psi _{i-1,r}), \;\;\; i=1,\ldots ,r-1 \end{aligned}$$

where $\beta _1,\ldots ,\beta _r-1$ are positive numbers.

3.2.4 Theorem 1

If the system  (26) has relative degree $r$ with respect to the output function $s$ and the condition  (25) on $\frac{\partial }{\partial u}s^r$ is satisfied, then with properly choosing the parameters $\beta _1,\ldots ,\beta _r-1$ the controller defined by

$$\begin{aligned} u = -\alpha sign\bigg [ \psi _{r-1,r} (s, \dot{s},\ldots ,s^{(r-1)}) \bigg ] \end{aligned}$$

(30)

assures the appearance of r-sliding mode $s\equiv 0$ while attracting all trajectories in finite time.

The parameters $\beta _1,\ldots ,\beta _r-1$ are chosen to be sufficiently large in the index ordering. Each choice specifies a family of controller applicable to all systems expressed as  (26) with relative degree $r$. The parameter $\alpha >0$ depends on the choice of positive constants $K_m$ and $K_M$. Coefficients of $J_{i,r}$ can be chosen as any positive numbers and $\alpha$ needs to be negative when $\frac{\partial }{\partial u}s^{r} < 0$.

There can be infinite many choices for $\beta _i$. A tested example for $\beta _i$ for $r=3$ is provided in Fridman and Levant (2002). The 3-sliding controller is given as

$$\begin{aligned} \nu = -\alpha sign\bigg ( \ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} sign\big (\dot{s} + {|s|}^{\frac{2}{3}}sign(s)\big ) \bigg ) \end{aligned}$$

(31)

The idea is that a 1-sliding mode is established on the smooth parts of the discontinuity set $\Lambda$ of  (31) described by the differential equation $\psi _{r-1,r} =0$. The resulting movement takes place in some close boundary of the $\Lambda$ satisfying $\psi _{r-2,r} =0$, transfers in finite time into some vicinity of the subset satisfying $\psi _{r-3,r} =0$ and so on. While the trajectory reaches the r-sliding set, set $\Lambda$ shrinks to origin in the coordinates $s, \dot{s},\ldots ,s^{(r-1)}$ (Levant 2012).

This controller placed in  (13) makes the overall control input for the system. The parameter $\alpha$ is a positive constant i.e. $\alpha >0$. For our system we take $\alpha =20$ with tolerance $\tau = 10^{-3}$ and Euler?s method for integration. The overall 3-sliding controller for the system becomes:

$$\begin{aligned} u&= -\frac{m L(x_1) (a+x_1)^2}{L_o a x_3} \Bigg (\frac{k}{m} z_3 - {\frac{L_o L_1 a x_2 {x}^2_3}{m L(x_1) (a+x_1)^3}} - {\frac{L_o a R{x}^2_3}{m L(x_1) (a+x_1)^2}} - a_2 z_3 \nonumber \\&- a_1 z_2 -\alpha sign\bigg ( \ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} sign\big (\dot{s} + {|s|}^{\frac{2}{3}}sign(s)\big ) \bigg ) \Bigg ) \end{aligned}$$

(32)

A maximum of $r$th order accuracy is attainable with the above mentioned 3-sliding controller and with proper choice of parameters $\beta _1,\ldots ,\beta _r-1$ the convergence time is reduced approximately $\kappa (\alpha )$ times where $0<\kappa \le 1$.

To analyze the controller performance for reaching phase (to guarantee that the trajectory reaches the manifold in finite time) we follow a similar procedure as for First Order Sliding Controller. Considering a Lyapunov function candidate:

$$\begin{aligned} V=\frac{1}{2} s^2 \Rightarrow \dot{V}=s\dot{s} \end{aligned}$$

Under the influence of the above mentioned 3-sliding controller, we get

$$\begin{aligned} \dot{V} \le -\alpha |s||\nu | \le -\alpha \lambda |s| \;\;\;\;\;\; ;\alpha > 0 \end{aligned}$$

where $\lambda$ is a positive class K function such that $\lambda = \mu + \omega , \omega >0$ and $|\nu |\le \mu , \mu > 0$ is calculated as follows: replacing the $sign$ function by its approximation i.e.

$$\begin{aligned} sign(s) = \frac{|s|}{s} \end{aligned}$$

results in

$$\begin{aligned} |\nu |= \frac{\Bigg | \ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} \frac{\Big |\dot{s} + {|s|}^{\frac{2}{3}} \frac{|s|}{s} \Big |}{\Big [ \dot{s} + {|s|}^{\frac{2}{3}} \frac{|s|}{s} \Big ]} \Bigg |}{\ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} \frac{\Big |\dot{s} + {|s|}^{\frac{2}{3}} \frac{|s|}{s} \Big |}{\Big [ \dot{s} + {|s|}^{\frac{2}{3}} \frac{|s|}{s} \Big ]}} \end{aligned}$$

using the Triangle Inequity, Preservation of division and Idempotence properties of absolute numbers we get

$$\begin{aligned} |\nu |&\le \frac{\Bigg | \ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} \frac{\Big |\dot{s} + {|s|}^{\frac{2}{3}}\Big |}{\Big |\dot{s} + {|s|}^{\frac{2}{3}}\Big |} \Bigg |}{\ddot{s} + 2{\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}}} \frac{\Big |\dot{s} + {|s|}^{\frac{2}{3}}\Big |}{\dot{s} + {|s|}^{\frac{2}{3}}}} \nonumber \\ \end{aligned}$$

(33)

we know that $\big ({|\dot{s}|}^3 + s^2\big )^{\frac{1}{6}} > 0$, using Triangle Inequity and further solving the inequity, we get

$$\begin{aligned} |\nu | \le |\ddot{s}| + \Big | \big (\dot{s} + s^2\big )^{\frac{1}{6}}\Big | \le |\ddot{s}| \le W \;\;\;\;\;\;\; ;W>0 \end{aligned}$$

which makes the Lyapunov function derivative negative definite, i.e.

$$\begin{aligned} \dot{V} < -\alpha W |s| \;\;\;\;\;\;\;\; ;\alpha > 0 \;\; \mathrm{and} \;\; W>0 \end{aligned}$$

Therefore, under the influence of the controller the trajectory reaches the sliding manifold ($s=0$) in finite time and once on the manifold it cannot leave it as $\dot{V}$ is negative definite. So until reaching the boundary layer in finite time, $|s(t)|$ is strictly decreasing and remains inside this set afterwards.

Inside the boundary layer (inside the set $\Omega _\epsilon$) a similar analysis can be carried out as in first order sliding mode controller (applying a change of variables and using Invariance Principle) to show that the application of the controller results in an asymptotically stable origin. The results for the controller are discussed in Analysis Section where it is shown that the 3-sliding controller results in much improved performance as compared to the First and Second Order SMC.

3.3 Output Feedback

In this section, we extend the state feedback design to output feedback by using a High Gain Observer (HGO) (Esfandiari and Hassan 1992; Atassi and Hassan 1999). Towards that end, we consider the observer as given by the following set of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \; \hat{\dot{\xi _1}} &{} = \hat{\xi _2} + h_1 ( y- \hat{\xi _1}) \\ \; \hat{\dot{\xi _2}} &{} = h_2( y- \hat{\xi _1}) \\ \; \hat{\dot{\xi _3}} &{} = h_3( y- \hat{\xi _1}) \end{array}\right. } \end{aligned}$$

(34)

in which the observer gains are chosen as follows:

$$\begin{aligned} \left[ \begin{array}{c} h_1\\ h_2 \\ h_3\\ \end{array} \right] = \left[ \begin{array}{c} 2/{\epsilon } \\ 1/{\epsilon ^2} \\ 1/{\epsilon ^3} \\ \end{array} \right] \end{aligned}$$

(35)

where $\epsilon$ is a design parameter. It is well established that by incorporating an HGO, one can recover the performance of the state feedback controller by a suitable choice of observer gains. This is achieved by choosing the design parameter $\epsilon$ sufficiently small which renders the estimation error $(\hat{\xi } - \xi )$ to zero as $\epsilon$ approaches zero. However, this process results in a large overshoot for a very limited time in the initial transient phase before the estimation error sharply decays to zero. This overshooting phenomenon is called peaking and is usually overcome by saturating the observer for a very brief initial interval during operation.

The output feedback controller incorporating the HGO  (34) for 3-sliding feedback controller is given as:

$$\begin{aligned} u&= -\frac{m L(x_1) (a+x_1)^2}{L_o a x_3} \Bigg (\frac{k}{m} \hat{z_3} - {\frac{L_o L_1 a x_2 {x}^2_3}{m L(x_1) (a+x_1)^3}} - {\frac{L_o a R{x}^2_3}{m L(x_1) (a+x_1)^2}} - a_2 \hat{z_3} \nonumber \\&\quad - a_1 \hat{z_2} -\alpha sign\bigg ( \ddot{\hat{s}} + 2{\big ({|\dot{\hat{s}}|}^3 + \hat{s}^2\big )^{\frac{1}{6}}} sign\big (\dot{\hat{s}} + {|\hat{s}|}^{\frac{2}{3}}sign(\hat{s})\big ) \bigg ) \Bigg ) \end{aligned}$$

(36)

This output feedback controller is applied to the original nonlinear system represented in strict feedback normal form. The inclusion of HGO recovers the performance of the full state feedback controller and, by suitable choice of gains, allows the output feedback to achieve semi-global asymptotic stabilization over a domain of interest.

3.3.1 Theorem 2

Consider the closed loop system comprising of the plant (5) and the output feedback controller (36). Suppose the origin of the closed loop system under state feedback control (32) is asymptotically stable and $\mathcal {R}$ is its region of attraction. Let $\mathcal {S}$ be any compact subset in the interior of $\mathcal {R}$ and $\mathcal {Q}$ be any compact subset of $\mathcal {R}^\rho$. Then

• There exists $\epsilon ^{*}_{1} > 0$ such that for every $0 < \varepsilon \le { \epsilon ^{*}_{1}}$, the solutions of the closed loop system (under state feedback $X(t)$ and under output feedback $(\hat{x}(t))$), starting in $\mathcal {S} \times \mathcal {Q}$, are bounded for all $t > 0$.

• Given any $\mu >0$, there exists $\epsilon ^{*}_{2} > 0$ and $T_2 > 0$, both dependent on $\mu$, such that, for every for every $0 < \varepsilon \le { \epsilon ^{*}_{2}}$, the solutions of the closed loop system, starting in $\mathcal {S} \times \mathcal {Q}$, satisfy

  $$\begin{aligned} ||X(t)||\le \mu \;\;\;\; ||\hat{x}(t)||\le \mu \;\;\;\; \forall \;t\ge T_2 \end{aligned}$$

• Given any $\mu >0$, there exists $\epsilon ^{*}_{3} > 0$, dependent on $\mu$, such that, for every for every $0 < \varepsilon \le { \epsilon ^{*}_{3}}$, the solutions of the closed loop system, starting in $\mathcal {S} \times \mathcal {Q}$, satisfy

  $$\begin{aligned} ||X(t)-X_{r}(t)||\le \mu \;\;\;\; \forall \;t\ge 0 \end{aligned}$$

  where $X_r$ is the solution of system under (32) starting at $X(0)$.

• If the origin of system under (32) is exponentially stable and that $f(z)$ is continuously differentiable in some neighborhood of $X=0$, then there exists $\epsilon ^{*}_{4} > 0$ such that, for every $0 < \varepsilon \le { \epsilon ^{*}_{4}}$, the origin of the closed loop system is exponentially stable and $\mathcal {S} \times \mathcal {Q}$ is a subset of its region of attraction.

3.3.2 Proof

The proof follows the general outline as given in [Hassan (2002), Sect. 14.5.2] with appropriate modifications as per the problem under consideration. In particular, proof of the theorem establishes that the output feedback controller recovers the performance of the state feedback controller for sufficiently small $\epsilon$. The performance recovery is evident in itself in three points. Firstly, recovery of exponential stability. Second, recovery of region of attraction in the sense that we can recover any compact set in its interior. Third, the solution $X(t)$ under output feedback reaches the solution under state feedback as $\epsilon$ tends to zero.

Remark 1

It is well known that if the state feedback controller achieves the state feedback controller achieves global or semi-global asymptotic stabilization with local exponential stability, then for sufficiently small $\epsilon$, the output feedback controller achieves semi-global stabilization with local exponential stability.

4 Performance Analysis

In this section a detailed analysis of the First Order Sliding Mode Controller and the Higher Order Sliding Controllers is carried out and simulation results are shown to demonstrate the performance of different controllers.

4.1 First Order Sliding Mode Controller

The controller $\nu =-\gamma sat{\big (\frac{s}{\epsilon }\big )}$ is called the First Order Sliding Mode Control.

Fig. 3

First order sliding mode control results

Fig. 4

Control input for sliding mode control

Fig. 5

Sliding phase results For $\epsilon = 0.001$(chattering)

• Transient Performance/Reaching Phase: The First Order SMC behaves poorly in the reaching phase and the system trajectory exhibits large overshoots before reaching the sliding manifold as shown in Fig. 3. But the controller (Fig. 4) guarantees that the trajectory reaches the sliding manifold $(s=0)$ in finite time and once on the manifold it cannot leave it as $\dot{V}$ is negative definite.

• Sliding Phase: Inside the boundary layer ${|s|\le \epsilon }$ the control reduces to the linear feedback law $\nu =-\gamma sat{\big (\frac{s}{\epsilon }\big )}$ and the closed loop system can be stabilized by suitable choice of the gain $\gamma$, to be large enough to overcome the max bound $\rho$ of the perturbation term $u_{eq}$ i.e. $\gamma > \rho + \beta _o, \beta _o > 0$. The parameter $\epsilon$ is a small constant i.e. $0< \epsilon \le 1$ defined as the maximum bound of the sliding manifold on either side of origin. So we get ultimate boundedness with an ultimate bound that can be reduced by decreasing $\epsilon$ i.e. $\epsilon \rightarrow 0$.

• Chattering Analysis and Stability: The controller is a Continuous Sliding Mode Controller using the $sat$ approximation of the discontinuous $sign$ function i.e. $\nu =-\gamma sat{\big (\frac{s}{\epsilon }\big )}$ to cater the “chattering” introduced in the system due to switching delay between the sign of s, which causes unwanted oscillations in the system as shown in Fig. 5. The value of $\epsilon$ needs to be carefully selected because when $\epsilon$ is reduced to zero, the continuous sliding controller approaches a discontinuous sliding controller, i.e. as $\epsilon \rightarrow 0 \Rightarrow sat(s) \rightarrow sign(s)$ and chattering starts to appear in the system and for the system with input defined as:

  $$\begin{aligned} u=\nu =Ri=i \end{aligned}$$

  it causes a continuous drawl of current from the source. So, with a proper choice of $\epsilon$ close to zero, the controller achieves ultimate boundedness as all trajectories starting off the manifold ${|s|\le \epsilon }$ reach it in finite time and stay there onwards. Then by choice of a high enough controller gain $\gamma$ the controller achieves semi-global asymptotic stability for the system. The simulation values for the controller $\epsilon =0.01$ and $\gamma =10$ are based on the same constraints discussed above for $\gamma$ and $\epsilon$, assuring a reasonable reaching phase time and chattering removal as shown in Fig. 6.

Fig. 6

Sliding phase results For $\epsilon = 0.01$(chattering removed)

Fig. 7

Output under 2-sliding controller

4.2 Higher Order Sliding Mode Controller

As discussed earlier, the main problem is that when the relative degree $\rho$ of the control variable $(s)$ is greater than one, the control methods, to completely remove chattering, generally require the knowledge of up to $(\rho -1)$ derivatives of $s$. For the current system with relative degree $\rho =3$, the usually unavailable quantities $\dot{s}$ and $\ddot{s}$ need to be incorporated for a controller design that completely removes chattering. Using the 2-sliding controller (Fig. 7) for the system also does not completely eliminate chattering as shown in Fig. 8, and the recommended practice is to use a 3-sliding controller.

Fig. 8

Control input for 2-sliding controller

Fig. 9

Output under 3-sliding controller with varying $\epsilon$

• Reaching Phase Elimination Time: Using the 2-sliding Twisting Controller and 3-sliding Controller the time required for the system trajectory to reach the sliding surface $(s)$ is considerably reduced as compared to first order sliding mode control results (Levant 2012). With proper choice of parameters $\beta _1,\ldots ,\beta _r-1$ the convergence time is reduced approximately $\kappa (\alpha )$ times where $0<\kappa \le 1$ under the constraints defined in (29–30). This is evident from the simulation results that the 3-sliding controller results in much faster global finite time convergence to the origin and the overall control is bounded as shown in Fig. 9.

• Implementation of the 3-sliding Controller: The 3-sliding controller implementation requires the availability of the sliding manifold and the knowledge of up to $(\rho -1)$ derivatives i.e. $s,\dot{s}$ and $\ddot{s}$ at all times. The usually unavailable quantities $s,\dot{s}$ and $\ddot{s}$ need to be incorporated for the controller design that completely removes chattering. With the introduction of these variables as auxiliary variables in the control design procedure, the controller effectively takes care of the discontinuities in the sliding variable $(s)$ and removes the vibrations (harmonics) that may arise due to its higher derivatives, as in the case of first order sliding mode controller. As a result the controller is a much smooth and bounded function of time in Lipschitz sense rather than a bounded but “infinite switching frequency/relay” controller, as shown in Fig. 10.

• Stability: The 3-sliding controller results are comparable with a full-state back-stepping controller, both very different in design parameters (differential inequalities instead of parametric uncertainties) and resulting performance (Levant 1999). Offering much higher accuracy and finite time convergence for complex non-linear systems, (systems with finite escape time) the proposed 3-sliding controller features a globally asymptotically stable closed loop system and in some cases locally exponentially stable systems. It is evident from Fig. 9 that the closed loop non-linear system (5) is stabilized and output is successfully regulated to the desired reference.

• Chattering Removal: The above mentioned technique of including the higher derivatives of the sliding manifold in the control design procedure also removes the chattering effect from the system even under very small HGO gain $\epsilon$ values (see for $\epsilon =0.005$ in Fig. 9). When we design the controller based on knowledge of higher derivatives of the sliding variable (s) and cater for the higher derivative terms, the unwanted oscillations (chattering) introduced in the system are considerably reduced. With the proper handling of HOSMC design constraints, chattering is completely removed and we get a local 3-sliding controller rather than the relay controller $u=-\gamma sign(s)$ while achieving a $3rd$ order sliding precision with respect to $\tau$ i.e. $O(\tau ^3)$ (Levant 2010). The inclusion of HGO for estimation of unmeasured system states in the design of output feedback controller does not degrade the controller performance or stability. The sliding manifold $(s)$ and its derivatives vanish in finite time as shown in Fig. 11.

  To show the controller efficiency and the performance recovery of the State Feedback Controller using the Output Feedback controller based on High Gain Observer, the observer convergence speed control parameter $\epsilon$ was varied from $0.1$ to $0.005$ to show the difference in the performance recovery. Other simulation parameters taken are: $\mu =0.01, V_M=50, V_m=15, \Gamma _m=0.5, \Gamma _M=1, a_1 = a_2=1\;\; \Phi =2, s_o=I_{ss}$.

Fig. 10

Control input for 3-sliding controller

Fig. 11

Sliding manifold and higher derivatives

• Discontinuity Regularization/Constraint Control: The Transient phase overshoot called peaking occurring due to the inclusion of HGO is reduced by putting some constraint on control input (regularizing the discontinuity), as per limits, using sat function (Fridman and Levant 2002), with the limits $[-2.5 \;\; I_{ss}]$. Due to this, the overshoot magnitudes are considerably reduced without degrading the controller performance as shown in Fig. 12. The control input becomes:

  $$\begin{aligned} u = sat\Bigg [-\frac{m L(x_1) (a+x_1)^2}{L_o a x_3} \Bigg (\frac{k}{m} \hat{z_3} - {\frac{L_o L_1 a x_2 {x}^2_3}{m L(x_1) (a+x_1)^3}} - {\frac{L_o a R{x}^2_3}{m L(x_1) (a+x_1)^2}} \nonumber \\ - a_2 \hat{z_3} - a_1 \hat{z_2} -\alpha sign\bigg ( \ddot{\hat{s}} + 2{\big ({|\dot{\hat{s}}|}^3 + \hat{s}^2\big )^{\frac{1}{6}}} sign\big (\dot{\hat{s}} + {|\hat{s}|}^{\frac{2}{3}}sign(\hat{s})\big ) \bigg ) \Bigg )\Bigg ] \end{aligned}$$

  (37)

Fig. 12

Output under constraint control input using 3-sliding controller

• Robustness Under Parametric Variations: To verify the robustness properties of the proposed 3-sliding controller, the system nominal parameters were perturbed by 10–20% while keeping the parameters of the controller unchanged. The controller, to stabilize the system at desired reference, has to exert some extra effort but the desired reference is achieved as shown in Fig. 13. The new control input, using nominal system parameters becomes:

  $$\begin{aligned} u=sat\bigg ( \frac{1}{\hat{g}(z)} \big (-\hat{f}(z) -a_2 \hat{z_3}-a_1 \hat{z_2}- \nu \big ) \bigg ) \end{aligned}$$

  (38)

The new parameters for system are given in Table 2.

Fig. 13

Output using 3-sliding controller under parametric uncertainties

Table 2 Varied system parameters

5 Conclusion

We focused on the problem of robust output feedback stabilization of a Magnetic Levitation System using Higher Order Sliding Mode Control (HOSMC) strategy. The traditional (first order) sliding mode control (SMC) design tool provides for a systematic approach to solving the problem of stabilization and maintaining a predefined (user specified) consistent performance of a minimum-phase nonlinear system in the face of modeling imprecision and parametric uncertainties. Recently reported variants of SMC commonly known as Higher Order Sliding Mode Control schemes have gained substantial attention since these provide for a better transient performance together with robustness properties.

We proposed an output feedback controller that robustly stabilizes the closed-loop system with an added objective of achieving an improvement in the transient performance. The proposed control scheme incorporates a higher-order sliding mode controller (HOSMC) to solve the robust semi-global stabilization problem in presence of a class of somewhat unknown disturbances and parametric uncertainties. The state feedback control design is extended to output feedback by including a high gain observer that estimates the unmeasured states. It is shown that by suitable choice of observer gains, the output feedback controller recovers the performance of state feedback and achieves semi-global stabilization over a domain of interest. A detailed analysis of the closed-loop system was given highlighting the various factors that lead to improvement in transient performance, robustness properties and elimination of chattering. Simulation results were included and a performance comparison was given for the traditional SMC and HOSMC designs employing the first, second and third order sliding modes in the controller structure.

A detailed performance analysis showed that the first order SMC was able to stabilize the system at the desired reference point. However, the transient performance of the same was degraded and showed large overshoot, and a slower reaching phase when compared to that of the second-order and third-order SMC, which showed superior transient performance, along with better robustness properties and removal of chattering.

5.1 Future Work

For future work the authors recommend the inclusion of some other observer design technique e.g. an Exact Differentiator or the Internal Model based approach to handle the output feedback control problem for the system. The concept can be extended to Output Regulation of the nonlinear system using the robust HOSMC algorithm based conventional/conditional compensator which may result in further improvement of transient performance and ability to asymptotically track unknown references while rejecting disturbance signals, both produced by some autonomous external system. A natural extension of the HOSMC framework is the control of non-minimum phase systems directly using high gain feedback or incorporate an extended high gain observer and design output feedback control. The incorporation of higher order sliding strategy in controller design opens new dimensions towards robust control design and performance enhancement.