Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Liquid storage tanks are one of the most important structures in several industries, such as oil refinery, aviation, chemical industries, power generation, etc. Failure of such tanks may lead to enormous losses directly or indirectly. Several researchers reported the catastrophic failure of liquid storage tanks during past earthquakes, leading to loss of human lives as well as massive economic loss (Haroun 1983a; Rammerstorfer et al. 1990). To safeguard such important structures against devastating earthquake, base isolation is considered as an efficient technique (Kelly and Mayes 1989; Jangid and Datta 1995a; Malhotra 1997; Deb 2004; Shrimali and Jangid 2004; Matsagar and Jangid 2008). Several international design guidelines (AWWA D-100-96 1996; EN 1998-4 2006; API 650 2007; AIJ 2010) are available which take into account the seismic action for analysis and design of liquid storage tanks deterministically. However, the reliability evaluation of structures under dynamic loading has drawn significant attention over the recent years (Chaudhuri and Chakraborty 2006; Gupta and Manohar 2006; Padgett and DesRoches 2007; Rao et al. 2009). Few studies were carried out on seismic fragility analysis of ground-supported fixed-base and base-isolated liquid storage tanks under base excitation due to earthquake (O’Rourke and So 2000; Iervolino et al. 2004; Saha et al. 2013a). However, only limited studies were reported on the reliability assessment of the base-isolated liquid storage tanks, under base excitation (Mishra and Chakraborty 2010). On the other hand, the current design codes are gradually shifting toward the reliability-based design philosophy, which requires probabilistic analysis of structures. It therefore mandates systematic reliability analysis of liquid storage tanks.

Herein, a detailed methodology for seismic reliability analysis of base-isolated liquid storage tanks, under base excitation in horizontal direction, is proposed duly accounting for uncertainties. Failure modes for the liquid storage tanks are considered from earlier research works in accordance with international guidelines. The uncertainties of the base isolator characteristics parameters are also considered in the evaluation of the seismic reliability. Generalized polynomial chaos (gPC) expansion technique is used to determine the response statistics under random horizontal base excitation considering the uncertainties in the isolation parameters. First order second moment (FOSM) theory was used to carry out probabilistic analyses of structures in several research works (Shinozuka 1983; Ayyub and Haldar 1984; Bjerager 1990). The FOSM theory is used here for reliability assessment of base-isolated liquid storage tanks. Monte Carlo (MC) simulation is also carried out to compare applicability of the FOSM theory to estimate the probability of failure of base-isolated liquid storage tanks.

The major objectives of this book chapter are: (1) to formulate the reliability of base-isolated liquid storage tanks under base excitation in horizontal direction; (2) to compare the effectiveness of the FOSM theory, with the MC simulation, to determine the reliability of base-isolated liquid storage tanks; and (3) to investigate the effect of the uncertainties in the isolator and the excitation parameters on the reliability of base-isolated liquid storage tanks under base excitation in horizontal direction.

2 Reliability Analysis of Structures

In structural design and analysis, reliability (R 0) is conveniently described as the complement of the probability of failure (p f). Reliability is defined as the probability that a structure will not exceed a specified limiting criterion during considered reference period or life of the structure (Ranganathan 1999). In mathematical form it is expressed as,

$$ {R}_0=1-{p}_{\mathrm{f}}. $$
(1)

Let the resistance (capacity or strength) is represented by Cap and the demand (action of the load, i.e., shear force, moment, etc.) is represented by Dem. The objective for the design is to achieve an acceptable condition, i.e., Cap ≥ Dem. Hence, the probability of failure is written as the probability of the case when Dem > Cap, in mathematical form,

$$ {p}_{\mathrm{f}}= P\left( \mathit{Dem}> \mathit{Cap}\right).$$
(2)

Considering Cap and Dem both as random variables, the probability of failure can be computed as (Ranganathan 1999),

$$ {p}_{\mathrm{f}}=1-{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{f}_1(\mathit{Cap}){F}_2(\mathit{Cap})\; d(\mathit{Cap})}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{f}_2(\mathit{Dem}){F}_1(\mathit{Dem})\; d(\mathit{Dem})} $$
(3)

where, f 1 and f 2 denote the probability density functions (PDF), and F 1 and F 2 denote the cumulative distribution functions (CFD) of the capacity and demand, respectively. However, in real life situations, obtaining solution of such integrals may be intractable. Moreover, many times proper identification of the PDF of the demand or capacity may not even be possible. Therefore, several numerical techniques are developed over the years to estimate the reliability of structures when a closed form analytical solution is unavailable.

2.1 First Order Second Moment (FOSM) Theory

The reliability evaluation procedures are divided into three levels (Ranganathan 1999), namely (1) 1st level procedure, where the reliability is defined simply in terms of safety factors; (2) 2nd level procedure, where safety checks are carried out at the selected points on the failure boundary or the failure surface to estimate the reliability; and (3) 3rd level procedure, also known as higher order reliability analysis, where all the points on the failure surface or failure boundary are considered. The higher order reliability analyses are capable of estimating the reliability of structures most accurately. Nevertheless, the FOSM theory, which is categorized as 2nd level procedure, is widely used for its simplicity.

In the FOSM theory, the failure function [F(Cap, Dem)] is defined in terms of the safety margin (S m) as,

$$ {S}_{\mathrm{m}}= F\left( \mathit{Cap}, \mathit{Dem}\right)= \mathit{Cap}- \mathit{Dem}. $$
(4)

The reliability is estimated in terms of first and second moments of the failure function (i.e., mean and variance of S m). It is also to be noted that when F(Cap, Dem) is a nonlinear function, made up of several basic input variables, then the first order approximation is used to evaluate the mean and variance of S m. Because of this reason, the method is known as the first order second moment (FOSM) theory. In this theory, the reliability is commonly expressed in the form of reliability index (β). Cornell (1969) defined the reliability in terms of the reliability index (β) as the ratio of the mean \( \left({\mu}_{\mathrm{S}_{\mathrm{m}}}\right) \) to the standard deviation \( \left({\sigma}_{\mathrm{S}_{\mathrm{m}}}\right) \) of the safety margin as,

$$ \beta =\frac{\mu_{\mathrm{S}_{\mathrm{m}}}}{\sigma_{\mathrm{S}_{\mathrm{m}}}}.$$
(5)

The probability of failure can be computed as,

$$ {p}_{\mathrm{f}}={\varPhi}^{-1}\left(-\beta \right) $$
(6)

where, Φ − 1 is the inverse of the standard normal density function. For normally distributed random variables and linear failure function, this relation (Eq. (6)) calculates accurate probability of failure. Moreover, this relation gives a preliminary estimation of probability of failure for other types of distributions as well.

2.2 Monte Carlo (MC) Simulation

In many cases, the probability of failure determined from the reliability index, using the FOSM theory, provides a reasonable estimate. However, the actual distribution of the demand may not be sufficiently represented by the first and second moment, i.e., the mean and standard deviation. In those cases, in the absence of the higher order reliability theory, the MC simulation is invariably used for variety of reliability analysis problems. Although this technique is not computationally efficient, with the help of the modern computing facilities the MC simulation is a widely used technique in risk and reliability engineering. In the MC simulation, a large number of sample points are generated from the predefined probability distributions of input random variables. Failure function is formulated in terms of the demand and capacity, which consists of several input random variables. Response of the structure is obtained deterministically for each set of the input variables to check the safety. The reliability analysis procedure using the MC simulation is summarized in the following steps.

  1. 1.

    The failure function (F) is written in terms of n input random variables (X i) as,

    $$ F= f\left({X}_1,{X}_2,{X}_3,\dots, {X}_{\rm n}\right) $$
    (7)

    where, the probability distribution of each random variable is known.

  1. 2.

    Realization (x ik) of each input variable is generated from its distribution, and by substituting it in Eq. (7), N sim number of realizations of F is obtained. The k th realization, F k is obtained as,

    $$ {F}_{\rm k}= f\left({x}_{1 {\rm k}},{x}_{2 {\rm k}},{x}_{3 {\rm k}},\dots, {x}_{\rm nk}\right) $$
    (8)

    where, k takes the values from 1 to N sim.

  1. 3.

    The failure criterion is checked for each set of input random variables, and the cases for which the failure occurs are counted, say N fail. Then the probability of failure is computed as,

    $$ {p}_{\mathrm{f}}=\frac{N_{\mathrm{f}\mathrm{ail}}}{N_{\mathrm{sim}}}. $$
    (9)

Total number of the simulations (i.e., N sim) depends on the required accuracy and the size of the problem. If sufficient computational facilities are available, and the probability distributions of the input random variables are known, then practically any reliability problem can be solved by the MC simulation.

Herein, the probability of failure (p f) of base-isolated liquid storage tank is estimated from the reliability index (β) using the FOSM theory and compared with the probability of failure obtained using the MC simulation. Based on the distribution and statistics of the input random variables, the mean and standard deviation of the demand are computed using the gPC expansion technique. Subsequently, the reliability index for the base-isolated liquid storage tank is computed and the probability of failure is estimated. However, when the failure function is not linearly related to the input parameters, and not normally distributed, the FOSM theory may not provide accurate estimate of the probability of failure. In such cases, it is necessary to compare the probability of failure estimated using the FOSM theory with the probability of failure evaluated using other higher order reliability theory or the MC simulation. Here, the MC simulation is carried out using the same distributions and statistics of the input random variables, as considered in the gPC expansion technique, to evaluate and compare the probability of failure.

3 Reliability Analysis of Base-Isolated Structures

Stochastic response and the reliability analysis of base-isolated structures have received considerable attention among the research community (Jangid and Datta 1995b; Pagnini and Solari 1999; Jangid 2000; Jacob et al. 2013). To study the reliability problem of a hysteretic system, Spencer and Bergman (1985) developed a procedure using Petrov-Galerkin finite element method for the determination of statistical moments. They compared the statistical moments obtained using the proposed method with direct MC simulation, however the reliability evaluation was not carried out. Pradlwarter and Schuëller (1998) carried out reliability analysis of multi-degree-of-freedom (MDOF) system equipped with hysteresis devices such as isolators, dampers, etc. They used direct MC simulation to compute the reliability and proposed a controlled MC simulation to reduce the sample sizes with better accuracy of the reliability estimate. Scruggs et al. (2006) proposed an optimization procedure for base isolation system with active controller, considering the system reliability under stochastic earthquake. They optimized the probability of failure considering the uncertain earthquake model parameters. Mishra et al. (2013) presented a reliability-based design optimization (RBDO) procedure considering the uncertainty in the earthquake parameters as well as in the isolation system. They observed significantly higher probability of failure in case of the RBDO approach, as compared to the deterministic approach, due to uncertainty involved in the system parameters. They concluded that the optimum design parameters obtained using deterministic approach overestimate the structural reliability.

Buildings remained the major concern while analyzing the reliability of base-isolated structures in most of the previous research works. However, only limited studies reported the reliability analysis of liquid storage tanks. Mishra and Chakraborty (2010) investigated the effect of uncertainties in the isolator parameters on the seismic reliability of tower mounted base-isolated liquid storage tanks. They concluded that the uncertainty in the earthquake motion dominates the variability in the reliability; however, the uncertainties in the isolator parameters also play a crucial role in the reliability estimation. Saha et al. (2013c) presented stochastic analysis of ground-supported base-isolated liquid storage tanks considering the uncertain isolator parameters under random base excitation. They used generalized polynomial chaos (gPC) expansion technique to consider the uncertainty in isolation parameters and base excitation, and compared the probability distributions of the peak response quantities. They demonstrated the necessity of considering the uncertainty in the dynamic analysis of fixed-base and base-isolated liquid storage tanks.

4 Failure of Steel Liquid Storage Tank

Selection of failure mechanism of the structure and defining the limiting criteria are important steps in any reliability analysis. Typical earthquake induced failures observed in cylindrical steel liquid storage tanks are: (1) buckling of the tank wall, (2) rupture of tank wall in hoop tension, (3) tank roof failure, (4) sliding and up-lifting of tank base, (5) failure of base plate, (6) anchorage failure, and (7) failure of connecting accessories.

Out of all the above-mentioned failure modes the buckling of tank wall received most attention in the research works, and the international guidelines differ in many ways to address this issue. Buckling of liquid filled thin walled steel tanks, under horizontal component of earthquake, is categorized into two types (EN 1998-4 2006), namely (1) elastic buckling and (2) elasto-plastic buckling. The elastic buckling is also referred to as diamond buckling which mainly occurs under severe vertical stress induced by the overturning moment and other vertical loads. When diamond shape buckling occurs in a tank wall, the buckled region generally bends inward, forming several wrinkles in circumferential direction on the wall surface (Fig. 1a). This kind of buckling mainly occurs when the hoop tension in the tank wall is less. Such type of tank wall buckling is more common in case of slender tank, i.e., height to radius ratio is high (Niwa and Clough 1982).

Fig. 1
figure 1

(a) Diamond shape and (b) elephant foot buckling of tanks (source: NISEE e-Library)

Full size image

Outward bulging of the tank wall under the horizontal earthquake excitation is known as elephant foot buckling (Fig. 1b). Niwa and Clough (1982) concluded from their experimental studies that elephant foot buckling occurs due to the combined action of hoop stress and axial compressive stress. When the axial compressive stress exceeded the axial buckling stress, at the same time the hoop stress was close to the material yield strength, elephant foot buckling was observed (Niwa and Clough 1982). Later, Akiyama (1992) also validated this observation by conducting a set of experiments on steel tanks. Elephant foot buckling was predominantly observed in broad tanks, i.e., for low height to radius ratio (Hamdan 2000). Such kind of tank wall buckling is classified as elasto-plastic buckling in EN 1998-4 (2006).

Some design guidelines relate the buckling of the tank wall to the axial compression developed due to the overturning moment (AWWA D-100-96 1996; API 650 2007). However, studies are reported which relate the buckling of the tank wall to the base shear in horizontal direction. Okada et al. (1995) presented a method to evaluate the effect of the shear force on the elasto-plastic buckling of cylindrical tank. Tsukimori (1996) examined the effect of interaction between the shear and bending loads on the buckling of thin cylindrical shell. Some of the present tank design guidelines provide checks for the shear buckling, along with the axial buckling (AIJ 2010).

The elastic buckling stress of a thin cylindrical tank is given by Timoshenko and Gere (1961),

$$ {\sigma}_{\mathrm{cr}}=\frac{1}{{\left[3\left(1-{\nu}^2\right)\right]}^{0.5}}\frac{E_{\mathrm{s}}{t}_{\mathrm{s}}}{R} $$
(10)

where, the Poisson’s ratio and modulus of elasticity of the tank wall material are denoted by E s and ν, respectively; t s is the tank wall thickness; and R is the radius of the tank wall. For steel tank wall (ν = 0.3) the expression becomes,

$$ {\sigma}_{\mathrm{cr}}=0.605\frac{E_{\mathrm{s}}{t}_{\mathrm{s}}}{R}.$$
(11)

The elastic shear buckling stress is given by,

$$ {\tau}_{\mathrm{cr}}=0.07708\frac{\pi^2{E}_{\mathrm{s}}}{{\left(1-{\nu}^2\right)}^{5}\!\left/ \!{8}\right.}\sqrt{\frac{H}{R}} {\left(\frac{R}{t_{\mathrm{s}}}\right)}^{-{5}\!\left/ \!{4}\right.} $$
(12)

where, H is height of the liquid column. The limiting overturning moment (M b,cr) and base shear (V b,cr), based on the elastic buckling stresses, are respectively written as (Okada et al. 1995),

$$ {M}_{\mathrm{b},\mathrm{cr}}={\sigma}_{\mathrm{cr}}\pi {R}^2{t}_{\mathrm{s}}$$
(13)

and

$$ {V}_{\mathrm{b},\mathrm{cr}}={\tau}_{\mathrm{cr}}\pi R{t}_{\mathrm{s}}.$$
(14)

5 Modeling of Base-Isolated Liquid Storage Tank

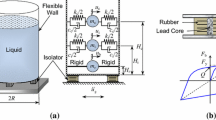
Appropriate modeling of base-isolated liquid storage tank is essential for dynamic analysis and response evaluation. Several international codes and design guidelines (AWWA D-100-96 1996; EN 1998-4 2006; API 650 2007; AIJ 2010) recommend the lumped mass mechanical analog to model cylindrical liquid storage tank. The lumped mass mechanical analog is also recommended for seismic analysis of liquid storage tanks using response spectrum approach. Simplified representation of the liquid storage tank is always required for using it routinely in the design offices. Haroun and Housner (1981) proposed a mechanical analog, with three degrees-of-freedom (DOF), for the dynamic analysis of liquid storage tanks. As per the analog, the liquid column is discretized into three lumped masses, namely (1) convective mass (m c), lumped at height H c above the base; (2) impulsive mass (m i), lumped at height H i above the base; and (3) rigid mass (m r), lumped at height H r above the base. The lumped mass model of a base-isolated liquid storage tank is shown in Fig. 2a. The lumped masses (m c, m i, and m r) are computed from the total mass of the liquid column (=πR 2 H), neglecting the mass of the tank wall. The deterministic dynamic behavior of liquid storage tanks, using this model, was validated with experimental results by Haroun (1983b). The model was widely used in earlier research works (Shrimali and Jangid 2002, 2004; Saha et al. 2013b) for the dynamic analyses of base-isolated liquid storage tanks. Here, laminated rubber bearing (LRB) is considered as the isolator in the base-isolated liquid storage tank system. The linear force-deformation behavior of the LRB is shown in Fig. 2b, where F b is the restoring force and x b is the isolator level displacement, relative to the ground.

Fig. 2
figure 2

(a) Model of base-isolated liquid storage tank and (b) laminated rubber bearing (LRB) with its force-deformation behavior

Full size image

The matrix form of the equations of motion for the base-isolated liquid storage tank is written as,

$$ \overline{M}\left\{\ddot{X}\right\}+\overline{C}\left\{\dot{X}\right\}+\overline{K}\left\{ X\right\}=-\overline{M}\left\{ r\right\}{\ddot{u}}_{\mathrm{g}} $$
(15)

where, {X} = {x c x i x b}T is the displacement vector; x c = (u c − u b), x i = (u i − u b) and x b = (u b - u g) are the relative displacements of the convective, impulsive, and rigid masses, respectively; and {r} = {0 0 1}T is the influence coefficient vector. Here, u c, u i, and u b represent the absolute displacements of the convective mass, the impulsive mass, and the isolator level, respectively. The uni-directional horizontal base acceleration is denoted by \( {\ddot{u}}_{\mathrm{g}} \). The mass matrix (\( \overline{M} \)), the damping matrix (\( \overline{C} \)), and the stiffness matrix (\( \overline{K} \)) are expressed as follows.

$$ \overline{M}=\left[\begin{array}{ccc} {m}_{\mathrm{c}}& 0& {m}_{\mathrm{c}} \\ {} 0& {m}_{\mathrm{i}}& {m}_{\mathrm{i}} \\ {} {m}_{\mathrm{c}}& {m}_{\mathrm{i}} & M \end{array}\right] $$
(16)

where, M = m c + m i + m r.

$$ \overline{C}=\left[\begin{array}{ccc} {c}_{\mathrm{c}}& 0& 0 \\ {} 0& {c}_{\mathrm{i}}& 0 \\ {} 0& 0& {c}_{\mathrm{b}}\end{array}\right] $$
(17)

where, c c, c i, and c b are damping of the convective mass, the impulsive mass, and the base isolator, respectively.

$$ \overline{K}=\left[\begin{array}{ccc} {k}_{\mathrm{c}} & 0 & 0 \\ 0 & {k}_{\mathrm{i}} & 0 \\ 0 & 0 & {k}_{\mathrm{b}} \end{array}\right] $$
(18)

where, k c, k i, and k b are stiffness of the convective mass, the impulsive mass, and the base isolator, respectively. The LRB is characterized by its viscous damping (c b = 4πMξ b/T b), where ξ b is the damping ratio and isolation time period \( \left({T}_{\mathrm{b}}=2\pi \sqrt{M/{k}_{\mathrm{b}}}\right) \).

Saha et al. (2013c) presented stochastic modeling of the base-isolated liquid storage tank using the gPC expansion technique. For simplicity, the base excitation is represented by a uni-directional sinusoidal acceleration input with random amplitude and frequency. Apart from the base excitation, the randomness in the characteristic parameters of the isolator is also considered in the stochastic modeling of the base-isolated liquid storage tank. Considering the uncertain parameters, the dynamic equations of motion (Eq. (15)) are rewritten in the matrix form as,

$$ \overline{M}\left\{\ddot{X}\left( t,\overline{\zeta}\right)\right\}+\overline{C}\left({\zeta}_{\rm c}\right)\left\{\dot{X}\left( t,\overline{\zeta}\right)\right\}+\overline{K}\left({\zeta}_{\rm k}\right)\left\{ X\left( t,\overline{\zeta}\right)\right\}=-\overline{M}\left\{ r\right\}{\ddot{u}}_{\rm g}\left( t,{\overline{\zeta}}_{\rm g}\right) $$
(19)

where, \( \left\{ X\left( t,\overline{\zeta}\right)\right\} \) is the unknown displacement vector which is random in nature; ζ c and ζ k represent the randomness in the damping and stiffness of the base-isolation system, respectively; and the vector \( {\overline{\zeta}}_{\rm g} \) represents the randomness in the base excitation. The vector \( \overline{\zeta} \) represents all the random variables involved in the system response.

6 Solution of the Stochastic Equations of Motion

Truncated gPC expansions are used to represent the uncertain damping and stiffness matrices as given by Saha et al. (2013c).

$$ \overline{C}\left({\overline{\zeta}}_{\rm c}\right)={\displaystyle \sum_{{i}_1=0}^{N_1}{\overline{c}}_{{i}_1}{\psi}_{{\rm i}_1}}\left({\zeta}_{\rm c}\right)$$
(20)
$$ \overline{K}\left({\overline{\zeta}}_{\rm k}\right)={\displaystyle \sum_{{i}_2=0}^{N_2}{\overline{k}}_{{i}_2}{\psi}_{{\rm i}_2}}\left({\zeta}_{\rm k}\right) $$
(21)

where, \( {\overline{c}}_{\mathrm{i}_1} \) and \( {\overline{k}}_{\mathrm{i}_2} \) are deterministic unknown coefficient matrices; \( {\psi}_{\mathrm{i}_1}\left({\zeta}_\mathrm{c}\right) \) and \( {\psi}_{\mathrm{i}_2}\left({\zeta}_\mathrm{k}\right) \) are the stochastic basis functions for damping and stiffness, respectively. Similarly, the random base acceleration and the unknown displacement vector are modeled as random fields and represented by the truncated gPC expansions as,

$$ {\ddot{u}}_\mathrm{g}\left( t,{\overline{\zeta}}_\mathrm{g}\right)={\displaystyle \sum_{{i}_3=0}^{N_3}{u_\mathrm{g}}_{\mathrm{i}_3}(t){\psi}_{{i}_3}}\left({\overline{\zeta}}_\mathrm{g}\right)$$
(22)
$$ \left\{ x\left( t,\overline{\zeta}\right)\right\}={\displaystyle \sum_{{i}_4=0}^{N_4}{\overline{x}}_{\mathrm{i}_4}(t){\psi}_{{i}_4}}\left(\overline{\zeta}\right) $$
(23)

where, at a particular time instant, \( {u}_{\mathrm{g}_{\mathrm{i}_3}}(t) \) represents the deterministic unknown base excitation coefficient, and \( {\overline{x}}_{\mathrm{i}_4}(t) \) represents the deterministic unknown response coefficient vector. The stochastic basis functions for the excitation and the response are defined by \( {\psi}_{\mathrm{i}_3}\left({\overline{\zeta}}_\mathrm{g}\right) \) and \( {\psi}_{\mathrm{i}_4}\left(\overline{\zeta}\right) \), respectively. Here, the uncertain stiffness (k b) of the LRB is represented in terms of the isolation time period (T b). The base excitation in horizontal direction is assumed as sinusoidal acceleration as,

$$ {\ddot{u}}_\mathrm{g}\left( t,{\overline{\zeta}}_\mathrm{g}\right)={A}_{\mathrm{m}}\left({\zeta}_\mathrm{a}\right) \sin \left[\omega \left({\zeta}_{\omega}\right) t\right] $$
(24)

where, random amplitude and frequency of the base excitation is denoted by A m(ζ a) and ω(ζ ω ), respectively.

Substitution of these expansions (Eqs. 20–23) in Eq. (19) yields an approximated stochastic form of the system equations. The stochastic approximation error, denoted by \( \varepsilon \left( t,\overline{\zeta}\right) \), is defined as,

$$ \begin{aligned}[b]\varepsilon \left( t,\overline{\zeta}\right)&=\overline{M}{\displaystyle \sum_{{i}_4=0}^{N_4}{\overline{\ddot{x}}}_{\mathrm{i}_4}(t)}{\psi}_{\mathrm{i}_4}\left(\overline{\zeta}\right)+{\displaystyle \sum_{{i}_1=0}^{N_1}{\overline{c}}_{\mathrm{i}_1}}{\psi}_{\mathrm{i}_1}\left({\zeta}_\mathrm{c}\right){\displaystyle \sum_{{i}_4=0}^{N_4}{\overline{\dot{x}}}_{\mathrm{i}_4}(t)}{\psi}_{\mathrm{i}_4}\left(\overline{\zeta}\right)\nonumber\\ {}&\quad+{\displaystyle \sum_{{i}_2=0}^{N_2}{\overline{k}}_{\mathrm{i}_2}}{\psi}_{\mathrm{i}_2}\left({\zeta}_\mathrm{k}\right){\displaystyle \sum_{{i}_4=0}^{N_4}{\overline{x}}_{\mathrm{i}_4}(t)}{\psi}_{\mathrm{i}_4}\left(\overline{\zeta}\right)+\overline{M}\left\{ r\right\}{\displaystyle \sum_{{i}_3=0}^{N_3}{u}_{\mathrm{g}_{\mathrm{i}_3}}(t)}{\psi}_{\mathrm{i}_3}\left({\overline{\zeta}}_\mathrm{g}\right).\end{aligned} $$
(25)

To solve the stochastic equation of motion, the stochastic basis function \( \psi \left(\overline{\zeta}\right) \) of each input random variable must be known or defined.

Once the \( \psi \left(\overline{\zeta}\right)\mathrm{s}\) are defined, the solution of the equations is reduced to the determination of the unknown displacement vector \( {\overline{x}}_{\mathrm{i}_4}(t) \) by minimizing the error \( \varepsilon \left( t,\overline{\zeta}\right) \). The error is deterministically equated to zero at specific points using a nonintrusive method. The nonintrusive method is same as the method of collocation points. The collocation points are generally chosen from the roots of the similar polynomials as used for the basis function. When more numbers of collocation points are required, roots of the higher order polynomials are chosen.

The response quantities of the base-isolated liquid storage tank, under base excitation in horizontal direction, are considered as the base shear (V b) and the overturning moment (M b). Deterministically, the base shear and the overturning moment are computed as,

$$ {V}_{\mathrm{b}}={m}_{\mathrm{c}}{\ddot{u}}_{\mathrm{c}}+{m}_{\mathrm{i}}{\ddot{u}}_{\mathrm{i}}+{m}_{\mathrm{r}}{\ddot{u}}_{\mathrm{b}} $$
(26)

and

$$ {M}_{\mathrm{b}}=\left({m}_{\mathrm{c}}{\ddot{u}}_{\mathrm{c}}\right){H}_{\mathrm{c}}+\left({m}_{\mathrm{i}}{\ddot{u}}_{\mathrm{i}}\right){H}_{\mathrm{i}}+\left({m}_{\mathrm{r}}{\ddot{u}}_{\mathrm{b}}\right){H}_{\mathrm{r}}.$$
(27)

Here, all the input random variables are assumed to be normally distributed and uncorrelated. Using 3rd order Hermite polynomial, the uncertain response quantities (V b and M b) are written in the following forms (Saha et al. 2013c).

$$ {V}_{\mathrm{b}}\left(\zeta, t\right)={y}_0^{\mathrm{v}}(t)+{y}_1^{\mathrm{v}}(t)\zeta +{y}_2^{\mathrm{v}}(t)\left({\zeta}^2-1\right)+{y}_3^{\mathrm{v}}(t)\left({\zeta}^3-3\zeta \right)$$
(28)

and

$$ {M}_{\mathrm{b}}\left(\zeta, t\right)={y}_0^{\mathrm{m}}(t)+{y}_1^{\mathrm{m}}(t)\zeta +{y}_2^{\mathrm{m}}(t)\left({\zeta}^2-1\right)+{y}_3^{\mathrm{m}}(t)\left({\zeta}^3-3\zeta \right) $$
(29)

where, y vi (t) and y mi (t) are the unknown deterministic coefficients at each time step corresponding to the base shear and the overturning moment, respectively.

Once the polynomial coefficients are determined, they are substituted back into Eqs. (28) and (29). Now, the response of the base-isolated liquid storage tank is expressed in terms of the uncertain input random variables, at each time step, and the response statistics are obtained. The mean and standard deviation of the base shear (\( {\mu}_{V_{\mathrm{b}}} \) and \( {\sigma}_{V_{\mathrm{b}}} \)) are calculated using the following equations (Sepahvand et al. 2010).

$$ {\mu}_{V_{\mathrm{b}}}={y}_0^{\mathrm{v}} $$
(30)

and

$$ {\sigma}_{V_{\mathrm{b}}}=\sqrt{{\displaystyle \sum_{{i}=1}^3{\left({y}_\mathrm{i}^{\mathrm{v}}\right)}^2{h}_\mathrm{i}^2}} $$
(31)

where, h 2i is the norm of the polynomial. For one-dimensional Hermite polynomial, with normally distributed uncertain parameters, h 21  = 1, h 22  = 2 and h 23  = 6.

Table 1 Geometrical and material properties of tanks
Full size table
Table 2 Considered distribution and statistics of input parameters
Full size table

Similarly, equations to calculate the mean and standard deviation of the overturning moment (\( {\mu}_{M_{\mathrm{b}}} \) and \( {\sigma}_{M_{\mathrm{b}}} \)) are given as,

$$ {\mu}_{M_{\mathrm{b}}}={y}_0^{\mathrm{m}} $$
(32)

and

$$ {\sigma}_{M_{\mathrm{b}}}=\sqrt{{\displaystyle \sum_{{i}=1}^3{\left({y}_\mathrm{i}^{\mathrm{m}}\right)}^2{h}_\mathrm{i}^2}}. $$
(33)

7 Numerical Studies

The reliability of base-isolated liquid storage tank under base excitation in horizontal direction is assessed through analysis of ground-supported cylindrical steel tanks with different slenderness ratio (S = H/R). The geometrical and material properties of the broad and slender tanks are summarized in Table 1, where ρ s and ρ w denote the mass density of the tank wall material and the liquid, respectively. The damping, corresponding to the convective mass and the impulsive mass, is assumed as 0.5 % and 2 %, respectively (Haroun 1983b). The type of distribution and statistics of the input parameters, considered in the present study, are presented in Table 2. The duration of the base excitation is considered as 15 s, with time increment 0.02 s, whereas the amplitude and the frequency are considered uncertain (Table 2). The uncertain parameters, which are assumed to be independent and normally distributed, are represented by the Hermite polynomial. Galerkin projection technique is used to represent the input parameters in terms of their mean and standard deviation. Nine collocation points (0, ±0.742, ±2.334, ±1.3556, and ±2.875) are chosen from the roots of the 4th and 5th order Hermite polynomials. Nine sets of the uncertain input parameters are generated from these collocation points using the Galerkin projection technique. Deterministic analyses are carried out, by numerically solving Eq. (15) using Newmark’s-β method, to obtain the response of the base-isolated liquid storage tanks for the nine sets of the uncertain input parameters. Regression analysis is performed to determine the unknown coefficients of the base shear and the overturning moment (Eqs. (28) and (29)).

Figure 3 shows the time histories of the polynomial coefficients for the peak base shear and peak overturning moment, both for the broad and slender tank configurations. The coefficient y 0 represents the mean, whereas the coefficient y 1 largely contributes to the deviation of the response from the mean response. Convergence in the response calculation using the gPC expansion technique is achieved when the higher order coefficients (i.e., y 2 and y 3) are smaller in amplitude as compared to y 0 and y 1. If desired convergence in the response calculation is not achieved, then higher order approximating polynomial is to be considered. Moreover, large amplitudes of the higher order coefficients also signify the nonlinear relation between the response and the input parameters. It is observed that the coefficients y 0 and y 1 are comparable in both the response quantities for the broad and slender tank configurations. This shows the significance of the considering uncertainty in the input parameters for the dynamic analysis of base-isolated liquid storage tanks. Moreover, the lower contributions from the higher order coefficients, y 2 and y 3, indicate that even with 3rd order Hermite polynomial, convergence of the response calculation can be achieved in the gPC expansion technique. Nevertheless, nonzero y 2 and y 3 indicate the nonlinear relation between the peak response quantities of the base-isolated liquid storage tanks and the considered input parameters.

Fig. 3
figure 3

Time history of the gPC expansion coefficients

Full size image

7.1 Computation of Reliability Index (β)

The peak of the mean base shear (\( {\mu}_{V_{\mathrm{b}}} \)) and mean overturning moment (\( {\mu}_{M_{\mathrm{b}}} \)) are determined from the time history of the response quantities, and the respective standard deviations (\( {\sigma}_{V_{\mathrm{b}}} \) and \( {\sigma}_{M_{\mathrm{b}}} \)) are computed at the corresponding time instant. The mean and standard deviation of the response quantities, computed using the gPC expansion technique, and the corresponding limiting values (capacity) are presented in Table 3. The limiting values are computed from Eqs. (13) and (14). The response quantities and the capacities are presented in normalized form with respect to the total weight (W = Mg), where g is the gravitational acceleration. The safety margin is expressed in terms of two criteria based on the limiting base shear and limiting overturning moment as,

Table 3 Statistics of tank response quantities using gPC expansion
Full size table
$$ {S}_{\mathrm{m}}={V}_{\mathrm{b},\mathrm{cr}}-{V}_{\mathrm{b}} $$
(34a)

or

$$ {S}_{\mathrm{m}}={M}_{\mathrm{b},\mathrm{cr}}-{M}_{\mathrm{b}}. $$
(34b)

The limiting base shear (V b,cr) and limiting overturning moment (M b,cr) are considered as deterministic, therefore the mean of the safety margin \( \left({\mu}_{S_{\mathrm{m}}}\right) \) is computed as,

$$ {\mu}_{S_{\mathrm{m}}}={V}_{\mathrm{b},\mathrm{cr}}-{\mu}_{V_{\mathrm{b}}} $$
(35a)

or

$$ {\mu}_{S_{\mathrm{m}}}={M}_{\mathrm{b},\mathrm{cr}}-{\mu}_{M_{\mathrm{b}}}. $$
(35b)

The standard deviation of the safety margin \( \left({\sigma}_{S_{\mathrm{m}}}\right) \) is given by,

$$ {\sigma}_{S_{\mathrm{m}}}={\sigma}_{V_{\mathrm{b}}} $$
(36a)

or

$$ {\sigma}_{S_{\mathrm{m}}}={\sigma}_{M_{\mathrm{b}}}.$$
(36b)

Once the first and second moment (i.e., the mean and standard deviation) of the safety margin are known, the reliability index (β) is computed using Eq. (5).

The reliability indices for the broad and slender tanks are computed and presented in Table 4. The reliability index corresponding to the exceedance of the base shear is considerably low which results in a high probability of failure in both the broad and slender tank configurations. However, the reliability index corresponding to the exceedance of the overturning moment is observed significantly high. Nevertheless, the probability of failure, under base excitation in horizontal direction, is more in slender tank as compared to the broad tank.

Table 4 Reliability index (β) and probability of failure (p f) using FOSM theory
Full size table

7.2 Computation of Probability of Failure (p f) using MC Simulation

A set of realizations is generated from the considered distribution of the input parameters, as given in Table 2. For each set of the input parameters, the tank model is analyzed deterministically to obtain the peak response quantities. The peak response quantities (V b and M b) are then compared with the limiting base shear (V b,cr) and limiting overturning moment (M b,cr). The total number of the simulations, when the demand exceeds the capacity is counted as N fail. The probability of failure is computed as the ratio between the numbers of failures to the total number of simulations (Eq. (9)). The number of simulations plays a crucial role in accurate estimation of the probability of failure; hence, a convergence study is carried out to find out the sufficient number of simulations. The probabilities of failure (p f) with respect to the number of simulations are presented in Table 5. To investigate the critical failure mode, number of failures due to exceedance of the limiting base share (n v) and limiting overturning moment (n m) are also counted and presented in Table 5. It is observed from Table 5 that the base shear criterion governs the failure in both the broad and slender tank configurations. Figure 4 also shows the convergence of the probability of failure with number of simulations. It is observed that with 10,000 simulations, estimation of the probability of failure converges for both broad and slender tank configurations. Further, it is observed that the probability of failure (0.0008), estimated using the FOSM theory for broad tank, is much lesser as compared to the probability of failure (0.0826) obtained from the MC simulations. However for slender tank, probability of failure estimated using the FOSM theory (0.508) is similar to the probability of failure obtained from the MC simulations.

Table 5 Convergence of probability of failure (p f) using MC simulation
Full size table
Fig. 4
figure 4

Convergence of probability of failure using (p f) MC simulation

Full size image

To explain this observation, the probability distribution of the peak base shear is plotted from the peak response computed using 50,000 MC simulations and compared with the distribution obtained through the gPC expansion technique. To obtain the probability distribution of the base shear using the gPC expansion, 50,000 standard normal variates are generated, and the response time history of the base shear is generated using Eq. (28). Figure 5 shows the comparison of the probability distributions of the base shear for both the broad and slender tank configurations. The limiting base shears (capacities) of the broad and slender tanks are also plotted for comparison purpose. It is observed that the overall distribution of the peak base shear, obtained using the gPC expansion technique closely matches to that predicted by the MC simulation. The computed limiting base shear (capacity) of the broad tank is significantly higher than the peak base shear demand, providing a higher safety margin. Furthermore, ordinates of the probability density for the broad tank, obtained from the MC simulation, differ from that obtained using the gPC expansion technique, specifically near the peak region and beyond the base shear capacity. Beyond the base shear capacity, the MC simulation distribution curve has considerably lower ordinates, as compared to the distribution curve using the gPC expansion technique. As the peak responses, greater than the capacity, are only considered in the computation, the deviation in the distribution in this region significantly influences the failure probability estimation. Hence, significant difference in the probability of failure estimation, using the FOSM theory and the MC simulation, for the broad tank, is observed.

Fig. 5
figure 5

Comparison of capacity and peak base shear distribution using gPC expansion and MC simulation

Full size image

On the other hand, in case of the slender tank the probability distributions of the peak base shear, obtained using the FOSM theory and the MC simulation, are matching closely near the peak region. Moreover, the base shear capacity of the slender tank is close to the demand with lesser safety margin. Hence, the marginal deviation in the peak response distribution, beyond the capacity, does not significantly increase the numbers of failures due to base shear exceedance. Owing to this fact, similar failure probability estimations are obtained, by the FOSM theory using the gPC expansion technique and the MC simulation, for the slender tank. It is concluded that the accuracy in estimating the probability of failure, for a base-isolated liquid storage tank, largely depends on the actual distribution of the peak response quantities and the available safety margin. Probability of failure estimated from the mean and standard deviation, using the FOSM theory, may not provide reasonable accuracy for base-isolated liquid storage tanks. Therefore, only the MC simulation is used to estimate the probability of failure in the following studies.

7.3 Effect of Individual Parameter Uncertainty on Probability of Failure (p f)

The effect of uncertainty in each parameter on the probability of failure of the base-isolated liquid storage tanks is investigated. The peak response quantities are obtained considering uncertainty in one parameter only at a time, while the other parameters are considered deterministic. The values of each uncertain parameter, taken in the analysis, are presented in Table 2. The mean values are taken as the deterministic inputs, while the standard deviations of the parameters are taken as zero, except for the parameter under consideration. The MC simulation is used to obtain the probability of failure (p f) with 10,000 realizations of the input variables. The number of simulations is considered 10,000 to avoid unnecessary computational effort since reasonable convergence of the probability of failure (p f) is observed in Fig. 4. Table 6 presents the variation of the probability of failure with respect to the individual uncertain parameters. It is observed that the effect of the individual uncertain parameters is significant on the probability of failure (p f) of the tanks. It is also observed that for the broad tank, probability of failure, estimated considering uncertainty only in the isolation damping, is lower as compared to the probability of failure when uncertainty is considered in the other input parameters. However for the slender tank, probability of failure, estimated considering uncertainty only in the isolation damping, is higher as compared to the probability of failure when uncertainty is considered in the other input parameters.

Table 6 Influence of individual uncertain parameter on probability of failure (p f) using MC simulation
Full size table

To explain this disparity, the distribution of the peak base shear is plotted in Fig. 6 for broad and slender tank configurations. It is observed that the simulated values of the peak base shear are distributed around the deterministic peak value (0.098 W). However, the effect of the uncertain damping is insignificant on the distribution of the peak base shear, and the simulated peak responses are distributed within a narrow band. For the broad tank, base shear capacity (0.19 W) is considerably higher than the mean peak base shear (0.099 W) when uncertainty is considered only in the isolation damping. Therefore, no failure is observed in case of the broad tank. However for the slender tank, the base shear capacity is same as the deterministic peak base shear (0.11 W). The maximum probability density of the peak base shear (with the mean value as 0.112 W) is also observed around the deterministic value for the slender tank when the uncertainty is considered only in the isolation damping. With marginal variation in the isolation damping, most of the peak responses exceed the capacity. Consequently, the probability of failure in case of the uncertain damping is evaluated to be significantly higher in case of the slender tank. Therefore, it is concluded that when the capacity is significantly more than the demand, the effect of uncertainty in the isolation damping is negligible. However, when the demand is marginally more than the capacity, uncertainty in the isolation damping significantly affects probability of failure.

Fig. 6
figure 6

Comparison of capacity and peak base shear distribution for uncertainty in individual input parameter using MC simulation

Full size image

7.4 Effect of Level of Uncertainty on Probability of Failure (p f)

The effect of the level of uncertainty on the probability of failure of the base-isolated liquid storage tanks is also investigated. The standard deviation, in terms of the % mean, is used to quantify the levels of uncertainty in each parameter. The range of the standard deviation is taken as 5–20 %, with an increment of 5 %, simultaneously for all the input parameters. In Fig. 4, it is shown that 10,000 MC simulations are sufficient to obtain convergence in the evaluation of probability of failure (p f). Therefore, the MC simulation is used to obtain the probability of failure (p f) with 10,000 realizations of the input variables at each level of the uncertainty for broad (S = 0.6) and slender (S = 1.85) tank configurations. Table 7 presents the variation in the probability of failure of the base-isolated broad and slender tanks with increasing level of uncertainty. It is observed that the probability of failure in the broad tank increases with the increase in the uncertainty, whereas the probability of failure in the slender tank decreases with increase in the uncertainty. The distributions of the peak base shear for the broad and slender tank configurations, at different levels of uncertainty in the input parameters, are shown in Fig. 7 to explain the observation. In case of the broad tank, with increase in the uncertainty level, more number of times the peak base shear exceeds the capacity which leads to increase in the probability of failure. It is also observed that with increasing uncertainty level in the isolator and the excitation parameters, the peak region of the peak base shear distribution shifts toward lower value, disturbing the symmetry of the distribution. Moreover, for the slender tank base shear capacity is same as the deterministic peak base shear (0.11 W). Owing to this fact, higher uncertainty in the input parameters leads to lesser numbers of cases, when the base shear demand exceeds the capacity. As a result, lower probability of failure is observed with increasing uncertainty in the input parameters for slender tank. Therefore, it is concluded that the higher level of uncertainties in the isolator and the excitation parameters disturb the symmetry of the peak base shear distribution of base-isolated liquid storage tanks. It is also concluded that the effects of the level of uncertainty on the probability of failure of the base-isolated liquid storage tanks depend on the difference between the designed capacity and demand (or safety margin) for the tanks.

Table 7 Effect of uncertainty level on probability of failure (p f) using MC simulation
Full size table
Fig. 7
figure 7

Comparison of capacity and peak base shear distribution for different levels of uncertainty in input parameters using MC simulation

Full size image

8 Summary and Conclusions

The first order second moment (FOSM) theory, in combination with the generalized polynomial chaos (gPC) expansion technique, is used to determine the reliability of base-isolated liquid storage tanks under base excitation in horizontal direction. The failure of the ground-supported cylindrical steel tanks is defined in terms of the limiting base shear and overturning moment in the elastic range. The effectiveness of the FOSM theory to estimate the seismic reliability is compared with the MC simulation. It is concluded that the accuracy in estimating the probability of failure, for base-isolated liquid storage tank, largely depends on the actual distribution of the peak response quantities and the available safety margin. Probability of failure estimated using the FOSM theory may not provide reasonable accuracy for base-isolated liquid storage tanks. The effect of uncertainties in the isolator and excitation parameters on the probability of failure (p f) of base-isolated liquid storage tanks is also investigated using the MC simulation.

It is concluded that the probability of failure (p f) is more in slender tank as compared to broad tank which indicates that the reliability of broad tank is more than the slender tank. The base shear predominantly governs the failure in both broad and slender tank configurations. The uncertainty of the isolation time period and the base excitation significantly influence the failure probability of the base-isolated broad and slender tanks. Further, it is concluded that when the demand is marginally more than the capacity, failure probability increases with the increase in isolation damping uncertainty. However, when the capacity is significantly more than the demand, the effect of uncertainty in the isolation damping is negligible. It is observed that the higher level of uncertainties in the isolator and excitation parameters disturb the symmetry of the peak base shear distribution of base-isolated liquid storage tanks. It is concluded that the effects of the level of uncertainty on the probability of failure of the base-isolated liquid storage tanks depend on the safety margin available for the tanks.