1 Introduction

Structural failures of liquid storage tanks during past earthquakes, which imparted enormous economic losses, are reported by several researchers (Haroun 1983a; Rammerstorfer et al. 1990; Zama et al. 2012). Therefore, enhancing the protection level of such tanks against devastating earthquake is crucial. Base isolation technique is effective to safeguard such important structures against devastating earthquake (Kelly 1986; Buckle and Mayes 1990; Jangid and Datta 1995; Deb 2004; Ibrahim 2008; Matsagar and Jangid 2008; Mishra and Chakraborty 2013). Several international standards and design guidelines explained the analysis and design of liquid storage tanks (IS: 803 1976; AWWA D-100-96 1996; EN 1998-4 2006; API 650 2007; AIJ 2010). A detailed review of the international standards and design guidelines, on the seismic analysis and design of liquid storage tanks, was carried out by Jaiswal et al. (2007). Analyses of base-isolated liquid storage tanks against seismic loading were carried out by several researchers considering different isolation systems and modeling approaches (Malhotra 1997; Shrimali and Jangid 2002, 2004; Saha et al. 2013a). They concluded that the base isolation is a suitable choice for the structural engineers to enhance seismic performance of liquid storage tanks by reducing the design forces. Nevertheless, uncertainties involved in the base isolation and excitation parameters are necessary to consider while assessing the seismic protection of the base-isolated liquid storage tanks (Saha et al. 2013b).

Seismic fragility curve is a convenient way to represent the seismic performance of a structure, duly considering uncertainties, for a range of seismic intensity levels. Different approaches for seismic fragility analysis of buildings and bridges were addressed in several studies (Choi et al. 2004; Gupta and Manohar 2006; Khan et al. 2006; Padgett et al. 2008; Kim and Leon 2013; Sudret and Mai 2013; Unnikrishnan et al. 2013). HAZUS (1999) assigned five damage states to categorize the failure of ground-supported fixed-base liquid storage tanks under seismic loading, and presented fragility curves corresponding to those damage states. O’rourke and So (2000) developed empirical seismic fragility curves for ground-supported liquid storage tanks based on post-earthquake investigation data. They used logistic regression analysis to derive the fragility curves and compared with the fragility curves presented earlier by HAZUS (1999). They concluded that the observed seismic performance of the tanks was better than the expected performance as specified by HAZUS (1999). Salzano et al. (2003) also evaluated the seismic risk of atmospheric storage tanks using fragility curves developed from observational data. Iervolino et al. (2004) presented a response surface based approach to obtain the seismic fragility of ground-supported unanchored industrial liquid storage tanks. They considered the liquid filling height and the friction at the base as the uncertain random variables while determining the probability of failure using first order reliability method (FORM). Razzaghi and Eshgi (2008) developed fragility curves for cylindrical oil storage tanks considering two different limit states, such as plastic deformation of wall without any elasto-plastic buckling and elephant foot buckling. Non-linear time history analyses were performed to obtain the failure corresponding to the defined limit states at different liquid heights. All the above studies were carried out for seismic fragility analysis of fixed-base liquid storage tanks; however, seismic fragility analysis of base-isolated liquid storage tanks is reported in limited number of studies (Saha et al. 2013c).

In majority of the earlier studies, seismic fragility of liquid storage tanks were obtained through observational data from past earthquakes or using recorded earthquake ground motions following judgmental or empirical approaches. However, the judgmental and empirical approaches to obtain the fragility curves of liquid storage tanks may not be suitable for the sites where observational data or recorded earthquake ground motions are unavailable or insufficient. Moreover, the non-stationarity of the earthquake ground motions, both in time domain and frequency domain, are not adequately addressed in seismic fragility evaluation of liquid storage tanks in earlier research works and in the present design guidelines. Furthermore, the fragility was obtained invariably with respect to the peak ground acceleration (PGA) of the selected recorded earthquakes. However, there is a need to investigate the correlation between the peak response quantities of the base-isolated liquid storage tanks and the earthquake intensity measure (IM) parameters.

Herein, seismic fragility of base-isolated liquid storage tanks is evaluated considering non-stationary stochastic earthquake inputs. Monte Carlo (MC) simulation is used to randomly generate artificial earthquake acceleration time histories based on non-stationary earthquake generation model. Lumped mass mechanical analog is used to model the base-isolated liquid storage tank. The isolation system is considered as lead-rubber bearing with non-linear force–deformation behavior. This type of bearing was first used in New Zealand (NZ), and commonly referred as NZ system (Jangid and Datta 1995; Ibrahim 2008). However, several international design guidelines and standards recommend equivalent linear modeling for the non-linear hysteretic behavior of the lead-rubber bearing (Naeim and Kelly 1999; EN 1998-1 2004; ASCE 7 2010; IBC 2012). Moreover, the characteristic parameters of the isolator and equivalent linearization of the isolator force–deformation behavior influence the seismic response of the base-isolated structures (Matsagar and Jangid 2004), especially in case of the liquid storage tanks (Curadelli 2013; Saha et al. 2014). Therefore, the effect of the equivalent linear modeling of the isolator, on the seismic fragility of base-isolated liquid storage tank, is also investigated in the present study. The specific objectives of the present study are: (1) to investigate the correlation between different earthquake IM parameters and the peak response quantities of the base-isolated liquid storage tanks, (2) to formulate the seismic fragility of the base-isolated liquid storage tanks under non-stationary earthquake ground motion using the MC simulation, (3) to compare the seismic fragility of the base-isolated liquid storage tanks with fixed-base tanks, (4) to study the influence of the important isolator parameters, such as period, damping, yield strength and yield displacement, on the seismic fragility of the base-isolated liquid storage tanks, and (5) to compare the seismic fragility of the base-isolated liquid storage tanks for non-linear hysteretic and equivalent linear modeling of the isolator.

2 Modeling of base-isolated liquid storage tank

Ground-supported liquid storage tanks, cylindrical in geometry having single compartment with no roof cover at the top and with sufficient freeboard, are considered in the present study. Lumped mass mechanical analog, proposed by Haroun and Housner (1981), is used here to model the cylindrical liquid storage tank. In this analog, the liquid column is lumped into three masses as shown in Fig. 1a. The sloshing or convective mass (m c), the impulsive mass (m i), and the rigid mass (m r) are lumped at the heights H c, H i, and H r, respectively, from the tank base. The height and the radius of the liquid column are denoted by H and R, respectively. The lumped masses, and the stiffness attached to them, depend on the total mass of the liquid column (\(= \pi R^{2} H\rho_{\text{w}}\)), thickness and material properties of the tank wall. Here, liquid mass density is denoted by ρw, and mass of the tank wall is neglected being typically less than 5 % of the liquid mass.

Fig. 1
figure 1

a Model of base-isolated liquid storage tank, and b lead-rubber bearing (NZ system) with its force–deformation behavior

Full size image

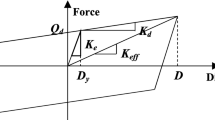
The lead-rubber bearings are placed below the tank base to isolate the tank from the ground. An idealized cross-section and force–deformation behavior of the lead-rubber bearing are shown in Fig. 1b. The isolation bearings, which support the tank, are considered to be placed on rigid foundation. The restoring force in the isolator is denoted by F b, and x b denotes the relative displacement at the isolation level with respect to the ground. The lead-rubber bearing is characterized by four important parameters such as (1) the isolation period (\(T_{\text{b}} = 2\pi \sqrt {{M \mathord{\left/ {\vphantom {M {k_{\text{b}} }}} \right. \kern-0pt} {k_{\text{b}} }}}\)), where M = m c + m i + m r is the total mass of the dynamical system, (2) the isolation damping (\(c_{\text{b}} = {{4\pi \xi_{\text{b}} } \mathord{\left/ {\vphantom {{4\pi \xi_{\text{b}} } {T_{\text{b}} }}} \right. \kern-0pt} {T_{\text{b}} }}\)), where ξb is the isolation damping ratio, (3) the yield strength (F y), and (4) the yield displacement (q). The yield strength is commonly expressed in normalized form as F y/W, where W = Mg is total weight of the base-isolated liquid storage tank, and g is the gravitational acceleration. The non-linear restoring force (F b) in the isolator is expressed by the hysteretic force–deformation relation proposed by Wen (1976). This relationship was used for modeling non-linear base isolation system by several researchers (Constantinou et al. 1990; Tsopelas et al. 1994a; Shrimali and Jangid 2002). As per this model, the restoring force is expressed as,

$$F_{\text{b}} = c_{\text{b}} \dot{x}_{\text{b}} + k_{\text{b}} x_{\text{b}} + \left( {1 - \alpha } \right)F_{\text{y}} Z$$
(1)

where α is the post-yield to pre-yield stiffness ratio, and Z denotes the non-dimensional hysteretic displacement component satisfying the following non-linear first order differential equation.

$$q\dot{Z} = A\dot{x}_{\text{b}} - \beta \left| {\dot{x}_{\text{b}} Z} \right|Z - \tau \dot{x}_{\text{b}} Z^{2}$$
(2)

where the constants A, β, and τ define the non-linear hysteretic loop of the isolator.

The equations of motion for the base-isolated liquid storage tank are written in the matrix form as,

$$\bar{M}\left\{ {\textit{\"{X}}} \right\} + \bar{C}\left\{ {\dot{X}} \right\} + \bar{K}\left\{ X \right\} + \left\{ F \right\} = - \bar{M}\left\{ r \right\}{\ddot{u}}_{\text{g}}$$
(3)

where {X} = {x c x i x b}T is the displacement vector; x c = (u c − u b) and x i = (u i − u b) are the relative displacements of the sloshing and impulsive masses, respectively, and \(\{ r\} = \{ \begin{array}{*{20}c} 0 & 0 & {1\}^{\text{T}} } \\ \end{array}\) is the influence coefficient vector. Here, u c, u i, and u b represent the absolute displacements of the sloshing mass, the impulsive mass, and the isolation level, respectively. The uni-directional horizontal ground acceleration is denoted by \({\ddot{u}}_{\text{g}}\). The hysteretic component of the restoring force is expressed by the vector {F} as,

$$\left\{ F \right\} = \left\{ {\begin{array}{*{20}c} 0 & 0 & {\left( {1 - \alpha } \right)F_{\text{y}} Z} \\ \end{array} } \right\}^{\text{T}} .$$
(4)

It can be noted here that the viscous damping (c b) is attributed to the material properties of the rubber, and the hysteretic component is attributed to the lead-core. Therefore, the term isolation damping ratio (ξb) does not indicate the total damping of the isolation system. This modeling approach for the lead-rubber bearing is considered in several earlier studies on the base-isolated structures (Jangid and Datta 1995; Shrimali and Jangid 2002; Matsagar and Jangid 2003).

The mass matrix (\(\bar{M}\)), the damping matrix (\(\bar{C}\)), and the stiffness matrix (\(\bar{K}\)) are expressed as follows.

$$\bar{M} = \left[ {\begin{array}{*{20}c} {m_{\text{c}} } & 0 & {m_{\text{c}} } \\ 0 & {m_{\text{i}} } & {m_{\text{i}} } \\ {m_{\text{c}} } & {m_{\text{i}} } & M \\ \end{array} } \right]$$
(5)

and

$$\bar{C} = \left[ {\begin{array}{*{20}c} {c_{\text{c}} } & 0 & 0 \\ 0 & {c_{\text{i}} } & 0 \\ 0 & 0 & {c_{\text{b}} } \\ \end{array} } \right]$$
(6)

where c c and c i are the damping coefficients corresponding to the sloshing mass and impulsive mass, respectively.

$$\bar{K} = \left[ {\begin{array}{*{20}c} {k_{\text{c}} } & 0 & 0 \\ 0 & {k_{\text{i}} } & 0 \\ 0 & 0 & {k_{\text{b}} } \\ \end{array} } \right]$$
(7)

where k c, k i, and k b are the stiffness corresponding to the sloshing mass, the impulsive mass, and the base isolator, respectively. The stiffness corresponding to the sloshing mass (k c) and the impulsive mass (k i) are given as,

$$k_{\text{c}} = 1.84(m_{\text{c}} g/R)\tanh (1.84H/R)$$
(8)

and

$$k_{\text{i}} = E_{\text{s}} m_{\text{i}} /\rho_{\text{s}} (P/H)^{2}$$
(9)

where E s and ρs are the modulus of elasticity and the density of the tank wall material, respectively; and P is a dimensionless parameter given by Haroun and Housner (1981) which depends on the tank wall material and thickness (t s). It is worth mentioning that this modeling approach using the lumped mass mechanical analog, to derive the equations of motion for the base-isolated liquid storage tank, was reported in several earlier works (Tsopelas et al. 1994b; Malhotra 1997). The damping coefficients corresponding to the sloshing mass (c c) and the impulsive mass (c i) are given as,

$$c_{\text{c}} = 2\xi_{\text{c}} \sqrt {m_{\text{c}} k_{\text{c}} }$$
(10)

and

$$c_{\text{i}} = 2\xi_{\text{i}} \sqrt {m_{\text{i}} k_{\text{i}} }$$
(11)

where ξc and ξi are the damping ratios corresponding to the sloshing mass and the impulsive mass, respectively.

The hysteretic force vector {F} in Eq. 3 becomes zero when the non-linear force–deformation behavior of the lead-rubber bearing is modeled with equivalent linear model. The damping and stiffness corresponding to the lead-rubber bearing are replaced by the effective damping (\(c_{\text{eff}} = 2\xi_{\text{eff}} \sqrt {Mk_{\text{eff}}}\)) and the effective stiffness (k eff), respectively. The effective damping ratio (ξeff) and the effective stiffness of the lead-rubber bearing are expressed as (Skinner et al. 1993; Naeim and Kelly 1999)

$$\xi_{\text{eff}} = {{2Q(D - q)} \mathord{\left/ {\vphantom {{2Q(D - q)} {(\pi k_{\text{eff}} D^{2} )}}} \right. \kern-0pt} {(\pi k_{\text{eff}} D^{2} )}}$$
(12)

and

$$k_{\text{eff}} = k_{\text{b}} + {Q \mathord{\left/ {\vphantom {Q D}} \right. \kern-0pt} D}$$
(13)

where \(Q = (F_{\text{y}} - q\,k_{\text{b}} )\) represents the strength corresponding to the intersection point between the post-yield stiffness and the force axis, and known as the characteristic strength; D is the specified design displacement of the bearing. Once the equations of motion are solved, the base shear (V b) in the tank wall and the overturning moment (M b) at the tank base are computed as,

$$V_{\text{b}} = m_{\text{c}} {\ddot{u}}_{\text{c}} + m_{\text{i}} {\ddot{u}}_{\text{i}} + m_{\text{r}} {\ddot{u}}_{\text{b}}$$
(14)

and

$$M_{\text{b}} = \left( {m_{\text{c}} {\ddot{u}}_{\text{c}} } \right)H_{\text{c}} + \left( {m_{\text{i}} {\ddot{u}}_{\text{i}} } \right)H_{\text{i}} + \left( {m_{\text{r}} {\ddot{u}}_{\text{b}} } \right)H_{\text{r}} .$$
(15)

It can be noted that the weight of the tank wall and the roof can be added to the impulsive mode for calculation of the base shear and overturning moment (Malhotra et al. 2000).

3 Stochastic ground motion model

To address the non-stationary nature of the earthquake ground motion, a stochastic ground motion model, proposed by Rezaeian and Kiureghian (2008), is considered here. According to this model, total duration (T N) of the ground motion is discretized into N steps (i.e. \(T_{\text{N}} =\Delta t \times N\)). Then the ground acceleration [\({\ddot{u}}_{\text{g}} (t)\)] is given by,

$${\ddot{u}}_{\text{g}} \left( t \right) = f(t)\sum\limits_{{{\text{i}} = 1}}^{\text{k}} a_{\text{i}} (t)v_{\text{i} , \,{\text{for}} \,t_{\text{k}} \le t < t_{{\text{k}} + 1}}$$
(16)

where k can be any integer between 1 and N; \(f(t)\) denotes the modulation function which defines the variation of the acceleration amplitude; \(a_{\text{i}} (t)\) denotes the filter function; and v i is any standard normal variable.

The modulating function is given by,

$$f(t) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\text{for}} \quad {t \le T_{0} } \hfill \\ {a_{\text{r,max}} \,\left( {\frac{{t - T_{ 0} }}{{T_{ 1} { - }T_{ 0} }}} \right)^{2} ,} \hfill & {\text{for}} \quad {T_{0} \le t \le T_{1} } \hfill \\ {a_{\text{r,max}} ,} \hfill & {\text{for}} \quad {T_{1} \le t \le T_{2} } \hfill \\ {a_{\text{r,max}} \,e^{{\left[ { - \kappa \left( {t - T_{2} } \right)^{\eta } } \right]}} ,} \hfill & {\text{for}} \quad {T_{2} \le t} \hfill \\ \end{array} } \right.$$
(17)

where the initiation of the process is denoted by the time instant, T 0; the time instants T 1 and T 2 denote the starting and ending of the strong motion phase with root mean square (RMS) acceleration, \(a_{\text{r,max}}\). The parameters κ and η define the decaying phase of the modulating function. The filter function is expressed as,

$$a_{\text{i}} (t) = {\frac{{h[(t - t_{\text{i}} ),\,\omega_{\text{f}} (t_{\text{i}} ),\,\zeta_{\text{f}} (t_{\text{i}} )]}}{{\sqrt {\sum\nolimits_{{{\text{j}} = 1}}^{\text{k}} {h^{ 2} [(t - t_{\text{j}} ),\,\omega_{\text{f}} (t_{\text{j}} ),\,\zeta_{\text{f}} (t_{\text{j}} )]} } }},} \quad {\text{for}}\quad {t_{\text{k}} \le t < t_{{{\text{k}} + 1}} \quad {\text{and}}\quad 0 < i \le k}$$
(18)

where the impulse response function (IRF), \(h[(t - t_{\text{i}} ),\,\omega_{\text{f}} (t_{\text{i}} ),\,\zeta_{\text{f}} (t_{\text{i}} )]\) represents the pseudo-acceleration response of a single-degree-of-freedom (SDOF) linear oscillator under a unit impulse. The IRF is expressed at time τ as,

$$h\left[(t - {\tau}_{\text{i}} ),\,\omega_{\text{f}} (\tau_{\text{i}} ),\,\zeta_{\text{f}} (\tau_{\text{i}} )\right] = \left\{ {\begin{array}{*{20}l} {\frac{{\omega_{\text{f}} (\tau )\,\exp [ - \zeta_{\text{f}} (\tau )\,\omega_{\text{f}} (\tau )\,(t - \tau )]}}{{\sqrt {1 - \zeta_{\text{f}}^{ 2} (\tau )} \,\,\left\{ {\sin [\omega_{\text{f}} (\tau )\sqrt {1 - \zeta_{\text{f}}^{ 2} (\tau )} \,(t - \tau )]} \right\}^{ - 1} }}\,\,,} \hfill & {\text{for}} \quad {\tau \le t} \hfill \\ {0,} \hfill & {\text{for}} \quad {\tau > t} \hfill \\ \end{array} } \right.$$
(19)

where \(\omega_{\text{f}} (\tau_{\text{i}} )\) and \(\zeta_{\text{f}} (\tau_{\text{i}} )\) denote the time dependent natural frequency and damping ratio of the filter, respectively. The natural frequency of the filter is considered to decay linearly as,

$$\omega_{\text{f}} (\tau ) = \omega_{0} + (\omega_{\text{N}} - \omega_{0} )\frac{\tau }{{(T_{\text{N}} - T_{0} )}}$$
(20)

where ω0 and ωN denote the natural frequencies at the time instances T 0 and T N, respectively. Extending the procedure, as described by Rezaeian and Kiureghian (2008), Jacob et al. (2013) presented a detailed methodology to identify the model parameters and generation of stochastic earthquake acceleration time history. Ten parameters of the model were identified, and probability distributions were assigned to each of the model parameters using a set of 100 recorded earthquakes. The probability distribution function (PDF), \(f(x)\) of the parameters are defined by Pearson type-I distribution using the following relationship.

$$f(x) = \left\{ {\begin{array}{*{20}l} {c_{ 1} (x - x_{1} )^{{{\text{c}}_{ 2} }} (x_{2} - x)^{{{\text{c}}_{ 3} }} ,} \hfill & {{\text{for}}\quad x_{1} \le x \le x_{2} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(21)

where c 1, c 2, c 3, x 1, and x 2 are the constants of the distribution. The distribution constants for the individual parameters are presented in Table 1 as reported by Jacob (2010). MC simulation is used to generate a pool of artificial earthquake acceleration time histories based on the assigned probability distributions of the model input parameters. Table 2 shows the statistics of the randomly generated 1000 earthquake ground motions.

Table 1 Details of PDF for ground motion generation parameters (Jacob 2010)
Full size table
Table 2 Statistics of randomly generated 1000 earthquake ground motions
Full size table

4 Solution of equations of motion

The base-isolated liquid storage tank is a non-classically damped system due to considerable difference between the isolation damping and the damping of the different lumped masses. Moreover, due to non-linear hysteretic behavior of the isolation system, modal superposition technique cannot be used to solve the equations of motion (Eq. 3). Therefore, Newmark’s step-by-step integration procedure, with linear variation of the acceleration, is used here to solve the equations of motion for seismic response analysis. Moreover, the first order differential equation (Eq. 2) is numerically solved using 4th order Runge–Kutta method to obtain the hysteretic displacement component of the isolator.

5 Seismic fragility analysis

Seismic fragility is defined as the probability of failure for a given level of considered seismic intensity measure (IM) parameter. The failure can be expressed as the condition when the seismic demand (load) exceeds the structural capacity (resistance). Therefore, the seismic fragility is expressed in the following simple form.

$$Fragility \approx P[Dem > Cap|{\text{IM}}]$$
(22)

where Dem represents the demand corresponding to specific level of a selected seismic intensity measure (IM), and Cap represents the structural capacity corresponding to a particular failure criterion.

5.1 Selection of intensity measure (IM) parameter

Selection of the seismic IM parameter for the fragility analysis is one of the important steps. Several researchers investigated the use of different seismic IM parameters for the fragility analysis of structures. Padgett et al. (2008) investigated the determination of optimal IM parameter for fragility analysis of highway bridges. They considered ten IM parameters and recommended that the PGA is a suitable choice for fragility analysis, specifically when classes of bridges are under consideration. For the present study, peak ground acceleration (PGA), peak ground velocity (PGV), peak ground displacement (PGD), and the peak spectral acceleration (S a) are chosen to compare the suitability as the IM parameter. The correlation between the peak seismic response quantities of the base-isolated liquid storage tanks and the selected IM parameters are evaluated to investigate their suitability. Nine earthquake ground motions, recorded at far-fault and near-fault locations, are selected for this study. Details of these nine recorded earthquake ground motions are presented in Table 3.

Table 3 Recorded earthquake ground motions used for IM parameter comparison
Full size table

The material and geometrical properties of the tanks are presented in Table 4; where S denotes the tank slenderness ratio (H/R). The liquid storage tanks with broad (S = 0.6) and slender (S = 1.85) configurations are considered for this study. The isolation period (T b) and damping ratio (ξb) are taken as 2.5 s and 0.05, respectively. The normalized yield strength (F y/W) and the yield displacement (q) of the isolator are taken as 0.05 and 2.5 cm, respectively. These are the commonly used parameters for designing of the lead-rubber bearing in practice. The other parameters of Eq. 2 are taken as A = 1 and β = τ = 0.5, to represent the non-linear force–deformation behavior of the lead-rubber bearing. Damping ratios corresponding to the sloshing mass and the impulsive mass are assumed as 0.5 % and 2 % of the critical damping, respectively (Haroun 1983b). The peak base shear (V b), peak overturning moment (M b), and peak isolation displacement (x b) are plotted against the increasing IM parameters in Fig. 2 for broad and slender tank configurations. Each point on the plot represents the peak response quantities of the base-isolated liquid storage tank for an individual earthquake. The correlation coefficient (r) between the selected IM parameters and the peak response quantities of the base-isolated liquid storage tank is computed as,

$$r = \frac{1}{5}\sum\limits_{i = 1}^{6} {\left( {\frac{{\chi_{\text{i}} - \bar{\chi }}}{{S_{\chi } }}} \right)\left( {\frac{{y_{\text{i}} - \bar{y}}}{{S_{\text{y}} }}} \right)}$$
(23)

where \(\chi_{\text{i}}\) denotes peak IM of the ith earthquake ground motion; \(\bar{\chi }\) represents mean of the peak IM for the nine selected earthquake ground motions; y i denotes the peak response quantity corresponding to the ith earthquake ground motion; \(\bar{y}\) represents mean of the peak response quantities under the nine selected earthquakes; the standard deviation of the peak IM parameters is represented by S χ; and the standard deviation of the peak response quantities is represented by S y. The evaluated correlation coefficients (r) are shown in Fig. 2. It is observed that the correlations between the IM parameter and the peak response quantities are more for PGA, and least for PGD in case of both the tank configurations. The peak responses are also observed to be well-correlated with S a for both the tank configurations. It is further observed that the peak responses of the slender tank are equally correlated with PGV as compared to PGA for the slender tank. However, the correlations with PGV vary significantly with the tank configurations. Therefore, PGA is considered as the suitable IM parameter to evaluate seismic fragility of the base-isolated liquid storage tanks for the present study.

Table 4 Geometric, material and dynamic properties of liquid storage tanks
Full size table
Fig. 2
figure 2

Correlation between IM parameters and peak response quantities of base-isolated liquid storage tanks

Full size image

5.2 Selection of failure criteria

The failure criteria is chosen based on: (1) elastic buckling strength of the tank wall, which is defined in terms of critical peak base shear (V b,cr) and critical overturning moment (M b,cr), and (2) in terms of the critical isolation displacement (D cr). The failure of the tank is assumed whenever any one of the considered critical values is exceeded by the corresponding seismic demand. The buckling of tank wall near the base is most critical, as any repair/replacement work at the tank base will halt all operations associated with the tank. The peak displacement at the isolation level (isolation displacement, x b) needs to be accommodated by providing adequate moat width around the tank. Possible pounding at the base isolation level may significantly increase the superstructure acceleration, which will induce additional base shear and overturning moment (Matsagar and Jangid 2003). Moreover, inadequate flexibility in the connections (to the piping and other accessories) may lead to severe loss due to excessive relative displacement. As a result, the maximum isolation displacement may play a crucial role in failure of the base-isolated liquid storage tanks. The present study considers only open tank with sufficient freeboard, therefore the damage of tank roof due to liquid sloshing is ignored. Further, damage to the roof or top of the tank wall due to the sloshing are less critical as compared to the damage at the tank base, evidently because it is possible to repair the damaged roof or the top wall without hindering the normal operations associated with the tank.

Okada et al. (1995) presented a methodology to compute the critical base shear and the critical overturning moment in terms of elastic buckling of the tank wall as follows.

$$V_{\text{b,cr}} =\uptau_{\text{cr}} {\uppi} Rt_{s}$$
(24)

and

$$M_{\text{b,cr}} =\upsigma_{\text{cr}} {\uppi} R^{2} t_{s}$$
(25)

where τcr and σcr are the elastic shear buckling stress and the elastic bending buckling stress, respectively. They are expressed as,

$$\uptau_{\text{cr}} = 0.07708\frac{{\uppi^{2} E_{s} }}{{(1 -\upupsilon^{2} )^{5/8} \sqrt {\frac{H}{R}} }}\left( {\frac{R}{{t_{s} }}} \right)^{ - 5/4}$$
(26)

and

$$\upsigma_{\text{cr}} = 0.605\frac{{E_{s} t_{s} }}{R}$$
(27)

where ν is the Poisson’s ratio of the tank wall material.

To compare the seismic demand and capacity of the base-isolated liquid storage tanks corresponding to tank wall buckling, ten artificial earthquake ground motions are generated randomly which are sufficient from statistical viewpoint. The PGA and the frequency content, corresponding to the peak fast Fourier transform (FFT) amplitude are presented in Table 5 for all the ten generated earthquake ground motions. All the ten earthquakes are then normalized to three PGA levels such as 0.5, 1, and 1.5 g, and seismic demands of the tanks are determined at each of the considered PGA levels. It is worthy to mention here, that Table 5 presents the characteristics of the randomly generated ten earthquake ground motions based on the input parameters reported by Jacob (2010). As these earthquake ground motions are randomly selected from a large pool, the range is only representative of the variation of the frequency content in the synthetically generated ground motions. For generation of particular site-specific earthquake ground motion, having narrow band or broad band frequency content, the model parameter inputs can be suitably selected. Figure 3 shows the peak base shear and peak overturning moment for the broad (S = 0.6) and slender (S = 1.85) base-isolated liquid storage tanks under the ten earthquake ground motions with normalized PGA. The capacity, i.e. the critical base shear and the critical overturning moment, for the considered tank configurations are also computed and compared with the seismic demand. It is noted that with increase in the PGA, the demand is evidently increasing. However, the demand is not same for all the earthquakes though their PGAs are same. The critical overturning moments are observed considerably higher than the respective seismic demands for both the tank configurations. However, the critical base shear is exceeded by the seismic demand in several occasions, even at lower PGA level. Hence, it is concluded that the critical base shear is the governing failure criteria for both the tank configurations, broad and slender, when the tank wall buckling is considered.

Table 5 Characteristics of randomly generated ten earthquake ground motions
Full size table
Fig. 3
figure 3

Comparison between tank wall buckling capacities and demands for base-isolated liquid storage tanks

Full size image

Deciding the critical isolation displacement (D cr) is not described in any current design guidelines for base-isolated liquid storage tanks. For bridges, the complete failure due to unseating of the deck is reported in the range of 150 to 250 mm (Choi et al. 2004). In most of the practical applications of the base isolation systems, the maximum design isolation displacement is considered as 250 mm; however, greater design displacement for the isolation systems is possible (Kelly et al. 2010). In the present study, the critical isolation displacement is considered as 250 mm. Although, no particular site condition is considered in the present study, it is worthy to mention that as per the ASCE 7 (2010), this maximum displacement corresponds to a base-isolated structure having effective period 2.5 s and 5 % effective damping located at a site where the expected spectral acceleration (at 1 s period) is 0.6 g.

5.3 Procedure for seismic fragility analysis

Once the PGA is selected as the IM parameter, the fragility is expressed in terms of the critical response quantities as,

$$Fragility \approx P[V_{\text{b}} > V_{\text{b,cr}} |{\text{PGA}}],$$
(28a)
$$Fragility \approx P[M_{\text{b}} > M_{\text{b,cr}} |{\text{PGA}}],$$
(28b)

or

$$Fragility \approx P[x_{\text{b}} > D_{\text{cr}} |{\text{PGA}}].$$
(28c)

The procedure followed for the seismic fragility analysis of the base-isolated liquid storage tanks under non-stationary earthquakes is described schematically in Fig. 4. Based on the identified probability distributions of the earthquake ground motion model parameters, N sim numbers of artificial earthquake acceleration time histories are generated using the MC simulation. All the earthquake time histories are then normalized to a PGA level within the considered range of variation. On the other hand, the capacities corresponding to the tank wall buckling (i.e. V b,cr and M b,cr) are computed using Eqs. 24 and 25 for a considered tank configuration of the liquid storage tank. Afterwards, the liquid storage tank model is analyzed for N sim number of earthquake acceleration time histories, and the peak response quantities are determined. Thereafter, the seismic demands are compared with the capacities of the tank. Probability of failure (p f) is computed for any particular PGA level as,

$$p_{f} = \frac{{N_{\text{fail}} }}{{N_{\text{sim}} }}$$
(29)

where N fail is the number of the cases when the demand exceeds the capacity. The probability of failure is plotted against the corresponding PGA level to obtain a failure point. The procedure is then repeated for a range of PGA levels, and then the fragility curve is obtained by joining the failure points.

Fig. 4
figure 4

Flowchart for seismic fragility analysis procedure used in this study

Full size image

5.4 Convergence of probability of failure

The number of simulations (N sim) plays a crucial role in determination of the probability of failure using the MC simulation. Therefore, a convergence study is carried out to find out the number of simulations necessary for reasonably accurate estimation of the probability of failure (p f). The number of simulations should be selected in such a way that it can provide convergence in the estimation of the probability of failure for a wide range of PGA level. Therefore, three levels of the PGA are considered here for both the broad (S = 0.6) and slender (S = 1.85) tank configurations. Figure 5 shows the plots of the probability of failure against the number of simulations for both the tank configurations. It is observed that 1000 simulations are sufficient to estimate the probability of failure with reasonable accuracy. It is also observed that the number of simulations is more sensitive for slender tanks, especially at the lower PGA level. Therefore, the number of simulations must be chosen cautiously depending upon the tank configuration and PGA level of the earthquake. In the present study, 1000 simulations are chosen for all the analyses presented hereafter.

Fig. 5
figure 5

Convergence of probability of failure (p f) with number of simulations (N sim)

Full size image

6 Numerical study

Seismic fragility of the base-isolated liquid storage tank is evaluated for both the broad and slender tank configurations as given in Table 4. The damping ratios corresponding to the sloshing mass and the impulsive mass are assumed as 0.5 and 2 %, respectively. The period (T b), damping ratio (ξb), normalized yield strength (F y/W), and yield displacement (q) of the lead-rubber bearing are taken as 2.5 s, 0.05, 0.05, and 2.5 cm, respectively. The non-linear force–deformation behavior of the lead-rubber bearing is represented using Eq. 2 by suitably selecting the parameters as A = 1 and β = τ = 0.5. The number of the simulations for the artificial earthquake generations are kept constant as 1000 for both the tank configurations. The PGA level is varied from 0.05–3 g with 0.1 g increment to determine the probability of failure of the base-isolated liquid storage tanks over a wide range of the PGA levels. Seismic performance of the base-isolated structures is significantly influenced by the isolation parameters such as isolation period (T b), isolation damping ratio (ξb), yield strength (F y), and yield displacement (q) of the isolator etc. as stated by Matsagar and Jangid (2004). Therefore, effectiveness of the seismic base isolation and the influence of the isolator characteristic parameters on the seismic fragility of base-isolated liquid storage tanks are presented in the following sections.

6.1 Fragility of fixed-base and base-isolated liquid storage tanks

The effectiveness of the base isolation technique, to improve the seismic performance of liquid storage tank, is investigated by comparing the fragility curves for the fixed-base and base-isolated liquid storage tanks. Two configurations of the tank, broad (S = 0.6) and slender (S = 1.85), are considered for both the fixed-base and base-isolated tanks. The critical isolation displacement (D cr) or the available moat width is assumed as 250 mm. Figure 6 shows the fragility curves corresponding to the tank wall buckling criterion and maximum isolation displacement criterion. It is observed that the tank wall buckling is the governing failure criterion for both the broad and slender tank configurations. It can be noted here that more the moat width provided, lesser the probability of base displacement exceeding the critical limit. Therefore, it is reasonable to assume, for lead-rubber bearing, that the failure due to the tank wall bucking is expected to occur before the peak isolation displacement exceeds the provided moat width. Consequently, in all the forthcoming study only the failure criterion corresponding to the tank wall buckling is considered. The seismic fragility curves of the fixed-base and base-isolated liquid storage tanks are compared in Fig. 7. The fragility curves are shown up to the PGA level of 2 g for the comparison. It is observed that the probability of failure for the slender tank is higher than the broad tanks. This is attributed to the fact that base isolation is more effective for comparatively stiff structures than the flexible structures. Further, substantial decrease in the probability of failure is observed when base isolation is introduced in the tank. It is evident from the study that base isolation helps to significantly increase the seismic performance of the liquid storage tanks. It is also observed that the fragility curve for the fixed-based tank is steeper as compared to that of the base-isolated tank. It indicates that the probability of failure for the fixed-base tank increases suddenly with small increase in the PGA level. However, for the base-isolated tank, increase in the probability of failure is not sudden, and the isolation helps in protecting the liquid storage tank up to higher level of PGA. This behavior indicates that the base isolation technique can be effectively used to protect important lifeline structures such as liquid storage tanks. From the fragility curves obtained for the base-isolated broad and slender tanks, it is concluded that seismic isolation is comparatively more effective in case of the broad tanks.

Fig. 6
figure 6

Comparison of failure criteria for seismic fragility analysis

Full size image
Fig. 7
figure 7

Comparison of seismic fragility for fixed-base and base-isolated liquid storage tanks

Full size image

6.2 Influence of isolation period on seismic fragility

The influence of the isolation period (T b) on the seismic fragility of the base-isolated liquid storage tanks is investigated by comparing the fragility curves obtained for three different T b values. The isolation periods (T b) considered are 2, 2.5, and 3 s, while the damping ratio (ξb) is kept constant at 0.05. Further, both the broad and slender configurations of the liquid storage tank are considered to demonstrate the influence. Figure 8 shows the effect of variation in the isolation period on the seismic fragility for the base-isolated liquid storage tanks with broad and slender tank configurations. It can be observed that slope of the fragility curve decreases with increase in the isolation period. It implies that with increase in the isolation period, the probability of failure at a particular PGA level decreases. Similar trend is observed for both the tank configurations, which can be explained in the context of dynamic analysis of structures. As the stiffness of the structure decreases, it attracts lesser force from the seismic excitation. With increase in the isolation period, the overall base-isolated liquid storage tank becomes more flexible, consequently attracts lesser seismic force.

Fig. 8
figure 8

Influence of isolation period (T b) on seismic fragility of base-isolated liquid storage tanks

Full size image

6.3 Influence of isolation damping on seismic fragility

Damping is another important parameter of the base isolation system which influences the seismic response of the structure. To examine the influence of the isolation damping on the seismic fragility of the base-isolated liquid storage tanks, three different values of the isolation damping are considered. The isolation damping ratios (ξb) considered are 0.05, 0.1, and 0.15, whereas the period (T b) is kept constant at 2.5 s. It can be noted here that only the viscous damping is varied. The parameters defining the hysteretic component of the force–deformation behavior are kept constant. Figure 9 shows the effect of the variation in isolation damping on the seismic fragility for both the broad and slender base-isolated liquid storage tanks. For both the cases, damping helps to decrease the seismic demand, as a result the probability of failure at a particular PGA level decreases with increase in the isolation damping. However, it is to be noted that influence of the damping on the seismic fragility of the base-isolated liquid storage tanks is less as compared to the period variation. The slope of the fragility curves marginally changes with change in the isolation damping within the considered range of variation. In general, the viscous damping has lesser effect on the peak responses as compared to the hysteretic component. Probably owing to this fact, less effect of isolation damping (ξb) is observed on seismic fragility of the base-isolated liquid storage tanks.

Fig. 9
figure 9

Influence of isolation damping (ξb) on seismic fragility of base-isolated liquid storage tanks

Full size image

6.4 Influence of yield strength and yield displacement of isolator on seismic fragility

The pre-yielding behavior of the lead-rubber bearing depends on its yield strength (F y) and yield displacement (q). The yield strength of the lead-rubber bearing is primarily contributed by the lead core. The effect of variation in the isolator yield strength (F y) on the seismic fragility is evaluated for the broad and slender tank configurations. Here, the yield strength is considered in the normalized form as F y/W. The isolation period (T b) and damping ratio (ξb) are kept constant at 2.5 s and 0.05, respectively. It can be noted here that in this study, the viscous damping is kept constant, while the hysteretic component of the force–deformation behavior are varied by changing the yield strength and yield displacement.

To investigate the influence of the yield strength, normalized yield strength (F y/W) of the lead-rubber bearing is varied from 0.05 to 0.1 with 0.025 increments. The isolator yield displacement (q) is kept constant at 2.5 cm. Figure 10 shows the variation in the seismic fragility for both the broad and slender tanks due to variation in the isolator yield strength. It is observed that for lower yield strength of the isolator, the slope of the fragility curve is reduced for both the tank configurations. It implies that the probability of failure of the liquid storage tank, at a particular PGA level, is more in case of higher yield strength of the isolator. The reduced fragility of the tanks for the lower yield strength of the isolator is attributed to the increased flexibility at post-yielding behavior. It is also observed that effect of the normalized yield strength is more pronounced in case of the slender tank as compared to the broad tank. Furthermore, effect of the isolator yield strength is less when the probability of failure approaches toward unity, i.e. at the higher level of the PGA.

Fig. 10
figure 10

Influence of normalized yield strength (F y/W) of isolator on seismic fragility of base-isolated liquid storage tanks

Full size image

The yield displacement (q) of the lead-rubber bearing is varied from 1 cm to 4 cm with 1.5 cm increments to investigate its influence on the seismic fragility of the base-isolated liquid storage tanks. The normalized yield strength (F y/W) of the lead-rubber bearing is kept constant at 0.05. Figure 11 shows the variation in the seismic fragility for both the broad and slender tanks due to variation in the isolator yield displacement. It is observed that probability of failure increases with increase in the isolator yield displacement for both the broad and slender tanks at a particular PGA level. However, the influence reduces as the PGA level increases. Therefore, it is concluded that increase in the isolator yield displacement, keeping the yield strength constant, increases the seismic fragility of the base-isolated liquid storage tank.

Fig. 11
figure 11

Influence of normalized isolator yield displacement (q) on seismic fragility of base-isolated liquid storage tanks

Full size image

6.5 Effect of the isolator modeling on seismic fragility

Effect of the equivalent linear modeling of non-linear hysteretic behavior of the isolator, on the seismic fragility of the base-isolated liquid storage tanks, is investigated. Both the broad (S = 0.6) and slender (S = 1.85) tank configurations are considered for this study. The isolator yield displacement is kept constant at 2.5 cm. Here, the effective period \((T_{\text{eff}} = 2\pi \sqrt {M/k_{\text{eff}} } )\) and the effective damping ratio (ξeff) of the lead-rubber bearing are considered as 2.5 s and 0.05, respectively. The parameters of the non-linear hysteretic model are determined using Eqs. 12 and 13 in such a way that the T eff and ξeff remain 2.5 s and 0.05, respectively for a given design displacement (D). The design displacement is considered as the maximum displacement at the isolation level of a rigid superstructure isolated by the equivalent linear isolation system having period and damping ratio as 2.5 s and 0.05, respectively. Figure 12 shows the comparison between the fragility curves obtained for the broad and slender tank configurations when the isolator hysteretic behavior is modeled as non-linear hysteretic and equivalent linear. The effect of the isolator modeling on the seismic fragility for both the tank configurations is observed to be insignificant. For slender tank configuration, the probability of failure is marginally less when the isolator hysteretic behavior is modeled as equivalent linear. However, for the broad tank the effect of the isolator modeling is negligible. Therefore, it is concluded that the equivalent linear modeling of the isolator’s non-linear hysteretic behavior does not affect the seismic fragility for the base-isolated liquid storage tanks significantly for the limit states of failure considered in the present study.

Fig. 12
figure 12

Effect of isolator modeling on seismic fragility of base-isolated liquid storage tanks

Full size image

7 Conclusions

Seismic fragility of the base-isolated liquid storage tanks under stochastic earthquake is evaluated using Monte Carlo (MC) simulation. The correlation between the selected earthquake intensity measure (IM) parameters and the peak response quantities of the base-isolated liquid storage tanks is examined. The effectiveness of the base isolation technique is studied by comparing the fragility curves for the fixed-base and base-isolated liquid storage tanks. The influence of the isolator characteristic parameters and modeling approaches on the seismic fragility of the base-isolated liquid storage tanks is investigated. The following major conclusions are derived from the present study.

  1. 1.

    It is observed that the PGA of the earthquake ground motion is largely correlated with the peak response quantities; therefore, it can be suitably used for seismic fragility analysis of the base-isolated liquid storage tanks.

  2. 2.

    Base isolation effectively decreases the probability of failure for liquid storage tanks as compared to the fixed-base case, and the effectiveness of the base isolation in terms of reduced failure probability is more in case of the broad tanks.

  3. 3.

    Increase in the isolation period decreases the probability of failure for both broad and slender tank configurations which in turn decreases the seismic fragility.

  4. 4.

    With increasing isolation damping, the probability of failure of the base-isolated liquid storage tanks decreases marginally, however its influence is less significant as compared to other isolator characteristic parameters.

  5. 5.

    The effect of the isolator yield strength is significant in slender tanks as compared to the broad tanks, and for higher isolator yield strength the probability of failure increases.

  6. 6.

    Increase in the isolator yield displacement, keeping the yield strength constant, increases the seismic fragility of the base-isolated liquid storage tank.

  7. 7.

    Equivalent linear modeling of the isolator non-linear hysteretic behavior insignificantly affect the seismic fragility for the base-isolated liquid storage tanks.

It can be noted here that the presented work is applicable only for the tank without roof and having sufficient freeboard. Herein, the damage due the liquid sloshing, which can trigger severe damage to the tank roof and upper portion of the tank wall, especially in case of covered tanks, is not considered. Further, the critical isolation displacement or the provided moat width is assumed constant in the present study. Significant difference in the developed fragility curves is expected when smaller moat width is available.