Sensitivity and Reliability Analysis of Engineering Structures: Sampling Based Methods

Abstract

This chapter intends to present an overview of Monte Carlo-type methods currently in use in the probabilistic analysis of large engineering structures. It starts with an introduction to the generation of multi-dimensional random quantities. Next, spatially distributed random properties, e.g., material or geometrical properties in continuum mechanics, are modeled as random fields. Approximations to random fields by means of Karhunen–Loève expansion and polynomial chaos expansion are introduced. These tools are employed to study the response of continuous structures with loads, material or geometrical properties given by random fields. The main focus is on sensitivity analysis of large engineering structures, where small Monte Carlo sample sizes are mandatory. The transition to reliability is undertaken by means of the concept of tolerance intervals. Further, current sampling methods for accurate reliability estimates are discussed, and practical applications are presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

4.1 Introduction

Engineering structures are usually modelled as input–output maps: the response Y is a function Y = g(X ₁, …, X _n ) of input parameters (X ₁, …, X _n ) like material properties, geometry, boundary conditions, and driving forces (dynamic or distributed loads, noise). It has been acknowledged since a long time that both the structural model (given by the function g) and the input parameters are uncertain. Traditionally, uncertainties have been dealt with by employing safety factors. That is, the traditional codes would require that the load carrying capacity of the structure exceeds the design loads by a certain factor > 1, typically 1.35 for permanent loads (such as dead weight) and 1.5–2.0 for temporary loads.

This state of affairs is unsatisfactory in as much as no information about the actual distance to failure can be extracted. The desire for a more analytical description of the uncertainties led to the introduction of the probabilistic safety concept in civil engineering, initiated by the pioneering work of Freudenthal [17], Bolotin [6], and others in the 1950s. Starting with the 1980s and 1990s, the European engineering codes have been changed into probability based codes. By now, this is the standard in civil engineering (see, e.g., EN 1990:2002 [15])—interestingly, the civil engineering community has been far ahead of the other engineering fields in adopting the probabilistic point of view.

Under this point of view, every relevant parameter of the engineering model is a random variable. There is no absolute safety, but rather a probability of failure. As a consequence, more information than just the nominal parameter values must be entered in the model, namely a description of the statistical distribution of the input. Further, the response is no longer deterministic, but rather a random variable, whose distribution must be computed in order to describe the behavior of the structure as well as the probability that certain limits are exceeded (described by a limit state function).

In practical applications, the structure is usually represented by a finite element model. These models are generally large, computationally costly, and partially black boxes. Practically, Monte Carlo simulation is the only way to numerically compute the statistics of the system response. Thereby, an artificial sample of X ₁, …, X _n , a data matrix of size N × n, is generated and N values of y = g(x ₁, …, x _n ) are calculated, producing a sample of size N of the response Y, which in turn can be evaluated statistically. This approach raises the computational cost dramatically, and so the need for cost-saving algorithms arises.

An adequate understanding of the uncertainties in an engineering task requires a number of actions, among them reflection about the choice of model and the failure mechanisms; assessing the variability of input and output variables and model parameters; sensitivity analysis (i.e., the determination of the relative influence of individual input parameters on the response); assessing the reliability of the structure. This involves a variety of activities to be performed, from laboratory experiments, data collection to model validation.

The reader is alerted that in the present contribution, only the comparatively narrow part of the numerical calculation of sensitivities and of reliability is addressed. As suggested in the title, the focus is on sampling based methods. In view of the need to employ as few model evaluations as possible, the choice of the sample becomes an important issue. This is dealt with under the heading design of experiment in Sect. 4.2. In due course, metamodels will be encountered there as well. Section 4.3 is devoted to the simulation of random fields, that is, spatially distributed random input. Section 4.4 starts off with sensitivity analysis, of interest in itself, but also the basis for model reduction. This becomes useful in Sect. 4.5, where reliability analysis is addressed. In Sect. 4.6, the concepts will be illustrated using a model from aerospace engineering, supplied by our industrial partner Intales GmbH Engineering Solutions.

The methods presented here have been developed, adapted, and implemented in a number of joint research projects with Intales GmbH Engineering Solutions.¹ Note that approaches to uncertainty analysis going beyond probability theory, such as interval analysis or the combination of both approaches in the form of random sets, are not addressed here. One instance of such a hybrid approach is in Chap. 3 of this volume. For further information the reader is referred to the recent surveys [4, 36].

4.2 Design of Experiment

In this section, the task of simulating the output Y = g(X ₁, …, X _n ) of an input–output function applied to random input (X ₁, …, X _n ) will be addressed. Direct Monte Carlo simulation consists in generating a sample $\mathbf{x}_{1},\ldots,\mathbf{x}_{N}$ of the n-dimensional random variable (X ₁, …, X _n ), collected in an N × n-matrix.² The sample has to be generated in such a way that the columns are statistically independent and each of them is distributed according to the distribution of the corresponding random variable. We are not going to detail this step—most scientific software packages come with a pseudorandom number generator that can produce high dimensional independent samples of most familiar statistical distributions [42] of sufficiently large size (the crucial question of accuracy will be addressed below). The term design of experiment refers to the choice of the sample so as to achieve certain desirable additional properties.

Subsequently, each sampled row $\mathbf{x}_{j} = (x_{\mathit{ji}},\ldots,x_{\mathit{jn}})$ is sent through the input–output map to produce a sample $y_{j} = g(x_{j1},\ldots,x_{\mathit{jn}})$, j = 1, …, N of the output Y.

The complete information about the statistical properties of the output Y is contained in its cumulative distribution function

$$\displaystyle{F_{Y }(y) = P(Y \leq y) = P(g(X_{1},\ldots,X_{n}) \leq y)}$$

which in turn can be written as an expectation value, namely as

$$\displaystyle{F_{Y }(y) = \mathrm{E}\big(h(Y )\big) = \mathrm{E}\big(h(g(X_{1},\ldots,X_{n})\big)}$$

where h is the indicator function of the interval (−∞, y], i.e., h(z) = 1 for z ≤ y and 0 otherwise. Similarly, all statistical properties of the output Y can be formulated in terms of expectation values of functions of Y. For example, the moments of Y are obtained by choosing h(z) = z ^m, m = 1, 2, 3, …. The core of Monte Carlo simulation is that these expectation values can be approximated by the corresponding sample mean, that is,

$$\displaystyle{\mathrm{E}\big(h(Y )\big) \approx \overline{h(Y )} = \frac{1} {N}\sum _{j=1}^{N}h(y_{ j}) = \frac{1} {N}\sum _{j=1}^{N}h\big(g(x_{\mathit{ ji}},\ldots,x_{\mathit{jn}})\big).}$$

By construction, y ₁, …, y _N is an independent random sample, hence statistical sampling theory tells us that the variance of the estimator $\overline{h(Y )}$ is given by

$$\displaystyle{\mathrm{V}\big(\overline{h(Y )}\big) = \frac{1} {N}\mathrm{V}\big(h(Y )\big) = \frac{{C}^{2}} {N} }$$

where n is the variance of $h(Y ) = h\big(g(X_{1},\ldots,X_{n})\big)$, a fixed number depending only on n, n, and the given distribution of (X ₁, …, X _n ). Thus the mean error of a Monte Carlo estimate is of order $1/\sqrt{N}$. For methods to generate random samples leading to a numerical error approximately below prescribed bounds see [19].

We note in passing that replacing the pseudorandom numbers by quasirandom numbers, generated from the so-called low-discrepancy sequences, allows one to improve the mean square error to order (logN)ⁿ∕N, but demonstrably not further [13, 34]. Rather than going into design of experiment based on quasirandom numbers, two sampling plans will be addressed which are of bigger importance in our setting.

Latin Hypercube Sampling The first issue is stratified sampling that is designed to avoid random clustering and produces sampled points with a balanced distribution over the parameter space. A prominent and easy-to-implement method of stratified sampling is Latin hypercube sampling. To obtain a sample of size N, the Latin hypercube sampling plan divides the range of each variable X _i into n disjoint subintervals of equal probability. First, N values of each variable X _i , i = 1, …, n, belonging to the respective subintervals are randomly selected. Then the N values for X ₁ are randomly paired without replacement with the N values for X ₂. The resulting pairs are then randomly combined with the N values of X ₃ and so on, until a set of Nn-tuples is obtained. This set forms the Latin hypercube sample. The advantage of Latin hypercube sampling is that sampled points are evenly distributed through design space, thereby hitting also regions of low probability possibly important for the input–output map which might be missed by direct Monte Carlo simulation. A Latin hypercube estimate is not necessarily more accurate than a standard Monte Carlo estimate at given N, but it can be shown that the variance of a Latin hypercube estimator is asymptotically smaller than the variance of the direct Monte Carlo estimator, and possibly markedly smaller when the input–output map is partially monotonic [53].

Correlation Control The second issue is correlation control, which is an essential ingredient in Monte Carlo simulation with small sample sizes (say, around N = 100 or less). As the reader may easily verify, the rows of an independently sampled matrix $\mathbf{X} = (x_{\mathit{ij}},i = 1,\ldots,N;j = 1,\ldots n)$ of independent random variables X ₁, …, X _n may turn out to have correlation coefficients up to 20 % in practice, when N is that small (this undesirable effect disappears for N ≈ 1, 000). Thanks to an empirical method due to Iman and Conover [21], it is possible to rearrange the entries of the sampled matrix in such a way that the new columns are nearly uncorrelated. In fact, the method allows one to construct a matrix $\mathbf{{X}}^{{\ast}}$ of any desired correlation structure $\mathbf{K}$. This is done as follows. The van der Waerden matrix $\mathbf{W}$ is defined by

$$\displaystyle{\mathbf{W} = \left (\begin{array}{*{10}c} w_{1}^{(1)} & \ldots & w_{1}^{(n)}\\ \vdots & & \vdots \\ w_{N}^{(1)} & \ldots & w_{N}^{(n)} \end{array} \right )}$$

where each column consists of a random permutation of the van der Waerden scores

$${\displaystyle{\varPhi }^{-1}\Big( \frac{j} {N + 1}\Big),\qquad j = 1,\ldots,N.}$$

Here Φ denotes the standard normal cumulative distribution function. Starting with the Cholesky factorizations

$$\displaystyle{\mathbf{K} =\mathbf{ P}\mathbf{{P}}^{\mathsf{T}},\quad \boldsymbol{\rho }_{ W} =\mathbf{ Q}\mathbf{{Q}}^{\mathsf{T}},}$$

with the correlation matrix $\boldsymbol{\rho }_{W}$ of $\mathbf{W}$, one can prove that

$$\displaystyle{\mathbf{{W}}^{{\ast}} =\mathbf{ W}\mathbf{{Q}}^{\mathsf{-T}}\mathbf{{P}}^{\mathsf{T}}}$$

has the target correlation structure $\mathbf{K}$. Empirical investigations [21] showed that the rank correlation matrix of the resulting matrix $\mathbf{{W}}^{{\ast}}$ is nearly the same, i.e., $\rho _{{W}^{{\ast}}} \approx \mathbf{ R}_{{W}^{{\ast}}}$. Therefore, rearranging the values in the columns of $\mathbf{X}$ corresponding to the rank order of the columns in $\mathbf{{W}}^{{\ast}}$ leads to a matrix $\mathbf{{X}}^{{\ast}}$ which approximately has the desired correlation structure:

$$\displaystyle{\rho _{{X}^{{\ast}}} =\rho _{{W}^{{\ast}}} \approx \mathbf{ R}_{{W}^{{\ast}}} =\mathbf{ K}.}$$

Further improvement can usually be achieved by iteration of the procedure. It should be noted that the described method of correlation control does not destroy the Latin hypercube structure of a sample and thus can be directly combined with Latin hypercube sampling. The efficiency of correlation control in dependence on the number of input variables has been studied in [37].

In all simulations presented in this paper, Latin hypercube sampling and correlation control have been routinely implemented.

Bootstrap Resampling The result of a Monte Carlo simulation is a single estimate $\overline{h(Y )}$ of one or more desired quantities h(Y ). One would like to be able to assess the accuracy of the estimate, i.e., the variance of the estimator, confidence intervals, etc., without additional calls of the expensive input–output map. A cost-saving method to achieve this is bootstrap resampling [14, 50]. The bootstrapping procedure consists in repeatedly drawing from the same sample with replacement to obtain new samples of the same size N. To obtain B = 1, 000, say, bootstrap samples of size N, one proceeds as follows.

From the original data sample, e.g., h(y ₁), …, h(y _N ), of size N one randomly draws N-times, so that each realization has equal probability of being drawn. The results are combined to produce a bootstrap sample of size N (note that some entries of the bootstrap sample may be repetitions of realizations of the original data sample). This is repeated B = 1, 000 times. The B = 1, 000 bootstrap samples now are used to compute B = 1, 000 realizations of $\overline{h(Y )}$, say, and the distribution of $\overline{h(Y )}$ can be estimated in this way. The reason why this works is that each bootstrap sample has a distribution which approximates the empirical distribution of the original sample.

In this way, the generation of a multitude of samples of the same distribution is mimicked and allows one to assess the variability of the individual sample estimators. For example, confidence intervals for $\overline{h(Y )}$ can be either obtained by computing the percentiles of the B = 1, 000 estimates of $\overline{h(Y )}$, or approximated by a Student’s t-distribution based on the empirical standard deviation of those values.

Metamodels Also known as surrogate models or response surfaces, metamodels attempt to save computational cost by approximating the input–output function by a simpler (deterministic) function. Typically, such an approximation is based on evaluating the input–output function at a smaller number of design points and suitable extrapolation. Large size Monte Carlo simulation can then be performed with the metamodel with little computational cost. Metamodels obtained by linear regression with possibly nonlinear shape functions have the advantage that the powerful diagnostic methods of regression analysis can be used. For example, partial coefficients of determination admit to quantify the relative importance of input variables with respect to the variability of the output in nonparametric ways [28, 32, 39]. Other metamodels are based on radial basis functions, smoothing splines, or Kriging (i.e., variance minimizing piecewise linear extrapolation); see, e.g., [25, 45]. The accuracy of a metamodel crucially depends on the degree of smoothness of the input–output function. Metamodels cannot be used, e.g., to accurately describe nonlinear bifurcation as in buckling analysis. On the other hand, given a sufficiently smooth model, the accuracy of a metamodel can be controlled by sequential design of experiment, in which additional design points are added in regions of lower accuracy, optimizing both the global error and the space filling properties of the experimental design, see, e.g., [23].

Stochastic Response Surfaces If the input variables (X ₁, …, X _n ) are Gaussian or have been transformed into standard Gaussian variables, the input–output function can be seen as a function on standard Gaussian space and approximated by a response surface on that space. As an illustration, consider the univariate case of a single random variable X with distribution function F(x). The transformed random variable $U {=\varPhi }^{-1}(F(X))$ has a standard Gaussian distribution. This transformation reduces the input–output map to a function of the Gaussian variable U as well, by means of $Y (U) = g\big({F}^{-1}(\varPhi (U))\big)$. For example, if X has a normal distribution with mean μ and variance σ ², the transformation is simply $X = {F}^{-1}(\varPhi (U)) =\mu +\sigma U$.

Recall that the Hermite polynomials h _n (u) form an orthonormal basis in the space of square integrable functions on the real line with respect to the Gaussian density ${\mathrm{e}}^{-{u}^{2}/2 }\,\mathrm{d}u/\sqrt{2\pi }$. The (normalized) Hermite polynomials are given by the recursion

$$\displaystyle{h_{n+1}(u) = \frac{u} {\sqrt{n + 1}}h_{n}(u) + \frac{n} {\sqrt{n(n + 1)}}h_{n-1}(u)}$$

with h ₀(u) = 1, h ₁(u) = u. Every function Y (U) of a Gaussian variable U such that Y (U) has finite second moments has a convergent Hermite expansion of the form

$$\displaystyle{Y (U) =\sum _{ k=0}^{\infty }c_{ k}h_{k}(U).}$$

The coefficients c _k can be obtained as the inner product E(Y (U)h _n (U)); alternatively, collocation and regression can be used to numerically compute them. More precisely, choose finitely many points ξ ₁, …, ξ _m in the domain of the input–output map g. Compute collocation points $u_{j} {=\varPhi }^{-1}(F(\xi _{j}))$ on the real line. Record the outputs $y_{j} = g(\xi _{j}) = g\big({F}^{-1}(\varPhi (u_{j}))\big)$. Evaluate the coefficients c ₁, …, c _M of a truncated Hermite expansion by linear regression on the data (u _j , y _j ) with the Hermite functions h _k , k = 1, …, M, as shape functions. This concludes the construction of a stochastic response surface Y _M (U) for the input–output function, given as a truncated Hermite series. Monte Carlo simulation is now done at no cost by sampling a standard Gaussian variable U and evaluating Y _M (U).

Note that this procedure requires only m evaluations of the costly input–output map on the points ξ ₁, …, ξ _m . The rest of the burden is put on the transformation $U {=\varPhi }^{-1}(F(X))$, thus parametric studies with differently distributed X, for example, with varying mean and variance, can be easily undertaken. In the one-dimensional case a low value of M, say around ten, and twice the number of collocation points usually suffices. For an application of this method, see, e.g., [35].

As is well-known, the procedure can be generalized to multiple expansions of functions of infinitely many Gaussian variables, known as the polynomial chaos expansion; the reader is referred to e.g., [18, 29].

4.3 Random Fields

Material and geometrical properties (e.g., modulus of elasticity, thickness) of a structure may vary randomly from point to point. Such a behavior can be captured by means of random fields, that is, stochastic processes that assign a random variable q(x) to every point x in a region in space. Usually, random fields are chosen so as to have continuous or even differentiable realizations, as opposed to random noise in stochastic mechanics. To define the field, the joint distributions of the values at any finite number of points q(x ₁), …, q(x _k ) should be specified. If the random field is stationary (i.e., the finite dimensional distributions are translation invariant) and Gaussian, it is completely specified by the mean value μ _q  = E(q(x)) and the second moments, i.e., the covariance COV(q(x), q(y)) for any two points x, y. Due to stationarity, the covariance depends only on the distance $\delta = \vert x - y\vert$ of the points and is of the form

$$\displaystyle{\mathrm{COV}(q(x),q(y)) = C(x,y) {=\sigma }^{2}c(\delta )}$$

with the variance σ ² and the autocorrelation function c(δ). A frequently used autocorrelation function is of the form

$$\displaystyle{ c(\delta ) =\exp \big (-\vert \delta \vert /\ell\big), }$$

(4.1)

where $\ell$ is the so-called correlation length. The indicator function of the interval $[-\ell,\ell]$ might be taken as a crude autocorrelation function with correlation equal to 1 for δ in the interval and 0 outside. The area under the curve (4.1) is the same as the area under this indicator function, whence the name correlation length. Other autocorrelation functions in use may be of Gaussian type, in higher dimensions also with anisotropic distance measure.

If measurement data are available, the autocorrelation function can be estimated from the empirical covariance matrix by arranging the values along the distance δ of the measured points and fitting a shape function as in (4.1), thereby estimating σ ² and $\ell$.

In order to simulate a random field, one discretizes the region under consideration with grid points x _i , i = 1, …, M, measures the distance between the grid points x _i , and sets up a covariance matrix $\mathbf{C} = (C_{\mathit{ij}},i,j = 1,\ldots,M)$ whose values are computed from (4.1) where δ is the distance between x _i and x _j . In case the random field is Gaussian, there are at least three methods to generate realizations of the field.

The first method is the standard simulation method for correlated Gaussian variables. It is based on the Cholesky factorization $\mathbf{C} =\mathbf{ A}\mathbf{{A}}^{\mathsf{T}}$. If $\mathbf{Y }$ is an M-dimensional Gaussian random variable with mean zero and independent components (i.e., its covariance matrix $\mathrm{E}(\mathbf{Y }\mathbf{{Y }}^{\mathsf{T}}) =\mathbf{ I}$, the identity matrix), then $\mathbf{X} =\mathbf{ A}\mathbf{Y }$ is a mean-zero Gaussian random variable whose covariance matrix is $\mathbf{C}$. This follows from the simple identities

$$\displaystyle{\mathrm{E}(\mathbf{X}\mathbf{{X}}^{\mathsf{T}}) =\mathrm{ E}(\mathbf{A}\mathbf{Y }\mathbf{{Y }}^{\mathsf{T}}\mathbf{{A}}^{\mathsf{T}}) =\mathbf{ A}\mathrm{E}(\mathbf{Y }\mathbf{{Y }}^{\mathsf{T}})\mathbf{{A}}^{\mathsf{T}} =\mathbf{ A}\mathbf{I}\mathbf{{A}}^{\mathsf{T}} =\mathbf{ C}.}$$

Accordingly, starting from a realization of the M-dimensional standard Gaussian random variable $\mathbf{Y }$, the transformation $\mathbf{X} =\mu _{q} +\mathbf{ A}\mathbf{Y }$ yields a realization of the desired random field q(x) in the grid points, i.e., X _i  = q(x _i ). This is repeated N times to obtain a Monte Carlo sample of the random field. It should be noted that this method works in any space dimension; it just requires enumerating the grid points and keeping track of their distance. The disadvantage of this method is that one cannot easily keep track of the error in terms of the number of grid points, that is, the accuracy of the autocovariance function of the simulated field.

The second method is advantageous in this respect. It is based on the Karhunen–Loève expansion of the field. In fact, the eigenvalue problem

$$\displaystyle{\int C(x,y)\varphi _{k}(y)\,\mathrm{d}y =\lambda _{k}\varphi _{k}(x)}$$

where C(x, y) is the autocovariance function of the random field, has a sequence of positive eigenvalues λ _k and orthonormal eigenfunctions $\varphi _{k}(x)$ (orthonormality in mean square). Then

$$\displaystyle{ q(x) =\sum _{ k=1}^{\infty }\sqrt{\lambda _{ k}}\xi _{k}\varphi _{k}(x) }$$

(4.2)

where the ξ _k are uncorrelated random variables with unit variance, see, e.g., [30]. If the process is Gaussian, the ξ _k are independent and distributed according to the standard normal distribution $\mathcal{N}(0,1)$.

For the numerical simulation, the spatial region is again discretized by a grid and the $\varphi _{k}$ are taken, e.g., piecewise constant on the grid elements. The eigenvalue problem becomes a matrix eigenvalue problem, and the series (4.2), with approximate eigenvalues and eigenfunctions, truncated after a finite number M of terms, can be used for Monte Carlo simulation of the field trajectories. Here the mean square error due to truncation after M terms is just the sum of the neglected eigenvalues; the discretization error can be estimated through the numerical integration error and its propagation through eigenvalue problems [5]. A further advantage of the method is that it can be directly based on a finite element discretization [46]. However, changing the field parameters, e.g., the correlation length, requires solving the eigenvalue problem with a different matrix anew, which can be costly.

This disadvantage is avoided in the third method, which is applicable in one space dimension. It is based on the observation that the autocorrelation function (4.1) coincides with the autocorrelation function of an Ornstein–Uhlenbeck process, namely the solution process of the Langevin stochastic differential equation

$$\displaystyle{ \mathrm{d}q(x) = -\tfrac{1} {\ell} q(x) + \sqrt{\tfrac{2} {\ell}} \,\sigma \,\mathrm{d}w(x),\quad q(0) \sim \mathcal{N}(0{,\sigma }^{2}), }$$

(4.3)

where w(x) denotes Wiener process on the real line, see e.g. [2]. Solutions of sufficient accuracy can be easily simulated from discrete white noise input by means of an explicit Euler scheme at little cost [26].

4.4 Sensitivity Analysis

Sensitivity analysis is a core ingredient in understanding the behavior of a structural model. It aims at determining the input parameters that have the largest influence on critical output. In addition, it can be used as a first step in reliability analysis or in optimizing structural properties.

Sensitivity analysis does not necessarily require knowledge of the probabilistic properties of the input and thus is a nonparametric method. If the input–output function is explicitly given and sufficiently smooth, one may use partial derivatives to assess the sensitivity, see, e.g., [40, 45]. In the context we envisage, the input–output function may be non-differentiable and a black box, in addition. For this reason we focus on derivative-free methods of sensitivity analysis, that is, on sampling based methods. The strategy is to produce a sample of the input data (X ₁, …, X _n ), to compute a sample of the output Y and to analyze the statistical input–output relations or the relations between different output quantities. For all variables, we take a uniform distribution centered around the nominal values μ _j with a spread of a certain equal percentage, say ± 15 %. Equally scaled spread and uniform distributions are chosen to avoid distortion of the relative weights of the input variables. If information about the actual statistical distribution of one or the other input variable is known, this knowledge first does not enter in the sensitivity analysis, but may be considered in a second stage.

The computationally least expensive methods are correlation based, which will be described first. An explorative analysis usually starts with inspecting scatterplots of individual variables vs. output. To obtain a refined diagnosis, methods are needed that quantify the correlations, assess their significance, and possibly remove hidden influences of the co-variates on the correlation between a given input variable and the output variable. The simplest indicator is the Pearson correlation coefficient (CC). It detects linear relationships between input and output. To recall the definition, assume given a sample $x_{j1},\ldots,x_{\mathit{jn}}$, and y _j , j = 1, …, N of the n-dimensional input and the corresponding output. Denote the mean values by $\overline{x}_{i}$ and $\overline{y}$, respectively. The empirical Pearson correlation coefficient of input number i with the output is defined as

$$\displaystyle{r(x_{i},y) = \frac{\sum _{j=1}^{N}(x_{\mathit{ji}} -\overline{x}_{i})(y_{j} -\overline{y})} {\sqrt{\sum _{j=1 }^{N }{(x_{\mathit{ji } } - \overline{x } _{i } )}^{2 } \sum _{j=1 }^{N }{(y_{j } - \overline{y } )}^{2}}}.}$$

It turns out that the correlation coefficient does not isolate the effect of x _i on the output y, but is influenced by the co-variates (inputs with numbers k ≠ i), especially when they have a nonzero correlation with x _i . Regression based indices may be used to mitigate this effect.

A brief recall of linear regression is in order. The goal of linear regression analysis is to fit a linear model $y =\beta _{0} +\beta _{1}x_{1} +\beta _{2}x_{2} +\ldots +\beta _{n}x_{n}$ to the data, that is, each value y _j is to be approximated by

$$\displaystyle{y_{j} =\beta _{0} +\beta _{1}x_{j1} +\beta _{2}x_{j2} +\ldots +\beta _{n}x_{\mathit{jn}} +\varepsilon _{j},\quad j = 1,\ldots,N}$$

with the errors $\varepsilon _{j}$. The estimated coefficients $\hat{\beta }_{0},\hat{\beta }_{1},\ldots,\hat{\beta }_{n}$ are obtained as the solution of the minimization problem

$$\displaystyle{L(\beta _{0},\beta _{1},\ldots,\beta _{n}) =\sum _{ j=1}^{N}\varepsilon _{ j}^{2} \rightarrow \min.}$$

The values predicted by the model and the residuals are, respectively,

$$\displaystyle{\hat{y}_{j} =\hat{\beta } _{0} +\hat{\beta } _{1}x_{j1} +\ldots +\hat{\beta }_{n}x_{\mathit{jn}},\qquad e_{j} = y_{j} -\hat{ y}_{j},}$$

j = 1, …, N. If there is no linear relation between input and output, the best prediction is the mean value $\overline{y}$, in which case the residuals coincide with the measured data y _j , centered at the mean. The other extreme is that the data points y _j already lie on a hyperplane $y_{j} =\beta _{0} +\beta _{1}x_{j1} +\beta _{2}x_{j2} +\ldots +\beta _{n}x_{\mathit{jn}}$, in which case the best prediction is simply the data point, $\hat{y}_{j} = y_{j}$, and the residuals are identically equal to zero.

It can be shown that the total square variability of y can be partitioned into two summands:

$$\displaystyle{\sum _{j=1}^{N}{(y_{ j} -\overline{y})}^{2} =\sum _{ j=1}^{N}{(\hat{y}_{ j} -\overline{y})}^{2} +\sum _{ j=1}^{N}{(y_{ j} -\hat{ y}_{j})}^{2}.}$$

The coefficient of determination is defined as ${R}^{2} =\sum _{ j=1}^{N}{(\hat{y}_{j} -\overline{y})}^{2}\big/\sum _{j=1}^{N}{(y_{j} -\overline{y})}^{2}$. By what has been said above about the residuals, it equals 1 if the data points already lie on a hyperplane and 0 when no linear relationship between input and output exists, and in general measures the explanatory power of the fitted regression model.

The regression coefficients as such cannot be used as indicators of the influence of the corresponding variables, because they are scale dependent. Rather, the standardized regression coefficients (SRC) can be used. These are the regression coefficients of the centered and normalized model, where the data x _ji are replaced by $(x_{\mathit{ji}} -\overline{x}_{i})\big/\sqrt{\sum _{j=1 }^{N }{(x_{\mathit{ji } } - \overline{x } _{i } )}^{2}}$, and similarly for the y _j . In case the n input columns x _j1, …, x _jn , j = 1, …, N are uncorrelated, the SRCs coincide with the CCs. In general, the expression for the CCs has an additional summand which depends on the correlated co-variates.

A more effective removal of the influence of the co-variates is achieved through the partial correlation coefficients (PCCs). The partial correlation between x _i and y, given the set of co-variates $x_{\setminus i} =\{ x_{1},\ldots,x_{i-1},x_{i+1},\ldots,x_{n}\}$ is defined as the correlation between the two residuals obtained by regressing x _i on $x_{\setminus i}$ and y on $x_{\setminus i}$, respectively. That is, one first constructs the two regression models

$$\displaystyle{\hat{x}_{i} =\hat{\alpha } _{0} +\sum _{k\neq i}\hat{\alpha }_{k}x_{k},\qquad \hat{y} =\hat{\beta } _{0} +\sum _{k\neq i}\hat{\beta }_{k}x_{k},}$$

obtaining the residuals $\mathbf{e}_{i}$ and $\mathbf{e}$ with components

$$\displaystyle{e_{\mathit{ji}} = x_{\mathit{ji}} -\hat{ x}_{\mathit{ji}},\qquad e_{j} = y_{j} -\hat{ y}_{j},}$$

j = 1, …, N. By construction, the residuals e _ji and e _j are those parts of x _i and y that remain after subtraction of the predicted linear part depending on $x_{\setminus i}$. Thus the PCC $\rho (\mathbf{e}_{i},\mathbf{e})$ quantifies the linear relationship between x _i and y after removal of any part of the variation due to the linear influence of the co-variates $x_{\setminus i}$.

The advantage of the PCCs is that they are more discriminating. In fact, if the input–output map is a truly linear function and the input parameters are uncorrelated, then the PCC of an input variable that enters with a non-zero coefficient is equal to plus or minus one. In reality, input–output maps are not ideally linear functions and so the effect is somewhat moderated. Still the PCCs are an accentuating measure of influence.

If the input–output function is decidedly nonlinear, but monotonic, sensitivities are better detected when one applies a rank transformation to the data. That is, the data x _j1, …, x _jn , and y _j , j = 1, …, N are ordered and only their rank information is kept. This leads to the Spearman rank correlation coefficients (RCC), the standardized rank regression coefficients (SRRC), and the partial rank correlation coefficients (PRCC). Having the computed Monte Carlo sample x _j1, …, x _jn , and y _j at hand, the calculation of the various coefficients produces no additional cost, thus it is recommended to evaluate all six of them to have a better overview. Finally, bootstrap resampling allows one to compute confidence intervals. If zero is outside the confidence interval, the corresponding coefficient can be considered to be significantly different from zero, and the corresponding input variable is classified as having a non-negligible influence on the output. The degree of influence can then be classified according to the magnitude of the six coefficients.

Alternative methods of sensitivity analysis are variance based. Pinching strategies consist in freezing individual variables at their central value and studying the change of variability in the output. If one produces a sample with X _i fixed to its nominal value μ _i , the reduction in variance says something about the influence of X _i on Y:

$$\displaystyle{\frac{\mathrm{V}(g(X_{1},\ldots,X_{i-1},\mu _{i},X_{i+1},\ldots,X_{n}))} {\mathrm{V}(g(X_{1},\ldots,X_{n}))} }$$

In fact, this is the proportion of total variance not explained by X _i . As can already be seen from the formulation, this strategy is costly because for each pinched variable a new Monte Carlo simulation is required.

A more sophisticated method is the partition of variance according to the groups of variables, the Sobol’ indices introduced in [51, 52]. It is based on an expansion of the input–output function into summands of increasing dimensionality.

For a survey of sampling based methods in sensitivity analysis, see [20].

4.5 Reliability Analysis

The central concept of reliability analysis is the failure probability. The system is considered in a failed state if a certain combination of the input parameters (X ₁, …, X _n ) and the output Y exceeds an admissible range. For the present purpose it is not necessary to distinguish into favorable (resistance increasing) and unfavorable (load or stress exerting) influences, as is done in the European civil engineering codes [15] with their partial safety factors, critical values and design values. Since Y is a function of the inputs (X ₁, …, X _n ), which subsume all random influences on the structure, failure can be described by a limit state function $\varPhi (X_{1},\ldots,X_{n})$ of the input alone. Failure is usually defined by $\varPhi (X_{1},\ldots,X_{n}) < 0$, while $\varPhi (X_{1},\ldots,X_{n}) \geq 0$ signifies a safe state. The failure region is the subset of design space (the domain of the input parameters) resulting in violation of the limit state condition, i.e.,

$$\displaystyle{\mathcal{F} =\{ (x_{1},\ldots,x_{n}):\varPhi (x_{1},\ldots,x_{n}) < 0\}.}$$

Then

$$\displaystyle{p_{f} = P\big((X_{1},\ldots,X_{n}) \in \mathcal{F}\big) = P\big(\varPhi (X_{1},\ldots,X_{n}) < 0\big)}$$

is the failure probability; $R = 1 - p_{f}$ is the reliability of the structure. Occasionally it is useful to describe failure as a ratio of actual and admissible values, leading to a failure region of the form $\varPsi (x_{1},\ldots,x_{n}) > 1$. To determine the probability p _f , the types and parameters of the probability distributions of (X ₁, …, X _n ) are needed. As opposed to sensitivity analysis, this requires detailed information about the statistical properties of the input parameters, obtained from experiments or previous studies.

The acceptable value of the failure probability depends on the circumstances. The civil engineering codes require that the designed structure obtains an instantaneous probability of failure of $p_{f} = 1{0}^{-6}$ and a long-term failure probability of $p_{f} = 1{0}^{-5}$. To credibly estimate tail probabilities of such a small magnitude, a lot of information is needed. In addition, if time dependent reliability is to be assessed, failure rates and the additional parameters of the time-dependent reliability function are required. The problems arising from this concept of failure probability have been discussed at many places, including the codes themselves [15, Annex C4(3)], see also [16, 36] and references therein. In technological development phases in aerospace engineering, a failure probability in the range of $p_{f} = 1{0}^{-3}$ may be acceptable, especially if it is not used as an absolute measure, but as an objective function in optimization (reliability based optimization).

Having performed a Monte Carlo sensitivity analysis of the model output Y = g(X ₁, …, X _n ), the question comes to mind if one could not use the generated sample for getting reliability estimates of the structure. This is indeed the case, albeit at a possibly low accuracy due to the small sample size of the sensitivity analysis. There are two ways of exploiting the existing sample. One way is by means of tolerance intervals to estimate credible upper and lower bounds for the output Y; another way is by reweighting the generated sample of (X ₁, …, X _n ) so as to mimic input distributions other than the uniform distributions used in the sensitivity analysis.

Tolerance Intervals While confidence intervals give an estimate for the distribution parameters λ of a random quantity Y, a tolerance interval gives an estimate of the range of possible observations of Y. More precisely, one wants to compute an interval [a, b] that contains a certain proportion p, say p = 90 %, of the population with a given confidence level 1 −α, say $1-\alpha = 95\,\%$. A non-parametric approach based on order statistics is especially attractive, since it is applicable without knowledge of the type of statistical distribution of Y. In fact, given whatever sample of whatever random variable, one may estimate the proportion p of the population that lies within the sample maximum Y _max (the largest value in the sample) and the sample minimum Y _min with a given confidence 1 −α, depending only on the sample size N. In this situation, the interval $[a,b] = [Y _{\mathrm{min}},Y _{\mathrm{max}}]$ is given and N is known. Thus depending on the desired confidence level, the proportion p lying within the boundaries [a, b] can be computed.

The derivation of a one-sided non-parametric tolerance interval with upper boundary the sample maximum is particularly easy, using only combinatorics. In fact, a proportion p of the population lies in the interval (−∞, Y _max] with confidence 1 −α if the relation

$$\displaystyle{{p}^{N} =\alpha }$$

holds. This can be seen as follows. Denote by Q _p the p-th quantile of Y. This means that P(Y ≤ Q _p ) = p. On the other hand, the interval $(-\infty,Y _{\mathrm{max}}]$ contains at least the proportion p of the population if $Q_{p} \leq Y _{\mathrm{max}}$. Thus it is required that

$$\displaystyle{P(Q_{p} \leq Y _{\mathrm{max}}) \geq 1 -\alpha.}$$

But $P(Q_{p} \leq Y _{\mathrm{max}}) = 1 - P(Y _{\mathrm{max}} < Q_{p})$. Observe that $Y _{\mathrm{max}} < Q_{p}$ if and only if each of the N independent realizations of Y in the sample is below Q _p , i.e., Y _j  < Q _p for j = 1, …, N. By definition, the probability of the event Y _j  < Q _p is exactly p. Collecting terms, one arrives at $1 - P(Y _{\mathrm{max}} < Q_{p}) = 1 - {p}^{N}$, whence the assertion.

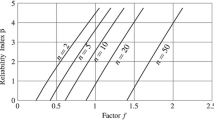
From there, universally valid estimates of the sample size N required so that a proportion p of values lies under the sample maximum at confidence 1 −α can be established, see e.g. Table 4.1. The same formula applies to one-sided intervals of the form [Y _min, ∞). Tolerance intervals with various proportions and confidence levels are tabulated, e.g., in the ISO standard [22]. For the theory, see, e.g., [27].

Table 4.1 Required sample size N for one-sided tolerance intervals at confidence 1 −α

Monte Carlo Reweighting As outlined in Sect. 4.2, the goal of Monte Carlo simulation is to estimate expectation values $\mathrm{E}\big(h(Y )\big) = \mathrm{E}\big(h(g(X_{1},\ldots,X_{n}))\big)$ of functions of the model output. Suppose we have already generated a sample $(x_{\mathit{ji}},\ldots,x_{\mathit{jn}})$ and computed the outputs y _j , j = 1, …, N, where the sample has been generated according to a certain probability distribution of the input, say with probability density f(x ₁, …, x _n ). Is it possible to use the same sample to estimate $\mathrm{E}\big(h(\tilde{Y })\big) = \mathrm{E}\big(h(g(\tilde{X}_{1},\ldots,\tilde{X}_{n}))\big)$ where the $\tilde{X}_{j}$ are random variables defined on the same range as the X _j , but with another probability distribution, say with probability density $\varphi (x_{1},\ldots,x_{n})$? To understand the positive answer, it is useful to write the expectation $\mathrm{E}\big(h(\tilde{Y })\big)$ as an integral:

$$\displaystyle\begin{array}{rcl} \mathrm{E}\big(h(g(\tilde{X}_{1},\ldots,\tilde{X}_{n}))\big)& =& \int \cdots \int h(g(x_{1},\ldots,x_{n}))\varphi (x_{1},\ldots,x_{n})\,\mathrm{d}x_{1}\cdots \mathrm{d}x_{n} {}\\ & =& \int \cdots \int h(g(x_{1},\ldots,x_{n})) \frac{\varphi (x_{1},\ldots,x_{n})} {f(x_{1},\ldots,x_{n})} {}\\ & & \times f(x_{1},\ldots,x_{n})\,\mathrm{d}x_{1}\cdots \mathrm{d}x_{n} {}\\ & =& \mathrm{E}\Big(h(g(X_{1},\ldots,X_{n})) \frac{\varphi (X_{1},\ldots,X_{n})} {f(X_{1},\ldots,X_{n})}\Big). {}\\ \end{array}$$

This shows that the computation of the new expectation value can be accomplished by computing the old expectation value of the input–output function, multiplied by a weight—the quotient of the two densities. In terms of Monte Carlo simulation, one has to compute

$$\displaystyle{\mathrm{E}\big(h(\tilde{Y })\big) \approx \frac{1} {N}\sum _{j=1}^{N}h\big(g(x_{\mathit{ ji}},\ldots,x_{\mathit{jn}})\big)\, \frac{\varphi (x_{\mathit{ji}},\ldots,x_{\mathit{jn}})} {f(x_{\mathit{ji}},\ldots,x_{\mathit{jn}})}.}$$

This causes no additional effort, because one can reuse the expensive computation of $h\big(g(x_{\mathit{ji}},\ldots,x_{\mathit{jn}})\big)$. The accuracy of the method depends on the degree of similarity of the old and the new distribution.

A typical application could consist in reusing the sample from the sensitivity analysis, based on uniform distributions, and place truncated Gaussians on the intervals. This concludes the remarks about what can be extracted from the sensitivity analysis towards a reliability assessment.

Importance Sampling When estimating failure probabilities of low value, one cannot expect that the rather small sample sizes of sensitivity analysis suffice. In fact, a standard Monte Carlo estimate of the failure probability is of the form

$$\displaystyle{p_{f} \approx \frac{1} {N}\sum _{j=1}^{N}{\chi }^{\mathcal{F}}(x_{ j1},\ldots,x_{\mathit{jn}})}$$

where ${\chi }^{\mathcal{F}}$ equals one if $(x_{j1},\ldots,x_{\mathit{jn}}) \in \mathcal{F}$ and zero otherwise. It thus can be seen as the mean value of an N-fold repetition of a zero-one experiment with success probability p _f . The variance of the Monte Carlo estimator of p _f is hence given by $p_{f}(1 - p_{f})/N$, whence the mean estimation error is approximately equal to $\sqrt{ p_{f}/N}$. This means that an accuracy of α ⋅ 100 % requires a sample size of N ≈ 1∕(α p _f ). Consequently, cost-saving methods need to be devised, two of which shall be discussed here.

The first one is importance sampling. As seen above, the probability of failure is estimated by counting the number of realizations of the input variables (X ₁, …, X _n ) that fall into the failure region. Since this number is expected to be small compared to the total number of simulated points, the probability density f(x ₁, …, x _n ) of the input variables will be small on $\mathcal{F}$. The idea of importance sampling is to generate a sample of another distribution, say with probability density $\varphi (x_{1},\ldots,x_{n})$, which may be concentrated in the region $\mathcal{F}$. The idea is similar to Monte Carlo reweighting, but this time a different sample is produced to begin with. In fact,

$$\displaystyle\begin{array}{rcl} p_{f}& =& \mathrm{E}\big({\chi }^{\mathcal{F}}(X_{ 1},\ldots,X_{n})\big) =\int { \cdots \int \chi }^{\mathcal{F}}(x_{ 1},\ldots,x_{n})f(x_{1},\ldots,x_{n})\,\mathrm{d}x_{1}\cdots \mathrm{d}x_{n} {}\\ & =& \int {\cdots \int \chi }^{\mathcal{F}}(x_{ 1},\ldots,x_{n})\frac{f(x_{1},\ldots,x_{n})} {\varphi (x_{1},\ldots,x_{n})} \,\varphi (x_{1},\ldots,x_{n})\,\mathrm{d}x_{1}\cdots \mathrm{d}x_{n} {}\\ & =& \mathrm{E}\Big({\chi }^{\mathcal{F}}(\tilde{X}_{ 1},\ldots,\tilde{X}_{n})\frac{f(\tilde{X}_{1},\ldots,\tilde{X}_{n})} {\varphi (\tilde{X}_{1},\ldots,\tilde{X}_{n})} \Big) {}\\ \end{array}$$

where the random variables $(\tilde{X}_{1},\ldots,\tilde{X}_{n})$ have the probability density $\varphi (x_{1},\ldots,x_{n})$. This leads to the following prescription. First, choose a probability density function $\varphi (x_{1},\ldots,x_{n})$ concentrated in the failure region. Next, generate a random sample $(z_{\mathit{ji}},\ldots,z_{\mathit{jn}})$ according to the corresponding probability distribution. Finally, estimate the failure probability by

$$\displaystyle{p_{f} \approx \frac{1} {N}\sum _{j=1}^{N}{\chi }^{\mathcal{F}}(z_{\mathit{ ji}},\ldots,z_{\mathit{jn}})\frac{f(z_{\mathit{ji}},\ldots,z_{\mathit{jn}})} {\varphi (z_{\mathit{ji}},\ldots,z_{\mathit{jn}})}.}$$

Of course, this begs the question how to find a probability density $\varphi (x_{1},\ldots,x_{n})$ concentrated in the failure region. After all, the failure region unfolds itself only after Monte Carlo evaluation of the limit state function. Various proposals have been made in this respect, notably Bucher’s adaptive sampling [7, 9]. This method starts with a pilot simulation with increased variance of the input variables (to rapidly produce a number of points in the failure region) and then uses certain shifted Gaussians as weight functions.

An interesting proposal has recently been made by Schwarz [49], developed for the situation where the input variables are supported in intervals (as, e.g., the uniform distributions used in sensitivity analysis or transformations thereof). There are two ingredients. First, one may expect that—in most cases—the failure region is concentrated in points near the boundaries of the intervals. Second, input variables with a larger influence on the output should have a larger weight. The starting point of the procedure is a sensitivity analysis with moderate sample size, from which the most important input variables and their correlation coefficients with the output are determined. Then a parametrized family of weight functions is placed on the input intervals, where the weight is just 1 for the unimportant parameters and is shifted more and more towards the boundaries of the input intervals, the larger the correlation.

Subset Simulation The subset simulation method was introduced by Au and Beck in [3]. The idea is to approximate the failure region $\mathcal{F}$ by a sequence of larger regions $\mathcal{F} = \mathcal{F}_{m} \subset \mathcal{F}_{m-1} \subset \ldots \subset \mathcal{F}_{1} \subset \mathcal{F}_{0}$ and to compute the failure probability by a product of conditional probabilities

$$\displaystyle{p_{f} = P(\mathcal{F}) = P(\mathcal{F}_{m}\vert \mathcal{F}_{m-1})P(\mathcal{F}_{m-1}\vert \mathcal{F}_{m-2})\ldots P(\mathcal{F}_{1}\vert \mathcal{F}_{0})P(\mathcal{F}_{0})}$$

where $\mathcal{F} = \mathcal{F}_{m}$ and $\mathcal{F}_{0}$ is the starting region. These conditional probabilities are appreciably larger than the failure probability and hence easier to simulate with smaller samples. In this case it is useful to describe the failure region by means of a ratio based limit state function $\mathcal{F} =\{ (x_{1},\ldots,x_{n}):\varPsi (x_{1},\ldots,x_{n}) > 1\}$. The intermediate regions are chosen of the form $\mathcal{F}_{i} =\{ (x_{1},\ldots,x_{n}):\varPsi (x_{1},\ldots,x_{n}) >\alpha _{i}\}$ with $0 <\alpha _{0} <\alpha _{1} <\ldots <\alpha _{m} = 1$. In fact, the choice of α _i is often made during the simulation such that $P(\mathcal{F}_{i}\big\vert \mathcal{F}_{i-1})$ has a fixed value, say p ₀ between 0.1 and 0.3, and the regions $\mathcal{F}_{i}$ are constructed recursively. The conditional distribution $P(\cdot \vert \mathcal{F}_{i})$ is just the original distribution, restricted to $\mathcal{F}_{i}$ and scaled by $P(\mathcal{F}_{i})$. The latter probability is unknown a priori. This suggests to use the Metropolis–Hastings algorithm, a Markov chain Monte Carlo algorithm, which requires knowledge of the sampling distribution only up to a multiplicative factor (see below).

In the sequel, it is assumed that at each level i, a sample of size N is generated. The algorithm is initiated by generating a sample of the original distribution using standard Monte Carlo simulation. From this sample, the worst p ₀ ⋅ 100 % realizations are declared to belong to $\mathcal{F}_{0}$. More precisely, the sample is ordered according to the Ψ-values. The threshold level α ₀ is chosen as the (1 − p ₀)N-th largest value among the Ψ-values attained in the sample, and $\mathcal{F}_{0}$ is defined to be the set $\{(x_{1},\ldots,x_{n}):\varPsi (x_{1},\ldots,x_{n}) >\alpha _{0}\}$. Further, $P(\mathcal{F}_{0}) = p_{0}$. In the next step, one or more of the points in $\mathcal{F}_{0}$ is/are chosen as the initial point (root) of a Markov chain whose elements are distributed according to $P(\cdot \vert \mathcal{F}_{0})$, this way generating a second sample of size N. Again, the worst p ₀ ⋅ 100 % realizations are declared to belong to $\mathcal{F}_{1}$, and α ₁ is chosen as the (1 − p ₀)N-th largest value among the Ψ-values attained in the second sample, and so on. The simulation stops at the first level m at which the Ψ-values of the worst p ₀ ⋅ 100 % bigger than 1. At this stage $P(\mathcal{F}_{m}\vert \mathcal{F}_{m-1})$ is estimated by M∕N where M is the number of failed realizations in the last sample. Finally, p _f is estimated as p ₀ ^m ⋅ M∕N.

Before discussing some details of the algorithm, a short introduction to Markov chain Monte Carlo simulation is in order. The ideas can be best explicated at the hand of the original Metropolis algorithm for simulating a one-dimensional distribution π(x). The goal is to generate a realization $\xi _{0},\xi _{1},\xi _{2},\ldots,\xi _{N}$ of a Markov chain whose stationary distribution is π(x). Since the chain will converge to the stationary distribution as N → ∞, the end-pieces ξ _M , …, ξ _N are approximately distributed according to π (for large M and N).

The algorithm proceeds as follows. Choose a transition kernel q(x, y) (proposal distribution) such that q(x, y) = q(y, x) for all x, y. (Often it is taken of the form q(x, y) = p(x − y) where p is a nowhere vanishing probability density.) Choose an initial distribution p ⁽⁰⁾(x).

• Sample a value ξ ₀ from p ⁽⁰⁾.

• For k = 1, …, N

  Sample a value η from the proposal distribution q(ξ _k−1, ⋅ ).

  Compute the ratio $r = \frac{\pi (\eta )} {\pi (\xi _{k-1})}$.

  • If r ≥ 1, the value η is accepted; set $\xi _{k} =\xi _{k-1}$.

  • If r < 1, the value η is accepted with probability r and rejected with probability 1 − r.

  Draw a random number ζ from the uniform distribution on [0, 1].

  • If ζ ≤ r, set ξ _k  = η.

  • If ζ > r, set $\xi _{k} =\xi _{k-1}$.

• ξ ₀, ξ ₁, …, ξ _N has π(x) as limiting distribution as N → ∞.

Observe that only the ratio r enters in the computation, so knowledge of π(x) is only required up to a multiplicative factor. The Metropolis–Hastings algorithm is similar, but the proposal distribution is not required to be symmetric. More theory can be found in [42].

If the distribution π(x ₁, …, x _n ) is multidimensional, it is advantageous to change only one coordinate in each step in order to keep the number of rejected trials at a moderate level. In its application to subset simulation, the target distribution is $P(\cdot \vert \mathcal{F}_{i-1})$ in each level. Thus one has to check whether $\xi _{k} \in \mathcal{F}_{i-1}$ for acceptance, in addition. By construction, each root of the generated Markov chain is already distributed according to $P(\cdot \vert \mathcal{F}_{i-1})$. It can be shown [3] that the elements of the whole chain at level i are not only asymptotically but also perfectly distributed according to $P(\cdot \vert \mathcal{F}_{i-1})$. As can be seen, there are a lot of screws that can be adjusted: choice of the proposal distribution, optimal acceptance/rejection rate, number and length of chains generated in level i—with the possibility of parallelization, choice of p ₀, and so on. Based on many recommendations to be found in the literature, subset simulation has developed into an efficient method for estimating failure probabilities. A critical comparison of various simulation methods in reliability analysis can be found in [47, 48].

4.6 Application

This section is devoted to demonstrating the methods at work in a practical application from aerospace engineering, namely in a finite element model of the frontskirt of the ARIANE 5 launcher. The frontskirt is the part of the launcher that connects the tanks section with the payload section and also has to support the booster loads. It consists of a light weight shell structure reinforced by struts. The full finite element model is composed of shell elements and solid elements, altogether with two million degrees of freedom. The models have been supplied by Intales GmbH Engineering Solutions (see Footnote 1). Models of varying complexity and material properties with up to 130 input and a similar number of output parameters have been analyzed.

For the sake of presentation, we shall focus on a smaller finite element model keeping the global structure with about ninety thousand degrees of freedom. Figure 4.1 depicts the model schematically; it is composed of two hemispheres and three cylinders, one of which is made up of composite material. The shadings indicate thickness variations of the tank skin, described by a random field. Booster loads are introduced at two opposite locations in the upper cylinder (not shown in Fig. 4.1). A selection of seventeen input parameters (all loads characterizing various flight scenarios) will be considered; their meaning is described in Table 4.2. As a representative output we start with the load proportionality factor (LPF), a decisive variable indicating buckling failure. It is defined as the limiting value in an incremental procedure in which the mechanical loads during a flight scenario are increased step by step until breakdown of the structure is reached. In the full model, the LPF is computed by means of a path following procedure that follows bifurcations until material failure occurs. In the simplified computations presented here, no distinction of bifurcation or material failure was made, so that the terminal value of the LPF was taken as that value at which the finite element program failed to converge. What concerns the computational effort, a single run of the input–output function computing the LPF in Abaqus takes around 1 h on a personal computer and 10 min on the supercomputer Leo-III of the University of Innsbruck.

Fig. 4.1

Simplified finite element model of frontskirt; shadings show random field (thickness of tank skin) [12]

Table 4.2 Description of input parameters no. 1–17 with their nominal values

Sensitivity Analysis As a basis for the sensitivity analysis, a sample of size N = 100 of the n = 17 input parameters was generated. Each parameter was taken uniformly distributed around its nominal value listed in Table 4.2 with a spread of ± 15 %. Latin hypercube sampling and correlation control was employed. The statistics of the computed LPF are listed in Table 4.3.

Table 4.3 Sample statistics of simulated load proportionality factor

Fig. 4.2

Scatterplots of 17 input variables vs. output (LPF) [24, 38]

The scatterplot of Fig. 4.2 gives a first impression of the influence of the input variables on the output. It is quite clearly seen that input parameter no. 13 (booster loads) exerts a big influence, whereas the diagrams for the other parameters are less conclusive. To quantify the influences, the six different correlation indices CC, PCC, SRC, RCC, PRCC, SPRC were computed. (A complete list of the values has been published in [38].) As an example, the PRCCs of the 17 input parameters vs. the LPF are visualized in Fig. 4.3 (left).

Fig. 4.3

Partial rank correlation coefficients (left) and 95 % bootstrap confidence intervals (right) [24, 38]

The resulting sensitivity indices induce a ranking of the input parameters according to their influence on the output. Note that the accuracy of the estimate for the correlation coefficients is in the range of $1/\sqrt{N} \cdot 100\,\% = 10\,\%$; this suffices to determine the ranking and confirms the observation that one can get along with small sample sizes for an assertive sensitivity analysis. To check whether the computed correlation indices are significantly different from zero, bootstrap 95 %-confidence intervals were computed (with bootstrap sample size B = 5, 000). As a basis for an overall assessment of the ranking, only those sensitivity estimates with a resultant confidence interval not including 0 have been regarded as significant. As an example, bootstrap confidence intervals for the PRCCs are displayed in Fig. 4.3 (right). Accordingly, only the PRCCs of the parameters X ₁, X ₃, X ₉, X ₁₃, and X ₁₄ test to be nonzero. The ranks of those parameters that tested to be significant according to at least one of the six indices are listed in Table 4.4. The table gives a good impression of the sensitivity assessment—if a single scale is required, one might use the average ranks.

Table 4.4 Ranks of the significant input parameters X _i according to the six measures of correlation input–output

Coefficient of Determination As discussed in Sects. 4.2 and 4.4, metamodels can be used to further quantify the influence of selected parameters. One way to achieve this is to fit a linear regression model

$$\displaystyle{Y =\beta _{0} +\beta _{1}X_{1} + \cdots +\beta _{n}X_{n}}$$

and then to compute the partial coefficients of determination. The sequential partial coefficient of determination of variable X _i is computed by first fitting the model $Y =\beta _{0} +\beta _{1}X_{1} + \cdots +\beta _{n}X_{i-1}$, then adjoining the variable X _i and recording the increase in the coefficient of determination R ². Averaging all partial coefficients of determination which can be obtained by adding the variable X _i to all possible combinations of the already included variables leads to a non-parametric measure of the contribution of variable X _i to the explanatory power of the model. The procedure is explained, e.g., in [28, 39]. The result can be conveniently displayed in the form of a pie chart. As an example, a linear model for the LPF has been set up with input parameters nos. 1, 3, 4, 7, 9, 13, 14. It resulted in the assessment of the influences depicted in Fig. 4.4, taken from [43]. The eminent influence of parameter X ₁₃ is once more confirmed. In the figure, the label Res refers to the residual proportion which remains unexplained through the linear model.

Fig. 4.4

Pie chart of relative explanatory power of LPF through various input variables [43]

Fig. 4.5

Plots of histogram and cumulative distribution function of LPF produced by random loads, no imperfections (left) and with random field turned on (right). Vertical line indicates LPF corresponding to nominal input values [41]

Random Fields In order to investigate the effect of geometric and material imperfections, the thickness, modulus of elasticity and yield stress were disturbed by two-dimensional random fields with an autocovariance function of the form (4.1). The distance function on the cylinders was taken as the sum of the axial and radial distance, whereas on the spheres, it was taken as the sum of the latitude and altitude, multiplied by the radius. A routine extracting the distances from the finite element grid was implemented by [41]. The nominal values were 1 mm (thickness), 70,000 MPa (modulus of elasticity), 320 MPa (yield stress) for the first sphere, with similar values for the other components of the frontskirt. A coefficient of variation of 10 % was applied throughout. In a parametric study, the correlation lengths were varied between 60 mm (corresponding to the dimension of two elements of the grid) and 1,600 mm, with various combinations in the two respective directions. Random fields were generated by means of the Karhunen–Loève expansion.

In a first investigation, the different effects of the random imperfections and the 17 random loads on the LPF were studied. Figure 4.5 shows one of the results, with a sample size of N = 100 both for loads and realizations of the random fields. The correlation lengths were set to 188.5 mm in all angular directions (cylinders and spheres), while the correlation length in axial direction was taken 450 and 900 mm for the cylinders. In the left figure, the distribution of the LPF is shown with the random loads from the sensitivity analysis, but with material and geometric properties kept at their nominal value. In the right figure, the random field is turned on, in addition. One can see that the random field has a stabilizing effect (larger values of LPF are attained), but at the same time increases the uncertainty of the outcome.

Interestingly, the application of random fields admits a structurally localized study of the correlations. After all, a realization of the random field induces a realization of the modelled quantity (e.g., thickness) in each element of the FE-grid. Thus one can do a standard sensitivity analysis with these variables. For example, cylinder no. 3 has 2,500 elements; the random field simulation produces N = 100 realizations of the 2,500 grid values of the thickness, elasticity modulus, yield stress. The spatial distribution of the influence on the LPF can thus be visualized. Figure 4.6 shows such a distribution in terms of the Pearson CC for the yield stress (left) and the thickness (right). In the same way, localized correlations of different output variables can be pictured.

Fig. 4.6

Spatial distribution of influence (measured by CC) of element-wise yield stress (left) and thickness (right) on the LPF, based on random field simulation [41]

Tolerance Intervals As a first step from sensitivity to reliability, tolerance intervals for the LPF can be established. Recall from Table 4.3 that the minimal sampled LPF was at LPF _min = 3. 4468. Based on the formula p ^N = α with N = 100, one can assess the proportions p of the possibly attainable LPF-values with a given confidence 1 −α. The results are summarized in Table 4.5.

Table 4.5 Proportion p of LPFs lying above $\mathit{LPF}_{\mathrm{min}} = 3.4468$ at confidence level 1 −α

Reliability Analysis In order to test various simulation methods for reliability, a benchmark study of the small launcher model was undertaken by [49], from where all results and tables in this paragraph are taken. For this study, an extended list of 35 input parameters was used. As a limit state function, a combination of allowable limits in the equivalent plastic strain (PEEQ), principal stress in the composite part (SP), and the absolute value of the smallest eigenvalue (EV) was employed:

$$\displaystyle{\varPsi (\mathbf{x}) =\max \left \{\frac{\mathit{PEEQ}(\mathbf{x})} {0.07}, \frac{\mathit{SP}(\mathbf{x})} {180}, \frac{0.001} {\mathit{EV }(\mathbf{x})}\right \}}$$

with failure defined by $\varPsi (\mathbf{x}) > 1$, $\mathbf{x} = (x_{1},\ldots,x_{35})$. The three criteria correspond to plastification in the metallic part, rupture in the composite part, and buckling of the structure.

A reference brute force Monte Carlo simulation of size N = 5, 000 was undertaken on the supercomputer Leo-III, with three strands in parallel. As in the previous sensitivity analysis, the 35 input variables were taken uniformly distributed on an interval of spread ± 15 % around their nominal values. The resulting failure probability turned out to be p _f  = 0. 0116. A 95 % bootstrap confidence interval was computed (bootstrap sample size B = 5, 000) as [0. 0088, 0. 0146]. A sensitivity analysis with the sample revealed that only 10 of the 35 parameters had a significant influence on the failure criterion Ψ, measured at a 90 % confidence level.

Next, an investigation was undertaken whether an estimate in the same range could be obtained with a smaller sample size by subset simulation or by importance sampling. Subset simulation was undertaken with p ₀ = 0. 2 (see Sect. 4.5). Since p ₀ ³ = 0. 008 is already smaller than the intended failure probability, three levels $\mathcal{F}_{0},\mathcal{F}_{1},\mathcal{F}_{2}$ suffice for the subset simulation algorithm. Experiments were undertaken with sample size N = 900 and N = 300 for each level. Recall that 20 % of the generated points 20 % of the generated points of $\mathcal{F}_{i-1}$ are assigned to $\mathcal{F}_{i}$ in each step. Since these points can be reused when going from level i − 1 to level i, the total number of generated points in the three levels is 2, 340 and 780, respectively. Further, it was tested whether including all 35 input influential ones in the simulation changes the value of the failure probability. In addition, bootstrap confidence intervals for the failure probability were computed.

To keep results comparable, the importance sampling procedure was done with a sample size N = 780. The method described in Sect. 4.5 was employed, by which the weights are computed in dependence on the magnitude of the correlation coefficient of the respective input parameter with the Ψ-value. This required the actual simulation to be preceded by a sensitivity analysis. The sensitivity analysis was done with a sample of size 99, so that a sample size of 681 remained for the importance sampling part. Correlation control was employed when simulating the input data. It was tested whether weighting of all parameters or weighting only the parameters significant at the 90 % level changes the outcome.

The joint results are recorded in Table 4.6. Here NR refers to the total number of realizations computed in the simulation, NV denotes the number of activated variables (subset simulation), respectively weighted variables (importance sampling); p _f is the failure probability and 95 % BSL/BSU refers to the lower/upper bound of the 95 % bootstrap confidence interval for p _f .

Table 4.6 Comparison of results of six different simulation procedures for the failure probability [49]

We conclude this section by reporting on a reweighting experiment. As a basis, the sample of size N = 5, 000 of the reference Monte Carlo simulation was taken. The uniformly distributed input was replaced, using reweighting, by truncated Gaussians. The mean values of the Gaussian distributions were taken as the interval midpoints, the variance was computed from assumed coefficients of variation (between 7.5 and 15 %), the truncation was effected at the interval endpoints. The change from uniform distributions to mid-pieces of Gaussians resulted in quite a change of the failure probability, namely to p _f  = 0. 0019 with a 95 % bootstrap confidence interval [0. 001, 0. 003].

4.7 Conclusion

The purpose of this chapter was twofold. On the one hand, it served to describe current core methods of Monte Carlo simulation, from design of experiment, random fields, metamodelling to concepts of sensitivity and reliability analysis. On the other hand, the chapter demonstrated the implementation of those methods in joint research projects with Intales GmbH Engineering Solutions over the past years.

A number of themes have deliberately not been addressed in order to keep the presentation concise. These include simulation of correlated input using copulas [33], also implemented in the mentioned projects [44], Bayesian methods of reliability analysis [31], Bayesian estimates of the distribution of the failure probability [49, 54], and optimization for finding worst case parameter combinations [12]. Further, the discussion of asymptotic sampling [8], though implemented in our toolbox [49], was omitted because its presentation would have required to go into some details about the safety index and FORM (the first order reliability method).