A New Discretization Method for the Convective Terms in the Incompressible Navier-Stokes Equations

Abstract

In this contribution we present the use of local one-dimensional boundary value problems (BVPs) to compute the interface velocities in the convective terms of the incompressible Navier-Stokes equations. This technique provides us with a better estimate for the interface velocities than linear interpolants.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

We present an accurate method to compute the interface velocities needed in the convective terms of the momentum equations by solving local one-dimensional BVPs. This method can be used as an improvement to a second-order accurate finite volume method on a staggered grid, with central difference discretization for the viscous and convective terms. Such a setup gives us an energy conserving discretization method for the incompressible Navier-Stokes equations [2]. The standard method for computing the interface velocities makes use of linear interpolation, i.e., by taking the average values, or alternatively, the upwind values. In this paper, we will solve a reduced form of the momentum equations, locally over a grid cell, in order to compute the interface velocities. The idea is inspired by the complete flux scheme for the advection-diffusion-reaction equation as presented in [3]. In this paper we consider the two-dimensional incompressible Navier-Stokes equations, the proposed method can be extended to the three-dimensional case.

In Sect. 2 of this paper, we outline the finite volume method for the incompressible Navier-Stokes equations. In Sect. 3 we describe the methods for solving the one-dimensional nonlinear BVPs. The computed interface velocities are then compared with highly accurate numerical solutions in Sect. 4. We conclude with results in Sect. 5.

2 Finite volume method

Consider the dimensionless incompressible Navier-Stokes equations, i.e.,

$$\begin{aligned} \nabla \cdot \mathbf u&= 0,\end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial \mathbf u }{\partial t} + \nabla \cdot (\mathbf u \mathbf u )&= -\nabla p + \frac{1}{\mathrm {Re}}\nabla ^2\mathbf u , \end{aligned}$$

(1b)

where $\mathbf u = (u,v)$ is the velocity of the fluid, $p$ the pressure and $\mathrm {Re}$ the Reynolds number. We use the second-order finite volume method to discretize the above system of equations, as discussed in [1]. The spatial discretization is done using a staggered Cartesian grid, with the pressure and the velocity components defined at different locations, see Fig. 1. The semi-discrete form of Eq. (1a) and (1b) then reads:

$$\begin{aligned} D u(t)&= r_1(t),\\ |\varOmega | u'(t)&= -C(u,v) + \frac{1}{\mathrm {Re}}Lu(t) - Gp(t) +r_2(t), \end{aligned}$$

where $D$, $C$, $L$ and $G$ represent the discrete divergence, convection, diffusion and gradient operators, respectively, and where $|\varOmega |$ represents the measure of the control volumes [1]. The terms $r_1(t)$ and $r_2(t)$ give the boundary conditions for the system of equations. In two dimensions, $|\varOmega |$ can be expressed as $|\varOmega | = \mathrm {diag}(|\varOmega ^u_{i,j}|, |\varOmega ^v_{i,j}|),$ with $|\varOmega ^u_{i,j}| = |\varOmega ^v_{i,j}| = \varDelta x\varDelta y$. Let us consider the convective discretization for the $u$-component, i.e.,

$$\begin{aligned} \big (C^u(u,v)\big )_{i,j}&= \varDelta y \big (u_{i\,+\,1/2,j}^2 - u_{i\,-\,1/2,j}^2 \big ) + \varDelta x\big (v_{i\,+\,1/2,j}\,u_{i,j\,+\,1/2}\nonumber \\&\quad - v_{i\,+\,1/2,j\,-\,1}\,u_{i,j\,-\,1/2}\big ). \end{aligned}$$

(2)

For computing $(C^u(u,v))_{i,j}$, we need methods to compute the interface velocities $u_{i\,+\,1/2,j}$, $v_{i\,+\,1/2,j}$ and $u_{i,j\,+\,1/2}$. In this paper we focus on the computation of $u_{i\,+\,1/2,j}$. The velocity $u_{i\,+\,1/2,j}$ can be simply taken as the average

$$ u_{i\,+\,1/2,j} = \frac{u_{i,j} + u_{i\,+\,1,j}}{2}. $$

In this paper, we aim to compute $u_{i\,+\,1/2,j}$ by solving a reduced form of the $u$-momentum equation locally. The $u$-momentum equation reads

Fig. 1

Staggered grid structure for spatial discretization

$$\begin{aligned} u_t + (uu)_x + (uv)_y = -p_x + \dfrac{1}{\mathrm{{Re}}}\big ( u_{xx} + u_{yy}\big ). \end{aligned}$$

Let us assume that the flow is locally steady and one-dimensional. Moreover, we ignore all terms involving $y$. Then the previous equation is reduced to

$$\begin{aligned} uu_x - \varepsilon u_{xx} = -p_x, \end{aligned}$$

(3)

where $\varepsilon = 1/\mathrm {Re}$. Thus, we are left with a nonlinear differential equation. In the following we ignore the $y$-dependence of $u$ and we simply write $u=u(x)$. We denote $u(x_i)$ as $u_{i}$. In order to get the interface velocity $u_{i\,+\,1/2}$ located at $x_{i\,+\,1}$ we solve Eq. (3) for $x \in \big (x_{i\,+\,1/2}, x_{i\,+\,3/2}\big )$ subject to the boundary conditions

$$\begin{aligned} u(x_{i\,+\,1/2}) = u_{i}, \quad u(x_{i\,+\,3/2}) = u_{i\,+\,1}. \end{aligned}$$

(4)

The following section details the computation of $u_{i\,+\,1/2,j}$ and briefly outlines the computation of $u_{i,j\,+\,1/2}$ and $v_{i\,+\,1/2,j}$.

3 Computing the Interface Velocities

The BVP (3)–(4) is difficult to solve due to the nonlinear term $uu_x$ and the pressure gradient $p_x$. We simplify this by first solving a linearized problem without the pressure gradient and subsequently solving the linearized problem along with the pressure term.

Let $U$ be in between $u_{i}$ and $u_{i\,+\,1}$, or equal to either $u_i$ or $u_{i\,+\,1}$. We linearize the nonlinear term of Eq. (3), to get

$$\begin{aligned} Uu_x - \varepsilon u_{xx} = -p_x. \end{aligned}$$

In the derivation that follows, it is convenient to introduce the following notation, $\mathsf {a} = U/\varepsilon$ and $(.)' = \partial /\partial x$. We define the local mesh Péclet number ($\mathsf {P}$) as

$$\begin{aligned} \mathsf {P} = \frac{U\varDelta x}{\varepsilon } = \mathsf {a}\varDelta x, \end{aligned}$$

(5)

and the normalized coordinate by

$$ \sigma (x) = \frac{x - x_{i\,+\,1/2}}{\varDelta x}\quad \;\;\text { for } x \in \big [x_{i\,+\,1/2}, x_{i\,+\,3/2}\big ]. $$

So the linearized equation can now be written as,

$$\begin{aligned} \varepsilon \big (u' - \mathsf {a}u\big )' = p'. \end{aligned}$$

(6)

The problem given by Eq. (6) with boundary conditions (4), can now be split in two cases, the homogeneous case, having $p' =0$, and the inhomogeneous case, in which we assume a piecewise linear pressure. We first consider the homogeneous case.

Homogeneous case. Using $u' - \mathsf {a} u = e^{\mathsf {a}x}\big (e^{-\mathsf {a}x} u\big )'$ and integrating Eq. (6) (with the assumption $p' = 0$), from $x_{i\,+\,1/2}$ to $x \in [x_{i\,+\,1/2}, x_{i\,+\,3/2}]$, and applying the boundary condition $u(x_{i\,+\,1/2}) = u_{i}$, gives

$$ e^{-\mathsf {a}x}u(x) - e^{-\mathsf {a}x_{i\,+\,1/2}}u_{i} = \dfrac{C_1}{\mathsf {a}}\big ( e^{-\mathsf {a}x_{i\,+\,1/2}} - e^{-\mathsf {a}x}\big ),\quad (\mathsf {a}\ne 0). $$

Formulating in terms of $\sigma$ and $\mathsf {P}$, and imposing the other boundary condition $u(x_{i\,+\,3/2}) = u_{i\,+\,1}$, gives

$$\begin{aligned} u(x) = \frac{e^{-\mathsf {P}(1-\sigma (x))} - 1}{e^{\mathsf {-P}} - 1} u_{i} + \frac{e^{\mathsf {P}\sigma (x)} - 1}{e^{\mathsf {P}} - 1} u_{i\,+\,1}. \end{aligned}$$

(7)

We assume that the grid is equidistant. Then putting $\sigma (x) = \frac{1}{2}$ in the above expression gives

$$\begin{aligned} u_{i\,+\,1/2}= A(-\mathsf {P}/2) u_{i} + A(\mathsf {P}/2)u_{i\,+\,1}, \end{aligned}$$

(8)

where $A(z) = \big (e^{z} + 1\big )^{-1}.$ Alternatively, $u_{i\,+\,1/2}$ can also be expressed as the sum of the average value and a correction term, as

$$\begin{aligned} u_{i\,+\,1/2} = \frac{(u_{i} + u_{i\,+\,1})}{2} + \Big (A(\mathsf {P}/2) - \frac{1}{2}\Big )(u_{i\,+\,1} - u_i). \end{aligned}$$

(9)

From Eq. (8), we see that $u_{i\,+\,1/2}$ is a weighted average of $u_i$ and $u_{i\,+\,1}$. It can be observed that in the limit $\mathsf {P} \rightarrow 0$, we recover the average value. For $\mathsf {P} = 0$, we have $\mathsf {a} = 0$, implying $\varepsilon u'' = 0$, which gives $u(x_{i+1}) = (u_i+u_{i+1})/2$. In the limit $|\mathsf {P}| \rightarrow \infty$, we get $A(|\mathsf {P/2}|) = 0$, thereby giving $u_{i+1/2} = u_i$ or $u_{i+1}$, depending on the direction of the flow.

We compute the velocity $u_{i+1/2}$ iteratively, by initializing $U = (u_i + u_{i+1})/2$ and $\mathsf {P}$ as given in Eq. (5) and then compute $u_{i+1/2}$ using Eq. (8). For the next iteration, we take $U$ to be the computed value of $u_{i+1/2}$ and update $\mathsf {P}$ accordingly, and then compute a new value of $u_{i+1/2}$ using Eq. (8). We continue this procedure until the values of $u_{i+1/2}$ computed after each iteration have converged, i.e., when the absolute difference between the values of $u_{i+1/2}$ computed at consecutive iterations has dropped below a fixed tolerance.

Inhomogeneous case In this case we solve the linearized boundary value problem given by Eq. (6), under the assumption that the pressure $p$ is piecewise linear. We initially proceed as we did in the homogeneous case, so we have

$$\begin{aligned} e^{\mathsf {a}x}\big (e^{-\mathsf {a}x}u\big )' = \frac{1}{\varepsilon }\mathrm {I}(x) + C_1, \quad \qquad \mathrm {I}(x) = \int _{x_{i+1}}^x p'(\xi )\mathrm {d}\xi , \end{aligned}$$

(10)

and Eq. (10) then becomes

$$\begin{aligned} \big (e^{-\mathsf {a}x}u\big )' = \frac{1}{\varepsilon }e^{-\mathsf {a}x}\mathrm {I}(x) + C_1e^{-\mathsf {a}x}. \end{aligned}$$

(11)

The value $I(x)$ can be calculated as

$$\begin{aligned} {I}(x) = {\left\{ \begin{array}{ll} \frac{1}{\varDelta x} (p_{i+1} - p_i)(x - x_{i+1}) = (p_{i+1} - p_i)(\sigma (x) - \frac{1}{2}), &{} \,\,\text {for}\,\, 0\le \sigma (x) \le \frac{1}{2}.\\ \frac{1}{\varDelta x} (p_{i+2} - p_{i+1})(x - x_{i+1}) = (p_{i+2} - p_{i+1})(\sigma (x) - \frac{1}{2}), &{}\,\,\text {for}\,\, \frac{1}{2}\le \sigma (x) \le 1. \end{array}\right. } \end{aligned}$$

Integrating Eq. (11) from $x_{i+1/2}$ to $x \in \big [x_{i+1/2}, x_{i+3/2}\big ]$ and using the boundary condition $u(x_{i+1/2}) = u_{i}$, we get

$$ u(x) - e^{\mathsf {P}\sigma (x)}u_{i} = \dfrac{1}{\varepsilon }\int _{x_{i+1/2}}^x e^{\mathsf {a}(x-\xi )}\mathrm {I}(\xi )\mathrm {d}\xi + \dfrac{C_1}{\mathsf {a}}(e^{\mathsf {P}\sigma (x)} - 1). $$

We define

$$ \mathrm {J}(x) \equiv \int _{x_{i+1/2}}^x e^{\mathsf {a}(x-\xi )}\mathrm {I}(\xi )\mathrm {d}\xi , $$

and use the boundary condition $u(x_{i+3/2}) = u_{i+1}$ to get the solution

$$\begin{aligned} u(x) = \frac{e^{-\mathsf {P}(1-\sigma (x))} - 1}{e^{-\mathsf {P}} - 1}u_{i} + \frac{e^{\mathsf {P}\sigma (x)}-1}{e^{\mathsf {P}}-1}u_{i+1} + \dfrac{1}{\varepsilon }\Big (\mathrm {J}(x) - \frac{e^{\mathsf {P}\sigma (x)}-1}{e^{\mathsf {P}}-1}\mathrm {J}(x_{i+3/2})\Big ). \end{aligned}$$

(12)

We now express the velocity $u(x)$ as the sum of a homogeneous part $u^h(x)$ and an inhomogeneous part $u^i(x)$ as

$$ u(x) = u^h(x) + u^i(x). $$

The homogeneous part $u^h(x)$ of the velocity, as given by Eq. (7), depends on the convection-diffusion operator, whereas the inhomogeneous part, $u^i(x)$, depends on the pressure gradient. Computing the values of the integrals $\mathrm {J}(x_{i+1})$ and $\mathrm {J}(x_{i+3/2})$, and introducing

$$ F(z) \equiv \frac{e^z - 1 - z}{z^2(e^{z} + 1)}, $$

gives us

$$\begin{aligned} u(x_{i+1})&= u^h(x_{i+1}) + u^i(x_{i+1}),\end{aligned}$$

(13a)

$$\begin{aligned} u^h(x_{i+1})&= \mathrm {A}(-\mathsf {P/2}) u_{i} + \mathrm {A}(\mathsf {P/2}) u_{i+1},\end{aligned}$$

(13b)

$$\begin{aligned} u^i(x_{i+1})&= -\frac{(\varDelta x)^2}{4\varepsilon }\Big [F(-\mathsf {P}/2)\frac{p_{i+1} - p_{i}}{\varDelta x} + F(\mathsf {P}/2)\frac{p_{i+2} - p_{i+1}}{\varDelta x}\Big ]. \end{aligned}$$

(13c)

In this case also the computation of $u(x_{i+1})$ is iterative, where we begin by taking $U = u^h = (u_{i,j}+u_{i+1,j})/2$ and $u^i = 0$ and compute $u(x_{i+1})$ using the above equations. Now proceed as in case of the homogeneous case, until the values converge.

Till now we have discussed the computation of the interface velocity $u_{i+1/2,j}$ but for computing the convective term as given by Eq. (2), we also require $u_{i,j+1/2}$ and $v_{i+1/2,j}$. These velocities can also be computed using local BVPs. The interface velocity $u_{i,j+1/2}$ is computed from the BVP

$$\begin{aligned} Vu_y - \varepsilon u_{yy} = 0,\quad y_j < y < y_{j+1},\end{aligned}$$

(14a)

$$\begin{aligned} u(y_j) = u_{j},\quad u(y_{j+1}) = u_{j+1}, \end{aligned}$$

(14b)

and $v_{i+1/2,j}$, from

$$\begin{aligned} Uv_x - \varepsilon v_{xx} = 0, \quad x_i < x < x_{i+1},\end{aligned}$$

(15a)

$$\begin{aligned} v(x_i) = v_{i},\quad v(x_{i+1}) = v_{i+1}. \end{aligned}$$

(15b)

These velocities are also computed iteratively. We begin the iterations by defining $V = (v_{i,j} + v_{i+1,j})/2$ and $\mathsf {P}_v = V\varDelta y/\varepsilon$ for BVP (14a) and (14b) and $U = (u_{i,j}+ u_{i,j+1})/2$, $\mathsf {P}_u = U\varDelta x/\varepsilon$ for BVP (15a) and (15b). We then compute $u_{i,j+1/2}$ and $v_{i+1/2,j}$ using an equation analogous to (8). For the next iteration, we assign $V$ the value of $v_{i+1/2,j}$ computed in the previous iteration and $U$ the value of $u_{i,j+1/2}$ computed in the previous iteration. With the new values of $V$ and $U$ we update $\mathsf {P}_v$ and $\mathsf {P}_u$ and recompute $u_{i,j+1/2}$ and $v_{i+1/2,j}$. We continue this procedure until the values converge. Computing the interface velocities in this manner results in the coupling between $u$ and $v$ interface velocities. The next section gives a validation of the method presented above.

4 Numerical Validation

In order to check the accuracy of the computed interface velocity $u_{i+1/2,j}$, we compare it with the value obtained by computing a very accurate numerical solution of the local boundary value problem.

Table 1 Validation for the homogeneous case, $u_{i+1/2,j}$ according to Eq. (8), ($\varDelta x = 10^{-3}$)

Table 2 Validation for inhomogeneous case, $u_{i+1/2,j}$ according to Eq. (13a)–(13c), ($\varDelta x = 10^{-3}$)

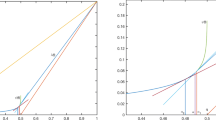
For the validation of our computed interface velocities, we take $u_{i,j} = 1.125$ and $u_{i+1,j} = 1.225$. For this setup the value of $u_{i+1/2,j}$ obtained by central averaging ($u_{\text {avg}}$) is 1.175 and by taking the upwind value ($u_{\text {up}}$) it is 1.125. Let $u_{\text {num}}$ denote the highly accurate numerically computed value of $u_{i+1/2,j}$. We next define the relative absolute differences $\mathrm {d}u_{\text {avg}} = \frac{|u_{\text {avg}} - u_{i+1/2,j}|}{|u_{\text {avg}}|}$ and $\mathrm {d}u_{\text {num}} = \frac{|u_{\text {num}} - u_{i+1/2,j}|}{|u_{\text {num}}|}$. The convergence criterion, i.e., the difference of the computed interface velocities from two consecutive iterations, is taken to be $10^{-7}$. Table 1 gives the results obtained for the homogeneous case. It can be observed that the computed interface velocity is very accurate (when compared to $u_{\text {num}}$) and attains the upwind value for higher Reynolds numbers. Similarly, for the inhomogeneous case, let $u(x_{i+1})$ be the velocity computed using Eq. (13a)–(13c), as the sum of $u^h(x_{i+1})$ and $u^i(x_{i+1})$. Table 2 gives the obtained results. For this case a constant pressure gradient of $-0.01175$ has been assumed. The inhomogeneous part of the velocity increases with increasing Reynolds number. The effect of adding a pressure gradient can be seen in Fig. 2, where we have plotted the interface velocity with increasing Reynolds number. In absence of a pressure gradient the computed interface velocity is almost equal to the numerical solution see Fig. 2a. On adding the pressure gradient, the homogeneous part of the velocity remains the same, and the addition of the inhomogeneous part corrects the interface velocity $u_{i+1/2,j}$, in a physically proper way.

5 Conclusions

To compute interface velocities, we have proposed an iterative discretization method that depends on the local mesh Péclet number, $\mathsf {P}$. For increasing $\mathsf {P}$, the homogeneous part of the velocity attains the upwind value, and for decreasing values of $\mathsf {P}$, it converges towards the average velocity. The pressure gradient plays an important role in the determination of $u_{i+1/2,j}$. For increasing pressure gradient, the difference between the approximations of $u_{i+1/2,j}$, $u^h$ and $u^h + u^i$ and the numerical solution $u_{ num}$ increases see Fig. 2b. For a negative pressure gradient, the interface velocity increases, whereas for a positive pressure gradient it decreases. The increment/decrement grows with an increase in the absolute value of the pressure gradient.

Fig. 2

Effect of adding a pressure gradient to the BVP, $u_i =1.125$, $u_{i+1} = 1.225$, $\varDelta x = 10^{-2}$ a Interface velocities in absence of a pressure gradient. b Interface velocities with a negative pressure gradient

We have applied the methods proposed in this paper to the two-dimensional flow in a lid-driven square cavity. It was observed that the difference in the velocities computed using the proposed iterative method and those computed using the average method is very small for small values of $\varDelta x/ \varepsilon$ but starts to increase as $\varDelta x/ \varepsilon$ increases. The gain of the present method is to be sought in the possibility to use much coarser grids, with the same accuracy as standard methods.