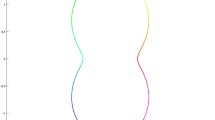The Bakhvalov mesh: a complete finite-difference analysis of two-dimensional singularly perturbed convection-diffusion problems

Abstract

A linear two-dimensional singularly perturbed convection-diffusion boundary-value problem is considered. The problem is discretized by the upwind finite-difference method. The analysis of this method on Shishkin-type meshes has been well-established, but the discretization mesh in this paper is the original Bakhvalov mesh, introduced in 1969 as the first layer-adapted mesh. We analyze the error of the numerical solution in the maximum norm and prove first-order pointwise accuracy, uniform in the perturbation parameter. This is the first complete analysis of this kind for two-dimensional convection-diffusion problems discretized on the Bakhvalov mesh. Our numerical experiments validate the theoretical analysis.

1 Introduction and the model problem

In this paper, we consider the two-dimensional singularly perturbed convection-diffusion problem

$$ \begin{array}{lll} -\varepsilon {\Delta} u- b_{1}(x,y)u_{x} -b_{2}(x,y)u_{y} +c(x,y)&u= f(x,y) & \quad \text{on}\quad {\varOmega}=(0,1)^{2},\\ &u=0 & \quad \text{on}\quad {\varGamma}=\partial {\varOmega}, \end{array} $$

(1)

where ε is the perturbation parameter such that 0 < ε ≤ ε^∗≪ 1, b₁, b₂, c and f are sufficiently smooth functions, and b₁(x,y) > β₁ > 0, b₂(x,y) > β₂ > 0, c(x,y) ≥ 0 for all $(x,y)\in \bar {{\varOmega }}$. We refer the reader to [9, 20] (see also [22, Theorem 7.17]) for a detailed exposition of the compatibility conditions guaranteeing that the problem (1) has a unique solution u in some suitable normed space. In general, the solution u of the problem (1) has exponential boundary layers along the edges x = 0 and y = 0. As opposed to this, when setting b₁(x,y) ≡ 0, b₂(x,y) ≡ 0, and c(x,y) > 0 on Ω in (1), one gets singularly perturbed reaction-diffusion problems whose solutions typically have characteristic boundary layers along all four edges of the unit square.

Singularly perturbed differential equations arise in various practical applications and mathematical models. For example, convection-diffusion problems are found in many formulations of fluid flow problems (such as the linearization of the Navier-Stokes equations and transport problems) and semi-conductor device simulation. More details on these two significant applications can be found in [30, pp. 1–4], whereas mathematical models involving systems of reaction-diffusion problems appear, for example, in simulation of chemical reactions, wave-current interaction, and biological applications [3, 6].

When solving singular perturbation problems such as (1) numerically, the goal is to design numerical methods that yield solutions that converge to the corresponding exact solutions uniformly in the perturbation parameter ε. This task is very challenging because the conventional numerical methods do not give satisfactory results when applied to singular perturbation problems [8]. Therefore, special methods are devised to achieve parameter-robust convergence. In the research literature, there are two main approaches: the use of exponentially fitted finite-difference operators on uniform meshes and the use of layer-adapted meshes with certain discretization methods. The former is less popular in spite of the fact that fitted schemes, like the Il’in-Allen-Southwell (I-A-S) scheme, work well when applied to the one-dimensional analogue of (1). However, their extensions to 2D problems are difficult to analyze, and even impossible in the case of reaction-diffusion equations [8, Example 2.2]. Indeed, a recent result due to Roos and Schopf [32] shows that one can achieve first-order convergence with the I-A-S scheme on uniform meshes for two-dimensional convection-dominated problems, but with restricted assumptions b₁(x,y) ≡ b₁(x) and b₂(x,y) ≡ b₂(y). A similar result is obtained in [10] for exponentially fitted Galerkin and Petrov-Galerkin methods. Another rare successful use of uniform meshes in a very unique setting to obtain ε-uniform convergence for one-dimensional quasilinear convection-diffusion problems is the inversion method introduced by Vulanović and Nhan [37], but this special approach remains inapplicable to 2D problems.

As opposed to the fitted-operator approach, the use of layer-adapted meshes—from their first appearance more than five decades ago—has attained much attention of singular perturbation researchers. As early as in 1969, Bakhvalov [2] introduced his phenomenal idea of the mesh construction for one- and two-dimensional reaction-diffusion equations in such a way that the mesh is dense inside the boundary layers and coarse outside the layers. Essentially, in the layers, the mesh points are generated by a function which corresponds to the inverse of the boundary layer function. Moreover, the Bakhvalov mesh-generating function is continuously differentiable on the whole interval of integration. The Bakhvalov-type meshes due to Vulanović [39] generalize the Bakhvalov mesh still retaining the elegant smooth property of the mesh-generating function. However, the smoothness of these Bakhvalov-type meshes generally results in implicitly defined transition points between the fine and coarse parts of the mesh. This makes the error analysis more complicated than in the case of the meshes with predefined transition points, such as Shishkin-type meshes in the sense of Roos and Linß [17, 29] (see also [27]). The Shishkin-type meshes modify the original piecewise uniform Shishkin mesh [34] keeping its transition point. They are distinct from the Bakhvalov-type meshes because their mesh-generating functions are not smooth. For more detailed exposition of the layer-adapted mesh design, we refer the reader to Roos’ most recent survey [33], as well as to the monographs [7, 22, 30, 36], where the analysis of numerical methods applied on these meshes can also be found.

Reaction-diffusion problems are more easily solved and analyzed [31, Section 1.1] than the convection-diffusion problem (1). For instance, when finite-difference methods are used for two-dimensional reaction-diffusion elliptic problems, the complete analysis for Shishkin meshes is given in [5, 13], whereas a simpler unified analysis for both Bakhvalov-type and Shishkin-type meshes can be found in [12]. On the other hand, when a convection-dominated problem is discretized by finite-difference methods on Bakhvalov-type meshes rather than Shishkin-type meshes, the analysis becomes much more difficult and delicate [33, Section 1.2]. Indeed, the analysis of Shishkin-type meshes for the problem (1) was accomplished in 1999 by Linß and Stynes [18, 19] (see also their 2003 survey [17] and the error-expansion analysis on the standard Shishkin mesh by Kopteva [16]). This happened even before the first central finite-difference error analysis of reaction-diffusion problems obtained in 2005 by Clavero et al. [5], and later in [4] for the use of a third-order HODIE finite-difference scheme. However, for Bakhvalov-type meshes no similar result, even for the standard upwind scheme, has been known for two decades (see [31, Question 6]). The very first attempt to solve this important open problem is given in a recent work by Nhan and Vulanović [28]. The main result in [28] is a complete analysis of the one-dimensional analogue of (1) discretized on the simplest Bakhvalov-type mesh from [39] for which the transition point can be written explicitly, but the authors also briefly outline an extended analysis for 2D problems. An early use of this simplest Bakhvalov-type mesh for two-dimensional problems can be found in [40], where a second-order hybrid finite-difference method is designed and analyzed. However, the problem considered there is much simpler than (1) (b₂(x,y) ≡ 0 and b₁(x,y) ≡ b₁(x) are assumed) and ε-uniform convergence is not proved.

The purpose of the current paper is to provide for the first time a complete analysis of the original Bakhvalov mesh when it is employed to discretize the stationary convection-diffusion problem (1) by the upwind scheme. Therefore, our result fills a long-standing theoretical gap in the analysis of the Bakhvalov-type meshes for higher-dimensional convection-diffusion problems. The analysis presented in this paper is even more compelling because, in 1D, several special techniques have been used to provide parameter-uniform convergence proofs for Bakhvalov-type meshes, such as the use of the hybrid-stability inequality [1, 14, 15, 23, 29] and the preconditioning-based analysis proposed recently in [24,25,26, 38], but none of them has been extended to 2D problems (cf. [22, Remark 9.2] and [24]). On the other hand, the truncation error and barrier function approach, which has been widely used in the analysis of Shishkin-type meshes [11, 18, 19, 21, 35], has not been applied to any Bakhvalov-type mesh even for 1D problems until the recent appearance of [28]. It is the same truncation error and barrier function approach from [28] that we follow here.

The paper is organized as follows. In the next section, we review some well-known preliminary results regarding the behavior of the exact solution and we also introduce the upwind difference discretization on an arbitrary mesh. This is followed by Section 3, where we describe the Bakhvalov mesh for the convection-diffusion problem (1) and established its important properties for the later analysis. A complete truncation error analysis is given in Section 4, and then an appropriate barrier function is constructed in Section 5 and used to prove the parameter-uniform convergence. Numerical results that support our theoretical findings are reported in Section 6. Finally, a short concluding remark is presented in the last section.

2 Preliminaries and the upwind discretization

In accordance with the established practice, we use C to denote a generic positive constant independent of ε and the discretization parameter N. Let $C^{n}(\bar {{\varOmega }})$ and $C^{n,1}(\bar {{\varOmega }})$ be the spaces of functions defined on $\bar {{\varOmega }}$ whose derivatives up to the n-th order are continuous and, respectively, Lipschitz-continuous. Let ∥⋅∥_n denote the $L^{\infty }$-type norm in $C^{n}(\bar {{\varOmega }})$ and |⋅|_n, |⋅|_n,1 denote the $L^{\infty }$-type seminorms in $C^{n}(\bar {{\varOmega }})$ and $C^{n,1}(\bar {{\varOmega }})$.

Lemma 1 (Shishkin-type decomposition)

Suppose that f satisfies the compatibility conditions (see, for instance, [19, Theorem 2.1]). Then the boundary-value problem (1) has a classical solution $u\in C^{3,1}\left (\bar {{\varOmega }}\right )$ and this solution can be decomposed as

$$ u=S+E_{1}+E_{2}+E_{12}, $$

where, for all $(x,y)\in \bar {{\varOmega }}$, we have

$$ \left\|S\right\|_{2} + \varepsilon\left|S\right|_{2,1} \le C, $$

(2)

$$ \left|\frac{\partial^{k+\ell}E_{1}}{\partial x^{k} \partial y^{\ell}}(x,y)\right|\le C \varepsilon^{-k}e^{-\beta_{1} x/\varepsilon}, $$

(3)

$$ \left|\frac{\partial^{k+\ell}E_{2}}{\partial x^{k} \partial y^{\ell}}(x,y)\right|\le C \varepsilon^{-\ell}e^{-\beta_{2} y/\varepsilon}, $$

(4)

and

$$ \left|\frac{\partial^{k+\ell}E_{12}}{\partial x^{k} \partial y^{\ell}}x,y)\right|\le C \varepsilon^{-(k+\ell)}e^{-(\beta_{1} x+\beta_{2} y)/\varepsilon}, $$

(5)

for 0 ≤ k + ℓ ≤ 3. Furthermore,

$$ \left|\mathcal{L}E_{1}(x,y)\right|\le C e^{-\beta_{1} x/\varepsilon}, $$

(6)

$$ \left|\mathcal{L}E_{2}(x,y)\right|\le C e^{-\beta_{2} y/\varepsilon}, $$

(7)

and

$$ \left|\mathcal{L}E_{12}(x,y)\right|\le C e^{-(\beta_{1} x+\beta_{2} y)/\varepsilon}. $$

(8)

Let ${\varOmega }^{N}=\left \{(x_{i},y_{j}):\ i,j=0,1,\ldots , N\right \}$ be the discretization mesh, where the mesh point coordinates x_i and y_j satisfy

$$ 0=x_{0}<x_{1}<\cdots<x_{N}=1\quad \text{and}\quad 0=y_{0}<y_{1}<\cdots<y_{N}=1. $$

We denote ${\varGamma }^{N}= {\varGamma } \bigcap {\varOmega }^{N}$, and also set $h_{x,i}=x_{i}-x_{i-1},\ \hbar _{x,i}=(h_{x,i+1}+h_{x,i})/2$ and $h_{y,j}=y_{j}-y_{j-1},\ \hbar _{y,j}=(h_{y,j+1}+h_{y,j})/2$. Given a mesh function $\{{w}_{ij}^{N}\}$ on Ω^N, we discretize the problem (1) by the standard upwind scheme as follows,

$$ \begin{array}{lll} \mathcal{L}^{N} {w}_{ij}^{N}:=\left( -\varepsilon({{D}_{x}^{2}} +{{D}_{y}^{2}})- b_{1,ij}{D}_{x}^{+} -b_{2,ij}{D}_{y}^{+}+c_{ij}\right)&w_{ij}^{N}&=f_{ij} \ \ \text{on}\ \ {\varOmega}^{N}\backslash {\varGamma}^{N},\\ &{w}_{ij}^{N}&=0 \ \ \text{on} \ \ {\varGamma}^{N}, \end{array} $$

(9)

with

$$ {{D}_{x}^{2}} {w}_{ij}^{N} = \frac{1}{\hbar_{x,i}}\left( {D}_{x}^{+}{w}_{ij}^{N} - D^{-}_{x}{w}_{ij}^{N}\right), \quad {{D}_{y}^{2}} {w}_{ij}^{N} = \frac{1}{\hbar_{y,j}}\left( {D}_{y}^{+}{w}_{ij}^{N} - {D}_{y}^{-}{w}_{ij}^{N}\right), $$

$$ D^{-}_{x}{w}_{ij}^{N}=\frac{{w}_{ij}^{N}-w^{N}_{i-1,j}}{h_{x,i}}, \quad {D}_{x}^{+}{w}_{ij}^{N}=\frac{w^{N}_{i+1,j}-w^{N}_{i,j}}{h_{x,i+1}}, $$

$$ {D}_{y}^{-}{w}_{ij}^{N}=\frac{{w}_{ij}^{N}-w^{N}_{i,j-1}}{h_{y,j}}, \quad {D}_{y}^{+}{w}_{ij}^{N}=\frac{w^{N}_{i,j+1}-w^{N}_{i,j}}{h_{y,j+1}}. $$

We split ${\mathscr{L}}^{N}$ into ${{\mathscr{L}}}_{x}^{N}+ {{\mathscr{L}}}_{y}^{N}$, where

$$ {\mathcal{L}}_{x}^{N}{w}_{ij}^{N}=\left( -\varepsilon {{D}_{x}^{2}} -b_{1,ij}{D}_{x}^{+}+c_{ij}\right){w}_{ij}^{N} \ \ \text{and} \ \ {\mathcal{L}}_{y}^{N}{w}_{ij}^{N}= \left( -\varepsilon {{D}_{y}^{2}} -b_{2,ij}{D}_{y}^{+}\right){w}_{ij}^{N}. $$

The matrix associated with the discrete operator ${\mathscr{L}}^{N}$ is an M-matrix. Therefore, the following discrete comparison principle holds.

Lemma 2

The operator ${\mathscr{L}}^{N}$ satisfies a discrete comparison principle, that is, if $\left \{v_{ij}\right \}$ and $\left \{w_{ij}\right \}$ are two mesh functions satisfying $\left |v_{ij}\right |\le w_{ij}$ on Γ^N, and $\left |{\mathscr{L}}^{N}v_{ij}\right |\le {\mathscr{L}}^{N} w_{ij}$ on Ω^N ∖Γ^N, then $\left |v_{ij}\right |\le w_{ij}$ on Ω^N.

We also have the standard truncation error bounds for the discrete operator ${\mathscr{L}}^{N}$ as below.

Lemma 3 (cf. Lemma 3.2 in 19 and Lemma 8 in [18])

Let g(x,y) be a smooth function defined on Ω. Then the following estimates for the truncation error hold:

$$ \left|{\mathcal{L}}_{x}^{N} g_{ij}-\left( \mathcal{L}_xg\right)_{ij}\right| \le C \left( h_{x,i}+h_{x,i+1}\right) \left( b_{ij}\left|\frac{\partial^2 g}{\partial x^2}(x,y)\right|_0 + \varepsilon\left|\frac{\partial^2 g}{\partial x^2}(x,y)\right|_{0,1}\right), $$

(10)

and

$$ \left|{\mathcal{L}}_{x}^{N} g_{ij}-\left( \mathcal{L}_xg\right)_{ij}\right| \le C \left( \varepsilon {\int}_{x_{i-1}}^{x_{i+1}}\left|\frac{\partial^3g}{\partial x^3} (\zeta,y_j)\right|d\zeta + {\int}_{x_{i-1}}^{x_i} \left|\frac{\partial^2g}{\partial x^2} (\zeta,y_j)\right|d\zeta \right), $$

(11)

for 0 < i, j < N, with analogous estimates for $\left |{{\mathscr{L}}}_{y}^{N} g_{ij}-\left ({\mathscr{L}}_{y}g\right )_{ij}\right |$.

3 The Bakhvalov mesh for convection-diffusion problems

The original Bakhvalov mesh is presented in [2] as a discretization mesh for the reaction-dominated problems with characteristic boundary layers. In this section, we adopt his idea and describe the version for the problem (1) with exponential layers. Furthermore, a careful analysis of mesh properties that are needed for the later error analysis is also given.

The coordinates of the mesh points, x_i and y_j, of the Bakhvalov mesh are generated by functions λ₁(t) and λ₂(t) with t ∈ [0,1] in the sense that x_i = λ₁(t_i) and y_i = λ₂(t_i), where t_i = i/N for i = 0,1,…,N. Then we form the mesh Ω^N using the Bakhvalov mesh points (x_i,y_j). For simplicity, from now on, we only consider identical mesh-generating functions λ₁ and λ₂, denoting them jointly by λ.

The mesh-generating function λ is defined as follows:

$$ \lambda(t)= \begin{cases} \psi(t), & t\in[0,\alpha],\\ \psi(\alpha)+\psi^{\prime}(\alpha)(t-\alpha), & t\in [\alpha,1], \end{cases} $$

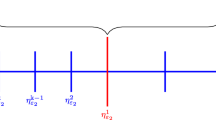
with ψ(t) = aεϕ(t) and $\phi (t):=\ln \frac {q}{q-t}$ for t ∈ [0,q), where a and q are fixed positive mesh parameters such that q ∈ (0,1) and $\psi ^{\prime }(0)<1$, that is, aε^∗ < q. Speaking of the mesh points on either the x- or the y-axis, the value of ψ(α) represents the transition point from the mesh graded in the layer to the uniform mesh outside the layer. The transition point is defined implicitly via α, which is the solution of the nonlinear equation

$$ \psi(\alpha) + \psi^{\prime}(\alpha)(1-\alpha) = 1 $$

(the part of λ on [α,1] is the tangent line from the point (1,1) to ψ, touching ψ at (α,ψ(α)).

Remark 1

If we want the points x_i and y_i, i = 0,1,…,N, to be generated by two different respective functions λ₁ and λ₂, then each function has its own constants a and q, and consequently, different values of α.

Since we do not know the point α in general, we consider auxiliary points α₁ and α₂ such that

$$ \psi^{\prime}(\alpha_{1}) = \frac{1}{1-q} \ \ \text{and} \ \ \psi^{\prime}(\alpha_{2}) = 1. $$

The line through the points (q,0) and (1,1) has the slope 1/(1 − q) and it is steeper than the tangent line from (1,1) to ψ(t), whose slope is $\psi ^{\prime }(\alpha )$. Therefore, α < α₁ < q because $\psi ^{\prime }(t)$ is monotonically increasing on [0,q). Similarly, we also have 0 < α₂ < α. Figure 1 illustrates this construction graphically.

Fig. 1

The Bakhvalov mesh-generating function, λ(t) on [0,1] (left) and its zoomed-in portion (right) for ε = 10^− 2, q = 1/2, and a = 2

We now prove some properties of the Bakhvalov mesh. We state them for h_i, which stands for both h_x,i and h_y,i, i = 1,2,…,N.

Lemma 4

$$ h_{i-1}\le h_{i}\le \frac{1}{(1-q)N}, \ \ i=2,3,\ldots, N, $$

(12)

and

$$ q-a\varepsilon < \alpha < q-a(1-q)\varepsilon. $$

(13)

Proof

It is easy to see that $\phi ^{\prime \prime }(t)=\frac {1}{(q-t)^{2}}>0$ for t ∈ [0,q), and

$$ \lambda^{\prime}(t)= \begin{cases} \psi^{\prime}(t), & t\in[0,\alpha],\\ \psi^{\prime}(\alpha), & t\in [\alpha,1]. \end{cases} $$

(14)

Therefore, $\lambda ^{\prime }(t)$ is non-decreasing and (12) follows from

$$ \begin{array}{ll} h_{i-1}&\le h_{i}={\int}_{t_{i-1}}^{t_i} \lambda^{\prime}(s) ds \le N^{-1} \lambda^{\prime}(t_i) \\ &\le N^{-1} \psi^{\prime}(\alpha) \le N^{-1} \psi^{\prime}(\alpha_{1}) =\frac{1}{(1-q)N}, \ \ i=2,\ldots, N. \end{array} $$

(15)

To show (13), use $\psi ^{\prime }(\alpha _{1})= \frac {1}{1-q}$ again to get

$$ a\varepsilon \phi^{\prime}(\alpha_{1})=\frac{a\varepsilon}{q-\alpha_{1}}=\frac{1}{1-q}. $$

It follows that α₁ = q − (1 − q)aε which yields the second inequality in (13). A similar work with $\psi ^{\prime }(\alpha _{2})=1$ yields the remaining estimate in (13). □

The estimates (13) imply important lower and upper bounds for q − α, which are occasionally used later in the error analysis:

$$ a(1-q)\varepsilon<q-\alpha<a\varepsilon. $$

(16)

Let J be the index such that

$$ t_{{J}-1} < \alpha \le t_{J}. $$

(17)

The next lemma provides more estimates of the mesh width in the layer region.

Lemma 5

Let t_J ≤ q. Then we have

$$ \frac{a\varepsilon}{q} N^{-1}\le h_{i}\le a\varepsilon , \quad i=1,2,\ldots,J-1 $$

(18)

Proof

By (17), for i ≤ J − 1 we have

$$ \begin{array}{ll} h_{i} &= a\varepsilon {\int}_{t_{i-1}}^{t_{i}}\phi^{\prime}(s) ds\ge \frac{a\varepsilon}{N}\phi^{\prime}(t_{i-1})\ge \frac{a\varepsilon}{N} \frac{1}{q-t_{i-1}} \ge \frac{a\varepsilon}{q} N^{-1}. \end{array} $$

On the other hand,

$$ \begin{array}{ll} h_{i} &= a\varepsilon {\int}_{t_{i-1}}^{t_{i}}\phi^{\prime}(s) ds\le \frac{a\varepsilon}{N}\phi^{\prime}(t_{i})= \frac{a\varepsilon}{N} \frac{1}{q-t_{i}} \le \frac{a\varepsilon}{N} \frac{1}{(t_{J}-t_{J-1})}\le a \varepsilon, \end{array} $$

which completes the proof of (18). □

Remark 2

Without the condition t_J ≤ q, the estimate in Lemma 5 are true for i ≤ J − 2.

We now consider step-size estimates for the case q < t_J. We also define

$$\displaystyle t_{J-1/2}=\frac{t_{J-1}+t_{J}}{2}=\frac{J-1/2}{N}.$$

Lemma 6

Let q < t_J. Then the following estimates are satisfied:

• When α ≤ t_J− 1/2, we have

  $$ h_{J}\ge \left( 2N\right)^{-1}. $$

  (19)

• When t_J− 1/2 < α, we have

  $$ h_{J-1}\le 2a\varepsilon. $$

  (20)

Proof

First, consider α ≤ t_J− 1/2. In this case, $h_{J}^{}=x_{J}^{}-x_{J-1}^{}=(x_{J}-x_{\alpha })+(x_{\alpha }-x_{J-1})$ with x_α = ψ(α). It follows that

$$ \begin{array}{ll} h_{J}&\ge x_{J}-x_{\alpha}=\psi^{\prime}(\alpha)(t_{J}-\alpha)=a\varepsilon \phi^{\prime}(\alpha)(t_{J}-\alpha)\\ &\ge \frac{a \varepsilon }{q-\alpha}\left( t_{J}-\alpha\right)\ge \frac{a \varepsilon }{q-\alpha}\left( t_{J}-t_{J-1/2}\right) \ge \frac{1}{2N}, \end{array} $$

where we used (16) in the last inequality.

Second, for t_J− 1/2 < α, because t_J− 1 < t_J− 1/2 < α < q, we have

$$ \begin{array}{ll} h_{J-1}&=a\varepsilon {\int}_{t_{J-2}}^{t_{J-1}}\phi^{\prime}(s) ds\le \frac{a\varepsilon}{N}\phi^{\prime}(t_{J-1}) \le \frac{a\varepsilon}{N}\cdot \frac{1}{q-t_{J-1} } \\ & \le \frac{a\varepsilon}{N}\cdot\frac{1}{t_{J-1/2}-t_{J-1}}\le 2a\varepsilon, \end{array} $$

which gives (20). □

4 The truncation error analysis

The numerical solution ${w}_{ij}^{N}$ of the upwind finite-difference discretization is decomposed analogously to its continuous counterpart:

$$ {w}_{ij}^{N} = S_{ij}^{N} + E_{1,ij}^{N} + E_{2,ij}^{N} + E_{12, ij}^{N}, $$

for which

$$ \mathcal{L}^{N}S_{ij}^{N}=\left( \mathcal{L}S\right)_{ij},\ \mathcal{L}^{N}E_{1,ij}^{N}=\left( \mathcal{L}E_{1}\right)_{ij}, \ \mathcal{L}^{N}E_{2,ij}^{N}=\left( \mathcal{L}E_{2}\right)_{ij}, \ \mathcal{L}^{N}E{}_{12,ij}^{N}=\left( \mathcal{L}E_{12}\right)_{ij}\ \text{on} \ {\varOmega}^{N}\setminus {\varGamma}^{N}, $$

and

$$ S_{ij}^{N}=S_{ij},\ E_{1,ij}^{N} = E_{1,ij},\ \ E_{2,ij}^{N} = E_{2,ij}, \ E_{12,ij}^{N} = E_{12,ij} \ \text{on}\ {\varGamma}^{N}. $$

(21)

Let

$$ \mathcal{L}^{N} \left( u_{ij}\right) -\left( \mathcal{L} u\right)_{ij} =\mathcal{L}^{N} \left( u_{ij}-{w}_{ij}^{N}\right),\quad 1\le i, j \le N-1, $$

be the truncation (consistency) error of the upwind discretization of the problem (1) on the Bakhvalov mesh. We establish the upper bounds for the truncation error by using

$$ \begin{array}{ll} \left|\mathcal{L}^{N} \left( u_{ij}-{w}_{ij}^{N}\right) \right|&\le \left|\mathcal{L}^{N} \left( S_{ij}-S_{ij}^{N}\right) \right| + \left|\mathcal{L}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\\ \qquad &+ \left|\mathcal{L}^{N} \left( E_{2,ij}-E_{2,ij}^{N}\right) \right|+\left|\mathcal{L}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right|\\ &\le {\tau}_{ij}^{x}+ \tau_{ij}^{y}, \end{array} $$

(22)

where we set

$$ \begin{array}{ll} {\tau}_{ij}^{x}:&= \left|{\mathcal{L}}_{x}^{N} \left( S_{ij}-S_{ij}^{N}\right) \right| + \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\\ \qquad&+\left|{\mathcal{L}}_{x}^{N} \left( E_{2,ij}-E_{2,ij}^{N}\right) \right|+\left|{\mathcal{L}}_{x}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right| \end{array} $$

and

$$ \begin{array}{ll} \tau_{ij}^{y}:&= \left|{\mathcal{L}}_{y}^{N} \left( S_{ij}-S_{ij}^{N}\right) \right| + \left|{\mathcal{L}}_{y}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\\ \qquad &+\left|{\mathcal{L}}_{y}^{N} \left( E_{2,ij}-E_{2,ij}^{N}\right) \right|+\left|{\mathcal{L}}_{y}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right|. \end{array} $$

We will bound each term of ${\tau }_{ij}^{x}$ and $\tau _{ij}^{y}$ separately. For the regular part S of the solution, the standard argument (see also [19]) is applied by invoking Lemma 1 and the first estimate in Lemma 3, as well as the mesh property (12) to obtain

$$ \left|{\mathcal{L}}_{x}^{N} \left( S_{ij}-S_{ij}^{N}\right) \right|\!\le CN^{-1} \text{ and } \left|{\mathcal{L}}_{y}^{N} \left( S_{ij}-S_{ij}^{N}\right) \right|\le CN^{-1}\quad \text{for}\quad 1\!\le i,\ j \!\le N-1. $$

(23)

Let

$$ \bar E_{ij}^{x}= \prod\limits_{k=1}^{i}\left( 1+ \frac{\beta_{1} h_{x,k}}{2\varepsilon}\right)^{-1} $$

and let $\bar E_{ij}^{y}$ be defined in the same way with β₂ instead of β₁.

In the next two lemmas we provide the truncation error estimate for the layer parts E₁ and E₂, as well as for the corner part E₁₂.

Lemma 7

Let aβ₁ ≥ 2. Then, for any j = 1,2,…,N − 1, the bound on $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{1,ij}-E_{1,ij}^{N}\right ) \right |$ can be given as follows.

• For i ≥ J,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\le CN^{-1}. $$

  (24)

• For i ≤ J − 2,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\le C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right). $$

  (25)

• For i = J − 1,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\le \begin{cases} C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right),& \text{if } \ h_{x,i}\le \varepsilon,\\ C\left( N^{-1}+h_{x,i+1}^{-1}\bar E_{ij}^{x}N^{-1}\right),&\text{if } \ h_{x,i}>\varepsilon. \end{cases} $$

  (26)

Also,

$$ \left|{\mathcal{L}}_{x}^{N} \left( E_{2,ij}-E^{N}_{2 ,ij}\right) \right|\le CN^{-1}. $$

(27)

Proof

Throughout the proof, let 1 ≤ j ≤ N − 1. For the detail of this proof technique, we refer the reader to [28, Lemma 3.1].

We begin by asserting (24) for i ≥ J + 1. We apply (11) to E₁, use (3), and note that in this case t_i− 1 ≥ t_J ≥ α. Then we have

$$ \begin{array}{ll} \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right| &\le CN^{-1}\lambda^{\prime}(t_{i+1})\varepsilon^{-2}e^{-\beta_{1}\lambda(t_{i-1})/\varepsilon}\le CN^{-1} \varepsilon^{-2} e^{-a\beta_{1} \phi(\alpha)} \\ &\le CN^{-1} \varepsilon^{-2} \left( e^{-\phi(\alpha)}\right)^{a\beta_{1}} \le CN^{-1} \varepsilon^{-2} \left( \frac{q-\alpha}{q}\right)^{a\beta_{1}}\le CN^{-1}, \end{array} $$

where we have used (16) and aβ₁ ≥ 2 in the last inequality.

To prove (24) for i = J, we consider two cases: ε ≤ N^− 1 and ε > N^− 1. First, for i = J and ε ≤ N^− 1, our approach is

$$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\le \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}\right) \right|+ \left|\left( \mathcal{L}_{x} E_{1}\right)_{ij} \right| $$

(28)

and then we bound each term on the right-hand side separately. Using the estimate (6) at i = J we get

$$ \begin{array}{ll} \left|\left( \mathcal{L}_{x} E_{1}\right)_{ij} \right| &\le Ce^{-\beta_{1} x_{J}/\varepsilon}\le C \left( e^{-\phi(\alpha)}\right)^{a\beta_{1}}\le C\left( \frac{q-\alpha}{q}\right)^{a\beta_{1}}\le C(\varepsilon)^{a\beta_{1}}\le CN^{-1}, \end{array} $$

(29)

where we used (16).As for $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{1,ij}\right ) \right |$, we have

$$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}\right) \right| \le P_{ij}^{x} + Q_{ij}^{x}+R_{ij}^{x}, $$

(30)

where $P_{ij}^{x}= \varepsilon \left |D_{x}^{^{2}} E_{1,ij}\right |, \ Q_{ij}^{x} = b_{1,ij}\left |D_{x}^{+}E_{1,ij}\right |, \ \ R_{ij}^{x}=c_{ij}\left |E_{1,ij}\right |,$ and

$$ \begin{array}{ll} P_{J,j}^{x} &\le C \hbar_{x,J}^{-1} e^{-\beta_{1} x_{J-1}/\varepsilon} \le C N\left( e^{-\phi(t_{J-1})}\right)^{a\beta_{1}} \le CN\left( \varepsilon+N^{-1}\right)^{a\beta_{1}}\le CN^{-1}, \end{array} $$

where we have used t_J− 1 < α ≤ t_J and (16) again. The same argument is employed to get $Q_{J,j}^{x}\le CN^{-1}$. For $R_{J,j}^{x}$, it is clear from (3) that

$$ R_{J,j}^{x}\le C e^{-\beta_{1} x_{J}/\varepsilon}\le CN^{-1}, $$

because of the arguments used in (29).

Second, for i = J and ε > N^− 1, it follows that h_x,J ≤ Cε because of (12). Therefore, we use (11) to continue as follows:

$$ \begin{array}{ll} \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|&\le CN^{-1} \varepsilon^{-2} e^{-\beta_{1} x_{J-1}/\varepsilon} \le CN^{-1} \varepsilon^{-2} e^{-\beta_{1} x_{J}/\varepsilon}\le CN^{-1}. \end{array} $$

This completes the proof of (24).

We combine the estimates (25) and (26) and prove them together. We consider two subcases:

• 1. when t_i− 1 ≤ q − 3/N, and

• 2. when q − 3/N < t_i− 1 < α.

• Subcase 1. Note that, when t_i− 1 ≤ q − 3/N, we have t_i+ 1 ≤ q − 1/N < q, so $\lambda ^{\prime }(t_{i+1}) \le a\varepsilon \phi ^{\prime }(t_{i+1})$ due to (14). Hence,

  $$ \begin{array}{ll} \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right| &\le CN^{-1}\lambda^{\prime}(t_{i+1})\varepsilon^{-2}e^{-\beta_{1} x_{i-1}/\varepsilon}\\ &\le C\varepsilon^{-1}N^{-1}\left( \frac{1}{q-t_{i+1}}\right)\left( e^{-\phi(t_{i-1})}\right)^{a\beta_{1}/2}e^{-\beta_{1} x_{i-1}/(2\varepsilon)}\\ &\le C\varepsilon^{-1}N^{-1}\bar{E}^{x}_{ij}. \end{array} $$

Here, for i = 1,2,…,J − 2, we used h_x,i ≤ aε due to Remark 2, and for i = J − 1, the assumption h_x,J− 1 ≤ ε in (26).

• Subcase 2. Note that in this case we have (q − t_i− 1) < 3N^− 1. Hence, we can proceed as follows:

  $$ \begin{array}{ll} \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right| &\le C\varepsilon^{-1} e^{-\beta_{1} x_{i-1}/2\varepsilon}e^{-\beta_{1} x_{i-1}/2\varepsilon}\\ &\le C\varepsilon^{-1} e^{-\beta_{1} x_{i}/(2\varepsilon)}e^{\beta_{1} h_{x,i}/(2\varepsilon)}\left( e^{-\phi(t_{i-1})}\right)^{a\beta_{1}/2}\\&\le C\varepsilon^{-1}\bar{E}^{x}_{ij}N^{-1}. \end{array} $$

  This completes the proof of (25) and the first estimate in (26).

Lastly, we show the second estimate in (26), that is, when i = J − 1 and h_x,i > ε, by considering the following cases:

$$ \left|{\mathcal{L}}_{x}^{N} \left( E_{1,ij}-E_{1,ij}^{N}\right) \right|\le \begin{cases} Ch_{x,i+1}^{-1}\bar{E}^{x}_{ij}N^{-1},& t_{J}\le q\\ CN^{-1}, &q<t_{J} \& \alpha\le t_{J-1/2}^{},\\ Ch_{x,i+1}^{-1}\bar{E}^{x}_{ij}N^{-1}, &q<t_{J} \& \alpha> t_{J-1/2}^{}. \end{cases} $$

(31)

First, when t_J ≤ q, due to (12), one gets ε ≤ CN^− 1. We again use the estimate in the form of (28), invoking (16) and (6) to get

$$ \begin{array}{ll} \left|\left( \mathcal{L}E_{1}\right)_{ij}\right|&\le C e^{-\beta_{1} x_{J-1}/\varepsilon} \le Ch_{x,J}^{-1} \bar{E}_{J-1,j}^{x}\left( e^{-\phi(t_{J-1})}\right)^{a\beta_{1}/2} \le Ch_{x,J}^{-1} \bar{E}_{J-1,j}^{x}N^{-1}. \end{array} $$

(32)

For $P_{J-1,j}^{x}$ (and analogously for $Q_{J-1,j}^{x}$), we use (16) and (18) again to obtain

$$ \begin{array}{ll} P_{J-1,j}^{x} &\le C \hbar_{x,J-1}^{-1} e^{-\beta_{1} x_{J-2}/\varepsilon} \le Ch_{x,J}^{-1} \bar{E}_{J-1,j}^{x}\left[\varepsilon+2N^{-1}\right] \le Ch_{x,J}^{-1} \bar{E}_{J-1,j}^{x}N^{-1}. \end{array} $$

(33)

This implies that $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{1,ij}\right ) \right | \le Ch_{x,J}^{-1} \bar {E}_{J-1,j}^{x}N^{-1}$ and, together with (32), asserts the first case of (31).

For h_x,i > ε, i = J − 1, $\alpha \le t_{J-1/2}^{}$ and q < t_J, we use (19) to get

$$ \begin{array}{ll} P_{J-1,j}^{x}&\le C\hbar_{x,J-1}^{-1}e^{-\beta_{1} x_{J-2}/\varepsilon}\le Ch_{x,J}^{-1}\left( e^{-\phi(t_{J-2})}\right)^{a\beta_{1}} \le C N \left( \frac{q-t_{J-2}}{q}\right)^{a\beta_{1}}\le CN^{-1} \end{array} $$

because t_J− 1 < q < t_J. We apply a similar argument to $Q_{J-1,j}^{x}$, and also

$$ \begin{array}{ll} \left|\left( \mathcal{L}E_{1}\right)_{ij}\right|&\le C e^{-\beta_{1} x_{J-1}/\varepsilon} \le C\left( e^{-\phi(t_{J-1})}\right)^{a\beta_{1}/2}\le C\left( \frac{q-t_{J-1}}{q}\right)^{a\beta_{1}/2}\le CN^{-1}. \end{array} $$

This implies that $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{1,ij}-E_{1,ij}^{N}\right ) \right |\le CN^{-1}$, which is the second estimate in (31).

For h_x,i > ε (again, ε ≤ CN^− 1 by (12)), i = J − 1, α > t_J− 1/2, and q < t_J, because of (20), we can bound $P_{J-1,j}^{x}$ and $Q_{J-1,j}^{x}$ as in (33), and $\left |\left ({\mathscr{L}}E_{1}\right )_{ij}\right |$ as in (32), which yields the last case of (31).

For $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{2,ij}-E_{2,ij}^{N}\right ) \right |$, because of (4) and (11), we can easily show that, with arbitrary h_y,j,

$$ \left|{\mathcal{L}}_{x}^{N} \left( E_{2,ij}-E_{2,ij}^{N}\right) \right|\le C\left( \varepsilon h_{x,i+1}+h_{x,i}\right) \le C N^{-1}, \quad 1\le i\le N-1, $$

where we used the property h_x,i ≤ CN^− 1,i = 1,2,…,N. This completes the proof. □

Lemma 8

Let aβ₁ ≥ 2. The upper bound on $\left |{{\mathscr{L}}}_{x}^{N} \left (E_{12,ij}-E{}_{12,ij}^{N}\right ) \right |$, for any j = 1,2,…,N − 1, satisfies the following.

• For i ≥ J,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right|\le CN^{-1}. $$

• For i ≤ J − 2,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right|\le C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right). $$

• For i = J − 1,

  $$ \left|{\mathcal{L}}_{x}^{N} \left( E_{12,ij}-E{}_{12,ij}^{N}\right) \right|\le \begin{cases} C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right)& \text{if } \ h_{x,i}\le \varepsilon,\\ C\left( N^{-1}+h_{x,i+1}^{-1}\bar E_{ij}^{x}N^{-1}\right) &\text{if } \ h_{x,i}>\varepsilon. \end{cases} $$

Proof

We observe the following two key estimates that make the analysis in the proof of Lemma 7 work for the E₁₂ component. Lemma 1 implies

$$\left| \mathcal{L}E_{12}(x,y)\right|\le C e^{-\beta_{1} x/\varepsilon}e^{-\beta_{2} y/\varepsilon}\le C e^{-\beta_{1} x/\varepsilon},$$

and

$$\left|\frac{\partial^{i} E_{12}}{\partial x^{i}}(x,y)\right|\le C \varepsilon^{-i}e^{-\beta_{1} x/\varepsilon}e^{-\beta_{2} y/\varepsilon}\le C \varepsilon^{-i}e^{-\beta_{1} x/\varepsilon}.$$

Hence, arguments analogous to those in the proof of Lemma 7 can be applied to prove the assertions. □

Combining Lemmas 7 and 8 with (23) and invoking (22), we arrive at the main result of this section, the truncation error estimate for the upwind discretization of the problem (1) on the Bakhvalov mesh.

Theorem 1

Let aβ₁ ≥ 2 and aβ₂ ≥ 2. Then the truncation error of the upwind discretization of the problem (1) on the Bakhvalov mesh satisfies

$$ \begin{array}{ll} \left|\mathcal{L}^{N} \left( u_{ij}\right) -\left( \mathcal{L} u\right)_{ij} \right| &\le {\tau}_{ij}^{x}+ \tau_{ij}^{y}, \end{array} $$

where for ${\tau }_{ij}^{x}$ and any j = 1,2,…,N − 1, we have,

• for i ≥ J,

  $$ {\tau}_{ij}^{x}\le CN^{-1}, $$

  (34)

• for i ≤ J − 2,

  $$ {\tau}_{ij}^{x}\le C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right) $$

• for i = J − 1,

  $$ {\tau}_{ij}^{x}\le \begin{cases} C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{x}N^{-1}\right) & \text{if } \ h_{x,i}\le \varepsilon,\\ C\left( N^{-1}+h_{x,i+1}^{-1}\bar E_{ij}^{x}N^{-1}\right) &\text{if } \ h_{x,i}>\varepsilon, \end{cases} $$

  (35)

whereas $\tau _{ij}^{y}$, for any i = 1,2,…,N − 1, can be bounded as follows:

• for j ≥ J,

  $$ \tau_{ij}^{y}\le CN^{-1}, $$

• for j ≤ J − 2,

  $$ \tau_{ij}^{y}\le C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{y}N^{-1}\right) $$

• for j = J − 1,

  $$ \tau_{ij}^{y}\le \begin{cases} C\left( N^{-1}+\varepsilon^{-1}\bar E_{ij}^{y}N^{-1}\right)& \text{if } \ h_{y,j}\le \varepsilon,\\ C\left( N^{-1}+h_{y,j+1}^{-1}\bar E_{ij}^{y}N^{-1}\right) &\text{if } \ h_{y,j}>\varepsilon. \end{cases} $$

5 The barrier function and uniform convergence result

We now proceed to form a barrier function. Set

$$ \gamma_{ij}=\gamma_{ij}^{x}+\gamma_{ij}^{y}, \ \ 1\le i,j\le N-1, $$

with

$$ \gamma_{ij}^{x}=C_{1}(1-x_{i})N^{-1} + C_{2}\bar E_{ij}^{x} N^{-1}\ \ \text{and} \ \ \gamma_{ij}^{y}=C_{3}(1-y_{j})N^{-1}+ C_{4}\bar E_{ij}^{y} N^{-1}, $$

where C_k, k = 1,2,3,4, are appropriately chosen positive constants independent of both ε and N.

Lemma 9

Let aβ₁ ≥ 2 and aβ₂ ≥ 2. Then, there exist sufficiently large constants C_k, k = 1,2,3,4, such that

$$ \mathcal{L}^{N}\gamma_{ij} = \mathcal{L}^{N}\gamma^{x}_{ij}+\mathcal{L}^{N}\gamma^{y}_{ij} \ge {\kappa}_{ij}^{x}+ {\kappa}_{ij}^{y}\ge {\tau}_{ij}^{x}+ \tau_{ij}^{y}, \ \ 1\le i,j\le N-1, $$

where

$$ {\kappa}_{ij}^{x} = C_{1}N^{-1}+C_{2}[\max\{\varepsilon,h_{x,i+1}\}]^{-1}\bar{E}^{x}_{ij}N^{-1}, $$

and

$$ {\kappa}_{ij}^{y} = C_{3}N^{-1}+C_{4}[\max\{\varepsilon,h_{y,j+1}\}]^{-1}\bar{E}^{y}_{ij}N^{-1}. $$

Proof

It is easy to verify that ${{\mathscr{L}}}_{x}^{N}\gamma _{ij}\ge {\kappa }_{ij}^{x}$ and ${{\mathscr{L}}}_{y}^{N}\gamma _{ij} \ge {\kappa }_{ij}^{y}$, see, for instance, [11, 27, 35]. Therefore, using Theorem 1, we will show that

$$ {\tau}_{ij}^{x}\le {\kappa}_{ij}^{x}, \quad 1\le j\le N-1, $$

for various values of the index i.

Let 1 ≤ j ≤ N − 1 throughout the proof again. It is clear from (34) that

$$ {\tau}_{ij}^{x} \le CN^{-1} \le C_{1}N^{-1}\le{\kappa}_{ij}^{x} , \quad i=J,J+1,\ldots, N-1. $$

It remains to prove that ${\tau }_{ij}^{x}\le {\kappa }_{ij}^{x}$ for i ≤ J − 1. If i ≤ J − 3, then h_x,i+ 1 ≤ aε because of Remark 2, in which the estimate (18) holds for i ≤ J − 2. Therefore,

$$ {\tau}_{ij}^{x}\le C\left( N^{-1}+\varepsilon^{-1}\bar{E}^{x}_{ij}N^{-1}\right) \le C_{1}N^{-1}+C_{2}\varepsilon^{-1}\bar{E}_{ij}^{x}N^{-1}\le {\kappa}_{ij}^{x}, \quad \text{for any } i\le J-3. $$

(36)

Next, for i = J − 2,J − 1, we consider two cases: h_x,i > ε and h_x,i ≤ ε. First, when h_x,i > ε, it is clear that h_x,i+ 1 ≥ h_x,i which immediately yields ${\tau }_{J-1,j}^{x} \le \kappa ^{x}_{J-1,j}$ because of (35).

For i = J − 2 and h_x,J− 2 > ε (which implies CN^− 1 > ε), we can also prove that

$${\tau}_{J-1,j}^{x} \le C (N^{-1}+ {h}_{x,J-1}^{-1}{\bar{E}}_{J-2,j}^{x}N^{-1}),$$

by invoking (28), (30), h_x,J− 2 ≤ aε by Remark 2, while analogous arguments can be used to obtain the bounds of $Q_{J-2,j}^{x}$, $\left |\left ({\mathscr{L}}E_{1}\right )_{J-2,j}\right |,$ and $\left |\left ({\mathscr{L}}E_{12}\right )_{J-2,j}\right |$.

Second, we consider h_x,i ≤ ε and i = J − 2,J − 1. If h_x,i+ 1 ≤ ε, we have the same situation as in the estimate (36). On the other hand, when h_x,i+ 1 > ε for i = J − 2,J − 1, this implies that $\max \limits \{\varepsilon , h_{x,i+1}\}=h_{x,i+1}$ and ε ≤ CN^− 1, so, by modifying the approach in (33), we can also show that

$$ {\tau}_{ij}^{x}\le C\left( N^{-1}+h_{x,i+1}^{-1}\bar{E}_{ij}^{x}N^{-1}\right). $$

Similar arguments, when applied to $Q^{x}_{ij},$ $\left |\left ({\mathscr{L}}_{x}E_{1}\right )_{ij}\right |,$ and $\left |\left ({\mathscr{L}}_{x}E_{12}\right )_{ij}\right |$ give,

$$ {\tau}_{ij}^{x}\le Ch_{x,i+1}^{-1}\bar{E}_{ij}^{x}N^{-1}\le {\kappa}_{ij}^{x}, \quad i=J-2,J-1. $$

Using analogous reasoning for $\tau _{ij}^{y}$, we are done. □

Theorem 2

Let aβ₁ ≥ 2 and aβ₂ ≥ 2. Then, for the upwind finite-difference method applied on the Bakhvalov mesh to the convection-diffusion problem (1), the error satisfies

$$ \left|u_{ij}-{w}_{ij}^{N}\right|\le CN^{-1}, \quad \text{for}\quad 0\le i,\ j\le N. $$

Proof

It is straightforward from (21) that

$$ \left|u_{ij}-{w}_{ij}^{N}\right|=0\le \gamma_{ij}\quad \text{on}\quad {\varGamma}^{N}. $$

Furthermore, Lemma 9 gives

$$ \left|\mathcal{L}^{N}\left( u_{ij}-{w}_{ij}^{N}\right)\right|\le \mathcal{L}^{N}\gamma_{ij} \quad \text{on}\quad {\varOmega}^{N}\setminus{\varGamma}^{N}. $$

Applying the discrete comparison principle, Lemma 2, we complete the proof. □

Remark 3

The above ε-uniform convergence result is more robust than what can be proved when the upwind scheme is used on the standard Shishkin mesh, in which case $\ln N$-factors occur in the error. Moreover, proofs of ε-uniform convergence on Shishkin-type meshes usually invoke the assumption ε ≤ N^− 1 (see [18, Assumption 3] and [22, page 12], for instance), which our proof method does not require.

6 Numerical results

In this section, we illustrate the numerical performance of the Bakhvalov mesh as the discretization mesh of the standard upwind difference scheme for the two-dimensional convection-diffusion problems of type (1). We consider two test problems. The first one is taken from [22, page 261],

$$ \begin{array}{lll} -\varepsilon {\Delta} u- (x+2)u_{x} -(y^{3}+3)u_{y} +&u= f(x,y) \quad &\text{on}\quad {\varOmega}=(0,1)^{2},\\ &u=0 \quad &\text{on}\quad {\varGamma}=\partial {\varOmega}, \end{array} $$

(37)

where f(x,y) is chosen so that

$$ u(x,y)= \cos\left( \frac{\pi x}{2}\right) \left( 1-e^{-2x/\varepsilon}\right) \left( 1-y\right)^{3}\left( 1-e^{-3y/\varepsilon}\right) $$

is the exact solution. It is clear that the solution has exponential boundary layers along the x = 0 and y = 0 edges. In this test problem, b₁(x,y) ≥ 2 and b₂(x,y) ≥ 3 for $(x,y)\in \bar {\varOmega }$. Therefore, the choice of the Bakhvalov mesh parameter a = 2 satisfies aβ₁ ≥ 2 and aβ₂ ≥ 2 as required by Theorem 2. We also choose q = 1/2.

The computed errors, denoted by E_N, are shown in Table 1, together with the rate of convergence ρ which is approximated numerically as

$$ \rho\approx \frac{\ln E_{N}- \ln E_{2N}}{\ln 2}. $$

Table 9.1 in [22] shows the errors for the same test problem with ε = 10^− 8 when the standard Shishkin mesh and the Bakhvalov-Shishkin mesh are used. We point out that the errors in Table 1 are less.

Table 1 Problem (37): errors and rates for the upwind discretization on the Bakhvalov mesh with a = 2 and q = 1/2

Our second test problem is

$$ \begin{array}{ll} -\varepsilon {\Delta} u- \left[x\sin\left( \frac{\pi}{4}y\right)+1\right]u_{x} -&\left[ye^{x}+1\right]u_{y} + \left[x^{2} + e^{2y}\right]u =5y\sin x\cos\left( \frac{\pi y}{2}\right)\\ &\quad \text{on}\quad {\varOmega}=(0,1)^{2},\\ &u=0 \quad \text{on}\quad {\varGamma} = \partial {\varOmega}, \end{array} $$

(38)

for which we do not know the exact solution. Therefore, we compute the errors by the double-mesh principle [7]. We use the same mesh parameters like above, a = 2 (here b_k(x,y) ≥ 1 for k = 1,2 and $(x,y)\in \bar {\varOmega }$) and q = 1/2. The upwind approximations and the rates of convergence are shown in Table 2. A computed solution when N = 2⁶ and ε = 10^− 3 is plotted in Fig. 2.

Table 2 Problem (38): errors and rates obtained by the double-mesh principle for the upwind discretization on the Bakhvalov mesh with a = 2 and q = 1/2

Fig. 2

The computed solution by double-mesh principle to the test problem (38)

7 Conclusion

Motivated by a long-standing open question in [31], related to the finite-difference analysis of convection-dominated problems, we generalized the new approach of the truncation error and barrier function technique, recently introduced in [28], from one-dimensional problems to 2D problems. Moreover, one of the simplest modifications of the Bakhvalov mesh was used in [28], whereas in the present paper, we considered the original Bakhvalov discretization mesh. For the upwind finite-difference scheme, we proved first-order convergence uniform in the perturbation parameter. We also confirmed the theoretical results experimentally. Our novel technical approach opens the door to the analysis of other unanswered questions related to Bakhvalov-type meshes in conjunction with convection-diffusion problems.