Keywords

Mathematics Subject Classification (2010)

1 Introduction

Solid bodies depart from their rest shape under the influence of applied loads. In case the applied loads or stresses are sufficiently small, many solids exhibit a linearly elastic and reversible behavior. If, however, the stress induced by the applied loads exceeds a certain threshold (the yield stress), the material behavior switches from the elastic to the so-called plastic regime. In this state, the overall loading process is no longer reversible and permanent deformations remain even after the loads are withdrawn. Mathematically, this leads to a description involving variational inequalities (VIs), or equivalently, complementarity conditions.

Plastic deformation is desired for instance as an industrial shaping technique of metal workpieces, as e.g. by deep-drawing of body sheets in the automotive industry. The task of finding appropriate time-dependent loads which effect a desired final deformation leads to optimal control problems for elastoplasticity systems. These problems are also motivated by the desire to reduce the amount of springback, i.e., the partial reversal of the final material deformation due to a release of the stored elastic energy once the loads are removed.

In this review, we concentrate for the sake of brevity on the model of static elastoplasticity with small strains in its so-called dual (stress-based) formulation, and with linear kinematic hardening. Within the project, similar results were achieved also for the more challenging quasi-static model, see [24–26] and the dissertation [23]. The system describing the quasi-static forward problem is given in Sect. 2.3. We also refer to [3] for the analysis of an optimal control problem involving the static primal (strain-based) counterpart.

According to the standard approach for infinite strains we do not distinguish between reference and actual configuration and identify \(\Omega \) with the workpiece under consideration. In its strong form, the static problem of elastoplasticity in its dual formulation with linear kinematic hardening reads

$$\displaystyle{ \left.\begin{array}{llll} \mathbb{C}^{-1}\boldsymbol{\sigma } + \boldsymbol{\varepsilon }(\boldsymbol{u}) +\lambda \, (\boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D}) & = \boldsymbol{0} &&\text{in }\Omega, \\ \mathbb{H}^{-1}\boldsymbol{\chi } +\lambda \, (\boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D}) & = \boldsymbol{0} &&\text{in }\Omega, \\ \mathrm{div} \boldsymbol{\sigma } & = -\boldsymbol{f} &&\text{in }\Omega, \\ \begin{array}{lll} \text{with complement. conditions}&&\;0 \leq \lambda \;\perp \;\phi (\boldsymbol{\Sigma })\\ \text{and boundary conditions} & &\;\boldsymbol{u} \end{array} &\begin{array}{ll} &\leq 0\\ & = \boldsymbol{0} \end{array} &&\begin{array}{ll} &\text{in }\Omega,\\ &\text{on } \Gamma _{ D}, \end{array} \\ \boldsymbol{\sigma }\,\mbox{ $\cdot$ }\,\boldsymbol{n} & = \boldsymbol{g} &&\text{on }\Gamma _{N}. \end{array} \quad \right \} }$$
(1.1)

The state variables consist of the stress \(\boldsymbol{\sigma }\) and back stress \(\boldsymbol{\chi }\), combined into the generalized stresses \(\boldsymbol{\Sigma } = (\boldsymbol{\sigma },\boldsymbol{\chi })\), plus the displacement \(\boldsymbol{u}\) and the plastic multiplier λ associated with the yield condition \(\phi (\boldsymbol{\Sigma }) \leq 0\) which we assume to be of von Mises type, see (2.1). The first two equations in (1.1), together with the complementarity conditions, represent the material law of static elastoplasticity. The tensors \(\mathbb{C}^{-1}\) and \(\mathbb{H}^{-1}\) are the inverses of the elasticity tensor (the compliance tensor) and of the hardening modulus, respectively, \(\boldsymbol{\sigma }^{D}\) denotes the deviatoric part of \(\boldsymbol{\sigma }\), while \(\boldsymbol{\varepsilon }(\boldsymbol{u})\) is the linearized strain. The third equation in (1.1) represents the equilibrium of forces. The boundary conditions correspond to clamping on \(\Gamma _{D}\) and the prescription of boundary loads \(\boldsymbol{g}\) on the remainder \(\Gamma _{N} = \Gamma \setminus \Gamma _{D}\).

Due to the complementarity between the plastic multiplier λ and the yield condition \(\phi (\boldsymbol{\Sigma })\), the optimal control of (1.1) leads to a mathematical program with complementarity constraints (MPCC) in function space. As is known already for finite dimensional MPCCs, classical constraint qualifications such as MFCQ fail to hold. To overcome these difficulties, several competing stationarity concepts tailored for MPCCs have been developed, see for instance [15, 21] for an overview in the finite dimensional case. For the infinite dimensional case, we refer to the classical works [1, 19, 20] and the recent contributions [14, 16, 22].

2 Optimal Control Problems in Small-Strain Static Elastoplasticity

In this section we present the optimal control problem under consideration. We set up some notation in Sect. 2.1. Afterwards, we discuss the static forward problem in Sect. 2.2 and state the quasi-static forward problem in Sect. 2.3. The optimal control problem of static plasticity is considered in Sect. 2.4. As mentioned in the introduction, we concentrate on the model of static elastoplasticity with small strains in its so-called dual formulation, and with linear kinematic hardening.

2.1 Notation and Standing Assumptions

2.1.1 Variables

Our notation follows [8] for the forward problem. Since the presentation of optimality conditions relies on adjoint variables and Lagrange multipliers associated with inequality constraints, additional variables are needed.

2.1.2 Function Spaces

Let \(\Omega \subset \mathbb{R}^{d}\) be a bounded domain with Lipschitz boundary \(\Gamma = \partial \Omega \) in dimension d ∈ { 2, 3}. We point out that the presented analysis is not restricted to the case d ≤ 3, but for reasons of physical interpretation we focus on the two and three dimensional cases. The boundary consists of two disjoint parts \(\Gamma _{N}\) and \(\Gamma _{D}\). We denote by \(\mathbb{S}:= \mathbb{R}_{\text{sym}}^{d\times d}\) the space of symmetric d-by-d matrices, endowed with the inner product \(\boldsymbol{A}: \boldsymbol{B} =\sum _{ i,j=1}^{d}A_{\mathit{ij}}B_{\mathit{ij}}\), and we define

$$\displaystyle\begin{array}{rcl} & & V = H_{D}^{1}(\Omega; \mathbb{R}^{d}) =\{ \boldsymbol{u} \in H^{1}(\Omega; \mathbb{R}^{d}): \boldsymbol{u} = 0\text{ on }\Gamma _{ D}\}, {}\\ & & S = L^{2}(\Omega; \mathbb{S}) {}\\ \end{array}$$

as the spaces for the displacement \(\boldsymbol{u}\), stress \(\boldsymbol{\sigma }\), and back stress \(\boldsymbol{\chi }\), respectively. The control \((\boldsymbol{f},\boldsymbol{g})\) belongs to the space

$$\displaystyle{ U = L^{2}(\Omega; \mathbb{R}^{d}) \times L^{2}(\Gamma _{ N}; \mathbb{R}^{d}). }$$

2.1.3 Yield Function and Admissible Stresses

We restrict our discussion to the von Mises yield function. In the context of linear kinematic hardening, it reads

$$\displaystyle{ \phi (\boldsymbol{\Sigma }) =\big (\vert \boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D}\vert ^{2} -\tilde{\sigma }_{ 0}^{2}\big)/2 }$$
(2.1)

for \(\boldsymbol{\Sigma } = (\boldsymbol{\sigma },\boldsymbol{\chi }) \in S^{2}\), where \(\vert \,\mbox{ $\cdot$ }\,\vert\) denotes the pointwise Frobenius norm of matrices,

$$\displaystyle{ \boldsymbol{\sigma }^{D} = \boldsymbol{\sigma } -\frac{1} {d}\,(\text{trace}\boldsymbol{\sigma })\,\boldsymbol{I} }$$

is the deviatoric part of \(\boldsymbol{\sigma }\), and \(\tilde{\sigma }_{0}\) is the yield stress. The yield function gives rise to the set of admissible generalized stresses

$$\displaystyle{ \mathcal{K} =\{ \boldsymbol{\Sigma } \in S^{2}:\phi (\boldsymbol{\Sigma }) \leq 0\quad \text{a.e. in }\Omega \}. }$$
(2.2)

Due to the structure of the yield function, \(\boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D}\) appears frequently and we abbreviate it and its adjoint by

$$\displaystyle{ \mathcal{D}\boldsymbol{\Sigma } = \boldsymbol{\sigma }^{D}+\boldsymbol{\chi }^{D}\quad \text{and}\quad \mathcal{D}^{\star }\boldsymbol{\sigma } = \left (\begin{array}{*{10}c} \boldsymbol{\sigma }^{D} \\ \boldsymbol{\sigma }^{D} \end{array} \right ) }$$

for matrices \(\boldsymbol{\Sigma } \in \mathbb{S}^{2}\) as well as for functions \(\boldsymbol{\Sigma } \in S^{2}\). When considered as an operator in function space, \(\mathcal{D}\) maps S 2 → S. For later reference, we also remark that

$$\displaystyle{ \mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma } = \left (\begin{array}{*{10}c} \boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D} \\ \boldsymbol{\sigma }^{D} + \boldsymbol{\chi }^{D}\\ \end{array} \right ) }$$

holds.

2.1.4 Operators and Forms

We begin by defining the bilinear forms associated with (1.1). For \(\boldsymbol{\Sigma } = (\boldsymbol{\sigma },\boldsymbol{\chi }) \in S^{2}\) and \(\boldsymbol{T} = (\boldsymbol{\tau },\boldsymbol{\mu }) \in S^{2}\), let

$$\displaystyle{ a(\boldsymbol{\Sigma },\boldsymbol{T}) =\int _{\Omega }\boldsymbol{\sigma }: \mathbb{C}^{-1}\boldsymbol{\tau }\,\text{d}x +\int _{ \Omega }\boldsymbol{\chi }: \mathbb{H}^{-1}\boldsymbol{\mu }\,\text{d}x. }$$
(2.3)

Here \(\mathbb{C}^{-1}(x)\) and \(\mathbb{H}^{-1}(x)\) are maps from \(\mathbb{S}\) to \(\mathbb{S}\) which may depend on the spatial variable x. For \(\boldsymbol{\Sigma } = (\boldsymbol{\sigma },\boldsymbol{\chi }) \in S^{2}\) and \(\boldsymbol{v} \in V\), let

$$\displaystyle{ b(\boldsymbol{\Sigma },\boldsymbol{v}) = -\int _{\Omega }\boldsymbol{\sigma }: \boldsymbol{\varepsilon }(\boldsymbol{v})\,\text{d}x. }$$
(2.4)

We recall that \(\boldsymbol{\varepsilon }(\boldsymbol{v}) = \frac{1} {2}\big(\nabla \boldsymbol{v} + (\nabla \boldsymbol{v})^{\top }\big)\) denotes the (linearized) strain tensor.

The bilinear forms induce operators

$$\displaystyle{ \begin{array}{llll} A &: S^{2} \rightarrow S^{2},&&\langle A\boldsymbol{\Sigma },\,\boldsymbol{T}\rangle = a(\boldsymbol{\Sigma },\boldsymbol{T}), \\ B &: S^{2} \rightarrow V ', &&\langle B\boldsymbol{\Sigma },\,\boldsymbol{v}\rangle = b(\boldsymbol{\Sigma },\boldsymbol{v}).\end{array} }$$

Here and throughout, \(\langle \,\mbox{ $\cdot$ }\,,\,\,\mbox{ $\cdot$ }\,\rangle\) denotes the dual pairing between V and its dual V ′, or the scalar products in S or S 2, respectively.

Assumptions.

  1. 1.

    The domain \(\Omega \subset \mathbb{R}^{d}\), d ≥ 2 is a bounded domain with Lipschitz boundary in the sense of [4, Chapter 1.2]. The boundary of \(\Omega \), denoted by \(\Gamma \), consists of two disjoint measurable parts \(\Gamma _{N}\) and \(\Gamma _{D}\) such that \(\Gamma = \Gamma _{N} \cup \Gamma _{D}\). While \(\Gamma _{N}\) is a relatively open subset, \(\Gamma _{D}\) is a relatively closed subset of \(\Gamma \). Furthermore \(\Gamma _{D}\) is assumed to have positive measure. In addition, the set \(\Omega \cup \Gamma _{N}\) is regular in the sense of Gröger, cf. [6]. A characterization of regular domains for the case d ∈ { 2, 3} can be found in [7, Section 5]. This class of domains covers a wide range of geometries.

    We make these assumptions in order to apply the regularity results in [10] pertaining to systems of nonlinear elasticity. The latter appear in the forward problem and its regularizations. Additional regularity leads to a norm gap, which is needed to prove the differentiability of the control-to-state map.

  2. 2.

    The yield stress \(\tilde{\sigma }_{0}\) is assumed to be a positive constant. It equals \(\sqrt{2/3}\,\sigma _{0}\), where σ 0 is the uni-axial yield stress.

  3. 3.

    \(\mathbb{C}^{-1}\) and \(\mathbb{H}^{-1}\) are elements of \(L^{\infty }(\Omega;\mathcal{L}(\mathbb{S}, \mathbb{S}))\), where \(\mathcal{L}(\mathbb{S}, \mathbb{S})\) denotes the space of linear operators \(\mathbb{S} \rightarrow \mathbb{S}\). Both \(\mathbb{C}^{-1}(x)\) and \(\mathbb{H}^{-1}(x)\) are assumed to be uniformly coercive. Standard examples are isotropic and homogeneous materials, where

    $$\displaystyle{ \mathbb{C}^{-1}\boldsymbol{\sigma } = \frac{1} {2\,\mu }\boldsymbol{\sigma } - \frac{\lambda } {2\,\mu \,(2\,\mu + d\,\lambda )}\text{trace}(\boldsymbol{\sigma })\,\boldsymbol{I} }$$

    with Lamé constants μ and λ. (These constants appear only here and there is no risk of confusion with the plastic multiplier λ or the Lagrange multiplier μ.) In this case \(\mathbb{C}^{-1}\) is coercive, provided that μ > 0 and d λ + 2 μ > 0 hold. A common example for the hardening modulus is given by \(\mathbb{H}^{-1}\boldsymbol{\chi } = \boldsymbol{\chi }/k_{1}\) with hardening constant \(k_{1} > 0\), see [8, Section 3.4].

Assumption (3) shows that \(a(\boldsymbol{\Sigma },\boldsymbol{\Sigma }) \geq \underline{\alpha }\,\Vert \boldsymbol{\Sigma }\Vert _{S^{2}}^{2}\) for some \(\underline{\alpha }> 0\).

2.2 The Forward Problem and Its Regularization

In this section, we address the lower-level problem of static plasticity. The weak formulation of (1.1) is given by

$$\displaystyle{ a(\boldsymbol{\Sigma },\boldsymbol{T}) + b(\boldsymbol{T},\boldsymbol{u}) +\int _{\Omega }\lambda \,\mathcal{D}\boldsymbol{\Sigma }: \mathcal{D}\boldsymbol{T} dx = 0\qquad\qquad \mathrm{for}\;\mathrm{all}\;\boldsymbol{T} \in S^{2}, }$$
(2.5a)
$$\displaystyle{ b(\boldsymbol{\Sigma },\boldsymbol{v}) =\langle \ell,\boldsymbol{v}\rangle\; \mathrm{for}\;\mathrm{ all }\;\boldsymbol{v} \in V, }$$
(2.5b)
$$\displaystyle{ 0 \leq \lambda \quad \perp \quad \phi (\boldsymbol{\Sigma }) \leq 0\;\mathrm{a.e. in }\;\Omega, }$$
(2.5c)

and it represents an energy minimization problem subject to a feasibility constraint for the generalized stresses. Here, \(\lambda \perp \phi (\boldsymbol{\Sigma })\) represents the pointwise a.e. complementarity condition \(\lambda \,\phi (\boldsymbol{\Sigma }) = 0\). It is well known that given ℓ ∈ V ′, (2.5) has a unique solution \((\boldsymbol{\Sigma },\boldsymbol{u},\lambda )\), see, e.g., [9, Proposition 3.1] and [12, Theorem 2.2]. The components \((\boldsymbol{\Sigma },\boldsymbol{u}) \in S^{2} \times V\) of the solution depend Lipschitz continuously on ℓ ∈ V ′. For the equivalence of (2.5) with a mixed VI of first kind, we refer to [11, Theorem 1.4] and [12, Theorem 2.2].

A standard way to derive qualified optimality conditions for the upper-level problem is based on the differentiability of the load-to-state map \(\ell\mapsto (\boldsymbol{\Sigma },\boldsymbol{u})\). However, the load-to-state operator associated with problem (2.5) is not Gâteaux-differentiable, since the directional derivative in turn involves a complementarity system and is thus not linear w.r.t. the direction, see [13]. What one can show is that the load-to-state map is Bouligand-differentiable under additional smoothness assumptions, see [2], but the nonlinearity of the directional derivative precludes the application of the standard adjoint approach.

To remedy the lack of Fréchet differentiability, we regularize the complementarity condition of the lower-level problem. This regularization is two-fold. First, the constraint \(\phi (\boldsymbol{\Sigma }) \leq 0\) is replaced by a quadratic penalty term in the lower-level objective. Second, the occurring max{0, ⋅ }-term is locally smoothed. We require that the smooth replacement \(\max \nolimits _{\varepsilon }\) of max{0, ⋅ } satisfies the following conditions: for all \(\varepsilon > 0\), the function \(\max \nolimits _{\varepsilon }: \mathbb{R} \rightarrow \mathbb{R}\) is of class C 1, 1 and satisfies

  1. 1.

    \(\max \nolimits _{\varepsilon }(x) \geq \max \{ 0,x\}\),

  2. 2.

    \(\max \nolimits _{\varepsilon }\) is monotone increasing and convex,

  3. 3.

    \(\max \nolimits _{\varepsilon }(x) =\max \{ 0,x\}\) for \(\vert x\vert \geq \varepsilon\).

It is easy to see that there exists a class of functions satisfying these requirements, and we refrain from fixing a certain choice of \(\max \nolimits _{\varepsilon }\) here. This leaves a choice for numerical implementations.

It is convenient to define

$$\displaystyle{ J_{\gamma,\varepsilon }(\boldsymbol{\Sigma }) = p_{\gamma,\varepsilon }(\vert \mathcal{D}\boldsymbol{\Sigma }\vert )\,\mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma }\quad \text{where}\quad p_{\gamma,\varepsilon }(x) =\max \nolimits _{\varepsilon }\big(\gamma \,(1 -\tilde{\sigma }_{0}/x)\big), }$$
(2.6)

which acts pointwise on functions in S 2. Here, γ > 0 is the penalty parameter.

In [12, Section 2.2] we obtained the following smoothed version of the optimality condition (2.5):

$$\displaystyle{ a(\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{T}) + b(\boldsymbol{T},\boldsymbol{u}_{\gamma,\varepsilon }) +\langle J_{\gamma,\varepsilon }(\boldsymbol{\Sigma }_{\gamma,\varepsilon }),\,\boldsymbol{T}\rangle = 0\quad \text{for all }\boldsymbol{T} \in S^{2}, }$$
(2.7a)
$$\displaystyle{ b(\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{v}) =\langle \ell,\boldsymbol{v}\rangle \quad \text{for all }\boldsymbol{v} \in V. }$$
(2.7b)

Note that the expression \(\langle J_{\gamma,\varepsilon }(\boldsymbol{\Sigma }_{\gamma,\varepsilon }),\,\boldsymbol{T}\rangle\) is well defined for \(\boldsymbol{T} \in S^{2}\), since \(J_{\gamma,\varepsilon }(\boldsymbol{\Sigma }_{\gamma,\varepsilon }) \in S^{2}\) due to \(p_{\gamma,\varepsilon }(\vert \mathcal{D}\boldsymbol{\Sigma }_{\gamma,\varepsilon }\vert ) \in L^{\infty }(\Omega )\). The existence and uniqueness of a solution can be shown by the theory of monotone operators. We obtain that for any ℓ ∈ V ′, (2.7) has a unique solution

$$\displaystyle{ G_{\gamma,\varepsilon }(\ell) = (G_{\gamma,\varepsilon }^{\boldsymbol{\Sigma }}(\ell),G_{\gamma,\varepsilon }^{\boldsymbol{u}}(\ell)) = (\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{u}_{\gamma,\varepsilon }) \in S^{2} \times V. }$$
(2.8)

Moreover, \(\boldsymbol{\Sigma }_{\gamma,\varepsilon }\) and \(\boldsymbol{u}_{\gamma,\varepsilon }\) depend Lipschitz continuously on ℓ, with a Lipschitz constant L independent of γ and \(\varepsilon\).

By using the L p-regularity result (with p > 2) of [10], we obtain the Fréchet differentiability of \(G_{\gamma,\varepsilon }\). The derivative at \((\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{u}_{\gamma,\varepsilon }) = G_{\gamma,\varepsilon }(\ell)\) in the direction δ ℓ ∈ U is given by the unique solution \((\delta \boldsymbol{\Sigma },\delta \boldsymbol{u})\) of

$$\displaystyle{ (A + J_{\gamma,\varepsilon }'(\boldsymbol{\Sigma }_{\gamma,\varepsilon }))\,\delta \boldsymbol{\Sigma } + B^{\star }\delta \boldsymbol{u} = \boldsymbol{0}, }$$
(2.9a)
$$B\;\delta\boldsymbol{\Sigma}\;=\;\delta l$$
(2.9b)
$$\displaystyle{ J_{\gamma,\varepsilon }'(\boldsymbol{\Sigma })\,\boldsymbol{T} = p_{\gamma,\varepsilon }'(\vert \mathcal{D}\boldsymbol{\Sigma }\vert )\,\frac{\mathcal{D}\boldsymbol{\Sigma }: \mathcal{D}\boldsymbol{T}} {\vert \mathcal{D}\boldsymbol{\Sigma }\vert } \,\mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma } + p_{\gamma,\varepsilon }(\vert \mathcal{D}\boldsymbol{\Sigma }\vert )\,\mathcal{D}^{\star }\mathcal{D}\boldsymbol{T} }$$
(2.10)

with

$$\displaystyle{ p_{\gamma,\varepsilon }'(x) =\max \nolimits _{\varepsilon }'\big(\gamma \,(1 -\tilde{\sigma }_{0}\,x^{-1})\big)\,\gamma \,\tilde{\sigma }_{ 0}\,x^{-2}. }$$

Let us remark that the differentiability of the solution operator of (2.7) is a non-trivial result. This can be appreciated when we reformulate (2.7) as the following quasi-linear system in \(\boldsymbol{u}\), where the principal part depends nonlinearly on the gradient of \(\boldsymbol{u}\):

$$\displaystyle{ B\,(A + J_{\gamma,\varepsilon })^{-1}(-B^{\star }\boldsymbol{u}_{\gamma,\boldsymbol{\varepsilon }}) =\ell. }$$

General differentiability results for such systems can be found in [27].

Finally, we obtain the convergence of the regularization. Let us denote by \((\boldsymbol{\Sigma },\boldsymbol{u},\lambda )\) the solution of (2.5) with right hand side ℓ ∈ V ′ and by \((\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{u}_{\gamma,\varepsilon })\) the solutions of the regularized problems (2.7) with right hand side \(\ell_{\gamma,\varepsilon }\) for \(\gamma,\varepsilon > 0\). Then we obtain

$$\displaystyle\begin{array}{rcl} & \Vert \boldsymbol{\Sigma } -\boldsymbol{\Sigma }_{\gamma,\varepsilon }\Vert _{S^{2}}^{2} \leq C\,\big(\Vert \ell-\ell_{\gamma,\varepsilon }\Vert _{V '}\Vert \boldsymbol{u} -\boldsymbol{u}_{\gamma,\varepsilon }\Vert _{V } +\gamma ^{-1}\,\Vert \ell\Vert _{V '}\Vert \ell_{\gamma,\varepsilon }\Vert _{V '}+\varepsilon \big),& {}\\ & \Vert \boldsymbol{u} -\boldsymbol{u}_{\gamma,\varepsilon }\Vert _{V } \leq C\,\big(\Vert \ell-\ell_{\gamma,\varepsilon }\Vert _{V '}\Vert \boldsymbol{u} -\boldsymbol{u}_{\gamma,\varepsilon }\Vert _{V } +\gamma ^{-1}\,\Vert \ell\Vert _{V '}\Vert \ell_{\gamma,\varepsilon }\Vert _{V '}+\varepsilon & {}\\ & +\Vert \boldsymbol{\Sigma } -\boldsymbol{\Sigma }_{\gamma,\varepsilon }\Vert _{S^{2}}\big), & {}\\ \end{array}$$

where C is independent of ℓ, \(\ell_{\gamma,\varepsilon }\), γ and \(\varepsilon\). In particular, we find \((\boldsymbol{\Sigma }_{\gamma,\varepsilon },\boldsymbol{u}_{\gamma,\varepsilon }) \rightarrow (\boldsymbol{\Sigma },\boldsymbol{u})\) if γ → ∞, \(\varepsilon \rightarrow 0\) and \(\ell_{\gamma,\varepsilon } \rightarrow \ell\) in V ′.

The comparison of (2.5a) and (2.7a) gives rise to the definition

$$\displaystyle{ \lambda _{\gamma,\varepsilon }:= p_{\gamma,\varepsilon }(\vert \mathcal{D}\boldsymbol{\Sigma }_{\gamma,\varepsilon }\vert ). }$$
(2.11)

From the definition of \(p_{\gamma,\varepsilon }\), we see that \(0 \leq \lambda _{\gamma,\varepsilon } \leq \max \{\gamma,\varepsilon \}\) holds. Finally, we obtain the convergence \(\lambda _{\gamma,\varepsilon } \rightarrow \lambda\) in \(L^{2}(\Omega )\) under the same assumptions as for the convergence of \((\boldsymbol{\Sigma },\boldsymbol{u})\).

Similar results are obtained in the case of quasi-static plasticity in [23, 25].

2.3 The Quasi-static Forward Problem

For convenience of the reader, we state the forward problem of quasi-static plasticity. This problem is time-dependent but rate-independent. We denote by H 1(0, T; X) the standard Bochner-Sobolev space of functions which map the interval [0, T] into the Banach space X and which possess a square-integrable weak derivative in time.

The time-dependent load ℓ ∈ H 1(0, T; V ′) satisfies ℓ(0) = 0. The associated states \((\boldsymbol{\Sigma },\boldsymbol{u}) \in H^{1}(0,T;S^{2} \times V )\) also satisfy homogeneous initial conditions \((\boldsymbol{\Sigma }(0),\boldsymbol{u}(0)) = \boldsymbol{0}\). In the case of a pre-loaded workpiece, non-zero initial conditions apply. Together with the plastic multiplier \(\lambda \in L^{2}(0,T;L^{2}(\Omega ))\), the system

$$\displaystyle{ A\dot{\boldsymbol{\Sigma }} + B^{\star }\dot{\boldsymbol{u}} +\lambda \, \mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma } =\boldsymbol{ 0}\quad \text{in }L^{2}(0,T;S^{2}), }$$
(2.12a)
$$\displaystyle{ B\boldsymbol{\Sigma } =\ell \quad \text{in }L^{2}(0,T;V '), }$$
(2.12b)
$$\displaystyle{ 0 \leq \lambda \quad \perp \quad \phi (\boldsymbol{\Sigma }) \leq 0\quad \text{a.e. in }(0,T) \times \Omega. }$$
(2.12c)

constitutes the forward problem. The existence and uniqueness of solutions can be found in [8, Sec. 8], regularity of the plastic multiplier was proved in [11], and continuity results are given in [5, 24].

2.4 An Optimal Control Problem

As was mentioned before, the volume and boundary forces \(\boldsymbol{f}\) and \(\boldsymbol{g}\) act as control variables. They induce in the forward system (2.5) the load \(\ell= R(\boldsymbol{f},\boldsymbol{g})\) defined by

$$\displaystyle{ \langle \ell,\boldsymbol{v}\rangle =\langle R(\boldsymbol{f},\boldsymbol{g}),\boldsymbol{v}\rangle:= -\int _{\Omega }\boldsymbol{f}\,\mbox{ $\cdot$ }\,\boldsymbol{v}\,\text{d}x -\int _{\Gamma _{N}}\boldsymbol{g}\,\mbox{ $\cdot$ }\,\boldsymbol{v}\,\text{d}s,\quad \boldsymbol{v} \in V }$$
(2.13)

for \((\boldsymbol{f},\boldsymbol{g}) \in U\). The optimal control, or upper-level problem under consideration reads

$$\displaystyle{ \left.\begin{array}{ll} \text{Minimize}\quad &\frac{1} {2}\Vert \boldsymbol{u} -\boldsymbol{u}_{d}\Vert _{L^{2}(\Omega;\mathbb{R}^{d})}^{2} + \frac{\nu _{1}} {2}\Vert \boldsymbol{f}\Vert _{L^{2}(\Omega;\mathbb{R}^{d})}^{2} + \frac{\nu _{2}} {2}\Vert \boldsymbol{g}\Vert _{L^{2}(\Gamma _{N};\mathbb{R}^{d})}^{2} \\ \text{where}\quad &(\boldsymbol{\Sigma },\boldsymbol{u},\lambda )\text{ solves the static plasticity problem (2.5)} \\ &\text{with right-hand side }\ell = R(\boldsymbol{f},\boldsymbol{g}). \end{array} \quad \right \} }$$
(p)

The desired displacement \(\boldsymbol{u}_{d}\) is an element of \(L^{2}(\Omega; \mathbb{R}^{d})\). Moreover, \(\nu _{1}\) and ν 2 are positive constants. The objective expresses the goal of reaching as closely as possible a desired deformation \(\boldsymbol{u}_{d}\). In the interest of not further complicating the presentation, control constraints are not considered but they could be easily included with obvious modifications.

The optimal control problem in the quasi-static case reads

Note that volume forces are not present. The control constraints on \(\boldsymbol{g}\) refer to an unloaded initial and terminal state. We mention that optimal control problems with more general objectives and additional control constraints are considered in [24].

Existence of solutions for problem (P) was proved in [9, Proposition 3.6] by using the compactness of R: U → V ′. The existence result in the quasi-static variant is a little bit more involved, since the pointwise application of R considered as a mapping H 1(0, T; U) → H 1(0, T; V ′) is not compact. However, one can show that the solution mapping is weakly continuous, which yields the existence of solutions, see [24, s 2.9].

Additionally, one can show that local solutions of (P) can be approximated by solutions of the regularized versions of (P), where (2.5) is replaced by (2.7). For the precise formulation of this approximation result, consult [12, Section 3.2]. Similar results in the case of quasi-static plasticity are obtained in [25, Section 4], see also [23].

3 Optimality Conditions

As was mentioned in the introduction, minimizers of MPCCs often do not fulfill the KKT conditions, and thus alternative stationarity concepts must be devised, along with tailored constraint qualifications. Briefly speaking, one disposes of the Lagrange multiplier pertaining to the complementarity conditions. One also redefines those multipliers belonging to the inequalities involved in the complementarity relation. In our setting, the latter comprise the multiplier μ (associated with the non-negativity of the plastic multiplier λ ≥ 0) and θ (associated with the yield condition \(\phi (\boldsymbol{\Sigma }) \leq 0\)). Existing stationarity concepts differ in what conditions are imposed for μ and θ.

Our first result provides an optimality system of C-stationary type. It is characteristic for this class that a sign is known only for the product θ μ, in the sense that θ μ ≥ 0 holds a.e. in \(\Omega \).

$$\displaystyle{ A\boldsymbol{\Sigma } +\lambda \, \mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma } + B^{\star }\boldsymbol{u} = \boldsymbol{0}, }$$
(3.1a)
$$\displaystyle{ B\boldsymbol{\Sigma } = R(\boldsymbol{f},\boldsymbol{g}), }$$
(3.1b)
$$\displaystyle{ 0 \leq \lambda \quad \perp \quad \phi (\boldsymbol{\Sigma }) \leq 0, }$$
(3.1c)
$$\displaystyle{ A\boldsymbol{\Upsilon } +\lambda \, \mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Upsilon } +\theta \, \mathcal{D}^{\star }\mathcal{D}\boldsymbol{\Sigma } + B^{\star }\boldsymbol{w} = \boldsymbol{0}, }$$
(3.2a)
$$\displaystyle{ B\boldsymbol{\Upsilon } = -(\boldsymbol{u} -\boldsymbol{u}_{d}), }$$
(3.2b)
$$\displaystyle{ (\nu _{1}\,\boldsymbol{f},\nu _{2}\,\boldsymbol{g}) - R^{\star }\boldsymbol{w} = \boldsymbol{0}, }$$
(3.3)
$$\displaystyle{ \mathcal{D}\boldsymbol{\Sigma }: \mathcal{D}\boldsymbol{\Upsilon }-\mu = 0, }$$
(3.4a)
$$\displaystyle{ \mu \,\lambda = 0, }$$
(3.4b)
$$\displaystyle{ \theta \,\phi (\boldsymbol{\Sigma }) = 0, }$$
(3.4c)
$$\displaystyle{ \theta \,\mu \geq 0. }$$
(3.4d)

The following result was proved in [12, Theorem 3.16] by means of a family of regularized optimal control problems, wherein the lower-level static plasticity problems are replaced by their approximations (2.7), and passage to the limit.

Theorem 1.

Let \((\boldsymbol{f},\boldsymbol{g})\) be a local optimal solution of (P). Let \((\boldsymbol{\Sigma },\boldsymbol{u})\) and λ denote the associated stresses, displacements, and plastic multiplier. Then there exist adjoint stresses and displacements \((\boldsymbol{\Upsilon },\boldsymbol{w}) \in S^{2} \times V\) and Lagrange multipliers \(\theta,\mu \in L^{2}(\Omega )\) such that the C-stationarity system(3.1)–(3.4) is satisfied.

C-stationarity was also obtained in the quasi-static setting for a semi-discretized in time problem, see [26, Section 2]. In passing to the limit in the time discretization parameter, the sign condition corresponding to θ μ ≥ 0 is lost. What remains is weak stationarity, see [26, Section 3].

A stronger stationarity concept than C-stationarity is strong stationarity, which asks for θ ≥ 0 and μ ≥ 0 on the so-called biactive set, defined by \(\mathcal{B}:=\{ x \in \Omega:\phi (\boldsymbol{\Sigma }(x)) =\lambda (x) = 0\}\). Results for various MPCC control problems in the literature which imply the strong stationarity of local minimizers have in common that the control functions must be sufficiently rich. A long-standing open question whether or not control constraints impede strong stationarity was recently resolved in [28]. Nevertheless, it still stands as a conjecture that the controls need to be distributed controls in the range space of the differential operators defining the forward problem, see (2.5a)–(2.5b). In accordance with this, we proved in [13, Theorem 4.5] a strong stationarity result for local minimizers of a modified problem with richer controls.

Moreover, we also obtained optimality conditions from the class of B-stationarity conditions. Rather than working with dual quantities, these conditions state that at a local minimizer, directional derivatives of the objective are non-negative in all directions from certain cones. By showing the weak directional differentiability of the control-to-state map, we obtained in [13, Corollary 3.12] the non-negativity of all directional derivatives of the reduced objective in tangential directions. It is noteworthy that the cone of tangential directions is taken to be the closure of the cone of feasible directions w.r.t. the weak topology. For the precise formulation of these results, we refer to [13].

Finally, sufficient second-order optimality conditions for the static problem were derived in [2]. For this purpose, the weak differentiability results from [13] had to be sharpened. To be more precise, it was shown that, under mild additional assumptions on the integrability of the hardening variable \(\boldsymbol{\chi }\), the control-to-state mapping is Bouligand differentiable from \(W_{D}^{1,p}(\Omega )'\) to S 2 × V, where p > 2. The associated remainder term property allows to deduce sufficient conditions by means of a second-order Taylor expansion of a particularly chosen Lagrange functional. The obtained sufficient conditions are comparable to the ones known from finite dimensional MPCCs, see e.g. [21]. However, one observes a substantial gap to the necessary optimality conditions, since the sufficient conditions involve a system which is even more rigorous compared to strong stationarity.

4 Numerical Results

Within this project, we also developed some algorithms to solve the optimal control problems. For the quasi-static variant of the optimal control problem (p q), we built a solver using the finite element library FEniCS, see [17]. The results shown below are based on a discretization by continuous, piecewise quadratic functions for the displacement, whereas the stresses are discretized only at the quadrature points. The temporal derivatives were replaced by an implicit Euler scheme. We used a globalized Newton-CG approach to compute stationary points of the discretized and regularized problem.

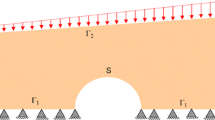
In Fig. 1 we present the computed (optimal) state for a problem with 96 time steps and 50,115 DoFs (per time step) for the displacement and 460,800 DoFs (per time step) for the stresses. The control boundary is located in the middle of the upper boundary, as can be seen from the red (pressure) and green (tension) arrows in Fig. 1. The observation boundary coincides with the control boundary. The desired final deformation is a deflection of the observation boundary by − 0. 1 in z-direction. The final deformation approaches this desired deformation very well, see Fig. 2.

Fig. 1
figure 1

The computed optimal state for different time steps \(t = i\,T/6\), i = 1, …, 6, where T is the final time. The control is shown by red (pressure) and green (tension) arrows. The workpiece is colored by the von Mises equivalent stress. The deformation is 20 times enlarged

Full size image
Fig. 2
figure 2

Final deformation, 500 times enlarged

Full size image

5 Further Results of the Project and Ongoing Work

We finally mention some further results of the project and related ongoing work in this section. In a recent manuscript [3] we considered an optimal control problem similar to (P), but with the static forward problem given in its primal (strain-based) formulation. The latter involves a variational inequality of the second kind in place of a complementarity system. Instead of the generalized stresses \(\boldsymbol{\Sigma }\) and plastic multiplier λ, the plastic strain \(\boldsymbol{p}\) appears as a state variable. By means of regularization, we obtained in [3, Theorem 1.1] a certain system of first-order necessary optimality conditions. Since a classification paralleling the notions of B-, C- or strong stationarity for optimal control problems involving variational inequalities of the second kind is not available in the literature, it is a priori not clear how strong this result is. Interestingly, we were able to show that the optimality system obtained is precisely equivalent to the C-stationarity conditions for the optimal control problem (P), i.e., when the formulation is replaced by the corresponding dual system (2.5).

Concerning the finite element error analysis for MPCCs in function space, optimal control problems governed by the obstacle problem were investigated in [18]. Quasi-optimal a priori error estimates for state and control were derived and confirmed by numerical examples. At the moment, a posteriori error representations based on the dual weighted residual approach are being developed in cooperation with A. Rademacher (TU Dortmund) and W. Wollner (University of Hamburg). The transfer of the a priori and a posteriori results to optimal control of elastoplastic deformation processes will be the subject of future research.

In the paper [28], we considered the distributed control of the obstacle problem subject to control constraints. As already mentioned, it was an long-standing open problem whether local minimizers (together with suitable multipliers) satisfy the strong stationarity conditions. We were able to prove that the answer is affirmative if certain mild conditions on the control constraints are satisfied. Moreover, it is possible to construct counter-examples when these conditions are violated.

Preprints and technical reports can be found at our publication page http://www.tu-chemnitz.de/mathematik/part_dgl/publications.php and at the preprint page of the DFG priority program SPP 1253 http://www.am.uni-erlangen.de/home/spp1253/wiki/index.php/Preprints.