Theoretical and Numerical Elastoplasticity

Abstract

This chapter presents an overview of the theory of classical elastoplasticity and associated variational problems. The flow theory is presented as a normality relation for a convex yield function, or equivalently in terms of the dissipation function. The latter formulation provides the basis for the variational theory, for which results on well-posedness are presented. Predictor-corrector algorithms based on the time-discrete problem are reviewed. Aspects of the large-deformation theory, including algorithmic aspects, are also presented.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The objective of this chapter is to present a reasonably self-contained overview of the theory of elastoplasticity, including aspects of the variational problems, discrete approximations, and associated solution algorithms. Both the small- and large-deformation theories are considered.

There are a number of works that deal in depth with the basic aspects of elastoplasticity presented in this chapter. For further background on classical plasticity the reader is referred to the texts by Gurtin et al. (2010) and Lubliner (1990). Comprehensive treatments of computational plasticity may be found for example in the works by de Souza Neto et al. (2008), Simo and Hughes (1998), while the monograph by Han and Reddy (2013) treats mathematical aspects as well as numerical analysis of problems of small-strain plasticity.

1.1 Elastic–Plastic Behaviour in One Dimension

Consider the stress–strain behaviour of a bar in uniaxial stress as shown in Fig. 1. Starting at the origin, the path OA is purely elastic. At $\sigma = \sigma _0$, where $\sigma _0$ is the initial yield stress, irreversible plastic behaviour becomes possible along the curve AB. The stress $\sigma _1$ at the point B is now the new or current yield stress: a further increase in stress will result in continued plastic behaviour along the path BC, while a decrease in stress will result in an elastic response, along the curve BD. This elastic behaviour will continue until the stress reaches the value $\sigma = -\sigma _1$ in the compressive range, beyond which plastic behaviour occurs once again along the curve DE.

Fig. 1

a Behaviour in uniaxial tension and compression of an elastic-plastic material; b the dissipation function $D(\dot{\varepsilon }^p)$

The total strain is made up additively of an elastic component $\varepsilon ^e$ and a plastic component $\varepsilon ^p$, with the elastic part of the strain given by Hooke’s law: that is,

$$ \varepsilon = \varepsilon ^e + \varepsilon ^p, \quad \sigma = E\varepsilon ^e = E(\varepsilon - \varepsilon ^p), $$

with E being Young’s modulus. Determination of the plastic strain requires information about the stress history and its evolution, and the plastic strain rate is as follows:

$$\begin{aligned} \dot{\varepsilon }^p = \left\{ \begin{array}{ll} 0 &{} \text {if } \sigma \in (-\sigma _1,\sigma _1 )\ \text {or } \ \sigma _1\dot{\sigma } <0, \\ \lambda \, \text {sgn}\,\sigma &{} \text {if } |\sigma | = \sigma _1 \ \text {and}\ \sigma _1\dot{\sigma }>0 . \end{array} \right. \end{aligned}$$

(1)

More concisely, we may write

$$\begin{aligned} \dot{\varepsilon }^p&= \lambda \frac{d\varphi }{d\sigma }, \qquad \lambda \ge 0, \ \varphi (\sigma ) \le 0,\ \lambda \,\varphi (\sigma ) = 0. \end{aligned}$$

(2)

The initial elastic range is the set of stresses $\sigma$ for which $\varphi _0 (\sigma ) = |\sigma | - \sigma _0 \le 0$, while the current elastic range, as a result of the plastic deformation, is given by $\varphi (\sigma ) = |\sigma | - \sigma _1 \le 0$.

The flow relation (2) can be ‘inverted’ in the sense that the stress may be given in terms of the plastic strain rate. The key quantity that makes this possible is the dissipation function D. From (2), since $\lambda = |\dot{\varepsilon }^p|$ and $|\sigma | = \sigma _1$ it follows by inverting this relation that

$$\begin{aligned} \sigma = \sigma _1\frac{\dot{\varepsilon }^p}{|\dot{\varepsilon }^p|} = \left. \frac{dD(q)}{dq}\right| _{q = \dot{\varepsilon }^p} \end{aligned}$$

(3)

where the dissipation function D is defined by

$$\begin{aligned} D (\dot{\varepsilon }^p) = \sigma _1|\dot{\varepsilon }^p|. \end{aligned}$$

(4)

This function is convex and positively homogeneous (that is, $D(c\dot{\varepsilon }^p) = |c|D(\dot{\varepsilon }^p)$), and differentiable everywhere except at $\dot{\varepsilon }^p = 0$ (Fig. 1b). With the dissipation function at our disposal, it is possible to capture the entire flow relation in a single inequality, viz

$$\begin{aligned} D (q) - D (\dot{\varepsilon }^p) - \sigma ( q - \dot{\varepsilon }^p) \ge 0\quad \text {for all}\ q. \end{aligned}$$

(5)

To see this, consider first the case of elastic behaviour, for which $\dot{\varepsilon }^p = 0$. Then (5) becomes

$$ \sigma q \le \sigma _1|q|\qquad \text {or}\qquad |\sigma | \le \sigma _1, $$

which is precisely the requirement that the stress lies in the elastic region. On the other hand, D is differentiable when $\dot{\varepsilon }^p \ne 0$, and in this case (5) is easily shown to be equivalent to the relation (3).

2 Three-Dimensional Elastoplastic Behaviour

We will assume isothermal conditions throughout for convenience. Furthermore, we develop a theory of rate-independent plasticity for quasistatic situations in which inertial terms may be neglected in the equation of motion. A further discussion of rate-independence can be found in Gurtin et al. (2010, p. 428). The appropriate extension to rate-dependent behaviour is the theory of viscoplasticity (see, for example, Gurtin et al. (2010), Lubliner (1990), Simo and Hughes (1998) for accounts of viscoplasticity).

Consider a body that occupies a domain $\Omega \subset {\varvec{\mathbb {R}}}^d$ $(d = 2, 3)$ with boundary $\Gamma$. The Cauchy stress tensor, denoted by ${\varvec{\sigma }}$, is symmetric and satisfies the equation of equilibrium

$$\begin{aligned} - \text {div}\,{\varvec{\sigma }}= {\varvec{b}}, \end{aligned}$$

(6)

where $\varvec{b}$ is the body force.

The linearized strain ${\varvec{\varepsilon }}$ is given by

$$\begin{aligned} {\varvec{\varepsilon }}({\varvec{u}}) = {\frac{1}{2}}\left( \nabla {\varvec{u}}+ [\nabla {\varvec{u}}]^T\right) . \end{aligned}$$

(7)

The boundary $\Gamma$ has unit outward normal ${\varvec{n}}$ and is partitioned into nonoverlapping subsets $\Gamma _u$ and $\Gamma _t$ such that $\Gamma _u \cup \Gamma _t = \Gamma$. Then possible boundary conditions would be

$$\begin{aligned}&{\varvec{u}}= \bar{{\varvec{u}}}\ \text {on}\ \Gamma _u, \quad {\varvec{\sigma }}{\varvec{n}}= \bar{{\varvec{t}}}\ \text {on}\ \Gamma _t. \end{aligned}$$

(8)

Here $\bar{{\varvec{u}}}$ and $\bar{{\varvec{t}}}$ are a prescribed displacement and surface traction, respectively.

Elastoplastic behaviour. The total strain ${\varvec{\varepsilon }}$ is assumed additively decomposable into an elastic part ${\varvec{\varepsilon }}^e$ and a plastic part ${\varvec{\varepsilon }}^p$: that is,

$$\begin{aligned} {\varvec{\varepsilon }}= {\varvec{\varepsilon }}^e + {\varvec{\varepsilon }}^p. \end{aligned}$$

(9)

The elastic component of strain satisfies the elastic constitutive relation; assuming isotropy this is given by

$$\begin{aligned} {\varvec{\sigma }}= {\mathbb {C}}{\varvec{\varepsilon }}^e = \lambda (\mathrm {tr}\,{\varvec{\varepsilon }}^e){\varvec{I}}+ 2\mu {\varvec{\varepsilon }}^e . \end{aligned}$$

(10)

Here ${\mathbb {C}}$ is the elasticity tensor and $\lambda$ and $\mu$ are the Lamé parameters.

An assumption based on physical behaviour is that of no change in volume accompanying plastic deformation; thus we impose the condition $\mathrm {tr}\, {\varvec{\varepsilon }}^p = \varepsilon ^p_{ii} = 0.$ To model hardening behaviour we introduce the back-stress ${\varvec{\alpha }}$, which is a symmetric second-order tensor and which accounts for kinematic hardening, and a scalar variable $\eta$ which accounts for isotropic hardening. A typical choice for $\eta$ is the accumulated plastic strain, so that

$$\begin{aligned} \dot{\eta } = |\dot{{\varvec{\varepsilon }}}^p|. \end{aligned}$$

(11)

We define two force-like variables: a symmetric tensor ${\varvec{a}}$ and a scalar g that are conjugate, respectively, to ${\varvec{\alpha }}$ and $\eta$. We collect these two pairs of variables in arrays $\mathsf {p}$ and $\mathsf {s}$ and write $\mathsf {p} = ({\varvec{\alpha }},\eta )\,,\ \mathsf {s} = ({\varvec{a}},g)\,,$ with inner product $\mathsf {s\circ p} = {\varvec{a}}:{\varvec{\alpha }}+ g\eta \,.$ To develop the equations for plastic flow within a thermodynamic framework, we define the free energy $\psi$ which is assumed to be an additive function of the elastic strain ${\varvec{\varepsilon }}^e$ and the internal variables $\mathsf {p}$: that is,

$$\begin{aligned} \psi = \psi ({\varvec{\varepsilon }}^e,\mathsf {p}) = \psi ^e ({\varvec{\varepsilon }}^e) + \psi ^p({\varvec{\alpha }},\eta ). \end{aligned}$$

(12)

The free-energy imbalance takes the form $\dot{\psi } \le {\varvec{\sigma }}: \dot{{\varvec{\varepsilon }}} + \mathsf {s}\circ \dot{\mathsf {p}}.$ For linear elastic materials $\psi ^e(\varvec{{\varvec{\varepsilon }}}^e) = {\frac{1}{2}}{\varvec{\varepsilon }}^e :{\mathbb {C}}{\varvec{\varepsilon }}^e$; from this relation and (10) the reduced dissipation inequality

$$\begin{aligned} {\varvec{\sigma }}: \dot{{\varvec{\varepsilon }}}^p + \mathsf {s}\circ \dot{\mathsf {p}}\ge 0 \end{aligned}$$

(13)

follows, where the conjugate forces are defined by

$$\begin{aligned} {\varvec{a}}= \displaystyle - \frac{\partial \psi ^p}{\partial {\varvec{\alpha }}}, \qquad g = \displaystyle - \frac{\partial \psi ^p}{\partial \eta }. \end{aligned}$$

(14)

For linear hardening behaviour, for example, the plastic part of $\psi$ has the quadratic form

$$\begin{aligned} \psi ^p({\varvec{\alpha }},\eta ) = \tfrac{1}{2} k_1|{\varvec{\alpha }}|^2 + \tfrac{1}{2} k_2\eta ^2 \end{aligned}$$

(15)

where $k_1$ and $k_2$ are nonnegative scalars associated with kinematic and isotropic hardening, respectively. The conjugate forces are immediately obtained from (14) and are

$$\begin{aligned} {\varvec{a}}= -k_1{\varvec{\alpha }},\qquad g = - k_2\eta . \end{aligned}$$

(16)

The case of perfect plasticity is recovered by setting $k_1 \equiv 0$ and $k_2 \equiv 0$.

The elastic region and plastic flow The classical theory of plasticity constrains the stresses to lie, pointwise, in a region of admissible stresses $\mathcal {E}$. Plastic flow takes place only when the stresses lie on the boundary $\mathcal {S}$ of $\mathcal {E}$, with its exterior assumed to be not attainable. The structure of the region $\mathcal {E}$ and the form taken by the flow relations are determined by the principle of maximum plastic work, which has its origins in the work of von Mises, Taylor, and Bishop and Hill (see Lubliner (1990) for further details). According to the principle in its original form, for the case of perfect plasticity, given a state of stress ${\varvec{\sigma }}\in \mathcal {E}$ and an associated plastic strain rate $\dot{{\varvec{\varepsilon }}}^p$, the pair $({\varvec{\sigma }},\dot{{\varvec{\varepsilon }}}^p)$ is such as to maximize the plastic work among all admissible stresses: that is,

$$\begin{aligned} {\varvec{\sigma }}: \dot{{\varvec{\varepsilon }}}^p \ge {\varvec{\tau }}: \dot{{\varvec{\varepsilon }}}^p\quad \text {for all}\ {\varvec{\tau }}\in \mathcal {E}. \end{aligned}$$

(17)

We generalize to hardening plasticity by defining the generalized stress $\mathsf {S}$ and generalized plastic strain $\mathsf {P}$ by

$$\begin{aligned} \mathsf {S} := ({\varvec{\sigma }},{\varvec{\alpha }},g),\quad \mathsf {P} = ({\varvec{\varepsilon }}^p,{\varvec{\alpha }},\eta ) \end{aligned}$$

(18)

and requiring that $\mathsf {S} \in \mathcal {E}$, a set of admissible generalized stresses. Purely elastic behaviour takes place when $\mathsf {S}$ lies in the interior of $\mathcal {E}$, while plastic loading may take place only when $\mathsf {S}$ lies on the yield surface $\mathcal {S}$. The postulate of maximum plastic work is now as follows: given a generalized stress $\mathsf { S}\in \mathcal {E}$ and an associated generalized plastic strain rate $\dot{{\mathsf {P}}}$, the pair $(\mathsf {S},\,\dot{\mathsf {P}})$ satisfies

$$\begin{aligned} \mathsf {S}\circ \dot{{\mathsf {P}}} \ge {\mathsf {T}}\circ \dot{{\mathsf {P}}}\ \ \text {for all}\ {\mathsf {T}}\in \mathcal {E}. \end{aligned}$$

(19)

Here the inner product between conjugate generalized quantities is defined by $\mathsf {S\,\circ }\,{\dot{\mathbf{P}}} = {\varvec{\sigma }}:\dot{{\varvec{\varepsilon }}} + {\varvec{a}}:\dot{{\varvec{\alpha }}} + g\dot{\eta }.$

Fig. 2

The elastic region, yield function, and normality relation in generalized stress space

There are two major consequences of the maximum plastic work inequality. First, it can be shown that the generalized plastic strain rate $\dot{{\mathsf {P}}}$ associated with a generalized stress $\mathsf {S}$ on the yield surface $\mathcal {S}$ is normal to the tangent hyper-plane at the point $\mathsf {S}$ to $\mathcal {S}$. This result is generally referred to as the normality law. Second, it can be shown that the region $\mathcal {E}$ is convex. These notions are illustrated in Fig. 2. We can describe the surface $\mathcal {S}$ and the elastic region $\mathcal {E}$ with the use of a function $\varphi$, called the yield function:

$$\begin{aligned} \begin{array}{l} \mathcal {S}:=\{ \mathsf {S} : \varphi (\mathsf {S}) = 0\}\quad \text {and}\quad \mathcal {E} := \{ \mathsf {S} :\varphi (\mathsf {S}) < 0\}. \end{array} \end{aligned}$$

(20)

Then plastic flow takes place only when $\mathsf {S}$ lies on the yield surface so that $\varphi (\mathsf {S}) = 0$, while it is necessarily zero for any $\mathsf {S}$ such that $\varphi (\mathsf {S}) < 0$. The requirement that $\varphi = \dot{\varphi } = 0$ during plastic loading is known as the consistency condition.

If the yield surface is smooth, the normality relation becomes

$$\begin{aligned} \dot{{\mathsf {P}}} = \lambda \, \nabla \phi (\mathsf {S}), \end{aligned}$$

(21)

where $\lambda$ is a nonnegative scalar, called the plastic multiplier. Further, we have the complementarity condition $\lambda \ge 0,\ \ \phi \le 0,\ \ \lambda \,\phi = 0.$ An equivalent form of stating this set of relations is through the inequality (cf. Fig. 2)

$$\begin{aligned} \dot{\mathsf {P}}\circ (\mathsf {T - S}) \le 0\quad \text {for all}\ \varphi (\mathsf {T}) \le 0. \end{aligned}$$

(22)

A flow law in which the yield function serves as a potential, in the sense that the generalized plastic strain rate lies in the normal to the yield surface, is called an associative flow law.¹

If the yield surface for the case of perfect plasticity is defined by the function $\varphi ({\varvec{\sigma }}) = \Phi ({\varvec{\sigma }}) - c_0 =0 ,$ where $c_0>0$ is a constant, then the extension to kinematic and isotropic hardening entails the introduction of terms that describe translation and expansion of the yield surface . That is, the yield function now becomes $\mathsf {S}= ({\varvec{\sigma }},{\varvec{a}},g)$,

$$\begin{aligned} \varphi (\mathsf {S}) = \Phi ({\varvec{\sigma }}+ {\varvec{a}}) + g - c_0 . \end{aligned}$$

(23)

From (21) when expanded we obtain

$$\begin{aligned} \dot{{\varvec{\varepsilon }}}^p = \lambda \displaystyle \frac{\partial \Phi ({\varvec{\sigma }}+ {\varvec{a}})}{\partial {\varvec{\sigma }}}, \ \ \ \dot{{\varvec{\alpha }}} = \lambda \displaystyle \frac{\partial \Phi ({\varvec{\sigma }}+ {\varvec{a}})}{\partial {\varvec{a}}} = \dot{{\varvec{\varepsilon }}}^p,\ \ \ \dot{\eta } = \lambda \displaystyle \frac{\partial \Phi (\mathsf {S})}{\partial g} = \lambda . \end{aligned}$$

(24)

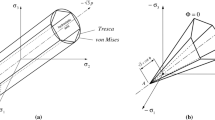
Examples of yield criteria We confine attention here to perfectly plastic behaviour, in which the hardening variables are absent. The assumption of plastic incompressibility permits a further simplification, in that it suffices to write $\varphi$ as a function of the invariants of the stress deviator $\text {dev}\,{\varvec{\sigma }}:= {\varvec{\sigma }}- \frac{1}{3}(\mathrm {tr}\,{\varvec{\sigma }}) {\varvec{I}}$.

The Mises–Hill yield criterion is based on the assumption that the threshold of elastic behaviour is determined by the elastic shear energy density, so that

$$\begin{aligned} \varphi ({\varvec{\sigma }}) = |\text {dev}\,{\varvec{\sigma }}| - c_0 . \end{aligned}$$

(25)

The normality law (21) is thus

$$\begin{aligned} \dot{{\varvec{\varepsilon }}}^p = \lambda \nabla \varphi ({\varvec{\sigma }}) = \lambda \frac{\text {dev}\,{\varvec{\sigma }}}{|\text {dev}\,{\varvec{\sigma }}|}. \end{aligned}$$

(26)

The Tresca yield criterion is based on the assumption that the elastic threshold is reached when the maximum shear stress reaches a critical value. In terms of the principal stresses ${\varvec{\sigma }}_i$, the maximum shear stress is given by ${\frac{1}{2}}\max _{i\ne j}{|\sigma _i - \sigma _j}|$ and the yield function is given by

$$\begin{aligned} \varphi ({\varvec{\sigma }}) = \max _{i\ne j}{|\sigma _i - \sigma _j}| - \sigma _0 = 0. \end{aligned}$$

(27)

The Tresca yield surface is not smooth so that the normality relation has to be suitably interpreted at corners or edges on this surface.

Fig. 3

Isotropic and kinematic hardening behaviour: A is the initial yield surface, B and C are subsequent yield surfaces after isotropic and kinematic hardening, respectively

Hardening laws. A typical choice for the isotropic hardening parameter is that of the equivalent plastic strain $\eta (t)$, defined in (11). For example, for the situation of biaxial stresses the Mises–Hill yield surface at any time is an ellipse B that is similar to the initial yield surface A, as shown in Fig. 3. The most common form of kinematic hardening is associated with the names of Prager and Ziegler. The variable ${\varvec{\alpha }}$ is taken to be the plastic strain tensor ${\varvec{\varepsilon }}^p$ and the plastic part of the free energy $\psi ^h ({\varvec{\alpha }})$ is given by the quadratic function $\psi ^h({\varvec{\varepsilon }}^p) = {\frac{1}{2}}k_1|{\varvec{\varepsilon }}^p|^2,$ in which $k_1 > 0$ is the hardening constant. The corresponding conjugate force ${\varvec{a}}$ is found from (16) to be ${\varvec{a}}= -k_1{\varvec{\varepsilon }}^p.$ The yield function then translates by an amount ${\varvec{a}}$ and is given by (Fig. 3)

$$\begin{aligned} \phi ({\varvec{\sigma }},{\varvec{a}}) = \Phi ({\varvec{\sigma }}+ {\varvec{a}}) -\sqrt{2/3}\,\sigma _0. \end{aligned}$$

(28)

The flow relation in terms of the dissipation function The three-dimensional version of the flow relation has an analogue to the inverted one-dimensional form (5). We define the dissipation function D by

$$\begin{aligned} D (\dot{\mathsf {P}}) = \sup \{ \mathsf {S}\circ \dot{\mathsf {P}}\ |\ \varphi (\mathsf {S}) \le 0 \}. \end{aligned}$$

(29)

Then the flow relation (21) or (22) can be written equivalently as

$$\begin{aligned} D(\mathsf {Q}) - D (\dot{\mathsf {P}}) - \mathsf {S}\circ (\mathsf {Q} - \dot{\mathsf {P}}) \ge 0\quad \text {for all}\ \mathsf {Q}. \end{aligned}$$

(30)

To see this, consider for example the case of perfect plasticity with the Mises flow relation, for which the yield function is given by (25). Then the dissipation is, from (29), $D(\dot{{\varvec{\varepsilon }}}^p) = c_0 |\dot{{\varvec{\varepsilon }}}^p|$. When $\dot{{\varvec{\varepsilon }}}^p\ne {\varvec{0}}$ the inequality (30) reduces to the equation

$$ {\varvec{\sigma }}= \left. \frac{\partial D}{\partial {\varvec{q}}}\right| _{q = \dot{\varepsilon }^p} = c_0 \frac{\dot{{\varvec{\varepsilon }}}^p}{|\dot{{\varvec{\varepsilon }}}^p|}, $$

which could be obtained directly by inversion of (26). On the other hand, when $\dot{{\varvec{\varepsilon }}}^p = {\varvec{0}}$ then (30) reduces to

$$ {\varvec{\sigma }}:{\varvec{q}}\le D({\varvec{q}})\quad \text {or}\quad |\text {dev}\,{\varvec{\sigma }}| \le c_0; $$

this states that the stress lies in the elastic region. Thus the inequality (30) captures in a single expression the possibilities of elastic behaviour or plastic flow. For the case of kinematic and isotropic hardening with $\mathsf {P} = ({\varvec{\varepsilon }}^p,\eta )$, it can be shown that the dissipation function is given by

$$\begin{aligned} D(\dot{\mathsf {P}}) = \left\{ \begin{array}{ll} c_0 |\dot{{\varvec{\varepsilon }}}^p | &{} |\dot{{\varvec{\varepsilon }}}^p| \le \dot{\eta } \,, \\ +\infty &{} \text {otherwise}. \end{array} \right. \end{aligned}$$

(31)

3 The Primal Variational Problem

There are two alternative formulations of the flow relations that are of interest, as set out in the previous section. We describe as the primal variational problem the version that uses the flow law (30) in terms of the dissipation, while the dual variational problem is formulated using the flow law (21) or (22) that makes use of the yield function. We focus here on the primal version, which has as its basic unknown variables the displacement ${\varvec{u}}$, plastic strain ${\varvec{\varepsilon }}^p$, and set of hardening variables $\mathsf {p} = ({\varvec{\alpha }},\eta )$. In what follows we shall equate ${\varvec{\alpha }}$ with the plastic strain ${\varvec{\varepsilon }}^p$. We are then required to find $({\varvec{u}},{\varvec{\varepsilon }}^p,\eta )$ that satisfy the equation of equilibrium (6), the elastic relation (10), and the flow relation in primal form (30). For convenience, we assume the homogeneous Dirichlet boundary condition ${\varvec{u}}= {\varvec{0}}$ on $\Gamma$.

The spaces V, Q, and M of displacements, plastic strains, and hardening variables are defined, respectively, by²

$$\begin{aligned} V&:= [H^1_0(\Omega )]^3, \nonumber \\ Q&:= \left\{ {\varvec{q}}= (q_{ij})_{3\times 3}:\ q_{ji} = q_{ij}, \ q_{ij} \in L^2(\Omega ),\ \mathrm {tr}\,{\varvec{q}}= 0\ \text {a.e. in}\ \Omega \right\} , \\ M&:= L^2(\Omega ). \end{aligned}$$

We set $W := V \times Q \times M$, which is a Hilbert space with the natural inner product $({\mathsf {w}},{\mathsf {z}})_{W}:= ({\varvec{u}},{\varvec{v}})_{V} + ({\varvec{\varepsilon }}^p,{\varvec{q}})_{Q} + (\eta ,\zeta )_M$ and the norm $\Vert {\mathsf {z}}\Vert _W := ({\mathsf {z}},{\mathsf {z}})^{1/2}_W$, where ${\mathsf {w}}=({\varvec{u}},{\varvec{\varepsilon }}^p,\eta )$ and ${\mathsf {z}}= ({\varvec{v}},{\varvec{q}},\zeta )$, and define the closed, convex subset

$$\begin{aligned} W_p = \left\{ {\mathsf {w}}\in W: \ |{\varvec{q}}| \le \zeta \ \text {a.e. in }\ \Omega \right\} . \end{aligned}$$

(32)

We assume that the elasticity tensor ${\mathbb {C}}$ is pointwise stable, so that for isotropic materials the Lamé constants in (10) satisfy $\mu > 0$ and $3 \lambda + 2\mu > 0$. We will pay particular attention to the special case of an elastoplastic material with linearly kinematic and isotropic hardening, together or separately, defined for example through (15) and (16). We assume that the hardening constants $k_1$ and $k_2$ satisfy

$$\begin{aligned}&k_1,k_2 \in L^\infty (\Omega ),\quad k_1 \ge 0,\quad k_2\ge 0, \quad k_1> 0 \ \text {or}\ k_2 > 0. \end{aligned}$$

(33)

The equilibrium equation. We take the scalar product of (6) with ${\varvec{v}}-\dot{{\varvec{u}}}$ for arbitrary ${\varvec{v}}\in V$, integrate over $\Omega$, and perform an integration by parts with the use of the elastic relation to obtain

$$\begin{aligned} \int _\Omega {\mathbb {C}}({\varvec{\varepsilon }}({\varvec{u}})-{\varvec{\varepsilon }}^p):({\varvec{\varepsilon }}({\varvec{v}})- {\varvec{\varepsilon }}(\dot{{\varvec{u}}}))\,dx =\int _\Omega {\varvec{f}}\cdot ({\varvec{v}}-\dot{{\varvec{u}}})\,dx\quad \forall \,{\varvec{v}}\in V. \end{aligned}$$

(34a)

The flow relation. We integrate the relation (30) over $\Omega$ and seek $(\dot{{\varvec{\varepsilon }}}^p,\dot{\eta })\in W_p$ that satisfies

$$\begin{aligned} \int _\Omega D({\varvec{q}},\zeta )\, dx&\ge \int _\Omega D(\dot{{\varvec{\varepsilon }}}^p,\dot{\eta })\, dx + \int _\Omega ({\varvec{\sigma }}({\varvec{u}},{\varvec{\varepsilon }}^p)- k_1{\varvec{\varepsilon }}^p):({\varvec{q}}- \dot{{\varvec{\varepsilon }}}^p) dx \nonumber \\&\quad - \int _\Omega k_2\eta \, (\zeta - \dot{\eta }) dx \end{aligned}$$

(34b)

for all $({\varvec{q}},\zeta )\in W_p$. The problem may be cast in the form of a variational inequality as follows: setting $\mathsf {w} = ({\varvec{u}},\varvec{\varepsilon }^p,\eta )$ and $\mathsf {z} = ({\varvec{v}},{\varvec{q}},\zeta )$ as before, we define

$$\begin{aligned}&a: W \times W \rightarrow {\varvec{\mathbb {R}}},\quad a ({\mathsf {w}},{\mathsf {z}}) = \int _\Omega \Big [{\varvec{\sigma }}({\varvec{u}},{\varvec{\varepsilon }}^p):{\varvec{\varepsilon }}({\varvec{v}}- {\varvec{q}}) + k_1{\varvec{\varepsilon }}^p:{\varvec{q}}+ k_2\eta \zeta \Big ]\ dx, \end{aligned}$$

(35a)

$$\begin{aligned}&j: W \times {\varvec{\mathbb {R}}}, \qquad \quad j({\mathsf {z}}) = \int _\Omega D({\varvec{q}},\zeta )\ dx, \end{aligned}$$

(35b)

$$\begin{aligned}&\ell : W \rightarrow {\varvec{\mathbb {R}}}, \qquad \quad \langle \ell ,{\mathsf {z}}\rangle = \int _\Omega {\varvec{f}}\cdot {\varvec{v}}\ dx. \end{aligned}$$

(35c)

The bilinear form $a(\cdot ,\cdot )$ is symmetric as a result of the symmetry properties of ${\mathbb {C}}$. From the properties of D, $j (\cdot )$ is convex, positively homogeneous, and nonnegative. We now add (34b) and (34a) to obtain the variational inequality

$$\begin{aligned} a({\mathsf {w}}(t),{\mathsf {z}}-\dot{{\mathsf {w}}}(t)) + j({\mathsf {z}}) - j(\dot{{\mathsf {w}}}(t)) \ge \langle \ell (t),{\mathsf {z}}- \dot{{\mathsf {w}}}(t)\rangle \quad \forall \,{\mathsf {z}}\in W. \end{aligned}$$

(36)

Note that the variational inequality is posed on the whole space W rather than $W_p$, observing that $j({\mathsf {z}})=\infty$ for ${\mathsf {z}}\not \in W_p$ and bearing in mind the requirement $\dot{{\mathsf {w}}}(t)\in W_p$. The primal variational problem of elastoplasticity thus takes the following form: given $\ell \in H^1(0,T;W^\prime )$, $\ell (0)={\mathsf {0}}$, find ${\mathsf {w}}=({\varvec{u}},{\varvec{\varepsilon }}^p,\eta ):[0,T] \rightarrow W$, ${\mathsf {w}}(0) = \mathsf {0}$, such that for almost all $t\in (0,T)$, $\dot{{\mathsf {w}}}(t)\in W_p$ and (36) is satisfied for all ${\mathsf {z}}\in W$.

It is readily shown that a solution to the classical problem solves the variational inequality (36). Conversely, it can be shown that if ${\mathsf {w}}$ is a smooth solution of (36) then ${\mathsf {w}}$ is also a solution to the classical problem.

Linearly kinematic hardening corresponds to the special case $k_2 = 0$. The variables in this case are the displacement ${\varvec{u}}$ and the plastic strain ${\varvec{\varepsilon }}^p$, and the spaces V and Q are as previously defined. The solution space is now $W_{\mathrm {kin}} := V \times Q$, with the inner product $({\mathsf {w}},{\mathsf {z}})_{W}:= ({\varvec{u}},{\varvec{v}})_{V} + ({\varvec{\varepsilon }}^p,{\varvec{q}})_{Q}$ and the norm $\Vert {\mathsf {z}}\Vert _{W_{\mathrm {kin}}} := ({\mathsf {z}},{\mathsf {z}})^{1/2}_{W_{\mathrm {kin}}}$, where ${\mathsf {w}}= ({\varvec{u}},{\varvec{\varepsilon }}^p)$ and ${\mathsf {z}}= ({\varvec{v}},{\varvec{q}})$. For this case the dissipation function (31) becomes $D({\varvec{q}})=c_0|{\varvec{q}}|\quad \forall \,{\varvec{q}}\in Q.$

The case of linearly isotropic hardening only is obtained by setting $k_1=0$ in (34b) and (35a).

The problem (34a) with (34b) has a unique solution $({\varvec{u}}(t),{\varvec{\varepsilon }}^p(t),\eta (t)) \in V\times Q\times M$ provided that either kinematic or isotropic hardening behaviour is present. The case of perfect plasticity requires a different approach altogether, in order to allow for discontinuities in the solution in the form of slip bands, for example.

4 Solution Algorithms

We focus in this section on time-discrete approximations, and refer to the texts mentioned in the introduction for details of finite element approximations. Time-discretization involves a uniform partitioning of the time interval [0, T] according to $0=t_0< t_1<\cdots <t_N=T,$ where $t_n - t_{n -1} =k$, $k=T/N$. We write $\ell _n = \ell (t_n)$ and define $\Delta w_n$ to be the backward difference $w_n-w_{n-1}$. Focusing for convenience on the problem with isotropic hardening, the time-discrete approximation of (34) is as follows: given all quantities at time $t_n$ and the loading ${\varvec{f}}_{n+1}$, find the displacement ${\varvec{u}}_{n+1}$, plastic strain ${\varvec{\varepsilon }}^p_{n+1}$ and hardening variable $\eta _{n+1}$ that satisfy (see 34)

$$\begin{aligned}&\int _\Omega {\mathbb {C}}({\varvec{\varepsilon }}({\varvec{u}}_{n+1})-{\varvec{\varepsilon }}^p_{n+1}):{\varvec{\varepsilon }}({\varvec{v}})\,dx =\int _\Omega {\varvec{f}}\cdot {\varvec{v}}\,dx\quad \forall \,{\varvec{v}}\in V, \\ \int _\Omega D({\varvec{q}},\zeta )\, dx&\ge \int _\Omega D(\Delta {\varvec{\varepsilon }}^p,\Delta \eta )\, dx + \int _\Omega \left( {\varvec{\sigma }}_{n+1}- k_1{\varvec{\varepsilon }}^p_{n+1}\right) :({\varvec{q}}-\Delta {\varvec{\varepsilon }}^p)\ dx \nonumber \end{aligned}$$

(37a)

$$\begin{aligned}&\quad + \int _\Omega g_{n+1} (\zeta -\Delta \eta ) dx , \end{aligned}$$

(37b)

where ${\varvec{\sigma }}_{n+1} = {\mathbb {C}}({\varvec{u}}_{n+1} - {\varvec{\varepsilon }}^p_{n+1})$ and $g_{n+1} = -k_2\eta _{n+1}$. This problem is equivalent to the minimization problem

$$ \mathsf {w}_n = \text {argmin} \,J(\mathsf {z}) := {\frac{1}{2}}a(\mathsf {z},\mathsf {z}) + j(\Delta \mathsf {z}) -\ell (\mathsf {z}_h) $$

where the bilinear form $a(\cdot ,\cdot )$, linear functional $\ell (\cdot )$, and functional $j(\cdot )$ are as defined in (35). We are interested in algorithms of predictor–corrector type for solving the problem (37). A now standard such algorithm is as follows:

Predictor step: Given ${\varvec{u}}_n,{\varvec{\varepsilon }}^p_n,\eta _n$, solve

$$\begin{aligned}&\int _\Omega {\mathbb {C}}({\varvec{\varepsilon }}({\varvec{u}}_{n+1}^{(i)} - {\varvec{\varepsilon }}^p_n - \Delta {\varvec{\varepsilon }}^{p*(i)}):{\varvec{\varepsilon }}({\varvec{v}})\ dx = \int _\Omega {\varvec{f}}_{n+1}\cdot {\varvec{v}}\ dx , \end{aligned}$$

(38a)

$$\begin{aligned}&D^{(i)}({\varvec{q}}) - D^{(i)}( \Delta {\varvec{\varepsilon }}^{p*(i)}) - {\varvec{\sigma }}^{*(i)}_{n+1}: ({\varvec{q}}- \Delta {\varvec{\varepsilon }}^{p*(i)}) - g^{*(i)}_{n+1}(\zeta - \Delta \eta ^{*(i)}) \ge 0 \end{aligned}$$

(38b)

for ${\varvec{u}}^{(i)}_{n+1}$, $\Delta {\varvec{\varepsilon }}^{p*(i)}$ and $\Delta \eta ^{*(i)}$, where $D^{(i)}$ is a smooth convex approximation of D which satisfies $D({\varvec{q}}) \le D^{(i)}({\varvec{q}})$ and (see Fig. 4a)

$$\begin{aligned} D^{(i)}|_{\Delta \varepsilon ^{p(i-1)}} = D|_{\Delta \varepsilon ^{p(i-1)}}, \nabla D^{(i)}|_{\Delta \varepsilon ^{p(i-1)}} = \nabla D|_{\Delta \varepsilon ^{p(i-1)}} . \end{aligned}$$

(39)

Fig. 4

a Approximation $D^{(i)}$ of D; b the closest-point projection in generalized stress space

Corrector step: Given ${\varvec{u}}^{(i)}_{n+1}$, solve for $\Delta {\varvec{\varepsilon }}^{p(i)}$ the flow relation

$$\begin{aligned} D({\varvec{q}}) - D( \Delta {\varvec{\varepsilon }}^{p(i)}) - {\varvec{\sigma }}^{(i)}_{n+1}: ({\varvec{q}}- \Delta {\varvec{\varepsilon }}^{p(i)}) - g^{(i)}_{n+1}(\zeta - \Delta \eta ^{(i)}) \ge 0 \end{aligned}$$

(40)

where ${\varvec{\sigma }}^{(i)}_{n+1} = {\mathbb {C}}({\varvec{\varepsilon }}({\varvec{u}}^{(i)}_{n+1} - {\varvec{\varepsilon }}^{p(i)}_{n+1}),\ g^{(i)}_{n+1} = - k\eta _{n+1}^{(i)}$.

The corrector step of the algorithm is equivalent to the displacement-driven return mapping algorithm (see for example Simo and Hughes (1998)), and may be interpreted as a closest-point projection. From (22) the corrector step (40) is equivalent to

$$\begin{aligned} \Delta {\varvec{\varepsilon }}^{p(i)}:({\varvec{\tau }}- {\varvec{\sigma }}^{(i)}) + \Delta \eta ^{(i)}(h - g) \le 0\quad \text {for}\ \varphi ({\varvec{\tau }},h) \le 0. \end{aligned}$$

(41)

Now the generalized stresses at time $t_{n+1}$ may be written as ${\varvec{\sigma }}_{n+1} = {\varvec{\sigma }}^{\mathrm {tr}}_{n+1} - {\mathbb {C}}\Delta {\varvec{\varepsilon }}^p,\quad g_{n+1} = g_n -k_2\Delta \eta$ where ${\varvec{\sigma }}^{\mathrm {tr}}_{n+1} = {\mathbb {C}}[{\varvec{\varepsilon }}({\varvec{u}}_{n+1}) - {\varvec{p}}_{n}]$ and $g^\mathrm{tr}_{n+1} = - k_2\eta _n$ are the trial values at time $t_{n+1}$ if no plastic flow were to take place in the time step $[t_{n},t_{n+1}]$. Setting $\mathsf {S} = ({\varvec{\sigma }},g)$, $\mathsf {T} = ({\varvec{\tau }},h)$, and $\mathsf {S}^{\mathrm {tr}} = ({\varvec{\sigma }}^{\mathrm {tr}},g^{\mathrm {tr}})$ the inequality (41) becomes, at time $t_{n+1}$,

$$ (\mathsf {T} - \mathsf {S}_{n+1}):\mathsf {G}^{-1}(\mathsf {S}^{\mathrm {tr}}_{n+1} - \mathsf {S}_{n+1}) \le 0\quad \text {for all}\ \mathsf {T} \in \mathcal {E} \quad \text {where} \quad \mathsf {G} = \left( \begin{array}{cc} {\mathbb {C}}&{} 0 \\ 0 &{} k \end{array} \right) . $$

In other words, the actual stress may be found as the orthogonal projection of the trial generalized stress $\mathsf {S}^{\mathrm {tr}}$ onto the elastic region, in the inner product generated by $\mathsf {G}^{-1}$. This is illustrated in Fig. 4b.

The problem may be formulated as the constrained minimization problem with the constraint $\mathsf {T} \in \mathcal {E}$ or $\varphi (\mathsf {T}) \le 0$ imposed through a Lagrange multiplier $\lambda$: that is,

$$\begin{aligned} \mathsf {S}_{n+1} = \text {argmin}\, (\mathsf {T} - \mathsf {S}^{\mathrm {tr}}_{n+1}):\mathsf {G}^{-1} (\mathsf {T} - \mathsf {S}^{\mathrm {tr}}_{n+1}) + \lambda \varphi (\mathsf {T}). \end{aligned}$$

(42)

For an account of the structure and implementation of the algorithm, see Simo and Hughes (1998), Chap. 3.

Examples of predictors (a) Elastic predictor. We set ${\varvec{\varepsilon }}^{p*(i)} = {\varvec{\varepsilon }}^{p(i-1)}$ so there is no need to define an approximate dissipation function $D^{(i)}$.

(b) Consistent tangent predictor. We define $D^{(i)}$ as the second order Taylor expansion of D about ${\varvec{\varepsilon }}^{p(i-1)}$. We put

$$\begin{aligned} D^{(i)}({\varvec{q}})&= D({\varvec{\varepsilon }}^{p(i-1)}) + \nabla D({\varvec{\varepsilon }}^{p(i-1)}):({\varvec{q}}- {\varvec{\varepsilon }}^{p(i-1)}) \nonumber \\&\quad + \tfrac{1}{2} ({\varvec{q}}- {\varvec{\varepsilon }}^{p(i-1)}):[{\varvec{H}}({\varvec{\varepsilon }}^{p(i-1)}) + \rho {\varvec{I}}]({\varvec{q}}- {\varvec{\varepsilon }}^{p(i-1)}) \end{aligned}$$

(43)

where ${\varvec{H}}:= \nabla ^2 D({\varvec{\varepsilon }}^{p(i-1)})$ and $\rho \ge 0$. With $\rho = 0$ and in a fully discrete setting, after the internal variables have been eliminated, (38a) and (38b) yield the set of displacement equations ${\varvec{K}}_{\mathrm {tan}}{\varvec{d}}= {\varvec{R}}^i$, where ${\varvec{K}}$ is the consistent tangent matrix and ${\varvec{R}}^i$ the residual.

Convergence of the algorithm The predictor–corrector algorithm can be shown to converge, for sufficiently large hardening (see Djoko et al. (2007)). For example, assuming linear isotropic hardening with a hardening coefficient $k_2$ as in (15), it can be shown that the predictor–corrector algorithm converges provided that $r \sim (\lambda + 2\mu )/(2\mu (1 + k_2)) < 1/3$, and that

$$ \Vert \mathsf {w - w^i}\Vert \le \left( \frac{2r}{1 - r}\right) ^i\Vert \mathsf {w^1 - w^0}\Vert , $$

where $\mathsf {w}^i$ denotes the ith iterate in the algorithm.

5 Elastoplasticity at Large Deformations

We present here a brief account of the extension of parts of the theory in the earlier sections to large-deformation elastoplasticity. For details of the relevant concepts from continuum mechanics and elastoplasticity see, for example, de Souza Neto et al. (2008), Gurtin et al. (2010), Simo and Hughes (1998).

We identify a body with a bounded domain $\Omega \subset {\varvec{\mathbb {R}}}^d\ (d=2,3)$ with boundary $\Gamma$. Points in $\Omega$ are denoted by ${\varvec{X}}$. For a given time interval [0, T] a motion of the body is described by a function ${\varvec{\varphi }}: \Omega \times [0,T] \rightarrow {\varvec{\mathbb {R}}}^d$, so that the position of a material point initially at ${\varvec{X}}$ is given by

$$\begin{aligned} {\varvec{X}}\in \Omega \rightarrow {\varvec{x}}= {\varvec{\varphi }}({\varvec{X}},t) = {\varvec{u}}({\varvec{X}},t) + {\varvec{X}}. \end{aligned}$$

(44)

Here ${\varvec{u}}$ is the displacement vector. The motion is assumed orientation-preserving, invertible, and such as to exclude interpenetration of matter: thus, the deformation gradient ${\varvec{F}}({\varvec{X}}) = \text {Grad}\,{\varvec{\varphi }}({\varvec{X}},t)$ satisfies $J = \text {det}\,{\varvec{F}}> 0$ in $\Omega .$

The right Cauchy–Green tensor ${\varvec{C}}$ and Green-Lagrange strain tensor ${\varvec{E}}$ are defined by

$$\begin{aligned} {\varvec{C}}&= {\varvec{F}}^T{\varvec{F}}, \end{aligned}$$

(45a)

$$\begin{aligned} {\varvec{E}}&= {\frac{1}{2}}({\varvec{C}}- {\varvec{I}}) = \tfrac{1}{2} \big (\text {Grad}\,{\varvec{u}}+ [\text {Grad}\,{\varvec{u}}]^T + [\text {Grad}\,{\varvec{u}}]^T\text {Grad}\,{\varvec{u}}\big ). \end{aligned}$$

(45b)

Here Grad denotes the gradient operator in the reference configuration: that is, in component form $(\text {Grad}\,{\varvec{u}})_{ij} = \partial u_i / \partial X_j$. The velocity ${\varvec{v}}$ is defined by ${\varvec{v}}= \bar{{\varvec{v}}} ({\varvec{X}},t) = \dot{{\varvec{\varphi }}}$. Using the invertibility of the motion it may be written alternatively as ${\varvec{v}}= \widehat{{\varvec{v}}}({\varvec{x}},t)$. The spatial gradient is denoted by grad, so that $(\text {grad}\,{\varvec{v}})_{ij} = \partial v_i/\partial x_j$ for ${\varvec{v}}= {\varvec{v}}({\varvec{x}},t)$. The velocity gradient ${\varvec{L}}$ is a spatial field related to the deformation gradient by ${\varvec{L}}= \text {grad}\,{\varvec{v}}= \dot{{\varvec{F}}}{\varvec{F}}^{-1}.$

For an elastic–plastic body, the standard Kröner multiplicative decomposition is assumed: that is,

$$\begin{aligned} {\varvec{F}}= {\varvec{F}}^e{\varvec{F}}^p, \end{aligned}$$

(46)

in which ${\varvec{F}}^e$ is the elastic part of the deformation, accounting for stretch and rotation of the lattice, while ${\varvec{F}}^p$ represents the irreversible plastic distortion, resulting from formation and motion of dislocations. Consistent with the requirement $J >0$, it is assumed that $\text {det}\,{\varvec{F}}^e> 0\ \text {and}\ \text {det}\,{\varvec{F}}^p > 0.$ Plastic deformation is further assumed to isochoric in nature, so that

$$\begin{aligned} \text {det}\,{\varvec{F}}^p = 1. \end{aligned}$$

(47)

The elastic and plastic parts ${\varvec{F}}^e$ and ${\varvec{F}}^p$ of the deformation gradient are not gradients of a vector field, unlike the situation for ${\varvec{F}}$. Corresponding to the Cauchy-Green and strain tensors in (45), elastic analogues may be defined according to

$$\begin{aligned} {\varvec{C}}^e = {\varvec{F}}^{eT}{\varvec{F}}^e\,,\qquad {\varvec{E}}^e = \tfrac{1}{2} ({\varvec{C}}^e - {\varvec{I}}). \end{aligned}$$

(48)

The velocity gradient ${\varvec{L}}$ may be decomposed additively into elastic and plastic parts; using the relation ${\varvec{L}}= \dot{{\varvec{F}}}{\varvec{F}}^{-1}$ together with (46), we define

$$\begin{aligned}&{\varvec{L}}^e = \dot{{\varvec{F}}}^e({\varvec{F}}^{e})^{-1},\quad {\varvec{L}}^p = \dot{{\varvec{F}}}^p[{\varvec{F}}^{p}]^{-1}, \quad {\varvec{L}}= {\varvec{L}}^e + {\varvec{F}}^e{\varvec{L}}^p[{\varvec{F}}^{e}]^{-1}. \end{aligned}$$

(49)

Quasistatic behaviour is assumed throughout this work, so that inertial terms may be neglected. The equation of equilibrium in the reference configuration is

$$\begin{aligned} - \text {Div}\,{\varvec{P}}= {\varvec{b}}_0, \end{aligned}$$

(50)

where ${\varvec{b}}_0$ is the body force per unit reference volume and ${\varvec{P}}$ is the first Piola–Kirchhoff stress, related to the Cauchy stress ${\varvec{\sigma }}$ by ${\varvec{P}}= J{\varvec{\sigma }}{\varvec{F}}^{-T}$.

Denoting by $\psi$ the specific free energy of the body and by $\rho _0$ the mass density per unit reference volume, the free-energy imbalance, which follows from the second law of thermodynamics, takes the form

$$\begin{aligned} \rho _0\dot{\psi } - {\varvec{P}}:\dot{{\varvec{F}}} \le 0. \end{aligned}$$

(51)

Two further useful stress measures, the elastic second Piola–Kirchhoff stress ${\varvec{S}}^e$, and the Mandel stress ${\varvec{M}}$, are defined by

$$\begin{aligned} {\varvec{S}}^e = J[{\varvec{F}}^e]^{-1}{\varvec{\sigma }}[{\varvec{F}}^{e}]^{-T},\quad {\varvec{M}}= J{\varvec{F}}^{eT}{\varvec{\sigma }}[{\varvec{F}}^{e}]^{-T} = {\varvec{C}}^e{\varvec{S}}^e. \end{aligned}$$

(52)

Then with the identity $\dot{{\varvec{E}}}^e = [{\varvec{F}}^{e}]^T{\varvec{D}}^e{\varvec{F}}^e$, the free-energy imbalance (51) can be recast in the form

$$\begin{aligned} \rho _0\dot{\psi } - {\varvec{S}}^e:\dot{{\varvec{E}}}^e - {\varvec{M}}:{\varvec{L}}^p \le 0. \end{aligned}$$

(53)

The free energy is assumed to be additively decomposable into an elastic part $\psi ^e ({\varvec{F}}^e)$ which captures the elastic response, and a plastic part $\psi ^p$ which captures features of the plastic behaviour such as hardening. Furthermore, the principle of material frame indifference requires the dependence to be on ${\varvec{C}}^e = [{\varvec{F}}^e]^T{\varvec{F}}^e$ or equivalently ${\varvec{E}}^e$. We restrict attention to isotropic hardening, which is captured by a scalar variable $\eta$, so that

$$\begin{aligned} \psi = \hat{\psi }^e({\varvec{E}}^e) + \hat{\psi }^p(\eta ). \end{aligned}$$

(54)

Application of the Coleman–Noll procedure leads, respectively, to the elastic relation, definition of the conjugate force g, and the reduced dissipation inequality:

$$\begin{aligned}&{\varvec{S}}^e = \rho _0\frac{\partial \hat{\psi }({\varvec{E}}^e)}{\partial {\varvec{E}}^e},\quad g := - \rho _0 \frac{\partial \psi }{\partial \eta },\quad {\varvec{M}}:{\varvec{L}}^p + g\dot{\eta } \ge 0. \end{aligned}$$

(55)

The flow relation. We introduce conjugate pairs $\mathsf {S}: = ({\varvec{M}},g)\ \text {and}\ \mathsf {L^p}:= ({\varvec{L}}^p,\dot{\eta }),$ and the region $\mathcal {E}$ of admissible generalized stresses, and assume its boundary to be given by the yield function $\varphi (\mathsf {S} ) = 0$: thus $\mathcal {E} = \{ \mathsf {S}:\, \varphi (\mathsf {S}) \le 0 \}.$ The flow relation may be written as the normality relation

$$\begin{aligned} \mathsf {L^p}: (\mathsf {T - S}) \le 0\quad \text {for all}\ \mathsf {T} \in \mathcal {E}\quad \text {or}\quad \mathsf {L}^\mathsf{p} = \lambda \frac{\partial \varphi }{\partial \mathsf {S}} \end{aligned}$$

(56)

together with the complementarity conditions $\lambda \ge 0, \varphi \le 0,\ \lambda \varphi = 0$. Equivalently, we introduce the convex, positively homogeneous dissipation function $D = \hat{D}(\mathsf {L^p})$ and a flow relation

$$\begin{aligned} D (\mathsf {Q}) \ge D( \mathsf {L^p} ) + {\varvec{M}}:({{\varvec{Q}}} - {\varvec{L}}^p) + g (\zeta - \dot{\eta }), \end{aligned}$$

(57)

where $\mathsf {Q} = ({\varvec{Q}},\zeta )$. Henceforth we make use of the Mises–Hill yield criterion with isotropic hardening relevant to large deformations, for which case the yield function and dissipation functions are

$$\begin{aligned} \varphi ( {\varvec{M}},g) = |\text {dev}\,{\varvec{M}}| + g - c_0 \le 0, \ \ \ D({\varvec{L}}^p,\dot{\eta }) = \left\{ \begin{array}{rl} c_0 |{\varvec{L}}^p | &{} \dot{\eta } \le |{\varvec{L}}^p |, \\ + \infty &{} \text {otherwise}. \end{array} \right. \end{aligned}$$

(58)

The initial-boundary value problem and variational problem. The boundary $\Gamma$ of the body is decomposed into nonoverlapping subsets $\Gamma _u$ and $\Gamma _t$ with $\Gamma _u \cup \Gamma _t = \Gamma$. The body force ${\varvec{b}}_0 : [0,T] \times \Omega \rightarrow {\varvec{\mathbb {R}}}^d$ and surface traction $\bar{{\varvec{t}}}: [0,T] \times \Gamma _t \rightarrow {\varvec{\mathbb {R}}}^d$ are assumed to be continuous in time. We also assume a prescribed, time-independent displacement $\bar{{\varvec{u}}}$ on $\Gamma _u$. Then the initial-boundary value problem for large-deformation plasticity is as follows: find the displacement field ${\varvec{u}}({\varvec{X}},t)$ and ${\varvec{F}}^p({\varvec{X}},t)$ that satisfy the equation of equilibrium (50), the elastic relation (55)$_1$, the kinematic relations (46) and (49), flow relation (56) or (57), and boundary conditions. The weak form of the equilibrium equation is given by

$$\begin{aligned} \int _\Omega {\varvec{P}}:\text {Grad}\, {\varvec{v}}\ dx = \int _\Omega {\varvec{b}}_0\cdot {\varvec{v}}\ dx + \int _{\Gamma _t} \bar{{\varvec{t}}}\cdot {\varvec{v}}\ ds. \end{aligned}$$

(59)

The variational problem is then one of finding the displacement ${\varvec{u}}$, plastic strain rate in the form ${\varvec{L}}^p$, and hardening variable $\eta$ that satisfy (56) or (57), and (59).

5.1 The Incremental Problem

The variational problem does not have an equivalent formulation as a minimization problem, but it is possible to formulate the corresponding incremental problem as an unconstrained minimization problem. As before the time interval is partitioned uniformly according to $0 = t_0< t_1< \cdots < t_N = T$. Then from (57) and (59) the incremental problem becomes one of finding $({\varvec{u}}_{n+1},{\varvec{L}}^p_{n+1},\eta _{n+1})$ that satisfy

$$\begin{aligned}&\int _\Omega {\varvec{P}}_{n+1}:\text {Grad}\,{\varvec{v}}\ dx = \int _\Omega {\varvec{b}}_{0,n+1}\cdot {\varvec{v}}\ dx\ + \int _{\Gamma _t} \bar{{\varvec{t}}}_{n+1}\cdot {\varvec{v}}\ ds , \end{aligned}$$

(60a)

$$\begin{aligned}&D (\mathsf {Q}) \ge D( {\mathsf {L^p}_{n+1}}) + {\varvec{M}}_{n+1}:({\varvec{Q}}- {\varvec{L}}^p_{n+1}) + \frac{1}{\Delta t}\int _\Omega g_{n+1} (\zeta - \Delta \eta ). \end{aligned}$$

(60b)

Here ${\varvec{M}}_{n+1}$ is found from (52)$_2$ with (52), and $g_{n+1} = \left. -\partial \psi ^h / \partial \eta \right| _{n+1} .$

Consider the functional

$$\begin{aligned} J({\varvec{v}},{\varvec{Q}},\zeta ) =&\int _\Omega \big [ \psi ^e({\varvec{E}}^e) + \psi ^h (\zeta ) \big ] \,dx + \int _\Omega D (\Delta t {\varvec{Q}},\Delta \zeta ) \, dx \nonumber \\&\quad - \int _\Omega {\varvec{b}}_{0,n+1}\cdot {\varvec{v}}\ dx - \int _{\Gamma _N} \bar{{\varvec{t}}}_{n+1}\cdot {\varvec{v}}\ ds. \end{aligned}$$

(61)

 

Theorem 5.1

If $({\varvec{u}}_{n+1},{\varvec{L}}_{n+1}^p,\Delta \eta )$ minimizes the functional (61) then $({\varvec{u}}_{n+1},{\varvec{L}}_{n+1}^p,\Delta \eta )$ is a solution to the variational problem (60).

For a proof of this result see for example Reddy (2013).

As for the small-deformation problem, the appropriate algorithm for solving (60) is one of predictor–corrector type. We focus here on the corrector step, which entails finding ${\varvec{F}}^e_{n+1}$ and $\eta _{n+1}$ for given displacement ${\varvec{u}}_{n+1}$ (determined in the predictor step) or equivalently ${\varvec{F}}_{n+1}$. Noting that

$$ \mathsf {L^p}_{n+1} = ({\varvec{L}}^p_{n+1}, \Delta \eta /\Delta t), $$

we introduce the approximate identity (de Souza Neto et al. (2008), Appendix B)

$$\begin{aligned} {\varvec{F}}^p_{n+1}&= ( \exp {\varvec{L}}^p_{n+1} ){\varvec{F}}^p_{n} \end{aligned}$$

(62)

in which $\exp$ is the matrix-valued exponential. Since ${\varvec{G}}_{n+1} := [{\varvec{F}}^p_{n+1}]^{-1} = {\varvec{G}}_{n} \exp (-{\varvec{L}}^p_{n+1} )$, for a given deformation ${\varvec{F}}_n$ at time $t_{n+1}$ it follows that

$$\begin{aligned} {\varvec{F}}^e_{n+1}&= {\varvec{F}}_{n+1}{\varvec{G}}_{n}\exp (-{\varvec{L}}^p_{n+1})] \nonumber \\&= {\varvec{F}}^{e,{\mathrm {tr}}}\exp (-\Delta \lambda _{n+1}{\varvec{N}}_{n+1})]. \end{aligned}$$

(63)

Here we have defined the trial elastic deformation gradient ${\varvec{F}}^{e,{\mathrm {tr}}}$ to be the value of ${\varvec{F}}^e$ assuming no plastic flow in the time step $[t_n,t_{n+1}]$, that is, ${\varvec{F}}^{e,{\mathrm {tr}}} = {\varvec{F}}_{n+1}{\varvec{G}}_n,$ and we have also used (56)$_2$ with ${\varvec{N}}_{n+1} = \text {dev}\,{\varvec{M}}/ |\text {dev}\,{\varvec{M}}|$. Using the identity det[exp $\ldots =$ exp [tr ($\ldots$)], we find that $\text {det}\,{\varvec{F}}^e_{n+1} = \text {det}\,{\varvec{F}}^{e,{\mathrm {tr}}}_{n+1}$ so that $J^e_{n+1} = J^{e,{\mathrm {tr}}}_{n+1}$ and hence $J^e_{n+1} = J^{e,{\mathrm {tr}}}_{n+1}$. Thus the plastic incompressibility constraint is satisfied exactly.

The corrector step then entails the following steps:

• (i) Given ${\varvec{F}}^{e,{\mathrm {tr}}}$ and $\eta ^{\mathrm {tr}} = \eta _n$, find $\mathsf {S}^{\mathrm {tr}} := ({\varvec{M}}^{\mathrm {tr}},g^{\mathrm {tr}})$ using (55)$_1$ and (55)$_2$.

• (ii) If $\varphi (\mathsf {S}^{\mathrm {tr}}) < 0$ then update with $\Delta \lambda = 0$.

• (iii) Otherwise, solve (63) and $\varphi (\mathsf {S}_{n+1}) = 0$ for ${\varvec{F}}^{e}_{n+1}$ and $\Delta \lambda$.

The return mapping algorithm can be simplified considerably by making use of the logarithmic elastic strain ${\varvec{\varepsilon }}^e$ whose components $\varepsilon ^e_A\ (A=1, 2, 3)$ in the spatial principal basis are given by $\varepsilon ^e_A = \log B^e_A$ and ${\varvec{B}}^e = [{\varvec{F}}^e]^T{\varvec{F}}^e$. Then with the yield function written as a function of the Kirchhoff stress ${\varvec{\tau }}= J{\varvec{\sigma }}$, the elastic strain update is found from

$$ {\varvec{\varepsilon }}^e = {\varvec{\varepsilon }}^{e,{\mathrm {tr}}} - \left. \Delta \lambda \frac{\partial \varphi ({\varvec{\tau }},g)}{\partial {\varvec{\tau }}}\right| _{n+1}. $$

Further details may be found in de Souza Neto et al. (2008), Simo and Hughes (1998).