Suspension Rheology

Abstract

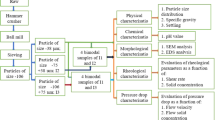
The importance of rheology in the mining industry derives from the fact that all materials being processed are suspensions, that is, mixtures of solid particles and fluids, usually in water. In mineral processing plants, water is mixed with ground ore to form a pulp that constitutes the mill feed. The mill overflow is mixed again with water to adjust the solid content for classification in hydrocyclones. Pulp characteristics are essential in the transport of products to their final destination. A suspension, like all types of materials, must obey the laws of mechanics under the application of forces. The flow patterns of suspensions in tubes depend on their concentrations and transport velocities. In diluted suspensions at low velocities particles will settle. The suspension is termed a settling suspension and the flow regime is considered heterogeneous. At a velocity beyond a value at which all particles are suspended gives a non-settling suspension and the flow regime is homogeneous with Newtonian behavior. Concentrated suspensions are usually homogenous with non-Newtonian behavior. The variables and field equations for all types of fluids are presented and constitutive equations differentiate between Newtonian and non-Newtonian behavior. Empirical models of non-Newtonian behavior are presented, including pseudo-plastic and dilatant behavior with Cross and Carreau and Power-law models, and yield-stress models with Bingham and Hershel-Bulkley models. The study of the operational effect on viscosity includes variable such as solid particle size and concentration, temperature, pressure, time and pH. Rheometry provides experimental methods to determine rheological parameters such as viscosity and yield stress.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

E. C. Bingham introduced the word rheology in 1929 to describe the study of deformation and flow of all types of materials. The axioms of mechanics and the mass and momentum balances are valid for all macroscopic bodies and the distinction among different materials is established by constitutive equations, that is, the response of materials to applied stresses. Strictly speaking, rheology covers the mechanical study of all matter considered as continua, but it is usually reserved for those with non-linear constitutive equations, therefore leaving out Hooken solids and Newtonian fluids. Rheology can be considered a description, with constitutive equations also called rheological equations of state, of material behavior and not of materials. A rheological study includes the formulation of constitutive equations and the experimental methods to determine corresponding parameters, which is called rheometry.

The importance of rheology in the mining industry derives from the fact that all materials being processed are suspensions, that is, mixtures of solid particles and fluids, usually water. In mineral processing plants these suspensions are termed pulps. In a grinding plant, water is mixed with ground ore to form a pulp that constitutes the mill’s feed. The mill overflow is mixed again with water to adjust the solid content required to be classified in hydrocyclones. Pulp characteristics are essential in the transport of products to their final destination in the flotation plant.

A suspension, like all types of materials, must obey the laws of mechanics under the application of forces. The flow patterns of suspensions in tubes depend on their concentrations and transport velocities. In diluted suspensions at low velocities particles will settle. The suspension is termed a settling suspension and the flow regime is considered heterogeneous. At a velocity beyond a value at which all particles are suspended gives us a non-settling suspension and the flow regime is homogeneous with Newtonian behavior. Concentrated suspensions are usually homogenous but with non-Newtonian behavior. Generally, mineral pulps have non-Newtonian behavior, therefore their rheological characteristics are essential in the different unit operations in a mineral processing plant.

10.1 Introduction to Rheology

The incompressible stationary shear flow of a fluid can be described with the following variables, (1) material density $\rho ({\varvec{r}},t)$, (2) velocity ${\varvec{v}}({\varvec{r}},t)$ and (3) the stress tensor ${\varvec{T}}({\varvec{r}},t)$, where ${\varvec{r}}\,{\text{and}}\,t$ are the position vector and time respectively. These three field variables must obey the mass and linear momentum field equations:

$$ \nabla \cdot {\varvec{v}} = 0 $$

(10.1)

$$ \rho \nabla {\varvec{v}} \cdot {\varvec{v}} = \nabla \cdot {\varvec{T}} + \rho {\varvec{g}}\, $$

(10.2)

where g is the gravitational constant vector.

Since there are three field variables and only two field equations, a constitutive equation must be postulated for the stress tensor:

$$ {\varvec{T}} = - p{\varvec{I}} + {\varvec{T}}^{E} ({\varvec{r}}) $$

(10.3)

where $p$ is the pressure and ${\varvec{T}}^{E}$ is the shear stress tensor or extra stress tensor.

The extra stress tensor defines the type of fluid, for example, a Newtonian fluid is ${\varvec{T}}^{E}$ given by:

$$ {\varvec{T}}^{E} = \mu \left({\nabla {\varvec{v}} + \nabla {\varvec{v}}^{T}} \right) $$

(10.4)

where $\mu$ is a constant called shear viscosity and $\nabla {\varvec{v}}$ is the shear rate tensor.

For a two-dimensional axi-symmetrical flow of a Newtonian fluid in the $x_{2}$ or z direction in case of a cylindrical tube, the shear stresses $T_{12} (x_{1} ,x_{2} ) < 0$ or $T_{r,z} (r,z) < 0$ reduces to:

$$ T_{12}^{E} = \mu \frac{{\partial v_{2} }}{{\partial x_{1} }}\quad T_{rz}^{E} = \mu \frac{{\partial v_{z} }}{\partial r} $$

(10.5)

The stresses are usually written in the form $T_{12}^{E} \equiv \tau$ or $T_{rz}^{E} \equiv \tau$ and the velocity gradient as $\partial v_{2} /\partial x_{1} = \dot{\gamma }\,\,{\text{or}}\,\,\partial v_{z} /\partial r = \dot{\gamma }$, then Eq. (10.5) is used in the form:

$$ \tau = \mu \dot{\gamma } $$

(10.6)

where the shear stress $\tau$ is measured in Pascal (Newton per meter) (Pa = N/m²), the shear rate $\dot{\gamma }$ in (s⁻¹) and the viscosity in (Pa s).

Figure 10.1 represents the shear stress for the flow in a cylindrical tube in the direction z, where $\tau_{w}$ is the shear rate at the wall of the tube (see Chap. 11).

Fig. 10.1

Shear stress distribution for the flow in a cylindrical tube for $p_{0} > p_{L}$

10.2 Constitutive Equations

Materials with a constant viscosity behave as Newtonian fluids. Common fluids like water and air have Newtonian behavior. For these types of fluids, the shear stress is a liner function of the shear rate.

10.2.1 Suspensions with Newtonian Behavior

Diluted non-settling suspensions have Newtonian behavior, that is, the viscosity is constant and the relationship between shear stress and the shear rate is represented by a straight line called a rheogram, see Fig. 10.2 for a suspension with 0.01 volume fraction of solids. Einstein’s constitutive equation applies; $\eta = \eta_{s} \times \left( {1 + 2.5\varphi } \right)$, where $\eta_{s}$ is the viscosity of the continuous phase.

Fig. 10.2

Rheogram for a diluted non-settling suspension with Newtonian behavior. a Flow curve. b Viscosity curve

10.2.2 Non-Newtonian Behavior

Figure 10.3 shows a general viscosity curve for suspensions with non-Newtonian behavior. At a low shear rate, the shear stress shows a constant viscosity region followed by a drastic fall, then a new constant viscosity region and finally, in some cases, an increase in viscosity at very high shear rates.

Fig. 10.3

General representation of the flow curve of non-Newtonian suspension

If we consider Newtonian behavior as a reference, see the red line in Fig. 10.4, non-Newtonian behavior present two additional rheograms: pseudo-plastic, also known as shear thinning behavior, typical of mineral suspensions and polymer solutions (see the blue line in Fig. 10.4), and dilatant, also known as shear thickening behavior, where viscosity increases with shear rate, see the magenta line.

Fig. 10.4

Rheogram of a fluid with a typical non-Newtonian behavior (Schramm 2000). a Flow curve. b Viscosity curve

A copper flotation tailing has non-Newtonian behavior, that is, the constitutive equation of the stress is a non-linear function of the shear rate. These types of constitutive equations are written the same as Newtonian equations. However, in this case, viscosity is not constant but rather is a function of the shear rate. Figure 10.5 shows an example.

$$ \tau = \eta (\dot{\gamma })\dot{\gamma } $$

(10.7)

where $\eta$ is the shear viscosity.

Fig. 10.5

Rheogram for flotation tailings. a Flow curve. b Viscosity curve

• (a) Pseudo Plastic and Dilatant Behavior

In general, materials with pseudo-plastic behavior present two Newtonian plateaus (constant viscosities; see Fig. 10.7), a first Newtonian plateau, with constant viscosity $\eta_{0}$ at low shear rates and a second Newtonian plateau, with viscosity $\eta_{\infty }$ at high shear rates. Sometimes the first Newtonian plateau is so high that it cannot be measured, in which case, the low shear rate behavior is described as an apparent yield stress $\tau_{y}$. Sometimes, the second Newtonian plateau is short and viscosity increases as the shear rate increases, which is termed dilatant behavior.

In mineral processing, we find discrete or agglomerate particle suspensions with different concentrations. At low concentrations, discrete particle suspensions have Newtonian behavior, as shown in Fig. 10.2, but with higher concentrations their behavior is viscoplastic, see Fig. 10.5. In general, mineral particles at rest present a negative surface charge when suspended in water (see Chap. 7) and consequently become hydrated. In slow motion particles stay hydrated and present a certain resistance to flow but with an increase in shear rate, the hydration layer is striped away and particles become oriented in the direction of the flow, causing decreases in flow resistance and viscosity, approaching an optimum constant orientation.

Dilatant flow behavior is found in highly concentrated suspensions and depends on the solid concentration, the particle size distribution and the continuous phase viscosity. The region of shear thickening generally follows that of shear thinning.

Densely packed particles have enough fluid inside to fill the void between particles. At rest or at low shear rates, water lubricates particle surfaces, allowing an easy positional change of particles when forces are applied and the suspension behaves as a shear thinning liquid. At critical shear rates, packed particles lose water, which causes an increase in interior concentration. Particle–particle interaction increases drag, causing dilatant behavior as shown in Fig. 10.6.

Fig. 10.6

Rheological behavior of a rougher flotation tailing with 56 % solids and pH 9.2

10.2.3 Empirical Rheological Models

Empirical constitutive equations are quantified with different mathematical models. We will describe Cross and Carreau models; Ostwal-de Waele, commonly known as the power law model, the Herschel-Bulkley model and Bingham model.

• (a) Cross and Carreau Models

Cross and Carreau models are represented by Eqs. (10.8) and (10.9), respectively. Given that $\dot{\gamma } = \tau /\eta$, the relationship between viscosity and shear rate is:

$$ \frac{{\eta - \eta_{\infty } }}{{\eta_{0} - \eta_{\infty } }} = \frac{1}{{1 + (\lambda \dot{\gamma })^{m} }}\quad \tau = \frac{\eta }{\lambda } \times \left( {\frac{{\eta_{0} - \eta_{\infty } }}{{\eta - \eta_{\infty } }} - 1} \right)^{1/m} $$

(10.8)

$${\text{Carreau}}\quad \frac{{\eta - \eta_{\infty } }}{{\eta_{0} - \eta_{\infty } }} = \frac{1}{{\left( {1 + (\beta \dot{\gamma })^{2} } \right)^{(1 - n)/2} }}{\quad}\tau = \frac{\eta }{\beta } \times \left[ {\left( {\frac{{\eta_{0} - \eta_{\infty } }}{{\eta - \eta_{\infty } }}} \right)^{{\frac{2}{1 - n}}} - 1} \right]^{0.5}$$

(10.9)

where $\eta_{0} \;{\text{and}}\;\eta_{\infty }$ are the viscosities at low and high shear rates plateaus, and $\lambda ,\,\beta ,\,m{\text{ and }}n$ are experimental constants. Figure 10.7 represents the two models in terms of $\eta = f\left( {\dot{\gamma }} \right)\,$, where $\lambda {\text{ and }}\beta$ are curve fitting parameters with the dimension of time and n as a constant.

Fig. 10.7

Viscosity versus shear rate for a given material

• (b) Power Law Model (Ostwal-de Waele)

Power law models represent pseudo-plastic and dilatant behavior with great accuracy. Equation (10.10) represents the viscosity and shear stress for material obeying the power law model:

$$ \eta = m\dot{\gamma }^{n - 1} \quad{\text{and}}\quad\tau = m\dot{\gamma }^{n} $$

(10.10)

where m is the consistency index, with units in ${\text{Pa}} \times {\text{s}}^{ 2}$ and n is the power index. Values of the power index $n < 1$ represent pseudo-plastic behavior and values of $n > 1$ dilatant behavior.

Problem 10.1

Determine the rheogram of the thickener underflow of a copper flotation tailing from the experimental data in Table 10.1, obtained with a rotational viscometer. Plot the rheogram and determine the parameters of the power law model.

Table 10.1 Rheological experiment

Results are shown in Eq. (10.11) and Figs. 10.8, 10.9, 10.10, where the points are the experimental values and the lines represent the simulation with the power law model.

$$ \eta = 1.723\dot{\gamma }^{0.727} \,\,[{\text{Pas}}]\quad \tau = 1.723\dot{\gamma }^{0.2468} \,\,[{\text{Pa}}] $$

(10.11)

Fig. 10.8

Shear stress versus shear rate of a thickener underflow of copper flotation tailings modeled by the power law

Fig. 10.9

Viscosity versus shear rate of thickener underflow of a copper flotation tailings modeled by the power law

Fig. 10.10

Rheogram of a fluid with non-Newtonian behavior. Circles are experimental data and the line is the potential model

• (c) Models with Yield Stress

In concentrated flocculated suspensions, particles aggregate as flocs, which interact with each other forming a network maintained by surface interaction forces extending throughout the entire volume of the suspension. The application of stresses to this structure deforms it elastically until the structure breaks down. This break down is related to the yield stress of the material and can be considered as the minimum shear stress at which the solid structure becomes liquid. Knowledge about yield stress is essential in transporting suspensions, especially in resuspending particles when they have settled in a pipeline or channel. See Chap. 11 for details.

There are two methods to measure the yield stress: (1) extrapolating the flow curve to a zero shear rate and (2) directly measuring shear stress when the flow begins. The first method depends on the rheological model in use, for example Bingham or Hershel-Bulkley models, which provide different values that are in both cases different from the yield stress determined by measuring with the vane method. We conclude that shear rate should be determined by the method that gives the best value for the application required.

• 1. Extrapolation from flow curves

• Bingham Model

mineral pulps in tubes and channels the range of shear rates is usually high, on the order of hundreds of seconds to minus one. At these ranges, viscosity is constant and equal to the slope of the line of the shear values. In this case, the extrapolation of this line to a zero shear rate gives an appropriate yield stress that, together with the constant viscosity, provides the required rheological parameters. Bingham proposed this method in 1922 with the constitutive equation:

$$ \tau = \tau_{y} + K\dot{\gamma } $$

(10.12)

where $\tau_{y}$ is the yield stress and $K$ is the constant plastic viscosity. Equation (10.12) shows that Bingham’s model is the combination of a yield stress $\tau_{y}$ with a Newtonian viscosity $K$. This model has the advantage of giving the result of the modeling in one plot.

Problem 10.2

Determine the parameters of Bingham’s model for the experimental data in Table 10.2. For high shear stress values, a tangent drawn to the shear stress-shear rate curve gives $\tau$ as the intercept of the tangent with the vertical axis and the viscosity as its slope. See Fig. 10.10.

$$ \tau_{y} = 12.5\,\,{\text{Pa and }}K = 0.0196\,\,{\text{Pa\,s}} $$

(10.13)

Table 10.2 Data of a rheogram for a copper flotation tailing

• Herschel-Bulkley Model

For processes at low shear rates, the stress-shear function is curved and Bingham’s model is inadequate since viscosity is not constant. In this case, the Herschel-Bulkley model can be used with the constitutive equation:

$$ \tau = \tau_{y} + k\dot{\gamma }^{z} $$

(10.14)

where $\tau_{y}$ is the yield stress, k is the consistency index, similar to the power law model, and n is the power index.

Problem 10.3

For the experimental data in Table 10.2, determine the rheological parameters of the Herschel-Bulkley model.

The following values were obtained by non-linear curve fitting for the Herschel-Bulkley rheological parameters: $\tau_{y} = 1.25,\,\,\,\,k = 2.37,\,\,\,z = 0.343$, see Figs. 10.11 and 10.12.

Fig. 10.11

Bingham model for data of Table 10.2

Fig. 10.12

Herschel-Bulkley model for data from Table 10.2

For the same experimental data, the power-law model better describes the shear stress in the whole range of shear rates. The drawback is that this model requires knowledge of the variable viscosity obtained from the viscosity plot versus shear rate, while Bingham’s model requires only the shear stress plot. We conclude that the power-law model is better for processes requiring low shear rate (lower than 150 s⁻¹ in Fig. 10.11). Engineers designing and operating pipelines in the mining industry prefer Bingham’s model because it gives them a constant viscosity and a yield stress value, which are important in transporting mineral pulps.

• (d) Pseudo-Plastic-Dilatant behavior

Under some conditions, copper flotation tailings present pseudo-plastic-dilatant behavior similar to that of Fig. 10.6. There are no models for this type of behavior, but a polynomial of degree three or four can describe the entire rheogram in the full range of shear rates.

Problem 10.4

Determine the parameters for a rougher flotation tailing with data given in Table 10.3 and represented in Fig. 10.13. The result with a four-power polynomial is:

$$ \tau = - 2.000 \times 10^{ - 9} \dot{\gamma }^{4} + 2.000 \times 10^{ - 6} \dot{\gamma }^{3} - 6.000 \times 10^{ - 4} \dot{\gamma }^{2} + 7.940 \times 10^{ - 2} \dot{\gamma } + 5.212 $$

(10.15)

Table 10.3 Dimension of the sensors

Fig. 10.13

Rheogram of a rougher flotation tailings of a copper ore at pH = 9.2 and 4 % solids modeled by a four power polynomial

10.2.4 Operational Effects on Viscosity

• (a) The effect of concentration

Solid concentration has the most important effect on suspensions. In general, properties such as yield stress and viscosity increase with solid concentration. The viscosity of suspensions at low concentration can be modeled by a polynomial extension of Einstein’s equation.

$$ \eta = \eta_{0} \left( {1 + k_{1} \varphi + k_{2} \varphi^{2} + k_{3} \varphi^{3} + \cdots } \right) $$

(10.16)

where $\eta_{0}$ is viscosity at zero concentration, $\varphi$ is the volume fraction of solids, $k_{1} = 2.5$ is Einstein’s parameter and $k_{2} ,\,k_{3} , \ldots k_{n}$ are fitting parameters. For concentrations of less than $0.01$ the suspension behaves Newtonian. See Fig. 10.14.

• Krieger-Daugherty

At higher concentrations, suspensions have non-Newtonian behavior. Several equations describe this behavior; one of the most commonly used is the Krieger-Daugherty equation (Krieger 1972), in which viscosity depends on maximum particle packing $\varphi_{\hbox{max} }$. See Eq. (10.17) and Fig. 10.14.

$$ \eta = \eta_{0} \left( {1 + \frac{\varphi }{{\varphi_{\text{m} } }}} \right)^{{a \times \varphi_{\text{m} } }} $$

(10.17)

• Exponential function

When using the power-law model for the rheogram, an exponential function sometimes gives a good fit for the effect of solid concentrations. Figures 10.15 and 10.16 give an example of a copper flotation tailing at a shear rate of 200 s⁻¹.

$$ \eta = 0.838 \times { \exp }\left( {0.142\;\% } \right)\dot{\gamma }^{ - 0.670} $$

(10.18)

Fig. 10.14

Shear stress versus shear rate plot for a copper tailing at several solid concentrations

Fig. 10.15

Shear viscosity versus shear rate for a copper flotation tailing with % solid by weight as a parameter. Symbols are experimental values and the lines are simulations with Eq. (10.18)

Fig. 10.16

Plot of viscosity versus particle concentration for data from Fig. 10.13

Shaheen (1972) presented an alternative model to describe the concentration effect:

$$ \eta = \eta_{0} a \times { \exp }\left( {\frac{b\varphi }{{1 - \left( {\varphi /\varphi_{m} } \right)}}} \right) $$

(10.19)

where a, b sand $\varphi_{m}$ are constant.

• (b) Effect of particle size

Particle size distribution affects viscosity in three ways: (1) through the maximum particle packing $\varphi_{m}$; (2) the presence of very small particles; and (3) particle size distribution. Fine particles can fit in a packed bed between larger particles, increasing the density and affecting the relative concentration $\varphi /\varphi_{m}$. Another effect of small particles is to transform the continuous phase, usually water, into a viscous suspension that directly affects overall viscosity. Finally, particle size distribution contributes to shear thickening of mineral pulps, as shown in Figs. 10.6 and 10.13.

Unfortunately, there is no theoretical information on how these variables influence suspension viscosity. Consequently, the maximum packing density $\varphi_{m}$ is usually obtained by curve fitting.

• (c) The effect of temperature

An exponential function (Tanner 1988) fits the effect of temperature on Newtonian liquids.

$$ \eta = A\;{ \exp }\left( {B/(T - T_{0} )} \right) $$

(10.20)

where $T$ is the absolute temperature and $A,\,B$ and $T_{0}$ are characteristic constants. In the absence of information on the effects of temperature on suspensions, the equation for Newtonian fluids is used.

In Barrientos et al. (1994) performed numerous rheological experiments with quartz samples of different sizes and concentrations. They proposed a general equation based on the Shaheen model (1972) for the suspension viscosity in terms of four dimensionless variables $x/x_{0}$, $\varphi$, $\text{Re} \,$ and ${^\circ}{\text{C}}$, where $x{\text{ and }}x_{0}$ are the average and a reference particle size, $\varphi$ is the solid volume fraction, $\text{Re} = \rho_{f} \dot{\gamma }x^{2} /\eta$ is the flow Reynolds number, $\rho_{0} {\text{ and }}\eta_{0}$ are the fluid density and viscosity, respectively, $\dot{\gamma }$ is the shear rate and °C is the temperature in Celsius. They separated the functional form of this equation into three terms, one for the effect of temperature, a second for the effect of concentration and a third for the interaction between these variables.

$$ \begin{aligned} \eta /\eta _{0} \;{\text{ = }}\; & {\text{p}}_{1} \exp \left( {\frac{{3.462 \times 10^{3} }}{T} + } \right) \times \exp \left( {\frac{{p_{2} \varphi }}{{1 - \left( {\varphi /p_{3} } \right)^{{p_{4} }} }}} \right) \\ \; & \times \left( {1 + \frac{{p_{5} \exp \left( { - p_{6} \varphi ^{{p_{7} }} } \right) \times \left( {x/x_{0} } \right)^{{p_{8} }} }}{{{\text{Re}}^{{1/p_{9} }} }}} \right)^{{p_{9} }} \\ \end{aligned} $$

(10.21)

Concha et al. (1999) performed 70 experiments with underflow material from the feed, overflow and underflow of a copper ore grinding-classification circuit and with ground underflow for several time ranges, temperatures from 5 to 25 °C and concentrations from 15 to 40 % solid by weight. After obtaining nine parameters of the four dimensional groups by non-linear curve fitting, they concluded by simulation that particle size has a significant effect on rheograms solely for shear rate values below $\dot{\gamma } \approx 200\;{\text{s}}^{ - 1}$.

• (d) Effect of pressure

In general, the effect of pressure on viscosity is small, except for materials such as oil subjected to very high pressures, where an exponential equation can be used (Tanner 1988).

$$ \eta = \eta (0){ \exp }\left( {p/\beta } \right) $$

where $p$ is the applied pressure, $\eta (0)$ is the viscosity at zero pressure and $\beta$ is a constant.

• (e) pH Effect

It is well know that plant operators add lime to thickener underflow of copper flotation tailings when it is too viscous for hydraulic transport. This does not always solve the problem because pH affects the slurry in a complicated way. Figure 10.17 show the viscosity of a copper flotation tailing for several particle concentrations at a shear rate of 200 s⁻¹.

Fig. 10.17

Effect of pH on the viscosity of a copper flotation tailing at a shear rate of 200 (s⁻¹)

Two minimum viscosities were present for this material at all concentrations, one at pH 7.5 and the second at pH 9.0, with more pronounced values at high concentrations. Several copper tailings present this behavior. To establish if this behavior is due to the silica content of the tailings, experiments were made with silica in distilled water. Figures 10.17 and 10.18 give the results. The two minimums are also shown but with somewhat higher pH values.

Fig. 10.18

Effect of pH on the viscosity of a suspension of silica of 2 % solids in distilled water at a shear rate of 200 (s⁻¹)

• (f) The effect of time

Time is important in materials that suffer structural changes during measurement. For example, some flocculated suspensions change structure while sheared, which produces a change in viscosity. This behavior may be thixotropic or rheopectic depending if the viscosity diminishes or increases with time. A schematic drawing of these behaviors is shown in Fig. 10.19.

Fig. 10.19

Material with thixotropic or rheopectic behaviors

10.3 Rheometry

Rheometry is that part of Rheology which provides experimental methods to determine rheological parameters such as viscosity and yield stress, that is, it establishes the methods to determine the constitutive equation of a fluid material. Simple shear flows permit obtaining exact solutions of the Navier–Stokes equations, which in turn provides the rheological parameters.

10.3.1 Simple Shear Stationary Flows

Simple shear are flows produced by a unidirectional shear rate, an example of which are the flows in a circular tube, rotational flows in the annular gap of concentric cylinders, torsion flow between two flat plates and flow between a cone and a plate, among other. These flows are of interest to mineral processing because they provide the tools to calculate pipes and pumps (see Chap. 11) and experimental methods to determine rheological properties; shear stress versus shear rate plots; yield stress and viscosity versus shear rate.

• (a) Flow in concentric cylinders

Consider the stationary rotational flow of a suspension of non-settling particles in two concentric cylinders of radius $R_{1} {\text{ and }}R_{2}$ produced by the rotation of the cylinders with angular velocities $\varOmega_{1} {\text{ and }}\varOmega_{2}$ respectively. Assume the cylinders are open to the atmosphere at one end. Figure 10.20 shows the cylinder.

Fig. 10.20

Rotational flow between two concentric cylinders

Considering a constant fluid density, variables for this problem are the viscosity of the suspension and the tangential velocity of the fluid. The field equation in cylindrical coordinates in laminar flow is:

$$ \eta \frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rv_{\theta } } \right)} \right) = 0 $$

(10.22)

with boundary conditions:

$$ v_{\theta } \left( {R_{1} } \right) = \varOmega_{1} R_{1} \,,\,\,v_{\theta } \left( {R_{2} } \right) = \varOmega_{2} R_{2} \,,\,\,v_{r} = v_{z} = 0 $$

where $v_{\theta } ,v_{r} {\text{ and }}v_{z}$ are the components of the velocity vector and $\varOmega_{1} {\text{ and }}\varOmega_{2}$ are the angular velocities of the cylinders with radius $R_{1} {\text{ and }}R_{2}$.

• Tangential velocity

Integrating Eq. (10.22) twice results in:

$$ v_{\theta } = \frac{{C_{1} }}{2}r + \frac{{C_{2} }}{r} $$

(10.23)

Applying boundary conditions, the constant $C_{1} {\text{ and }}C_{2}$ are:

$$ C_{1} = \frac{{2\left( {R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} } \right)}}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}}\quad C_{2} = \frac{{R_{1} R_{2}^{2} \left( {\varOmega_{1} - \varOmega_{2} } \right)}}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} $$

(10.24)

and

$$ v_{\theta } \left( r \right) = \frac{1}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}}\left( {\left( {R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} } \right)r + \frac{{R_{1} R_{2}^{2} \left( {\varOmega_{1} - \varOmega_{2} } \right)}}{r}} \right) $$

(10.25)

• Shear Rate

Integrating Eq. (10.22) once yields:

$$ \frac{{\partial v_{\theta } }}{\partial r} = C_{1} - \frac{{v_{\theta } }}{r} $$

(10.26)

Substituting $C_{1}$ gives:

$$ \frac{{\partial v_{\theta } }}{\partial r} = \frac{{R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} }}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} - \frac{{v_{\theta } }}{r} $$

(10.27)

To obtain the average shear rate calculate the average of (10.27) for radius $R_{1}$ and $R_{2}$:

$$ \bar{\dot{\gamma }} = \frac{1}{2}\left( {\left. {\frac{{\partial v_{\theta } }}{\partial r}} \right|_{{r = R_{1} }} +\; \left. {\frac{{\partial v_{\theta } }}{\partial r}} \right|_{{r = R_{2} }} } \right) $$

(10.28)

Applying boundary conditions:

$$ \begin{aligned} \left. {\frac{{\partial v_{\theta } }}{\partial r}} \right|_{{r = R_{1} }} &= \;\frac{{R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} }}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} - \varOmega_{1} \\ \left. {\frac{{\partial v_{\theta } }}{\partial r}} \right|_{{r = R_{2} }} &= \;\frac{{R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} }}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} - \varOmega_{2} \\ \bar{\dot{\gamma }} &= \;\frac{{R_{2}^{2} \varOmega_{2} - R_{1}^{2} \varOmega_{1} }}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} - \left( {\varOmega_{2} + \varOmega_{1} } \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\text{s}}^{ - 1} \\ \end{aligned} $$

(10.29)

• (b) Flow in a capillary

Consider the stationary laminar axial flow of a fluid in a cylindrical tube, see Fig. 10.21. From Chap. 11 the flow rate and the shear stress at the wall of the tube are given by:

Fig. 10.21

Axial flow in cylindrical tube. a Velocity distribution. b Shear stress distribution

Since the shear rate is linear in r, the average value of $\bar{\dot{\gamma }}$ is given by:

$$ \bar{\dot{\gamma }} = \frac{{4 \times \bar{v}_{z} }}{D},\quad \bar{\dot{\gamma }} = \frac{5.1 \times Q}{{D^{3} }} $$

(10.30)

10.3.2 Types of Viscometers

There are two types of viscometers used in mineral processing, rotational and capillary. Searle-type rotational viscometers are used for mineral pulps while capillary viscometers are used for polymers.

• (a) Rotary viscometers

The relative rotation of two concentric cylinders of a viscometer induces shear rate in the fluid. Usually one cylinder rotates while the other is fixed. In a Searle viscometer, the inner cylinder rotates while the outer cylinder is fixed. The system is called Couette. See Figs. 10.22 and 10.23.

Fig. 10.22

Systems types used in rotary viscometers

Fig. 10.23

Searle type of measuring system. Shear rate is measured on the rotor axis and the outer cylinder is fixed

During measurement, the fluid to be tested is allowed into the gap between the two cylinders. The relative motion of the cylinder induces a simple shear to the fluid, which produces a torque in the other cylinder that is measured by a suitable device. If the gap between the cylinders is small, the viscosity in the gap is constant as shown in Fig. 10.22.

The Searle system is the most commonly used for mineral pulps.

For a Searle system from Eq. (10.29), the shear rate is given by:

$$ \dot{\gamma } = \frac{{\varOmega_{1} R_{2}^{2} }}{{\left( {R_{2}^{2} - R_{1}^{2} } \right)}} $$

(10.31)

To determine a rheogram, a given shear rate $\dot{\gamma }$ is established in the equipment by imposing a rotational speed $N_{1}$ given in terms of $\dot{\gamma }$ by Eq. (10.32)

$$ N_{1} = \frac{60}{2\pi }\left( {1 - \left( {\frac{{R_{1} }}{{R_{2} }}} \right)^{2} } \right)\dot{\gamma }\;\;\left[ {\text{rpm}} \right] $$

(10.32)

where $N_{1}$ is the rotational speed in rpm of the inner cylinder with a radius of $R_{1} {\text{ and }}R_{2}$ is the radius outer cylinder.

A good example of a robust rotational viscometer for mineral pulps is the Haake RV-20 viscometer under ISO standard 3219. Figure 10.24 shows this instrument.

Fig. 10.24

Haake RV-20 rotational viscometer

Figure 10.25 shows typical sensors for suspensions. The grooves on the outside of the inner cylinder and on the inside of the outer cylinder avoid slippage of particles along the walls.

Fig. 10.25

Grooved sensors type MV

10.3.3 Standard Rheological Measurement (Rheogram ISO 3219)

• 1. Select the correct measuring system.

• 2. Fill the cup with a representative sample of slurry to the designated point.

• 3. Place the cup on the laboratory jack centered below the viscometer bob.

• 4. Slowly raise the jack so that the bob completely penetrates the slurry sample.

• 5. Fix the cup to the viscometer using the designated mounting screw.

• 6. Use the software from the rotational rheometer to produce a rheogram of the slurry sample.

• 7. Present a rheogram of shear stress versus shear rate between 0 and 450 s⁻¹.

• 8. Repeat for different concentrations.

Problem 10.5

The measurement of copper flotation tailings with a rotational viscometer at 65 % solids gave the data in Table 10.4. Obtain the complete rheogram and determine the rheological parameters with Bingham, Power-law and Herschel-Bulkley model.

Table 10.4 Experimental data of a copper mineral at 65 % solids

• Bingham Model

The Bingham model is characterized by a yield stress $\tau_{y}$ and a constant plastic viscosity K. Results are given in Fig. 10.26.

$$ \tau_{y} = 40\,\,{\text{Pa}}\quad{\text{and}}\quad{\text{K = 0}} . 1 9 7\,\,{\text{Pa}}\;{\text{s}} $$

Fig. 10.26

Bingham parameters for data from Table 10.4 by extrapolation of the rheological curve

• Power law model

The power law model is described by the constitutive equation: $\tau = m\dot{\gamma }^{n}$

$$ m = 6.958\;{\text{Pa}}\;{\text{and}}\;n = 0. 4 5 7 $$

The result is shown in Fig. 10.27.

Fig. 10.27

Simulation with power law model of data of Table 10.4

• Herschel-Bulkley Model

Herschel-Bulkley model combines a yield stress with a power-law model. Here Fig. 10.28:

$$ \tau_{y} = 1.25\;{\text{Pa}};\quad k = 2.37\;{\text{Pa}}\;{\text{s}}^{\text{z}} \,;\quad z = 0.343 $$

Fig. 10.28

Simulation with Herschley-Bulkley model for data from Table 10.4

• Determination of the yield stress with vanes

Given the importance of yield stress in transporting mineral pulps, it needs to be determined accurately. The best way determine yield stress for values above 10 Pa is direct measurement at shear rate tending to zero. Measuring yield stress of mineral pulps at very low shear rates with rotary viscometers presents the problem of particle slip at the rotating cylinder. To avoid this problem, the vane method is used. This method consists of using a rotating vane, as shown in Fig. 10.29, to measure the yield stress under static conditions. The vane is submerged in the pulp, rotated at a speed of less than 10 [rpm] and torque is slowly increased. After a linear elastic deformation of the shear surface formed, a maximum torque $T_{M}$ is reached as shown in Fig. 10.30. Appropriate operating conditions are $D_{T} > 3d$ and $N < 10\;[{\text{rpm}}]$. Three (kg) are needed for each test.

Fig. 10.29

Vane rotor to determine yield stress

Fig. 10.30

Torque curve versus time showing the maximum torque reached

With vane measurements an approximate value of the yield stress is obtained from Eq. (10.33) with values 20–30 % lower than the real value. This is because the shear distribution is not uniform, the sides of the shear surface having different values from each other. In the absence of theoretical knowledge, Nguyen and Boger (1985) assumed a potential distribution with power m, and obtained the equation:

$$ T_{m} = \frac{{\pi d^{3} }}{2}\left( {\frac{\ell }{d} + \frac{1}{3}} \right)\tau_{y} $$

(10.33)

Due to the presence of two unknowns, $\tau_{y} {\text{ and }}m$, in equation, it is necessary to perform more than one test, usually three, with vanes of different shapes $\ell /d$ to obtain the values of these unknowns simultaneously.

Writing Eq. (10.33) in the form:

$$ \frac{{2T_{m} }}{{\pi d^{3} }} = \frac{\ell }{d}\tau_{y} + \frac{{\tau_{y} }}{m + 3} $$

(10.34)

a plot of $2T_{M} /\pi d^{3} \;{\text{vs}} .\;\ell /d$ gives a straight line. The slope of the line is $\tau_{y}$ and the intercept with the vertical axis is $\tau_{y} /(m + 3)$, which gives the value of m. See Fig. 10.31. In the case of Fig. 10.31:

$$ \frac{{\tau_{y} }}{m + 3} = 2.8551\; \to \;\tau_{y} = 32.444\; \to \;m\,{ = 8} . 3 6 $$

(10.35)

Fig. 10.31

Yield stress determination with the vane method

• (b) Capillary viscometers

A capillary viscometer is a straight cylindrical tube with diameter D and length L, through which the sample to be tested flows with constant velocity v. The time t for a given volume Q to flow between levels of the tube at a constant pressure gradient is measured. If the material has a Newtonian behavior, the Hagen-Poiseuille equation relates these variables. See Eq. (10.36).

$$ Q = \frac{1}{8}\frac{{\pi R^{4} }}{\eta }\frac{\Updelta p}{L}\;\left[ {{\text{m}}^{ 3} /{\text{s}}} \right] $$

(10.36)

Since $Q = \bar{v}_{z} /t$, where $\bar{v}_{z}$ is the average velocity. The flow is gravity driven with $\Updelta p/L = \rho g$, and the kinematical viscosity is $\nu = \eta /\rho$, we have:

$$ \nu = \frac{\pi }{32}\frac{{gD^{2} }}{{\bar{v}_{z} }}t\;\left[ {{\text{cm}}^{ 2} /{\text{s}}} \right] $$

(10.37)

For a determined capillary and constant velocity, Eq. (10.37) is written in the form:

$$ \nu = K \times t\;{\text{cm}}^{ 2} /{\text{s}};\quad{\text{where}}\quad K = \frac{\pi }{32}\frac{{gD^{2} }}{{\bar{v}_{z} }} $$

(10.38)

Manufacturers have automated and standardized capillary viscometers and give the constant K for each capillary to facilitate its use. An example is the Cannon–Fenske capillary viscometer with Lauda control. See Fig. 10.32.

Fig. 10.32

Cannon-Fenske Capillary Viscometer with Lauda Control

• Selection of capillary diameters

It is important that the material to be tested behave as a Newtonian fluid, because of which the above equation was developed. To ensure this requirement, the flow in the capillary must give a shear rate $\dot{\gamma }$ within the Newtonian range. In Chap. 11 we establish the following equation for the average shear rate in the flow in a tube:

$$ \bar{\dot{\gamma }} = 6.8\frac{Q}{{D^{3} }} $$

(10.39)

For example, the flow of 15 mm/s in a capillary of 1.01 mm gives a shear rate of $\bar{\dot{\gamma }} = 99\,{\text{s}}^{ - 1}$, which is in the Newtonian range (see Chap. 11) and corresponds to a Cannon–Fenske capillary N° 200.