Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this chapter we will introduce common numeric methods designed to solve initial value problems. Within our discussion of the Kepler problem in the previous chapter we introduced four concepts, namely the implicit Euler method, the explicit Euler method, the implicit midpoint rule, and we mentioned the symplectic Euler method. In this chapter we plan to put these methods into a more general context and to discuss more advanced techniques.

Let us define the problem: We consider initial value problems of the form

$$\begin{aligned} \left\{ \begin{aligned} \dot{y}(t)&= f(y,t), \\ y(0)&= y_0, \end{aligned}\right. \end{aligned}$$
(5.1)

where \(y(t) \equiv y\) is an \(n\)-dimensional vector and \(y_0\) is referred to as the initial value of \(y\). Let us make some remarks about the form of Eq. (5.1).

(i) We note that by posing Eq. (5.1), we assume that the differential equation is explicit in \(\dot{y}\); i.e. initial value problems of the form

$$\begin{aligned} \left\{ \begin{aligned} G(\dot{y})&= f(y,t), \\ y(0)&= y_0, \end{aligned}\right. \end{aligned}$$
(5.2)

are only considered if \(G(\dot{y})\) is analytically invertible. For instance, we will not deal with differential equations of the form

$$\begin{aligned} \dot{y} + \log \left( \dot{y} \right) = 1. \end{aligned}$$
(5.3)

(ii) We note that Eq. (5.1) is a first order differential equation in \(y\). However, this is in fact not a restriction since we can transform every explicit differential equation of order \(n\) into a coupled set of explicit first order differential equations. Let us demonstrate this. We regard an explicit differential equation of the form

$$\begin{aligned} y^{(n)} = f(t; y, \dot{y}, \ddot{y}, \ldots , y^{(n-1)}), \end{aligned}$$
(5.4)

where we defined \(y^{(k)} \equiv \frac{\mathrm{{d}}^k}{\mathrm{{d}}t^k} y\). This equation is equivalent to the set

$$\begin{aligned} \dot{y}_1&= y_2, \nonumber \\ \dot{y}_2&= y_3, \nonumber \\ \vdots&\vdots \nonumber \\ \dot{y}_{n-1}&= y_{n}, \nonumber \\ \dot{y}_{n}&= f(t, y_1,y_2,\ldots ,y_{n}), \end{aligned}$$
(5.5)

which can be written as Eq. (5.1). Hence, we can attenuate the criterion discussed in point (i), i.e. that the differential equation has to be explicit in \(\dot{y}\), to the criterion that the differential equation of order \(n\) has to be explicit in the \(n\)-th derivative of \(y\), namely \(y^{(n)}\).

There is another point required to be discussed before moving on. The numerical treatment of initial value problems is of inestimable value in physics because many differential equations, which appear unspectacular at first glance, cannot be solved analytically. For instance, consider a first order differential equation:

$$\begin{aligned} \dot{y} = t^2 + y^2. \end{aligned}$$
(5.6)

Although this equation appears to be simple, one has to rely on numerical methods in order to obtain a solution. However, Eq. (5.6) is not well posed since the solution is ambiguous as long as no initial values are given. A numerical solution is only possible if the problem is completely defined. In many cases, one uses numerical methods although the problem is solvable with the help of analytic methods, simply because the solution would be too complicated. A numerical approach might be justified, however, one should always remember that [1], quote:

                  “Numerical methods are no excuse for poor analysis.”

This chapter is augmented by a chapter on the double pendulum, which will serve as a demonstration of the applicability of Runge-Kutta methods and by a chapter on molecular dynamics which will demonstrate the applicability of the leap-frog algorithm.

2 Simple Integrators

We start by reintroducing the methods already discussed in the previous chapter. Again, we discretize the time coordinate \(t\) via the relation \(t_n = t_0 + n \varDelta t\) and define \(f_n \equiv f(t_n)\) accordingly. In the following we will refrain from noting the initial condition explicitly for a more compact notation. We investigate Eq. (5.1) at some particular time \(t_n\):

$$\begin{aligned} \dot{y}_n = f(y_n,t_n). \end{aligned}$$
(5.7)

Integrating both sides of (5.7) over the interval \([t_n, t_{n+1}]\) gives

$$\begin{aligned} y_{n+1} = y_n + \int \limits _{t_n}^{t_{n+1}} \mathrm d t' f[y(t'),t']. \end{aligned}$$
(5.8)

Note that Eq. (5.8) is exact and it will be our starting point in the discussion of several paths to a numeric solution of initial value problems. These solutions will be based on an approximation of the integral on the right hand side of Eq. (5.8) with the help of the methods already discussed in Chap. 3.

In the following we list four of the best known simple integration methods for initial value problems:

(1)

Applying the forward rectangular rule (3.9) to Eq. (5.8) yields

$$\begin{aligned} y_{n+1} = y_n + f(y_n,t_n) \varDelta t+ {\fancyscript{O}}(\varDelta t^2), \end{aligned}$$
(5.9)

which is the explicit Euler method we encountered already in Sect. 4.3. This method is also referred to as the forward Euler method . In accordance to the forward rectangular rule, the leading term of the error of this method is proportional to \(\varDelta t^2\) as was pointed out in Sect. 3.2.

(2)

We use the backward rectangular rule (3.10) in Eq. (5.8) and obtain

$$\begin{aligned} y_{n+1} = y_n + f(y_{n+1},t_{n+1}) \varDelta t+ {\fancyscript{O}}(\varDelta t^2), \end{aligned}$$
(5.10)

which is the implicit Euler method, also referred to as backward Euler method . As already highlighted in Sect. 4.3, it may be necessary to solve Eq. (5.10) numerically for \(y_{n+1}\) (Some notes on the numeric solution of non-linear equations can be found in Appendix B).

(3)

The central rectangular rule (3.13) approximates Eq. (5.8) by

$$\begin{aligned} y_{n+1} = y_n + f(y_{n+\frac{1}{2}},t_{n+\frac{1}{2}} )\varDelta t + {\fancyscript{O}}(\varDelta t^3), \end{aligned}$$
(5.11)

and we rewrite this equation in the form:

$$\begin{aligned} y_{n+1} = y_{n-1} + 2 f(y_{n},t_{n} )\varDelta t + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.12)

This method is sometimes referred to as the leap-frog routine or Störmer-Verlet method. We will come back to this point in Chap. 7. Note that the approximation

$$\begin{aligned} y_{n+\frac{1}{2}} \approx \frac{y_n + y_{n+1}}{2}, \end{aligned}$$
(5.13)

gives the implicit midpoint rule as it was introduced in Sect. 4.3.

(4)

Employing the trapezoidal rule (3.15) in an approximation to Eq. (5.8) yields

$$\begin{aligned} y_{n+1} = y_n + \frac{\varDelta t}{2} \left[ f(y_n,t_n) + f(y_{n+1},t_{n+1}) \right] + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.14)

This is an implicit method which has to be solved for \(y_{n+1}\). It is generally known as the Crank-Nicolson method or simply as trapezoidal method.

Methods (1), (2), and (4) are also known as one-step methods, since only function values at times \(t_n\) and \(t_{n+1}\) are used to propagate in time. In contrast, the leap-frog method is already a multi-step method since three different times appear in the expression. Basically, there are three different strategies to improve these rather simple methods:

  • Taylor series methods: Use more terms in the Taylor expansion of \(y_{n+1}\).

  • Linear Multi-Step methods: Use data from previous time steps \(y_k\), \(k < n\) in order to cancel terms in the truncation error.

  • Runge-Kutta method: Use intermediate points within one time step.

We will briefly discuss the first two alternatives and then turn our attention to the Runge-Kutta methods in the next section.

Taylor Series Methods From Chap. 2 we are already familiar with the Taylor expansion (2.7) of the function \(y_{n+1}\) around the point \(y_n\),

$$\begin{aligned} y_{n+1} = y_n + \varDelta t \dot{y}_n + \frac{\varDelta t^2}{2} \ddot{y}_n + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.15)

We insert Eq. (5.7) into Eq. (5.15) and obtain

$$\begin{aligned} y_{n+1} = y_n + \varDelta t\,f(y_n,t_n) + \frac{\varDelta t^2}{2} \ddot{y}_n + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.16)

So far nothing has been gained since the truncation error is still proportional to \(\varDelta t^2\). However, calculating \(\ddot{y}_n\) with the help of Eq. (5.7) gives

$$\begin{aligned} \ddot{y}_n = \frac{{\mathrm {d}}}{{\mathrm {d}}t} f (y_n,t_n) = \dot{f}(y_n,t_n) + f'(y_n,t_n) \dot{y}_n = \dot{f}(y_n,t_n) + f'(y_n,t_n) f(y_n,t_n), \end{aligned}$$
(5.17)

and this results together with Eq. (5.16) in:

$$\begin{aligned} y_{n+1} = y_n + \varDelta t\,f(y_n,t_n) + \frac{\varDelta t^2}{2} \left[ \dot{f}(y_n,t_n) + f'(y_n,t_n) f(y_n,t_n) \right] + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.18)

This manipulation reduced the local truncation error to orders of \(\varDelta t^3\). The derivatives of \(f(y_n,t_n)\), \(f'(y_n,t_n)\) and \(\dot{f}(y_n,t_n)\) can be approximated with the help of the methods discussed in Chap. 2, if an analytic differentiation is not feasible.

The above procedure can be repeated up to arbitrary order in the Taylor expansion (5.15).

Linear Multi-Step Methods

A \(k\)-th order linear multi-step method is defined by the approximation

$$\begin{aligned} y_{n+1} = \sum _{j = 0}^k a_j y_{n-j} + \varDelta t \sum _{j = 0}^{k+1} b_i\,f(y_{n+1-j},t_{n+1-j}), \end{aligned}$$
(5.19)

of Eq. (5.8). The coefficients \(a_j\) and \(b_j\) have to be determined in such a way that the truncation error is reduced. Two of the best known techniques are the so called second order Adams–Bashford methods

$$\begin{aligned} y_{n+1} = y_n + \frac{\varDelta t}{2} \left[ 3 f(y_{n},t_n) - f(y_{n-1},t_{n-1}) \right] \end{aligned}$$
(5.20)

and the second order rule (backward differentiation formula)

$$\begin{aligned} y_{n+1} = \frac{1}{3} \left[ 4 y_n - y_{n-1} + \frac{\varDelta t}{2} f(y_{n+1}, t_{n+1} ) \right] . \end{aligned}$$
(5.21)

We note in passing that the backward differentiation formula of arbitrary order can easily be obtained with the help of the operator technique introduced in Sect. 2.4, Eq. (2.30). One simply replaces the first derivative on the left hand side by the function \(f(y_n,t_n)\) according to Eq. (5.7) and calculates the backward difference series on the right hand side to arbitrary order.

In many cases, multi-step methods are based on the interpolation of previously computed values \(y_k\) by Lagrange polynomials. This interpolation is then inserted into Eq. (5.8) and integrated. However, a detailed discussion of such procedures is beyond the scope of this book. The interested reader is referred to Refs. [2, 3].

Nevertheless, let us make one last point. We note that Eq. (5.19) is explicit for \(b_0 = 0\) and implicit for \(b_0 \ne 0\). In many numerical realizations one combines implicit and explicit multi-step methods in such a way that the explicit result (solve Eq. (5.19) with \(b_0 = 0\)) is used as a guess to solve the implicit equation (solve Eq. (5.19) with \(b_0 \ne 0\)). Hence, the explicit method predicts the value \(y_{n+1}\) and the implicit method corrects it. Such methods yield very good results and are commonly referred to as predictor–corrector methods [4].

3 Runge-Kutta Methods

In contrast to linear multi-step methods, the idea in Runge-Kutta methods is to improve the accuracy by calculating intermediate grid-points within the interval \([t_n,t_{n+1}]\). We note that the approximation (5.11) resulting from the central rectangular rule is already such a method since the function value \(y_{n+\frac{1}{2}}\) at the grid-point \(t_{n+\frac{1}{2}} = t_n + \frac{\varDelta t}{2}\) is taken into account. We investigate this in more detail and rewrite Eq. (5.11):

$$\begin{aligned} y_{n+1} = y_n + f(y_{n+\frac{1}{2}},t_{n+\frac{1}{2}} )\varDelta t + {\fancyscript{O}}(\varDelta t^3). \end{aligned}$$
(5.22)

We now have to find appropriate approximations to \(y_{n+\frac{1}{2}}\) which will increase the accuracy of Eq. (5.11). Our first choice is to replace \(y_{n+\frac{1}{2}}\) with the help of the explicit Euler method, Eq. (5.9),

$$\begin{aligned} y_{n+\frac{1}{2}} = y_n + \frac{\varDelta t}{2} \dot{y}_n = y_n + \frac{\varDelta t}{2} f(y_n,t_n), \end{aligned}$$
(5.23)

which, inserted into Eq. (5.22) yields

$$\begin{aligned} y_{n+1} = y_n + f \left[ y_n + \frac{\varDelta t}{2} f(y_n,t_n), t_n + \frac{\varDelta t}{2} \right] \varDelta t + {\fancyscript{O}}(\varDelta t^2). \end{aligned}$$
(5.24)

We note that Eq. (5.24) is referred to as the explicit midpoint rule. In analogy we could have approximated \(y_{n+\frac{1}{2}}\) with the help of the implicit Euler method (5.10) which yields

$$\begin{aligned} y_{n+1} = y_n + f \left[ y_n + \frac{\varDelta t}{2} f(y_{n+1},t_{n+1}), t_n + \frac{\varDelta t}{2} \right] \varDelta t + {\fancyscript{O}}(\varDelta t^2). \end{aligned}$$
(5.25)

This equation is referred to as the implicit midpoint rule. Let us explain how we obtain an estimate for the error in Eqs. (5.24) and (5.25). In case of Eq. (5.24) we investigate the term

$$\begin{aligned} y_{n+1} - y_n - f \left[ y_n + \frac{\varDelta t}{2} f(y_n,t_n), t_n + \frac{\varDelta t}{2} \right] \varDelta t. \end{aligned}$$

The Taylor expansion of \(y_{n+1}\) and \(f(\cdot )\) around the point \(\varDelta t = 0\) yields

$$\begin{aligned} \varDelta t \left[ \dot{y}_n - f(y_n,t_n) \right] + \frac{\varDelta t^2}{2} \left[ \ddot{y} - \dot{f}(y_n,t_n) - f'(y_n, t_n) \dot{y}_n \right] + \cdots . \end{aligned}$$
(5.26)

We observe that the first term cancels because of Eq. (5.7). Consequently, the error is of order \(\varDelta t^2\). A similar argument holds for Eq. (5.25).

Let us introduce a more convenient notation for the above examples before we concentrate on a more general topic. It is presented in algorithmic form, i.e. it defines the sequence in which one should calculate the various terms. This is convenient for two reasons, first of all it increases the readability of complex methods such as Eq. (5.25) and, secondly, it can be easily identified which part of the method involves an implicit step which has to be solved separately for the corresponding variable. For this purpose let us introduce variables \(Y_i\) of some index \(i \ge 1\) and we use a simple example to illustrate this notation. Consider the explicit Euler method (5.9). It can be written as

$$\begin{aligned} Y_1&= y_n, \nonumber \\ y_{n+1}&= y_n + f(Y_1,t_n) \varDelta t. \end{aligned}$$
(5.27)

In a similar fashion we write the implicit Euler method (5.10) as

$$\begin{aligned} Y_1&= y_n + f(Y_1,t_{n+1}) \varDelta t, \nonumber \\ y_{n+1}&= y_n + f(Y_1,t_{n+1}) \varDelta t. \end{aligned}$$
(5.28)

It is understood that the first equation of (5.28) has to be solved for \(Y_1\) first and this result is then plugged into the second equation in order to obtain \(y_{n+1}\). One further example: the Crank–Nicolson (5.14) method can be rewritten as

$$\begin{aligned} Y_1&= y_n, \nonumber \\ Y_2&= y_n + \frac{\varDelta t}{2} \left[ f(Y_1,t_n) + f(Y_2,t_{n+1}) \right] , \nonumber \\ y_{n+1}&= y_n + \frac{\varDelta t}{2} \left[ f(Y_1,t_n) + f(Y_2,t_{n+1}) \right] , \end{aligned}$$
(5.29)

where the second equation is to be solved for \(Y_2\) in the second step.

In analogy, the algorithmic form of the explicit midpoint rule (5.24) is defined as

$$\begin{aligned} Y_1&= y_{n}, \nonumber \\ Y_2&= y_n + \frac{\varDelta t}{2} f\left( Y_1,t_n + \frac{\varDelta t}{2} \right) , \nonumber \\ y_{n+1}&= y_n + \frac{\varDelta t}{2} f\left( Y_2,t_n + \frac{\varDelta t}{2} \right) , \end{aligned}$$
(5.30)

and we find for the implicit midpoint rule (5.25):

$$\begin{aligned} Y_1&= y_n + \frac{\varDelta t}{2} f \left( Y_1, t_n + \frac{\varDelta t}{2} \right) , \nonumber \\ y_{n+1}&= y_n + \varDelta t\,f \left( Y_1, t_n + \frac{\varDelta t}{2} \right) . \end{aligned}$$
(5.31)

The above algorithms are all examples of the so called Runge-Kutta methods. We introduce the general representation of a \(d\)-stage Runge-Kutta method:

$$\begin{aligned} Y_i&= y_n + \varDelta t \sum _{j = 1}^d a_{ij}\,f\left( Y_j, t_n + c_j \varDelta t \right) , \qquad i = 1, \ldots , d,\nonumber \\ y_{n+1}&= y_n +\varDelta t \sum _{j = 1}^d b_i\,f \left( Y_j, t_n +c_j \varDelta t \right) . \end{aligned}$$
(5.32)

We note that Eq. (5.32) it is completely determined by the coefficients \(a_{ij}\), \(b_j\) and \(c_j\). In particular \(a = \{a_{ij} \}\) is a \(d \times d\) matrix, while \(b = \{b_j \}\) and \(c = \{ c_j \}\) are \(d\) dimensional vectors.

Butcher tableaus are a very useful tool to characterize such methods. They provide a structured representation of the coefficient matrix \(a\) and the coefficient vectors \(b\) and \(c\):

$$\begin{aligned} \begin{array}{c | c c c c} c_1 &{} a_{11} &{} a_{12} &{} \ldots &{} a_{1d} \\ c_2 &{} a_{21} &{} a_{22} &{} \ldots &{} a_{2d} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ c_d &{} a_{d1} &{} a_{d2} &{} \ldots &{} a_{dd} \\ \hline &{} b_1 &{} b_2 &{} \ldots &{} b_d \end{array} \end{aligned}$$
(5.33)

We note that the Runge-Kutta method (5.32) or (5.33) is explicit if the matrix \(a\) is zero on and above the diagonal, i.e. \(a_{ij} = 0\) for \( j \ge i\). Let us rewrite all the methods described here in the form of Butcher tableaus:

Explicit Euler:

$$\begin{aligned} \begin{array}{c | c} 0 &{} 0 \\ \hline &{} 1 \end{array} \end{aligned}$$
(5.34)

Implicit Euler:

$$\begin{aligned} \begin{array}{c | c} 1 &{} 1 \\ \hline &{} 1 \end{array} \end{aligned}$$
(5.35)

Crank-Nicolson:

$$\begin{aligned} \begin{array}{c | c c} 0 &{} 0 &{} 0 \\ 1 &{} \frac{1}{2} &{} \frac{1}{2}\\ \hline \\ &{} \frac{1}{2} &{} \frac{1}{2} \end{array} \end{aligned}$$
(5.36)

Explicit Midpoint:

$$\begin{aligned} \begin{array}{c | c c} 0 &{} 0 &{} 0 \\ \frac{1}{2} &{} \frac{1}{2} &{} 0\\ \hline \\ &{} \frac{1}{2} &{} \frac{1}{2} \end{array} \end{aligned}$$
(5.37)

Implicit Midpoint:

$$\begin{aligned} \begin{array}{c | c} \frac{1}{2} &{} \frac{1}{2} \\ \hline &{} 1 \end{array} \end{aligned}$$
(5.38)

With the help of Runge–Kutta methods of the general form (5.32) one can develop methods of arbitrary accuracy. One of the most popular methods is the explicit four stage method (we will call it e-RK-4) which is defined by the algorithm:

$$\begin{aligned} Y_1&= y_n, \nonumber \\ Y_2&= y_n + \frac{\varDelta t}{2} f(Y_1, t_n), \nonumber \\ Y_3&= y_n + \frac{\varDelta t}{2} f\left( Y_2, t_n + \frac{\varDelta t}{2} \right) , \nonumber \\ Y_4&= y_n + \varDelta t\,f\left( Y_3 , t_n +\frac{\varDelta t}{2} \right) , \nonumber \\ y_{n+1}&= y_n + \frac{\varDelta t}{6} \left[ f(Y_1,t_n) + 2 f \left( Y_2, t_n \,{+}\,\frac{\varDelta t}{2} \right) \right. \nonumber \\&\left. +\,2 f \left( Y_3, t_n +\frac{\varDelta t}{2} \right) + f(Y_4,t_n) \right] . \end{aligned}$$
(5.39)

This method is an analogue to the Simpson rule of numerical integration as discussed in Sect. 3.4. However, a detailed compilation of the coefficient array \(a\) and coefficient vectors \(b\), and \(c\) is quite complicated. A closer inspection reveals that the methodological error of this method behaves as \(\varDelta t^5\). The algorithm e-RK-4, Eq. (5.39), is represented by a Butcher tableau of the form

$$\begin{aligned} \begin{array}{c|cccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{1}{2} &{}\frac{1}{2} &{} 0 &{} 0&{}0 \\ \frac{1}{2} &{}0 &{}\frac{1}{2} &{}0 &{}0\\ 1 &{} 0 &{} 0 &{} 1 &{}0\\ \hline \\ &{} \frac{1}{6} &{} \frac{1}{3} &{}\frac{1}{3} &{}\frac{1}{6}\\ \end{array} \end{aligned}$$
(5.40)

Another quite popular method is given by the Butcher tableau

$$\begin{aligned} \begin{array}{c | c c} \frac{1}{2} - \frac{\sqrt{3}}{6} &{} \frac{1}{4} &{} \frac{1}{4} - \frac{\sqrt{3}}{6}\\ \frac{1}{2} + \frac{\sqrt{3}}{6} &{} \frac{1}{4} + \frac{\sqrt{3}}{6} &{} \frac{1}{4} \\ \hline \\ &{} \frac{1}{2} &{}\frac{1}{2} \end{array} \end{aligned}$$
(5.41)

We note that this method is implicit and mention that it corresponds to the two point Gauss-Legendre quadrature of Sect. 3.6.

A further improvement of implicit Runge-Kutta methods can be achieved by choosing the \(Y_i\) in such a way that they correspond to solutions of the differential equation (5.7) at intermediate time steps. The intermediate time steps at which one wants to reproduce the function are referred to as collocation points. At these points the functions are approximated by interpolation on the basis of Lagrange polynomials, which can easily be integrated analytically. However, the discussion of such collocation methods [4] is far beyond the scope of this book.

In general Runge-Kutta methods are very useful. However one always has to keep in mind that there could be better methods for the problem at hand. Let us close this section with a quote from the book by Press et al. [5]:

“For many scientific users, fourth-order Runge-Kutta is not just the first word on ODE integrators, but the last word as well. In fact, you can get pretty far on this old workhorse, especially if you combine it with an adaptive step-size algorithm. Keep in mind, however, that the old workhorse’s last trip may well take you to the poorhouse: Bulirsch-Stoer or predictor-corrector methods can be very much more efficient for problems where high accuracy is a requirement. Those methods are the high-strung racehorses. Runge-Kutta is for ploughing the fields.”

4 Hamiltonian Systems: Symplectic Integrators

Let us define a symplectic integrator as a numerical integration in which the mapping

$$\begin{aligned} \varPhi _{\varDelta t}: y_n \mapsto y_{n+1}, \end{aligned}$$
(5.42)

is symplectic. Here \(\varPhi _{\varDelta t}\) is referred to as the numerical flow of the method. If we regard the initial value problem (5.1) we can define in an analogous way the flow of the system \(\varphi _t\) as

$$\begin{aligned} \varphi _t(y_0) = y(t). \end{aligned}$$
(5.43)

For instance, if we consider the initial value problem

$$\begin{aligned} \left\{ \begin{array}{ll} &{} \dot{y} = A y, \\ &{} y(0) = y_0, \end{array}\right. \end{aligned}$$
(5.44)

where \(y \in {\mathbb R}^n\) and \(A \in {\mathbb R}^{n \times n}\), then the flow of the system \(\varphi _t\) is given by:

$$\begin{aligned} \varphi _t(y_0) = \exp ( A t) y_0. \end{aligned}$$
(5.45)

On the other hand, if we regard two vectors \(v, w \in {\mathbb R}^2\), we can express the area \(\omega \) of the parallelogram spanned by these vectors as

$$\begin{aligned} \omega (v,w) = \det (v w) = v \left( \begin{array}{c c} 0 &{} 1 \\ -1 &{} 0 \end{array} \right) w = ad - bc, \end{aligned}$$
(5.46)

where we put \(v = (a, b)^T\) and \(w = (c,d)^T\). More generally, if \(v, w \in {\mathbb R}^{2d}\), we have

$$\begin{aligned} \omega (v,w) = v \left( \begin{array}{c c} 0 &{} I \\ -I &{} 0 \end{array} \right) w \equiv v J w, \end{aligned}$$
(5.47)

where \(I\) is the \(d \times d\) dimensional unity matrix. Hence (5.47) represents the sum of the projected areas of the form

$$\begin{aligned} \det \left( \begin{array}{c c} v_i &{} w_i \\ v_{i+d} &{} w_{i+d} \end{array} \right) . \end{aligned}$$
(5.48)

If we regard a mapping \(M: {\mathbb R}^{2d} \mapsto {\mathbb R}^{2d}\) and require that

$$\begin{aligned} \omega (M v, Mw) = \omega (v,w), \end{aligned}$$
(5.49)

i.e. the area is preserved, we obtain the condition that

$$\begin{aligned} M^T J M = J, \end{aligned}$$
(5.50)

which is equivalent to \(\det (M) = 1\). Finally, a differentiable mapping \(f: {\mathbb R}^{2d} \mapsto {\mathbb R}^{2d}\) is referred to as symplectic if the linear mapping \(f'(x)\) (Jacobi matrix) conserves \(\omega \) for all \(x \in {\mathbb R}^{2d}\). One can easily prove that the flow of Hamiltonian systems (energy conserving) is symplectic, i.e. area preserving in phase space. Every Hamiltonian system is characterized by its Hamilton function\(H(p,q)\) and the corresponding Hamilton equations of motion:

$$\begin{aligned} \dot{p} = - \nabla _q H(p,q) \qquad \text { and }\, \dot{q} = \nabla _p H(p,q). \end{aligned}$$
(5.51)

We define the flow of the system via

$$\begin{aligned} \varphi _t(x_0) = x(t), \end{aligned}$$
(5.52)

where

$$\begin{aligned} x_0 = \left( \begin{array}{c} p_0 \\ q_0 \end{array} \right) \quad \text { and } \quad x(t) = \left( \begin{array}{c} p(t) \\ q(t) \end{array} \right) . \end{aligned}$$
(5.53)

Hence we rewrite (5.51) as

$$\begin{aligned} \dot{x} = J^{-1} \nabla _x H(x), \end{aligned}$$
(5.54)

and note that \(x \equiv x(t,x_0)\) is a function of time and initial conditions. In a next step we define the Jacobian of the flow via

$$\begin{aligned} P_t(x_0) = \nabla _{x_0} \phi _t(x_0), \end{aligned}$$
(5.55)

and calculate

$$\begin{aligned} \dot{P}_t(x_0)&= \nabla _{x_0} \dot{x} \nonumber \\&= J^{-1} \nabla _{x_0} \nabla _x H(x) \nonumber \\&= J^{-1} \varDelta _x H(x) \nabla _{x_0} x \nonumber \\&= J^{-1} \varDelta _x H(x) P_t(x_0) \nonumber \\&= \left( \begin{array}{cc} - \nabla _{qp} H(p,q) &{} -\nabla _{qq} H(p,q) \\ \nabla _{pp} H(p,q) &{} \nabla _{pq} H(p,q) \end{array} \right) P_t(x_0). \end{aligned}$$
(5.56)

Hence, \(P_t\) is given by the solution of the equation

$$\begin{aligned} \dot{P}_t = J^{-1} \varDelta _x H(x) P_t. \end{aligned}$$
(5.57)

Symplecticity ensures that the area

$$\begin{aligned} P_t^T J P_t = \text {const}, \end{aligned}$$
(5.58)

which can be verified by calculating \(\frac{{\mathrm {d}}}{{\mathrm {d}} t} \left( P_t^T J P_t \right) \) where we keep in mind that \(J^T = -J\). Hence,

$$\begin{aligned} \frac{{\mathrm {d}}}{\mathrm{{d}} t}P_t^T J P_t&= \dot{P}_t^T J P_t + P_t^T J \dot{P}_t \nonumber \\&= P_t^T \varDelta _x H(x) (J^{-1} )^T J P_t + P_t^T J J^{-1} \varDelta _x H(x) P_t \nonumber \\&= 0, \end{aligned}$$
(5.59)

if the Hamilton function is conserved, i.e.

$$\begin{aligned} \frac{\partial }{\partial t} H(p,q) \mathop {=}\limits ^{!}0. \end{aligned}$$
(5.60)

This means that the flow of a Hamiltonian system is symplectic, i.e. area preserving in phase space.

Since this conservation law is violated by methods like e-RK-4 or explicit Euler, one introduces so called symplectic integrators, which have been particularly designed as a remedy to this shortcoming. A detailed investigation of these techniques is far too engaged for this book. The interested reader is referred to Refs. [6–9].

However, we provide a list of the most important integrators.

Symplectic Euler

$$\begin{aligned} q_{n+1}&= q_n + a(q_n, p_{n+1}) \varDelta t, \end{aligned}$$
(5.61a)
$$\begin{aligned} p_{n+1}&= p_n + b(q_n, p_{n+1})\varDelta t. \end{aligned}$$
(5.61b)

Here \(a(p,q) = \nabla _p H(p,q)\) and \(b(p,q) = - \nabla _q H(p,q)\) have already been defined in Sect. 4.3.

Symplectic Runge – Kutta

It can be demonstrated that a Runge-Kutta method is symplectic if the coefficients fulfill

$$\begin{aligned} b_i a_{ij} +b_j a_{ji} = b_i b_j, \end{aligned}$$
(5.62)

for all \(i,j\) [7]. This is a property of the collocation methods based on Gauss points \(c_i\).

5 An Example: The Kepler Problem, Revisited

It has already been discussed in Sect. 4.3 that the Hamilton function of this system takes on the form

$$\begin{aligned} H(p,q) = \frac{1}{2} \left( p_1^2 + p_2^2 \right) - \frac{1}{\sqrt{q_1^2 + q_2^2}}, \end{aligned}$$
(5.63)

and Hamilton’s equations of motion read

$$\begin{aligned} \dot{p}_1&= - \nabla _{q_1} H(p,q) = -\frac{q_1}{(q_1^2 + q_2^2)^{\frac{3}{2}}}, \end{aligned}$$
(5.64a)
$$\begin{aligned} \dot{p}_2&= - \nabla _{q_2} H(p,q) = -\frac{q_2}{(q_1^2 + q_2^2)^{\frac{3}{2}}}, \end{aligned}$$
(5.64b)
$$\begin{aligned} \dot{q}_1&= \nabla _{p_1} H(p,q) = p_1, \end{aligned}$$
(5.64c)
$$\begin{aligned} \dot{q}_2&= \nabla _{p_2} H(p,q) = p_2. \end{aligned}$$
(5.64d)

We now introduce the time instances \(t_n = t_0 + n \varDelta t\) and define \(q_i^n \equiv q_i(t_n)\) and \(p_i^n \equiv p_i(t_n)\) for \(i = 1,2\). In the following we give the discretized recursion relation for three different methods, namely explicit Euler, implicit Euler, and symplectic Euler.

Explicit Euler

In case of the explicit Euler method we have simple recursion relations

$$\begin{aligned} p_1^{n+1}&= p_1^n -\frac{q^n_1 \varDelta t}{[(q^n_1)^2 + (q^n_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.65a)
$$\begin{aligned} p_2^{n+1}&= p_2^n -\frac{q^n_2 \varDelta t}{[(q^n_1)^2 + (q^n_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.65b)
$$\begin{aligned} q_1^{n+1}&= q_1^n + p_1^n \varDelta t, \end{aligned}$$
(5.65c)
$$\begin{aligned} q_2^{n+1}&= q_2^n + p_2^n \varDelta t. \end{aligned}$$
(5.65d)

Implicit Euler

We obtain the implicit equations

$$\begin{aligned} p_1^{n+1}&= p_1^n -\frac{q^{n+1}_1 \varDelta t}{[(q^{n+1}_1)^2 + (q^{n+1}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.66a)
$$\begin{aligned} p_2^{n+1}&= p_2^n -\frac{q^{n+1}_2 \varDelta t}{[(q^{n+1}_1)^2 + (q^{n+1}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.66b)
$$\begin{aligned} q_1^{n+1}&= q_1^n + p_1^{n+1} \varDelta t, \end{aligned}$$
(5.66c)
$$\begin{aligned} q_2^{n+1}&= q_2^n + p_2^{n+1} \varDelta t. \end{aligned}$$
(5.66d)

These implicit equations can be solved, for instance, by the use of the Newton method discussed in Appendix B.

Symplectic Euler

Employing Eqs. (5.61) gives

$$\begin{aligned} p_1^{n+1}&= p_1^n -\frac{q^{n}_1 \varDelta t}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.67a)
$$\begin{aligned} p_2^{n+1}&= p_2^n -\frac{q^{n}_2 \varDelta t}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.67b)
$$\begin{aligned} q_1^{n+1}&= q_1^n + p_1^{n+1} \varDelta t, \end{aligned}$$
(5.67c)
$$\begin{aligned} q_2^{n+1}&= q_2^n + p_2^{n+1} \varDelta t. \end{aligned}$$
(5.67d)

These implicit equations can be solved analytically and we obtain

$$\begin{aligned} p_1^{n+1}&= p_1^n -\frac{q^{n}_1 \varDelta t}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.68a)
$$\begin{aligned} p_2^{n+1}&= p_2^n -\frac{q^{n}_2 \varDelta t}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.68b)
$$\begin{aligned} q_1^{n+1}&= q_1^n + p_1^n \varDelta t-\frac{q^{n}_1 \varDelta t^2}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.68c)
$$\begin{aligned} q_2^{n+1}&= q_2^n + p_2^n \varDelta t -\frac{q^{n}_2 \varDelta t^2}{[(q^{n}_1)^2 + (q^{n}_2)^2]^{\frac{3}{2}}}. \end{aligned}$$
(5.68d)

A second possibility of the symplectic Euler is given by Eq. (4.41). It reads

$$\begin{aligned} p_1^{n+1}&= p_1^n -\frac{q^{n+1}_1 \varDelta t}{[(q^{n+1}_1)^2 + (q^{n+1}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.69a)
$$\begin{aligned} p_2^{n+1}&= p_2^n -\frac{q^{n+1}_2 \varDelta t}{[(q^{n+1}_1)^2 + (q^{n+1}_2)^2]^{\frac{3}{2}}}, \end{aligned}$$
(5.69b)
$$\begin{aligned} q_1^{n+1}&= q_1^n + p_1^{n} \varDelta t, \end{aligned}$$
(5.69c)
$$\begin{aligned} q_2^{n+1}&= q_2^n + p_2^{n} \varDelta t. \end{aligned}$$
(5.69d)

The trajectories calculated using these four methods are presented in Figs. 5.1 and 5.2, the time evolution of the total energy of the system is plotted in Fig. 5.3. The initial conditions were [7]

$$\begin{aligned} p_1(0) = 0, \qquad q_1(0) = 1-e, \end{aligned}$$
(5.70)

and

$$\begin{aligned} p_2(0) = \sqrt{\frac{1+e}{1-e}}, \qquad q_2(0) = 0, \end{aligned}$$
(5.71)

with \(e = 0.6\) which gives \(H = -1/2\). Furthermore, we set \(\varDelta t = 0.01\) for the symplectic Euler methods and \(\varDelta t = 0.005\) for the forward and backward Euler methods in order to reduce the methodological error. The implicit equations were solved with help of the Newton method as discussed in Appendix B. The Jacobi matrix was calculated analytically, hence no methodological error enters because approximations of derivatives were unnecessary.

Fig. 5.1
figure 1

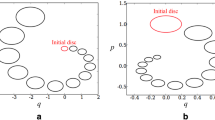
Kepler trajectories in position space for the initial values defined in Eqs. (5.70) and (5.71). They are indicated by a solid square. Solutions have been generated (a) by the explicit Euler method (5.65), (b) by the implicit Euler method (5.66), (c) by the symplectic Euler method (5.68), and (d) by the symplectic Euler method (5.69)

Full size image

According to theory the \(q\)-space and \(p\)-space projections of the phase space trajectory are ellipses. Furthermore, energy and angular momentum are conserved. Thus, the numerical solutions of Hamilton’s equations of motion (5.64) should reflect these properties. Figures 5.1a, b and 5.2a, b present the results of the explicit Euler method, Eq. (5.65), and the implicit Euler method, Eq. (5.66), respectively. Obviously, the result does not agree with the theoretical expectation and the trajectories are open instead of closed. The reason for this behavior is the methodological error of the method which is accumulative and, thus, causes a violation of energy conservation. This violation becomes apparent in Fig. 5.3 where the total energy \(H(t)\) is plotted versus time \(t\). Neither the explicit Euler method (dashed line) nor the implicit Euler method (short dashed line) conform to the requirement of energy conservation. We also see step-like structures of \(H(t)\). At the center of these steps an open diamond symbol and in the case of the implicit Euler method an additional open circle indicate the position in time of the perihelion of the point-mass (point of closest approach to the center of attraction). It is indicated by the same symbols in Fig. 5.1a, b. At this point the point-mass reaches its maximum velocity, the pericenter velocity, and it covers the biggest distances along its trajectory per time interval \(\varDelta t\). Consequently, the methodological error is biggest in this part of the trajectory which manifests itself in those steps in \(H(t)\). As the point-mass moves ‘faster’ when the implicit Euler method is applied, again, the distances covered per time interval are greater than those covered by the point-mass in the explicit Euler method. Thus, it is not surprising that the error of the implicit Euler method is bigger as well when \(H(t)\) is determined.

Fig. 5.2
figure 2

Kepler trajectories in momentum space for the initial values defined in Eqs. (5.70) and (5.71). They are indicated by a solid square. Solutions have been generated (a) by the explicit Euler method (5.65), (b) by the implicit Euler method (5.66), (c) by the symplectic Euler method (5.68), and (d) by the symplectic Euler method (5.69)

Full size image
Fig. 5.3
figure 3

Time evolution of the total energy \(H\) calculated with the help of the four methods discussed in the text. The initial values are given by Eqs. (5.70) and (5.71). Solutions have been generated (a) by the explicit Euler method (5.65) (dashed line), (b) by the implicit Euler method (5.66) (dotted line), (c) by the symplectic Euler method (5.68) (solid line), and (d) by the symplectic Euler method (5.69) (dashed-dotted line)

Full size image

These results are in strong contrast to the numerical solutions of Eqs. (5.64) obtained with the help of symplectic Euler methods which are presented in Figs. 5.1c, d and 5.2c, d. The trajectories are almost perfect ellipses for both symplectic methods Eqs. (5.68) and (5.69). Moreover, the total energy \(H(t)\) (solid and dashed-dotted lines in Fig. 5.3) varies very little as a function of \(t\). Deviations from the mean value can only be observed around the perihelion which is indicated by a solid square. Moreover, these deviations compensate because of the symplectic nature of the method. This proves that symplectic integrators are the appropriate technique to solve the equations of motion of Hamiltonian systems.

Summary

We concentrated on numerical methods to solve the initial value problem. The methods discussed here rely heavily on the various methods developed for numerical integration because we can always find an integral representation of this kind of ordinary differential equations. The simple integrators known from Chap. 4 were augmented by the more general Crank-Nicholson method which was based on the trapezoidal rule introduced in Sect. 3.3. The simple single-step methods were improved in their methodological error by Taylor series methods, linear multi-step methods, and by the Runge-Kutta method. The latter took intermediate points within the time interval \([t_n,t_{n+1}]\) into account. In principle, it is possible to achieve almost arbitrary accuracy with such a method. Nevertheless, all those methods had the disadvantage that because of their methodological error energy conservation was violated when applied to Hamiltonian systems. As this problem can be remedied by symplectic integrators a short introduction into this topic was provided and the most important symplectic integrators have been presented. The final discussion of Kepler’s two-body problem elucidated the various points discussed throughout this chapter.

Problems

  1. 1.

    Write a program to solve numerically the Kepler problem. The Hamilton function of the problem is defined as

    $$\begin{aligned} H(p,q) = \frac{1}{2} \left( p_1^2 + p_2^2 \right) - \frac{1}{\sqrt{q_1^2 + q_2^2}}, \end{aligned}$$

    and the initial conditions are given by

    $$\begin{aligned} p_1(0) = 0, \quad q_1(0) = 1-e, \quad p_2(0) = \sqrt{\frac{1+e}{1-e}}, \quad q_2(0) = 0, \end{aligned}$$

    where \(e = 0.6\). Derive Hamilton’s equations of motion and implement an algorithm which solves these equations based on the following methods

    1. (a)

      Explicit Euler,

    2. (b)

      Symplectic Euler.

  2. 2.

    Plot the trajectories and the total energy as a function of time. You can use the results presented in Figs. 5.1 and 5.2 to check your code. Modify the initial conditions and discuss the results! Try to confirm Kepler’s laws of planetary motion with the help of your algorithm.