Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

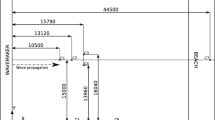
An example of a system formed by a channel connected to an open domain (see Fig. 1) is a river flushing into a lake or the open sea. The tides induce a flow between both domains, in fact, during the stage of positive flow rate (positive is considered when flow is directed toward the open domain) a pair of vortices is formed. This is a coherent structure known as a dipole. The evolution of dipole depends on a dimensionless parameter, the Strouhal number \(S\), defined as follow:

$$\begin{aligned} S=\frac{H_1}{UT} \end{aligned}$$
(1)
Fig. 1
figure 1

System geometry under study, consisting of a channel connected to a basin

Full size image

where \(H_1\) is the channel width, \(U\) is the maximum speed at the channel and \(T\) is the forcing period. Considering a potential flow composed of a linear sink (or source, depending of the stage) and two counter rotating point vortices, Wells and Van Heijst (2003) shown that when \(S < 0.13\) the dipole escapes, and when \(S > 0.13\) the dipole returns to the channel. The numerical code described in this manuscript provides a detailed knowledge of the vortex formation or another features of the flow, like the coexistence of multiple dipoles, interaction among them or even the coalescence of vortices. All these facts are important because is well known the ability of dipoles to carry particles from one region to another. There are some previous works about both dipoles and particle transport. For instance Duran-Matute et al. (2010) made a numerical simulation of a dipole assuming as initial condition the velocity field of a Lamb-Chaplygin vortex in the horizontal plane and a Poiseuille velocity profile for the vertical coordinate. The relevant parameters are the Reynolds number \(Re\) and the aspect ratio \(\delta =H/R_0\), where \(H\) is the fluid-layer depth and \(R_0\) is the radius of the Lamb-Chaplygin vortex. They found that the three-dimensional nature of the flow depends on the single parameter \(K=\delta ^2Re\). When \(K < 6 \) the flow remains bidimensional, and when \(K >15 \) the flow becomes three dimensional with a spanwise vortex in front of dipole. From the experimental side Lacaze et al. (2010) and Albagnac (2010) produced a dipole by rotating two vertical plates in a rectangular basin. They also observed a spanwise vortex in front of the dipole and report that intensities of the spanwise vortex and the dipole are comparable.

Concerning the mass flow Angilella (2010) investigated the transport of dust in the vicinity of a pair of identical point vortices rotating about a common center and that remain in a vertical plane. To this end the equation of motion for trajectories is solved in a rotating reference frame, then Coriolis and centrifugal forces are included in addition to gravity and drag. The motivation of the research was to test the idea that the particle dispersion increases with the presence of a co-rotating vortex pair. When drag is the dominant force, the particle trajectories exhibit chaotic behavior, so mixing is enhanced.

Shaden et al. (2007) made experiments to determine the particle transport during the formation and growth of an annular vortex, which was produced with a piston-cylinder apparatus immersed in a water tank. They found that in the early stage, most of the fluid that enters the region of nonzero vorticity comes from the cylinder, and as the vortex ring grows and moves, fluid outside this cylinder is entrained.

The goal of this work is to calculate the trajectories of solid particles from an equation deduced from first principles (Maxey and Riley 1983) in which drag, added mass and history forces are included. For the integration of this equation the velocity field of the flow in the system shown in Fig. 1 is required. The solution obtained allows to determine the regions from which the particles are expeled and the regions where the particles are deposited .

The paper is organized as follows: In Sect. 2, we introduce the equation for particle motion equation, then it is written in dimensionless form. After we present the governing parameters and describe the methodology. In Sect. 3, we present data obtained for different values of \(S\) and \(Re\) and we compare them with some experimental results and, finally, we draw conclusions in Sect. 4.

2 Theoretical Background

In the flow the driving force is introduced through a periodic flow rate given by

$$\begin{aligned} Q=Q_0\sin \left( \frac{2\pi }{T} t\right) \end{aligned}$$
(2)

where \(T\) is the driving period. This choice allows periodic reversal of the flow. In dimensionless variables the flow rate is:

$$\begin{aligned} Q=\sin \left( 2 \pi S t\right) \end{aligned}$$
(3)

In order to describe all equations and results in dimensionless form we need to introduce a second parameter, namely, the Reynolds number, defined as: \(Re=\frac{UH_{1}}{\nu }\). Here \(H_1\) as the channel width, \(U = Q_0/H_1\) is the maximum velocity in the channel and \(\nu \) the kinematical viscosity. For the calculation of trajectories we solve a second order differential equation deduced by (Maxey and Riley 1983):

$$\begin{aligned} m_{p}\frac{d\mathbf{{v}}_{p}}{dt}&= (m_{p}-m_{f})\mathbf{{g}}+m_f\frac{D\mathbf{{u}}}{Dt}\nonumber \\&\quad +6\pi r\mu _f(\mathbf{{u}}-\mathbf{{v}}_p)+\frac{m_f}{2}\frac{D(\mathbf{{u}}-\mathbf{{v}}_p)}{Dt}\\&\quad +6r^{2}\sqrt{\pi \mu _f\rho _f}\int _0^{t}\frac{\frac{D(\mathbf{{u}}-\mathbf{{v}}_p)}{D\tau }}{\sqrt{t-\tau }}d\tau&\nonumber \end{aligned}$$
(4)

in which it is assumed that solid particles are spheres. Here, \(\mathbf u\) is the fluid velocity at the particle position (if the particle was removed), \(\mathbf{{v}}_p\) is particle velocity, \(m_p\) is its mass, \(m_f\) is the mass of fluid displaced by the solid sphere, \(\mu _f\) is the dynamic viscosity, \(g\) is gravity, and \(r\) is the radius of the particle. The first term on the right-hand side is the sum of gravity and the buoyant force. The second term is the Stokes force, which is proportional to the difference between particle and fluid velocities. The third term is the added-mass term, and the last term is the history force (Mordant 2001). In the last equation the velocity field of the flow is required. This field has been obtained in a previous paper (Lopez and Ruiz 2013). Now we write this equation in non dimensional form:

$$\begin{aligned} \frac{d\mathbf{{v}}_p}{dt}=&-\left( \frac{\rho _p}{\rho _f}-1\right) Fr\hat{z}+ \frac{3}{\left( \frac{2\rho _p}{\rho _m}+1\right) }\frac{D\mathbf{{u}}}{Dt} \\&+\frac{9(\mathbf{{u}}-\mathbf{{v}}_p)}{\left( \frac{2\rho _p}{\rho _m}+1\right) Re}\left( \frac{H_1}{r}\right) ^2+\frac{9}{\left( \frac{2\rho _p}{\rho _m}+1\right) \sqrt{\pi Re}}\left( \frac{H_1}{r}\right) \int _0^{t}\frac{\frac{D(\mathbf{{u}}-\mathbf{{v}}_p)}{D\tau }}{\sqrt{t-\tau }}d\tau \nonumber \end{aligned}$$
(5)

where \(\rho _p\) is the particle density, \(\rho _f\) is the fluid density and \(\hat{z}\) is a unit vector in the vertical direction. \(Fr =gH_1/U^2\) is the Froude number. For this calculation we make the approximation:

$$\begin{aligned} \frac{d(\mathbf{{u}}-\mathbf{{v}}_p)}{dt}\approx \frac{D\mathbf{{u}}}{Dt}-\frac{d\mathbf{{v}}}{dt} \end{aligned}$$
(6)

Equation (5) is solved in two dimensions, so gravity and buoyancy are dropped and consequently the Froude number does not enter in the calculations.

For the integration we use \(\rho _p = 2400\) kg/m\(^3\) (tipical sand density) and \(r = 5\times 10^{-4}\) m (the radius of the solid particles). We present results for particle transport in the flow using various values for \(S\) and \(Re\). The calculation were made in some selected initial positions and we assume that the initial velocity is zero.

3 Particle Transport

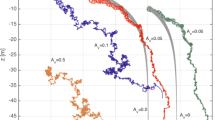
Before to describe the motion of particles we present a result about the vorticity field obtained by solving equations of fluid dynamics in the vorticity - stream function formulation. Figure 2 shows the vorticity field for \(S=0.05\) and \(Re=667\). Multiples dipoles appear, each one is formed during a cycle. The solution was calculated using a pseudo-spectral method, based on Chebyshev polinomial for the space, and an Adams-Bashford semi-implicit schema for the time. In order to have a picture of the motion induced by the flow, some trajectories of solid particles and fluid elements are plotted in Fig. 3. The values of Reynolds and Strouhal numbers are respectively 67 and 0.0075. A comparison between motion of solid particles and fluid elements reveals that at the early stage both kind of trajectories resembles each to other. However, after a while trajectories separate which is a signature of the influence of drag and other forces acting on the solid particles.

Fig. 2
figure 2

Vorticity at \(t= 3.24\) T. Multiple dipoles are present

Full size image
Fig. 3
figure 3

Trajectories of both the solid particle (continuous) and the fluid elements (dotted) for two initial points \(p_1=(1.1,1.4)\) and \(p_2=(3.5,-1)\), for the case \(Re=67\), \(S=0.0075\)

Full size image

In Fig. 3, the particle initially located at the point \(p_1=(1.1,1.4)\) moves away from the axis of symmetry. Then, due to the passage of the first dipole it is pulled back to the centerline and for a while it follows a nearly parallel path to the x-axis and after it make several curls. This kind of motion is induced by the presence of the dipole, which pulls and drives the particle. On the other side the particle initially located at the second point \(p_2=(3.5,-1)\) has in the early stage a similar behavior as first one, in the sense that it is moved away and pulled back to the axis of symmetry. Furthermore the path between \(x=6\) and \(x=28\) do not follow any curl. Finally, the curve made a curl, which is related to the presence of the second dipole.

An overall picture of the transport of particles is obtained if the calculation of trajectories is performed for many particles. For this reason the entire domain is divided in a set of cells. In each one a fixed number of particles (9 in this work) is placed there at initial time. The size of a cell is \(0.88\times 0.96\). Then we integrate Eq. (5) for all these particles. With this procedure we can identify regions where particles accumulate or where particles are expelled. In Fig. 4 initial (upper graphs) and final (lower graphs) position are plotted. The assertion “initial position” includes only those particles that remain in the domain at the final time of integration. Blanks in the graphs indicate regions where particles are expelled outside the domain. These blanks correspond to erosion zones. The lower graphs correspond to final position of particles. Figure 4a shows the erosion zones until the time \(t\)=0.94\(T\). Figure 4b shows areas of erosion until the time \(t\)=1.9\(T\). The particle distributions at time \(t\)=0.94\(T\) and \(t\)=0.94\(T\) are shown in Figs.  4c and 4d respectively. In those graphs the passage of dipole is clearly observed. Particle transport can be outlined by the calculation of the histogram of the particle position. We proceed as follow: First, we chose a set of uniformly distributed particles, so that the probability density function (PDF) is the same elsewhere. After a while a new distribution of particles is obtained because the particles are constantly moving. The particles may remain inside the domain or may leave it. In the latter case the final particle position is unknown and consequently this particle position is not considered in the histogram.

Fig. 4
figure 4

Solid particles position at two times for \(S = 0.0075\), and \(Re = 67\). (a) and (c) Show the initial position of the particles and the white spaces indicate erosion zones. (c) and (d) Show the particles distribution at the time indicated in each panel

Full size image

A histogram of particle position for \(t = 5.6\) T, \(S = 0.05\), and \(Re = 333\) is presented in Fig. 5. For this histogram the size of cells is \(\varDelta x = 0.56\) and \(\varDelta y = 0.54\). In Fig. 5 left, we see that the particle concentration rises to 50 in a small region inside the channel.

The right side of Fig. 5 shows a picture of a experiment in which the same parameters were used in the histogram. We place sea sand uniformly distributed and after various periods, we can observe an accumulation of particles within the channel near the outlet. In addition in front of the channel there is a region where the particles were removed by the flow.

Fig. 5
figure 5

Left Histogram of particle positions at \(t = 5.6T\), \(S = 0.05\), and \(Re = 333\). Right Experimental setup

Full size image

A description of the sand barriers position in tidal inlet system is made by de Swart and Zimmerman (2009). The tidal currents induce the formation of a barrier in front of the inlet. The results presented above are in some agreement with these observational data.

4 Conclusions

In this paper we have made a study of the motion of solid particles in a flow with periodic forcing. In this flow one or more dipoles can coexist. The calculation of trajectories was made by the integration of a second order differential equation in which drag, added mas and history forces are included. The results show the existence of regions where particles are expelled outside the entire domain. Otherwise, there are also regions where particles concentrate. Some of these results are in agreement with observational and experimental data, even if trajectories were calculated in 2D and gravity was not taken into account.