1 Introduction

The processes of passive tracer dispersion in wave dominated environments are of significant importance for understanding transport properties of many hydrodynamic systems, such as aerosol dispersion in atmosphere, shock tube flows, acoustical levitation, dusted plasmas flows and solar wind among others (see, for example, Falkovich 2009; Shukla and Mamun 2001; Zukas and Walters 1997; Anisimov et al. 2013; Falkovich et al. 2001; Nazarenko 2011; Skvortsov et al. 2013; Ruderman 2006 and references therein). In the ocean, the mixing caused by surface waves contribute to pollutant spread, upper layer dynamics and impacts on the marine life habitat (Polzin and Ferrari 2004; Ledwell et al. 1993).

The Stokes Drift is an important vector component that appears often in wave-averaged dynamics, a nonlinear phenomenon first identified by George Stokes (1847). Mathematically, the Stokes Drift is the mean difference between Eulerian and Lagrangian velocities and can be thought of as the near-surface ocean current induced from the wave action. Trajectories to leading-order are closed orbits and the mean Eulerian velocities, at one fixed point in space, must be zero. However, the actual orbits of linear waves are not closed and over time there is a depth-dependent drift. Even though this is a second-order effect, the magnitudes of these near-surface currents can be significant. A passive tracer, therefore, will experience a second-order velocity in the wave propagation direction, given by the mean Stokes Drift current. In a random sea, composed as the superposition of numerous statistically independent waves each one with its own velocity, the Stokes Drift current randomly fluctuates around a mean value. Calculation of the Stokes Drift fluctuations is a challenging problem and since the seminal paper by Herterich and Hasselmann (1982b) there have been a body of publications on this topic and it is still an area of active research (Buick et al. 2001; Herbers and Janssen 2016; Huang and Law 2018, among others). The main mathematical difficulties are related to the fact that the Stokes Drift itself is a nonlinear quantity and a rigorous estimation of its fluctuations requires higher order terms in perturbation theory expansion and incorporation of viscous and induced flow effects (Jansons 2007; Lukaschuk et al. 2007; Vucelja et al. 2007). There is rich variety of analytical methods that can be employed for this purpose. A review and comparison of these methods are outside of the scope of the present study.

There are several scientific ways to think about the Lagrangian dispersion problem. Taylor (1921) was the first to quantify the motion of Lagrangian particles in terms of an effective diffusion coefficient (K). Shortly thereafter, Richardson (1926) noted that in turbulent flows the diffusivity must be a function of spatial scale, as opposed to being constant, as implied by Taylor (1921). By employing empirical data fit for diffusivity, Richardson (1926) arrived at his celebrated scaling law, \({D^{2}_{r}}\sim K t^{3}\), where Dr is the mean square of inter-particle separation (Boffetta and Sokolov 2002).

There are a number of comprehensive studies where wave turbulent diffusion has been investigated either theoretically (Falkovich 2009; Balk 2001, 2002, 2006) or with experimental observations (Falkovich 2009; Polzin and Ferrari 2004; Ledwell et al. 1993; Herterich and Hasselmann 1982a). Moreover, similar experiments were performed to estimate the wave-induced diffusion of particle pairs in a large wave tank (Buick et al. 2001) and in a flume (Huang and Law 2018). The turbulent dispersion experienced by surface drifters is similar to the diffusion caused by turbulent velocity fluctuations as originally described by Taylor in his seminal paper (Batchelor and Townsend 1956). The difference with the wave induced diffusion is that the ‘randomness’ of the velocity field in this case is caused by a superposition of random waves rather than fluctuations of velocity in the flow. Therefore, the wave-induced turbulent dispersion experienced by a passive tracer can theoretically be described as random fluctuations relative to the underlying mean advection velocity—the Stokes Drift current (Falkovich 2009; Balk 2001, 2002, 2006; Herterich and Hasselmann 1982a; Weichman and Glazman 1999). The process is anisotropic and depends on the shape of the spectrum, in particular its directional spreading. The diffusion is significantly larger, naturally, in the mean wave propagation direction.

The growth of wind waves in deep water is, mainly, a function of three dynamic processes: wind input, energy dissipation by breaking and nonliear wave-wave interactions. Phillips (1958) suggested that in the frequency range between 1.5 and 3 times the spectral peak exists a saturation in which these processes balance each other. Therefore, the shape of the spectrum beyond the peak frequency is in a stage of saturation in which a balance between wind pumping and loss by dissipation is achieved. Using dimensional arguments, Phillips (1958) proposed that the spectral tail that describes this frequency range is E(ω) ∝ ω−n with n = 5, where E(ω) is the frequency spectrum. Thirty years later, Phillips (1985) reconsidered his analysis and pointed out that a ω− 4 decay is more appropriate.

Zakharov and Filonenko (1966) and Kitaigorodskii (1983) proposed an energy balance in which wind pumping dominates the region around the spectral peak and dissipation is confined to much higher frequencies, with the nonlinear interactions acting in a frequency band in between these two limits. The energy is transferred from low to high frequencies by a constant flux, in analogy with Kolmogorov’s theory of isotropic weak turbulence (Zakharov 1984; Zakharov et al. 2019), which supports a ω− 11/3 spectral tail. Despite the fact that the directional spectrum is anisotropic, this corroborates the hypothesis of a ω− 4 decay. The concept of Kolmogorov’s equilibrium range requires that the action of the terms of wind input and dissipation are clearly separated in frequency space, with the so-called inertial subrange lying in between. Also, within the inertial subrange, wind input and dissipation are expected to be much smaller than the nonlinear interactions.

In general there is still a lack of consensus about the existence of a single value for the exponent n. In Violante-Carvalho et al. (2004), among some examples, the authors measured E(ω) with a heavy-pitch-roll buoy moored in deep water. They computed n in which most values were equally spaced between − 4 and − 6, with a mean value of − 5.01. The validity of the assumption of a inertial subrange for wind waves is also debatable, with a no obvious separation between the wind input and dissipation terms in frequency space (Polnikov 2018). On the contrary, according to Polnikov and Uma (2014), in general both terms are simultaneously acting along the high-frequency band. To account for the finite depth effects, a model with n = 6 has also been proposed (Denissenko et al. 2007). Moreover, based on experimental data, Babanin (2010) discussed that both decays ω− 4—this one closer to the spectral peak—and ω− 5 are simultaneously present at the spectral tail. The transitional frequency between the subintervals in oceanic waves is dependent on the ratio U10/cp, where U10 is the wind speed measured at a height of 10 m and cp is the phase speed at the peak frequency.

Through numerical simulations, Balk (2001, 2002) validated the proposed theory about the behaviour of passive tracers under the influence of turbulence caused by large scale, planetary waves, typically with wavelengths greater than 500 km. One of the author’s assumptions was that the energy spectrum of the velocity field presents a long and well-defined inertial subrange. The velocity field was assumed to be generated by a superposition of random waves, which enables to solve the analytical problem using perturbation methods. The main consideration is about the particle’ paths simulated during the time interval characterised by the inertial subrange, which is considered to describe an anomalous behaviour. Their mean square displacement—D(t)—has the form D(t) ∝ tλ, where the exponent λ is validated numerically.

For this reason the mathematical treatment of dispersion of passive markers by a random wave field is inartistically connected to that of conventional turbulent dispersion. As for the case of hydrodynamic turbulence the results are typically formulated in terms of the scaling law of particle cluster size as a function of time. The cluster size is defined as the mean-square separation of two particles \(D (t) = \langle |\textbf {r}^{2}_{i} (t) - \textbf {r}^{2}_{j} (t)|\rangle \), where 〈⋅〉 implies a statistically averaged quantity, and the scaling exponent λ = const is one of the main parameters of interest. The important difference is that for hydrodynamic turbulence λ is completely determined by the turbulence energy spectrum whereas for waves it is also determined by the dispersion relation.

Different values of exponent λ correspond to different mechanisms of transport processes. Conversely, a particular value of parameter λ, estimated from particle-marker statistics, can be helpful in identifying a specific transport mechanism. For instance, λ = 2 correspond to ballistic separation (the particle moves with different, but constant velocities) and λ = 1 is a diffusion spread. For shear dominated dispersion 4 ≤ λ ≤ 6. The process within 0 ≤ λ ≤ 1 is usually referred to as sub-diffusive and with λ ≥ 2 as super-diffusive (Balk 2001, 2002, 2006). The exponent λ may change during the particle cluster evolution depending on the amplitude of separation compared to the spatial scale of the fluctuating velocity field. It is noteworthy that for Kolmogorov’ turbulence this change is non-monotonic: initially λ = 2 (ballistic), then λ = 3 (super-diffusive, the celebrated Richardson law), and λ = 1 as \(t\rightarrow \infty \), the Taylor diffusion. For the surface wave turbulence, the value of λ in the intermediate range corresponding to the inertial energy interval is somewhat different.

The main goal of the present paper is an experimental investigation of the dispersion of particles—drifters—advected by a random wave field. We determine the scaling laws experimentally, estimate the exponent λ and compare it with analytical predictions. To further investigate these ubiquitous transport phenomena, the trajectories of surface drifters released in a large wave tank are tracked down using optical cameras under a variety of spectral conditions.

The remaining is organised as follows. In Section 2, a description of the theoretical approach and terminology are presented, whereas the methodology is discussed in Section 3. The main results are described in Section 4. Finally, Section 5 presents our conclusions.

2 Theoretical framework

The behaviour of passive drifters can be described in terms of marker positions. Considering r(x,y) as the position vector in a 2D space of a Lagrangian particle evolving as dr/dt = U(x,y,t), where U(x,y,t) is an Eulerian velocity field . For a large ensemble of N ≫ 1 particles, passively advected by the given velocity field, the following averaged quantities can be defined

$$ \langle \textbf{r}\rangle = M (t), ~~ \langle \textbf{r}^{2}\rangle = D(t) + M^{2}(t), $$
(1)

where M(t) is the mean drift of a ‘cluster’ of tracer particles and D(t) is the mean variance with respect to the initial position at the origin—t = 0. According to Balk (2001, 2002, 2006), if a wavefield follows the weak turbulence model—therefore with an extensive inertial interval with Kolmogorov-type spectra—then functions M(t) and D(t) obey the following scaling laws

$$ M(t) \propto t^{\mu}, ~~ D(t) \propto t^{\lambda}. $$
(2)

A non-zero drift is only possible if the underlying velocity field is compressible or anisotropic, otherwise μ ≡ 0 (Balk 2002). The power exponents—μ and λ—have the analytic expressions in terms of the characteristics of the wave field (Balk 2001, 2002, 2006).

For t ≤ τcor, where τcor is the time correlation of the velocity field, the particle moves with initial (constant) velocity, so D(t) ∝ t2 and μ = 1, λ = 2. For an isotropic velocity field when \(D \gg L^{2}_{cor}\), where Lcor is the correlation scale of a random velocity field, M(t) = 0 and D(t) ∝ t (diffusion spread, Taylor mechanism) and μ = 0, λ = 1. The limiting values λ = 1 and λ = 2 are the universal values that are valid irrespectively of the nature of the underlying velocity field—i.e. waves or hydrodynamic turbulence.

Consider a random wave field with frequencies within a inertial subrange [ωmin,ωmax]. At the short-time limit, t ≪ 1/ωmax, where ωmax is the maximal frequency of wave spectrum, the tracer dispersion follows a ‘ballistic’ regime, 〈r〉2 ∝〈r2〉∝ t2, so

$$ \mu = 1, ~~~ \lambda = 2. $$
(3)

In the long-time limit t ≫ 1/ωmin, where ωmin is the minimal frequency of the wave spectrum, the exponents become

$$ \mu = 1, ~~~ \lambda = 1, $$
(4)

and a normal diffusion with a constant drift and a constant diffusivity is expected, in the form

$$ M(t)~=~V_{0} t, ~~~D(t)~=~K_{0} t, $$
(5)

where V0 and K0 are constants.

Finally, in the intermediate limit, 1/ωmax ≪ t ≪ 1/ωmin, we have an ‘anomalous’ diffusion. For the wave turbulence model—delta correlated ensemble of nonlinear surface waves—Balk (2001, 2002, 2006) derived the following scaling relation

$$ \mu = \lambda - \frac{1}{\alpha}, ~~~ \lambda = 2 + \frac{\nu - d }{\alpha}, $$
(6)

where d is the dimensionality of the problem—d = 2 for the 2D case here discussed—and parameters α and ν are power exponents from the dispersion relation and wave energy spectrum, respectively

$$ {\Omega}_{k} = Bk^{\alpha}, ~~~ E_{k} = Ck^{-\nu}, $$
(7)

where B and C are constants. For deep water waves, here considered, α = 1/2. The ν parameter depends on the spectral shape and can be estimated fitting an exponential function in the wavenumber spectra decay. Theoretically, E(ω) ∝ ω−n corresponds to E(k) ∝ k−ν, with n = 5 (Phillips spectrum) and n = 4 (Zakharov-Filonenko spectrum) equivalent to ν = 3 and ν = 5/2, respectively (Zakharov et al. 2019; Donelan et al. 1992).

Our main goal is to investigate the dispersion of drifters on the water surface in the presence of a random wave field. We aim an experimental validation of the scaling laws given by Eqs. 2–6 and comparisons with the predictions of the weak turbulence theory.

3 Methodology and experimental setup

The estimation of M(t) and D(t)—Eq. 1—is based on the mean drift and mean variance between particles. To investigate the dispersion induced by turbulence of punctually released drifters, waves were mechanically generated in a wide tank with several distinct spectral features. Their trajectories were automatically tracked down using down-looking optical cameras.

3.1 The experiment in the wave tank

The wave tank at the Rio de Janeiro Federal University is one of the largest and deepest in the world (Fig. 1): 40 m long, 30 m wide and with an adjustable depth of up to 15 m via a moving floor. Waves are mechanically generated by 75 identical rectangular flap type plungers, individually driven by a sinusoidal signal generator. Regular and irregular waves are generated with periods ranging from 0.5 to 5 s and wave heights up to 50 cm. To mitigate reflection and to provide dissipation, a parabolic beach is located 35 m away from the wavemakers. One of the sides of the tank has a vertical wall, whereas a second beach is located in the opposite side, with the same slope and design as the one at the end of the tank.

Fig. 1
figure 1

Top view of the wave tank and position of the seven optical cameras—C1 to C7—employed to track down the drifters. Down-looking cameras 1, 2, 3 and 4 are located at the ceiling, four meters above the water surface. Cameras 5, 6 and 7 are on the floor along the tank’s walk paths. The arrows are distance in millimetres

Full size image

In our experiment, several spectral configurations were employed to investigate the wave induced dispersion—see Table 1. The main variable parameters are the wave steepness ak—a is the wave amplitude and k is the wavenumber—the directional spreading s and the JONSWAP peak enhancement factor γ. The tank’s floor was not allowed to move and all generated waves were propagating in deep water. Three conductivity-based liquid wave gauges were deployed, with accuracy of 1.5 mm and sampling rate of 60 Hz. They were located near the drifters’ launching point, at the centre of the wave tank and in one of its sides. The surface displacement measurements were employed to compute the wave spectra to validate those generated by the wavemaker.

Table 1 Wave tank configuration (on the left) and measured parameters (on the right)
Full size table

Four down-looking full HD cameras were used to track down the balls, with 1920 × 1080 pixel resolution—the position of the cameras are depicted in Fig. 1. Additionally, three HD front-looking cameras, with 1440 × 1080 pixel resolution, were also located on ground level. The down-looking cameras were synchronised with the Streampix 5 recording software and the frames time-stamped with microsecond precision.

The drifters were released simultaneously in a small circular area close to the wavemaker (Fig. 2). They consisted of multi-coloured plastic spherical balls and acrylic plastic resin balls, known as Polymethyl Methacrylate or PMMA, with diameters of 74 mm and 39 mm, respectively. The experiments were always performed with only one type of drifter, therefore different types of balls were never mixed together during the measurements.

Fig. 2
figure 2

Views from the wave tank ceiling. The apparatus to hold the balls together on the launching point (a). The balls being released (b) but no waves were generated yet. The initial dispersion of the balls caused by the mechanically generated waves (c), propagating from left to right. Every single ball has to be identified in every frame and its position tracked down along the duration of the record

Full size image

It has been found that if one accounts for the mass of the floating particles that may lead to a new phenomenon, particle clustering in standing waves (Lukaschuk et al. 2007; Vucelja et al. 2007; Jansons 2007; Derevyanko et al. 2007; Falkovich and Pumir 2007). This clustering is opposite to the particle dispersion and in standing waves this may affect the rate of particle cluster spread. For the relatively small particles (a fraction of mm) surface tension may become important and depending on hydrophobic properties of the particle surface (plastic, glass hollow sphere, pollen grain or even a droplet of oil) this effect can be translated to a change of effective mass of the particle (Lukaschuk et al. 2007; Vucelja et al. 2007). The aggregated importance of both particle size and its density can universally be captured by the so-called Stokes number, the nondimensional coefficient of the viscous drag term in the particle equation of motion (Derevyanko et al. 2007; Ouellette et al. 2008). The effects of viscosity and mean induced flow may be important for consistent estimation of the Stokes Drift fluctuations (Vucelja et al. 2007; Jansons 2007; Herbers and Janssen 2016).

Initially, a circular apparatus—diameter 360 mm—was employed to hold the balls on the still water surface (Fig. 2a), then to be pulled off by a pulley (Fig. 2b). At this point, the wavemaker is started and the drifters dispersion is initiated (Fig. 2c). Each video record has a duration of two minutes at 30 fps with several different wave configurations.

The diffusion process is strongly anisotropic, mainly in the wave propagation direction. The plastic balls used as tracers are very light and much smaller than the generated wavelengths, in this regard they can be treated as particles. However, their vertical sizes are comparable with the wave heights and that can be a potential source of error. They may also have some friction against the air, so they are not exactly an analogue of floating debris but can be considered as a proxy.

3.2 Algorithm for automatic detection of drifters in a moving wavy background

A detailed description of the proposed algorithm for automatic drifters detection appears in Pereira et al. (2019). Here, for completeness, the most relevant aspects are summarised with the specific references therein listed. The algorithm consists of three stages. Firstly, the video record is pre-processed by six steps. The record is subdivided into time stamped frames, each one converted to a grayscale image and then Gaussian filtered with a 2D pixel window. Reflections from the tank bottom or ceiling hinder the drifters detection. They are mitigated through Background Subtraction, which turns the background water into black and the drifters white, with well demarcated contours. The Hough Circle Transform is the most commonly employed technique for detection of circular objects in digital images, a robust model-based technique for the identification of the balls released on the tank as drifters. The output of the pre-processing stage is a matrix with the coordinates of each circular drifter (x,y) and their radiuses r, for each video frame.

For the second stage, the cross-assignment of a given drifter position over consecutive frames, a fast least square distance method is employed. A drifter with coordinate (x1,y1) in time t1 = t0 + Δt, where Δt is the camera’s sampling rate, is cross-assigned with its counterpart (x0,y0) in the previous frame t0, and then successively for each frame over the record duration. The output of the processing stage are the drifters raw trajectories.

The last and third stage, the post-processing, aims to eliminate erroneous cross-assignments. A possible wrong selection causes inconsistencies that appear as random trajectories, not along the expected wave propagation direction. Based on the maximum distance that a drifter experiences during consecutive frames, an additional selection parameter for a new cross-assignment is used. The modulus of the displacement vector, which depends on the wave steepness, is therefore employed stipulating a maximum possible drift distance. The final output are the post-processed, more precise qualified trajectories.

The drifters trajectories were assessed through two different quality tests. The first one takes into account the rhythmical back and fro balls’ displacements, with a net transport in the wave propagation direction. Their oscillations are expected to peak at the waves’ peak frequency. The drifters displacement spectra were validated against the wave variance spectra measured by the conductivity gauges, for distinct wave steepnesses, with perfect agreement. Additionally, the most straightforward—and laborious—test is to determine manually the trajectory of one single drifter and compare it to the automatically detected one. The visual assurance of proper assignment, despite that inaccuracy can occur with the manual selection of the drifters centre, yielded a robust validation with high correlation and small errors. The assessment tests instilled confidence in the fast and efficient proposed technique.

The experimental setup was designed to employ four synchronised down-looking cameras—C1 to C4 in Fig. 1. C1 and C2 were deployed along the tank’s longitudinal axis whereas C3 and C4 were deployed side by side along the transversal axis. The four cameras, with slight superposition areas, formed a T shaped single field of view aimed to extend the duration of the drifters records. However, due to the lateral dispersion, the number of successfully tracked drifters was reduced in each camera along their trajectories. Therefore, in the following, to increase the number of analysed points, only the drifters tracked with C1 will be discussed.

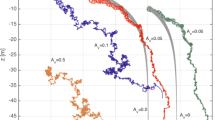
Each of the five distinct wave configurations listed in Table 1 was repeated at least three times. Figure 3a and b illustrate the technique to track down the drifters at the camera 1 field of view (C1 in Fig. 1), with their positions plotted alongside with M(t) in Fig. 3b. The displacement of the particles is much more accentuated in the direction of the wave propagation with respect to the transverse direction. The turbulent diffusion rate is, as expected, anisotropic. As shown in Table 1, the number of drifters successfully tracked and used in the following analysis varied from 27 to 10 in the five experiments, and were on average around 60 s in the camera’s field of view.

Fig. 3
figure 3

Example of one of the several test cases for different wave steepnesses. In a, the raw paths of every drifter are plotted with their coordinates (x,y) over the duration of the video record. The waves are propagating from left to right, the horizontal line is aligned with the tank’s longitudinal axis. In b, the same case shown in a, the blue lines are the qualified paths of individual drifters, whereas the red line depicts their mean path M(t)

Full size image

The number of drifters effectively tracked down is a limitation, as their individual trajectories may deviate markedly from each other (Fig. 3b). In numerical experiments (Balk 2001, 2002), thousands of trajectories were analysed statistically, over many realisations. In our experiment, 16 drifters on average were successfully tracked down, which is statistically questionable. However, it is not feasible in practical terms to monitor thousands of drifters in a wave tank.

4 Results

Irregular waves were generated according to a directional spectrum, described as

$$ E (\omega,\theta) = E(\omega) D(\theta), $$
(8)

where ω and θ are frequency and direction for a given wave component. Functions E and D are, respectively, a JONSWAP frequency spectrum model and a power-cosine directional spreading model—see for example Massel (2013). Of particular interest for the discussion, the peak enhancement factor γ is related to the peakedness of the sea state, ranging from 1 (fully developed, a Pierson-Moskowitz spectrum model) to 7, with 3.3 usually adopted as an average wind sea. These are the three values generated in the wave tank. Additionally, the power-cosine function (\(\cos \limits ^{2s}\theta \)) is employed for the angular distribution of the wave energy, which is termed directional spreading. The spreading parameter s can be assumed as a constant, or, as well as wind or frequency dependent. Increasing the power s causes a narrowing of the spread, typical of long crested swell. In our experiments, three values were employed, ranging from 10 (narrow distribution) to 1 (broad distribution).

Figure 4 illustrates one of the experiments with the fitted parameters λ and μ, respectively, from the plots D(t) and M(t) versus time—which are representative of all the other ones listed in Table 1. The drifters were released around 11 meters from the wavemaker and the computation initiated when the first wave hits them. Initially, the markers moved as a whole, possibly due to surface tension and viscosity (Denissenko et al. 2006). According to Lukaschuk et al. (2007) and Vucelja et al. (2007), at the very initial moments, the collisions among markers may also have a contribution to the particle cluster diffusivity because the time between collisions becomes the correlation time that determines the diffusion process (cluster spread). Under the effects of to surface tension and viscosity conditions the markers tended to cluster, which is the opposite trend to the diffusion spread expected (Lukaschuk et al. 2007; Vucelja et al. 2007). However, the effective attraction force being of hydrodynamic nature rapidly decays with floater separations and can be disregarded after this initial delay (Lukaschuk et al. 2007). From this point on, the values of μ and λ were computed and listed in Table 1, with any transient regime being disregarded—therefore, the effect of collisions among drifters is assumed as irrelevant.

Fig. 4
figure 4

Mean square displacement D(t) (a) and mean drift M(t) (b) over time, for experiment T100_010300—see Table 1. The black line is the fit, with the computed parameters λ and μ, respectively. In the initial 10 wave cycles the drifters move as a whole, when they separate from each other

Full size image

The average drift M(t) grows linearly with time (Fig. 4b), as predicted by Stokes (1847), with the mean fitted value of μ equals to 0.99. The variance of the markers position D(t) (Fig. 4a), on the other hand, is not in agreement with Taylor’s dispersion theory of a single particle, which predicts a diffusive motion (λ = 1) for homogeneous, isotropic turbulence given a long enough time span. The mean fitted λ equals 2.6, with standard deviation of 0.7, hence characterising a super-diffusive asymptotic behaviour, as reported for instance in Balk (2001, 2002, 2006). Moreover, to compare our results with previous studies we use experimental data for wave estimated diffusivity presented in Buick et al. (2001). From an approximate fit of data (in theirs Fig. 3), we can deduce K ∝ ta, where a = 0.76. Then, from D2 ∝ Kt, we derive λ ∝ 1.87, which is close to our experimental finding. Our results (Table 1) are also in good agreement with the data and field observations recently reported in Soomere et al. (2011) with λ = 2.5. It is noteworthy that both Buick et al. (2001) and Soomere et al. (2011) reported the two-step regime of tracer particles spread with the first step characterised by a much lower value of λ—equal to 0.27 in Soomere et al. (2011). This is in line with our observations. In general, the observed marker dispersion can be a combination of a number of dispersion mechanisms—for instance, wave induced dispersion and turbulent dispersion (Buick et al. 2001). Each mechanism can be characterised by its own diffusion coefficient Kn and scaling exponent λn, so the overall mean square displacement can be estimated as

$$ D = \sum K_{n} t^{\lambda_{n}} $$
(9)

As \(t\rightarrow \infty \) the mechanism with largest λn dominates and this can be used for the dominant mechanism identification. For turbulent dispersion λ = 3, for conventional diffusion λ = 1, and since we observe λ close to 2 it is an indication of the wave dominated dispersion.

Taylor dispersion due to mass transport predicts a diffusive motion, so the variance follows the scaling law D(t) ∝ t for large times. In the presence of random waves, with anisotropic turbulence, this behaviour was not found in our experiments. The diffusive motion predicted by Taylor’s theory assumes that the autocorrelation function of the particle velocities decays to zero rapidly as the lag increases, therefore the velocities are uncorrelated in a very short time interval. In Fig. 5, the mean velocity over time and its autocorrelation function are displayed. Considering the relatively short time interval of the measurements, the autocorrelation function indeed goes to zero. However, apparently not very fast, which might be in disagreement with one of the basic principles of the theory. The drifters velocities, hence, have a short memory about their initial conditions which does not satisfy the assumptions for a scaling law λ = 1.

Fig. 5
figure 5

Autocorrelation function of the mean velocity, experiment T100_050300, see Table 1 (a). Velocity of all drifters, experiment T100_050300 (b). The thick, black line is the mean velocity. These plots are representative of the other experiments

Full size image

Figure 6a depicts the relationship between the directional spreading parameter s configured from the wavemaker against the fitted parameter λ for the first three experiments highlighted with different shades of gray in Table 1, with parameters Hs, Tp and γ kept constant while only s varied. For a directional spreading of the type \(\cos \limits ^{2s}\theta \), for higher values of the parameter s the waves become less spread or more unidirectional, which would decrease the expected wave-induced diffusion. However, there is no obvious correlation, with an inverse relationship between λ and s not evident, with λ fluctuating around its mean value (λ = 2.6).

Fig. 6
figure 6

The relationship between the directional spreading parameter s and the fitted λ for the first three experiments with Hs, Tp and γ kept constant, only s varying, see Table 1 (a). The relationship between the high frequency decay exponent n and fitted λ for the first three experiments, for values of n greater or equal to 5 (b)

Full size image

On the other hand, there is a clear direct proportional relation between the high frequency decay exponent n and the fitted λ. In Fig. 6b, also keeping Hs, Tp and γ constant but s, and retaining only the values of n higher or equal to 5, its correlation with λ is clear. The higher the exponent n, the higher the parameter λ, with a correlation of 0.94. Therefore, λ is apparently more sensitive to the high frequency tail, rather than to the energy directional distribution.

Balk (2002) considered theoretically the effect of wave-induced turbulent diffusion, deriving relationships for its anomalous behaviour (Eq.6). Assuming a bi-dimensional case (d = 2), waves propagating in deep water (α = 1/2) and the theoretical values of ν (5/2 or 3, see Eq. 7), consequently the predicted values of the parameter λ are, respectively, λ = 3 or λ = 4. The fitted high frequency part of the measured 1D frequency spectra from the wave probe measurements is also shown in Table 1—parameter n, with mean value of 5.2 which roughly corresponds to ν = 3. The values of parameter λ for a super-diffusive behaviour predicted in Eq. 6 have similar magnitudes of the fitted λ from our data set.

The behaviour of the spectral tail is discussed in Babanin (2010), with the transitional frequency between subintervals ω− 4 and ω− 5 reported as dependent on the stage of wave development. For shorter waves, with peak frequencies higher than 0.7 Hz, for most wind conditions the ratio between transitional frequency and peak frequency is less than one, which means the existence of the ω− 5 tail only. In our measurements with comparatively shorter wavelengths, the existence of a single ω− 5 decay is also clear. The Kolmogoroff cascade at higher frequencies is therefore not expected, with a broad subinertial interval being questionable, violating one of the main assumptions in Balk (2002). However, our fitted λ are of the same magnitude of the theoretical ones, indicating that the wave-induced dispersion presents a super-diffusive behaviour.

5 Discussions and conclusion

A random wave field produces surface dispersion and here we aim to investigate the diffusion mechanisms, with the nonlinear dispersion of surface drifters experimentally carried out in a large wave tank. The transport properties are of significant theoretical and practical importance and diffusion experiments in the ocean necessarily have the cumbersome task to isolate the several space and time scales involved in the net dispersion. In a wave tank, the sole effect of wave-induced diffusion can be investigated in a controlled environment. In this context, JONSWAP wave spectra with distinct values of significant wave height, peak period, enhancement parameter γ and directional spreading were generated in deep water with plastic balls released and tracked down employing optical cameras. Their positions were determined over the duration of several video records, around 60 + s each, and the absolute dispersion investigated as the variance of the particle displacement. The scaling laws given by Eqs. 2–6 and predictions of the weak turbulence theory described in Balk (2002) were assessed.

No clear evidence of dependence of diffusion on directional spreading has emerged. That might be a result of the relatively short duration of the video records, which was a limitation caused by the dispersion of the balls and the short periods in which they remained in the cameras field of view. Several cameras were deployed in order to retain the maximum number of balls over their propagation, but as they moved from camera to camera the number was strongly reduced. Hence, only one camera was effectively used, which led to a relatively short duration. Keeping in mind such an experiment in a large and long wave tank, video records much longer than the ones here discussed are unlikely.

However, the scattering behaviour is better correlated with the high-frequency tail, which we believe does nor scatter the tracers as such but is diagnostic of the random waves. In our data, the tracers are scattered by large waves with random phases mainly via the spectrum tail, rather than via the angular spreading.

Our main finding is that the measured wave-induced dispersion shows a super-diffusive behaviour, in contrast with the diffusive motion predicted by Taylor’s theory. Considering a well defined inertial subrange, Balk (2002) proposed a mean squared displacement D(t) ∝ tλ, with the theoretical λ varying between 3 and 4 depending on the high frequency tail of the wave spectrum, respectively a Zakharov-Filonenko spectrum (E(ω) ∝ ω− 4) and a Phillips spectrum (E(ω) ∝ ω− 5). The scaling laws were experimentally determined and the exponent λ computed. The fitted λ has a mean value of 2.6 and standard deviation of 0.7, therefore close to the limits predicted by Balk (2002). One possibility for the discrepancy is that for relatively short waves, as the ones here discussed, a broad inertial subrange is not present, violating one of the main assumptions (Balk 2002). The wave spectra under these conditions will not have a Kolmogoroff cascade at higher frequencies, being better described by a Phillips spectrum. Our results have, therefore, important implications in the manner that wave-induced dispersion is implemented in numerical models.