On Hierarchical Convergence of the Heterogeneous Multiscale Finite Element Method Using Polyhedral Supports

Abstract

Numerical simulation of physical processes in such complex formations as permafrost is impossible without modern multiscale methods. For example, the heterogeneous multiscale finite element method (FE-HMM) can be used to simulate elastic deformation of solids. However, it is necessary to have some control tools of computational errors as well as a priori information on limitations of the method in solving practical problems. In this article, we investigate the influence of different mesh hierarchy levels on the accuracy and speed of solving the elastic deformation problem using FE-HMM with polyhedral supports at the macrolevel and with tetrahedral supports at the microlevel. The obtained estimates allow us to adjust the planning strategies of computational experiments, which are largely related to the construction of a set of meshes with different accuracy. We apply the h-refinement technology at the edges of macro-polyhedra in the microlevel mesh. Increasing in accuracy of computational solution up to two orders of magnitude with maintaining the total size of discretizations is obtained. Also, the applicability of the method for numerical simulation of physical processes in media with elongated inhomogeneities intersecting several macroelements is shown.

1 Introduction

Structural complexity of rocks imposes certain limitations on the computational schemes used. For example, direct methods (such as the Galerkin method [1]) lead to discretizations with a large number of parameters. It is critical situation even using modern computing machines. Therefore, methods based on decomposition of the initial domain into some subdomains are applied to simulate physical processes in heterogeneous multiscale media. However, in this case it is necessary to construct special boundary operators to ensure the continuity of the solution at interfaces. The most general and easy-to-use mathematical tools for constructing such operators are offered by multiscale finite element methods. For example, in the heterogeneous multiscale finite element method (FE-HMM) [2,3,4], the solution space has a hierarchical structure and contains two or more levels. Each of levels corresponds to one physical or geometric scale of the problem under consideration. At each level of the hierarchy, special subproblems are formulated to construct local subspaces. The procedures for matching the hierarchy levels are chosen according to the specifics of the processes being simulated. This strategy ensures sufficient flexibility and adaptability of the method.

In this paper, we recall the upper mesh level as a macrolevel taking into account the effective properties of the medium. We recall the lower mesh level as a microlevel. The microlevel allows to take into account all inhomogeneities of the medium. To simulate the elastic deformation of a heterogeneous solid using the two-level FE-HMM, let us formulate the main stages:

• 1. Construction of the mesh hierarchy: partitioning of the entire modelling domain into subdomains (macroelements) without overlapping and without strictly considering the internal geometric structure. Then each of the macroelements is independently partitioned into microelements, taking into account the internal structure.

• 2. Construction of a functional hierarchy. To construct the macroscale shape functions and to ensure smoothness of the solution, we consider series of subproblems on each macroelements using microelement meshes.

Despite the sufficient representation of FE-HMM in the literature, including for modelling elastic deformation [5], some mathematical and corresponding technological aspects of this method should be developed for each specific physical problem. In addition, at the upper level of the hierarchy (hereinafter referred to as the macrolevel) finite element of a simple shape with an equal number of faces (tetrahedrons or parallelepipeds) are traditionally used to simplify the construction of functional subspaces of the solution. However, to simulate the elastic deformation of heterogeneous solids, it is more efficient to use polyhedral macroelements with a non-fixed number of faces. We have proposed and implemented technologies for automating construction of mesh discretizations at the macrolevel, and approaches to construct the macroscale shape functions ensuring the required accuracy of the numerical solution.

2 Problem Statement and Solution Method

Let $\Omega = [0,1] \times [0,1] \times [0,1]$ be a homogeneous modelling domain. We consider a sandstone with Young’s modulus 5 GPa and Poisson’s ratio 0.27 GPa.

The lower base of the area is rigidly fixed. We assume that the upper base is displaced upward along the Z axis by 0.1 m. The side surface is free. The force of gravity is not taken into account in this case. Thus, the boundary elastic deformation problem is presented as:

$$ - \nabla \cdot \left( {{\mathbf{D}}:\nabla_{s} {\mathbf{U}}\left( {\mathbf{x}} \right)} \right) = 0, $$

(1)

$$ \left. {\mathbf{U}} \right|_{lower\_base} = \left( {0,0,0} \right)^{T} , $$

(2)

$$ \left. {\mathbf{U}} \right|_{upper\_base} = \left( {0,0,0.1} \right)^{T} , $$

(3)

$$ \left. {{\mathbf{n}} \cdot {{\varvec{\upsigma}}}} \right|_{side\_surface} = (0,0,0)^{T} . $$

(4)

If the domain is inhomogeneous, the above formulation is valid, but the corresponding ideal contact conditions at the interfaces are added.

2.1 Discretization of Computational Domain

This work does not deal with the construction of adaptive tetrahedral meshes in complex three-dimensional domains. For this purpose, the open integrated numerical modelling platform SALOME is used. It provides a wide range of tools for working with geometric objects and with mesh structures.

Polyhedral meshes are constructed as duals to the primary tetrahedral mesh. The nodes of the polyhedral mesh are the barycenters of geometric elements of the primary mesh. This approach is based on the Voronoi diagram [6], which is dual to the Delaunay triangulation [7]. There are different realizations of this approach in the two-dimensional and three-dimensional domains [8,9,10,11,12]. The approach is usually related with the choice of the way of constructing boundary elements, since in the basic formulation, the Voronoi diagram is constructed in the infinite domain.

Let ${\rm T}\left( \Omega \right) = \left\{ {{\rm T}^{3D} ,{\rm T}^{2D} ,{\rm T}^{1D} ,{\rm T}^{0D} } \right\}$ be some primary tetrahedral mesh constructed in a single-connected domain $\Omega$ with the non-smooth external boundary $\partial \Omega.$

The ${\rm T}\left( \Omega \right)$ consists of a subset of tetrahedra ${\rm T}^{3D} = \left\{ {t_{i}^{3D} ,i = \overline{{1,n_{{{\rm T}^{3D} }} }} } \right\}$, faces ${\rm T}^{2D} = \left\{ {t_{i}^{2D} ,i = \overline{{1,n_{{{\rm T}^{2D} }} }} } \right\}$, edges ${\rm T}^{1D} = \left\{ {t_{i}^{1D} ,i = \overline{{1,n_{{{\rm T}^{1D} }} }} } \right\}$, and nodes ${\rm T}^{0D} = \left\{ {t_{i}^{0D} ,i = \overline{{1,n_{{{\rm T}^{0D} }} }} } \right\}$. We recall $\Pi \left( \Omega \right) = \left\{ {\Pi^{3D} ,\Pi^{2D} ,\Pi^{1D} ,\Pi^{0D} } \right\}$ as a polyhedral mesh. We have implemented the most general approach, which consists of the sequential processing of the following basic mappings:

$$ V_{0D} :\left( {{\rm T}^{0D} } \right) \mapsto \Pi_{{}}^{3D} , $$

(5)

$$ F_{1D} :\left( {{\rm T}^{1D} } \right) \mapsto \Pi_{{}}^{2D} , $$

(6)

$$ E_{2D} :\left( {{\rm T}_{{}}^{2D} } \right) \mapsto \Pi_{{}}^{1D} , $$

(7)

$$ N_{3D} :{\rm T}^{3D} \mapsto \Pi_{{}}^{0D} , $$

(8)

where $V_{0D}$ is mapping, which corresponds to a node of the primary mesh to a polyhedron; $F_{1D}$ is mapping, which corresponds the edge of the primary mesh element to the polyhedral mesh edge (Fig. 1a); $E_{3D}$ is mapping, which corresponds to the inner edge of the primary mesh element to the polyhedral mesh edge (Fig. 1b); $N_{3D}$ is mapping, matching the barycenters of the primary mesh elements to the polyhedral mesh nodes.

Fig. 1.

Action of mapping operators from an edge of the primary mesh to a polyhedral mesh edge (a) and mapping from a primary mesh edge to a polyhedral mesh edge (b)

In addition, external boundaries $\partial \Omega$ give rise to additional special cases. For example, we need have a mapping that maps a primary mesh node lying on an external boundary $\partial \Omega$ to a polyhedral mesh edge (Fig. 2):

$$ F_{0D} :\left\{ {t^{0D} |t^{0D} \in {\rm T}^{0D} \,\,\,\,\exists t^{2D} \in {\rm T}_{ext}^{2D} :\,\,t^{2D} \cap t^{0D} = t^{0D} } \right\} \mapsto \Pi_{0D}^{2D} , $$

(9)

Fig. 2.

Action of the mapping operator from a primary mesh node lying on the external boundary $\partial \Omega$ to a polyhedral mesh edge

The considered approach of polyhedral mesh construction has some disadvantages, such as the possibility of non-planar faces and non-convex polyhedra. However, for the computational schemes based on multiscale methods proposed in this paper, this is not a critical situation.

2.2 Heterogeneous Multiscale Finite Element Method

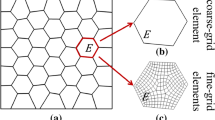
We consider a polyhedral consistent irregular mesh $\Pi_{{}}^{H} \left( \Omega \right) = \left\{ {K_{i}^{{\tilde{p}}} ,\,\,\,i = \overline{1,N} } \right\}$ of the entire computational domain. Where $K_{i}^{{\tilde{p}}}$ is a nonoverlapping polyhedron (Fig. 3a), and the $\tilde{p}$ is the number of the polyhedron vertices.

Fig. 3.

Structure of the computational domain and examples of meshes: a – the macromesh $\Pi_{{}}^{H} \left( \Omega \right)$ consists of 1290 polyhedra; b – the micromesh ${\rm T}_{{}}^{h} \left( {K_{i}^{{\tilde{p}}} } \right)$ in the polyhedron

Let us introduce a finite-dimensional subspace on the set $\Pi_{{}}^{H} \left( \Omega \right)$:

$$ \left[ {L^{2} \left( \Omega \right)} \right]^{3} \supset {\mathbf{V}}^{H} = \left\{ {{\mathbf{u}}|{\mathbf{u}} \in \left[ {L^{2} \left( \Omega \right)} \right]^{3} :{\mathbf{u}} \in \left[ {\Im^{H} \left( {\Pi_{{}}^{H} \left( \Omega \right)} \right)} \right]^{3} } \right\}, $$

(10)

where $\Im^{H} \left( {\Pi_{{}}^{H} \left( \Omega \right)} \right) = \left\{ {{{\varvec{\Psi}}}_{p} ,p = \overline{1,P} } \right\}$ is the space of non-polynomial finite shape functions associated with mesh nodes $p = \overline{1,P}$. Since the functions ${{\varvec{\Psi}}}_{p}$ are finite and satisfy the “unit partitioning”-condition by the FE-HMM requirements [13], we construct consistent irregular tetrahedral meshes ${\rm T}_{{}}^{h} \left( {K_{i}^{{\tilde{p}}} } \right) = \left\{ {\tau_{j} ,\,\,j = \overline{{1,n_{i} }} } \right\}$, $\forall i = \overline{1,N}$ (see Fig. 3b) on each of the polyhedral macroelement $K_{i}^{{\tilde{p}}}$ independently. To construct them, we define the next subspaces on corresponding finite element:

$$ \left[ {L^{2} \left( \Omega \right)} \right]^{3} \supset {\mathbf{V}}^{h} = \left\{ {{{\varvec{\Psi}}}|{{\varvec{\Psi}}} \in \left[ {L^{2} \left( \Omega \right)} \right]^{3} :{{\varvec{\Psi}}} \in \left[ {\Upsilon^{h} \left( {\tau_{j} } \right)} \right]^{3} \forall \tau_{j} \in {\rm T}^{h} \left( \Omega \right)} \right\}, $$

(11)

where $\Upsilon^{h} \left( {\tau_{j} } \right)$ is a space of first-degree polynomials (in the general case polynomials have the degree $m$). Then let us formulate discrete variational formulations at the microlevel for $K_{i}^{{\tilde{p}}}$, $\forall p = \overline{{1,\tilde{p}}}$, $\forall i = \overline{1,N}$:

$$ \left\{ {\begin{array}{*{20}c} {{\text{find}}\,\,{{\varvec{\Psi}}}_{p}^{h} \in {\mathbf{V}}_{{}}^{h} + \widetilde{{{\varvec{\Psi}}}}_{p} \left( {\partial K_{i}^{{\tilde{p}}} } \right)\,\,\,{\text{such that}}} \\ {\int\limits_{\Omega } {\nabla {{\varvec{\Psi}}}_{p}^{h} :{\mathbf{D}}:\nabla {\mathbf{v}}^{h} d\Omega } = 0,\,\,\forall {\mathbf{v}}^{h} \left( {\mathbf{x}} \right) \in {\mathbf{V}}_{{}}^{h} ,} \\ \end{array} } \right. $$

(12)

where $\widetilde{{{\varvec{\Psi}}}}_{p} \left( {\partial K_{i}^{{\tilde{p}}} } \right)$ is the value of the function ${{\varvec{\Psi}}}_{p}^{h}$ on the external boundary of the polyhedron. The function can be found from the solution of a similar problem with the lower dimensionality. Thus, we need to solve the quasi-dimensional problem on the boundary (Fig. 4b). Also, the values of the desired function along the edges are required (Fig. 4c). They can be obtained by using the simple interpolation from $\left( {0,0,0} \right)^{T}$ to $\left( {1,1,1} \right)^{T}$. If the edge is not crossed by an inclusion, in this case we construct one-dimensional subproblems along the edges with the boundary conditions $\left( {0,0,0} \right)^{T}$ or $\left( {1,1,1} \right)^{T}$ depending on the function index. Thus, the weight of the resulting function ${{\varvec{\Psi}}}_{p}^{h}$ and degree-of-freedom corresponding to the vertex with the index $p$ equals to the value $\left( {1,1,1} \right)^{T}$. All other weights associated with the macroelement vertices are equal to $\left( {0,0,0} \right)^{T}.$

Fig. 4.

The hierarchical system of meshes in a macroelement for a series of nested subproblems to construct the nonpolynomial shape functions: a – the tetrahedral mesh in the whole macroelement; b – the triangular mesh on the face (extracted from the tetrahedral mesh); c – the one-dimensional mesh on the edge (extracted from triangular meshes)

Also, by definition FE-HMM the shape functions must fulfill the property (Fig. 5):

$$ \sum\limits_{p = 1}^{{\tilde{p}}} {{{\varvec{\Psi}}}_{p}^{h} \left( {\mathbf{x}} \right)} = \left( {1,1,1} \right)^{T} ,\,\,\,\forall {\mathbf{x}} \in K_{i}^{{\tilde{p}}} . $$

(13)

Fig. 5.

Example of the x-component of the shape function on a polyhedron (a) and one of the sections (b)

The discrete variational formulation at the macrolevel has the form:

$$ \left\{ {\begin{array}{*{20}c} {{\text{find}}\,\,\,{\mathbf{U}}^{H} \in {\mathbf{V}}^{H} \left( {\Pi^{H} \left( \Omega \right)} \right) + {\mathbf{U}}_{D} \left( {\Gamma_{D} } \right)\,\,\,{\text{such as}}} \\ \begin{gathered} \int\limits_{\Omega } {\nabla {\mathbf{U}}^{H} :{\mathbf{D}}^{H} :\nabla {\mathbf{v}}^{H} d\Omega } = \int\limits_{{\Gamma_{N} }} {{\mathbf{G}}_{Ng} {\mathbf{v}}^{H} \left( {\mathbf{x}} \right)d\left( {\partial \Omega } \right)} + \int\limits_{\Omega } {{\mathbf{Fv}}^{H} d\Omega } ,\,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall {\mathbf{v}}^{H} \left( {\mathbf{x}} \right) \in {\mathbf{V}}^{H} \left( {\Pi^{H} \left( \Omega \right)} \right), \hfill \\ \end{gathered} \\ \end{array} } \right. $$

(14)

where ${\mathbf{D}}^{H}$ is a homogenized material coefficient.

Thus, the solution of the problem (1)–(4) is represented at each point of the domain $\Omega$ as a decomposition over the corresponding shape functions:

$$ {\mathbf{U}}^{H} \left( {\mathbf{x}} \right) = \sum\limits_{{K_{i}^{{\tilde{p}}} \in \Pi^{h} \left( \Omega \right)}}^{{}} {\sum\limits_{p = 1}^{{\tilde{p}}} {{\mathbf{q}}_{p}^{H} \Psi_{p}^{h} \left( {\mathbf{x}} \right)} } = \sum\limits_{{K_{i}^{{\tilde{p}}} \in \Pi^{h} \left( \Omega \right)}}^{{}} {\sum\limits_{p = 1}^{{\tilde{p}}} {{\mathbf{q}}_{p}^{H} \sum\limits_{r} {{\mathbf{q}}_{r}^{p,h} {{\varvec{\upxi}}}_{r}^{h} \left( {\mathbf{x}} \right)} } } , $$

(15)

where ${\mathbf{q}}_{p}^{H}$ and ${\mathbf{q}}_{r}^{p,h}$ are the weights of degrees of freedom obtained from the solution of (12) and (14), respectively, ${{\varvec{\upxi}}}_{r}^{h} \left( {\mathbf{x}} \right) \in {\mathbf{V}}^{h} \left( {K_{i}^{{\tilde{p}}} } \right)$ are the basis functions from the space defined in (11).

3 Numerical Estimation of FE-HMM Accuracy

3.1 Homogeneous Computational Domain

Let the solution ${\mathbf{U}}^{FEM}$ of the problem (1)–(4) be obtained by the classical finite element method using a detailed mesh (more than 10 million tetrahedra). We consider ${\mathbf{U}}^{FEM}$ as an exact solution for all variants. To calculate the relative error of the z-component of the solution obtained by using the heterogeneous multiscale finite element method, we apply the $L_{2}$-norm as:

$$ err = \frac{{\left\| {U_{z}^{FEM} - U_{z}^{FE - HMM} } \right\|_{{L_{2} }} }}{{\left\| {U_{z}^{FEM} } \right\|_{{L_{2} }} }} = \left( {\frac{{\int\limits_{\Omega } {\left( {U_{z}^{FEM} - U_{z}^{FE - HMM} } \right)^{2} d\Omega } }}{{\int\limits_{\Omega } {\left( {U_{z}^{FEM} } \right)^{2} d\Omega } }}} \right)^{1/2} . $$

(16)

Fig. 6.

Micromeshes of a macroelement with equal initial criteria for fineness of partitions: a – without adaptation, b – with additional sub-partitioning.

Table 1 shows a comparison of two approaches to the construction of meshes at the microlevel: without adaptation and with adaptation. In the variant with adaptation, additional subdivision of the tetrahedral mesh was performed on those edges of the polyhedron, where at the standard step of construction there were less than 5 nodes of the tetrahedral mesh (see Fig. 6).

As can be seen from the analysis of the results in the Table 1, the convergence of FE-HMM is hierarchical. The relative error of the solution decreases both by increasing the number of polyhedra at the macrolevel, and by splitting the mesh at the microlevel. However, in the variant with the micromesh without adaptation, there is a limit of the fineness at the macrolevel. Namely, on the mesh with 1290 polyhedra, the relative error is higher than on the meshes with fewer polyhedra for comparable fineness of the micromeshes. This is due to the fact that at a given criterion of micromeshes the necessary accuracy is not achieved when constructing the macrolevel shape functions even in a homogeneous medium. The introduction of an additional criterion of mesh adaptation along the edges allows to control this accuracy. This strategy significantly increases the total number of the degrees of freedom at the microlevel.

Table 1. Numerical characterization of computational meshes for a homogeneous sample and comparison of the two approaches to constructing meshes at the microlevel ($N^{h}$ is the total number of tetrahedra at the microlevel)

3.2 Computational Domain with Inclusions

One of the basic problems of multiscale methods is to realize a technology that allows to work with unstructured media. In these media, it is impossible to construct a macromesh that its internal boundaries do not cross medium interfaces, and inclusions lie in some macroelement strictly inside. Polyhedral media allow us to reduce such intersections, since the shape of the macroelements can be varied over a wide range. However, it is not always realizable. For example, it is impossible for media with lenticular inclusions (Fig. 7a).

Fig. 7.

Idealized macrostructure of permafrost rock.

To investigate the accuracy of the solution obtained in inhomogeneous objects, let us consider a two-component medium in the form of a cube with the edges of 1 m. The object consists of a matrix and inclusions of different configurations (Fig. 7). The matrix is sandstone (Young’s modulus is 5 GPa, Poisson’s ratio is 0.27) similar to the homogeneous sample from the point above. The inclusions are ice with Young’s modulus 9.8 GPa and the Poisson’s ratio 0.34. We assume the inclusions can be represented by the lenticular formations (two axises have fixed length 0.4 m, the third axis length varies randomly from 0.05 to 0.1 m) and the classical porous (diameter of spheres is 0.12 m).

For physically correct accounting of such peculiarities and preserving the continuity of the solution at the intersection boundaries, additional reduced subproblems (12) are solved to construct the macrolevel shape functions. The Table 2 shows the relative errors for the samples with lenticular inclusions (Fig. 7a) and spheres inclusions (Fig. 7b), for which the intersection of macroelements boundaries was also not controlled. The micromeshes were constructed with a conditional fineness criterion of “0.01” and with adaptation, since the most reliable results on a homogeneous sample were obtained at such parameters.

As in the case of the homogeneous sample (Table 1), the convergence with polyhedral mesh refinement is observed with a comparable number of tetrahedrons at the microlevel. However, 1290 polyhedra do not give a significant increase in accuracy, even when the number of microelements increases. The errors of the solutions for the sample with relatively large inclusions-lenses are comparable to the results for the samples with inclusions-spheres. Thus, our modification allows us to fully apply FE-HMM for media with inhomogeneities whose characteristic size exceeds the characteristic size of macroelements.

Table 2. Numerical characterization of the computational meshes and the relative errors of the solution for the sample with inclusions-lenses and inclusions-spheres ($N^{h}$ is the total number of tetrahedrons at the microlevel)

4 Parallelization of Computing Schemes

In this this paper, we will exclude the procedures for constructing hierarchical finite element meshes, as it is difficult to evaluate them in terms of the required resources, since a third-party software package SALOME is involved. For each macroelement the micromesh is also constructed independently.

In terms of implementation, the algorithm of the heterogeneous multiscale finite element method consists of the following steps:

• 1. A polyhedral macromesh is read and processed (e.g., a neighborhood relation is formed).

• 2. For each macroelements non-polynomial shape functions are independently constructed:

  • a. the tetrahedral mesh of the macroelement is read and processed (including submeshes on each face and on each edge);

  • b. the edges are analyzed and the traces of the shape function are formed along the one-dimensional boundary: if there are no homogeneities on the edge, the analytical relation is substituted, if there are homogeneities on the edge, the subproblems are solved;

  • c. form traces of shape functions on quasi two-dimensional faces (in the general case the faces may not be planar) through the solution of a series of subproblems;

  • d. systems of linear algebraic equations (SLAE) are formed and solved for each of the shape functions taking into account the corresponding traces on the boundaries.

• 3. Assembling the SLAU taking into account global boundary conditions and solving.

• 4. Analysis and output of results.

As it is not difficult to see, both algorithmic and software optimization are possible at each of the stages. However, in any case, the second stage generates a large number of additional subproblems since in a polyhedral medium, the number of shape functions coincides with the number of vertices which can be more than 30. Nevertheless, the processing on each of the macroelements in FE-HMM can be performed completely independently of the neighboring elements. Within the framework of this work a parallel version of the algorithm based on the OpenMP technology was realized. The Fig. 8 shows measurements of the solution time of the problem (1)–(4) for the homogeneous sample in the different variants of the meshes containing 26, 76, and 135 polyhedrons and preserving the fineness of micro-partitioning (about 1 million tetrahedrons).

The computational experiments were performed by using a computer with AMD Ryzen Threadripper PRO 3975WX 32-Cores (3.50 GHz) processor.

Fig. 8.

Dependence of the problem solution time on the number of processors used.

5 Conclusions

A parallel modification of the heterogeneous multiscale finite element method using polyhedral supports is proposed for solving the problem of elastic deformation of a heterogeneous solid.

The developed algorithms and computational schemes are analyzed in terms of numerical convergence and requirements to computational resources. The “two-level” convergence specific to hierarchical finite element methods has been shown experimentally. The solution accuracy can be controlled by varying the discretization at the macrolevel as well as at the microlevel. In this case, to achieve the best accuracy of the solution, it is necessary to maintain a balance in mesh refinement both in the construction of nonpolynomial shape functions at the micro- and macrolevels. The proposed automatic adaptation of the mesh at the microlevel near the edges of the polyhedron allows to obtain a more accurate solution (up to two orders of magnitude) at comparable sizes of discretizations. The approach in parallel realization of computational schemes used within the framework of this stage allowed to reduce the solution time up to 10 times on 32 threads. Also, in the future, it is planned to modify the technology of load distribution over processor threads to increase efficiency.