1. Introduction

Mathematical modeling of problems involving phase transition in the cryolithozone plays an essential role in constructing and designing various facilities on permafrost soils. Soil thawing and freezing processes can cause mechanical deformation and damage to structures erected on permafrost [1]–[3]. At the same time, the structures themselves are also capable of generating heat and can contribute to the melting of the subsoil of the foundation. For ground heating prevention and ensuring the stability of all structures, engineering structures and buildings in the cryolithozone are usually built on pile foundations [4]–[6]. Ground thawing can also damage bridges, roads, and railroads. We note that these processes are of a multiphysical nature. Their accurate description requires considering both thermal effects and mechanical deformations.

Many studies have been devoted to the development of mathematical models with phase transitions and effective methods of their numerical implementation (see, e.g., [7]–[11]). In [7], a coupled thermo-hydro-mechanical (THM) model of the rock mass under freezing/thawing conditions of moisture and ice saturating the pore space was derived and investigated. The finite-difference method implemented in FLAC3D [12] was used to numerically solve the obtained mathematical model. In [8], an elastic–plastic model was developed to simulate soil freezing and thawing. Those studies present the mathematical model that describes frost heaving using the porosity change rate function that models the growth of ice lenses as an average porosity growth. The finite-element method based on the ABAQUS program [13] was used to numerically implement the model. In [9], a stabilized THM model with elastic–plastic reactions and the influence of phase transitions was presented. For its numerical solution, a stabilized finite-element method was applied using the Deal.II library [14]. A THM model with water–ice phase transition was presented in [10]. In that study, the temperature dependence of displacements was implemented using the linear thermal expansion coefficient of the solid matrix without considering the change in porosity caused by the water–ice phase transition. The numerical solution was based on FLAC3D software. In our previous work [11], we developed a mathematical model of thermoelasticity with a phase transition, in which ground deformations occur due to changes in porosity caused by the difference between water and ice densities. This model is a simplified version of the model presented in [8]. It was solved numerically using the finite-element method with Picard iterations and linearization by determining the coefficients from the preceding time layer. The implementation was based on the FEniCS computation package [15].

It is worth noting that finding an analytic solution for most applied problems of thermoelasticity with a phase transition is impossible. This requires using numerical methods. The finite-element method is widely used for poroelasticity and thermoelasticity problems [16]–[18]. This method is well suited for numerical solutions of problems defined on complex computational domains, allowing the construction of unstructured meshes. But the numerical solution of thermoelasticity problems with phase transition in heterogeneous media involves computational difficulties. Mathematical models with phase transitions are characterized by strong nonlinearity. Consequently, various linearization methods, such as iterative Picard [15] and Newton [19] methods should be used. Because the solution of such problems does not change much in one time step, it is reasonable to use linearization by determining the coefficients from the preceding time layer (one iteration of the Picard method).

One of the main difficulties in numerically solving problems with phase transitions is tracing the phase transition interface. The enthalpy method of the numerical solution, in which the effective heat capacity is determined by various methods of smoothing the discontinuous coefficients has gained wide popularity [20]–[23]. In [24], a new method of smoothing in one spatial interval (cell) was presented. The results of numerical solutions of one-dimensional and two-dimensional two-phase Stefan problems using the respective finite-difference and finite-element methods were presented. This approach has demonstrated high accuracy due to the automatic selection of the smoothing interval.

Accounting for various environmental heterogeneities, including many piles and seasonal-cooling devices, requires generating very fine meshes, which is a computational difficulty in numerical implementations of thermomechanical models of the interaction of engineering structures and buildings erected in the cryolithozone. Such meshes significantly increase the size of discrete problems. Multiscale and homogenization methods are widely used to reduce the required computational resources [25]–[27]. The generalized multiscale finite-element method (GMsFEM) [26] has demonstrated its high efficiency for various problems in heterogeneous media [28]–[30]. This method has been successfully implemented for poroelasticity and thermoelasticity problems (without phase transition) in heterogeneous media [31], [32]. The GMsFEM has also been implemented for heat transfer problems with phase transition [33]–[35].

In this paper, we develop a multiscale method for solving the problem of thermoelasticity with phase transition in heterogeneous media based on the GMsFEM. The finite-element method with standard linear basis functions is used in the fine-grid numerical solution. A simplified model of thermoelasticity with phase transitions is used as a mathematical model where ground deformations occur due to changes in porosity caused by differences in water and ice densities. We test the accuracy of the proposed multiscale method on two- and three-dimensional model problems. We compare the multiscale solution with the fine-grid solution for different coarse grids and numbers of basis functions in local domains.

The paper is organized as follows. In Sec. 1, we review the literature. In Sec. 2, we present the mathematical model of thermoelasticity with phase transitions. Section 3 is devoted to the construction of a finite-element approximation on a fine grid. The approximation on a coarse grid using the GMsFEM method is presented in Sec. 4. In Sec. 5, we discuss the numerical results of the solutions of two-dimensional and three-dimensional model problems. We conclude in Sec. 6.

2. Mathematical model

In this section, we describe a thermoelastic model in saturated porous media with the phase transition of pore moisture to ice and back. The model is a nonlinear system of equations for mechanical displacements \(u\) and temperature \(T\). We consider a simplified mathematical model of freezing/thawing soil in which mechanical deformations of the medium occur due to changes in porosity caused by differences between water and ice densities. A detailed derivation of this model can be found in [11].

Before presenting the model, we introduce some auxiliary functions. First, we define a water content function \(w(T)\) and its derivative \(w'(T)\) with respect to temperature

$$ \begin{aligned} \, &w(T)=\begin{cases} \bar w, & T\geqslant T_{ \mathrm f },\\ \bar w e^{\alpha(T-T_{ \mathrm f })}, & T<T_{ \mathrm f }, \end{cases} \\ &w'(T)=\frac{\partial w(T)}{\partial T}=\begin{cases} 0, & T\geqslant T_{ \mathrm f },\\ \alpha\bar w\kern1pt e^{\alpha(T-T_{ \mathrm f })}, & T<T_{ \mathrm f }, \end{cases} \end{aligned}$$
(1)

where \(\bar w\) is the maximum water content, \(T\) is the temperature, \(T_{ \mathrm f }\) is the freezing temperature, and \(\alpha\) is a model parameter describing the rate of decay.

Using \(w(T)\), we can determine the porosity function \(\phi(T)\) as

$$ \phi(T)=\frac{w(T)+(\bar w-w(T)) \frac{\rho_{ \mathrm w }}{\rho_{ \mathrm i }}}{\frac{\rho_{ \mathrm w }}{\rho_{ \mathrm s }}+w(T)+(\bar w-w(T))\frac{\rho_{ \mathrm w }}{\rho_{ \mathrm i }}},$$
(2)

where \(\rho_{ \mathrm w }\), \(\rho_{ \mathrm i }\), and \(\rho_{ \mathrm s }\) are water, ice, and solid densities. We note that the maximum water content \(\bar w\) can be determined in terms of the maximum porosity \(\bar\phi\) as

$$\bar w=\biggl(\frac{\bar\phi}{1-\bar\phi}\biggr)\frac{\rho_{ \mathrm w }}{\rho_{ \mathrm s }}.$$
(3)

Next, we determine water, ice, and solid fraction volumes

$$ \begin{aligned} \, &\Theta_{ \mathrm w }(T)=w(T)\frac{\rho_{ \mathrm s }}{\rho_{ \mathrm w }}(1-\phi(T)), \\ &\Theta_{ \mathrm i }(T)=(\bar w-w(T))\frac{\rho_{ \mathrm s }}{\rho_{ \mathrm i }} (1-\phi(T)), \\ &\Theta_{ \mathrm s }(T)=1-\phi(T). \end{aligned}$$
(4)

We note that for a fully saturated porous medium, \(\Theta_{ \mathrm w }(T)+\Theta_{ \mathrm i }(T)+\Theta_{ \mathrm s }(T)=1\).

As a result, the mathematical model of thermoelasticity with the pore moisture phase transition in the region \(\Omega\subset\mathbb{R}^d\) (\(d=2,3\)) is described by the system of equations for the temperature \(T\) and displacement \(u\) for \(x\in\Omega\), \(t>0\):

$$(c\rho(T)+D(T)w'(T))\frac{\partial T}{\partial t}-\nabla\cdot(k(T)\nabla T)=0,$$
(5a)
$$\nabla(\mu\,\nabla du)+\nabla[(\lambda+\mu)\nabla\cdot du]+\nabla(\beta(T)\,d\phi(T))=0.$$
(5b)

The following notation is used here:

  1. •

    \(c\rho (T)\) is the volumetric heat capacity of the medium,

    $$ c\rho(T)=\Theta_{ \mathrm s }(T)c_{ \mathrm s }\rho_{ \mathrm s }+ \Theta_{ \mathrm i }(T)c_{ \mathrm i }\rho_{ \mathrm i }+\Theta_{ \mathrm w }(T)c_{ \mathrm w }\rho_{ \mathrm w },$$
    (6)

    where \(c_{ \mathrm s }\), \(c_{ \mathrm i }\), and \(c_{ \mathrm w }\) are solid, ice, and water specific heat capacities;

  2. •

    \(k(T)\) is the thermal conductivity coefficient of the medium [36],

    $$ k(T)=k_{ \mathrm s }^{\Theta_{ \mathrm s }(T)}k_{ \mathrm i }^{\Theta_{ \mathrm i }(T)}k_{ \mathrm w }^{\Theta_{ \mathrm w }(T)},$$
    (7)

    where \(k_{ \mathrm s }\), \(k_{ \mathrm i }\), and \(k_{ \mathrm w }\) are solid, ice, and water thermal conductivity coefficients;

  3. •

    \(\lambda\), \(\mu\) are Lamé parameters

    $$ \lambda=\frac{\nu E}{(1+\nu)(1-2\nu)},\qquad \mu=\frac{E}{2(1+\nu)},$$
    (8)

    where \(\nu\) is Poisson’s ratio and \(E\) is the elastic modulus of the medium;

  4. •

    \(\beta(T)\) is the thermal expansion of the medium caused by a change in porosity:

    $$ \beta(T)=\frac{3\lambda+2\mu}{3(1-\phi(T))};$$
    (9)
  5. •

    \(D(T)\) is the phase transition heat,

    $$ D(T)=L\rho_{ \mathrm s }\biggl[ (1-\phi(T))+(\bar w-w(T))\frac{\partial\phi(T)}{\partial w(T)}\biggr],$$
    (10)

    where \(L\) is the specific phase transition heat.

System of equations (5) is supplemented by the initial conditions

$$ T=T_0,\quad u=u_0\quad\text{for}\quad x\in\overline\Omega,\quad t=0$$
(11)

and boundary conditions

$$-k(T)\nabla T\cdot n=0 \;\; \text{for}\;\;x\in\Gamma_1, \qquad {-k(T)}\nabla T\cdot n=\gamma(T-T_1)\;\; \text{for}\;\; x\in\Gamma_2,$$
(12a)
$$\sigma(u)\cdot n=0 \;\; \text{for}\;\;x\in\Gamma_3, \qquad u=0\;\; \text{for}\;\;x\in\Gamma_4,$$
(12b)

where \(T_1\) is the ambient medium temperature and \(n\) is the unit vector normal to \(\partial\Omega=\Gamma_1\cup\Gamma_2=\Gamma_3\cup\Gamma_4\).

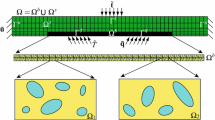
We note that (12) represent a general formulation of the boundary conditions. In Fig. 1, we show a possible variant of the domain \(\Omega\) and its boundaries (for two- and three-dimensional cases). In this variant, \(\Gamma_2\subset\Gamma_{\text{top}}\) (the darker section of the boundary), \(\Gamma_1=\partial\Omega\setminus\Gamma_2\) (dotted line), \(\Gamma_3=\Gamma_{\text{top}}\) (solid line), \(\Gamma_4=\partial\Omega\setminus\Gamma_3\) (dashed line).

Fig. 1.
figure 1

Schematic representation of a possible variant of the domain \(\Omega\) and its boundaries. Left: two-dimensional case. Right: three-dimensional case.

Full size image

We note that in (12b), \(\sigma (u)\) denotes the stress tensor defined as

$$\sigma (u)=2\mu\varepsilon(u)+\lambda\operatorname{tr}(\varepsilon(u))\,\mathcal I,\quad\varepsilon (u)=\frac{1}{2}(\nabla u+(\nabla u)^{\mathrm T}),$$

where \(\varepsilon(u)\) is the deformation tensor and \(\mathcal I\) is a unit matrix.

3. Approximation on a fine grid

To discretize problem (5) , (11), (12) in spatial variables on a fine grid, we use the finite-element method with standard linear basis functions. The time approximation is carried out using an implicit time scheme

$$ \frac{\partial T}{\partial t}\approx\frac{T^{m+1}-T^m}{\tau},$$
(13)

where \(m=\overline{0,N_t-1}\) is the time step ordinal number, \(N_t\) is a count of time steps, \(\tau=t_{\max}/N_t\) is a time step, and \(t_{\max}\) is the simulation time.

Variational formulation

Let \(Q\) and \(V\) be the respective functional spaces for temperature and displacement, such that

$$Q=H_1(\Omega),\qquad V=\{v\in[H_1(\Omega)]^d\colon v(x)=0\;\,\text{for}\;\,x\in\Gamma_4\},$$

where \(H_1\) is a Sobolev space and \(d=2,3\) is the geometric dimensionality of the problem. Multiplying Eqs. (5a) and (5b) by respective test functions \(r\in Q\) and \(v\in V\) and integrating by parts with boundary conditions (12), we obtain the following variational formulation. Find \(T\in Q\) and \(u\in V\) such that

$$\begin{alignedat}{3} &s\biggl(\frac{T^{m+1}-T^m}{\tau},r\biggr)+a_T(T^{m+1},r)=l(r) &\qquad &\forall r\in Q, \\ &a_u(u^{m+1}-u^m,v)=b(T^{m+1}-T^m,v) &\qquad &\forall v\in V, \end{alignedat}$$

where the bilinear and linear forms are

$$\begin{aligned} \, &s(T,r)=\int_{\Omega}[(c\rho)^m+(Dw')^m]T\kern1pt r\,dx,\qquad a_T(T,r)=\int_{\Omega}k^m\nabla T\cdot\nabla r\,dx+\int_{\Gamma_2}\gamma T\kern1pt r\,dx, \\ &l(r)=\int_{\Gamma_2}\gamma T_1r\,dx, \\ &a_u(u, v)=\int_{\Omega}\sigma(u):\varepsilon(v)\,dx,\qquad b(T,v)=\int_{\Omega}[\beta(T)\phi(T)\mathcal I]:\varepsilon(v)\,dx. \end{aligned}$$

Here, \((c\rho)^m=c\rho(T^m)\), \((Dw')^m=Dw'(T^m)\), \(k^m=k(T^m)\), and the colon denotes the inner product of tensors. To obtain a discrete linear analogue of the quasilinear heat transfer equation, we take the coefficients from the preceding time layer. We assume here that the influence of mechanical strains on heat transfer is negligible, and we can therefore solve the equations for temperature and displacement separately. In each time step, we first solve the equation for temperature and then, using the temperature distribution found on the upper time layer, solve the discrete analogue of the equation for displacements.

Discrete formulation

Let \(\mathcal T^h=\bigcup_{i=1}^{N_{ \mathrm c }^h} K_i^h\) be a grid partition of the computational domain \(\Omega\) into finite elements \(K_i^h\). We define the finite-dimensional spaces \(V_h\subset V\) and \(Q_h\subset Q\) on the grid \(\mathcal T^h\). Let the respective spaces \(Q_h\) and \(V_h\) be composed of piecewise linear basis functions \(\psi_j\) and \(\Phi_j\) on grid cells. We then obtain the following discrete problems on the fine grid for \(m=\overline{0,N_t-1}\).

  1. •

    Temperature. Find the vector \(T_h^{m+1}=(T_{h,1}^{m+1},\ldots, T_{h, \kern0.4pt\mathrm{dof\kern0.3pt} _{\text f}^T}^{m+1})^{\mathrm T}\) such that

    $$\begin{aligned} \, &S\frac{T_h^{m+1}-T_h^m}{\tau}+A_T T_h^{m+1}=F, \\ &S=[s_{ij}],\quad s_{ij}=s(\psi_i,\psi_j),\qquad A_T=[a_{T,ij}],\quad a_{T,ij}=a_T (\psi_i,\psi_j), \\ &F_T=\{f_j\},\qquad f_j=l(\psi_j). \end{aligned}$$
  2. •

    Displacement. Find the vector \(U_h^{m+1}=(U_{h,1}^{m+1},\ldots, U_{h, \kern0.4pt\mathrm{dof\kern0.3pt} _{\text f}^u}^{m+1})^{\mathrm T}\) such that

    $$A_u (U_h^{m+1}-U_h^m)=B^{m+1}-B^m,$$

    where \( \kern0.4pt\mathrm{dof\kern0.3pt} _{\text f}^u=d\cdot N^h_{ \mathrm v }\), and the matrix and the right-hand side are defined as

    $$\begin{aligned} \, &A_u=[a_{u,ij}],\qquad a_{u,ij}=a_u(\Phi_i,\Phi_j), \\ &B^m=\{b^m_j\},\quad b^m_j=b(T^m,\Phi_j),\qquad B^{m+1}=\{b^{m+1}_j\},\quad b^{m+1}_j=b(T^{m+1},\Phi_j). \end{aligned}$$

We note that the solutions of the discrete problems at each time step can be represented as a linear combination of the basis functions

$$T^m_{\text f}=\sum_{j=1}^{ \kern0.4pt\mathrm{dof\kern0.3pt} _{\text f}^{T}}T_{h,j}^{m+1}\psi_j^{},\qquad u^m_{\text f}=\sum_{j=1}^{ \kern0.4pt\mathrm{dof\kern0.3pt} _{\text f}^u} U_{h,j}^{m+1}\Phi_j^{}.$$

4. Approximation on a coarse grid

We use the GMsFEM [26] to approximate the problem on a coarse grid. This method is a systematic approach to constructing multiscale basis functions that take the heterogeneities of the medium into account. We note that the GMsFEM allows considering complex types of heterogeneities, for example, without scale separation, and with high contrast.

To further describe the GMsFEM, we introduce some notation. Let \(\mathcal T^H\) be a coarse grid and \(K_i^H\) be the cells of \(\mathcal T^H=\bigcup_{i=1}^{N_{ \mathrm c }^H} K_i^H\). We define local domains \(\omega_i^{}=\bigcup_{j}K_j^H\), where each cell \(K_j^H\) contains the \(i\)th node of the coarse grid.

We can divide the multiscale algorithm into two stages: offline and online. We generate the coarse grid, define the local domains, and construct snapshot spaces for each local domain at the offline stage. Next, we compute the multiscale basis functions on the found snapshot spaces.

Offline stage:

  1. 1.

    generation of the coarse grid \(\mathcal T^H\) and local domains \(\omega_i\);

  2. 2.

    construction of snapshot spaces for each local domain \(\omega_i\) by solving local problems;

  3. 3.

    construction of a multiscale space by solving local spectral problems;

  4. 4.

    generation of the projection matrix into the multiscale space.

The online stage consists in generating the system of equations on the coarse grid and the computational implementation.

Online stage:

  1. 1.

    construction of the discrete problem on the coarse grid using the projection matrix;

  2. 2.

    solving the discrete problem on the coarse grid;

  3. 3.

    reconstructing the solution on the fine grid.

Because the thermoelastic model under consideration allows solving the problem in a split manner, we construct the multiscale basis functions for temperature and displacements separately.

4.1. Construction of multiscale basis functions for temperature

We assume that the coarse grid \(\mathcal{T}^H\) and the local domains \(\omega_i\) have already been constructed. In that case, it is necessary to construct a snapshot space for each local domain \(\omega_i\). Wherever possible, we omit the subscript \(i\) in the notation for the local domain. Thus, we need to solve the following local problems for each local region \(\omega\). Find \(\varphi_j^{\omega,\,\text{snap}}\) such that

$$ \int_\omega k\,\nabla\varphi_j^{\omega,\,\text{snap}}\cdot\nabla r\,dx=0,$$
(14)

with the Dirichlet boundary conditions

$$ \varphi_j^{\omega,\,\text{snap}}=\delta_j^h (x)\quad\text{for}\quad x\in\partial\omega,$$
(15)

where \(\delta_j^h (x)=\delta_{j,k}\) for \(j,k\in J_h(\omega)\), and \(J_h(\omega)\) is the set of all fine-grid nodes on the boundary \(\partial\omega\). Thus, we need to solve \(N^{\partial\omega}\) local problems, where \(N^{\partial\omega}\) is the number of fine-grid nodes on \(\partial\omega\). For each local domain, we then construct the snapshot spaces and projection matrices

$$ \begin{aligned} \, Q_{\text{snap}}^{}(\omega)&=\operatorname{span}\{\varphi_j^{\omega,\,\text{snap}}\colon 1\leqslant j\leqslant N^{\partial\omega}\}, \\ R_{T,\,\text{snap}}^{}&=(\varphi_1^{\omega,\,\text{snap}},\ldots,\varphi_{N^{\partial\omega}}^{\omega,\,\text{snap}}). \end{aligned}$$
(16)

The next stage of the GMsFEM is constructing the multiscale space and the projection matrix. We first need to solve the following local spectral problems for each local domain:

$$ \tilde A_T^{}\tilde\varphi_k^{\omega}=\lambda_k^{}\widetilde S_T^{}\tilde\varphi_k^{\omega},$$
(17)

where

$$\begin{aligned} \, &\tilde A_T^{}=(R_{T,\,\text{snap}})^{\mathrm T}A_T^{}R_{T,\,\text{snap}}^{},\qquad \widetilde S_T^{}=(R_{T,\,\text{snap}})^{\mathrm T}S_T^{}R_{T,\,\text{snap}}^{}, \\ &A_T=[a_{T,ij}],\qquad a_{T,ij}=\int_{\omega}k\,\nabla\psi_i\cdot\nabla\psi_j\,dx,\qquad S_T=[s_{T,ij}],\quad s_{T,ij}=\int_{\omega} k\psi_i\psi_j\,dx. \end{aligned}$$

Next, we sort the eigenvalues in ascending order and select the eigenvectors corresponding to the \(M_T\) smallest eigenvalues. To transfer the eigenvectors back from the snapshot space to the original space, we again use the projection matrix of the snapshot space

$$ \varphi_k^{\omega}=R_{T,\,\text{snap}}^{}\tilde\varphi_k^{\omega}.$$
(18)

Then we multiply the obtained eigenvectors by a partition of unity function \(\chi_i\). This function is continuous and linear in \(\omega\), equal to 1 at the \(i\)th node of the coarse grid and 0 at all other coarse-grid nodes,

$$ \varphi_{i, k}=\chi_i\varphi_k^{\omega_i},\qquad 1\leqslant i\leqslant N_{ \mathrm v }^H,\quad 1\leqslant k\leqslant M_T,$$
(19)

where \(N_{ \mathrm v }^H\) is the count of nodes of the coarse grid \(\mathcal T^H\).

After calculating all local multiscale basis functions, we can construct the multiscale space and its projection matrix

$$ \begin{aligned} \, &Q_{\mathrm{ms}}=\operatorname{span}\{\varphi_{i,k}\colon 1\leqslant i\leqslant N_{ \mathrm v }^H\;\,\text{and}\;\,1\leqslant k\leqslant M_T\}, \\ &R_T=(\varphi_{1,1},\ldots,\varphi_{1,M_T},\ldots,\varphi_{N_{ \mathrm v }^H,1},\ldots,\varphi_{N_{ \mathrm v }^H, M_T}), \end{aligned}$$
(20)

4.2. Construction of multiscale basis functions for displacements

The multiscale basis functions for displacements are constructed in the same way. First, we need to construct the snapshot space for each local domain. We need to solve the following problems in each local domain \(\omega\). Find \(\Psi_j^{\omega,\,\text{snap}}\) such that

$$ \int_\omega\sigma(\Psi_j^{\omega,\,\text{snap}}):\varepsilon(v)\,dx=0,$$
(21)

with the Dirichlet boundary conditions

$$ \Psi_j^{\omega,\,\text{snap}}=\bar\delta_j^h(x)\quad\text{for}\quad x\in\partial\omega,$$
(22)

where \(\bar\delta_j^h(x)\) is either \((\delta_{j,k},0,0)^{\mathrm T}\) or \((0,\delta_{j,k},0)^{\mathrm T}\), or \((0,0,\delta_{j,k})^{\mathrm T}\) for \(j,k\in J_h(\omega_i)\). Thus, we need to solve \(d\cdot N^{\partial\omega}\) local problems. Further, we can construct the snapshot space and the projection matrix

$$ \begin{aligned} \, &V_{\text{snap}}(\omega)^{}=\operatorname{span}\{\Psi_j^{\omega,\,\text{snap}}\colon 1\leqslant j\leqslant d\cdot N^{\partial\omega}\}, \\ &R_{u,\,\text{snap}}^{}=(\Psi_1^{\omega,\,\text{snap}},\ldots,\Psi_{d\cdot N^{\partial\omega}}^{\omega,\,\text{snap}}). \end{aligned}$$
(23)

Then, for each local domain, we need to solve the spectral problems in the found snapshot spaces

$$ \tilde A_u^{}\widetilde\Psi_k^{\omega}=\lambda_k^u\widetilde S_u^{}\widetilde\Psi_k^{\omega},$$
(24)

where

$$\begin{aligned} \, &\,\tilde A_u^{}=(R_{u,\,\text{snap}})^{\mathrm T} A_u^{}R_{u,\,\text{snap}}^{},\qquad \widetilde S_u^{}=(R_{u,\,\text{snap}})^{\mathrm T}S_T^{}R_{u,\,\text{snap}}^{}, \\ &\begin{alignedat}{3} &A_u=\{a_{u,ij}\},&\qquad a_{u,ij}&=\int_{\omega}\sigma(\Phi_j):\varepsilon(\Phi_{ \mathrm i })\,dx, \\ &S_u=\{s_{u,ij}\},&\qquad s_{u,ij}&=\int_{\omega} (\lambda+2\mu)\Phi_{ \mathrm i }\cdot\Phi_j\,dx. \end{alignedat} \end{aligned}$$

As we did for the temperature, we sort the eigenvalues in ascending order and select the eigenvectors corresponding to the \(M_u\) smallest eigenvalues. We project the obtained eigenvectors back to the original space:

$$ \Psi_k^{\omega}=R_{u,\,\text{snap}}\widetilde\Psi_k^{\omega}.$$
(25)

To obtain conforming basis functions, we multiply the eigenvectors by the partition of unity function

$$ \Psi_{i,k}^{}=\xi_i\Psi_k^{\omega_i},\qquad 1\leqslant i\leqslant d\cdot N_{ \mathrm v }^H,\quad 1\leqslant k\leqslant M_u.$$
(26)

After calculating the basis functions in all local domains, we can construct the multiscale space and the corresponding projection matrix:

$$\begin{aligned} \, &V_{\mathrm{ms}}=\operatorname{span}\{\Psi_{i,k}\colon 1\leqslant i\leqslant d\cdot N_{ \mathrm v }^H\;\,\text{and}\;\, 1\leqslant k\leqslant M_u\}, \\ &R_u=(\Psi_{1, 1},\ldots,\Psi_{1, M_u},\ldots,\Psi_{d\cdot N_{ \mathrm v }^H, 1},\ldots,\Psi_{d\cdot N_{ \mathrm v }^H, M_u}). \end{aligned}$$
(27)

4.3. System on a coarse grid

Using the obtained projection matrices \(R_T\) and \(R_u\), we transfer the equations for temperature and displacements from the fine grid to the coarse grid. As a result, we obtain the following discrete problems on the coarse grid for \(m=\overline{0, N_t-1}\).

  1. •

    Temperature. Find the vector \(T_H^{m+1}=(T_{H,1}^{m+1},\ldots, T_{H, \kern0.4pt\mathrm{dof\kern0.3pt} _{\text c}^T}^{m+1})^{\mathrm T}\) such that

    $$S_H^{}\frac{T_H^{m+1}-T_H^m}{\tau}+A_{T,H}^{}T_H^{m+1}=F_H^{},$$

    where \( \kern0.4pt\mathrm{dof\kern0.3pt} _{\text c}^T=M_T\cdot N_{ \mathrm v }^H\), and the matrices and vectors are defined as

    $$S_H^{}=(R_T)^{\mathrm T} SR_T^{},\quad A_{T,H}^{}=(R_T)^{\mathrm T}A_T^{}R_T^{},\quad F_H^{}=(R_T)^{\mathrm T}F,\quad T_H^m=(R_T)^{\mathrm T}T_h^m.$$
  2. •

    Displacement. Find the vector \(U_H^{m+1}=(U_{H,1}^{m+1},\ldots,U_{H, \kern0.4pt\mathrm{dof\kern0.3pt} _{\text c}^u}^{m+1})^{\mathrm T}\) such that

    $$A_{u,H}^{}(U_H^{m+1}-U_H^m)=B_H^{m+1}-B_H^m,$$

    where \( \kern0.4pt\mathrm{dof\kern0.3pt} _{\text c}^u=d\cdot M_u\cdot N_{ \mathrm v }^H\), and the matrix and vectors are defined as

    $$A_{u,H}^{}=(R_u)^{\mathrm T}A_u^{}R_u^{},\quad B_H^m=(R_u^{})^{\mathrm T}B^m,\quad B_H^{m+1}=(R_u^{})^{\mathrm T}B^{m+1},\quad U_H^m=(R_u^{})^{\mathrm T}U_h^m.$$

We can reconstruct the solutions on the fine grid as

$$ T_{\mathrm{ms}}^{m+1}=R_T^{}T_H^{m+1},\qquad U_{\mathrm{ms}}^{m+1}=R_u^{}U_H^{m+1}.$$
(28)

Thus, it is possible to reconstruct the fine-grid solution with minimal error by solving the coarse-grid system. In the next section, we present numerical results for two- and three-dimensional model problems.

5. Numerical results

In this section, we present numerical results for two- and three-dimensional problems of thermoelasticity with phase transition in heterogeneous media. The numerical implementation is based on the FEniCS computational package [15]. We consider the following computational domains and grids.

  1. •

    Two-dimensional problem. For the two-dimensional problem, we consider the computational domain \(\Omega=[0,L_x]\times [0,L_y]\;\text{m}^2\), where \(L_x=L_y=6\;\text{m}\). We use a fine grid with 10201 vertices and 20000 triangular cells. For the proposed multiscale method, we consider two coarse grids: a) a uniform \(5\times 5\) coarse grid with 36 vertices and 25 rectangular cells; b) a uniform \(10\times 10\) coarse grid with 121 vertices and 100 rectangular cells (see Fig. 2a).

  2. •

    Three-dimensional problem. For the three-dimensional problem, we consider the computational domain \(\Omega=[0,L_x]\times [0,L_y]\times[0,L_z]\;\text{m}^3\), where \(L_x=L_y=L_z=6\;\text{m}\). We use a fine grid with 9261 vertices and 48000 tetrahedral cells. For the proposed multiscale method, we consider a uniform \(5\times 5\times 5\) coarse grid with 216 vertices and 125 cubic cells (see Fig. 2b).

Fig. 2.
figure 2

Computational grids. (a) two-dimensional case; (b) three-dimensional case. Darker color shows the \(\Gamma_H\) boundary.

Full size image

We set the following boundary conditions.

For the temperature,

$$\begin{alignedat}{3} &-k\nabla T\cdot n=\gamma_C (T-T_C)&\quad\text{for}\quad &x\in\Gamma_C, \\ &-k\nabla T\cdot n=\gamma_H (T-T_H)&\quad\text{for}\quad &x\in\Gamma_H, \\ &-k\nabla T\cdot n=0&\quad\text{for}\quad &x\in\partial\Omega\setminus (\Gamma_C\cup\Gamma_H), \end{alignedat}$$

where \(\Gamma_C=\Gamma_{\text{top}}\setminus\Gamma_H\), \(T_C=-15\,{}^\circ\text{C}\), \(\gamma_C=14\;\text{W}\cdot\text{m}^{-2}\cdot{}^\circ\text{C}^{-1}\), \(T_H=10\,{}^\circ\text{C}\) and \(\gamma_H=20\;\text{W}\cdot\text{m}^{-2}\cdot{}^\circ\text{C}^{-1}\).

For displacements in the two-dimensional problem,

$$\begin{alignedat}{5} &\sigma_1=0\;\text{Pa}, &\quad u_2&=0\;\text{m}&\quad\text{for}&\quad x_2=0\;\text{m}, \\ &\sigma_2=0\;\text{Pa},&\quad u_1&=0\;\text{m}&\quad\text{for}&\quad x_1=0\;\text{m}\quad\text{or}&\quad x_1=L_x\;\text{m}, \\ &\sigma\cdot n=0\;\text{Pa}\quad\kern1.5pt\text{at other boundaries}.\kern-180pt \end{alignedat}$$

For displacements in the three-dimensional problem,

$$\begin{alignedat}{5} &\sigma_1=\sigma_2=0\;\text{Pa},&\quad u_3&=0\;\text{m}&\quad\text{for}&\quad x_3=0\;\text{m}, \\ &\sigma_2=\sigma_3=0\;\text{Pa},&\quad u_1&=0\;\text{m}&\quad\text{for}&\quad x_1=0\;\text{m}\quad\text{or}\quad x_1=L_x\;\text{m}, \\ &\sigma_1=\sigma_3=0\;\text{Pa},&\quad u_2&=0\;\text{m}&\quad\text{for}&\quad x_2=0\;\text{m}\quad\text{or}\quad x_2=L_y\;\text{m}, \\ &\sigma\cdot n=0\;\text{Pa}\quad\kern1.5pt\text{at other boundaries}.\kern-180pt \end{alignedat}$$

We set \(u_0=(0,0,0)^{\mathrm T}\;\text{m}\) as the initial condition for displacements. For the temperature, we set the initial condition \(T_0=2\,{}^\circ\text{C}\). Thus, we consider the process of ground freezing in the presence of a heat-generating object.

Fig. 3.
figure 3

Heterogeneous coefficients, from left to right: the solid elastic modulus \(E_{ \mathrm s }\;[\text{Pa}]\), the solid specific heat capacity \(c_{ \mathrm s }\;[\text{J}\cdot\text{kg}^{-1}\cdot{}^\circ\text{C}^{-1}]\), the solid density \(\rho_{ \mathrm s }\;[\text{kg}\cdot\text{m}^{-3}]\), the solid thermal conductivity \(k_{ \mathrm s }\;[\text{W}\cdot\text{m}^{-1}\cdot{}^\circ\text{C}^{-1}]\), and the maximum porosity \(\bar\phi\). The first line is the two-dimensional case, the second line is the three-dimensional case.

Full size image

For both problems, we set the simulation time \(t_{\max}=30\;\text{days}\) with 50 time steps. The heterogeneous coefficients \(E_{ \mathrm s }\;[\text{Pa}]\), \(c_{ \mathrm s }\;[\text{J}\cdot\text{kg}^{-1}\cdot{}^\circ\text{C}^{-1}]\), \(\rho_{ \mathrm s }\;[\text{kg}\cdot\text{m}^{-3}]\), \(k_{ \mathrm s }\;[\text{W}\cdot\text{m}^{-1}\cdot {}^\circ\text{C}^{-1}]\), and \(\bar\phi\) for the two-dimensional and three-dimensional problems are shown in Fig. 3. The other parameters are as follows.

Ice: \(\rho_{ \mathrm i }=917.0\;\text{kg}\cdot\text{m}^{-3}\), \(c_{ \mathrm i }=2000.0\;\text{J}\cdot\text{kg}^{-1}\cdot {}^\circ\text{C}^{-1}\), and \(k_{ \mathrm i }= 2.24\;\text{W}\cdot\text{m}^{-1}\cdot {}^\circ\text{C}^{-1}\).

Water: \(\rho_{ \mathrm w }=1000.0\;\text{kg}\cdot\text{m}^{-3}\), \(c_{ \mathrm w }=4180.0\;\text{J}\cdot\text{kg}^{-1}\cdot {}^\circ\text{C}^{-1}\), and \(k_{ \mathrm w }= 0.56\;\text{W}\cdot\text{m}^{-1}\cdot {}^\circ\text{C}^{-1}\).

Solid: \(\nu = 0.3\).

Model parameters: \(L=333000.0\;\text{J}\cdot\text{kg}^{-1}\), \(T_{ \mathrm f }=0.0\,{}^\circ\text{C}\), and \(\alpha=0.3\,{}^\circ\text{C}^{-1}\).

Because it is apparently impossible to find an analytic solution for problems of thermoelasticity with phase transitions in heterogeneous media, we compare the multiscale solution with the solution on the fine grid. For this, we use the relative \(L_2\) errors

$$ \varepsilon_{L_2}^{\mathrm T}=\sqrt{\frac{\int_\Omega (T-T_{\mathrm{ms}})^2\,dx}{\int_\Omega T^2\,dx}}\cdot 100\%,\qquad \varepsilon_{L_2}^u=\sqrt{\frac{\int_\Omega(u-u_{\mathrm{ms}})^2\,dx}{\int_\Omega u^2\,dx}}\cdot 100\%$$
(29)

and the relative energy errors

$$ \begin{aligned} \, &\varepsilon_{\mathrm e}^{\mathrm T}=\sqrt{\frac{a_T (T-T_{\mathrm{ms}},T-T_{\mathrm{ms}})}{a_T (T, T)}}\cdot 100\%, \\ &\varepsilon_{\mathrm e}^u=\sqrt{\frac{a_u(u-u_{\mathrm{ms}},u-u_{\mathrm{ms}})}{a_u(u,u)}}\cdot 100\%, \end{aligned}$$
(30)

where \(T\) and \(u\) are the temperature and displacements calculated on the fine grid, and \(T_{\mathrm{ms}}\) and \(u_{\mathrm{ms}}\) are the temperature and displacement calculated on the coarse grid.

Fig. 4.
figure 4

Temperature and displacement magnitude distributions (deformed with a 30 times increased displacement value) at the final time moment for the two-dimensional problem (from left to right). The phase transition lines in the temperature distribution are highlighted by dash lines. (a) The solution on the fine grid, (b) the multiscale solution using 12 basis functions on the \(10\times 10\) coarse grid.

Full size image

5.1. Two-dimensional problem

The numerical results for the two-dimensional problem are shown in Fig. 4. The figure shows the temperature and displacement distributions at the final time moment \(t=\tau\cdot N_t\). The phase transition lines in the temperature distribution are highlighted by dashed lines. The displacements are deformed with an increase in values by a factor of 30. We can see that the ground heaving areas correspond to the areas where the phase transition occurred. The ground deformations were due to changes in porosity caused by the difference between water density and ice density. The first line presents the solution results on the fine grid, and the second line presents the results of a multiscale solution on the coarse grid \(10 \times 10\) using 12 multiscale basis functions in local domains. The results are very similar, which indicates that the proposed multiscale approach can provide a good approximation to the fine-grid solution.

We present relative errors for the two-dimensional problem in Table 1. Here, \(M\) is a count of multiscale basis functions in each local domain of the coarse grid, and it remains the same for both temperature and displacements. The \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm c }^T\) and \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm c }^u\) columns show the number of degrees of freedom of discrete problems for temperature and displacements on the coarse grid, respectively.

Table 1. Relative errors (%) for the temperature and displacement using different numbers of multiscale basis functions for the two-dimensional problem. \(5 \times 5\) and \(10 \times 10\) coarse grids. \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm f }^T=10201\), \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm f }^u=20402\)
Full size table

For both coarse grids, the errors decrease as the number of basis functions in the local domains of the coarse grid increases. The values of the energy errors are larger than the \(L_2\) errors. This phenomenon can be explained by the fact that the energy errors represent gradients of solutions. Using a coarse grid \(5 \times 5\), one can achieve good accuracy with a few basis functions. For example, with 4 basis functions, \(L_2\) errors are just over 5% for temperature and just over 7% for displacement. With 8 basis functions, the \(L_2\) errors for temperature are less than 3% and less than 5% for displacement.

The relative errors using the coarse grid \(10 \times 10\) are smaller than those using the coarse grid \(5 \times 5\). For example, when using 4 basis functions, the relative \(L_2\) errors are less than 2% for temperature and just over 3% for displacement. With 8 basis functions, the relative \(L_2\) errors are less than 1% for temperature and smaller than 2% for displacement. The energy errors for the coarse grid \(10 \times 10\) are also more minor than for the coarse grid \(5 \times 5\). For example, with 12 basis functions, the relative energy errors are less than 7% for temperature and less than 10% for displacement. For the coarse grid \(5 \times 5\) with 12 basis functions, the energy errors are larger than 15% for temperature and slightly larger than 17% for displacements. However, it is worth noting that the GMsFEM is a spectral approach and does not guarantee error reduction when we refine the mesh. For this reason, the CEM-GMsFEM was developed in [37].

5.2. Three-dimensional problem

The numerical results for the three-dimensional problem are shown in Fig. 5. The figure depicts distributions of temperature, temperature slice with the phase transition interface, displacement magnitude at the final time moment. The displacement distribution is also deformed with 30-time increased values. As in the two-dimensional case, the ground heaving zones correspond to the areas where the phase transition occurred. The ground deformations were due to changes in porosity caused by the difference between water density and ice density. The first line shows the results of the fine grid solution, and the second line shows the multiscale solution using 12 multiscale basis functions in local domains of the coarse grid \(5\times 5\times 5\). As in the two-dimensional problem, all distributions are very similar. Thus, our multiscale method can also provide good accuracy for the three-dimensional problem.

Fig. 5.
figure 5

Distributions of temperature, temperature slice with phase transition interface, displacement magnitude (deformed with 30 times increased displacement value) at the final time moment for the three-dimensional problem (from left to right). The first line is the solution on the fine grid (a), and the second line is the multiscale solution using 12 basis functions on the coarse grid \(5\times 5\times 5\) (b).

Full size image
Table 2. Relative errors (%) for temperature and displacement using different numbers of multiscale basis functions for the three-dimensional problem. Coarse grid \(5\times 5\times 5\); \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm f }^T=9261\), \( \kern0.4pt\mathrm{dof\kern0.3pt} _{ \mathrm f }^u=27783\)
Full size table

In Table 2, we present relative errors for the three-dimensional problem. As in the two-dimensional case, we observe a decrease in the errors as the number of multiscale basis functions increases. The table shows that the multiscale method can achieve good solution accuracy when using a small number of basis functions. For example, with six basis functions, the relative \(L_2\) errors are less than 5% for the temperature and a little more than 3% for the displacement. With 16 basis functions, the relative \(L_2\) errors are less than 2% for both fields.

6. Conclusion

We have discussed a model of thermoelasticity with phase transitions in which deformations of the medium occur due to changes in porosity caused by differences between the densities of water and ice. We have used the finite-element method with standard linear basis functions for spatial approximation on the fine grid. The multiscale solution method on the coarse grid is based on the GMsFEM. Time approximation was carried out using an implicit scheme, and the coefficients were determined from the preceding time layer for linearization of the discrete analogue of the nonlinear heat conduction equation.

We presented numerical results for two- and three-dimensional model problems with heterogeneous coefficients. The relative \(L_2\) and energy errors were calculated for different numbers of basis functions to compare the multiscale and fine-grid solutions. The results show that the proposed multiscale method can provide a good approximation to the solution on the fine grid with a significant reduction in the degrees of freedom.

In future work, we plan to consider more complex mathematical models of thermoelasticity with phase transitions. We also plan to consider the Online GMsFEM.