Secure Outsourced Matrix Multiplication with Fully Homomorphic Encryption

Abstract

Fully Homomorphic Encryption (FHE) is a powerful cryptographic tool that enables the handling of sensitive encrypted data in untrusted computing environments. This capability allows for the outsourcing of computational tasks, effectively addressing security and privacy concerns. This paper studies the secure matrix multiplication problem, a fundamental operation used in various outsourced computing applications such as statistical analysis and machine learning. We propose a novel method to solve the secure matrix multiplication $A_{m\times l}\times B_{l\times n}$ with arbitrary dimensions, which requires only O(l) rotations and $\min (m,l,n)$ homomorphic multiplications. In comparison to the state-of-the-art method [14], our approach stands out by achieving a remarkable reduction in the number of rotations by a factor of $O(\log \max (l,n))$, as well as a reduction in the number of homomorphic multiplications by a factor of $O(l/\min (m,l,n))$. We implemented [14, 21], and our method using the BGV scheme supported by the HElib library. Experimental results show that our scheme has the best performance for matrix multiplication of any dimension. For example, for $A_{16\times 128}\times B_{128\times 4}=C_{16\times 4}$, the runtime of our method is 32 s, while both [14, 21] take 569 seconds.

1 Introduction

In the era of cloud computing, accessing storage and computing resources through network-based services has become an economical alternative to construct and maintain costly IT systems. However, the protection of data privacy poses a significant challenge, particularly when dealing with sensitive information in domains such as economics and medicine. Fully Homomorphic Encryption (FHE) offers a natural solution by enabling computations to be performed on encrypted data, thereby ensuring data privacy guarantees for outsourced computing tasks in cloud-based applications.

FHE has emerged as a promising post-quantum cryptography, primarily due to the security assumptions it relies on, such as the Learning with Errors (LWE) problem. In contrast, other privacy-preserved computing technologies like traditional secure multi-party computation depend on additional security assumptions and offer relatively weaker data protection. Gentry [8] introduced the groundbreaking FHE scheme, which theoretically allows for the evaluation of any function on ciphertexts. Since then, extensive research efforts have been devoted to enhancing the efficiency of FHE schemes both in theory and practice (e.g., [1,2,3,4, 15, 23, 26]). Second-generation FHE schemes, including BFV [6], BGV [1], and CKKS [3], have gained widespread support from mainstream FHE libraries(e.g., SEAL [18], HElib [13]), owing to their support for SIMD (Single Instruction Multiple Data) batch processing.

Matrix multiplication is a fundamental operation extensively utilized in scientific, engineering, and machine learning applications, and often demands substantial computational resources. However, outsourcing matrix computations to untrusted servers raises concerns about data confidentiality. Consequently, the development of an efficient and highly secure matrix multiplication scheme becomes imperative for secure outsourced data processing. Based on FHE, this paper investigates this problem, and an efficient matrix multiplication scheme that can adapt to any matrix dimension is proposed.

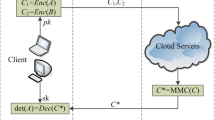
1.1 System Model

To perform matrix multiplication, a client with limited computational resources first encrypts the two input matrices with a public key and sends the ciphertexts with evaluation keys to the computationally powerful cloud server. Then, the cloud server computes the secure matrix multiplication by performing a series of homomorphic operations on the ciphertexts. Finally, the client receives the computation result from the cloud server, and decrypts it by the private key. In this paper, we adopt a semi-honest model [10], where the server executes the protocol correctly but tries to obtain additional information from the client data.

1.2 Fully Homomorphic Encryption and Hypercube Structure

In this paper, we specifically study the Ring-LWE variant [9] of the BGV scheme [1], which is worked over a polynomial ring modulo a cyclotomic polynomial $\mathbb {A}=\mathbb {Z}[X]/\phi _{M}(X)$, where $\phi _{M}(X)$ is the M-th cyclotomic polynomial. Given a plaintext space $\mathcal {M}$ and a ciphertext space $\mathcal {C}$, an FHE scheme is specified by five algorithms: KeyGen, Enc, Dec, Add and Mult, which represent key generation, encryption, decryption, homomorphic addition and multiplication, respectively. We use Add $(ct_1,ct_2)=ct_1\oplus ct_2$ and Mult $(ct_1,ct_2)=ct_1\odot ct_2$ to denote the homomorphic addition and multiplication, respectively, where $ct_1,ct_2\in \mathcal {C}$. In addition, the symbol $\odot$ is also used to represent scalar multiplication between ct and U, denoted as CMult(ct, U), where $ct\in \mathcal {C}$ and $U \in \mathcal {M}$ is scalar.

An important property of RLWE-based FHE schemes is the packing technique [24], which enables SIMD homomorphic operations. Using this method, every homomorphic operation over ciphertexts implies element-wise operations over plaintext slots. The packing technique also supports a basic data movement operation called rotation. Utilizing these operations can reduce space and time complexity while avoiding the need to repack plaintext data. The BGV scheme incorporates the hypercube structure for organizing plaintext and its associated rotation operation [11]. This operation rotates hypercolumns in specific dimension within a multi-dimensional hypercube structure. This paper uses a two-dimensional hypercube structure to represent the plaintext matrix. Rotate1D(ct, 0, k) denotes each column of the matrix rotated down by k positions, and Rotate1D(ct, 1, k) denotes each row of the matrix rotated right by k positions. Note that k can also be negative, resulting in the plaintext slots’ upward or leftward rotation. Figure 1 describes the operations mentioned above. Among these operations, Mult and Rotate1D are the most expensive. Therefore, to design efficient algorithms, our priority is to reduce the number of Mult and Rotate1D.

Fig. 1.

Typical operations on plaintext slot data in the hypercube structure

1.3 Related Works

For secure matrix multiplication $A_{m\times l}\times B_{l\times n}=C_{m\times n}$, a straightforward approach is to encrypt each matrix element into a ciphertext. However, this method requires a significant number of element-wise multiplication operations, totaling mln. Recognizing that each element of C is the inner product of a row of A and a column of B, [25] encrypts each row/column of the matrix into a ciphertext in the SIMD environment. The number of rotations and homomorphic multiplications required are $mn\log l$ and mn, respectively.

By applying the encoding methods [20, 27] to an RLWE-based FHE scheme, [5] proposed a scheme that encodes a matrix into a constant polynomial in the plaintext space. This method requires only a single homomorphic multiplication operation. Subsequently, [19] proposed an improved scheme built upon this work. However, this approach results in meaningless terms in the resulting ciphertext. When performing more computations, decryption, and re-encoding procedure are required to remove these terms, resulting in limited performance in practical applications.

[16] proposed an efficient square matrix multiplication scheme, which exploits a row ordering encoding map to transform an $l\times l$ matrix as a vector of dimension $l^2$. This method requires O(l) rotations and homomorphic multiplication operations. Although [16] extends the square matrix multiplication to rectangular matrix multiplication $A_{m\times l}\times B_{l\times n}=C_{m\times n}$, it considers only the case where $m \mid l$ and $l=n$. By exploiting the idle slots of the ciphertext, [22] reduces the number of homomorphic multiplications of [16] to O(1). However, a disadvantage of this method is that it only works with very few available matrix entries.

The most relevant works [14, 17, 21], which are based on the Fox Matrix multiplication method [7], can be regarded as an extension of the diagonal-order method for solving matrix-vector multiplication [11]. Specifically, given two $l \times l$ square matrices A and B and a hypercube structure, the method first extracts the i-th diagonal of A, i.e., $A_i = \{a_{0,i},a_{1,i+1},...,a_{l-1,i+l-1}\}$ , where $i=\{0,1,...,l-1\}$. Then, $A_i$ is replicated along the row to get $\hat{A_i}$, and each column of B is rotated upward by i positions to get $B_i$, i.e., $B_i=\textsf {Rotate1D}(B,0,-i)$. The multiplication of A and B is obtained by $A\cdot B=\sum _{i=0}^{l-1}\hat{A_i} \odot B_i$. Below we give an example with $l=3$.

$$\begin{aligned} \begin{aligned} \left( \begin{matrix} a_{00}&{}a_{01}&{}a_{02}\\ a_{10}&{}a_{11}&{}a_{12}\\ a_{20}&{}a_{21}&{}a_{22} \end{matrix} \right) \cdot \left( \begin{matrix} b_{00}&{}b_{01}&{}b_{02}\\ b_{10}&{}b_{11}&{}b_{12}\\ b_{20}&{}b_{21}&{}b_{22} \end{matrix} \right) & = \left( \begin{matrix} a_{00}&{}a_{00}&{}a_{00}\\ a_{11}&{}a_{11}&{}a_{11}\\ a_{22}&{}a_{22}&{}a_{22} \end{matrix} \right) \odot \left( \begin{matrix} b_{00}&{}b_{01}&{}b_{02}\\ b_{10}&{}b_{11}&{}b_{12}\\ b_{20}&{}b_{21}&{}b_{22} \end{matrix} \right) \\ \oplus \left( \begin{matrix} a_{01}&{}a_{01}&{}a_{01}\\ a_{12}&{}a_{12}&{}a_{12}\\ a_{20}&{}a_{20}&{}a_{20} \end{matrix} \right) \odot \left( \begin{matrix} b_{10}&{}b_{11}&{}b_{12}\\ b_{20}&{}b_{21}&{}b_{22}\\ b_{00}&{}b_{01}&{}b_{02} \end{matrix} \right) & \oplus \left( \begin{matrix} a_{02}&{}a_{02}&{}a_{02}\\ a_{10}&{}a_{10}&{}a_{10}\\ a_{21}&{}a_{21}&{}a_{21} \end{matrix} \right) \odot \left( \begin{matrix} b_{20}&{}b_{21}&{}b_{22}\\ b_{00}&{}b_{01}&{}b_{02}\\ b_{10}&{}b_{11}&{}b_{12} \end{matrix} \right) . \end{aligned} \end{aligned}$$

[17, 21] use the above method to compute the secure square matrix multiplication, with the difference that the former packs each row of each matrix into a ciphertext with a linear array structure, while the latter packs the entire matrix into a ciphertext with a two-dimension hypercube structure. [14] extends the method to rectangular matrix multiplication. Although the replication procedure for calculating $\hat{A_{i}}$ can be implemented by CMult, Rotate1D and Add, this procedure requires high rotations and space complexities. Motivated by this, we revisit the secure matrix multiplication problem in this paper.

1.4 Our Contribution

We propose a novel scheme for square matrix multiplication of dimension l using the hypercube structure based on FHE. Compared to existing methods [14, 21], our scheme asymptotically reduces the number of rotations from $O(l\log l)$ to O(l). Moreover, we extend the square matrix multiplication to rectangular matrix multiplication. For matrix multiplication $A_{m\times l}\times B_{l\times n}=C_{m\times n}$ of arbitrary dimensions, our scheme requires only O(l) rotations and $\min (m,l,n)$ homomorphic multiplications, while [14] requires $O(l\log \max (l,n) )$ rotations and l homomorphic multiplications. The experimental results also demonstrate the superiority of our algorithms.

2 Secure Matrix Multiplication Scheme with FHE

For general matrix multiplication $A_{m\times l}\times B_{l\times n}=C_{m\times n}$, we discuss the following four cases and give different strategies for each: (1) $m=l=n$; (2) $l=\min \{m,l,n\}$; (3) $l=\text {median} \{m,l,n\}$; (4) $l=\max \{m,l,n\}$.

2.1 Square Matrix Multiplication

Suppose the input matrices are $A_{l \times l}$ and $B_{l \times l}$, we let the hypercube structure be an $l \times l$ matrix, then A and B can be put exactly into their hypercube structures. Based on the most efficient scheme [16], the following equality describes the square matrix multiplication using the hypercube structure for the case of $l=3$.

$$\begin{aligned} \begin{aligned} \left( \begin{matrix} a_{00}&{}a_{01}&{}a_{02}\\ a_{10}&{}a_{11}&{}a_{12}\\ a_{20}&{}a_{21}&{}a_{22} \end{matrix} \right) \cdot \left( \begin{matrix} b_{00}&{}b_{01}&{}b_{02}\\ b_{10}&{}b_{11}&{}b_{12}\\ b_{20}&{}b_{21}&{}b_{22} \end{matrix} \right) &= \left( \begin{matrix} a_{00}&{}a_{01}&{}a_{02}\\ a_{11}&{}a_{12}&{}a_{10}\\ a_{22}&{}a_{20}&{}a_{21} \end{matrix} \right) \odot \left( \begin{matrix} b_{00}&{}b_{11}&{}b_{22}\\ b_{10}&{}b_{21}&{}b_{02}\\ b_{20}&{}b_{01}&{}b_{12} \end{matrix} \right) \\ \oplus \left( \begin{matrix} a_{01}&{}a_{02}&{}a_{00}\\ a_{12}&{}a_{10}&{}a_{11}\\ a_{20}&{}a_{21}&{}a_{22} \end{matrix} \right) \odot \left( \begin{matrix} b_{10}&{}b_{21}&{}b_{02}\\ b_{20}&{}b_{01}&{}b_{12}\\ b_{00}&{}b_{11}&{}b_{22} \end{matrix} \right) & \oplus \left( \begin{matrix} a_{02}&{}a_{00}&{}a_{01}\\ a_{10}&{}a_{11}&{}a_{12}\\ a_{21}&{}a_{22}&{}a_{20} \end{matrix} \right) \odot \left( \begin{matrix} b_{20}&{}b_{01}&{}b_{12}\\ b_{00}&{}b_{11}&{}b_{22}\\ b_{10}&{}b_{21}&{}b_{02} \end{matrix} \right) . \end{aligned} \end{aligned}$$

(1)

The homomorphic scheme is described as follows.

Step 1: Denote by ct.A and ct.B the two ciphertexts of input matrices A and B after being encrypted, respectively. This step obtains $ct.A_0$ by rotating the k-th row of ct.A by k positions, and obtains $ct.B_0$ by rotating the k-th column of ct.B by k positions $(k=\{0,1,...,l-1\})$.

Taking the calculation of $ct.A_0$ as an example, in round k, we first extract the k-th row of ct.A using the multiplication mask operation to get $ct.d_k$, and then rotate $ct.d_k$ by k positions per row. Finally, all $ct.d_k$ are summed by homomorphic addition to get $ct.A_0$. The calculation of $ct.A_0$ can be represented as

$$ct.A_0=\sum _{k}ct.d_k=\sum _{k} \textsf {Rotate1D} (U_k\odot ct.A, 1,-k),$$

where $k=\{0,1,...,l-1\}$, $U_k$ is an $l \times l$ plaintext matrix and is defined by

$$U_k[I][J]=\left\{ \begin{aligned} &1 \quad \text {If } I=k; \\ &0 \quad \text {otherwise.} \end{aligned} \right. .$$

For the convenience of later discussion, we propose a general algorithm in Algorithm 1. We denote by RotateAlign(ct.X, 1, l) the rotation of the k-th row of ct.X by $k \mod l$ positions, which can be achieved by Algorithm 1. Similarly, we use RotateAlign(ct.X, 0, l) to denote the rotation of the k-th column of ct.X by $k \mod l$ positions. The complexity of this step is about 2l additions, 2l constant multiplications, and 2l rotations.

For step 1, here is an example when $l = 3$. Let

then

By performing homomorphic addition on all $ct.d_k$, we get

In fact, RotateAlign requires only $O(\sqrt{l})$ rotations by utilizing the baby-step/giant-step approach (BSGS) [12]. If we select the good dimensions for the hypercube structure, Rotate1D(ct, d, k) applies one automorphism denoted by $\rho _{g_d}^k$. RotateAlign can be rewritten as $\sum _{k=0}^{l-1} U_k\rho _{g_d}^k(ct) = \sum _{i=0}^{h-1}\rho _{g_d}^{fi}\left[ \sum _{j=0}^{f-1}U'_{j+fi}\cdot \right.$ $\Bigl .\rho _{g_d}^j(ct)\Bigr ]$, where $h,f\approx \sqrt{l}$ and $U'_{j+fi}=\rho _{g_d}^{-fi}(U_{j+fi})=U_{j+fi}$. Then we compute $\rho _{g_d}^j(ct)$ only once during the inner loop for baby steps.

Step 2: There are l rounds in this step. In round i, where $i=\{0,1,...,l-1\}$, two rotations and a homomorphic multiplication operation are performed to calculate $\textsf {Rotate1D}(ct.A_0,1,-i)\odot \textsf {Rotate1D}(ct.B_1,0,-i)$. Then the results of these l rounds are summed by the homomorphic addition operation, i.e.,

$$\begin{aligned} ct.A \cdot ct.B=\sum _{i}\textsf {Rotate1D}(ct.A_0,1,-i)\odot \textsf {Rotate1D}(ct.B_0,0,-i). \end{aligned}$$

(2)

The complexity of this step is about l homomorphic multiplications, l additions, and 2l rotations. An example of step 2 is Eq. (1).

Actually, the above two steps with slight adjustments are also used heavily in the case of rectangular matrix multiplication. Therefore, for simplicity, we call the above two steps the fully homomorphic encryption matrix multiplication main procedure. Assuming that the input matrices are $A_{m\times l}$ and $B_{l\times n}$ and the hypercube structure is $D_0\times D_1$, we present FHE-MatMultMain $(ct.A,ct.B,m,l,n,D_0,D_1)$ in Algorithm 2, which implements step 1 and step 2. Table 1 summarizes the time complexity and depth of each step in Algorithm 2. When $m=l=n=D_0=D_1$, Algorithm 2 is the secure square matrix multiplication algorithm.

Table 1. Time Complexity and Depth of Algorithm 2

2.2 Rectangular Matrix Multiplication

Suppose the input matrices are $A_{m\times l}$ and $B_{l\times n}$, for different matrix dimensions we divide into three cases and give efficient schemes for each. Consider that for any matrix, we can transform it into a matrix whose two dimensions are both to the power of 2 by zero padding. The matrix size increases by up to 4 times after zero-padding. For the sake of simplicity, we assume that the dimensions m, l, and n are all to the power of 2.

Rectangular Matrix Multiplication with $\boldsymbol{l=\min \{m,l,n\}.}$ Let the hypercube structure be $m \times n$ in this case. Let $A_{m \times l}$ be put into the $m \times n$ hypercube structure by padding the right of A with zeros, and let the $B_{l\times n}$ be put into the $m \times n$ hypercube structure by padding the bottom of B with zeros. The homomorphic scheme is described as follows.

Step 1: This step replicates ct.A along the rows to get $ct.A_0$ and ct.B along the columns to get $ct.B_0$. Specifically, let the hypercube structure of a ciphertext ct.A be $D_0\times D_1$ and its dim-th dimension has $d_{dim}$ non-zero elements, where $dim=\{0,1\}$ and $d_{dim}\le D_{dim}$. We denote by Replicate1D$(ct, dim,d_{dim})$ the replicating of $d_{dim}$ non-zero elements to the whole hypercube structure along the dim-th dimension. We give a scheme description in Algorithm 3, which uses a “repeated doubling” method. Note that in line 3, $\log (D_{dim}/d_{dim}))$ is an integer since $D_i$ and $d_i$ are all to the power of 2. Since there are l non-zero elements in each row of ct.A, this step takes about $\log \frac{n}{l}$ rotations and additions to get $ct.A_0$. Similarly, this step takes about $\log \frac{m}{l}$ rotations and additions to get $ct.B_0$.

For step 1, here is an example when $m=4$, $l=2$, and $n=8$. Let A be a $4 \times 2$ matrix and B be a $2 \times 8$ matrix, then the hypercube structure is $4\times 8$, and

$$\begin{aligned} ct.A= \left( \begin{matrix} a_{00}&{}a_{01}&{}0&{}0&{}0&{}0&{}0&{}0\\ a_{10}&{}a_{11}&{}0&{}0&{}0&{}0&{}0&{}0\\ a_{20}&{}a_{21}&{}0&{}0&{}0&{}0&{}0&{}0\\ a_{30}&{}a_{31}&{}0&{}0&{}0&{}0&{}0&{}0 \end{matrix} \right) , ct.B= \left( \begin{matrix} b_{00}&{}b_{01}&{}b_{02}&{}b_{03}&{}b_{04}&{}b_{05}&{}b_{06}&{}b_{07}\\ b_{10}&{}b_{11}&{}b_{12}&{}b_{13}&{}b_{14}&{}b_{15}&{}b_{16}&{}b_{17}\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{matrix} \right) . \end{aligned}$$

(3)

Given ct.A and ct.B in Eq. (3), $ct.A_0$ and $ct.B_0$ are

(4)

Table 2. Time Complexity and Depth of Algorithm 4 ($l=\min \{m,l,n\}$)

Step 2: This step performs the FHE matrix multiplication main procedure with $ct.A_0$ and $ct.B_0$ as input, i.e., $ct.C\leftarrow$ FHE-MatMultMain $(ct.A_0,ct.B_0,m,l,n,m,n)$. The complexity of this step is about l homomorphic multiplications, 3l additions, 2l constant multiplications, and 2l rotations (see Table 1). For example, given $ct.A_0$ and $ct.B_0$ in Eq. (4), ct.C is obtained as

We describe the homomorphic matrix multiplication scheme with $l=\min \{m,l,n\}$ in Algorithm 4. Table 2 summarizes the time complexity and depth of each step in Algorithm 4.

Rectangular Matrix Multiplication with $\boldsymbol{l=\text {median}\{m,l,n\}.}$ In this case, if $m\ge l\ge n$, we let the hypercube structure be $m \times l$. Otherwise, if $n\ge l\ge m$, we let the hypercube structure be $l \times n$. For simplicity, we discuss the case of $m\ge l\ge n$ in detail, and the case of $n \ge l\ge m$ is similar.

For $m\ge l\ge n$, let $A_{m\times l}$ be put into the $m\times l$ hypercube structure, and let $B_{l \times n}$ be put into the $m\times l$ hypercube structure by padding the right and bottom of B with zeros. The homomorphic scheme is described as follows.

Step 1: This step first replicates ct.B along the rows to get $ct.d_0$, and then replicates $ct.d_0$ along the columns to get $ct.d_1$. The generation of $ct.d_0$ and $ct.d_1$ can be achieved by Algorithm 3. Since there are n non-zero elements in each row of ct.B, this step takes about $\log \frac{l}{n}$ additions and rotations to get $ct.d_0$. Similarly, this step takes about $\log \frac{m}{l}$ additions and rotations to get $ct.d_1$. For step 1, here is an example when $m=4$, $l=4$, and $n=2$. Let A be an $8 \times 4$ matrix and B be a $4 \times 2$ matrix, then the hypercube structure is $8\times 4$, and

(5)

Step 2: This step performs the FHE matrix multiplication main procedure with ct.A and $ct.d_1$ as input, i.e., $ct.C_0\leftarrow$ FHE-MatMultMain $(ct.A,ct.d_1,m,l,n,m,l)$. The complexity of this step is about n homomorphic multiplications, $2l+n$ additions, 2l constant multiplications, and $2l+2n$ rotations (see Table 1). For example, given ct.A and $ct.d_1$ in Equation (5), $ct.C_0$ is obtained as

(6)

Step 3: The $m\times l$ ciphertext $ct.C_0$ can be divided into $\frac{l}{n}$ column blocks, where each block has size $m\times n$. By rotation and homomorphic addition operations, this step adds all other column blocks to a column block by exploiting the “repeated doubling” method, and gets a ciphertext ct.C that encrypts the $m\times n$ matrix $C=AB$ in each column block. This step talks about $\log \frac{l}{n}$ rotations and $\log \frac{l}{n}$ additions to get ct.C. For example, given $ct.C_0$ in Eq. (6), ct.C is obtained as

which encrypts the $8\times 2$ matrix $C=AB$ in its first two columns.

For the convenience of later discussion, we give a general algorithm in Algorithm 5. Let the hypercube structure of a ciphertext ct be $D_0\times D_1$, which can be viewed as $\frac{D_1}{d_1}$ matrice blocks of size $D_0\times \frac{D_1}{d_1}$ ($D_1\ge d_1$ and $d_1\mid D_1$ ). We denote by Sum1D$(ct, 1,d_1)$ the summation of these $\frac{D_1}{d_1}$ matrices along the rows. Similarly, we denote by Sum1D$(ct, 0,d_0)$ the summation of $\frac{D_0}{d_0}$ matrices with size $\frac{D_0}{d_0}\times D_1$ along the columns. The summation can be achieved by Algorithm 5

Table 3. Time Complexity and Depth of Algorithm 6 ($m\ge l\ge n$)

From the above description, we give the homomorphic matrix multiplication algorithm with $m\ge l \ge n$ in Algorithm 6. Table 3 summarizes the time complexity and depth of each step in Algorithm 6.

Rectangular Matrix Multiplication with $\boldsymbol{l=\max \{m,l,n\}.}$ In this case, let the hypercube structure be $l \times l$, a natural scheme is to transform it into a square matrix multiplication by zero padding, and then call Algorithm 2. From Table 1, the homomorphic multiplication of this scheme is $l=\max \{m,l,n\}$.

We give an improved scheme, which requires only $\min \{m,l,n\}$ homomorphic multiplications. We discuss in detail the case of $l\ge m\ge n$ below, and the case of $l \ge n\ge m$ is similar.

Step 1: This step replicates ct.A along the columns to get $ct.A_0$, and replicates ct.B along the rows to get $ct.B_0$. Since there are m non-zero elements in each column of ct.A, this step takes about $\log \frac{l}{m}$ rotations and additions to get $ct.A_0$. Similarly, this step takes about $\log \frac{l}{n}$ rotations and additions to get $ct.B_0$. For step 1, here is an example when $m=2$, $l=4$, and $n=1$. Let A be a $2 \times 4$ matrix and B be a $4 \times 1$ matrix, then the hypercube structure is $4\times 4$, and

(7)

Step 2: This step performs the FHE matrix multiplication main procedure with $ct.A_0$ and $ct.B_0$ as input, i.e., $ct.C_0\leftarrow$ FHE-MatMultMain $(ct.A_0,ct.B_0,m,l,n,l,l)$. The complexity of this step is about n homomorphic multiplications, $2l+n$ additions, 2l constant multiplications, and $2l+2n$ rotations (see Table 1). For example, given $ct.A_0$ and $ct.B_0$ in Eq. (7), $ct.C_0$ is obtained as

(8)

Table 4. Time Complexity and Depth of Algorithm 7 ($l\ge m\ge n$)

Step 3: The $l\times l$ ciphertext $ct.C_0$ is divided into $\frac{l}{n}$ matrices by column where each matrix has size $l\times n$. This step gets ct.C by summing these $\frac{l}{n}$ blocks along the rows, which can be achieved by Algorithm 5. The complexity of this step is about $\log \frac{l}{n}$ additions and $\log \frac{l}{n}$ rotations. For example, given $ct.C_0$ in Eq. (8), by Algorithm 5,

which encrypts the $2\times 1$ matrix $C=AB$ in its first two rows and first column.

We describe the scheme in Algorithm 7. Table 4 summarizes the time complexity and depth of each step in Algorithm 7.

3 Complexity Analysis

In this section, we give a comparison of the complexity between our algorithm and the state-of-the-art algorithms [14, 16, 21]. Note that [16, 21] deal mainly with secure square matrix multiplication. For rectangular matrix multiplication, a trivial method is to transform rectangular matrices into square matrices by zero padding and then solve the problem using the existing method. Suppose the input matrices are $A_{m\times l}$ and $B_{l\times n}$, we denote by $k_1=\max \{m,l,n\}$, $k_2=\text {median}\{m,l,n\}$, $k_3=\min \{m,l,n\}$, and $t=\max \{l,n\}$. Table 5 summarizes the complexities of existing methods and our scheme. It can be found that in all cases, the number of Mult of our method is the lowest, as $k_3=\min \{m,l,n\}$. Compared to [14, 21], the Rot of our method is asymptotically reduced by $\frac{k_1\log k_1}{l}$ and $\log t$ times, respectively.

Table 5. Complexity comparison between our method and existing methods

4 Experimental Evaluation

4.1 Experimental Setup

Our experiments were conducted on a machine equipped with an Intel(R) Xeon(R) Platinum 8475B@2.5 GHz(16 Cores), accompanied by 128 GB of memory. The machine is operated on Ubuntu 22.04.2. Our implementation of secure matrix computation was built upon the foundation provided by the BGV scheme in HElib, and the code was compiled using g++ version 11.3.0. We utilized the openMP library to implement a multi-threaded version, and the number of threads in the implementation is up to 32.

For any given matrix dimensions, we compare the running time of our method with [14, 21]. Both methods are implemented using HElib and perform better than [16]. Since [21] is a secure square matrix multiplication method, we adopt the zero padding strategy utilized in [14] for rectangular matrices. For the choice of parameters p, M and $(m_0,m_1)$, we follow the method of [21], where p is the plaintext modulus, M defines the M-th cyclotomic polynomial, $(m_0,m_1)$ is the actual dimensions of the hypercube structure. Based on the conditions specified in [21]: (1) $M=k\cdot m_0\cdot m_1+1$; (2) $k, m_0$ and $m_1$ are pairwise coprime; (3) ord$(p)=k$. We can find two generators $g_1$ and $g_2$ with orders $m_0$ and $m_1$ in $\mathbb {Z}_M^*$ such that $\mathbb {Z}_M^*/\langle p\rangle =\langle g_0,g_1 \rangle$. Thus we achieve a hypercube with two good dimensions $m_0$ and $m_1$. More details can be found in [21]. The Appendix A.1 contains a discussion of implementation challenges and their corresponding solutions arising from choosing good dimensions.

The selection of other parameters in HElib maintains the default, except for setting $\textsf {bits}=600$ for the minimal bit length of the ciphertext modulus and $H=120$ for the Hamming weight of the secret key. The value of H differs from the experiments of other work(i.e., 64) in order to meet the minimum requirements of the latest HElib version. For all the experiments, these settings ensure a minimum security level of 80 bits. (We remark that the assessment of the security level in HElib is more stringent and distinct from the homomorphic encryption standard. It encompasses not only considerations related to polynomial degrees and ciphertext modulus.)

Fig. 2.

The running time (s) of [14, 21], our method and speedup ([14] vs. our method).

4.2 Results and Analysis

We compare the performance of our method with existing methods in Fig. 2. It can be found that for all cases, the execution time (MatMult) of our algorithm is the lowest. In the case of square matrix multiplication, [14, 21] have equal MatMult time, and our method has the best performance because it requires $O(\log l)$ times fewer rotations (see Table 5). For the same reason, we have a higher speedup as the matrix dimension increases. In the case of rectangular matrix multiplication, the MatMult time of [14, 21] and our method are positively correlated with $\max (m,l,n)$, l and $\min (m,l,n)$, respectively. This is because different methods require different numbers of Mult (see Table 5). Since our method requires $l/\min (m,l,n)$ times fewer homomorphic multiplications, when $l/\min (m,l,n)$ is maximum $((m,l,n)=(16,128,4))$, we can achieve the highest speedup, up to 18X.

Fig. 3.

Operating-level runtime breakdown (%).

Figure 3 shows the runtime breakdown at the operational level. The analysis reveals that a significant portion of the runtime in [14, 21] is dedicated to rotation operations. Due to 2 times more CMult operations than the other methods, the percentage of CMult runtime is greater in our method. We also provide noise testing and analysis, interested readers can refer to Appendix A.3.

In addition to the single-threaded implementation shown in Fig. 2, we also utilize multi-threaded (MT) to implement our method in parallel. We mainly parallelize the most time-consuming rotations in RotateAlign, and the degree of parallelism is at most l. Therefore, when the number of threads is greater than l, the increase in the number of threads does not further reduce the running time of MatMult. When the number of threads is less than l, the running time of MatMult decreases almost linearly with the number of threads, which means that our method has high scalability (Fig. 4).

Fig. 4.

Multi-threaded runtime of our method.

5 Conclusion

In this work, we propose an efficient secure matrix multiplication of arbitrary dimensions based on BGV fully homomorphic encryption scheme. This method leverages the plaintext slots of the hypercube structure and special homomorphic operations on them. We conducted extensive microbenchmark tests, employing parameters closely aligned with real-world applications. The results demonstrated significant performance enhancements when compared to the state-of-the-art methods.

It is worth noting that applications built upon the hypercube structure not only encompass one-dimensional linear structures but also hold potential for further optimization at the algorithmic complexity level. When our proposed algorithm serves as a building block in a larger secure computation, temporarily adjusting parameters is infeasible. It demonstrates scalability on par with one-dimensional linear structures, coupled with additional options. For instance, in situations where there are many non-data dependent matrix multiplications, and the parameters allow encoding multiple matrices at once, the algorithm can be easily adapted to enable single-ciphertext multi-matrix computations. In situations where only one single small matrix multiplication is involved, the extended version can be used to achieve slight performance improvements. Furthermore, due to the characteristics of hypercube encoding, such an adaptation simplifies the implementation of general homomorphic linear transformation with fewer homomorphic operations, leading to asymptotic reductions in computationally expensive homomorphic operations such as homomorphic multiplication and rotation throughout the entire application. Consequently, we posit that this work can serve as a valuable source of inspiration for subsequent work utilizing hypercube structure packing techniques.

In our future work, we aim to expand the algorithm’s capabilities to handle considerably large matrices, thereby facilitating its utility in big data privacy applications that involve massive datasets as inputs.

A Appendix

1.1 A.1 Practical Implementation Issues and Solutions

Choosing the good dimensions in the hypercube can minimize the overhead of a Rotation1D. Therefore, for performance reasons, the implementation always prioritizes the hypercube with good dimensions. However, to meet this requirement, the actual hypercube size chosen is usually larger than the expected minimum size. For example, when using Algorithm 2 to calculate a $3\times 3$ square matrix multiplication, the expected hypercube size is $3\times 3$, while the actual size that fulfills the requirement is $3\times 4$ (refer to the first matrix in Fig. 5a). Calling RotateAlign directly becomes incorrect due to the presence of redundant columns. By observing the terminal error state(i.e., the second matrix in Fig. 5a), it becomes apparent that the correction can be performed in a single step, utilizing 2 CMult, 1 Rotate1D, and 1 Add(see the changes brought by the first arrow in Fig. 5b). Subsequent operations of Rotate1D can also be corrected by employing an additional CMult and Add, as illustrated in Fig. 5b. These corrections only introduce a few constant operations.

Fig. 5.

An overview of the error in raw RotateAlign and the modified algorithms addressing the issue in subsequent steps.

One alternative is to expand the dimensions of the hypercube, although this may not always be feasible. Specifically, we can set the expected value of $m_1$ to $3m^*_1-2$($m^*_1$ denotes the minimum number of columns required in the aforementioned algorithm), thereby ensuring the correctness of all subsequent steps without requiring the correction steps shown in Fig. 5b. Figure 6 depicts the state of the extended version after performing a raw RotateAlign. All the columns required for subsequent steps have been prepared. This extension may seem to degrade performance due to an increase in M. However, the constraints of k, $m_0$, and $m_1$ as mentioned in Sect. 4.1, allow for generating similar values of M when the expected size is selected as $(m^*_0, 3m^*_1-2)$ or $(m^*_0, m^*_1)$. More details and suggestions for leveraging the extended version can be found in Appendix A.2.

Fig. 6.

Modified algorithm in the extended version.

1.2 A.2 Speedup of Extended and Non-extended Versions

In practical implementations, a minimum value for M is typically set to meet security requirements. This leads to selecting p of ord(p) is large when the matrix dimension is small. When ord$(p)\ge 3$, switching to an extended version provides the opportunity to fully utilize the potential of generating a larger hypercube structure with a large M, thereby achieving a certain degree of performance improvement. The performance comparison results and parameter sets $\mathcal {P}_1$ and $\mathcal {P}_2$ for the two scenarios are shown in Table 6. The extended version achieved $3.1\times$ speedup compared to [21] when the dimension is 64. The slight improvement over the non-extended version indicates that the correction steps have a limited impact. Considering the potential performance improvement, it is applicable in real-world applications to generate parameters using two different expected hypercube sizes: $(m^*_0, m^*_1)$ and $(m^*_0, 3m^*_1 - 2)$. If the value of M generated by the extended version parameter setting is similar to that of the non-extended version, the extended version can offer performance benefits.

Table 6. Performance(seconds) of homomorphic square matrix multiplication and speedup $\mathcal {S}$( [21] and non-extended version vs. extended version). The parameter sets $\mathcal {P}_1$ and $\mathcal {P}_2$ correspond to $(m_0, m_1, \text {ord}(p))$ and M for the non-extended and extended versions, respectively.

1.3 A.3 Noise Testing and Analysis

The experiments originally aimed to test larger matrix dimensions, such as a hypercube size exceeding $256\times 256$. However, when maintaining the aforementioned parameter settings, [21] encountered decryption failures due to excessive noise. Consequently, we examined how the noise varied with the increase in matrix dimensions for different methods. In HElib, the logarithm of the ratio of the modulus to the noise bound is referred to as capacity. Here, we use noise to represent the difference between the initial capacity and the remaining capacity. The breakdown of the initial capacity is illustrated in Fig. 7, with the shaded part representing the noise generated by evaluation and the light part representing the remaining capacity. While [11] asserts that Rot introduces less noise than Mult and CMult, the depth of Rot also significantly contributes to noise growth, particularly in the case of the prominently dominant Rot illustrated in Fig. 3. Compared to [21], our method increases Add but heavily decreases Rot, resulting in slower growth of noise with increasing matrix dimension.

Fig. 7.

Noise generation volume. The bottom (shaded) part represents generated noise, while the top (light) part represents the remaining capacity.