GMS: an efficient fully homomorphic encryption scheme for secure outsourced matrix multiplication

Abstract

Fully homomorphic encryption (FHE) is capable of handling sensitive encrypted data in untrusted computing environments. The efficient application of FHE schemes in secure outsourced computation can effectively address security and privacy concerns. This paper presents a novel fully homomorphic encryption scheme called GMS, based on the n-secret learning with errors (LWE) assumption. By utilizing block matrix and decomposition technology, GMS achieves shorter encryption and decryption times and smaller ciphertext sizes compared to existing FHE schemes. For secure outsourced matrix multiplication ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}$ with arbitrary dimensions, GMS only requires $O(\max \{m,n,l\})$ rotations and one homomorphic multiplication. Compared to the state-of-the-art methods, our approach stands out by achieving a significant reduction in the number of rotations by a factor of $O(\log \max \{n, l\})$, along with a decrease in the number of homomorphic multiplications by a factor of n and $O(\min \{m, n, l\})$. The experimental results demonstrate that GMS shows superior performance for secure outsourced matrix multiplication of any dimension. For example, when encrypting a $64\times 64$-dimensional matrix, the size of the ciphertext is only 1.27 MB. The encryption and decryption process takes approximately 0.2 s. For matrix multiplication ${\textbf {A}}_{64\times 64}\cdot {\textbf {B}}_{64\times 64}$, the runtime of our method is 39.98 s, achieving a speedup of up to 5X and 2X.

1 Introduction

Cloud computing technology provides clients with instant access to shared storage and computing resources, reducing investment and IT system maintenance costs. The rapid development of cloud computing has led to the widespread use of cloud outsourcing. This allows clients with limited computing resources to delegate intensive and complex computing tasks to high-performance cloud servers. However, the rapid development of cloud computing still faces several challenges:

• (1) Data privacy: Data outsourced by clients to cloud servers is typically confidential, such as medical or trade secret information. It is important to ensure that this data is kept secure and protected from unauthorized access. The shared characteristics of cloud servers can potentially expose private data, making it difficult to ensure privacy during outsourced computation.

• (2) Efficiency: Outsourced computation currently employs privacy protection technology to ensure the confidentiality of data. Incorporating privacy protection directly, however, can result in significant costs. Therefore, clients require an efficient process for outsourced computational tasks while still ensuring privacy.

Privacy protection technologies, such as fully homomorphic encryption (FHE), secure multi-party computing (MPC) [1], and disguise-based techniques [2], are commonly used to ensure data privacy in secure outsourced computation. It is important to note that while these technologies provide enhanced privacy, they may also impact performance. Secure multi-party computing is a general framework for such tasks, but it can result in high communication overhead and require multiple rounds of interaction between the client and the cloud server. The process of secure outsourced computation based on MPC may not be very efficient. The disguise-based technique utilizes the unique properties of matrices to create a specialized protocol for secure matrix multiplication. However, the representation of security symbols in various protocols is not standardized, which can potentially lead to information leakage. The flaw in the current disguise-based secure outsourced computation poses a significant threat to data privacy. However, achieving composability has not been possible with this technique. On the other hand, secure outsourced computation based on FHE is non-interactive and incurs a very low communication cost for uploading and downloading. Furthermore, secure outsourced computation based on FHE relies on encryption and decryption techniques from cryptography. This approach ensures data privacy, prevents information disclosure, and enables data composability. As a result, secure outsourced computation based on fully homomorphic encryption technology offers significant advantages and is widely used.

Most scholars focus on secure outsourced computation for matrix multiplication. Matrix multiplication is a widely used operation in scientific and engineering fields, such as statistical analysis, image processing, and machine learning. It can solve many practical problems. For instance, the training and prediction process of deep learning models can be simplified to a series of fundamental matrix operations. Additionally, an image can be represented and stored as a matrix based on its pixel characteristics, and the image processing process can be transformed into a matrix operation process. Efficient and secure outsourced computation for matrix multiplication is crucial for secure computation applications. However, the current fully homomorphic encryption scheme used to secure outsourced matrix multiplication has limitations. It usually involves a packaging process [3,4,5] that matches the data type of the plaintext. Additionally, it is restricted to applications involving binary matrices [6]. These limitations present challenges. Therefore, designing and implementing an efficient and secure outsourced matrix multiplication based on fully homomorphic encryption technology has become an important research problem.

1.1 Related work

Currently, secure outsourced matrix multiplication based on fully homomorphic encryption is typically implemented using existing schemes. This section provides an introduction to fully homomorphic encryption techniques, as well as a discussion of the advantages and limitations of current research on secure outsourced matrix multiplication using fully homomorphic encryption.

1.1.1 Fully homomorphic encryption

Fully homomorphic encryption allows computations on the ciphertext without requiring knowledge of the private key, making it an important tool for privacy protection. Most existing fully homomorphic encryption schemes are based on the AGCD assumption [7], the LWE assumption [8] and the NTRU assumption [9]. Fully homomorphic encryption based on the AGCD assumption revolves around integer encryption. This is considered to be the first generation of fully homomorphic encryption. It is easy to understand but requires a large public key and has low efficiency. The NTRU assumption is a non-standard assumption, and many researchers have questioned its security. The work of L$\acute{o}$peze-Alt et al. [9] has received considerable criticism in recent years. Fully homomorphic encryption based on the NTRU assumption is primarily used in application scenarios with low security requirements. A significant number of existing fully homomorphic encryption schemes are based on the learning with errors (LWE) assumption, first proposed by Regev in 2009 [8]. In 2010, Regev elaborated on the hardness of the LWE problem, which can be reduced to a worst-case hard problem [10]. Since there is currently no effective quantum solution algorithm for the LWE assumption, the encryption scheme based on the LWE assumption is considered to be resistant to quantum attacks. For example, the second generation of fully homomorphic encryption BGV [11], the third generation of fully homomorphic encryption GSW [12], and the fourth generation of fully homomorphic encryption CKKS [13], among others, are all based on the LWE assumption. The following discussion primarily focuses on the fully homomorphic encryption scheme based on the LWE assumption.

The second generation of the fully homomorphic encryption scheme BGV [11] operates on the integer polynomial ring. It cleverly utilizes modulus switching and key switching to achieve ciphertext refreshing, opening up new avenues for research in fully homomorphic encryption. Examples of other fully homomorphic encryption schemes include TFHE [14] and CKKS [13]. However, BGV has higher parameter requirements, necessitating a larger module and storage space. The fourth generation of the fully homomorphic encryption scheme CKKS [13] is a significant improvement over BGV [11]. It introduces an encoding and decoding process that allows the plaintext space to be expanded into a complex vector space. This enhancement allows the scheme to support floating-point arithmetic. The third generation of the fully homomorphic encryption scheme GSW [12] is ingenious. It exploits the properties of the eigenvalues and eigenvectors of the matrix and uses matrix decomposition to control noise expansion. As a result, the matrix decomposition technique has found widespread applications. These applications, which include schemes such as [6, 15,16,17,18], are often referred to as GSW-like schemes. These schemes primarily involve fully homomorphic encryption for matrices. HAO [6] is the first homomorphic encryption scheme for matrix that effectively controls ciphertext expansion. However, it can only encrypt plaintext for square matrices with elements in $\{0,1\},$ which has limitations. GGH [17] is a proposed scheme based on HAO [6]. GGH [17] can encrypt square matrices without the restriction of $\{0,1\},$ offering greater efficiency and versatility. However, since matrix multiplication does not satisfy the commutative property, the encryption process also requires the private key, essentially making it a form of symmetric encryption. It is necessary to introduce the encryption of fundamental matrices as public keys to convert it into an asymmetric encryption scheme. Subsequently, Pereira also proposed a GSW-like scheme [18], which can encrypt vectors and matrices and modify the base matrix decomposition. This scheme demonstrates relatively high efficiency. However, it still requires the introduction of $n^{2}$ base matrix encryption as public keys to achieve asymmetric encryption.

It can be seen that the existing fully homomorphic encryption schemes cannot be easily and directly applied to secure outsourced matrix multiplication. For BGV [11], TFHE [14], CKKS [13], and other fully homomorphic encryption schemes over the integer polynomial ring, the plaintext is typically represented in polynomial form. Implementing secure outsourced matrix multiplication requires packaging the matrix according to the plaintext format. There will undoubtedly be additional overhead. For GGH [17] and other fully homomorphic encryption schemes for matrices, they are inherently symmetric. This means that there are private keys involved in the encryption process that cannot be disclosed. To achieve secure matrix multiplication, it is necessary to introduce several basic matrix encryptions as public keys. However, this approach naturally leads to larger key sizes and storage requirements, which reduces efficiency. Therefore, if the fully homomorphic encryption scheme for matrices is asymmetric, then FHE-based secure outsourced matrix multiplication can eliminate the need for packaging different data types or introducing the encrypted matrix result as a public key. This can potentially lead to increased efficiency.

1.1.2 FHE-based secure outsourced matrix multiplication

Most of the existing secure outsourced matrix multiplication methods are based on fully homomorphic encryption and disguise-based technology, each of which has its own advantages. However, there are still several shortcomings in these approaches. We classify them according to the technology used. Table 1 presents the following details about the scheme: whether it supports arbitrary matrices, whether it is composable, the number of ciphertexts corresponding to a matrix ($\#$Ciphertext), the number of homomorphic multiplications in secure outsourced matrix multiplication ($\#$Multiplication), and the security level of the scheme. See Table 1 for more details, where n presents the dimension of matrix.

Table 1 Properties of each method

It is clear from Table 1 that the current disguise-based secure outsourced matrix multiplication generally has a low level of security. Even the only security measure that achieves CPA security [2] carries the risk of information leakage due to the use of security symbols. Performing secure outsourced matrix multiplication using fully homomorphic encryption is clearly the superior option. Then, we will introduce secure outsourced matrix multiplication based on fully homomorphic encryption in detail. In addition, we will review the existing work based on its utilization of the fully homomorphic encryption scheme.

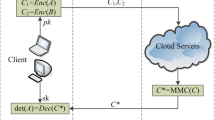
The concept of secure outsourced matrix multiplication based on fully homomorphic encryption originates from the secure matrix–vector multiplication proposed by Halevi et al. [22]. The implementation process of secure outsourced matrix multiplication based on fully homomorphic encryption is introduced in detail in [3, 25, 26] and other literature, making it a gradually emerging research topic. The specific process of secure outsourced matrix multiplication based on fully homomorphic encryption can be described by Fig. 1. Users P1 and P2 have matrices ${\textbf {A}}$ and ${\textbf {B}},$, respectively, and do not want anyone to know about them. User P3 needs to obtain the product ${\textbf {A}}\cdot {\textbf {B}}$ without knowing the matrices ${\textbf {A}}$ and ${\textbf {B}}.$ This can be achieved by implementing fully homomorphic encryption.

• Users P1 and P2 encrypt their respective matrices and upload the encrypted ciphertext to the cloud server.

• The cloud server performs homomorphic multiplication on the ciphertext as required and sends the result to user P3.

• User P3 receives the result and decrypts it to obtain ${\textbf {A}}\cdot {\textbf {B}}.$

Fig. 1

FHE-based secure outsourced matrix multiplication

Only [6] extended the existing fully homomorphic encryption scheme to achieve secure matrix multiplication. Hirmasa et al. [6] developed a GSW-like homomorphic encryption scheme for matrices. In this scheme, each matrix only requires one ciphertext to represent it, and each secure matrix multiplication corresponds to a homomorphic multiplication. The computational and storage overhead of this method is smaller, but it only applies to the case of a binary square matrix, specifically ${\textbf {A}}_{n\times n}\cdot {\textbf {B}}_{n\times n},$ where each component is either 0 or 1. There are limits to its practical application.

Halevi et al. [22] used the BGV fully homomorphic encryption to introduce the first secure matrix–vector multiplication, represented as ${{\varvec{w}}}={\textbf {A}}_{n\times n}\cdot {{\varvec{v}}},$ where ${{\varvec{v}}}$ and ${{\varvec{w}}}$ are vectors, and ${\textbf {A}}_{n\times n}$ is a matrix. However, its efficiency is not high because each matrix requires n ciphertexts to represent it, and a secure matrix multiplication requires $n^{2}$ homomorphic multiplication operations. Lu et al. [23] and Wang et al. [24] used the BGV scheme to extend secure matrix–vector multiplication to secure matrix–matrix multiplication based on row order and column order, respectively. However, a matrix still requires n ciphertexts to represent it, and a secure matrix multiplication corresponds to $n^{2}$ homomorphic multiplication operations; therefore, the efficiency is still not high. Duong et al. [3] and Lu et al. [25] combined matrix coding with the BGV scheme. In this approach, only one ciphertext is needed to represent a matrix, which reduces the storage cost. However, a disadvantage is that the result of secure multiplication does not match the encrypted format of the matrix. Therefore, the result obtained can only be decoded and output; it cannot be used for the next multiplication. This limitation hinders its practicality in terms of composability. Jiang et al. [26] combined the coding technique with CKKS/BGV fully homomorphic encryption, enabling each matrix to be represented by a single ciphertext. A secure matrix multiplication corresponds to only one homomorphic multiplication operation. The square matrix multiplication can be extended to a special form of matrix multiplication, namely ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times n},$ where $m\le n.$ Huang et al. [4] and Zhu et al. [5] are new studies that propose a secure outsourced matrix multiplication scheme for rectangular matrices, i.e., ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l},$ which has a wider range of applications. Huang’s work [4] can be accomplished by utilizing the CKKS/BGV scheme. Zhu et al. [5] have made further improvements building on the work of Huang et al. [4], which reduces the number of rotation operations and homomorphic multiplications using a novel approach. Their research aims to minimize matrix multiplication time by using the BGV scheme supported by the HElib library, which is distinguished by achieving a significant reduction in the number of rotations by a factor of $O(\log \max \{n,l\}),$ as well as a decrease in the number of homomorphic multiplications by a factor of $O(n/ \min \{m,n,l\}).$ However, the method still requires n homomorphic multiplications for each secure matrix multiplication, and the matrix must be converted into polynomials through encoding. This introduces additional overhead.

To summarize, supporting BGV, CKKS, and other fully homomorphic encryption schemes for polynomials requires encoding and packaging, which inevitably leads to additional overhead. Additionally, there is no efficient fully homomorphic encryption scheme directly available for arbitrary matrices. Therefore, designing an efficient fully homomorphic encryption scheme for arbitrary matrices can reduce the necessity for extra processing steps, like encoding and packaging. This would simplify the representation of a matrix with only one ciphertext, enable secure outsourced matrix multiplication using just one homomorphic multiplication, and ensure that the ciphertext possesses desirable properties, such as composability. Our focus is on designing efficient fully homomorphic encryption for arbitrary matrices. These improvements will undoubtedly enhance the efficiency of secure outsourced matrix multiplication based on this scheme.

1.2 Technical details and our contribution

We start by explaining the symbols and their meanings. We denote matrices using bold capital letters. For a positive integer q, the set $\mathbb {Z}_q$ is defined as $\{0,1,\ldots ,q-1\}.$ It is evident that $\mathbb {Z}_q$ forms a ring under addition and multiplication modulo q. The integer operation $\lfloor z \rceil$ is used to find the integer closest to z that satisfies $\left\lfloor z \right\rceil \in \left( z-\frac{1}{2},z+\frac{1}{2}\right] .$ The specific formula for the modular operation is $z\bmod q=z-q\left\lfloor \frac{z}{q}\right\rceil.$ For a matrix ${\textbf {Y}}=\left( y_{ij}\right) ,$ where $y_{ij}$ is the component in the ith row and jth column of the matrix ${\textbf {Y}},$ the modulo operation can be expressed as ${\textbf {Y}}\bmod q=\left( y_{ij}\bmod q\right) ,$ which calculates the modulus of each component of the matrix. The general overview and core techniques of our scheme are shown in Fig. 2.

Fig. 2

Technical overview diagram

We construct a fully homomorphic encryption scheme for matrices based on the n-secret LWE assumption and name it GMS. The n-secret LWE assumption can be expressed as ${\textbf {B}}=\left( {\textbf {A}} {\textbf {S}}_{1}+{\textbf {E}}\right) \bmod q.$ Here, ${\textbf {A}}\in \mathbb {Z}_q^{n\times m},$ ${\textbf {B}}\in \mathbb {Z}_q^{n\times n},$ and ${\textbf {E}}\in \mathbb {Z}_q^{n\times n}.$ Each component of ${\textbf {E}}$ is sampled from a discrete Gaussian distribution (error distribution) $\chi .$ To simplify the notation, we introduce several block matrices: ${\textbf {D}}=\left( \alpha {\textbf {B}}|{\textbf {A}}\right) \in \mathbb {Z}_{q}^{n\times (n+m)},$ ${\textbf {V}}=\left( {\textbf {I}}_{n}|{\textbf {O}}_{n\times m}\right) \in \mathbb {Z}_{q}^{n\times (n+m)},$ ${\textbf {S}}=\left( \begin{array}{c}{\beta {\textbf {I}}_n} \\ {-t{\textbf {S}}_{1}} \end{array}\right) \in \mathbb {Z}_q^{(n+m)\times n},$ and ${\textbf {T}}=\left( \begin{array}{c}{{\textbf {I}}_n} \\ {-{\textbf {T}}_{1}} \end{array}\right) \in \mathbb {Z}_q^{(n+m)\times n},$ where $\alpha ,\beta$ and $t=\alpha \beta$ are all small integers. Note that ${\textbf {S}}_{1}$ and ${\textbf {T}}_{1}$ are smaller matrices with a reduced matrix norm. We utilize the non-unique inverse property of the block matrix ${\textbf {V}}$ to illustrate the asymmetry of the scheme. This implies that disclosing the matrix ${\textbf {V}}$ does not jeopardize the security of the scheme. The matrix decomposition function $G^{-1}(\cdot ),$ which follows a sub-Gaussian distribution, is introduced in the scheme to reduce the matrix norm and effectively control the increase of noise. The encryption process is defined as ${\textbf {C}}=\left( {\textbf {GTMV}}+{\textbf {RD}}\right) \bmod q,$ where the gadget matrix ${\textbf {G}}$ is commonly used for matrix decomposition, such as ${\textbf {G}}={{\varvec{g}}}\otimes {\textbf {I}}_{n+m}.$ The decryption process is defined as ${\textbf {M}}=\left( {\textbf {G}}^{-1}\left( \eta {\textbf {V}}\right) {\textbf {CS}}\bmod q\right) \bmod t,$ which involves a private key ${\textbf {S}}$ that satisfies ${\textbf {DS}}=t{\textbf {E}}$ and ${\textbf {VS}}=\beta {\textbf {I}}_{n},$ simplifying the decryption process. Matrix decomposition is also introduced in homomorphic operations to reduce noise amplification. Homomorphic addition is defined as ${\textbf {C}}_{add}=\left( {\textbf {C}}_{1}+{\textbf {C}}_{2}\right) \bmod q,$ and homomorphic multiplication is defined as ${\textbf {C}}_{mul}=G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {C}}_{2}\bmod q.$ Additionally, for homomorphic multiplication, the rotation operation of ciphertext matrices is introduced to further enhance the efficiency of homomorphic multiplication. In addition, modulus switching and key switching techniques are defined to facilitate the process of refreshing the ciphertext and the increase in noise can be effectively controlled.

Due to the block matrix and decomposition technology utilized in the scheme design, GMS can achieve a smaller ciphertext size and lower noise expansion, resulting in shorter encryption, decryption, and evaluation times compared to existing FHE schemes. GMS can be extended directly to achieve secure outsourced matrix multiplication for arbitrary matrices by populating the matrix. Since GMS is an asymmetric encryption method for matrices, secure matrix multiplication using GMS can be implemented without the need for additional packaging or encoding. This simplifies the process and enhances efficiency.

On this basis, we are considering implementing secure outsourced matrix multiplication using GMS. We will analyze the efficiency and performance of the scheme from two perspectives: theoretical analysis and simulation experiments. The theoretical analysis primarily compared the time complexity of our scheme with existing works, while the simulation experiment tested the efficiency and performance of the scheme using C++. Specifically, we used the HElib library [22] in C++ to implement the scheme. We then ran the program on a personal laptop equipped with an 11th generation Intel(R) Core(TM) i5-11260 H CPU running at a frequency of 2.60GHz. Encryption and decryption time, ciphertext size, and homomorphic multiplication time were tested. In addition, we implemented the security outsourced matrix multiplication using GMS and replicated the last two tasks [4, 5], analyzing the time taken for matrix multiplication. Compared to existing methods [4, 5], our scheme reduces the number of homomorphic multiplications required for a matrix multiplication from n to 1. We extend the square matrix multiplication to include rectangular matrix multiplication. From the perspective of time complexity, for the matrix multiplication ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}$ of arbitrary dimensions, our approach only requires $O(\max \{m,n,l\})$ rotations, whereas [4] requires $O(n \log \max \{n, l\})$ rotations. The experimental results also demonstrate the superiority of our method.

2 Preliminaries

All matrices in this paper are defined over $\mathbb {Z}_q,$ and the symbol $\left\| \cdot \right\|$ is consistently used to represent the maximum norm of a matrix. The norm $\left\| \textbf{Y} \right\|$ refers to the maximum norm of the matrix ${\textbf {Y}},$ which is defined as $\left\| \textbf{Y} \right\| =\max _{i,j} \{|y_{i,j}|\}.$ Here, $y_{ij}$ represents the component of the matrix ${\textbf {Y}}$ at the ith row and jth column position. The addition norm and multiplication norm of the matrices ${\textbf {Y}}$ and ${\textbf {W}}$ satisfy the following inequalities: $\left\| {{\textbf {Y}}+{\textbf {W}}} \right\| \le \left\| {{\textbf {Y}}} \right\| +\left\| {{\textbf {W}}} \right\|$ and $\left\| {{\textbf {Y}}\cdot {\textbf {W}}} \right\| \le n\left\| {{\textbf {Y}}} \right\| \cdot \left\| {{\textbf {W}}} \right\|$. Here, n represents the number of columns in matrix ${\textbf {Y}},$ which is also equal to the number of rows in matrix ${\textbf {W}}.$

2.1 Distributions

This section focuses on the distributions required in our scheme: discrete Gaussian distributions and sub-Gaussian distributions. The error distribution in the LWE assumption follows a discrete Gaussian distribution, while the matrix decomposition follows a sub-Gaussian distribution. We will also cover gadget matrix and matrix decomposition in detail.

2.1.1 Discrete Gaussian distribution

The discrete Gaussian distribution on $\mathbb {Z}$ is introduced. This distribution is used to sample the private key in our scheme.

Definition 2.1

[27] Let c be the center and $\sigma$ be the parameter of the Gaussian function over $\mathbb {Z},$ which is defined as $\rho _{\sigma ,c}(x)=e^{-\frac{\left| x-c\right| ^{2}}{2\sigma ^{2}}},$ where $\sigma ,c>0.$ Additionally, let $\rho _{\sigma ,c}(\mathbb {Z})=\sum _{i=-\infty }^{\infty }\rho _{\sigma ,c}(i)$ be the discrete integral over $\mathbb {Z}.$ Define $\mathcal {D}_{\sigma }(X=x)=\frac{\rho _{\sigma ,c}(x)}{\rho _{\sigma ,c}(\mathbb {Z})}$ as a discrete Gaussian distribution with the expectation for c and the standard deviation of $\sigma .$

If $c=0,$ we denote this special distribution as $\chi .$ We use the notation $x\leftarrow \chi$ to indicate drawing x from the distribution $\chi .$ Similarly, for a set X we use the notation $x\leftarrow X$ to indicate drawing x uniformly at random from X.

2.1.2 Sub-Gaussian distribution

The sub-Gaussian distribution is introduced. This distribution is used for matrix decomposition.

Definition 2.2

[28] A variable $X\in \mathbb {R}$ is considered sub-Gaussian, for all $t\in \mathbb {R},$ it satisfies $\textrm{E}\left[ \textrm{exp}\left( 2\pi tX\right) \right] \le \textrm{exp}\left( \pi s^{2}t^{2}\right) .$ In this case, X follows a sub-Gaussian distribution with parameter s.

Sub-Gaussian random variables have the following two properties that can be easily obtained from the definition of sub-Gaussian random variables:

• Homogeneity: If the sub-Gaussian random variable X has parameter s,  then cX is sub-Gaussian with parameter cs.

• Pythagorean additivity: For two sub-Gaussian random variables $X_{1}$ and $X_{2}$ (that is independent from $X_{1}$) with parameter $s_{1}$ and $s_{2},$ respectively, $X_{1}+X_{2}$ is sub-Gaussian with parameter $\sqrt{s_{1}^{2}+s_{2}^{2}}.$

The above statement can be expanded to include vectors. A random vector ${{\varvec{x}}}$ is sub-Gaussian with parameter s,  if for all real unit vectors ${{\varvec{u}}},$ their marginal $\langle {{\varvec{u}}},{{\varvec{x}}}\rangle$ is sub-Gaussian with parameter s. It is evident from the definition that the concatenation of sub-Gaussian variables or vectors, each with a parameter s and independent of the previous one, is also sub-Gaussian with parameter s. The homogeneity and Pythagorean additivity also hold due to the linearity of vectors. It is known that the Euclidean norm of a sub-Gaussian random vector has the following upper bound.

Lemma 2.1

[28] Let ${{\varvec{x}}}\in \mathbb {R}^{n}$ be a random vector that has independent sub-Gaussian coordinates with parameter s. Then there exists a universal constant C such that $\textrm{Pr}\left[ \left\| {{\varvec{x}}}\right\| >C\cdot s\sqrt{n}\right] \le 2^{-\Omega (n)}.$

Next, we introduce the matrix decomposition that follows the sub-Gaussian distribution. This technique is widely used in fully homomorphic encryption and has a positive impact on controlling noise growth. Let q be a positive integer, $q\ge b\ge 2.$ Set $a=\left\lceil \log _b q \right\rceil$ and define a column vector ${{\varvec{g}}}=\left( 1,b,b^2,\ldots ,b^{a-1}\right) ^{T}.$ Define the gadget matrix ${\textbf {G}}={\textbf {I}}_{m} \otimes {{\varvec{g}}}\in \mathbb {Z}^{M\times m},$ where ${\textbf {I}}_{m}$ is the $m\times m$ dimensional identity matrix, $M=m\cdot a,$ $\otimes$ denotes the tensor product. $G^{-1}(\cdot )$ represents the basis b decomposition of each component of the element $\cdot ,$ and is a flattening process applied to the matrix. So, for a matrix ${\textbf {Y}},$ its decomposition is unique, and $G^{-1}({\textbf {Y}})\cdot {\textbf {G}}={\textbf {Y}},$ with the condition that $\left\| {\textbf {Y}}\right\| .$ Meanwhile, [28] has shown that the matrix decomposition function $G^{-1}(\cdot )$ follows a sub-Gaussian distribution with arguments O(1).

Lemma 2.2

[28] There is a randomized, efficiently computable function $G^{-1}:$ $\mathbb {Z}_{q}^{n}\rightarrow \mathbb {Z}^{n\cdot \lceil \log q\rceil }$ such that for any ${{\varvec{a}}}\in \mathbb {Z}_{q}^{n},$ ${{\varvec{x}}}\leftarrow G^{-1}({{\varvec{a}}})$ is sub-Gaussian with parameter O(1) and ${{\varvec{a}}}={\textbf {G}}{{\varvec{x}}}\bmod q.$

2.2 Learning with errors

The learning with errors (LWE) assumption, originally proposed by Regev [8], has two common versions: the search version and the decision version. These versions are mutually reducible and equally secure. The security analysis of our scheme includes the decision LWE (DLWE) assumption, and the specific definitions of DLWE and security reduction are described below.

Definition 2.3

(DLWE) [8] For a security parameter $\lambda ,$ let $n=n(\lambda )$ be an integer dimension, let $q=q(\lambda )\ge 2$ be an integer modulus, and let $\chi =\chi (\lambda )$ be an error distribution over $\mathbb {Z}.$ $\mathcal {DLWE}_{n,q,\chi }$ is the problem to distinguish the following two distributions: In the first distribution, a tuple $\left( {{\varvec{a}}}_{i},b_{i}\right)$ is sampled from uniform over $\mathbb {Z}_{q}^{n}\times \mathbb {Z}_{q};$ In the second distribution, ${{\varvec{s}}}\leftarrow \mathbb {Z}_{q}^{n}$ and then a tuple $\left( {{\varvec{a}}}_{i},b_{i}\right)$ is sampled by sampling ${{\varvec{a}}}_{i}\leftarrow \mathbb {Z}_{q}^{n},$ $e_{i}\leftarrow \chi ,$ and setting $b_{i}=\left\langle {{\varvec{a}}}_{i},{{\varvec{s}}}\right\rangle +e_{i}\bmod q.$ The $\mathcal {DLWE}_{n,q,\chi }$ assumption is that $\mathcal {DLWE}_{n,q,\chi }$ is infeasible.

Recall that $\textrm{GapSVP}_{\gamma }$ is the promise problem to distinguish between the case in which the lattice has a vector shorter than $r\in \mathbb {Q},$ and the case in which all the lattice vectors are greater than $\gamma \cdot r.$ $\textrm{SIVP}_{\gamma }$ is the problem to find the set of short linearly independent vectors in a lattice. $\mathcal {DLWE}_{n,q,\chi }$ has reductions to the standard lattice assumptions as follows. These reductions take $\chi$ to be a discrete Gaussian distribution $\mathcal {D}_{\mathbb {Z},\alpha q}$ (that is centered around 0 and has parameter $\alpha q$ for some $\alpha <1$).

Corollary 2.1

[8] Let $q=q(n)\in \mathbb {N}$ be a power of primes $q=p^{r}$ or a product of distinct prime numbers $q=\prod _{i}q_{i}$ ($q_{i}=\textrm{poly}(n)$ for all i), and let $\alpha \ge \frac{\sqrt{n}}{q}.$ If there exists an efficient algorithm that solves (average-case) $\mathcal {DLWE}_{n,q,\mathcal {D}_{\mathbb {Z},\alpha q}},$

• there exists an efficient quantum algorithm that can solve $\textrm{GapSVP}_{\tilde{O}\left( \frac{n}{\alpha }\right) }$ and $\textrm{SIVP}_{\tilde{O}\left( \frac{n}{\alpha }\right) }$ in the worst-case for any n-dimensional lattices.

• if in addition we have $q\ge \tilde{O}\left( 2^{\frac{n}{2}}\right) ,$ there exists an efficient classical algorithm that can solve $\textrm{GapSVP}_{\tilde{O}\left( \frac{n}{\alpha }\right) }$ in the worst-case for any n-dimensional lattices.

On this basis, one can select n secret vectors ${{\varvec{s}}}$ to create the matrix ${\textbf {S}}\in \mathbb {Z}_{q}^{m\times n},$ which leads to the definition of the n-secret LWE assumption.

Definition 2.4

(n-secret LWE) [17] For a security parameter $\lambda ,$ let $n=n(\lambda )$ and $m=m(\lambda )$ be integer dimension, let $q=q(\lambda )\ge 2$ be an integer modulus, and let $\chi =\chi (\lambda )$ be an error distribution over $\mathbb {Z}.$ $n\text {-}\mathcal {LWE}_{n,m,q,\chi }$ is the problem to distinguish the following two distributions: In the first distribution, a tuple $\left( {\textbf {A}},{\textbf {B}}\right)$ is sampled from uniform over $\mathbb {Z}_{q}^{n\times m}\times \mathbb {Z}_{q}^{n\times n};$ In the second distribution, ${\textbf {S}}\leftarrow \mathbb {Z}_{q}^{m\times n}$ and then a tuple $\left( {\textbf {A}},{\textbf {B}}\right)$ is sampled by sampling ${\textbf {A}}\leftarrow \mathbb {Z}_{q}^{n\times m},$ ${\textbf {E}}\leftarrow \chi ^{n\times n},$ and setting ${\textbf {B}}=\left( {\textbf {AS}}+{\textbf {E}}\right) \bmod q.$ The $n\text {-}\mathcal {LWE}_{n,m,q,\chi }$ assumption is that $n\text {-}\mathcal {LWE}_{n,m,q,\chi }$ is infeasible.

The security of our scheme is based on the n-secret LWE assumption, and we describe our construction of fully homomorphic encryption in detail below.

3 Fully homomorphic encryption scheme for matrix

This section mainly introduces the fully homomorphic encryption scheme for matrices, provides a detailed proof of its decryption correctness, homomorphic properties, and noise analysis. Furthermore, we utilize modulus switching and key switching technologies in our scheme to refresh the ciphertext and achieve noise reduction. Finally, we also provide a security analysis of our scheme.

3.1 Our scheme—GMS

Let $\lambda$ be the security parameter. The plaintext space $\mathcal {M}$ is the set of $n\times n$-dimensional matrix, where each component of the matrix is an element in the set $\{-t,-(t-1),\ldots ,-1,0,1,\ldots ,t-1,t\}.$ This means that the norm of $\mathcal {M}$ is less than or equal to t,  denoted as $\left\| {\mathcal {M}}\right\| \le t.$ where t is a positive integer. Let q be a large integer, $q\gg t,$ $a=\lceil \log _b q\rceil ,$ $N=na,$ and $M=ma.$ We also have integer values for $\alpha ,$ $\beta ,$ and $\eta$ that satisfy $\alpha \beta =t,$ $\alpha <\beta$ and $\beta$ and $\eta$ are invertible modulo q,  satisfying $\beta ^{-1}\bmod q=\eta ,$ which means that $\beta \eta \bmod q=1.$

• KeyGen$(1^{\lambda },pk,sk):$ Randomly and uniformly choose an $n\times m$-dimensional matrix ${\textbf {A}}\leftarrow \mathbb {Z}^{n\times m}_{t}.$ Randomly and secretly choose two $m\times n$-dimensional matrix ${\textbf {S}}_{1},{\textbf {S}}_{2}\leftarrow \mathbb {Z}_{q}^{m\times n},$ where each component is in the set $\{-1,0,1\}.$ The error matrix ${\textbf {E}}\leftarrow \mathbb {Z}_{q}^{n\times n},$ and each component of ${\textbf {E}}$ follows the error distribution $\chi .$ Compute ${\textbf {B}}=\left( {\textbf {AS}}_{1}+{\textbf {E}}\right) \bmod q,$ and let ${\textbf {D}}=\left( \alpha {\textbf {B}}|{\textbf {A}}\right) \in \mathbb {Z}_{q}^{n\times (n+m)},$ ${\textbf {T}}_{1}=\alpha \left( {\textbf {S}}_{1}+{\textbf {S}}_{2}\right) \in \mathbb {Z}_{q}^{m\times n}.$ Set ${\textbf {V}}=\left( {\textbf {I}}_{n}|{\textbf {O}}_{n\times m}\right) \in \mathbb {Z}_{q}^{n\times (n+m)},$ ${\textbf {S}}=\left( \begin{array}{c}{\beta {\textbf {I}}_n} \\ {-t{\textbf {S}}_{1}} \end{array}\right) \in \mathbb {Z}_q^{(n+m)\times n},~{\textbf {T}}=\left( \begin{array}{c}{{\textbf {I}}_n} \\ {-{\textbf {T}}_{1}} \end{array}\right) \in \mathbb {Z}_q^{(n+m)\times n},$ Then we have ${\textbf {DS}}=t{\textbf {E}},~{\textbf {VS}}=\beta {\textbf {I}}_{n},~{\textbf {DT}}=\alpha \left( {\textbf {E}}-{\textbf {AS}}_{2}\right) ,~{\textbf {VT}}={\textbf {I}}_{n}.$ The secret key $sk={\textbf {S}},$ the public key $pk=\left( {\textbf {T}},{\textbf {V}},{\textbf {D}}\right) .$

• Encrypt$(pk,{\textbf {M}}):$ Given the plaintext ${\textbf {M}}\in \mathcal {M},$ randomly and uniformly choose an $(N+M)\times n$-dimensional matrix ${\textbf {R}},$ each component of ${\textbf {R}}$ is an element in the set $\{-1,0,1\},$ i.e., ${\textbf {R}}\leftarrow \{-1,0,1\}^{(N+M)\times n}.$ Output the ciphertext ${\textbf {C}}=\left( {\textbf {GTMV}}+{\textbf {RD}}\right) \bmod q,$ where ${\textbf {G}}={\textbf {I}}_{n+m}\otimes {{\varvec{g}}}$ is a gadget matrix.

• Decrypt$(sk,{\textbf {C}}):$ Output ${\textbf {M}}^{\prime }=\left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {CS}}\bmod q\right) \bmod t.$

• Eval-Add$(pk,{\textbf {C}}_{1},{\textbf {C}}_{2})$: Given ciphertexts ${\textbf {C}}_{1}$ and ${\textbf {C}}_{2},$ output ${\textbf {C}}_{add}=\left( {\textbf {C}}_{1}+{\textbf {C}}_{2}\right) \bmod q.$

• Eval-Mult$(pk,{\textbf {C}}_{1},{\textbf {C}}_{2})$: Given ciphertexts ${\textbf {C}}_{1}$ and ${\textbf {C}}_{2},$ output ${\textbf {C}}_{mult}=G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {C}}_{2}\bmod q.$

• Refresh$({\textbf {C}},ksk,q_{1},q_{2})$: Given ciphertext ${\textbf {C}}$ and modulus $q_{1}>q_{2},$ run ${\textbf {C}}^{\prime }\leftarrow \mathrm{\textbf{ModSwitch}}({\textbf {C}}),$ where ${\textbf {C}}^{\prime }$ is encrypted under the same key with ${\textbf {C}}$ for a different modulus $q_{2}.$ Then run ${\textbf {C}}^{"}\leftarrow \mathrm{\textbf{KeySwt}}({\textbf {C}}^{\prime },ksk),$ where ${\textbf {C}}^{"}$ is encrypted under a different key $(pk^{\prime },sk^{\prime })$ for the same modulus with ${\textbf {C}}^{\prime }.$

3.2 Correctness of decryption

In this section, we mainly verify the correctness of decryption. For ${\textbf {C}},$ which is the encryption of ${\textbf {M}},$ consider the decryption process of ${\textbf {C}}:$

$$\begin{aligned} \begin{array}{ccl} {\textbf{Decrypt}}\left( sk,{\textbf {C}}\right) & =& \left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {CS}}\bmod q\right) \bmod t \\ & =& \left( G^{-1}\left( \eta {\textbf {V}}\right) \left( {\textbf {GTMV}}+{\textbf {RD}}\right) {\textbf {S}}\bmod q\right) \bmod t \\ & =& \left( \left( \eta {\textbf {VTMVS}}+G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RDS}}\right) \bmod q\right) \bmod t \\ & =& \left( \eta \beta {\textbf {M}}+tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}\bmod q\right) \bmod t \\ & =& \left( {\textbf {M}}+tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}\right) \bmod t \\ & =& {\textbf {M}}. \end{array} \end{aligned}$$

(1)

It is easy to see that decrypting the ciphertext ${\textbf {C}}$ yields the plaintext ${\textbf {M}}.$ In other words, the decryption is correct.

3.3 Homomorphic properties

In this section, we first define the operations of homomorphic addition and homomorphic multiplication in our scheme. We then proceed to verify their homomorphic properties.

• Homomorphic addition: ${\textbf {C}}_{add}=\left( {\textbf {C}}_{1}+{\textbf {C}}_{2}\right) \bmod q.$

  $$\begin{aligned} \begin{array}{ccl} {\textbf {C}}_{add}& =& \left( {\textbf {C}}_{1}+{\textbf {C}}_{2}\right) \bmod q \\ & =& \left( {\textbf {GTM}}_{1} {\textbf {V}}+{\textbf {R}}_{1} {\textbf {D}}\right) +\left( {\textbf {GTM}}_{2} {\textbf {V}}+{\textbf {R}}_{2} {\textbf {D}}\right) \bmod q \\ & =& \left( {\textbf {GT}}\left( {\textbf {M}}_{1}+{\textbf {M}}_{2}\right) {\textbf {V}}+\left( {\textbf {R}}_{1}+{\textbf {R}}_{2}\right) {\textbf {D}}\right) \bmod q. \end{array} \end{aligned}$$

  (2)

  Decrypt ${\textbf {C}}_{add},$ the specific decryption process is as follows:

  $$\begin{aligned} \begin{array}{ccl} \mathrm{\textbf{Decrypt}}\left( sk,{\textbf {C}}_{add}\right) & =& \left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {C}}_{add} {\textbf {S}}\bmod q\right) \bmod t \\ & =& \left( \left( \eta {\textbf {VT}}\left( {\textbf {M}}_{1}+{\textbf {M}}_{2}\right) {\textbf {VS}}+G^{-1}\left( \eta {\textbf {V}}\right) \left( {\textbf {R}}_{1}+{\textbf {R}}_{2}\right) {\textbf {DS}}\right) \bmod q\right) \bmod t \\ & =& \left( \left( \eta \beta \left( {\textbf {M}}_{1}+{\textbf {M}}_{2}\right) +tG^{-1}\left( \eta {\textbf {V}}\right) \left( {\textbf {R}}_{1}+{\textbf {R}}_{2}\right) {\textbf {E}}\right) \bmod q\right) \bmod t \\ & =& \left( \left( {\textbf {M}}_{1}+{\textbf {M}}_{2}\right) +tG^{-1}\left( \eta {\textbf {V}}\right) \left( {\textbf {R}}_{1}+{\textbf {R}}_{2}\right) {\textbf {E}}\right) \bmod t \\ & =& {\textbf {M}}_{1}+{\textbf {M}}_{2}. \end{array} \end{aligned}$$

  (3)

  Easy to know, ${\textbf {C}}_{add}$ corresponds to the encryption of the plaintext ${\textbf {M}}_{1}+{\textbf {M}}_{2}.$

• Homomorphic multiplication ${\textbf {C}}_{mult}=G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {C}}_{2}\bmod q.$

  $$\begin{aligned} \begin{array}{ccl} {\textbf {C}}_{mult}& =& G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {C}}_{2}\bmod q \\ & =& G^{-1}\left( {\textbf {C}}_{1}\right) \left( {\textbf {GTM}}_{2} {\textbf {V}}+{\textbf {R}}_{2} {\textbf {D}}\right) \bmod q \\ & =& \left( \left( {\textbf {GTM}}_{1} {\textbf {V}}+{\textbf {R}}_{1} {\textbf {D}}\right) {\textbf {TM}}_{2} {\textbf {V}}+G^{-1}\left( {\textbf {C}}_1\right) {\textbf {R}}_{2} {\textbf {D}}\right) \bmod q \\ & =& \left( {\textbf {GT}}\left( {\textbf {M}}_{1} {\textbf {M}}_{2}\right) {\textbf {V}}+\alpha {\textbf {R}}_{1}\left( {\textbf {E}}-{\textbf {AS}}_{2}\right) {\textbf {M}}_{2} {\textbf {V}}+G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {R}}_{2} {\textbf {D}}\right) \bmod q. \end{array} \end{aligned}$$

  (4)

  Decrypt ${\textbf {C}}_{mult},$ the specific decryption process is as follows:

  $$\begin{aligned} \begin{array}{ccl} & & \mathrm{\textbf{Decrypt}}\left( sk,{\textbf {C}}_{mult}\right) \\ & =& \left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {C}}_{mult} {\textbf {S}}\bmod q\right) \bmod t \\ & =& \left( \left( \eta \beta {\textbf {M}}_{1} {\textbf {M}}_{2}+\alpha \beta G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {R}}_{1}\left( {\textbf {E}}-{\textbf {A}} {\textbf {S}}_{2}\right) {\textbf {M}}_{2}+tG^{-1}\left( \eta {\textbf {V}}\right) G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {R}}_{2} {\textbf {E}}\right) \bmod q\right) \bmod t \\ & =& \left( {\textbf {M}}_{1} {\textbf {M}}_{2}+tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {R}}_{1}\left( {\textbf {E}}-{\textbf {A}} {\textbf {S}}_{2}\right) {\textbf {M}}_{2}+tG^{-1}\left( \eta {\textbf {V}}\right) G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {R}}_{2} {\textbf {E}}\right) \bmod t \\ & =& {\textbf {M}}_{1} {\textbf {M}}_{2}. \end{array} \end{aligned}$$

  (5)

  Easy to know, ${\textbf {C}}_{mult}$ corresponds to the encryption of the plaintext ${\textbf {M}}_{1} {\textbf {M}}_{2}.$

On this basis, we can further optimize the process of homomorphic multiplication. $G^{-1}\left( {\textbf {C}}_{1}\right)$ is a $(N+M)\times (N+M)$-dimensional matrix, ${\textbf {C}}_{2}$ is a $(N+M)\times (n+m)$-dimensional matrix, which can be expressed as

$$\begin{aligned} G^{-1}\left( {\textbf {C}}_{1}\right) =\left( \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1,N+M} \\ a_{21} & a_{22} & \cdots & a_{2,N+M} \\ \vdots & \vdots & \vdots & \vdots \\ a_{N+M,1} & a_{N+M,2} & \cdots & a_{N+M,N+M} \end{array} \right) ,{\textbf {C}}_{2}=\left( \begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1,n+m} \\ b_{21} & b_{22} & \cdots & b_{2,n+m} \\ \vdots & \vdots & \vdots & \vdots \\ b_{N+M,1} & b_{N+M,2} & \cdots & b_{N+M,n+m} \end{array} \right) . \end{aligned}$$

(6)

Rotate these two matrices by their diagonal elements to obtain the matrices ${\textbf {A}}$ and ${\textbf {B}}.$ The specific rotation operation is as follows.

$$\begin{aligned} {\textbf {A}}= & \textrm{Rotate}\left( G^{-1}\left( {\textbf {C}}_{1}\right) \right) =\left( \begin{array}{ccccc} a_{11} & a_{12} & \cdots & a_{1,N+M-1} & a_{1,N+M} \\ a_{22} & a_{23} & \cdots & a_{2,N+M} & a_{21} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{N+M,N+M} & a_{N+M,1} & \cdots & a_{N+M,N+M-2} & a_{N+M,N+M-1} \end{array} \right) , \end{aligned}$$

(7)

$$\begin{aligned} {\textbf {B}}= & \textrm{Rotate}\left( {\textbf {C}}_{2}\right) =\left( \begin{array}{cccc} b_{11} & b_{22} & \cdots & b_{n+m,n+m} \\ b_{21} & b_{32} & \cdots & b_{n+m+1,n+m} \\ \vdots & \vdots & \vdots & \vdots \\ b_{N+M-1,1} & b_{N+M,2} & \cdots & b_{n+m-2,n+m} \\ b_{N+M,1} & b_{12} & \cdots & b_{n+m-1,n+m} \end{array} \right) . \end{aligned}$$

(8)

Then use the $(N+M)$-dimensional column vector ${{\varvec{a}}}_{i}~(1\le i\le N+M)$ to represent each column element of the matrix ${\textbf {A}}$, and use the $(N+M)$-dimensional row vector ${{\varvec{b}}}_{j}^{T}~(1\le j\le N+M)$ to represent each row element of the matrix ${\textbf {B}},$ that is, ${\textbf {A}}=\left( {{\varvec{a}}}_{1},{{\varvec{a}}}_{2},\ldots ,{{\varvec{a}}}_{N+M}\right) ,$ ${\textbf {B}}=\left( {{\varvec{b}}}_{1}^{T},{{\varvec{b}}}_{2}^{T},\ldots ,{{\varvec{b}}}_{N+M}^{T}\right) ^{T}.$ Let the $(N+M)\times (n+m)$-dimensional matrix ${\textbf {A}}_{i}~(1\le i\le N+M)$ and ${\textbf {B}}_{j}~(1\le j\le N+M)$ be pressed as follows:

$$\begin{aligned} {\textbf {A}}_{1}= & \left( {{\varvec{a}}}_{1},{{\varvec{a}}}_{2},\ldots ,{{\varvec{a}}}_{n+m}\right) ,{\textbf {A}}_{2}=\left( {{\varvec{a}}}_{2},{{\varvec{a}}}_{3},\ldots ,{{\varvec{a}}}_{n+m+1}\right) ,{\textbf {A}}_{3}=\left( {{\varvec{a}}}_{3},{{\varvec{a}}}_{4},\ldots ,{{\varvec{a}}}_{n+m+2}\right) , \nonumber \\ & \ldots ,{\textbf {A}}_{N+M-1}=\left( {{\varvec{a}}}_{N+M-1},{{\varvec{a}}}_{N+M},\ldots ,{{\varvec{a}}}_{n+m-2}\right) ,{\textbf {A}}_{N+M}=\left( {{\varvec{a}}}_{N+M},{{\varvec{a}}}_{1},\ldots ,{{\varvec{a}}}_{n+m-1}\right) . \end{aligned}$$

(9)

$$\begin{aligned} {\textbf {B}}_{1}= & \left( {{\varvec{b}}}_{1}^{T},{{\varvec{b}}}_{2}^{T},\ldots ,{{\varvec{b}}}_{N+M-1}^{T},{{\varvec{b}}}_{N+M}^{T}\right) ^{T}, {\textbf {B}}_{2}=\left( {{\varvec{b}}}_{2}^{T},{{\varvec{b}}}_{3}^{T},\ldots ,{{\varvec{b}}}_{N+M}^{T},{{\varvec{b}}}_{1}^{T}\right) ^{T}, {\textbf {B}}_{3}=\left( {{\varvec{b}}}_{3}^{T},{{\varvec{b}}}_{4}^{T},\ldots ,{{\varvec{b}}}_{1}^{T},{{\varvec{b}}}_{2}^{T}\right) ^{T},\nonumber \\ & \ldots , {\textbf {B}}_{N+M}=\left( {{\varvec{b}}}_{N+M}^{T},{{\varvec{b}}}_{1}^{T},\ldots ,{{\varvec{b}}}_{N+M-2}^{T},{{\varvec{b}}}_{N+M-1}^{T}\right) ^{T}. \end{aligned}$$

(10)

So the homomorphic multiplication process can be transformed into

$$\begin{aligned} G^{-1}\left( {\textbf {C}}_{1}\right) \cdot {\textbf {C}}_{2}=\sum _{i=1}^{N+M} {\textbf {A}}_{i}\odot {\textbf {B}}_{i}=\sum _{i=1}^{N+M}\textrm{Rotate}\left( {\textbf {A}},0,-i\right) \odot \textrm{Rotate}\left( {\textbf {B}},1,-i\right) , \end{aligned}$$

(11)

where $\odot$ represents the element-wise multiplication of the matrix, $\textrm{Rotate}\left( {\textbf {A}},0,-i\right)$ indicates rotating each element of the matrix ${\textbf {A}}$ by i positions to the left, and $\textrm{Rotate}\left( {\textbf {B}},1,-i\right)$ indicates rotating each element of the matrix ${\textbf {B}}$ by i positions upwards. This can convert one ciphertext matrix multiplication into O(n) rotations and O(n) constant multiplications, which is more efficient.

3.4 Noise analysis

The noise in the scheme arises from the modular operation during the decryption process. let

$$\begin{aligned} \mathcal {N}({\textbf {C}})=G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {CS}}\bmod q-{\textbf {M}}=tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}. \end{aligned}$$

(12)

• Initial noise: $\left\| \mathcal {N}({\textbf {C}})\right\| =\left\| tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}\right\| \le t(N+M)n\left\| G^{-1}\left( \eta {\textbf {V}}\right) \right\| \left\| {\textbf {R}}\right\| \left\| {\textbf {E}}\right\| \le t(N+M)nb\left\| {\textbf {E}}\right\| .$

• Additional noise: $\left\| \mathcal {N}({\textbf {C}}_{add})\right\| =\left\| \mathcal {N}({\textbf {C}}_{1})\right\| +\left\| \mathcal {N}({\textbf {C}}_{2}) \right\| \le 2t(N+M)nb\left\| {\textbf {E}}\right\| .$

• Multiplication noise:

  $$\begin{aligned} \begin{array}{ccl} \left\| \mathcal {N}({\textbf {C}}_{mul})\right\| & =& \left\| tG^{-1}\left( \eta {\textbf {V}}\right) \left( {\textbf {R}}_{1}\left( {\textbf {E}}-{\textbf {AS}}_{2}\right) {\textbf {M}}_{2}+G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {R}}_{2} {\textbf {E}}\right) \right\| \\ & \le & t(N+M)\left\| G^{-1}\left( \eta {\textbf {V}}\right) \right\| \left( \left\| {\textbf {R}}_{1}\left( {\textbf {E}}-{\textbf {AS}}_{2}\right) {\textbf {M}}_{2}\right\| +\left\| G^{-1}\left( {\textbf {C}}_{1}\right) {\textbf {R}}_{2} {\textbf {E}}\right\| \right) \\ & \le & t(N+M)b\left( n^{2}\left\| {\textbf {R}}_{1}\right\| \left\| {\textbf {E}}-{\textbf {AS}}_{2}\right\| \left\| {\textbf {M}}_{2}\right\| +(N+M)n\left\| G^{-1}\left( {\textbf {C}}_{1}\right) \right\| \left\| {\textbf {R}}_{2}\right\| \left\| {\textbf {E}}\right\| \right) \\ & \le & t(N+M)b\left( n^{2}t\left( \left\| {\textbf {E}}\right\| +m\left\| {\textbf {A}}\right\| \left\| {\textbf {S}}_{2}\right\| \right) +(N+M)nb\left\| {\textbf {E}}\right\| \right) \\ & \le & t(N+M)b\left( \left( n^{2}+m\right) t+(N+M)nb\right) \left\| {\textbf {E}}\right\| . \end{array} \end{aligned}$$

  (13)

In summary, both initial noise and additional noise can be expressed as $O\left( n^{2}tbae\right) ,$ while multiplication noise can be expressed as $O\left( n^{3}t^{2}b^{2}a^{2}e\right) ,$ where e represents the maximum value of the norm of error matrix ${\textbf {E}},$ i.e., $\left\| {\textbf {E}}\right\| \le e.$ Therefore, the upper bound N of noise can be expressed as $N=O\left( n^{3}t^{2}b^{2}a^{2}e\right) ,$ and the parameter selection of the scheme is closely related to N and needs to satisfy $|N|<\frac{q}{2}.$

3.5 Ciphertext refreshing

According to the previous sections, it is evident that the accuracy of our scheme primarily relies on the modular operation $\bmod t.$ Specifically, the noise component should be $\le \frac{q}{2}.$ Based on the aforementioned analysis of noise, the maximum limit of noise can be achieved by selecting appropriate parameters. In order to enhance the efficiency of secure matrix multiplication and reduce the inclusion of redundant items in the operation, we introduce a ciphertext refreshing program in this section.

Similar to the ciphertext refreshing technique used in BGV [11], modulus switching technology is employed to convert the ciphertext from a large modulus to a small modulus. Subsequently, key switching technology is applied to change the ciphertext under different keys. This entire refreshing process transforms the ciphertext into another ciphertext under a different key and a smaller modulus, while still representing the same plaintext. The newly introduced modulus switching and key switching technologies are described below.

3.5.1 Modulus switching

Similar to the existing modulus switching technology, we need to define a mapping from a large modulus to a small modulus in order to implement the modulus switching process $\mathrm{\textbf{ModSwitch}}.$ The specific steps are as follows:

• Define a mapping from a large modulus $q_{1}$ to a small modulus $q_{2}$: For any integer a,  $[a]_{q_{1}\rightarrow q_{2}}=\left\lfloor \frac{q_{2}}{q_{1}}a\right\rfloor +r,$ where $r\in \{0,1\}.$

• For the ciphertext ${\textbf {C}}=\left( c_{ij}\right) ,1\le i\le N+M,1\le j\le n+m,$ the modulus mapping of each component can be defined as a pair. The specific definition of modulus switching is $\mathrm{\textbf{ModSwitch}}({\textbf {C}})=\left( [c_{ij}]_{q_{1}\rightarrow q_{2}}\right) .$

Let ${\textbf {C}}^{\prime }=\mathrm{\textbf{ModSwitch}}({\textbf {C}})=\left( [c_{ij}]_{q_{1}\rightarrow q_{2}}\right) ,$ then ${\textbf {C}}^{\prime }\approx \frac{q_{2}}{q_{1}} {\textbf {C}},$ the noise also becomes the original $\frac{q_{2}}{q_{1}}.$ Modulus switching, denoted as $\mathrm{\textbf{ModSwitch}},$ has the effect of reducing noise. The ciphertext ${\textbf {C}},$ which is encrypted using the modulo $q_{1},$ is transformed into a new ciphertext ${\textbf {C}}^{\prime }$ using a different modulo $q_{2}.$ In this case, it represents the same plaintext ${\textbf {M}},$ but the noise is reduced by approximately $\frac{q_{2}}{q_{1}}.$

3.5.2 Key switching

Similar to the existing key switching, our program also consists of two steps: first, generating a key switching key ksk,  and then using this ksk to publicly implement the ciphertext conversion. Our goal is to convert a ciphertext matrix ${\textbf {C}}$ determined by the key $\left( pk_{1},sk_{1}\right)$ to a ciphertext matrix ${\textbf {C}}^{\prime }$ determined by the key $\left( pk_{2},sk_{2}\right) .$

• KeySwtGen$(pk_{1},pk_{2},sk_{1},sk_{2}):$ Define one key pair is $pk_{1}=\left( {\textbf {T}}_{1},{\textbf {V}},{\textbf {D}}_{1}\right) ,$ $sk_{1}={\textbf {S}}_{(1)}$ and another key pair is $pk_{2}=\left( {\textbf {T}}_{2},{\textbf {V}},{\textbf {D}}_{2}\right) ,$ $sk_{2}={\textbf {S}}_{(2)}.$ The process of generating a key switching key is as follows:

  • 1. Define ${{\varvec{g}}}=\left( 1,b,b^{2},\ldots ,b^{a-1}\right) ^{T},$ and ${\textbf {G}}={\textbf {I}}_{m+n} \otimes {{\varvec{g}}}\in \mathbb {Z}^{(M+N)\times (m+n)}.$

  • 2. Randomly and uniformly choose a matrix ${\textbf {W}}\leftarrow \{-1,0,1\}^{(N+M)\times n}.$

  • 3. Output key switching key $ksk=\left( {\textbf {G}}+{\textbf {WD}}_{1}\right) {\textbf {S}}_{(1)} {\textbf {V}}\in \mathbb {Z}_{q}^{(N+M)\times n}.$

• KeySwt$({\textbf {C}}_{1},ksk):$ Given a ciphertext ${\textbf {C}}\in \mathbb {Z}_{q}$ and a key switching key $ksk\in \mathbb {Z}_{q}^{(N+M)\times (n+m)},$ define ${\textbf {Y}}={\textbf {GT}}_{2}G^{-1}\left( \eta {\textbf {V}}\right) G^{-1}({\textbf {C}})\in \mathbb {Z}_{q}^{(N+M)\times (N+M)},$ and output ${\textbf {C}}^{\prime }={\textbf {Y}}\cdot ksk\bmod q\in \mathbb {Z}_{q}.$

3.5.3 Correctness of modulus switching and key switching

The correctness of modulus switching is relatively easy and will not be verified in detail here. The main consideration is the correctness of key switching technology. First, calculate

$$\begin{aligned} \begin{array}{ccl} {\textbf {C}}^{\prime }& =& {\textbf {Y}}\cdot ksk\bmod q\\ & =& {\textbf {GT}}_{2}G^{-1}(\eta {\textbf {V}})G^{-1}({\textbf {C}})\left( {\textbf {G}}+{\textbf {WD}}_{1}\right) {\textbf {S}}_{(1)} {\textbf {V}}\bmod q\\ & =& {\textbf {GT}}_{2}G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {C}} {\textbf {S}}_{(1)} {\textbf {V}}+{\textbf {GT}}_{2}G^{-1}(\eta {\textbf {V}})G^{-1}({\textbf {C}}){\textbf {WD}}_{1} {\textbf {S}}_{(1)} {\textbf {V}}\bmod q\\ & =& {\textbf {GT}}_{2}\left( \eta \beta {\textbf {M}}+tG^{-1}\left( \eta {\textbf {V}}\right) {\textbf {R}} {\textbf {E}}_{1}\right) {\textbf {V}}+t{\textbf {GT}}_{2} G^{-1}(\eta {\textbf {V}})G^{-1}({\textbf {C}}){\textbf {WE}}_{1} {\textbf {V}}\bmod q\\ & =& {\textbf {GT}}_{2} {\textbf {MV}}+t\left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}_{1} {\textbf {V}}+{\textbf {GT}}_{2}G^{-1}\left( \eta {\textbf {V}}\right) G^{-1}\left( {\textbf {C}}\right) {\textbf {WE}}_{1} {\textbf {V}}\right) . \end{array} \end{aligned}$$

(14)

We know that the ciphertext ${\textbf {C}}^{\prime }$ is the encryption of plaintext ${\textbf {M}}.$ Its noise is $t\left( G^{-1}\left( \eta {\textbf {V}}\right) {\textbf {RE}}_{1} {\textbf {V}}+{\textbf {GT}}_{2}G^{-1}\left( \eta {\textbf {V}}\right) G^{-1}\left( {\textbf {C}}\right) {\textbf {WE}}_{1} {\textbf {V}}\right) ,$ which is still a multiple of t,  and it has the same form as the noise. This noise, which can be eliminated by subsequent operations using modulo t,  can be decrypted correctly. Therefore, the ciphertext ${\textbf {C}}^{\prime }$ can be decrypted correctly, and the homomorphic evaluation can be performed accurately.

3.6 Security analysis

Here, we prove the following theorem, which asserts the security of our scheme.

Theorem 3.1

Assuming DLWE (Definition 2.3) and n-secret LWE (Definition 2.4), the security of our scheme only depends on n-secret LWE assumption, and the fully homomorphic encryption scheme we constructed satisfies IND-CPA security [29].

Proof

To prove the security, we need to prove the indistinguishability of the following two distributions.

Distribution $\mathcal {D}_{1}:$ $\mathcal {D}_{1}=\left\{ {\textbf {C}}\leftarrow \left( {\textbf {GTMV}}+{\textbf {RD}}\right) \bmod q|pk=\left( {\textbf {T}},{\textbf {V}},{\textbf {D}}\right) ,sk={\textbf {S}}\right\} .$

Distribution $\mathcal {D}_{2}:$ $\mathcal {D}_{2}=\left\{ {\textbf {C}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}|pk=\left( {\textbf {T}},{\textbf {V}},{\textbf {D}}\right) ,sk={\textbf {S}}\right\} .$

We can see that $\mathcal {D}_{1}$ and $\mathcal {D}_{2}$ represent the adversary’s views when the plaintext ${\textbf {M}}$ is encrypted and randomly chosen, respectively. From the keyGen process, we have ${\textbf {D}}=\left( \alpha {\textbf {B}}|{\textbf {A}}\right) .$ Therefore, to demonstrate that the distributions $\mathcal {D}_{1}$ and $\mathcal {D}_{2}$ are computationally indistinguishable, we need to establish that the following two distributions are computationally indistinguishable:

Distribution $\mathcal {D}_{1}^{'}:$ $\mathcal {D}_{1}^{'}=\left\{ {\textbf {C}}\leftarrow \left( {\textbf {GTMV}}+{\textbf {R}}\left( \alpha {\textbf {B}}|{\textbf {A}}\right) \right) \bmod q|{\textbf {B}}=\left( {\textbf {AS}}+{\textbf {E}}\right) \bmod q\right\} .$

Distribution $\mathcal {D}_{2}^{'}:$ $\mathcal {D}_{2}^{'}=\left\{ {\textbf {C}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}\right\} .$

From the above discussion, it suffices to prove Lemma 3.1 in the following to complete the proof of Theorem 3.1.

Lemma 3.1

Distributions $\mathcal {D}_{1}^{'}$ and $\mathcal {D}_{2}^{'}$ are computationally indistinguishable under the hardness assumption of DLWE and n-secret LWE.

Proof

We prove the lemma via the following hybrids.

$\mathcal {G}_{0}:$ This is same as $\mathcal {D}_{1}^{'}.$

$\mathcal {G}_{1}:$ In this hybrid, the challenger computes ${\textbf {C}}$ as ${\textbf {C}}=\left( {\textbf {GTMV}}+{\textbf {R}}\left( \alpha {\textbf {B}}|{\textbf {A}}\right) \right) \bmod q,$ where ${\textbf {B}}=\left( {{\varvec{b}}}_{1},\ldots ,{{\varvec{b}}}_{n}\right) ,$ and ${{\varvec{b}}}_{i}=\left( {\textbf {A}}{{\varvec{s}}}_{i}+{{\varvec{e}}}_{i}\right) \bmod q,$ where each component of ${\textbf {A}}$ is selected from a random uniform distribution, and each component of ${{\varvec{e}}}_{i}$ is selected from an error distribution $\chi .$

$\mathcal {G}_{2}:$ The challenger computes ${\textbf {C}}=\left( {\textbf {GTMV}}+{\textbf {U}}\right) \bmod q,$ where ${\textbf {U}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}.$

$\mathcal {G}_{3}:$ In this hybrid, the challenger randomly and uniformly selects ${\textbf {C}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}.$

It is easy to see that the distribution of $G_{3}$ is the same as the distribution $\mathcal {D}_{2}^{'}$. We prove the indistinguishability of the distribution in the following way.

First, prove that $\mathcal {G}_{0}\equiv \mathcal {G}_{1}.$ Since only the selection method of ${\textbf {B}}$ is different in $\mathcal {G}_{0}$ and $\mathcal {G}_{1}$, it is easy to see that ${\textbf {B}}=\left( {\textbf {AS}}+{\textbf {E}}\right) \bmod q$ represents the standard DLWE assumption. ${{\varvec{b}}}_{i}=\left( {\textbf {A}}{{\varvec{s}}}_{i}+{{\varvec{e}}}_{i}\right) \bmod q$ represents the spliced form of the n secret vectors ${{\varvec{s}}}_{i}$, ensuring the equivalence of $\mathcal {G}_{0}$ and $\mathcal {G}_{1}.$

Then prove that $\mathcal {G}_{1}\approx _{c}\mathcal {G}_{2}$ due to DLWE. Since only the second half of the random selection in $\mathcal {G}_{1}$ and $\mathcal {G}_{2}$ is different, we know that the DLWE distribution and the uniform random distribution are computationally indistinguishable. In other words, $\left\{ \left( {\textbf {B}},{\textbf {A}}\right) \right\}$ and $\mathbb {Z}_ {q}^{(N+M)\times (n+m)}$ are computationally indistinguishable. By the definition of the cipher, ${\textbf {R}}\leftarrow \{-1,0,1\} ^{(N+M)\times (n+m)},$ so the distributions of ${\textbf {R}}\left( \alpha {\textbf {B}},{\textbf {A}}\right)$ and ${\textbf {U}}$ are computationally indistinguishable. Therefore, the distributions of $\mathcal {G}_{1}$ and $\mathcal {G}_{2}$ are computationally indistinguishable under the standard DLWE assumption.

Next, it is proven that $\mathcal {G}_{2}\approx _{s}\mathcal {G}_{3}.$ Since the public keys ${\textbf {T}}$ and ${\textbf {V}}$ are both public, and ${\textbf {G}}$ is the gadget matrix, ${\textbf {GTMV}}$ can be treated as a constant. Therefore, $\left( {\textbf {GTMV}}+{\textbf {U}}\right) \bmod q$ and ${\textbf {C}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}$ are statistically indistinguishable, where ${\textbf {U}}\leftarrow \mathbb {Z}_{q}^{(N+M)\times (n+m)}.$ means that the distributions of $\mathcal {G}_{2}$ and $\mathcal {G}_{3}$ are statistically indistinguishable.

Combined with the above analysis, it is easy to see that the distributions of $\mathcal {G}_{0}$ and $\mathcal {G}_{3}$ are computationally indistinguishable.

In summary, the distributions $\mathcal {D}_{1}^{'}$ and $\mathcal {D}_{2}^{'}$ are computationally indistinguishable, implying that the distributions $\mathcal {D}_{1}$ and $\mathcal {D}_{2}$ are also computationally indistinguishable. This implies that our scheme is IND-CPA if the n-secret LWE problem is computationally hard.

Thus, if the IND-CPA security of the underlying fully homomorphic encryption scheme can be guaranteed, it implies that the ciphertexts of any two messages are computationally indistinguishable. Since all computations in the public cloud are performed on encrypted data, the cloud cannot access any information from the encrypted data. Therefore, we can ensure the confidentiality of the data when using semi-honest servers for secure outsourced computation.

4 Secure matrix multiplication based on GMS

Since our scheme GMS is an asymmetric encryption scheme for matrices, the secure matrix multiplication procedure can be easily implemented. GMS can achieve rectangular matrix multiplication ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}$ by padding with zeros. This can be elaborated upon by considering the following three cases: (1) $\max \{m,n,l\}=m;$ (2) $\max \{m,n,l\}=n;$ (3) $\max \{m,n,l\}=l.$ The padding operation is as follows.

• (1) If $\max \{m,n,l\}=m,$ then first fill the matrices ${\textbf {A}}$ and ${\textbf {B}}$ into a square matrix, that is, ${\textbf {A}}^{'}_{m\times m}=\left( \begin{array}{cc} {\textbf {A}}_{m\times n}&{\textbf {O}}_{m\times (m-n)}\end{array}\right) ,$ ${\textbf {B}}^{'}_{m\times m}=\left( \begin{array}{cc} {\textbf {B}}_{n\times l} & {\textbf {O}}_{n\times (m-l)}\\ {\textbf {O}}_{(m-n)\times l} & {\textbf {O}}_{(m-n)\times (m-l)}\end{array}\right) .$ We have

  $$\begin{aligned} {\textbf {A}}^{'}\cdot {\textbf {B}}^{'}=\left( \begin{array}{cc} {\textbf {A}}&{\textbf {O}}\end{array}\right) \cdot \left( \begin{array}{cc} {\textbf {B}} & {\textbf {O}}\\ {\textbf {O}} & {\textbf {O}}\end{array}\right) =\left( \begin{array}{cc} {\textbf {A}}\cdot {\textbf {B}}_{m\times l}&{\textbf {O}}_{m\times (m-l)}\end{array}\right) . \end{aligned}$$

  So $\textrm{Enc}\left( \begin{array}{cc} {\textbf {A}}\cdot {\textbf {B}}&{\textbf {O}}\end{array}\right)$ can be obtained by passing $\textrm{Enc}\left( \begin{array}{cc} {\textbf {A}}&{\textbf {O}}\end{array}\right)$ and $\textrm{Enc}\left( \begin{array}{cc} {\textbf {B}} & {\textbf {O}}\\ {\textbf {O}} & {\textbf {O}}\end{array}\right)$ through the homomorphic multiplication operation, where $\textrm{Enc}$ represents the encryption algorithm of our scheme.

• (2) If $\max \{m,n,l\}=n,$ then first fill the matrices ${\textbf {A}}$ and ${\textbf {B}}$ into a square matrix, that is, ${\textbf {A}}^{'}_{n\times n}=\left( \begin{array}{c} {\textbf {A}}_{m\times n}\\ {\textbf {O}}_{(n-m)\times n}\end{array}\right) ,$ ${\textbf {B}}^{'}_{n\times n}=\left( \begin{array}{cc} {\textbf {B}}_{n\times l}&{\textbf {O}}_{n\times (n-l)}\end{array}\right) .$ We have

  $$\begin{aligned} {\textbf {A}}^{'}\cdot {\textbf {B}}^{'}=\left( \begin{array}{c} {\textbf {A}}\\ {\textbf {O}}\end{array}\right) \cdot \left( \begin{array}{cc} {\textbf {B}}&{\textbf {O}}\end{array}\right) =\left( \begin{array}{cc} {\textbf {A}}\cdot {\textbf {B}}_{m\times l} & {\textbf {O}}_{m\times (n-l)}\\ {\textbf {O}}_{(n-m)\times l} & {\textbf {O}}_{(n-m)\times (n-l)}\end{array}\right) . \end{aligned}$$

  So $\textrm{Enc}\left( \begin{array}{cc} {\textbf {A}}\cdot {\textbf {B}} & {\textbf {O}}\\ {\textbf {O}} & {\textbf {O}}\end{array}\right)$ can be obtained by passing $\textrm{Enc}\left( \begin{array}{c} {\textbf {A}}\\ {\textbf {O}}\end{array}\right)$ and $\textrm{Enc}\left( \begin{array}{cc} {\textbf {B}}&{\textbf {O}}\end{array}\right)$ through the homomorphic multiplication operation, where $\textrm{Enc}$ represents the encryption algorithm of our scheme.

• (3) If $\max \{m,n,l\}=l,$ then first fill the matrices ${\textbf {A}}$ and ${\textbf {B}}$ into a square matrix, that is, ${\textbf {A}}^{'}_{l\times l}=\left( \begin{array}{cc} {\textbf {A}}_{m\times n} & {\textbf {O}}_{m\times (l-n)}\\ {\textbf {O}}_{(l-m)\times n} & {\textbf {O}}_{(l-m)\times (l-n)}\end{array}\right) ,$ ${\textbf {B}}^{'}_{l\times l}=\left( \begin{array}{c} {\textbf {B}}_{n\times l}\\ {\textbf {O}}_{(l-n)\times l}\end{array}\right) .$ We have

  $$\begin{aligned} {\textbf {A}}^{'}\cdot {\textbf {B}}^{'}=\left( \begin{array}{cc} {\textbf {A}} & {\textbf {O}}\\ {\textbf {O}} & {\textbf {O}}\end{array}\right) \cdot \left( \begin{array}{c} {\textbf {B}}\\ {\textbf {O}}\end{array}\right) =\left( \begin{array}{c} {\textbf {A}}\cdot {\textbf {B}}_{m\times l}\\ {\textbf {O}}_{(l-m)\times l}\end{array}\right) . \end{aligned}$$

  So $\textrm{Enc}\left( \begin{array}{c} {\textbf {A}}\cdot {\textbf {B}}\\ {\textbf {O}}\end{array}\right)$ can be obtained by passing $\textrm{Enc}\left( \begin{array}{cc} {\textbf {A}} & {\textbf {O}}\\ {\textbf {O}} & {\textbf {O}}\end{array}\right)$ and $\textrm{Enc}\left( \begin{array}{c} {\textbf {B}}\\ {\textbf {O}}\end{array}\right)$ through the homomorphic multiplication operation, where $\textrm{Enc}$ represents the encryption algorithm of our scheme.

Therefore, secure outsourced matrix multiplication based on GMS for rectangular matrices requires the user to fill the matrix before encryption. Subsequently, the filled square matrix is encrypted and uploaded to the cloud server. The recipient can then download it from the cloud. The results obtained are decrypted on the server, and then, the first m rows and the first l columns of the matrix are extracted based on the desired dimensions. Therefore, our solution can be applied to secure outsourced matrix multiplication of any dimension, i.e., ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}.$

Next, we will focus on the simulation experiment, which will be presented in detail in three parts: parameter selection, theoretical comparison, and simulation experiment. Our simulation experiment first implemented the fully homomorphic encryption scheme we constructed and then proceeded to implement secure outsourced matrix multiplication. The experiment was based on the HElib library [22] in C++, running on a personal laptop with a 2.60GHz CPU configuration of the 11th generation Intel(R) Core(TM) i5–11260 H. Finally, a detailed analysis and conclusions were provided based on the data obtained from the simulation experiment.

4.1 Parameter selection

As shown in Sect. 3.6, our system assumes that the client is honest and that the only threat comes from a curious server. Note that our scheme GMS has been proven to be indistinguishable under the chosen plaintext attack model (IND-CPA). This means that the ciphertexts of two messages are computationally indistinguishable. Since the server does not have access to the secret key and can only see the ciphertexts during the secure matrix multiplication, it does not learn anything from the ciphertexts. Thus, it is safe to conclude that our secure outsourced matrix multiplication scheme is secure against a curious server in the IND-CPA model.

Therefore, the choice of parameters can be determined based on the fully homomorphic encryption scheme that we have designed. The security parameter setting assumed by the DLWE assumption generally requires a security level of either 128 bits or 256 bits. To ensure the comparability of experimental data, we set the security parameter $\lambda =128.$ This means that the modulus q is a positive integer with a length of 128 bits. In order to minimize the impact of noise on the system and the experiment, we chose to set the value of t as a positive integer with a length of 19 bits, based on the analysis in Sect. 3.4. The parameters corresponding to the different plaintext dimensions n are shown in Table 2.

Table 2 Parameter selection corresponding to different plaintext dimensions n

4.2 Theoretical analysis

In this section, we will primarily analyze the performance of our secure outsourced matrix multiplication. We compare our GMS-based secure matrix multiplication with the methods proposed by Jiang et al. [26], Hiromasa et al. [6], Huang et al. [4], and Zhu et al. [5]. As shown in Table 3. “$\#$Ciphs” represents the number of ciphertexts needed to encrypt a matrix. “$\#$HEMult” is the number of homomorphic multiplications required to perform a secure outsourced matrix multiplication. “Matrix dims” represent the applicable dimensions of the matrix. For the time complexity, let “Add” and “Mult” denote the ciphertext-ciphertext addition and ciphertext-ciphertext multiplication, respectively. Let “Cmult” denote plaintext-ciphertext multiplication. “Rot” denotes the rotation operation of a ciphertext along a row (or a column), and “Depth” denotes the depth of the multiplicative circuit. $D_{1}$ and $D_{2}$ denote the circuit depths of plaintext-ciphertext multiplication and ciphertext-ciphertext multiplication, respectively. Let $k_{1}=\max \{m, n, l\},$ $k_{2}=\textrm{median}\{m, n, l\},$ $k_{3}=\min \{m, n, l\}.$ The specific values are provided in Table 3.

Table 3 Comparison of the existing works with ours

Obviously, compared to Jiang et al. [26] and Hiromasa et al. [6], our method can be applied to a wider range of matrix multiplication cases, requiring lower time complexity and circuit depth. Huang et al. [4], Zhu et al. [5] and our method can be used for matrix multiplication of arbitrary dimensions. The number of Add, Cmult, and Rot required is of the same order of magnitude, while our method only requires one homomorphic multiplication to perform a matrix multiplication. The Mult of our method is asymptotically reduced by n and $k_{3}$ times, respectively. Therefore, our GMS-based secure outsourced matrix multiplication has a lower time complexity and is more efficient compared to existing methods.

4.3 Simulation experiment

In this section, we will verify and analyze the actual performance of our scheme, through a simulation experiment. We used the parameters listed in Table 2 to implement our constructed fully homomorphic encryption scheme, GMS. In this scheme, we randomly selected and retained the plaintext ${\textbf {M}}.$ We then decrypted it and compared it with the original plaintext. If they are not the same, an error will be returned. If they are the same, we recorded the encryption and decryption time, as well as the time taken for the homomorphic multiplication they were involved in. The entire program runs smoothly, and no errors are reported. Table 4 presents the size of ciphertext, the encryption and decryption times for different plaintext dimensions n,  along with the time required for homomorphic multiplication with varying homomorphic multiplication times k. CipherSize denotes the size of the ciphertext. EncTime(s) represents the encryption time. DecTime(s) is the decryption time. The right side of Table 4 represents the time it takes to perform k homomorphic multiplications on the ciphertext. The data in Table 4 represent a random sample of the program run multiple times.

Table 4 Ciphertext size, encryption time, decryption time, and homomorphic multiplication time

As shown in Table 4, the size of the ciphertext corresponding to a $64 \times 64$-dimensional plaintext is approximately only 1 MB. The encryption and decryption time for a $128\times 128$-dimensional plaintext is only about 1 second. The homomorphic multiplication time for a $32\times 32$-dimensional plaintext is only about 6 seconds. The fully homomorphic encryption scheme GMS that we constructed has a small ciphertext size and requires less time for encryption and decryption, resulting in high efficiency.

Next, we implemented the GMS-based secure outsourced matrix multiplication using the HElib library [22] and provided a detailed comparison of the resulting data obtained from the different secure matrix multiplication methods. Depending on the dimension of the matrix, it is divided into four cases: (1) Square matrix; (2) $\max \{m,n,l\}=m;$ (3) $\max \{m,n,l\}=n;$ (4) $\max \{m,n,l\}=l.$ We compare the performance of our method with existing methods in Fig. 3.

Fig. 3

The running time(s) of [4, 5], our method and speedup ([4, 5] vs our method)

From the data in Fig. 3, it is evident that in all cases, the execution time (matrix multiplication time) of our algorithm is the lowest. In the case of square matrix multiplication, our method demonstrates superior performance as it requires n times fewer homomorphic multiplications compared to other methods. Additionally, our approach requires the same number of rotations as the method proposed in [5], but significantly fewer rotations compared to the approach in [4] by a factor of $O(\log n)$ (refer to Table 3). As a result, we experience a greater speedup as the matrix dimension increases. When $(m,n,l)=(128,128,128),$ we achieve the highest speedup, up to 5X and 2X, respectively. In the case of rectangular matrix multiplication, the superiority of our approach compared to [5] is not readily apparent. This is because the matrix multiplication time of our method, [4] and [5], is positively correlated with $\max \{m,n,l\},$ n,  and $\min \{m,n,l\},$ respectively. When the dimensions of the matrices are significantly different, for example, $(m,n,l)=(16,128,4)$, our method is more frequently utilized for CMult and Rot compared to the method proposed in [5]. Consequently, the time required for matrix multiplication remains essentially unchanged; however, there is a substantial growth rate compared to the results reported in [4], up to 9X.

5 Conclusion

In this paper, we propose an efficient fully homomorphic encryption scheme called GMS for matrices. The scheme has a smaller ciphertext size and less noise expansion, which allows for efficient updating of the ciphertext through key switching and modulus switching. Furthermore, GMS has significant applications in secure outsourced matrix multiplication. Through theoretical analysis and simulation experiments, our scheme demonstrates lower time complexity and superior performance compared to existing methods. It can be applied to arbitrary matrices, i.e., ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}.$ Compared to existing methods, the secure outsourced matrix multiplication based on GMS has shown significant performance improvements and higher overall efficiency. Our GMS-based secure outsourced matrix multiplication is expected to be widely used in schemes that require matrix multiplication for secure outsourced computation.

In our future work, we have two goals. One goal is to enhance and extend the capacity and ability to process and handle significantly large amounts of data, thereby promoting applicability and utility in large data protection applications that utilize extensive datasets as input. The other goal is to optimize and implement multiple parallel operations to enhance the efficiency of the algorithm.