Abstract
The Non-Interactive Anonymous Router (NIAR) model was introduced by Shi and Wu [SW21] as an alternative to conventional solutions to the anonymous routing problem, in which a set of senders wish to send messages to a set of receivers. In contrast to most known approaches to support anonymous routing (e.g. mix-nets, DC-nets, etc.), which rely on a network of routers communicating with users via interactive protocols, the NIAR model assumes a single router and is inherently non-interactive (after an initial setup phase). In addition to being non-interactive, the NIAR model is compelling due to the security it provides: instead of relying on the honesty of some subset of the routers, the NIAR model requires anonymity even if the router (as well as an arbitrary subset of senders/receivers) is corrupted by an honest-but-curious adversary.
In this paper, we present a protocol for the NIAR model that improves upon the results from [SW21] in two ways:
-
Improved computational efficiency (quadratic to near linear): Our protocol matches the communication complexity of [SW21] for each sender/receiver, while reducing the computational overhead for the router to polylog overhead instead of linear overhead.
-
Relaxation of assumptions: Security of the protocol in [SW21] relies on the Decisional Linear assumption in bilinear groups; while security for our protocol follows from the existence of any rate-1 oblivious transfer (OT) protocol (instantiations of which are known to exist under the DDH, QR and LWE assumptions [DGI+19, GHO20]).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
As the collection and access of digital information in our daily lives becomes ever-more ubiquitous (internet, local networks, mobile networks, IoT), so too does the need for the development of technologies to protect access and transmission of this data. While protecting the integrity and access to sensitive data remain important tasks, there has been a growing need for anonymity in protecting data access and communications between users. Throughout this paper, anonymity will refer to the inability to associate which nodes in a network are communicating with each other; i.e. the unlinkability between one or more senders and the associated receiver(s). The conventional approach to providing such protection (onion routing, mix-nets, and others) relies on a network of routers relaying messages, where anonymity is only guaranteed if there are sufficiently many uncorrupted routers. A markedly different approach to this problem was recently introduced by Shi and Wu [SW21], who proposed using cryptographic techniques to hide connectivity patterns. Namely, they introduce the Non-Interactive Anonymous Router (NIAR) model, in which a set of N receiving nodes wish to receive information from a set of N sending nodes, with all information passing through a central router. Anonymity in their model is defined to be the inability to link any sender to the corresponding receiver, even if the router and (up to \(N-2\)) various (sender, receiver) pairs are susceptible to attack by an (honest-but-curiousFootnote 1) adversary.
There are a number of real-world scenarios in which the NIAR model as described above is relevant. The important characteristics of any such application is that a number of (sender, receiver) pairs wish to anonymously communicate with each other through a central server, where the messages to be transmitted are large and/or the communication channels are non-ephemeral/indefinite. These conditions are exhibited, for example, in the following scenarios:
Anonymous Peer-to-Peer Communication. Relevant in settings where a large set of users wish to communicate anonymously through a central server, e.g. for a Messaging app, where every communication link is established as a separate pair of (anonymous) virtual users.
Pub/Sub with Privacy. Because our solution is quasi-linear in message size, the additional overhead of storing all messages is minimal. We can therefore view the central router of the NIAR model as delivering each stream of messages it receives from the N senders into N storage units, rather than delivering them directly to receivers. In this way, the set of receivers can (privately) subscribe to an information service/source, and periodically receive updates. Furthermore, our protocol allows receivers to (privately) subscribe to multiple services at the same time, without revealing which services they are subscribed to.
Multi-Client PIR/PIW. In a similar spirit as the previous point, viewing the receivers as storage units, the messages being streamed from the senders can accumulate (or update previous messages), thus implementing a form of Private Information Writing (PIW). Depending on the application (in terms of which users will ultimately access/read the PIW server), hiding the linkage between which location each sender writes to versus which location each receiver reads from may require stronger security requirements, e.g. for our protocol, any receiver colluding with the central router will learn which sender it is reading from.
Oblivious Shuffle. A common scenario encountered in MPC protocols is when two or more parties are secret sharing a list of values, and need to obliviously permute the list, so that no party knows the permutation. Our protocol can be used to implement this oblivious shuffle, by viewing one party as acting as all N senders (for its list of N secret shared values), and sending the permuted shares via the “central router” (also being simulated by the sending party) to the other party (who is acting as all N receivers). This process is then reversed, with the other party sending its shares to the first party, via the same permutation. There are subtleties that need to be specified, such as ensuring that the permutation remains unknown to each party (which can be handled as part of the Setup procedure), and how to amortize the process to ensure efficiency (so the Setup does not dominate overall cost), but in general a solution in the NIAR model can be viewed as an instantiation of oblivious shuffle.
Permutation Routing with Anonymity. There has been substantial work in researching permutation routing (e.g. [AKS83, Lei84, Upf89, MS92]), which was inspired due to its relevance to parallel computing (for timing the connections between processors and memory) and fault tolerant routing. Since the NIAR model is essentially permutation routing with anonymity, any applications of permutation routing that stand to benefit from hiding the permutation are relevant to our work.
1.1 Technical Challenges
Notice that (assuming PKI) an immediate solution to anonymity in the NIAR model is to have each sender encrypt their message (under the desired receiver’s public key or using a shared secret key with the recipient), send the encrypted message to the center router, and then simply have the router flood all N (encrypted) messages to each of the N receivers. While this naïve approach satisfies anonymity (as well as privacy, in that receivers only receive messages intended for them), it has the pitfall of excessive communication: O(N) for each receiver, and \(O(N^2)\) for the router. Shi and Wu [SW21] present a protocol which, under the Decisional Linear assumption (on certain bilinear groups), achieves anonymity with minimal communication overhead.
Having re-framed the goal of anonymity to the NIAR model and with the toolbox of cryptographic techniques at hand, a natural observation is that Private Information Retrieval (PIR) can be used as a potential solution. In a (single server) PIR protocol [KO97], a server stores a database DB of N elements, and a client issues a query to the server to retrieve the \(i^{th}\) element DB[i], for i of its choice. Security in the PIR model means that the server does not learn any information about the index i being queried. Thus, if N senders encrypt their messages and send them to the router, we can let the router act as a PIR server with the N concatenated (encrypted) messages forming the contents of the PIR database. Each receiver can then issue a PIR query to fetch the appropriate message, and anonymity follows from the security of PIR. As with the protocol of [SW21], this solution enjoys both the requisite security features, as well as having minimal communication overhead (e.g. \(\log N\) overhead, depending on the PIR protocol; see survey of PIR results in [OS07]).
An important metric in determining the feasibility of a protocol in the NIAR model is the end-to-end message transmission time, which depends on the computational burden on each user, and especially that of the central router.
A significant drawback of both the protocol of [SW21]Footnote 2 and the naïve PIR solution described above is that they require quadratic (in terms of the number of users) computation at the router. As this computation cost is likely prohibitive (or at least extremely inefficient) when there are a large number of users, we set out to explore the possibility of a NIAR protocol that maintained the minimal communication burden of the naïve PIR and [SW21] solutions, but reduced computation overhead (at the router) from \(O(N^2)\) closer to the optimal O(N).
Our first observation is that the NIAR model is similar to so-called “permutation routing” (see Sect. 2.1), but with an additional anonymity requirement. Namely, permutation routing seeks to connect N senders to N receivers through a network, which (from a communication standpoint) is what is required in the NIAR model. Our main idea was to leverage the efficient routing (and therefore minimal overhead) of a permutation-routing network, but then to administer PIR at each node to keep each routing decision hidden, thereby allowing for the anonymity required by the NIAR model. In particular, we envisioned a solution in which the central router simulates a virtual permutation-routing network by itself, where the actual path the messages take (from each of the N senders on one end of the network to the N receivers at the other end) is hidden (from the central router) by using PIR along each edge. Namely, at each node of the (virtual) network, a PIR query is applied to each of the node’s outgoing edges, where the PIR query (privately) selects a message from one of the node’s incoming edges.
While the above idea captures the spirit of our solution (and indeed, the idea of layering PIR on top of various routing networks/protocols may have other interesting applications for anonymizing communication), there are several complications that required additional consideration:
-
1.
(Virtual) Network Size. Since each outgoing edge in the routing network is assigned a PIR query, and this PIR query is applied to a (virtual) database whose size is the number of incoming edges of the node in question, the computation cost of simulating routing in a virtual network is roughly \(O(E \cdot I)\), where E is the number of edges and I is the number of incoming edges per node. Since E is necessarily at least \(\varOmega (N)\), having a NIAR protocol with only polylog computation overhead requires that E is at most
 and I is
and I is  .
. -
2.
Standard PIR Won’t Work. Even if network size is small (\(O(N \cdot polylog(N))\)), if the depth (number of nodes a message passes through from sender to receiver) is not constant, then standard PIR schemes will not work, since each invocation of PIR typically has O(polylog(N)) bits in the PIR server’s response, and hence the message size will incur an exponential blow-up with network depth. For example, even log-depth networks will have messages of size \(O(2^{\log N}) = O(N)\) by the time they reach the last layer of the network, which is no better than the naïve PIR approach mentioned above.
-
3.
Correctness Requires Edge-Disjoint Paths. Since PIR is being used to hide routing decisions made at each node/routing gate in the network, this requires that each outgoing edge forwards the message on (at most) one of the node’s incoming edges. In particular, if any two paths connecting two different sender-receiver pairs in the permutation network contain a common edge, then correctness is compromised. Since a random path selection algorithm will be crucial to proving anonymity, the given (virtual) permutation network must have the property that, with high probability, a random sample of paths connecting the sender-receiver pairs are edge-disjoint.
-
4.
Edge-Disjoint Property is Insufficient for Anonymity. While having edge-disjoint paths is necessary for correctness, it is not sufficient to ensure anonymity. For example, if the central router is colluding with (N-2) sender-receiver pairs (and therefore only needs to determine the linkage amongst the remaining two senders and two receivers), then knowledge that all paths are edge-disjoint can give the router an advantage in identifying the linkage between the remaining two senders and two receivers. Namely, the router knows (via collusion) N-2 paths, and thus can eliminate available options for the remaining two paths. For example, this attack is viable in the Beneš network (which is commonly used in permutation routing literature; see Sect. 3.1) making it unsuitable when anonymity is required, and justifying our usage of a more complex network. Indeed, since permutation-routing networks have been studied outside of the context of anonymity, to our knowledge there has not been any research into understanding how network properties and path selection protocols impact anonymity.
1.2 Overview of Our Results
Our solution to the NIAR problem, which blends techniques from permutation routing with techniques for hiding routing decisions made at each node of the (virtual) permutation network, overcomes the challenges outlined in the previous section as follows. By using familiar permutation-routing networks, which are inherently small (\(O(N \cdot polylog(N))\)), we ensure the network size is suitably small, thus addressing the first potential issue. Furthermore, a common (and well-studied) feature of many permutation-routing networks is the edge-disjoint property, which inspired our choice to use an (extended) Beneš permutation Network, thus addressing the third issue. We observe that there is an inherent tension between network topology (number of nodes, edges, and depth) in terms of achieving correctness and anonymity versus low router computation. Our solution includes carefully selecting appropriate network parameters to balance these trade-offs. Meanwhile, recent works [DGI+19, GHO20, CGH+21] present so-called rate-1 PIR protocols, which can address the second issue of exponential growth of message size per network layer.
Addressing the fourth issue is one of our key technical achievements. In spirit, the edge-disjoint property is related to anonymity, but as mentioned above, it is in general insufficient. Identifying a property that is sufficient (and simultaneously not over-cumbersome in terms of network size), and then using such a property to formally argue anonymity, requires some thought and careful analysis. Informally, this property states that not only are N randomly chosen permutation paths through the network edge-disjoint (w.h.p), but even if the permutation swaps the output nodes of any two input nodes and two new paths are created to join these, then the collection of the old edges plus the two new sets of edges are still edge disjoint (w.h.p); see Definition 4.
Assuming rate-1 PIR, we present in Fig. 3 a routing protocol for the NIAR model that achieves \(O(\log N)\) per-party communication and \(O(N \cdot polylog(N))\) router computation. At a high level, our protocol dictates that the central router emulates routing in a permutation network, whereby each routing gate is (virtually) obliviously evaluated using a rate-1 PIR query/response for each outgoing edge. Our protocol consists of a setup phase in which the PIR queries that correspond to all outgoing edges of every routing gate are prepared, and then an online routing phase where a stream of (encrypted) messages are injected by the senders and routed to the receivers (re-using the setup).
A succinct comparison of our results to other relevant works is in Sect. 2.3.
2 Previous Work
2.1 Permutation Routing
In permutation routing [AKS83, Lei84, Upf89, MS92], messages from a set of N “input” nodes are routed through a network G to a set of N distinct “output” nodes. Such works attempt to identify networks G with various desired properties, and protocols within these networks that can efficiently route these messages, for any possible permutation \(\sigma \) that dictates which input node is connected to which output node. While our work is partially inspired by the routing networks considered in this line of work, the NIAR model is quite different than the permutation routing model, both because of the number of routers (one versus \(\varTheta (N \log N)\)) and due to the required privacy of the permutation \(\sigma \). In other words, we do not route the messages over a physical routing network (which is an iterative process that depends on the “depth” of the network), but rather we design our non-interactive routing protocol using a virtual sorting network.
2.2 PIR
There has been an extensive amount of work done on the original PIR problem [CGKS95, KO97] and its variants. Here, we discuss only a few of these works that are most relevant to us.
Multi-Client PIR. As discussed in the introduction, the NIAR problem can be solved using multi-client PIR. Indeed, a solution to generic multi-client PIR in which the PIR server’s work does not scale with the number of users would imply an efficient solution for NIAR. While no such result is known, we discuss a few relevant works and why they are insufficient for the NIAR model.
In [IP07], it is demonstrated how a single user can efficiently issue multiple queries to a PIR server. However, their results rely on a single decoding algorithm, whereas the NIAR model would require distinct decoding keys for each of the N receivers. [HOWW19] present a related notion of private anonymous data access; we note that the results in their model do not scale to the full corruption threshold (\(N-2\)) required in the NIAR security model. Finally, results in the related areas of Batch Codes [IKOS04] and Public-Key Encryption with amortized updates [COS10] address a different model, and consequently do not seem to be directly applicable to the NIAR model.
Rate-1 PIR. A recent line of work [DGI+19, GHO20, CGH+21] has demonstrated the viability of rate-1 PIR, in which the server response is comparable in size to the database entry being fetched. Formally, for a database of N elements each of size B, rate-1 PIR means that the ratio of B to the server response size approaches 1 as \(N \rightarrow \infty \). Stated differently, a rate-1 PIR scheme has an additive constant-stretch term \(\delta _{{ PIR}}\), such that the server’s response has size \(B + \delta _{{ PIR}}\). Rate-1 PIR is known to exist under the DDH, QR and LWE assumptions [DGI+19, GHO20].
Doubly Efficient PIR (DEPIR). In a recent result of Lin et al. [LMW22], they demonstrate a PIR protocol that, after a pre-processing phase that costs \(O(N^{1 + \epsilon })\) in server computation, enjoys polylog N communication and computation for each PIR query. If this DEPIR protocol were to be used to solve the NIAR problem (as per the straightforward application described in Sect. 1.1), the resulting protocol would have \(O(N^{1 + \epsilon })\) computation at the router for each new message packet/bit of the senders (since each database update would trigger a new “pre-processing” phase of the PIR server).
Various security requirements/settings relevant to the NIAR model. All four scenarios include collusion with router C, plus: - Top Setting (N-2 Pairs): Corruption of up to N-2 (sender, receiver) pairs; - Left Setting (Sender Collusion): Corruption of all senders (and N-2 receivers); - Right Setting (Receiver Collusion): Corruption of all receivers (and N-2 senders); - Bottom Setting (Arbitrary): Corruption of any \(2N - 2\) senders/receivers. The implication arrows indicate that a protocol that is secure in one setting is automatically secure in the other.
2.3 Comparison with Other Results in NIAR Model
The NIAR model was introduced in [SW21], which included several variants of the security requirement, and offered solutions for these variants. As mentioned, our results improve upon those of [SW21] in three main ways: (i) Reduced router overhead (\(O(N \cdot polylog N)\) versus \(O(N^2)\)); (ii) Seemingly simpler protocol based on weaker/more standard cryptographic assumptions; (iii) Improved practical/observed efficiency (not empirically verified). On the other hand, the protocol of [SW21] provides protection in different scenarios of security requirements. Namely, in terms of Fig. 1, our protocol focuses on the top and left settings, while [SW21] covers the top, right, and bottom settings. However, for all of the motivating examples discussed in the Introduction, security in the top and left settings (which our protocol provides) is sufficient.
A recent work of Fernando et al. [FSSV22] improves upon the work of [SW21], by reducing router computation to \(O(N \cdot polylog N)\), which (asymptotically) matches our result. However, the other comparisons between our work and that of [SW21] are still valid; namely, our protocol benefits from simpler assumptions and protocol complexity (e.g. we do not require obfuscation) as well as practical efficiency, but ours does not offer protection against full receiver collusion.
A summary of the comparison of our results to other relevant results can be found in the table below, where \(\widetilde{N} = O(N \cdot polylog N)\) denotes quasi-linear:
Protocol | Anonymity Level\(^a\) | Crypto Assumptions | Comm. | Router Comp. |
|---|---|---|---|---|
Permutation Routing | None | N/A | \(\widetilde{N}\) | \(\widetilde{N}\) |
Naïve PIR | Sender Collusion | PIR | \(\widetilde{N}\) | \(N^2\) |
DEPIR [LMW22]\(^b\) | Sender Collusion | Ring LWE | \(\widetilde{N}\) | \(N^{1 + \epsilon }\) |
Original NIAR[SW21] | Receiver Collusion | DLIN | \(\widetilde{N}\) | \(N^2\) |
Arbitrary | Obfuscation | \(\widetilde{N}\) | \(N^2\) | |
Improved NIAR [FSSV22] | Arbitrary | Obfuscation | \(\widetilde{N}\) | \(\widetilde{N}\) |
Our Results | Sender Collusion | DDH or QR or LWE | \(\widetilde{N}\) | \(\widetilde{N}\) |
3 Preliminaries
3.1 Beneš Network
(The networks mentioned here are common in the permutation routing literature, see for example [AKS83, Lei84, Upf89, MS92]. Figures depicting each of the networks described below can be found in the extended version of this paper). In a butterfly network, N input nodes are connected to N output nodes via a leveled network of \((1 + \log N)\) levels, each with N nodes. A Beneš network appends a second (inverted) butterfly network to the first; and more generally an extended Beneš network appends many “blocks” of butterfly networks together. We continue expanding on this model by replicating each node and edge c times, which can be conceptualized as coloring them with c distinct colors. Finally, our protocol will assume wide edges, which means that each edge can simultaneously route w messages (requiring specification of which of the w “slots” each message occupies).
3.2 Non-Interactive Anonymous Routing (NIAR)
We adopt the NIAR model of [SW21], in which N senders each has a series of m (e.g. single-bit) messages they wish to send to a distinct receiver anonymously. The anonymity guarantee refers to the unlinkability of each sender-receiver pair, and crucially it must be preserved even if the central router colludes with a subset of the senders/receivers. Depending on the application, there are various collusion patterns that may be of interest, see e.g. Fig. 1.
In this paper, we demonstrate our protocol is secure against the top and left settings (in Fig. 1). We do not consider the right and bottom settings (Receiver Collusion and Arbitrary) in this paper for two reasons: First, in the main application areas for the NIAR model (see Introduction above), the receivers already know the senders they wish to connect to, so anonymity of the senders (in the case that all receivers are colluding) is irrelevant. The second reason is because providing protection in settings when all Receivers collude with the router requires additional techniques than those considered in this paper. For example in [SW21] and [FSSV22], the protocol description, performance, and cryptographic hardness assumptions are all more complex in the Arbitrary collusion setting.
Formally, the (reformulated) NIAR model of [SW21] is as follows:
(Trusted) Setup. Upon input security parameters \((1^{\lambda _c}, 1^{\lambda _s})\), number of senders/receivers N, and permutation \(\sigma : [N] \rightarrow [N]\), the Setup algorithm outputs sender keys \(\{pk_i\}_{i \in [N]}\), receiver keysFootnote 3 \(\{(sk_i, \kappa _i)\}_{i \in [N]}\), and token \(\textsf{q}\) for router C:  .
.
Once Setup has been run, the Senders \(\{S_i\}\) can communicate arbitrary messages \(\{m_i\} = \{m_{i,\alpha }\}\) with the Receivers \(\{R_i\}\) through router C.
Send Message. Using key \(pk_i\), each Sender \(S_i\) encodes message \(m_i = m_{i,\alpha }\) (where \(\alpha \) denotes the \(\alpha ^{th}\) bit of message \(m_i\)), and sends the result to router C:  .
.
Route Message. Upon inputs \(\{c_i\}_{i \in [N]}\) from each Sender \(S_i\), and using key \(\textsf{q}\), router C prepares messages \(\{z_i\}_{i \in [N]}\), and sends these to each Receiver \(R_i\):  .
.
Decode Message. Using keys \((sk_i, \kappa _i)\), each Receiver \(R_i\) decodes the message \(z_i = z_{i,\alpha }\) received from router C, and outputs \(\widetilde{m}_i = \widetilde{m}_{i, \alpha }\):  .
.
Correctness. An oblivious permutation routing protocol has:
 : If each receiver \(R_i\) outputs message \(\widetilde{m}_i\)\(\scriptstyle {=}\)\(m_i\) with probability 1.
: If each receiver \(R_i\) outputs message \(\widetilde{m}_i\)\(\scriptstyle {=}\)\(m_i\) with probability 1.
 : If each receiver \(R_i\) outputs message \(\widetilde{m}_i\) \(\scriptstyle {=}\) \(m_i\) with probability at least \(\left( 1 - \frac{1}{2^{\lambda _c}}\right) \), for security parameter \(\lambda _c\).
: If each receiver \(R_i\) outputs message \(\widetilde{m}_i\) \(\scriptstyle {=}\) \(m_i\) with probability at least \(\left( 1 - \frac{1}{2^{\lambda _c}}\right) \), for security parameter \(\lambda _c\).
Security. Informally, anonymity means that if a subset of parties collude (including router C), the permutation \(\sigma \) (namely, its restriction to non-colluding parties) should remain unknown. Formally, let \(\mathcal {A}\) denote a (computationally bounded, honest-but-curious) adversary. Consider the following challenge game:
-
1.
On input security parameter \(\lambda \), Adversary \(\mathcal {A}\) chooses N, two distinct permutations \(\sigma _0, \sigma _1\) on [N], a set of sender indices \(S_{\mathcal {A}} \subseteq [N]\) to corrupt, and a set of receiver indices \(R_{\mathcal {A}} \subseteq [N]\) to corrupt, subject to the following constraints:
-
(a)
\(|R_{\mathcal {A}}| \le N - 2\);
-
(b)
\(\sigma _0\) and \(\sigma _1\) match for all receivers in \(R_{\mathcal {A}}\):
 .
.
-
(a)
-
2.
Adversary \(\mathcal {A}\) sends \(\{\sigma _0, \sigma _1\}\) to Challenger \(\mathcal {C}\).
-
3.
Challenger \(\mathcal {C}\) chooses \(\sigma _b \in \{\sigma _0, \sigma _1\}\) for \(b \leftarrow \{0,1\}\) (e.g. by flipping a coin).
-
4.
Challenger \(\mathcal {C}\) chooses router token \(\textsf{q}\), encryption keys \(\{\textsf{pk}_i\}_{i\in [N]}\), and decryption keys \(\{\textsf{sk}_i\}_{i \in [N]}\). \(\mathcal {C}\) sends \(\textsf{q}\), \(\{\textsf{pk}_i\}_{i\in S_{\mathcal {A}}}\), and \(\{\textsf{sk}_i\}_{i \in R_{\mathcal {A}}}\) to \(\mathcal {A}\).
-
5.
For each round \(\alpha \):
-
(a)
Based on knowledge of all prior ciphertexts \(\{c_{i,\alpha '}\}_{\alpha ' < \alpha }\) (see next step), Adversary \(\mathcal {A}\) chooses messages \(\{m^{(0)}_{i,\alpha }\}_{i \in [N]}\) and \(\{m^{(1)}_{i,\alpha }\}_{i \in [N]}\), subject to the constraint that all messages bound for a corrupt receiver match:
 s.t. \(i = \sigma _0^{{-}1}(j)\) for some \(j \in R_{\mathcal {A}}\): \(m^{(0)}_{i,\alpha } = m^{(1)}_{i,\alpha }\). \(\mathcal {A}\) sends \(\{m^{(0)}_{i,\alpha }\}\), \(\{m^{(1)}_{i,\alpha }\}\) to \(\mathcal {C}\).
s.t. \(i = \sigma _0^{{-}1}(j)\) for some \(j \in R_{\mathcal {A}}\): \(m^{(0)}_{i,\alpha } = m^{(1)}_{i,\alpha }\). \(\mathcal {A}\) sends \(\{m^{(0)}_{i,\alpha }\}\), \(\{m^{(1)}_{i,\alpha }\}\) to \(\mathcal {C}\). -
(b)
Challenger \(\mathcal {C}\) outputs to \(\mathcal {A}\) ciphertexts \(\{c_{i,\alpha }\}_{i \in [N]}\), where each ciphertext is computed as (with b as chosen in Step 3): \(c_{i,\alpha } = Enc_{\textsf{pk}_i}(m^{(b)}_{i,\alpha })\).
-
(a)
-
6.
Adversary \(\mathcal {A}\) outputs a guess \(b' \in \{0,1\}\) of which permutation \(\{\sigma _0, \sigma _1\}\) Challenger \(\mathcal {C}\) chose.
A NIAR protocol is \(\mathsf {\lambda _{s}}\) -secure if the probability that any computationally bounded adversary \(\mathcal {A}\) guesses b correctly is bounded by:

3.3 Emulating Oblivious Routing in a Virtual Routing Network
In this section, we present the main ideas that connect the NIAR model to the permutation routing problem. At a high level, the idea is to have the NIAR router emulate message transmission through a (virtual) routing network that supports permutation routing between N senders and receivers. In particular, we view the N senders as input nodes in the routing network, and the N receivers as the output nodes, and then choose paths through the routing network connecting each sender to its receiver. The NIAR router then passes messages from each sender to the designate receiver by routing messages along this path. Note that this entire network, except the input nodes (corresponding to the senders) and output nodes (corresponding to the receivers), together with message routing within it, is entirely simulated by the NIAR router.
In order to preserve anonymity in terms of linkage between each (sender, receiver) pair, the paths that each message takes through this (virtual) routing network must remain hidden to the NIAR router. The key primitive that we utilize to achieve this is called an oblivious routing gate., informally defined as:
Definition 1
(Informal). An oblivious routing gate describes a process in which the messages on w incoming wires of a gate are routed to its w outgoing wires, in such a way that the process that is performing the routing is unaware of the linkage between (incoming wire, outgoing wire) of each message.
Notice that PIR can be used to instantiate an oblivious routing gate, by using PIR queries to secretly select the incoming edge to read from, and then having the PIR server (that is doing the actual routing) write its corresponding PIR response along that outgoing edge; see Fig. 2.
Routing in the NIAR model can be achieved by combining the oblivious routing gate paradigm with ordinary routing through a permutation network, as follows:
Definition 2
(Informal). Denote NIAR parameters: N, permutation \(\sigma : [N] \rightarrow [N]\), “central router” party C, “sender” parties \(\{S_i\}_{_{i \in [N]}}\) with messages \(\{m_{i,\alpha }\}\), “receiver” parties \(\{R_i\}_{_{i \in [N]}}\), and let G denote a given routing network. An emulated permutation routing protocol \(\varPi _{EPR}\) performs NIAR routing by having C route the \(\alpha ^{th}\) message of each sender \(\{m_i\}\) through the (emulated) network G, in which messages are routing from the incoming edge of a network node to an outgoing edge via the oblivious routing gate paradigm.
Due to space limitations, the formal definitions of oblivious routing gate and emulated permutation routing, as well as example instantiations via PIR, appear in the extended version.
4 Our Protocol
4.1 Overview of Our Solution
Given N pairs of (sender, receiver) nodes and central router C, our protocol routes messages from the senders to the corresponding receivers via a virtual routing network G that C emulates where, for each node in the network, the router C obliviously executes a routing gate by simulating the functionality of a (rate-1) PIR query. Namely, (as part of trusted setup) each outgoing edge of a routing gate will have an assigned PIR query, and each incoming edge will have a value (which represents an encrypted message from one of the senders). Then the router C obliviously produces a message on each outgoing edge of the routing gate by running the associated PIR query on this wire against the (virtual) PIR database of messages (from the incoming wires). The determination of which incoming edge that a given PIR query (on a routing gate’s outgoing edge) should specify is established offline during a setup phase, and specifically it is determined by choosing a random path \(\mathcal {P}_i\), for each (sender\(_i\), receiver\(_i\)) pair, through the (virtual) routing network G. Notice that once PIR queries are assigned (during an offline setup phase) as per all chosen paths \(\{\mathcal {P}_i\}\), they may be reused indefinitely during the online routing phase to continuously route new messages for each (sender, receiver) pair. The main features of our solution are as follows:
-
Correctness. Ensuring each receiver gets every message reduces to showing that the paths \(\{\mathcal {P}_i\}\) connecting each (sender\(_i\), receiver\(_i\)) pair are edge-disjoint.
-
Privacy. Since each sender encrypts their messages under the intended receiver’s public key, receivers can only decipher messages intended for them.
-
Anonymity. This property is obtained so long as the paths \(\{\mathcal {P}_i\}\) chosen are “sufficiently edge-disjoint” (for details see Definition 23).
-
Communication. To limit the expansion of message size through each (virtual) routing gate, we employ rate-1 PIR, which ensures the final message size is proportional to the length of the chosen path \(\mathcal {P}\) through the (virtual) routing network G; and that any such path is short (i.e. of polylogN length).
-
End-to-End Time. Computation of central router C (which, together with communication, determines end-to-end transmission time) will depend on the size of the virtual graph \(G = (V, E)\). Thus, in order to minimize computational overhead, |E| should be close to N (e.g. \(N\cdot polylog N\)). Notice that there is inherent tension in minimizing end-to-end time versus satisfying the Correctness and Anonymity properties: the former requires small |V| and |E|, while the latter two are readily achieved for larger |V| and |E|. Our protocol finds appropriate (minimal) parameters to achieve correctness and anonymity, while introducing minimal end-to-end overhead.
We stress that some relaxed approaches to the NIAR problem actually fail to provide anonymity. Specifically, the approach of deploying an arbitrary permutation-routing network (without the extra features that we require), and the approach of just replacing each gate in the routing network (even a properly selected network) with PIR, do not seem sufficient, which we argue as follows.
While PIR is the main tool that hides (from central router C and any other parties it colludes with) the linkage between uncorrupted (sender, receiver) pairs, applying it naïvely will not provide the desired protection. Namely, if any two of the paths \(\{\mathcal {P}_i\}\) through the virtual routing network have an edge in common, then a PIR query cannot be assigned to that edge, as there will be conflicting input edge indices (and conflicting messages on those edges) to select. Since, in proving anonymity, path selection must be a randomized process (in particular, edge conflicts cannot be deliberately avoided), our protocol will handle edge conflicts by producing garbage PIR queries for such edges. While this approach introduces failures in terms of delivering messages along the conflicting paths that were chosen for any such (sender, receiver) pairs, the threat to correctness is overcome by ensuring enough redundancy in the system to account for (the low probability event of) edge conflicts. However, edge conflicts (and the lack of edge conflicts), also threatens anonymity: for example, the router C could observe many messages from (sender, receiver) pairs it has corrupted all pass through a common node, and the router may also know that the message from an uncorrupted sender has some probability of passing through this same node. Thus, the presence or absence of an edge conflict on the set of outgoing edges of this node may give the router an advantage in determining if the uncorrupted sender’s path goes through this node, and if so, some probabilistic advantage in knowing which outgoing edge the path used; and these advantages then threaten anonymity since the router may be able to have an advantage in guessing the ultimate destination (i.e. receiving node) of this path. Demonstrating that this approach cannot be used to give the router a non-negligible advantage in linking uncorrupted (sender, receiver) pairs will require: (i) Identifying what property a network should have to avoid this attack; (ii) Generating such a routing network that also supports the desired complexity and correctness requirements; (iii) An appropriate analysis that this property indeed proves anonymity. For example, the natural candidate property of exhibiting (with high probability on randomly chosen paths) the edge-disjoint property is insufficient, as it is susceptible to the above attack.
Figure 3 below gives pseudocode of our \(\varPi _{APR}\) protocol (due to space constraints, the full protocol can be found in the extended version).
4.2 Analysis of Our Protocol
Theorem 3
Assuming the existence of rate-1 PIR, following trusted setup,Footnote 4 the protocol presented in Fig. 3 is \(\lambda _s\)-secure with \(\lambda _c\)-statistical correctness, \(O(\log N)\) per-party communication, and  router computation.
router computation.
Remark. Instead of trusted setup, under appropriate cryptographic hardness assumptions the ideal functionality \(\varPi _{ORG}(G,\widehat{c},r,l,\varPi _{1{-}PIR})\) could instead be realized via generic secure multiparty computation (MPC) techniques. This would contribute  to the asymptotic cost of the protocol (to deal the
to the asymptotic cost of the protocol (to deal the  rate-1 queries and
rate-1 queries and  reconstruction keys), but because \(\varPi _{ORG}(G,\widehat{c},r,l,\varPi _{1{-}PIR})\) is utilized only in the Setup Phase, this would be incurred as a one-time cost and would not impact cost of the Routing Phase.
reconstruction keys), but because \(\varPi _{ORG}(G,\widehat{c},r,l,\varPi _{1{-}PIR})\) is utilized only in the Setup Phase, this would be incurred as a one-time cost and would not impact cost of the Routing Phase.
Proof
(Theorem 3, Sketch). Let  . Then the specific permutation network \(G = B(\widehat{N},b,c,w)\) used in \(\varPi _{APR}\) is a wide-edged, extended and colored Beneš network (see Sect. 3.1) with parameters \(\widehat{N} = N\), \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+\log N)\) (for \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)).
. Then the specific permutation network \(G = B(\widehat{N},b,c,w)\) used in \(\varPi _{APR}\) is a wide-edged, extended and colored Beneš network (see Sect. 3.1) with parameters \(\widehat{N} = N\), \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+\log N)\) (for \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)).
Cost. Per-party computation and communication costs for the routing phase are:

where:
-
\(|E| = (2 \log N + c) \cdot (c \cdot w \cdot N \cdot (1+b)) \hbox {isthenumberofedgesinnetworkB(N,b,c,w).}\)
-
\(Cost(\varPi _{Enc})\) is the (computation) cost of encrypting a message m.
-
\(Cost(\varPi _{Dec})\) is the (computation) cost of decrypting a ciphertext \(Enc_{pk_i}(m)\).
-
\(c_{_{Enc}}\) is the size of a ciphertext \(Enc_{pk_i}(m)\).
-
\(\delta _{{ PIR}}\) is the constant stretch of the underlying rate-1 PIR protocol \(\varPi _{1{-}PIR}\).
-
\(Cost(\varPi _{PIR{-}Query})\) is the PIR server cost of \(\varPi _{1{-}PIR}(c \cdot w, c_{_{Enc}}+ (1+b) \cdot \delta _{{ PIR}})\).
-
\(Cost(\varPi _{PIR{-}Rec})\) is the cost of running the reconstruction algorithm (on a PIR response) for \(\varPi _{1{-}PIR}(c \cdot w, c_{_{Enc}}+ (1+b) \cdot \delta _{{ PIR}})\).
Correctness. The intuition for the proof is as follows: Independent of adversarial presence, we first demonstrate bounds of certain properties of routing in the Beneš network, as per the protocols described in Fig. 3. Namely, we demonstrate in Corollary 19 that, with overwhelming probability, for any row index \(i \in [N]\) there will exist (at least) one experiment \(m \in [M]\) for which the path \(\mathcal {P}_{m,i}\) is edge-disjoint from all other paths \(\{\mathcal {P}_{m,j}\}_{j \ne i}\). Then as per protocol \(\varPi _{APR}\) specification (Step 2b of the Output Parties portion of the Routing Phase; see Fig. 3), the existence of an edge-disjoint path \(\mathcal {P}_i\) means that \(R_{\sigma (i)}\) will update \(\widetilde{w}_i \leftarrow \widetilde{w}_{m,i}\). By the correctness property of the ideal functionality of \(\varPi _{ORG}\), this value will be correct (i.e. it will equal \(p_i\)).
Formally, with  , Lemma 19 states that the probability that there exists some row index \(i \in [N]\) for which \(\mathcal {P}_{m,i}\) is not edge-disjoint for every experiment \(m \in [M]\) is bounded by:
, Lemma 19 states that the probability that there exists some row index \(i \in [N]\) for which \(\mathcal {P}_{m,i}\) is not edge-disjoint for every experiment \(m \in [M]\) is bounded by:

Security. As with the Correctness proof, we first demonstrate (probability bounds for) a version of the edge-disjoint property in the Beneš graph G (Sect. 3.1) used in Fig. 3. Namely, we demonstrate in Corollary 27 that, using the parameters as per \(\varPi _{APR}\) (Fig. 3), with overwhelming probability (in \(\lambda _s\)), for any pair of row indices \(i,i' \in [N]\) and for every experiment \(m \in [M]\), there will exist a block in which the chosen paths \(\mathcal {P}_{m,i}\) and \(\mathcal {P}_{m,i'}\) as well as their alternate paths \(\mathcal {P}'_{ m,i}\) and \(\mathcal {P}'_{ m,i'}\) are each edge-disjoint from all other paths in this block. Effectively, this means that for any two uncorrupted receiver nodes \(i, i' \notin R_{\mathcal {A}}\), that for each experiment there exists some block in which the Adversary will necessarily lose all ability to distinguish between \(\mathcal {P}_{m,i}\) and \(\mathcal {P}_{m,i'}\) by the time these paths cross through this block. We then use a hybrid argument to show that the existence of an adversary that can distinguish between two arbitrary permutations (as per (1)) implies the existence of an adversary who can distinguish (with a smaller probability) between two permutations that differ only on two points; and then this contradicts the existence of a block in which any two paths become indistinguishable after that block.
Formally, the proof reduces the NIAR security game (with Challenger invoking the protocol \(\varPi _{APR}\) of Fig. 3) to Challenge Game 2, and then uses the indistinguishability of Challenge Game 2 (Lemma 29). To match notation of \(\varPi _{APR}\) with the communication sent to adversary \(\mathcal {A}\) in the NIAR security game:
-
For Step 4 of the NIAR security game:
-
Encryption keys \(\{\textsf {pk}_i\}\): The \(\{pk_i\}\) from Step 1 of the Setup Phase (Fig. 3).
-
Decryption keys \(\{\textsf {sk}_i\}\): The \(\{sk_i\}\) from Step 1 of the Setup Phase, together with the reconstruction keys \(\{\kappa _i\} = \{(\mu , j, \kappa _{\mu ,j})\}\) from Step 2b of the Setup.
-
Router token \(\textsf{q}\): The rate-1 PIR queries \(\{q_{\mu ,j}\}\) from Step 2b of the Setup.
-
-
For Step 5b of the NIAR security game:
-
Ciphertexts \(\{c_{i,\alpha }\}\): The encrypted messages \(\{Enc_{pk_i}(m_{i,\alpha })\}\) from Sender’s Step 1 of the Routing Phase (Fig. 3).
-
First observe that indistinguishability of the distribution of ciphertexts \(\{c_{i,\alpha }\} = \{Enc_{pk_i}(m_{i,\alpha })\}\) under \(b=0\) versus \(b=1\) follows from the security of the encryption scheme, together with the constraint that all messages bound for a corrupt receiver must match for \(b=0\) and \(b=1\) (see the specified constraint in Step 5a of the NIAR security game). Thus, for any ciphertext \(c_{i,\alpha }\) for which Adversary \(\mathcal {A}\) does not hold the decryption key, the security of the encryption scheme ensures indistinguishability of this as a ciphertext of \(m^{(0)}_{i,\alpha }\) versus \(m^{(1)}_{i,\alpha }\); and for any ciphertext \(c_{i,\alpha }\) for which Adversary \(\mathcal {A}\) does hold the decryption key, the constraint in Step 5a of the NIAR security game dictates that this ciphertext encodes a common message \(m^{(0)}_{i,\alpha } = m^{(1)}_{i,\alpha }\).
Next we argue indistinguishability of the encryption keys \(\{pk_i\}_{i \in S_{\mathcal {A}}}\) and the decryption keys \(\{sk_i\}_{i \in R_{\mathcal {A}}}\). Notice first that due to the constraint in Step 1b of the NIAR security game, the distribution of decryption keys \(\{sk_i\}_{i \in R_{\mathcal {A}}}\) looks the same for \(b=0\) and \(b=1\), since \(\sigma _0\) and \(\sigma _1\) necessarily agree here (i.e. they each map some index \(j \in [N]\) to i. Meanwhile, for the distribution of encryption keys, we focus on indices \(i \in [N]\) for which \(\sigma _0(i) \ne \sigma _1(i)\). Fix any such i, and define \(j = \sigma _0(i)\) and \(j' = \sigma _1(i)\), so \(j \ne j'\). Again due to the constraint in Step 1b of the NIAR security game, we have that neither j nor \(j'\) is in \(R_{\mathcal {A}}\). This means that Adversary \(\mathcal {A}\) does not hold the corresponding decryption key for \(pk_i\) regardless of whether \(b=0\) or \(b=1\), and thus by the security of the encryption scheme, the distribution of \(pk_i\) for \(b=0\) appears identical as the distribution when \(b=1\).
For indistinguishability of the router token \(\textsf{q}=\{q_{\mu ,j}\}\): for a given \(q_{\mu ,j}\) for which Adversary \(\mathcal {A}\) does not hold the corresponding reconstruction key \(\kappa _{\mu ,j}\), indistinguishability follows from the security of the underlying rate-1 PIR scheme. Conversely, for a given \(q_{\mu ,j}\) for which Adversary \(\mathcal {A}\) does hold the corresponding reconstruction key \(\kappa _{\mu ,j}\), \(\mathcal {A}\) learns the input wire index that \(q_{\mu ,j}\) is selecting. However, the paths chosen through G (see Step (3a) of Setup Phase) are random and independent of each other and depend only on the given (sender, receiver) indices. Also, \(\mathcal {A}\) knows reconstruction key \(\kappa _{\mu ,j}\) if and only if outgoing edge \((\mu , j)\) is on the path leading to a corrupt receiver \(i \in R_\mathcal {A}\). Therefore, we again rely on the constraint in Step 1b of the NIAR security game to argue that \(\sigma _0\) and \(\sigma _1\) must agree on the (sender, receiver) indices for this path, so the input wire index that \(q_{\mu ,j}\) is selecting is the same.
It remains to argue indistinguishability of the reconstruction keys \(\{\kappa _i\}_{i \in R_\mathcal {A}}= \{(\mu , j, \kappa _{\mu ,j})\}\). If for a given tuple \((\mu , j, \kappa _{\mu ,j})\) the last component is a valid reconstruction key (i.e. \(\kappa _{\mu ,j} \ne \bot \)), then indistinguishability follows the same argument as above for the router token. On the other hand, if \(\kappa _{\mu ,j} \ne \bot \), then as per the Correctness property of any \(\varPi _{ORG}\) protocol, Adversary \(\mathcal {A}\) learns that at least two distinct paths chose outgoing edge \((\mu , j)\). Since this is the exact scenario as Challenge Game 2, the proof now follows from Lemma 29.
5 Correctness and Security
In this section, we present a series of definitions and lemmas that allow us to argue our main protocol (Fig. 3) satisfies the correctness and security properties of the NIAR model (Sect. 3.2). The main technical work lies in proving Security; this requires first defining a key property that networks can exhibit (Definition 23), then demonstrating that the Beneš Network we use satisfies this property (Corollary 27), and finally demonstrating how this property ensures security (see Challenge Games 1 and 2 in Sect. 5.3). As there are a number of lemmas and definitions to go through, to preserve the flow and focus on the main ideas, all proofs appear at the end of the paper.
5.1 Probabilities in a Beneš Network
The main goal of this section is to define a property of graphs that will allow us to formally argue that anonymity is achieved. As mentioned in the Introduction, this property is a stronger variant of edge-disjointness, which we call “local reversal edge-disjoint.” Informally:
Definition 4
(Informal). Given any permutation on N sets of (sender, receiver) pairs, a pairwise\(_{i,j}\) reversal refers to swapping the receivers of senders i and j. When viewing a “block” of a permutation network (which also has N input nodes and N output nodes), a local pairwise\(_{i,j}\) reversal refers to swapping the output nodes of two input nodes. A set of \(N+2\) paths through a block, which include one path for each (sender, receiver) pair plus two ex tra paths connecting sender i to receiver j (and sender j to receiver i) is said to be local pairwise\(_{i,j}\) reversal edge-disjoint if these \(N+2\) paths are edge-disjoint. A permutation network is said to enjoy the local reversal edge-disjoint property if, for any pair of indices (i, j), w.h.p. there exists a block that is local pairwise\(_{i,j}\) reversal edge-disjoint for \(N+2\) randomly chosen paths.
Formally, Definitions 23 and 26 define the “local reversal edge-disjoint” property, and it is used to prove security via Corollary 27 and in the analysis of (12)).
Lemma 5
Suppose that for each input node \(\{\nu _i\}_{i=1}^{N}\) of a butterfly network, a random path \(\mathcal {P}_i\) of \(\log N\) steps is performed. For any node \(\mu _{l}\) (at level \(l \in [0,\log N]\)), let \(X_{\mu _l}\) denote the random variable that indicates how many of the paths \(\{\mathcal {P}_i\}\) pass through node \(\mu _l\). Then for any integer \(k \ge 1\):

Lemma 6
Suppose that for each input nodeFootnote 5 \(\{\nu _i\}_{i=1}^{N}\) of a colored butterfly network (with replication factor c), a random path \(\mathcal {P}_i\) of \((1+\log N)\) steps is performed (the first step chooses the color \(\widehat{c} \in [c]\)). For any node \(\mu _l = \mu _{\widehat{c},r,l}\) (at level \(l \in [0,\log N]\), row \(r \in [N]\), and color \(\widehat{c} \in [c]\)), let \(X_{\mu _l}\) denote the random variable that indicates how many of the paths \(\{\mathcal {P}_i\}\) pass through node \(\mu _l\). Then for any integer \(k \ge 1\):

Lemma 7
Suppose that for each input node \(\{\nu _i\}_{i=1}^{N}\) of a colored butterfly network (with replication factor c), a random path \(\mathcal {P}_i\) of \((1+\log N)\) steps is performed (the first step chooses the color \(\widehat{c} \in [c]\)). For any integer \(k \ge 1\), let \(X_k\) denote an indicator variable on whether there exists any node \(\mu \) (in the entire colored butterfly network) that has more than k (of the N total) random paths \(\{\mathcal {P}_i\}\) pass through it. Then:

We now extend a (colored) butterfly network by concatenating several “blocks,” each block consisting of \(\log N\) levels, and then finishing with one final level that is the mirror reflection of a butterfly network:
Definition 8
An extended (colored) Beneš network with b blocks consists of b butterfly networks concatenated together, followed by a single (reflected) butterfly network. Additionally, where each pair of blocks are connected, there is a single level inserted which consists of edges connecting all colors of each node (at each “row”) to each other. A block \(\textsf{j}\), for \(j \in [1, (1+b)]\), refers to the \((1+\log N)\) levels (and edges) between levels \((j-1) \cdot (1+\log N)\) and \(j \cdot (1 + \log N)\). That is, a block corresponds to a contiguous set of \((1+\log N)\) levels, whose first \(\log N\) levels are a butterfly network, and the last level is the “connecting” level that consists of all edges connecting the different colors of all nodes on the same “row.”Footnote 6 The input level of a block \(j \in [1, 1+b]\) is level \((j-1)\cdot (1+\log N)\), and the output level is \(j \cdot (1+\log N)\) (notice the input level of block b is the same as the output level of block \(b-1\)).
The following is analogous to Lemma 7, but bounds the probability with respect to each block of an extended, colored Beneš network:
Lemma 9
Let \(\sigma : [N] \rightarrow [N]\) be an arbitrary permutation on N items. Suppose that for each input node \(\{\nu _i\}_{i=1}^{N}\) of an extended, colored Beneš network with replication factor c and b blocks, a random path \(\mathcal {P}_i\) of \((1+ b \cdot (1+\log N))\) steps is performed, and then each such path is extended (from level \((b \cdot (1+\log N))\) to level \((1+b) \cdot (1+\log N)\)) by traversing the unique path from the current node (on level \((b \cdot (1+\log N))\)) to \(\sigma (i)\). For any  and for any integer \(k \ge 1\), let \(X_{j,k}\) denote an indicator variable on whether there exists any node \(\mu _j\) within block j (i.e. between levels
and for any integer \(k \ge 1\), let \(X_{j,k}\) denote an indicator variable on whether there exists any node \(\mu _j\) within block j (i.e. between levels  that has more than k (of the N total) random paths \(\{\mathcal {P}_i\}\) pass through it. Then:
that has more than k (of the N total) random paths \(\{\mathcal {P}_i\}\) pass through it. Then:

5.2 Permutation Routing Problem
We begin with the definitions that are needed to describe the Permutation Routing Problem and the desired properties that a successful solution must exhibit.
Definition 10
Given a graph \(G=(V,E)\) and a collection of paths \(\{\mathcal {P}_i\}\) within the graph, we say that any given path \(\mathcal {P}_i\) is edge-disjoint from the others if no edge in \(\mathcal {P}_i\) is contained/traversed by any other path. We say the entire collection of paths \(\{\mathcal {P}_i\}\) is edge-disjoint if each individual edge is edge-disjoint.
Definition 11
A Permutation Routing Problem\((N, \sigma , G)\) is defined as follows: For input integer \(N \in \mathbb {N}\), permutation \(\sigma : [N] \rightarrow [N]\), and graph G that has N designated “input” nodes \(\{I_1, I_2, \dots , I_{N}\}\) and N designated “output” nodes \(\{O_1, O_2, \dots , O_{N}\}\), construct N edge-disjoint paths through G that connect each input-output pair \((I_i, O_{\sigma (i)})\).
We extend the notion of the extended, colored Beneš network to a wide-edged variant, in which each edge has been replicated w times (which can equivalently be viewed as each edge having capacity w):
Definition 12
A wide-edged, extended, colored Beneš network B(N, b, c, w) is an extended and colored Beneš network in which, for each level \(l \in [1, (b + (1+b) \cdot \log N)]\), each edge connecting levels (l-1, l) is replicated w times.
Notice that the added color and edge-width features serve a similar purpose: they each reduce the probability of an edge conflict (i.e. increase the probability of being edge-disjoint, as per Definition 10); but they do so in slightly different ways: the color feature not only introduces new edges, but also additional nodes, so that once a path chooses a color for a particular block (which happens only at the start of each block, when there is a transition between levels in which each edge connects the various “colors” corresponding to the nodes on a common “row;” it will not conflict (on the present block) with paths that chose another color. In contrast, the edge-width feature reduces the chances that two paths conflict across a given edge; but those same paths may still end up in the same node at the far end of this edge, and thus may conflict in a later edge.
We now describe a naïve protocol for randomly choosing paths through a Beneš network:
Definition 13
Given permutation \(\sigma : [N] \rightarrow [N]\) and a wide-edged, extended, colored Beneš network \(G = B(N,b,c,w)\), the Naïve Random Path algorithm defines N paths \(\{\mathcal {P}_i\}\) through G, connecting each input node to each output node as per \(\sigma \), as follows: Path \(\mathcal {P}_i\), which starts at input node \(I_i\), chooses random edges for each level through the first b blocks of \(G=B(N, b, c, w)\). Then from its current node on level \((b\cdot (1+\log N))\), it follows the unique path to destination node \(O_{\sigma (i)}\) (by choosing one of the w replicates of each edge along this path).
Definition 14
Given a wide-edged, extended, colored Beneš network B(N, b, c, w), and given a routing algorithm \(\varPi = \varPi _{N, \sigma , B(N,b,c,w)}\) that attempts to solve the Permutation Routing Problem (Definition 11), for each \(i \in [N]\) and for each block \(1 \le j \le (1+b)\), let \(\mathsf {X_{\varPi }(i,j)}\) denote the boolean random variable that indicates whether \(\varPi \) constructs an edge-disjoint path on the \(\mathbf {j^{th}}\) block for the pair \((I_i, O_{\sigma (i)})\). That is, \(X_{\varPi }(i,j) = 1\) if the path connecting \(I_i\) and \(O_{\sigma (i)}\) within the \(j^{th}\) block (as specified by \(\varPi \)) is edge-disjoint from all other paths specified by \(\varPi \).
We now demonstrate several properties that the Naïve Random Path algorithm (Definition 13) satisfies:
Lemma 15
Let \(\varPi = \varPi _{\sigma _{_{N}}}\) denote the Naïve Random Path algorithm (Definition 13) on a wide-edged, extended, and colored Beneš network \(B(N,b,c\ge 2,w)\). Then for any \(i \in [0,N]\), for any \(1 \le j \le (1+b)\), and for any \(1 \le k \le N\), the probability that \(X_{\varPi }(i,j) = 0\) (as per Definition 14) is bounded by:

We now extend Definition 14 (and in particular the indicator random variable \(X_{\varPi }(i,j) = 0\)) to a statement about a path \(\mathcal {P}_i\) being edge-disjoint across the entire network G:
Definition 16
Given a routing algorithm \(\varPi = \varPi _{N, \sigma , G}\) that attempts to solve the Permutation Routing Problem (Definition 11), for each \(i \in [N]\), let \(\mathsf {X_{\varPi }(i)}\) denote the boolean random variable that indicates whether \(\varPi \) constructs an edge-disjoint path for the pair \((I_i, O_{\sigma (i)})\). That is, \(X_{\varPi }(i) = 1\) if the path connecting \(I_i\) and \(O_{\sigma (i)}\) (as specified by \(\varPi \)) is edge-disjoint from all other paths specified by \(\varPi \).
Lemma 17
Let \(\varPi = \varPi _{\sigma _{_{N}}}\) denote the Naïve Random Path algorithm (Definition 13) on a wide-edged, extended, and colored Beneš network \(B(N,b,c\ge 2,w)\). Then for any \(i \in [N]\) and for any \(1 \le k \le N\), the probability that \(X_{\varPi }(i) = 0\) (as per Definition 16) is bounded by:

Proof
This follows immediately from Lemma 15 by applying a union bound on the \((1+b)\) blocks of the Beneš network B(N, b, c, w).
We are now ready to present the final definition and corresponding statement that will be required for the correctness property of the protocol in Fig. 3.
Definition 18
Given an (independent) collection \(\{\varPi _m\}\) of M routing algorithms that attempt to solve the Permutation Routing Problem (see Definition 11) in a wide-edged, extended and colored Beneš network B(N, b, c, w), let \(\textsf{X}\) denote the boolean random variable that indicates if, for every \(i \in [N]\), there exists (at least) one experiment \(m \in [M]\) in which \(X_{\varPi _m}(i) = 1\) (where \(X_{\varPi _m}(i)\) is the random variable in Definition 16).
Corollary 19
For any security parameter \(\lambda \) and for any input parameters \(2^n=N \ge 64\), \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+ \log N)\) (forFootnote 7 \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)), if the Naïve Random Path algorithm (Definition 13) is repeated \(M:=\lambda \) times, then the probability that \(X=0\) (Definition 18) is bounded by:

Ultimately, Corollary 19 will demonstrate correctness of our routing protocol (3). However, for the security property, we will need to consider two sets of (input, output) node pairs. The following definition (which extends Definition 14, but for two sets of (input, output) pairs of nodes) will be used to capture the requisite probabilities for our security proof.
Definition 20
Given a wide-edged, extended, colored Beneš network \(B(N,b,c,w)\) and two routing algorithms \(\varPi = \varPi _{N, \sigma , G=B(N,b,c,w)}\) and \(\varPi ' = \varPi '_{N, \sigma , G=B(N,b,c,w)}\) that attempt to solve the Permutation Routing Problem (Definition 11), for any pair of row indices \((i,i') \in [N]\) and for any block \(1 \le j \le (1+b)\), let \(\mathsf {Y_{\varPi ,\varPi '}(i,i',j)}\) denote the boolean random variable that indicates whether each of the four paths \(\{\mathcal {P}_{i}, \mathcal {P}_{i'}, \mathcal {P'}_{i}, \mathcal {P'}_{i'}\}\) are edge-disjoint from all other paths on block j.
Aside. Notice that Definition 20 is only concerned about what happens on a single block of a wide-edged, extended, and colored Beneš network B(N, b, c, w). In particular, we do not actually require two routing algorithms \(\varPi \), \(\varPi '\) to be defined on the full network B(N, b, c, w) in order to evaluate whether \(Y_{\varPi ,\varPi '}(i,i',j)\) equals zero or one on a given block \(j \in [1, 1+b]\) (as per Definition 20); rather, we only need to know what each algorithm does on block j. Also notice that there is no requirement that the four paths be edge-disjoint from each other.
Definition 21
Given a wide-edged, extended, and colored Beneš network \(G=B(N,b,c,w)\), and a routing algorithm \(\varPi = \varPi _{N, \sigma , G}\) that attempts to solve the Permutation Routing Problem (Definition 11), and given any pair of row indices \(i,i' \in [N]\) and any block index \(j \in [1,(1+b)]\), define the block \(\textsf{j}\) alternate routing algorithm \(\mathsf {\varPi '_{i,i',j}}\) as follows:
-
\(\varPi '_{i,i',j}\) is identical to \(\varPi \) on the first \((j-1)\) blocks.
-
On the \(j^{th}\) block:
-
For all \(\widehat{i} \notin \{i, i'\}\): \(\varPi '_{i,i',j}\) is identical to \(\varPi \).
-
Let \(\mu _i\) (respectively \(\mu _{i'}\)) denote the node on the output level (which has level index \(j \cdot (1+\log N)\)) of block j that \(\mathcal {P}_i\) (respectively \(\mathcal {P}_{i'}\)) passes through. Then \(\varPi '_{i,i',j}\) is identical to \(\varPi \) except that the choice of \(\mu _i\) versus \(\mu _{i'}\) is swapped in Step 2a for i and \(i'\).Footnote 8
-
-
For all blocks beyond the \(j^{th}\) block:
-
For all \(\widehat{i} \notin \{i, i'\}\): \(\varPi '_{i,i',j}\) is identical to \(\varPi \).
-
For \(i,i'\): \(\varPi '_{i,i',j}\) is identical to \(\varPi \), except that it has swapped paths \(\mathcal {P}_{i}\) and \(\mathcal {P}_{i'}\).Footnote 9
-
With these definitions in hand, we provide an analogous probability bound for \(Y_{\varPi ,\varPi '}(i,i',j)\) as Lemma 15 provided for \(X_{\varPi }(i,j)\).
Lemma 22
Let \(\varPi = \varPi _{\sigma _{_{N}}}\) denote the Naïve Random Path algorithm (Definition 13) on a wide-edged, extended, and colored Beneš network \(B(N,b,c\ge 2,w)\). Fix any pair of row indices \(i,i' \in [N]\) and any block index \(j \in [1,(1+b)]\), and let \(\varPi ' = \varPi '_{i,i',j}\) denote the “block j alternate routing protocol” (Definition 21). Then for any \(1 \le k \le N\), the probability that \(Y_{\varPi ,\varPi '}(i,i',j) = 0\) (as per Definition 20) is bounded by:

Just as \(\mathsf {X_{\varPi }(i,j)}\) (Definition 14) and the corresponding bound for it (Lemma 15) were extended from variables/statements about blocks to variables/statements about the entire network (in the corresponding Definition 16 and Lemma 17), we likewise extend \(Y_{\varPi ,\varPi '}(i,i',j)\) (Definition 20) and the corresponding Lemma 22 to variables/statements about the entire network. However, these extensions differ slightly from before, as ultimately we only need the existence of a block that satisfies the key property, as opposed to requiring that all blocks satisfy some property.
Definition 23
Given a wide-edged, extended, and colored Beneš network \(G=B(N,b,c,w)\), and given two routing algorithms \(\varPi = \varPi _{N, \sigma , G}\) and \(\varPi ' = \varPi '_{N, \sigma , G}\) that attempt to solve the Permutation Routing Problem (Definition 11), for any pair of row indices \((i,i') \in [N]\), let \(\mathsf {Y_{\varPi ,\varPi '}(i,i')}\) denote the boolean random variable that indicates whether there exists some block \(j \in [1,(1+b)]\) in which the four paths \(\{\mathcal {P}_{i}, \mathcal {P}_{i'}, \mathcal {P'}_{i}, \mathcal {P'}_{i'}\}\) are each edge-disjoint from all other paths on block j.
Definition 24
Given a wide-edged, extended, and colored Beneš network \(G=B(N,b,c,w)\), and a routing algorithm \(\varPi = \varPi _{N, \sigma , G}\) that attempts to solve the Permutation Routing Problem (Definition 11), and given any pair of row indices \(i,i' \in [N]\), define the alternate routing algorithm \(\mathsf {\varPi '_{i,i'}}\) as follows:
-
1.
 , let \(\varPi '_j = \varPi '_{i,i' ,j}\) denote the block j alternate routing algorithm (Definition 21).
, let \(\varPi '_j = \varPi '_{i,i' ,j}\) denote the block j alternate routing algorithm (Definition 21). -
2.
Construct \(\varPi '_{i,i'}\) from the family of alternate routing algorithms \(\{\varPi _{j}\}\) as follows:
-
a.
If there exists an index \(j \in [1,(1+b)]\) such that \(Y_{\varPi ,\varPi '_j}(i,i',j) = 1\) (as per Definition 14), then let \(\varPi '_{i,i'}= \varPi '_j\) (for the minimal j satisfying \(Y_{\varPi ,\varPi '_j}(i,i',j) = 1\)).
-
b.
Otherwise, define \(\varPi '_{i,i'} = \varPi \).
-
a.
Lemma 25
Let \(\varPi = \varPi _{\sigma _{_{N}}}\) denote the Naïve Random Path algorithm (Definition 13) on a wide-edged, extended, and colored Beneš network \(B(N,b,c\ge 2,w)\), let \(i,i' \in [N]\) be any two row indices, and let \(\varPi ' = \varPi '_{i,i'}\) be the alternate routing algorithm (as per Definition 24). Then for any \(1 \le k \le N\), the probability that \(Y_{\varPi ,\varPi '}(i,i') = 0\) (as per Definition 23) is bounded by:

We are now ready to present the final definition and corresponding statement that will be required for the security proof of the protocol in Fig. 3.
Definition 26
Given an (independent) collection \(\{\varPi _m\}\) of M routing algorithms that attempt to solve the Permutation Routing Problem (Definition 11) in a wide-edged, extended and colored Beneš network B(N, b, c, w), let \(\textsf{Y}\) denote the boolean random variable that indicates if, for every \(\varPi _m\) and every pair of row indices \(i,i' \in [N]\), that \(Y_{\varPi _{_m}, \varPi '_{m}}(i,i')=1\) (where \(\varPi '_m = \varPi '_{m,i,i'}\) is the alternate routing algorithm (Definition 24) and \(Y_{\varPi _{_m}, \varPi '_{m}}(i,i')\) is the corresponding random variable (Definition 23)).
Corollary 27
ForFootnote 10 any security parameter \(\lambda \ge 8\) and any input parameters \(2^n=N \ge 64\), \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+\log N)\) (for \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)), if the Naïve Random Path algorithm (Definition 13) is repeated \(M:=\lambda \) times, then the probability that \(Y= 0\) (Definition 26) is bounded by:

5.3 Security
Succinctly, security (anonymity) will follow for the routing protocol of Fig. 3 from:

In this section, we define Challenge Games 1 and 2, and then demonstrate the first two implications in (12) (the third implication was already presented in the proof of Theorem 3).
Challenge Game 1
Input Parameters:
-
Number of input/output nodes \(2^n=N \ge 64\).
-
Security parameter \(\lambda \ge 8\).
-
A wide-edged, extended and colored Beneš network \(G=B(N, b, c, w)\), with parameters as per Corollaries 19 and 27: \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+\log N)\) (for \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)).
-
There are N “global input nodes” on level \(-1\) of the Beneš network \(G=B(N, b, c, w)\), which are denoted: \(\mathcal {I} = \{I_1, I_2, \dots , I_{N}\}\), and N global output nodes \(\mathcal {O} = \{O_1, O_2, \dots , O_{N}\}\).
-
Set the experiment replication amount \(M = \lambda \).
Challenge Game:
-
1.
Challenger \(\mathcal {C}\) chooses a permutation \(\sigma \) on N elements \(\sigma : [N] \rightarrow [N]\).
-
2.
For each experiment \(m \in [M]\): Challenger \(\mathcal {C}\) performs the Naïve Random Path algorithm (Definition 13) \(\varPi _m = \varPi _{m,N,\sigma _b,G}\) (for \(G=B(N,b,c,w)\)). For each \(i \in [N]\), let \(\mathcal {P}_{m,i}\) denote the path chosen (by \(\varPi _m\)) that connects nodes \((I_i,\sigma _b(I_i))\).
-
3.
Let Y be the boolean random variable from Definition 26. If \(Y=0\), Challenger \(\mathcal {C}\) aborts (Adversary \(\mathcal {A}\) wins).
-
4.
Challenger \(\mathcal {C}\) chooses any two distinct indices \(i,i' \in [N]\), and givesFootnote 11
 to Adversary \(\mathcal {A}\), which is the mapping of \(\sigma \) on all indices except i and \(i'\). Notice that since \(\sigma \) is a permutation, Adversary \(\mathcal {A}\) now has complete knowledge of \(\sigma \), except for what \(\sigma \) does to i and \(i'\). In particular, there are two range indices \(\sigma (i),\sigma (i') \in [N]\) that are not mapped to (based on what \(\mathcal {C}\) gives to \(\mathcal {A}\)). Let \(\tau \) denote the permutation that is identical to \(\sigma \), except that it swaps where i and \(i'\) are mapped to (so \(\tau (i) = \sigma (i')\) and \(\tau (i') = \sigma (i)\)). Notice that after this step, Adversary \(\mathcal {A}\) knows that the permutation chosen by Challenger \(\mathcal {C}\) is either \(\sigma \) or \(\tau \).
to Adversary \(\mathcal {A}\), which is the mapping of \(\sigma \) on all indices except i and \(i'\). Notice that since \(\sigma \) is a permutation, Adversary \(\mathcal {A}\) now has complete knowledge of \(\sigma \), except for what \(\sigma \) does to i and \(i'\). In particular, there are two range indices \(\sigma (i),\sigma (i') \in [N]\) that are not mapped to (based on what \(\mathcal {C}\) gives to \(\mathcal {A}\)). Let \(\tau \) denote the permutation that is identical to \(\sigma \), except that it swaps where i and \(i'\) are mapped to (so \(\tau (i) = \sigma (i')\) and \(\tau (i') = \sigma (i)\)). Notice that after this step, Adversary \(\mathcal {A}\) knows that the permutation chosen by Challenger \(\mathcal {C}\) is either \(\sigma \) or \(\tau \). -
5.
(If this step is reached) Since \(Y=1\), for each run \(1 \le m \le M\) of the experiment, we have that alternate routing algorithm \(\varPi '_{m,i,i'}\) must have been constructed as per Step 2a of Definition 24 (as opposed to Step 2b). Therefore, let \(j_m \in [1,(1+b)]\) denote the block index for which \(\varPi '_{m,i,i'}\) is defined as in Step 2a; i.e. \(j_m\) (is the minimal index that) satisfies \(Y_{\varPi _m,\varPi '_m,j_m}(i,i',j_m) = 1\). Then, for each experiment \(m \in [M]\):
-
(a)
[Block Index]: Challenger \(\mathcal {C}\) gives Adversary \(\mathcal {A}\) the block index \(j_m\) (recall this is the first block for which \(Y_{\varPi _m,\varPi '_m,j_m}(i,i',j_m) = 1\)).
-
(b)
[All Non-Interesting Paths]: Challenger \(\mathcal {C}\) gives Adversary \(\mathcal {A}\) all paths \(\{\mathcal {P}_{m,\widehat{i}}\}_{\widehat{i} \notin \{i,i'\}}\).
-
(c)
[Interesting Paths Before Block \(j_m]\): Challenger \(\mathcal {C}\) gives Adversary \(\mathcal {A}\), through the first \((j_m \)-1) blocks only, paths \(\mathcal {P}_{m,i}\) and \(\mathcal {P}_{m,i'}\).
-
(d)
[Interesting Paths \(+\) Alternate Paths for Block \(j_m]\): Denote the two sub-paths of \(\mathcal {P}_{m,i}\) and \(\mathcal {P}_{m,i'}\) that are restricted to block \(j_m\) (i.e. just the edges of these paths within block \(j_m\)) and their two alternate sub-paths (as specified by alternate routing protocol \(\varPi '_{i,i'}\) (Definition 24)) as: \(\{\mathcal {P}_{m,i,j_m},\mathcal {P}_{m,i',j_m},\mathcal {P'}_{m,i,j_m},\mathcal {P'}_{m,i',j_m}\}\). Then Challenger \(\mathcal {C}\) gives Adversary \(\mathcal {A}\) the unordered set \(\{\mathcal {P}_{m,i,j_m},\mathcal {P}_{m,i',j_m},\mathcal {P'}_{m,i,j_m},\mathcal {P'}_{m,i',j_m}\}\).
-
(e)
[(Unordered) Interesting Paths Beyond Block \(j_m]\): For each level with index \(j_m \cdot (1+\log N) \le l \le (1+b) \cdot (1+\log N)\) in \(G=B(N, b, c, w)\) that lies after block \(j_m\), Challenger \(\mathcal {C}\) gives Adversary \(\mathcal {A}\) the unordered set of edges \(\{\mathcal {P}_{m,i,l}, \mathcal {P}_{m,i',l}\}_{_l}\), where \(\mathcal {P}_{m,i,l}\) (resp. \(\mathcal {P}_{m,i',l}\)) denotes the \(l^{th}\) edge on the path \(\mathcal {P}_{m,i}\) (resp. on the path \(\mathcal {P}_{m,i'}\)). In other words, \(\mathcal {A}\) learns the edges (beyond block \(j_m\)) traversed by paths \(\mathcal {P}_{m,i}\) and \(\mathcal {P}_{m,i'}\), but \(\mathcal {A}\) is not explicitly told which edges belong to which path (\(\mathcal {P}_{m,i}\) versus \(\mathcal {P}_{m,i'}\)).
-
(a)
-
6.
Adversary \(\mathcal {A}\) outputs a guess whether Challenger’s permutation was \(\sigma \) or \(\tau \).
The Adversary \(\mathcal {A}\) wins Challenge Game 1 either if Challenger \(\mathcal {C}\) aborts in Step 3, or if \(\mathcal {A}\)’s output guess in Step 6 is correct.
The main result for Challenge Game 1 (which is the first implication in (12)) is:
Lemma 28
The probability that an (unbounded) Adversary \(\mathcal {A}\) wins Challenge Game 1 is bounded by:

Challenge Game 2
Input Parameters:
-
Number of input/output nodes \(2^n=N \ge 64\).
-
Security parameter \(\lambda _s\). Let \(\lambda := 2\log N + \max (\lambda _s, 2 + \log \log N)\).
-
A wide-edged, extended and colored Beneš network \(G=B(N, b, c, w)\), with parameters as per Corollaries 19 and 27: \(b=\lambda -1\), \(c = 4\cdot a_{\lambda }\), and \(w=1.2 \cdot \lambda \cdot \log N \cdot (1+\log N)\) (for \(a_{\lambda }:=\max (2, \lambda ^{1/(\log N-1)})\)).
-
There are N “global input nodes” on level \(-1\) of the Beneš network \(G=B(N, b, c, w)\), which are denoted: \(\mathcal {I} = \{I_1, I_2, \dots , I_{N}\}\), and N global output nodes \(\mathcal {O} = \{O_1, O_2, \dots , O_{N}\}\).
-
Set the experiment replication amount \(M = \lambda \).
Challenge Game:
-
1.
On input security parameter \(\lambda \), Adversary \(\mathcal {A}\) chooses N, two distinct permutations \(\sigma _0, \sigma _1\) on [N], a set of sender indices \(S_{\mathcal {A}} \subseteq [N]\) to corrupt, and a set of receiver indices \(R_{\mathcal {A}} \subseteq [N]\) to corrupt; subject to constraints:
-
(a)
\(|R_{\mathcal {A}}| \le N - 2\);
-
(b)
\(\sigma _0\) and \(\sigma _1\) match for all receivers in \(R_{\mathcal {A}}\):
 .
.
-
(a)
-
2.
Adversary \(\mathcal {A}\) sends \(\{\sigma _0, \sigma _1\}\) to a Challenger \(\mathcal {C}\).
-
3.
Challenger \(\mathcal {C}\) chooses \(b \in \{0,1\}\) and selects \(\sigma _b \in \{\sigma _0, \sigma _1\}\).
-
4.
For each experiment \(m \in [M]\):
-
(a)
Challenger \(\mathcal {C}\) performs the Naïve Random Path algorithm (Definition 13) \(\varPi _m = \varPi _{m,N,\sigma _b,G}\) (for \(G=B(N,b,c,w)\)). For each \(i \in [N]\), let \(\mathcal {P}_{m,i}\) denote the path chosen (by \(\varPi _m\)) that connects nodes \((I_i, O_{\sigma _b(i)})\).
-
(b)
Adversary \(\mathcal {A}\) is given the following information:
-
For each \(i \in R_\mathcal {A}\): all edges \(e \in \mathcal {P}_{m,i}\) that are edge-disjoint from all other paths \(\mathcal {P}_{m,j}\) (for \(j \ne i\)).
-
The list of edges \(\{e\} \in G\) that have at least two distinct paths \(\mathcal {P}_{m,i}, \mathcal {P}_{m,i'}\) pass through them, with \(i' \ne i\) and \(i \in R_\mathcal {A}\). Notice that \(\mathcal {A}\) is given only the identity of the set of edges \(\{e\}\); in particular, \(\mathcal {A}\) is not given the information of which (nor even how many) indices in \([N] \setminus R_\mathcal {A}\) traverse each such edge.
-
-
(a)
-
5.
Let Y be the boolean random variable from Definition 26. If \(Y=0\), Challenger \(\mathcal {C}\) aborts (Adversary \(\mathcal {A}\) wins).
-
6.
Adversary \(\mathcal {A}\) outputs a guess \(b' \in \{0,1\}\) of which permutation \(\{\sigma _0, \sigma _1\}\) Challenger \(\mathcal {C}\) chose.
We say that the Adversary wins the above challenge if its output is correct.
The main result for Challenge Game 2 (which is the second implication in (12)) is:
Lemma 29
The probability that an (unbounded) Adversary \(\mathcal {A}\) wins Challenge Game 2 is bounded by:  .
.
Notes
- 1.
Our limitation to HBC adversaries is only needed to ensure Correctness of our protocol - that receivers get the correct messages. We note that requiring HBC for correctness is unavoidable, as a malicious router can, for example, not forward any message (like in PIR and other related primitives). In terms of Security (privacy of the senders-receivers permutation): so long as the one-time Setup is performed properly, then security of our protocol will hold in the Malicious adversary setting.
- 2.
Router computation is not explicitly measured in the protocol of [SW21], our analysis of their protocol yields \(O(N^2)\) computation load on the router: their Multi-Client Functional Encryption (MCFE) protocol is invoked N times by the router, with each invocation processing N ciphertexts.
- 3.
The sender keys \(\{pk_i\}\) are associated with the receiver keys \(\{sk_i\}\) via the permutation \(\sigma \); namely, secret key \(sk_{\sigma (i)}\) can decrypt messages encrypted under \(pk_i\).
- 4.
Trusted setup is required for establishing public/secret key pairs for encryption and for instantiating ideal functionality \(\varPi _{ORG}(G,\widehat{c},r,l,\varPi _{1{-}PIR})\).
- 5.
A colored butterfly network can be viewed as c disjoint butterfly networks overlaid on top of one another. Alternatively, we can view a colored butterfly network as a single (connected) graph by adding an extra input level (with level index \(-1\)) on the far left, consisting of N input nodes. Then there are c edges emanating from each input node, connecting it to each of the c colored nodes in level 0 of the corresponding row.
- 6.
In the special case of the (1+\(b)^{th}\) block, the first \(\log N\) levels of this block are a reflected butterfly network, and the last level of the block is the final “output” level of the entire network.
- 7.
Notice \(a_\lambda = 2\) if \(\lambda \le N/2\).
- 8.
Notice that if \(\mu _i = \mu _{i'}\), then \(\varPi '_{i,i',j}\) is identical to \(\varPi \) (for all paths \(\{\mathcal {P}_i\}\)) on all blocks through j (including block j).
- 9.
Swapping paths is only necessary for the sake of making sure the paths link up/connect between blocks (since output node \(\mu _i\) and \(\mu _{i'}\) were swapped in block j). However, as was noted in the Aside note following Definition 20, the details of what \(\varPi '_{i,i',j}\) does beyond block j will be irrelevant for the context of Lemmas 22 and 25.
- 10.
Notice that these parameter values all match those in the hypothesis of Corollary 19.
- 11.
This information is also available indirectly from what \(\mathcal {C}\) gives to \(\mathcal {A}\) in Step 5 a below.
References
Ajtai, M., Komlós, J., Szemerédi, E.: An o(n log n) sorting network. In: Proceedings of the 15th Annual ACM Symposium on Theory of Computing, 25–27 April 1983, pp. 1–9. ACM (1983)
Chase, M., Garg, S., Hajiabadi, M., Li, J., Miao, P.: Amortizing rate-1 OT and applications to PIR and PSI. In: Nissim, K., Waters, B. (eds.) TCC 2021. LNCS, vol. 13044, pp. 126–156. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90456-2_5
Chor, B., Kushilevitz, E., Goldreich, O., Sudan, M.: Private information retrieval. In: 36th Annual Symposium on Foundations of Computer Science, Milwaukee, Wisconsin, USA, 23–25 October 1995, pp. 41–50. IEEE Computer Society (1995)
Chandran, N., Ostrovsky, R., Skeith, W.E.: Public-key encryption with efficient amortized updates. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 17–35. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_2
Döttling, N., Garg, S., Ishai, Y., Malavolta, G., Mour, T., Ostrovsky, R.: Trapdoor hash functions and their applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 3–32. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_1
Fernando, R., Shi, E., Soni, P., Vanjani, N.: Non-interactive anonymous router with quasi-linear router computation. IACR Cryptology ePrint Archive, Paper 1395 (2022)
Garg, S., Hajiabadi, M., Ostrovsky, R.: Efficient range-trapdoor functions and applications: rate-1 OT and more. In: Pass, R., Pietrzak, K. (eds.) TCC 2020. LNCS, vol. 12550, pp. 88–116. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64375-1_4
Hamlin, A., Ostrovsky, R., Weiss, M., Wichs, D.: Private anonymous data access. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 244–273. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_9
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Batch codes and their applications. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, pp. 262–271. ACM (2004)
Ishai, Y., Paskin, A.: Evaluating branching programs on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 575–594. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_31
Kushilevitz, E., Ostrovsky, R.: Replication is NOT needed: SINGLE database, computationally-private information retrieval. In: 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, 19–22 October 1997, pp. 364–373. IEEE Computer Society (1997)
Leighton, F.T.: Tight bounds on the complexity of parallel sorting. In: Proceedings of the 16th Annual ACM Symposium on Theory of Computing, pp. 71–80. ACM (1984)
Lin, W.-K., Mook, E., Wichs, D.: Doubly efficient private information retrieval and fully homomorphic RAM computation from ring LWE. IACR Cryptology ePrint Archive, Paper 1703 (2022)
Maggs, B.M., Sitaraman, R.K.: Simple algorithms for routing on butterfly networks with bounded queues (ext. abstract). In: 24th Annual ACM Symposium on Theory of Computing, pp. 150–161. ACM (1992)
Ostrovsky, R., Skeith, W.E.: A survey of single-database private information retrieval: techniques and applications. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 393–411. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_26
Shi, E., Wu, K.: Non-interactive anonymous router. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12698, pp. 489–520. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77883-5_17
Upfal, E.: An o(log N) deterministic packet routing scheme (preliminary version). In: Proceedings of the 21st Annual ACM Symposium on Theory of Computing, pp. 241–250. ACM (1989)
Acknowledgements
This material is based upon work supported by the United States Air Force and DARPA – Distribution Statement “A” (Approved for Public Release, Distribution Unlimited) – under Contract No. FA8750-19-C-0031, DARPA under Cooperative Agreement HR0011-20-2-0025, the Algorand Centers of Excellence program managed by Algorand Foundation, NSF grants CNS-224635, CCF-2220450, CNS-2001096, US-Israel BSF grant 2018393, ISF grant 2774/20, Amazon Faculty Award, Cisco Research Award and Sunday Group. Any views, opinions, findings, conclusions or recommendations contained herein are those of the author(s) and should not be interpreted as necessarily representing the official policies, either expressed or implied, of DARPA, the Department of Defense, the United States Air Force, the Algorand Foundation, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes not withstanding any copyright annotation therein.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Bunn, P., Kushilevitz, E., Ostrovsky, R. (2023). Anonymous Permutation Routing. In: Rothblum, G., Wee, H. (eds) Theory of Cryptography. TCC 2023. Lecture Notes in Computer Science, vol 14371. Springer, Cham. https://doi.org/10.1007/978-3-031-48621-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-48621-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48620-3
Online ISBN: 978-3-031-48621-0
eBook Packages: Computer ScienceComputer Science (R0)




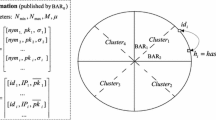
 and I is
and I is  .
.
 .
. s.t.
s.t. 

 , let
, let  to Adversary
to Adversary  .
.