Abstract
The field of distributed certification is concerned with certifying properties of distributed networks, where the communication topology of the network is represented as an arbitrary graph; each node of the graph is a separate processor, with its own internal state. To certify that the network satisfies a given property, a prover assigns each node of the network a certificate, and the nodes then communicate with one another and decide whether to accept or reject. We require soundness and completeness: the property holds if and only if there exists an assignment of certificates to the nodes that causes all nodes to accept. Our goal is to minimize the length of the certificates, as well as the communication between the nodes of the network. Distributed certification has been extensively studied in the distributed computing community, but it has so far only been studied in the information-theoretic setting, where the prover and the network nodes are computationally unbounded.
In this work we introduce and study computationally bounded distributed certification: we define locally verifiable distributed \(\textsf{SNARG}\)s ( s), which are an analog of \(\textsf{SNARG}\)s for distributed networks, and are able to circumvent known hardness results for information-theoretic distributed certification by requiring both the prover and the verifier to be computationally efficient (namely, PPT algorithms).
s), which are an analog of \(\textsf{SNARG}\)s for distributed networks, and are able to circumvent known hardness results for information-theoretic distributed certification by requiring both the prover and the verifier to be computationally efficient (namely, PPT algorithms).
We give two  constructions: the first allows us to succinctly certify any network property in \({\textsf{P}}\), using a global prover that can see the entire network; the second construction gives an efficient distributed prover, which succinctly certifies the execution of any efficient distributed algorithm. Our constructions rely on non-interactive batch arguments for \({\textsf{NP}}\) (\(\textsf{BARG}\)s) and on \(\textsf{RAM}~\textsf{SNARG}\)s, which have recently been shown to be constructible from standard cryptographic assumptions.
constructions: the first allows us to succinctly certify any network property in \({\textsf{P}}\), using a global prover that can see the entire network; the second construction gives an efficient distributed prover, which succinctly certifies the execution of any efficient distributed algorithm. Our constructions rely on non-interactive batch arguments for \({\textsf{NP}}\) (\(\textsf{BARG}\)s) and on \(\textsf{RAM}~\textsf{SNARG}\)s, which have recently been shown to be constructible from standard cryptographic assumptions.
R. Oshman’s research is supported by ISF grant no. 2801/20. E. Boyle’s research is supported in part by AFOSR Award FA9550-21-1-0046 and ERC Project HSS (852952). R. Cohen’s research is supported in part by NSF grant no. 2055568 and by the Algorand Centres of Excellence programme managed by Algorand Foundation. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of Algorand Foundation. T. Moran’s research is supported by ISF grant no. 2337/22.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Distributed algorithms are algorithms that execute on multiple processors, with each processor carrying out part of the computation and often seeing only part of the input. This class of algorithms encompasses a large variety of scenarios and computation models, ranging from a single computer cluster to large-scale distributed networks such as the internet. Distributed algorithms are notoriously difficult to design: in addition to the inherent unpredictability that results from having multiple processors that are usually not tightly coordinated, distributed algorithms are required to be robust and fault-tolerant, coping with an environment that can change over time. Moreover, distributed computation introduces bottlenecks that are not present in centralized computation, including communication and synchronization costs, which can sometimes outweigh the cost of local computation at each processor. All of these reasons make distributed algorithms hard to design and to reason about.
In this work we study distributed certification, a mechanism that is useful for ensuring correctness and fault-tolerance in distributed algorithms: the goal is to efficiently check, on demand, whether the system is in a legal state or not (here, “legal” varies depending on the particular algorithm and its purpose). To that end, we compute in advance auxiliary information in the form of certificates stored at the processors, and we design an efficient verification procedure that allows the processors to interact with one another and use their certificates to verify that the system is in a legal state. The certificates are computed once, and therefore we are traditionally less interested in how hard they are to compute; however, the verification procedure may be executed many times to check whether the system state is legal, and therefore it must be highly efficient. Since we do not trust that the system is in a legal state, we think of the certificates as given by a prover, whose goal is to convince us that the system is in a legal state even when it is not. One can therefore view distributed certification as a distributed analog of \({\textsf{NP}}\).
Distributed certification has recently received extensive attention in the context of distributed network algorithms, which execute in a network comprising many nodes (processors) that communicate over point-to-point communication links. The communication topology of the network is modeled as an arbitrary undirected network graph, where each node is a vertex; the edges of the graph represent bidirectional communication links. The goal of a network algorithm is to solve some global problem related to the network topology, and so the network graph is in some sense both the input to the computation and also the medium over which the computation is carried out. Typical tasks in this setting include setting up network infrastructure such as low-weight spanning trees or subgraphs, scheduling and routing, and various forms of resource allocation; see the textbook [Pel00] for many examples. We usually assume that the network nodes initially know only their own unique identifier (UID), their immediate neighbors, and possibly a small amount of global information about the network, such as its size or its diameter. An efficient network algorithm will typically have each node learn as little as possible about the network as a whole, as this requires both communication and time. This is sometimes referred to as locality [Pel00].
Distributed certification arises naturally in the context of fault tolerance and correctness in network algorithms (even in early work, e.g., [APV91]), but it was first formalized as an object of independent interest in [KKP05]. A certification scheme for a network property \(\mathcal {P}\) (for example, “the local states of the network nodes encode a valid spanning tree of the network”) consists of a prover, which is usually thought of as unbounded, and a verification procedure, which is an efficient distributed algorithm that uses the certificates. Here, “efficiency” can take many forms (see the textbook [Pel00] for some), but it is traditionally measured only in communication and in number of synchronized communication rounds, not in local computation at the nodes. (A synchronized communication round, or round for short, is a single interaction round during which each network node sends a possibly-different message on each of its edges, receives the messages sent by its neighbors, and performs some local computation.) At the end of the verification procedure, each network node outputs an acceptance bit, and the network as a whole is considered to accept if and only if all nodes accept; it suffices for one node to “raise the alarm” and reject in order to indicate that there is a problem. Our goal is to minimize the length of the certificates while providing soundness and completeness, that is — there should exist a certificate assignment that convinces all nodes to accept if and only if the network satisfies the property \(\mathcal {P}\).
To our knowledge, all prior work on distributed certification is in the information-theoretic setting: the prover and the network nodes are computationally unbounded, and we are concerned only with space (the length of the certificates) and communication (at verification time). As might be expected, some strong lower bounds are known: while any property of a communication topology on n nodes can be proven using \(O(n^2)\)-bit certificates by giving every node the entire network graph, it is shown in [GS16] that some properties do in fact require \(\Omega (n^2)\)-bit certificates in the deterministic setting, and similar results can be shown when the verification procedure can be randomized [FMO+19].
Our goal in this work is to circumvent the hardness of distributed certification in the information-theoretic setting by moving to the computational setting: we introduce and study computationally sound distributed proofs, which we refer to as locally verifiable distributed \(\textsf{SNARG}\)s ( s), extending the centralized notion of a succinct non-interactive argument (\(\textsf{SNARG}\)).
s), extending the centralized notion of a succinct non-interactive argument (\(\textsf{SNARG}\)).
Distributed \(\textsf{SNARG}\)s. In recent years, the fruitful line of work on delegation of computation has culminated in the construction of succinct, non-interactive arguments (\(\textsf{SNARG}\)s) for all properties in \({\textsf{P}}\) [CJJ21b, WW22, KLVW23, CGJ+22]. A \(\textsf{SNARG}\) is a computationally sound proof system under which a PPT prover certifies a statement of the form “\(x \in \mathcal {L}\)”, where x is an input and \(\mathcal {L}\) is a language, by providing a PPT verifier with a short proof \(\pi \). The verifier then examines the input x and the proof \(\pi \), and decides (in polynomial time) whether to accept or reject. It is guaranteed that an honest prover can convince the verifier to accept any true statement with probability 1 (perfect completeness), and at the same time, no PPT cheating prover can convince the verifier to accept with non-negligible probability (computational soundness).
In this work, we first ask:
Can we construct locally verifiable distributed \(\textsf{SNARG}\)s (
s), a distributed analog of \(\textsf{SNARG}\)s which can be verified by an efficient (i.e., local) distributed algorithm?
In contrast to prior work on distributed verification, here when we say “efficient” we mean in communication and in rounds, but also in computation, combining both distributed and centralized notions of efficiency. (We defer the precise definition of our model to Sect. 2.
We consider two types of provers: first, as a warm-up, we consider a centralized prover, which is a PPT algorithm that sees the entire network and computes succinct certificates for the nodes. We show that in this settings, there is an  for any property in \({\textsf{P}}\), using \(\textsf{RAM}\) \(\textsf{SNARG}\)s [KP16, KLVW23] as our main building block.
for any property in \({\textsf{P}}\), using \(\textsf{RAM}\) \(\textsf{SNARG}\)s [KP16, KLVW23] as our main building block.
The centralized prover can be applied in the distributed context by first collecting information about the entire network at one node, and having that node act as the prover and compute certificates for all the other nodes. However, this is very inefficient: for example, in terms of total communication, it is easy to see that collecting the entire network topology in one location may require \(\Omega (n^2)\) bits of communication to flow on some edge. In contrast, “efficient” network algorithms use sublinear and even polylogarithmic communication.Footnote 1 This motivates us to consider another type of prover – a distributed prover—and ask:
If a property can be decided by an efficient distributed algorithm, can it be succinctly certified by an efficient distributed prover?
Of course, we still require that the verifier be an efficient distributed algorithm, as in the case of the centralized prover above. We give a positive answer to this question as well: given a distributed algorithm \(\mathcal {D}\), we construct a distributed prover that runs alongside \(\mathcal {D}\) with low overhead (in communication and rounds), and produces succinct certificates at the network nodes.
We give more formal statements of our results in Sect. 1.3 below, but before doing so, we provide more context and background on distributed certification and on delegation of computation.
1.1 Background on Distributed Certification
The classical model for distributed certification was formally introduced by Korman, Kutten and Peleg in [KKP05] under the name proof labeling schemes (PLS), but was already present implicitly in prior work on self-stabilization, such as [APV91]. To certify a property \(\mathcal {P}\) of a network graph \(G = (V,E)\),Footnote 2 we first run a marker algorithm (i.e., a prover), a computationally-unbounded algorithm that sees the entire network, to compute a proof in the form of a labeling \(\ell : V \rightarrow \left\{ {0,1} \right\} ^*\). We refer to these labels as certificates; each node \(v \in V\) is given only its own certificate, \(\ell (v)\). We refer to this as the proving stage.
Next, whenever we wish to verify that the property \(\mathcal {P}\) holds, we carry out the verification stage: each node \(v \in V\) sends its certificate \(\ell (v)\) to its immediate neighbors in the graph. Then, each node examines its direct neighborhood, its certificates, and the certificate it received from its neighbors, and deterministically outputs an acceptance bit.
The proof is considered to be accepted if and only if all nodes accept it. During the verification stage, the nodes are honest; however, the prover may not be honest during the proving stage, and in general it can assign arbitrary certificates to any and all nodes in the network. We require soundness and completeness: the property \(\mathcal {P}\) holds if and only if there exists an assignment of certificates to the nodes that causes all nodes to accept.
The focus in the area of distributed certification is on schemes that use short certificates. Even short certificates can be extremely helpful: to illustrate, and to familiarize the reader with the model, we describe a scheme from [KKP05] for certifying the correctness of a spanning tree: each node \(v \in V\) is given a parent pointer \(p_v \in V \cup \left\{ {\bot } \right\} \), and our goal is to certify that the subgraph induced by these pointers, \(\left\{ { ( v, p_v ) : v \in V \text { and } p_v \ne \bot } \right\} \), is a spanning tree of the network graph G. In the scheme from [KKP05], each node \(v \in V\) is given a certificate \(\ell (v) = (r_v, d_v)\), containing the following information:
-
The purported name \(r_v\) of the root of the tree, and
-
The distance \(d_v\) of v from the root \(r_v\).
(Note that even though the tree has a single root, the prover can try to cheat by claiming different roots at different nodes, and hence we use the notation \(r_v\) for the root given to node v.) To verify, the nodes send their certificates to their neighbors, and check that:
-
Their root \(r_v\) is the same as the root \(r_u\) given to each neighbor u, and
-
If \(p_v \ne \bot \), then \(d_{p_v} = d_v - 1\), and if \(p_v = \bot \), then \(d_v = 0\).
This guarantees the correctness of the spanning tree,Footnote 3 and requires only \(O(\log n)\)-bit certificates, where n is the number of nodes in the network; the verification stage incurs communication \(O(\log n)\) on every edge, and requires only one round (each node sends one message to each neighbor). In contrast, generating a spanning tree from scratch requires \(\Omega (D)\) communication rounds, where D is the diameter of the network; verifying without certificates that a given (claimed) spanning tree is correct requires \(\tilde{\Omega }(\sqrt{n}/B)\) communication rounds, if each node is allowed to send B bits on every edge in every round [SHK+12].
The original model of [KKP05] is highly restricted: it does not allow randomization, and it allows only one round of communication, during which each node sends its certificate to all of its neighbors (this is the only type of message allowed). Subsequent work studied many variations on this basic model, featuring different generalizations and communication constraints during the verification stage (e.g., [GS16, OPR17, PP17, FFH+21, BFO22]), different restrictions on how certificates may depend on the nodes’ identifiers (e.g., [FHK12, FGKS13, BDFO18]), restricted classes of properties and network graphs (e.g., [FBP22, FMRT22]), allowing randomization [FPP19, FMO+19] or interaction with the prover (e.g., [KOS18, NPY20, BKO22]), and in the case of [BKO22], also preserving the privacy of the nodes using a distributed notion of zero knowledge. We refer to the survey [Feu21] for an overview of much of the work in this area.
To our knowledge, all work on distributed certification so far has been in the information-theoretic setting, which requires soundness against a computationally unbounded prover, and does not take the local computation time of either the prover or the verifier into consideration as a complexity measure (with one exception, [AO22], where the running time of the nodes is considered, but perfect soundness is still required). Information-theoretic certification is bound to run up against barriers arising from communication complexity: it is easy to construct synthetic properties that essentially encode lower bounds from nondeterministic or Merlin-Arthur communication complexity into a graph problem. More interestingly, it is possible to use reductions from communication complexity to prove lower bounds on some natural problems: for example, in [GS16] it was shown that \(\Omega (n^2)\)-bit certificates are required to prove the existence of a non-trivial automorphism, or non-3-colorability. In addition to this major drawback, in the information-theoretic setting there is no clear connection between whether a property is efficiently checkable in the traditional sense (\({\textsf{P}}\), or even \({\textsf{NP}}\)) and whether it admits a short distributed proof: even computationally easy properties, such as “the network has diameter at most k” (for some constant k), or “the identifiers of the nodes in the network are unique,” are known to require \(\tilde{\Omega }(n)\)-bit certificates [FMO+19]. (These lower bounds are, again, proven by reduction from 2-party communication complexity.) In this work we show that introducing computational assumptions allows us to efficiently certify any property in \({\textsf{P}}\), overcoming the limitations of the information-theoretic model.
1.2 Background on Delegation of Computation
Computationally sound proof systems were introduced in the seminal work of Micali [Mic00], who gave a construction for such proofs in an idealized model, the random-oracle model (ROM). Following Micali’s work, extensive effort went into obtaining non-interactive arguments (\(\textsf{SNARG}\)s) in models that are closer to the plain model, such as the Common Reference String (CRS) model. Earlier work in this line of research, such as [ABOR00, DLN+04, DL08, Gro10, BCCT12], relied on knowledge assumptions, which are non-falsifiable; for languages in \({\textsf{NP}}\), Gentry and Wichs [GW11] proved that relying on non-falsifiable assumptions is unavoidable. This led the research community to focus some attention on delegating efficient deterministic computation, that is, computation in \({\textsf{P}}\).
Initial progress on delegating computation in \({\textsf{P}}\) assumed the weaker model of a designated verifier, where the verifier holds some secret that is related to the CRS [KRR13, KRR14, KP16, BKK+18, HR18]. However, a recent line of work has led to the construction of publicly-verifiable \(\textsf{SNARG}\)s for deterministic computation, first for space-bounded computation [KPY19, JKKZ21] and then for general polynomial-time computation [CJJ21a, WW22, KLVW23]. These latter constructions exploit a connection to non-interactive batch arguments for \({\textsf{NP}}\) (\(\textsf{BARG}\)s), which can be constructed from various standard cryptographic assumptions [BHK17, CJJ21a, WW22, KLVW23, CGJ+22]. We use \(\textsf{BARG}\)s as the basis for the distributed prover that we construct in Sect. 4.
1.3 Our Results
We are now ready to give a more formal overview of our results, although the full formal definitions are deferred to the Sect. 2. For simplicity, in this overview we restrict attention to network properties that concern only the topology of the network—in other words, in the current section, a property \(\mathcal {P}\) is a family of undirected graphs. (In the more general case, a property can also involve the internal states of the network nodes, as in the spanning tree example from Sect. 1.1. This will be discussed in the Technical Overview.)
Defining  s. Like centralized \(\textsf{SNARG}\)s,
s. Like centralized \(\textsf{SNARG}\)s,  s are defined in the common reference string (CRS) model, where the prover and the verifier both have access to a shared unbiased source of randomness.
s are defined in the common reference string (CRS) model, where the prover and the verifier both have access to a shared unbiased source of randomness.
An  for a property \(\mathcal {P}\) consists of
for a property \(\mathcal {P}\) consists of
-
A prover algorithm: given a network graph \(G = (V,E)\) of size \(|V| = n\) and the common reference string (CRS), the prover algorithm outputs an assignment of \(O({\text {poly}}(\lambda , \log n))\)-bit certificates to the nodes of the network. The prover may be either a PPT centralized algorithm, or a distributed algorithm that executes in G in a polynomial number of rounds, sends messages of polynomial length on every edge, and involves only PPT computations at each network node.Footnote 4
-
A verifier algorithm: the verifier algorithm is a one-round distributed algorithm, where each node of the network simultaneously sends a (possibly different) message of length \(O({\text {poly}}(\lambda , \log n))\) on each of its edges, receives the messages sent by its neighbors, carries out some local computation, and then outputs an acceptance bit.
Each message sent by a node is produced by a PPT algorithm that takes as input the CRS, the certificate stored at the node, and the input and neighborhood of the node; the acceptance bit is produced by a PPT algorithm that takes the CRS, the certificate of the node, the messages received from its neighbors, the input and the neighborhood.
We require that certificates produced by an honest execution of the prover in the network be accepted by all verifiers with overwhelming probability, whereas for any graph failing to satisfy the property \(\mathcal {P}\), certificates produced by any poly-time cheating prover (allowing stronger, centralized provers in both cases) will be rejected by at least one node with overwhelming probability, as a function of the security parameter \(\lambda \).Footnote 5 We refer the reader to Sect. 2.1 for the formal definition.
 s with a global prover. We begin by considering a global (i.e., centralized) prover, which sees the entire network graph G. In this setting, we give a very simple construction that makes black-box use of the recently developed \(\textsf{RAM}\) \(\textsf{SNARG}\)s for \({\textsf{P}}\) [KP16, CJJ21b, KLVW23, CGJ+22] to obtain the following:
s with a global prover. We begin by considering a global (i.e., centralized) prover, which sees the entire network graph G. In this setting, we give a very simple construction that makes black-box use of the recently developed \(\textsf{RAM}\) \(\textsf{SNARG}\)s for \({\textsf{P}}\) [KP16, CJJ21b, KLVW23, CGJ+22] to obtain the following:
Theorem 1
Assuming the existence of \(\textsf{RAM}\) \(\textsf{SNARG}\)s for \({\textsf{P}}\) and collision-resistant hash families, for any property \(\mathcal {P}\in {\textsf{P}}\), there is an  with a global prover.
with a global prover.
 s with a distributed prover. As explained in Sect. 1, one of the main motivations for distributed certification is to be able to quickly check that the network is in a legal state. One natural special case is to check whether the results of a previously executed distributed algorithm are still correct, or whether they have been rendered incorrect by changes or faults in the network. To this end, we ask whether we can augment any given computationally efficient distributed algorithm \(\mathcal {D}\) with a distributed prover, which runs alongside \(\mathcal {D}\) and produces an
s with a distributed prover. As explained in Sect. 1, one of the main motivations for distributed certification is to be able to quickly check that the network is in a legal state. One natural special case is to check whether the results of a previously executed distributed algorithm are still correct, or whether they have been rendered incorrect by changes or faults in the network. To this end, we ask whether we can augment any given computationally efficient distributed algorithm \(\mathcal {D}\) with a distributed prover, which runs alongside \(\mathcal {D}\) and produces an  certifying the execution of \(\mathcal {D}\) in the specific network. The distributed prover may add some additional overhead in communication and in rounds, but we would like the overhead to be small.
certifying the execution of \(\mathcal {D}\) in the specific network. The distributed prover may add some additional overhead in communication and in rounds, but we would like the overhead to be small.
We show that indeed this is possible:
Theorem 2
Let \(\mathcal {D}\) be a distributed algorithm that runs in \({\text {poly}}(n)\) rounds in networks of size n, where in each round, every node sends a \({\text {poly}}(\log n)\)-bit message on every edge, receives the messages sent by its neighbors in the current round, and then carries out \({\text {poly}}(n)\) local computation steps.
Assuming the existence of \(\textsf{BARG}\)s for \({\textsf{NP}}\) and collision-resistant hash families, there exists an augmented distributed algorithm \(\mathcal {D}'\), which carries out the same computation as \(\mathcal {D}\), but also produces an  certificate attesting that \(\mathcal {D}\)’s output is correct.
certificate attesting that \(\mathcal {D}\)’s output is correct.
-
The overhead of \(\mathcal {D}'\) compared to \(\mathcal {D}\) is an additional \(O({{\,\textrm{diam}\,}}(G))\) rounds, during which each node sends only \({\text {poly}}(\lambda , \log n)\)-bit messages, for security parameter \(\lambda \).
-
The certificates produced are of size \({\text {poly}}(\lambda , \log n)\).
Using known constructions of \(\textsf{RAM}~\textsf{SNARG}\)s for \({\textsf{P}}\) and of \(\textsf{SNARG}\)s for batch-\({\textsf{NP}}\) [CJJ21b, CJJ21a, WW22, KLVW23, CGJ+22], we obtain both types of  s (global or distributed prover) for \({\textsf{P}}\) from either \(\textsf{LWE}\), \(\textsf{DLIN}\), or subexponential \(\textsf{DDH}\).
s (global or distributed prover) for \({\textsf{P}}\) from either \(\textsf{LWE}\), \(\textsf{DLIN}\), or subexponential \(\textsf{DDH}\).
Distributed Merkle trees (\(\textsf{DMT}\)s). To construct our distributed prover, we develop a data structure that we call a distributed Merkle tree (\(\textsf{DMT}\)), which is essentially a global Merkle tree of a distributed collection of 2|E| values, with each node u initially holding a value \(x_{u \rightarrow v}\) for each neighbor v. (At the “other end of the edge”, node v also holds a value \(x_{v \rightarrow u}\) for node v. There is no relation between the value \(x_{u \rightarrow v}\) and the value \(x_{v \rightarrow u}\).)
The unique property of the \(\textsf{DMT}\) is that it can be constructed by an efficient distributed algorithm, at the end of which each node u holds both the root of the global Merkle tree and a succinct opening to each value \(x_{(u,v)}\) that it held initially.
The \(\textsf{DMT}\) is used in the construction of the  of Theorem 2 to allow nodes to “refer” to messages sent by their neighbors. We cannot afford to have node v store these messages, or even a hash of the messages v received on each of its edges, as we do not want the certificates to grow linearly with the degree. Instead, we construct a \(\textsf{DMT}\) that allows nodes to “access” the messages sent by their neighbors: we let each value \(x_{v \rightarrow u}\) be a hash of the messages sent by node v to node u, and construct a \(\textsf{DMT}\) over these hashes. When node u needs to “access” a message sent by v to construct its proof, node v produces the appropriate opening path from the root of the \(\textsf{DMT}\), and sends it to node u. All of this happens implicitly, inside a \(\textsf{BARG}\) proof asserting that u’s local computation is correct.
of Theorem 2 to allow nodes to “refer” to messages sent by their neighbors. We cannot afford to have node v store these messages, or even a hash of the messages v received on each of its edges, as we do not want the certificates to grow linearly with the degree. Instead, we construct a \(\textsf{DMT}\) that allows nodes to “access” the messages sent by their neighbors: we let each value \(x_{v \rightarrow u}\) be a hash of the messages sent by node v to node u, and construct a \(\textsf{DMT}\) over these hashes. When node u needs to “access” a message sent by v to construct its proof, node v produces the appropriate opening path from the root of the \(\textsf{DMT}\), and sends it to node u. All of this happens implicitly, inside a \(\textsf{BARG}\) proof asserting that u’s local computation is correct.
The remainder of the paper gives a technical overview of our results.
2 Model and Definitions
In this section, we give a more formal overview of our network model; this model is standard in the area of distributed network algorithms (see, e.g., the textbook [Pel00]). We then formally define  s, the object we aim to construct.
s, the object we aim to construct.
Modeling Distributed Networks. A distributed network is modeled as an undirected, connectedFootnote 6 graph \(G = (V,E)\), where the nodes V of the network are the processors participating in the computation, and the edges E represent bidirectional communication links between them.
For a node \(v\in V\), we denote by \(N_G(v)\) (or by N(v), if G is clear from context) the neighborhood of v in the graph G. The communication links (i.e., edges) of node v are indexed by port numbers, with \(I_{u \rightarrow v} \in [n]\) denoting the port number of the channel from v to its neighbor u. The port numbers of a given node need not be contiguous, nor do they need to be symmetric (that is, it might be that \(I_{v \rightarrow u} \ne I_{u \rightarrow v}\)). We assume that the neighborhood N(v) and the port numbering at node v are known to node v during the verification stage; the node does not necessarily need to have them stored in memory at the beginning of the verification stage, but it should be able to generate them at verification time (e.g., by probing its neighborhood, opening communication sessions with its neighbors one after the other; or, in the case of a wireless network, by running a neighbor-discovery protocol).
In addition to knowing their neighborhood, we assume that each node \(v \in V\) has a unique identifier; for convenience we conflate the unique identifier of a node v with the vertex v representing v in the network graph. We assume that the UID is represented by a logarithmic number of bits in the size of the graph. No other information is available; in particular, we do not assume that the nodes know the size of the network, its diameter, or any other global properties.
A (synchronous) distributed network algorithm proceeds in synchronized rounds, where in each round, each node \(v \in V\) sends a (possibly different) message on each edge \(\left\{ {v, u} \right\} \in E\). The nodes then receive the messages sent to them, perform some internal computation, and then the next round begins. Eventually, each node halts and produces some output.
Distributed Decision Tasks. In the literature on distributed decision and certification, network properties are referred to as distributed languages. A distributed language is a family of configurations (G, x), where G is a network graph and \(x : V \rightarrow \left\{ {0,1} \right\} ^*\) assigns a string x(v) to each node \(v \in V\). The assignment x may represent, for example, the input to a distributed computation, or the internal states of the network nodes. We assume that |x(v)| is polynomial of the size of the graph. We usually refer to x as an input assignment, since for our purposes it represents an input to the decision task.
A distributed decision algorithm is a distributed algorithm at the end of which each node of the network outputs an acceptance bit. The standard notion of acceptance in distributed decision [FKP13] is that the network accepts if and only if all nodes accept; if any node rejects, then the network is considered to have rejected.
Notation. When describing the syntax (interface) of a distributed algorithm, we describe the input to the algorithm as a triplet \((\alpha ; G; \beta )\), where
-
\(\alpha \) is a value that is given to all the nodes in the network. Typically this will be the common reference string.
-
\(G = (V,E)\) is the network topology on which the algorithm runs.
-
\(\beta : V \rightarrow \left\{ {0,1} \right\} ^*\) is a mapping assigning a local input to every network node. Each node \(v \in V\) receives only \(\beta (v)\) at the beginning of the algorithm, and does not initially know the local values \(\beta (u)\) of other nodes \(u \ne v\).
We frequently abuse notation by writing a sequence of values or mappings instead of a single one for \(\alpha \) or \(\beta \) (respectively); e.g., when we write that the input to a distributed algorithm is (a, b; G; x, y), we mean that every node \(v \in V(G)\) is initially given a, b, x(v), y(v), and the algorithm executes in the network described by the graph G.
The output of a distributed algorithm in a network \(G = (V,E)\) is described by a mapping \(o : V \rightarrow \left\{ {0,1} \right\} ^*\) which specifies the output o(v) of each node \(v \in V\). In the case of decision algorithms, the output is a mapping \(o : V \rightarrow \left\{ {0,1} \right\} \), and we say that the algorithm accepts if and only if all nodes output 1 (i.e., \(\bigwedge _{v \in V} o(v) = 1\)). We denote this event by “\(\mathcal {D}( \alpha ; G ; \beta ) = 1\)”, where \(\mathcal {D}\) is the distributed algorithm, and \((\alpha ; G ; \beta )\) is its input (as explained above).
In general, when describing objects that depend on a specific graph G, we include G as a subscript: e.g., the neighborhood of node v in G is denoted \(N_G(v)\). However, when G is clear from the context, we omit the subscript and write, e.g., N(v).
2.1 Locally Verifiable Distributed \(\textsf{SNARG}\)s
In this section we give the formal definition of locally-verifiable distributed \(\textsf{SNARG}\)s ( s). This definition allows for provers that are either global (centralized) or distributed.
s). This definition allows for provers that are either global (centralized) or distributed.
Syntax. A locally verifiable distributed \(\textsf{SNARG}\) consists of the following algorithms.
\(\textsf{Gen}(1^\lambda , n)\rightarrow \textsf{crs}.\) A randomized algorithm that takes as input a security parameter \(1^\lambda \) and a graph size n, and outputs a common reference string \(\textsf{crs} \).
\(\mathcal {P}(\textsf{crs}; G; x)\rightarrow \pi .\) A deterministic algorithm (centralized or distributed)Footnote 7 that takes a \(\textsf{crs} \) obtained from \(\textsf{Gen}(1^{\lambda }, n)\) and a configuration (G, x), and outputs an assignment of certificates to the nodes \(\pi : V(G)\rightarrow \left\{ {0,1} \right\} ^*\).
\(\mathcal {V}(\textsf{crs}; G; x, \pi )\rightarrow b.\) A distributed decision algorithm that takes a common reference string \(\textsf{crs} \) obtained from \(\textsf{Gen}(1^{\lambda }, n)\), an input assignment \(x : V \rightarrow \left\{ {0,1} \right\} ^*\), and a proof \(\pi : V \rightarrow \left\{ {0,1} \right\} ^*\), and outputs acceptance bits \(b : V \rightarrow \left\{ {0,1} \right\} ^*\). In the distributed algorithm, each node v is initially given the \(\textsf{crs} \), its own local input x(v) (which is assumed to include its unique identifier), and its own proof \(\pi (v)\). During the algorithm nodes communicate with their neighbors over synchronized rounds, and eventually each node produces its own acceptance bit b(v).
Definition 1
Let \(\mathcal {L}\) be a distributed language. An  \((\textsf{Gen}, \mathcal {P}, \mathcal {V})\) for \(\mathcal {L}\) must satisfy the following properties:
\((\textsf{Gen}, \mathcal {P}, \mathcal {V})\) for \(\mathcal {L}\) must satisfy the following properties:
Completeness. For any \((G,x)\in \mathcal {L}\),

Soundness. For any PPT algorithm \(\mathcal {P}^*\), there exists a negligible function \({\text {negl}}(\cdot )\) such that

Succinctness. The \(\textsf{crs} \) and the proof \(\pi (v)\) at each node v are of length at most \({\text {poly}}(\lambda , \log n)\).
Verifier Efficiency. \(\mathcal {V}\) runs in a single synchronized communication round, during which each node sends a (possibly different) message of length \({\text {poly}}(\lambda , \log n)\) to each neighbor. At each node v, the local computation executed by \(\mathcal {V}\) runs in time \({\text {poly}}(\lambda , |\pi (v)|) = {\text {poly}}(\lambda , \log n)\).
Prover Efficiency. If the prover \(\mathcal {P}\) is centralized, then it runs in time \({\text {poly}}(\lambda , n)\). If the prover \(\mathcal {P}\) is distributed, then it runs in \({\text {poly}}(\lambda , n)\) rounds, sends messages of \({\text {poly}}(\lambda , \log n)\) bits, and uses \({\text {poly}}(\lambda , n)\) local computation time at every network node.
3  s with a Global Prover
s with a Global Prover
We begin by describing a simple construction for  s with a global prover for any property in \({\textsf{P}}\). (When we refer to \({\textsf{P}}\) here, we mean from the centralized point of view: a distributed language \(\mathcal {L}\) is in \({\textsf{P}}\) iff there is a deterministic poly-time Turing machine that takes as input a configuration (G, x) and accepts iff \((G,x) \in \mathcal {L}\).)
s with a global prover for any property in \({\textsf{P}}\). (When we refer to \({\textsf{P}}\) here, we mean from the centralized point of view: a distributed language \(\mathcal {L}\) is in \({\textsf{P}}\) iff there is a deterministic poly-time Turing machine that takes as input a configuration (G, x) and accepts iff \((G,x) \in \mathcal {L}\).)
Throughout this overview, we assume for simplicity that the nodes of the network are named \(V = \left\{ {1,\ldots ,n} \right\} \), with each node knowing its own name (but not necessarily the size n of the network).
Commit-and-Prove. Fix a language \(\mathcal {L}\in {\textsf{P}}\) and an instance \((G,x) \in \mathcal {L}\). A global prover that sees the entire instance G can use a (centralized) \(\textsf{SNARG}\) for the language \(\mathcal {L}\) in a black-box manner, to obtain a succinct proof for the statement “\((G,x) \in \mathcal {L}\).” However, regular \(\textsf{SNARG}\)s (as opposed to \(\textsf{RAM}~\textsf{SNARG}\)s) assume that the verifier holds the entire input whose membership in \(\mathcal {L}\) it would like to verify; in our case, no single node knows the entire instance G, so we cannot use the verification procedure of the \(\textsf{SNARG}\) as-is.
Our simple work-around to the nodes’ limited view of the network is to ask the prover to give the nodes a commitment with local openings C to the entire network graph (for instance, a Merkle tree [Mer89]), and to each node, a proof \(\pi _{\textsf{SNARG}}\) that the graph under the commitment is in the language \(\mathcal {L}\).
Note that the language for which \(\pi _{\textsf{SNARG}}\) is a \(\textsf{SNARG}\) proof is a set of commitments, not of network configurations—it is the language of all commitments to configurations in \(\mathcal {L}\). However, this leaves us with the burden of relating the commitment C to the true instance (G, x) in which the verifier executes, to ensure that the prover did not choose some arbitrary C that is unrelated to the instance at hand. To that end, we ask the prover to provide each node v with the following:
-
The commitment C and proof \(\pi _{\textsf{SNARG}}\). The nodes verify that they all received the same values by comparing with their neighbors, and they verify the \(\textsf{SNARG}\) proof \(\pi _{\textsf{SNARG}}\).
-
A succinct opening to v’s neighborhood. Node v verifies that indeed, C opens to its true neighborhood N(v).
Intuitively, by verifying that the commitment is consistent with the view of all the nodes, and by verifying the \(\textsf{SNARG}\) that the graph “under the commitment” is in the language \(\mathcal {L}\), we verify that the true instance (G, x) is in fact in \(\mathcal {L}\).
Although the language \(\mathcal {L}\) is in \({\textsf{P}}\), if we proceed carelessly, we might find ourselves asking the prover to prove an \({\textsf{NP}}\)-statement, such as “there exists a graph configuration (G, x) whose commitment is C, such that \((G,x) \in \mathcal {L}\).” Moreover, to prove the soundness of such a scheme, we would need to extract the configuration (G, x) from the proof \(\pi _{\textsf{SNARG}}\), in order to argue that a cheating adversary that produces a convincing proof of a false statement can be used to break either the \(\textsf{SNARG}\) or the commitment scheme. Essentially, we would require a \(\textsf{SNARK}\), a succinct non-interactive argument of knowledge for \({\textsf{NP}}\), but significant barriers are known [GW11] on constructing \(\textsf{SNARK}\)s from standard assumptions. To avoid this, we use \(\textsf{RAM}~\textsf{SNARG}\)s rather than plain \(\textsf{SNARG}\)s.
\(\textsf{RAM}~\textsf{SNARG}\)s for \({\textsf{P}}\). A \(\textsf{RAM}~\textsf{SNARG}\) ([KP16, BHK17]) is a \(\textsf{SNARG}\) that proves that a given \(\textsf{RAM}\) machine MFootnote 8 performs some computation correctly; however, instead of holding the input x to the computation, the verifier is given only a digest of x—a hash value, typically obtained from a hash family with local openings (for instance, the root of a Merkle tree of x). In our case, we ask the prover to use a polynomial-time machine \(M_\mathcal {L}\) that decides \(\mathcal {L}\) as the \(\textsf{RAM}\) machine for the \(\textsf{SNARG}\), and the commitment C as the digest; the prover computes a \(\textsf{RAM}~\textsf{SNARG}\) proof for the statement “\(M_\mathcal {L}(G,x) = 1\).”
Defining the soundness of \(\textsf{RAM}~\textsf{SNARG}\)s is delicate: because the verifier is not given the full instance but only a digest of it, there is no well-defined notion of a “false statement”—a given digest d could be the digest of multiple instances, some of which satisfy the claim and some of which do not. However, the digest is collision resistant, so intuitively, it is hard for the adversary to find two instances that have the same digest. We adopt the original \(\textsf{RAM}~\textsf{SNARG}\) soundness definition from [KP16, BHK17, KLVW23], which requires that it be computationally hard for an adversary to prove “contradictory statements”; given the common reference string, it must be hard for an adversary to find:
-
A digest d, and
-
Two different proofs \(\pi _0\) and \(\pi _1\), which are both accepted with input digest d, such that \(\pi _0\) proves that the output of the computation is 0, and \(\pi _1\) proves that the output of the computation is 1.
In our construction, the prover is asked to provide the nodes with a digest C, which is a commitment to the configuration (G, x), and a \(\textsf{RAM}~\textsf{SNARG}\) proof \(\pi _{\textsf{SNARG}}\) for the statement “\((G,x) \in \mathcal {L}\),” which the prover constructs using a RAM machine \(M_{\mathcal {L}}\) that decides membership in \(\mathcal {L}\) in polynomial time.
Tying the Digest to the Real Network Graph. By themselves, the digest C and the \(\textsf{RAM}~\textsf{SNARG}\) proof \(\pi _{\textsf{SNARG}}\) do not say much about the actual instance (G, x) that we have at hand. As we explained above, we can relate the digest to the real network by having every node verify that it opens correctly to its local view (neighborhood). However, this is not quite enough: the prover can commit to (i.e., provide a digest of) a graph \(G' \in \mathcal {L}\) that is larger than the true network graph G, such that \(G'\) agrees with G on the neighborhoods of all the “real nodes” (the nodes of G).Footnote 9 We prevent the prover from doing this by:
-
Asking the prover to provide the nodes with the size n of the network, and a certificate proving that the size is indeed n. There is a simple and elegant scheme for doing this [KKP05], based on building and certifying a rooted spanning tree of the network; it has perfect soundness and completeness, and requires \(O(\log n)\)-bit certificates.
-
The Turing machine \(M_\mathcal {L}\) that verifies membership in \(\mathcal {L}\) is assumed to take its input in the form of an adjacency list \(L_{G,x} = ( (v_1, x(v_1), N(v_1) ), \ldots , (v_n, x(v_n), N(v_n), \bot )\), where \(\bot \) is a special symbol marking the end of the list, and each triplet \((v_i, x(v_i), N(v_i))\) specifies a node \(v_i\), its input \(x(v_i)\), and its neighborhood \(N(v_i)\). Since \(\bot \) marks the end of the list, the machine \(M_\mathcal {L}\) is assumed (without loss of generality) to ignore anything following the symbol \(\bot \) in its input.
-
Recall that we assumed for simplicity that \(V = \left\{ {1,\ldots ,n} \right\} \). The prover computes a digest C of \(L_{G,x}\), and gives each node i the opening to the \({i}^{th}\) entry. Each node verifies that its entry opens correctly to its local view (name, input, and neighborhood).
-
The last node, node n, is also given the opening to the \({(n+1)}^{th}\) entry, and verifies that it opens to \(\bot \). Node n knows that it is the last node, because the prover gave all nodes the size n of the network (and certified it).
To prove the soundness of the resulting scheme, we show that if all nodes accept, then C is a commitment to some adjacency list \(L'\) which has \(L_{G,x}\) as a prefix—in the format outlined above, including the end-of-list symbol \(\bot \). Since the machine \(M_{\mathcal {L}}\) interprets \(\bot \) as the end of its input, it ignores anything past this point, and thus, the prover’s \(\textsf{SNARG}\) proof is essentially a proof for the statement “\(M_{\mathcal {L}}\) accepts (G, x).” If we assume for the sake of contradiction that \((G,x) \not \in \mathcal {L}\) then we can generate an honest \(\textsf{SNARG}\) proof \(\pi _0\) for the statement “\(M_{\mathcal {L}}\) rejects (G, x),” using the same digest C,Footnote 10 and this breaks the soundness of the \(\textsf{SNARG}\).
4  with a Distributed Prover
with a Distributed Prover
One of the main motivations for distributed certification is to help build fault-tolerant distributed algorithms. In this setting, there is no omniscient global prover that can provide certificates to all the nodes. Instead, the labels must themselves be produced by a distributed algorithm, and comprise a proof that a previous execution phase completed successfully and that its outputs are still valid (in particular, they are still relevant given the current state of the communication graph and the network nodes). Formally, given a distributed algorithm \(\mathcal {D}\), we want to construct a distributed prover \(\mathcal {D}'\) that certifies the language
Furthermore, \(\mathcal {D}'\) should not have much overhead compared to \(\mathcal {D}\) in terms of communication and rounds.
Certifying the execution of the distributed algorithm \(\mathcal {D}\) essentially amounts to proving a collection of “local” statements, each asserting that at a specific node \(v \in V(G)\), the algorithm \(\mathcal {D}\) indeed produces the claimed output y(v) when it executes in G. The prover at node v can record the local computation at node v as \(\mathcal {D}\) executes, including the messages that node v sends and receives. As a first step towards certifying that \(\mathcal {D}\) executes correctly, we could store at each node v a (centralized) \(\textsf{SNARG}\) proving that in every round, v produced the correct messages according to \(\mathcal {D}\), handled incoming messages correctly, and performed its local computation correctly, eventually outputting y(v). However, this does not suffice to guarantee that the global computation is correct, because we must verify consistency across the nodes: how can we be sure that incoming messages recorded at node v were indeed sent by v’s neighbors when \(\mathcal {D}\) ran, and vice-versa?
A naïve solution would be for node v to record, for each neighbor \(u \in N(v)\), a hash \(H_{(v,u)}\) of all the messages that v sends and receives on the edge \(\left\{ {v,u} \right\} \); at the other end of the edge, node u would do the same, producing a hash \(H_{(u,v)}\). At verification time, nodes u and v could compare their hashes, and reject if \(H_{(v,u)} \ne H_{(u,v)}\). Unfortunately, this solution would require too much space, as node v can have up to \(n - 1\) neighbors; we cannot afford to store a separate hash for each edge as part of the certificate. Our solution is instead to hash all the messages sent in the entire network together, but in a way that allows each node to “access” the messages sent by itself and its neighbors. To do this we use an object we call a distributed Merkle tree (\(\textsf{DMT}\)), which we introduce next.
Distributed Merkle Trees. A \(\textsf{DMT}\) is a single Merkle tree that represents a commitment to an unordered collection of values \(\left\{ { x_{u \rightarrow v} } \right\} _{\left\{ {u,v} \right\} \in E}\), one value for every directed edge \(u \rightarrow v\) such that \(\left\{ {u,v} \right\} \in E\). (The total number of values is 2|E|.) It is constructed by a distributed algorithm called \(\textsf{Dist}\textsf{Make}\), at the end of which each node v obtains the following information:
-
\(\textsf{val}\): the global root of the \(\textsf{DMT}\).
-
\(\textsf{rt} _v\): the “local root” of node v, which is the root of a Merkle tree over the local values \(\left\{ { x_{v \rightarrow u} } \right\} _{u \in N(v) } \).
-
\(I_v\) and \(\rho _v\): the index of \(\textsf{rt} _v\) inside the global \(\textsf{DMT}\), and the corresponding opening path \(\rho _v\) for \(\textsf{rt} _v\) from the global root \(\textsf{val}\).
-
\(\beta _v = \left\{ { (I_{v \rightarrow u}, \rho _{v \rightarrow u} ) } \right\} _{u \in N(v) }\): for each neighbor \(u \in N(v)\), the index \(I_{v \rightarrow u}\) is a relative index for the position of \(x_{v \rightarrow u}\) under the local root \(\textsf{rt} _v\), and the opening path \(\rho _{v \rightarrow u}\) is the corresponding relative opening path from \(\textsf{rt} _v\). For every pair of neighbors v and u, the index \(I_{v\rightarrow u}\) also equals the number of the port of u in v’s neighborhood.
The \(\textsf{DMT}\) is built such that for any value \(x_{v \rightarrow u}\), the index of the value in the \(\textsf{DMT}\) is given by \(I_v \parallel I_{v \rightarrow u}\), and the corresponding opening path is \(\rho _v \parallel \rho _{v \rightarrow u}\). Thus, node v holds enough information to produce an opening and to verify any value that it holds.Footnote 11 (Here and throughout, \(\parallel \) denotes concatenation; we treat indices as binary strings representing paths from the root down (with “0” representing a left turn, and “1” a right.)
The novelty of the \(\textsf{DMT}\) is that it can be constructed by an efficient distributed algorithm, which runs in O(D) synchronized rounds (where D is the diameter of the graph), and sends \({\text {poly}}(\lambda , \log n)\)-bit messages on every each in each round. We remark that it would be trivial to construct a \(\textsf{DMT}\) in a centralized manner, but the key to the efficiency of our distributed prover is to provide an efficient distributed construction; in particular, we cannot afford to, e.g., collect all the values \(\left\{ { x_{u \rightarrow v} } \right\} _{\left\{ {u,v} \right\} \in E}\) in one place, as this would require far too much communication. We avoid this by giving a distributed construction where each node does some of the work of constructing the \(\textsf{DMT}\), and eventually obtains only the information it needs.
We give an overview of the construction of the \(\textsf{DMT}\) in Sect. 5, but first we explain how we use it in the distributed prover.
Using the \({\boldsymbol{\textsf{DMT}.}}\) We assume for simplicity that in each round r, instead of sending and receiving messages on all its edges, each node v either sends or reads a message from one specific edge, determined by its current state. We further assume that each message sent is a single bit. (Both assumptions are without loss of generality, up to a polynomial blowup in the number of rounds.)
While running the original distributed algorithm \(\mathcal {D}\), the distributed prover stores the internal computation steps, the messages sent and the messages received at every node.Footnote 12 For each node v and neighbor u, node v computes two hashes:
-
A hash \(h_{v \rightarrow u}\) of the messages v sent to u, and
-
a hash \(h_{u \rightarrow v}\) of the messages v received from u.
A message sent in round r is hashed at index r. Note that both endpoints of the edge \(\left\{ { u,v } \right\} \) compute the same hashes \(h_{u \rightarrow v}\) and \(h_{v \rightarrow u}\), but they “interpret” them differently: node v views \(h_{u \rightarrow v}\) as a hash of the messages it received from u, while node u views it as a hash of the messages it sent to v, and vice-versa for \(h_{v \rightarrow u}\).
The messages hashes are used to construct the proof, but they are discarded at the end of the proving stage, so as not to exceed our storage requirements. We use a hash family with local openings, so that node v is able to produce a succinct opening from \(h_{v \rightarrow u}\) or \(h_{u \rightarrow v}\) to any specific message that was sent or received in a given round.
Next we construct a \(\textsf{DMT}\) over the values \(\left\{ { h_{u \rightarrow v }} \right\} _{ \left\{ {u,v} \right\} \in E}\). Let \(\textsf{val}^{\textsf{msg}}\) be the root of the \(\textsf{DMT}\). For each neighbor \(u \in N(v)\), node v obtains from the \(\textsf{DMT}\) the index and opening for the message hash \(h_{v \rightarrow u}\), and it sends them to the corresponding neighbor u.
For a given node v and a neighbor of it, u, let \(I^{ \textsf{msg} }_{v,u,r}\) be the index in the \(\textsf{DMT}\) of the message sent by node v to node u in round r, which is given by \(I_v \parallel I_{v \rightarrow u} \parallel r\) (recall that r is the index of the r-round message inside \(h_{v \rightarrow u}\)). Node v is able to compute both \(I^{ \textsf{msg} }_{v,u,r}\) and \(I^{ \textsf{msg} }_{u,v,r}\) and the corresponding opening paths, since it holds both hashes \(h_{v \rightarrow u}\) and \(h_{u \rightarrow v}\), learns \(I_v\) and \(\beta _v = \left\{ { I_{v \rightarrow u}} \right\} _{u \in N(v)}\) during the construction of the \(\textsf{DMT}\), and receives \(I_u \parallel I_{u \rightarrow v}\) from node v.
With these values in hand, the nodes can jointly use \(\textsf{val}^{\textsf{msg}}\) as a hash of all the messages sent or received during the execution of \(\mathcal {D}\). Each node v holds indices and openings for all the messages that it sent or received during the execution. Note that this is the only information that v obtains; although \(\textsf{val}^{\textsf{msg}}\) is a hash of all the messages sent in the network, each node can only access the messages that it “handled” (sent or received) during its own execution. This is all that is required to certify the execution of \(\mathcal {D}\), because a message that was neither sent nor received by a node does not influence its immediate execution.
Modeling the Distributed Algorithm in Detail. Before proceeding with the construction we must give a formal model for the internal computation at each network node, as our goal will be to certify that each step of this computation was carried out correctly. It is convenient to think of each round of a distributed algorithm as comprising three phases:
-
1.
A compute phase, where each node computes the messages it will send in the current round and writes them on a special output tape. In this phase nodes may also change their internal state.
-
2.
A send phase, where nodes send the messages that they produced in the compute phase. The internal states of the nodes do not change.
-
3.
A receive phase, where nodes receive the messages sent by their neighbors and write them on a special tape. The internal states of the nodes do not change.
The compute phase at each node is modeled by a RAM machine \(M_{\mathcal {D}}\) that uses the following memory sections:
-
\(\textsf{Env}\): a read-only memory section describing the node’s environment—its neighbors and port numbers, and any additional prior information it might have about the network before the computation begins.
-
\(\textsf{In}\): a read-only memory section that contains the input to the node.
-
\(\textsf{Read}\): a read-only input memory section that contains the messages that the node received in the previous round.
-
\(\textsf{Mem}\): a read-write working memory section, which contains the node’s internal state.
-
\(\textsf{Write}\): a write-only memory section where the machine writes the messages that the node sends to its neighbors in the current round. In the final round of the distributed algorithm, this memory section contains the final output of the node.
The state of the RAM machine, which we denote by \(\textsf{st} \), includes the following information:
-
Whether the machine will read or write in the current step,
-
The memory location that will be accessed,
-
If the next step is a write, the value to be written and the next state to which the RAM machine will transition after writing,
-
If the next step is a read, the states to which the RAM machine will transition upon reading 0 or 1 (respectively).
(We assume for simplicity that the memory is Boolean, that is, each cell contains a single bit.)
The send and receive phases can be thought of as follows:
-
The send phase is a sequence of 2|E| send steps, each indexed by a directed edge \(v \rightarrow u\), ordered lexicographically, first by sender v and then by receiver u. In send step \(v \rightarrow u\) the message created by v for u in the current round is sent on the edge between them.
-
The receive phase is similarly a sequence of 2|E| receive steps, indexed by the directed edges of the graph, and ordered lexicographically, again first by the sending node and then the receiving node. In receive step \(v \rightarrow u\) the message created by v for u in the current round is received at node u.
Intuitively, using the same ordering for both the send and the receive phase means that messages are received in the exact same order in which they are sent.
Certifying the Computation of One Node. After constructing the \(\textsf{DMT}\), each node has access to hashes of the messages it received during the execution of the algorithm. It would be tempting think of these hashes as input digests, since in some sense incoming messages do serve as inputs, and to use a \(\textsf{RAM}~\textsf{SNARG}\) in a black-box manner to certify that the node carried out its computation correctly. The problem with this approach is the notion of soundness we require, which is similar to that of a plain \(\textsf{SNARG}\), but differs from the soundness of a \(\textsf{RAM}~\textsf{SNARG}\): in our model, the nodes have access to their neighborhoods and their individual inputs at verification time, so in some sense they jointly have the entire input to the computation. We require that the prover should not be able to prove a false statement, that is, find a configuration (G, x) and a convincing proof that \(\mathcal {D}(G,x)\) outputs a value y which is not the true output of \(\mathcal {D}\) on (G, x). In contrast, the \(\textsf{RAM}~\textsf{SNARG}\) verifier has only a digest of the input—although it may also have a short explicit input, the bulk of the input is implicit and is “specified” only by the digest, i.e., it is not uniquely specified. The soundness of \(\textsf{RAM}~\textsf{SNARG}\)s, in turn, is weaker: they only require that the prover not be able to find a single digest and two convincing proofs for contradictory statements about the same digest. Because of this difference, we cannot use \(\textsf{RAM}~\textsf{SNARG}\)s as a black box, and instead we directly build the  from the same primary building block used in recent \(\textsf{RAM}~\textsf{SNARG}\) constructions [CJJ21b, KLVW23]: a non-interactive batch argument for \({\textsf{NP}}\) (\(\textsf{BARG}\)).
from the same primary building block used in recent \(\textsf{RAM}~\textsf{SNARG}\) constructions [CJJ21b, KLVW23]: a non-interactive batch argument for \({\textsf{NP}}\) (\(\textsf{BARG}\)).
A (non-interactive) \(\textsf{BARG}\) is an argument that proves a set (a batch) of \({\textsf{NP}}\) statements \(x_1,\ldots ,x_k\in \mathcal {L}\), for an \({\textsf{NP}}\) language \(\mathcal {L}\), such that the size of the proof increases very slowly (typically, polylogarithmically) with the number of statements k. (This is not a \(\textsf{SNARG}\) for \({\textsf{NP}}\), since the proof size does grow polynomially with the length of one witness.) Several recent works [CJJ21a, KLVW23] have constructed from standard assumptions \(\textsf{BARG}\)s with proof size \({\text {poly}}(\lambda , s, \log k)\), where s is the size of the circuit that verifies the \({\textsf{NP}}\)-language. These \(\textsf{BARG}\)s were then used in [CJJ21b, KLVW23] to construct \(\textsf{RAM}~\textsf{SNARG}\)s for \({\textsf{P}}\). Following their approach, we use \(\textsf{BARG}\)s to construct our desired  . Roughly, our method is as follows.
. Roughly, our method is as follows.
At each node v, we use a hash family with local openings to commit to the sequence of RAM machine configurations that v goes through: for example, if the history of the memory section \(\textsf{Read}\) at node v is given by \(\textsf{Read}_v^0, \textsf{Read}_v^1, \ldots \) (with \(\textsf{Read}_v^0\) being the initial contents of the memory section, \(\textsf{Read}_v^1\) being the contents following the first step of the algorithm, and so on), then we first compute individual hashes of \(\textsf{Read}_v^0, \textsf{Read}_v^1, \ldots \), and then hash together all these hashes to obtain a hash \(\textsf{val}^{\textsf{Read}}_v\) representing the sequence of contents on this memory section at node v. Similarly, let \(\textsf{val}^{\textsf{Mem}}_v, \textsf{val}^{\textsf{Write}}_v\) be commitments to the memory section contents of \(\textsf{Mem}\) and \(\textsf{Write}\) at v, and let \(\textsf{val}^{\textsf{st}}_v\) be a hash of the sequence of internal RAM machine states that node v went through during the execution of \(\mathcal {D}\) (in all rounds).
We now construct a \(\textsf{BARG}\) to prove the following statement (roughly speaking): for each round r and each internal step i of the compute phase of that round, there exist openings of \(\textsf{val}^{\textsf{Read}}_v\), \(\textsf{val}^{\textsf{Mem}}_v\), \(\textsf{val}^{\textsf{Write}}_v\) and \(\textsf{val}^{\textsf{st}}_v\) in indices (r, i) and \((r,i+1)\) to values \(\textsf{st} _{r,i},\textsf{st} _{r,i},\textsf{h}\textsf{Read}_{r,i},\textsf{h}\textsf{Read}_{r,i+1}, \textsf{h}\textsf{Mem}_{r,i}, \textsf{h}\textsf{Mem}_{r,i+1},\textsf{h}\textsf{Write}_{r,i}, \textsf{h}\textsf{Write}_{r,i+1}\), such that the following holds:
-
If i is a step of the compute phase, and \(\textsf{st} _{r,i}\) indicates that the machine reads from location \(\ell \) in memory section \(\textsf{TP}\in \left\{ {\textsf{Read},\textsf{Mem},\textsf{Write}} \right\} \), then there exists an opening of \(\textsf{h}\textsf{TP}_{r,i}\) in location \(\ell \) to a bit b such that upon reading b, \(M_\mathcal {D}\) transitions to \(\textsf{st} _{r,i+1}\). Moreover, the hash values of the memory sections \(\textsf{h}\textsf{Read},\textsf{h}\textsf{Mem},\textsf{h}\textsf{Write}\) do not change in step (r, i): we have \(\textsf{h}\textsf{Read}_{r,i}=\textsf{h}\textsf{Read}_{r,i+1}\), \(\textsf{h}\textsf{Mem}_{r,i} = \textsf{h}\textsf{Mem}_{r,i+1}\), and \(\textsf{h}\textsf{Write}_{r,i} = \textsf{h}\textsf{Write}_{r,i+1}\).
-
If i is a step of the compute phase, and \(\textsf{st} _{r,i}\) indicates that the machine writes the value b to location \(\ell \) in memory section \(\textsf{TP}\in \left\{ {\textsf{Mem},\textsf{Write}} \right\} \), then there exists an opening of \(\textsf{h}\textsf{TP}_{r,i+1}\) in location \(\ell \) to the bit b. Moreover, the hash values of the other memory sections \(\left\{ {\textsf{h}\textsf{Read},\textsf{h}\textsf{Mem},\textsf{h}\textsf{Write}} \right\} \backslash {\textsf{TP}}\) do not change in step (r, i).
-
If i is a step of the send phase indexed by \(v\rightarrow u\) (i.e., a step where v sends a message to u), then there exists a message m such that \(\textsf{val}^{\textsf{msg}}\) opens to m in index \(I^{ \textsf{msg} }_{v,u,r}\) and \(\textsf{h}\textsf{Write}\) opens to m in index d.
-
If i is a step of the receive phase indexed by \(u \rightarrow v\) (i.e., a step where v receives a message from u), and u is the \({d}^{th} \) neighbor of v, then there exists a message m such that \(\textsf{val}^{\textsf{msg}}\) opens to m in index \(I^{ \textsf{msg} }_{u,v,r}\) and \(\textsf{h}\textsf{Read}\) opens to m in index d.
In addition to the requirements above, we ust ensure that whenever the contents of a memory section change, they change only in the location to which the machine writes, and the hash value for the memory section changes accordingly; for example, if in step i of the compute phase of round r the machine writes value b to location \(\ell \) of memory section \(\textsf{TP}\), then we must ensure not only that \(\textsf{TP}_{r,i+1}\) opens to b in location \(\ell \), but also that \(\textsf{h}\textsf{TP}_{r,i}\) and \(\textsf{h}\textsf{TP}_{r,i+1}\) are hash values of arrays that differ only in location \(\ell \). To do so, we use a hash family that also supports write operations (in addition to local openings), as in the definition of a hash tree in [KPY19]. For example, a Merkle tree [Mer89] satisfies all of the requirements for a hash tree.
We use the hash write operations to include the following additional requirements as part of our \(\textsf{BARG}\) statement:
-
For each step i of the compute phase of each round r, if \(\textsf{st} _{r,i}\) indicates that the machine writes value b to location \(\ell \) in memory section \(\textsf{TP}\in \left\{ {\textsf{Mem},\textsf{Write}} \right\} \), then there exists an opening showing that \(\textsf{h}\textsf{TP}_{r,i}\) and \(\textsf{h}\textsf{TP}_{r,i+1}\) differ only in location \(\ell \).
-
For each step of the receive phase of each round r, if the message received in this step is written to location \(\ell \) of \(\textsf{Read}\), then there exists an opening showing that \(\textsf{h}\textsf{Read}_{r,i},\textsf{h}\textsf{Read}_{r,i+1}\) differ only location \(\ell \).
There is one main obstacle remaining: in all known \(\textsf{BARG}\) constructions, the \(\textsf{BARG}\) is only as succinct as the circuit that verifies the statements it claims. In our case, the statements involve the indices \(I^{ \textsf{msg} }_{v,u,r}\), as well as port numbers of the various neighbors of v, and the corresponding opening paths. These must be “hard-wired” into the circuit, because they are obtained from the \(\textsf{DMT}\), i.e., they are external to the \(\textsf{BARG}\) itself. Each node v may need to use up to \(n - 1\) indices and openings, one for every neighbor, so we cannot afford to use a circuit that explicitly encodes them.
Indirect Indexing. To avoid hard-wiring the indices and openings into the \(\textsf{BARG}\), each node v computes a commitment to the indices, in the form of a locally openable hash of the following arrays:
-
\(\textsf{Ind}^{ in }(v)\), an array containing at each index \(I_{v\rightarrow u}\) the value \(I_v \parallel I_{v \rightarrow u}\).
-
\(\textsf{Ind}^{ out }(v)\), an array containing at each index \(I_{v\rightarrow u}\) the value \(I_u \parallel I_{u \rightarrow v}\).
-
\(\textsf{Port}(v)\), an array containing at each index k the value \(\bot \) if \(v_k\notin N(v)\), or the value d if \(v_k\) is the \({d}^{th} \) neighbor of v.
Denote these hash values by \(\textsf{val}^{ in }(v)\), \(\textsf{val}^{ out }(v)\), and \(\textsf{val}^{\textsf{Port}}(v)\), respectively.
Now we can augment the \(\textsf{BARG}\), and have it prove the following: at every round r and step i of the send phase, there exists a port number d, an index I, a message m, and appropriate openings to the hash values \(\textsf{val}^{\textsf{Port}},\textsf{val}^{ out } ,\textsf{h}\textsf{Write}_{r,i},\textsf{val}^{\textsf{msg}}\) such that
-
\(\textsf{val}^{\textsf{Port}}\) opens to d in location \(\ell \) such that \(v_\ell \) is the node that v sends a message to in step i of every send phase,
-
\(\textsf{val}^{ out }\) opens to I in location d,
-
\(\textsf{h}\textsf{Write}_{r,i}\) opens to m in location d, and
-
\(\textsf{val}^{\textsf{msg}}\) opens to m in location \(I \parallel r\).
Similarly, at every round r and step i of the receive phase, there exist a port number d, an index I, a message m, and appropriate openings to the hash values \(\textsf{val}^{\textsf{Port}},\textsf{val}^{\in } ,\textsf{h}\textsf{Read}_{r,i+1},\textsf{val}^{\textsf{msg}}\) such that
-
\(\textsf{val}^{\textsf{Port}}\) opens to d in location k such that \(v_k\) is the node that v receives a message to in step i of every send phase,
-
\(\textsf{val}^{ in }\) opens to I in location d,
-
\(\textsf{h}\textsf{Read}_{r,i+1}\) opens to m in location d,Footnote 13 and
-
\(\textsf{val}^{\textsf{msg}}\) opens to m in location \(I \parallel r\).
The circuit verifying this \(\textsf{BARG}\)’s statement requires only the following values to be hard-wired: \(\textsf{val}^{\textsf{st}}\), \(\textsf{val}^{\textsf{msg}}\), \(\textsf{val}^{ in }\), \(\textsf{val}^{ out }\), \(\textsf{val}^{\textsf{Port}}\), \(\textsf{val}^{\textsf{Read}}\), \(\textsf{val}^{\textsf{Mem}}\), \(\textsf{val}^{\textsf{Write}}\). During verification, however, node v must verify that indeed, the hashes \(\textsf{val}^{ in }(v)\), \(\textsf{val}^{ out }(v), \textsf{val}^{\textsf{Port}}(v)\) are correct: node v can do this by re-computing the hashes, using the index \(I_v\) which is stored as part of its certificate, the port numbers \(\left\{ { I_{v \rightarrow u} } \right\} _{u \in N(v)}\) that it accesses during verification, and also indices \(\left\{ { I_u } \right\} _{u \in N(v)}\) and port numbers \(\left\{ { I_{u \rightarrow v} } \right\} _{u \in N(v)}\) that v’s neighbors can provide in verification time.
The Soundness of our Construction. Following [KLVW23], instead of using regular \(\textsf{BARG}\)s, we use somewhere extractable \(\textsf{BARG}\)s (\(\textsf{seBARG}\)s): an \(\textsf{seBARG}\) is a \(\textsf{BARG}\) with the following somewhere argument of knowledge property: for some index i, using the appropriate trapdoor, the \(\textsf{seBARG}\) proof completely reveals an \({\textsf{NP}}\)-witness for the \({i}^{th}\) statement. Importantly, the trapdoor is generated alongside the \(\textsf{crs} \) and the \(\textsf{crs} \) hides the binding index i: the (computationally bounded) prover cannot tell from the \(\textsf{crs} \) alone the binding index i. Conveniently, \(\textsf{BARG}\)s can be easily transformed into \(\textsf{seBARG}\)s [CJJ21b, KLVW23], without adding more assumptions.
The overall idea of our soundness proof is similar to the one in [CJJ21b, KLVW23], although there are some complications (e.g., the need to switch between different nodes of the network as we argue correctness). Assume for the sake of contradiction that a cheating prover is able to convince the network to accept a false statement with non-negligible probability. We proceed by induction over the rounds and internal steps (inside each compute, send and receive phase) of the distributed algorithm: in the induction we track the true state of the distributed algorithm, and compare witnesses extracted from the \(\textsf{seBARG}\) to this state. Informally speaking, we prove that from a proof that is accepted, using the appropriate trapdoor and crs, we can extract at each step a witness that must be compatible with the true execution of the distributed algorithm, otherwise we break the \(\textsf{seBARG}\). In the last round, this means that the output encoded in the witness is the correct output of the distributed algorithm. But this contradicts our assumption that the adversary convinces the network of a false statement.
5 Distributed Merkle Trees
Finally, we briefly sketch the construction of the distributed Merkle tree used in the previous section.
The Structure of the \(\textsf{DMT}\). Recall that our goal with the distributed Merkle tree (\(\textsf{DMT}\)) is to hash together all the messages sent during the execution of the distributed algorithm, in such a way that a node can produce openings for its own sent messages. Accordingly, we construct the \(\textsf{DMT}\) in several layers (see Fig. 1):
-
At the lowest level, for each node v and neighbor \(u \in N(v)\), node v hashes together the messages \((m_1^{v \rightarrow u}, m_2^{v \rightarrow u},\ldots )\) that it sent to node u, obtaining a hash \(\textsf{rt} _{v \rightarrow u}\).
-
At the second level, each node v hashes together the hashes of its different edges, \(\left\{ { \textsf{rt} _{v \rightarrow u} } \right\} _{u \in N(v)}\), ordered by the port numbers \(I_{v \rightarrow u}\), obtaining a hash \(\textsf{rt} _v\) which we refer to as v’s local root.
-
Finally, the nodes collaborate to hash their local roots \(\left\{ { \textsf{rt} _v } \right\} _{v \in V}\) together to obtain a global root \(\textsf{val}\). The nodes are initially not ordered, but during the creation of the \(\textsf{DMT}\), the local roots \(\left\{ { \textsf{rt} _v } \right\} _{v \in V}\) are ordered; and each node v obtains an index \(I_v\) for its local root, and the corresponding opening path from \(\textsf{val}\) to \(\textsf{rt} _v\).
Constructing the \(\textsf{DMT}\). After each node computes the hash values \(\textsf{rt} _{v\rightarrow u}\) for each of its neighbors \(u\in N(v)\), we continue by having the network nodes compute a spanning tree \( ST \) of the network, with each node v learning its parent \(p_v \in N(v) \cup \left\{ {\bot } \right\} \), and its children \(C_v \subseteq N(v)\). The root \(v_0\) of the spanning tree is the only node that has a null parent, i.e., \(p_{v_0} = \bot \).
We note that using standard techniques, a rooted spanning tree can be constructed in O(D) rounds in networks of diameter D, using \(O(\log n)\)-bit messages in every round; this can be done even if the nodes do not initially know the diameter D or the size n of the network, and it does not require the root to be chosen or known in advance [Lyn96].
After constructing the spanning tree, we compute the \(\textsf{DMT}\) in three stages: in the first stage nodes compute a Merkle tree of their own values, in the second we go “up the spanning tree” to compute the global Merkle tree, and the third stage goes “down the tree” to obtain the indices and the openings.
Stage 1: Local Hash Trees. Let \({\textbf{x}}_v\) be a vector containing the values \(\left\{ { \textsf{rt} _{v\rightarrow u} } \right\} _{u \in N(v)}\) held by node v, ordered by the port number of the neighbor \(u \in N(v)\) at node v (padded up to a power of 2, if necessary). For each node v and neighbor \(u \in N(v)\), let \(I_{v \rightarrow u}\) be a binary representation of the port number of u at v (again, possibly padded).
Each node v computes its local root \(\textsf{rt} _v\) by building a Merkle tree over the vector \(\textbf{x}_v\), as well as an opening \(\rho _{v\rightarrow u}\) for the index \(I_{v \rightarrow u}\), for each neighbor \(u \in N(v)\). We let \(\beta _v = \left\{ {(I_{v\rightarrow u}, \rho _{v\rightarrow u})} \right\} _{u\in N(v)}\).
Stage 2: Spanning Tree Computation. The nodes jointly compute a spanning tree \( ST \) of the network, storing at every node v the parent \(p_v \in N(v)\) of v and the children \(C_v \subseteq N(v)\) of v. In the sequel, we denote by \(v_0\) the root of the spanning tree.
Stage 3: Convergecast of hash-tree forests. In this stage, we compute the global hash tree up the spanning tree ST, with each node v merging some or all of the hash-trees received from its children and sending the result upwards in the form of a set of \(\textsf{HT}\)-roots annotated with height information.
Each node v receives from each child \(c \in C_v\) a set \(S_c\) of pairs \((\textsf{rt}, h)\), where \(\textsf{rt} \) is a Merkle-tree root, and \(h \in \mathbb {N}\) is the cumulative height of the Merkle tree. Node v now creates a forest \(F_v\), as follows:
-
1.
Initially, \(F_v\) contains the roots sent up by v’s children, and a new leaf representing v’s local hash tree: \(F_v = \left\{ { ( \textsf{rt} _v, 0 ) } \right\} \cup \bigcup _{c \in C_v} S_c\).
-
2.
While there remain two trees in \(F_v\) whose roots \(\textsf{rt} _0\) and \(\textsf{rt} _1\) have the same cumulative height h (note—we do not care about the actual height of the trees in the forest \(F_v\), but rather about their cumulative height, represented by the value h in the node \((\textsf{rt}, h)\)): node v chooses two such trees and merges them, creating a new root \(\textsf{rt} \) of cumulative height \(h+1\) and placing \((\textsf{rt} _0, h)\) and \((\textsf{rt} _1, h)\) as the left and right children of \((\textsf{rt}, h+1)\), respectively.
-
3.
When there no longer remain two trees in \(F_v\) whose roots have the same cumulative height:
-
If \(v \ne v_0\) (that is, v is not the root of the spanning tree), node v sends its parent, \(p_v\), the set \(S_v\) of tree-roots in \(F_v\). The size of this set is at most \(O(\log n)\), since it contains at most one root of any given cumulative height (if there were two roots of the same cumulative height, node v would merge them).
-
At the root \(v_0\), we do not want to halt until \(F_v\) is a single tree. If \(F_v\) is not yet a single tree, node \(v_0\) must pad the forest by adding “dummy trees” so that it can continue to merge. To do so, node \(v_0\) finds the tree-root \((\textsf{rt}, h)\) that has the smallest cumulative height h in \(F_v\). It then creates a “dummy” Merkle-tree of height h, with root \((\bot , h)\), and adds it to \(F_{v_0}\). Following this addition, there exist two tree-roots of cumulative-height h (the original tree-root \((\textsf{rt}, h)\) and the “dummy” tree-root \((\bot , h)\)), which \(v_0\) now merges. It continues on with this process, at each step choosing a tree with the smallest remaining height, and either merging it with another same-height tree if there is one, or creating a dummy tree and merging the shortest tree with it.
-
When the last stage completes, the forest \(F_{v_0}\) computed by node \(v_0\) (the root of the spanning tree) is in fact a single tree, whose root is the root of the global Merkle tree. Let \(\textsf{val}\) be this root.
Stage 4: Computing Hash-Tree Indices and Openings. In this stage we proceed down the spanning tree, forwarding the global root \(\textsf{val}\) downwards. In addition, as we move down the tree, each node v annotates its forest \(F_v\) with indices and opening paths: first, it receives from its parent \(p_v\) an index and opening for every tree-root \((\textsf{rt}, h) \in F_v\) that it sent upwards to \(p_v\). Then, it extends this information “downwards” inside \(F_v\), annotating each inner node and leaf in \(F_v\) with their index and opening path from the global root \(\textsf{val}\): for example, if \((\textsf{rt} _0, h)\) and \((\textsf{rt} _1, h)\) are the left and right children of \((\textsf{rt}, h+1)\) in \(F_v\), and the index and opening path for \((\textsf{rt}, h+1)\) are already known to be I and \(\rho \) (resp.), then the index and opening path for \((\textsf{rt} _0, h)\) are \(I \parallel 0\) and \(\rho \parallel \textsf{rt} _1\) (resp.).
Outputs. The final output at node v is \((\textsf{val}, \textsf{rt} _v, I_v, \rho _v, \beta _v)\). (For the  , at the end of the proving stage, \(\beta _v\) is discarded, as it is too long to store. However, \(\textsf{val}, \textsf{rt} _v, I_v\) and \(\rho _v\) are part of node v’s certificate.)
, at the end of the proving stage, \(\beta _v\) is discarded, as it is too long to store. However, \(\textsf{val}, \textsf{rt} _v, I_v\) and \(\rho _v\) are part of node v’s certificate.)
We remark that for our purposes, it is not necessary for the nodes to certify that they computed the \(\textsf{DMT}\) correctly: after obtaining the global root and the relevant openings, the nodes simply use the \(\textsf{DMT}\) as they would use a centralized hash with local openings. The completeness proof of our  relies on the fact that a correctly-computed \(\textsf{DMT}\) will open to the correct information everywhere, but the soundness proof does not rely the details of the construction, only on the fact that the value obtained by opening various locations of the \(\textsf{DMT}\) matches the true execution of the algorithm.
relies on the fact that a correctly-computed \(\textsf{DMT}\) will open to the correct information everywhere, but the soundness proof does not rely the details of the construction, only on the fact that the value obtained by opening various locations of the \(\textsf{DMT}\) matches the true execution of the algorithm.
Notes
- 1.
As just one example of many, in [KP98] it is shown that one can construct a k-dominating set of the network graph in \(\tilde{O}(k)\) communication per edge, and this is used to construct a minimum-weight spanning tree in \(\tilde{O}(\sqrt{n})\) communication per edge.
- 2.
In general, the nodes of the network may have inputs, on which the property may depend, but for simplicity we ignore inputs for the time being and discuss only properties of the graph topology itself.
- 3.
Assuming the underlying network is connected, which is a standard assumption in the area; otherwise additional information, such as the size of the network, is required.
- 4.
In fact, as we mentioned in Sect. 1, a centralized prover can also be implemented by a distributed algorithm where one node learns the entire network graph and then generates the certificates. This is easy to do in polynomial rounds and message length.
- 5.
The schemes we construct actually satisfy adaptive soundness: there is no PPT algorithm that can, with non-negligible probability, output a network graph and certificates for all the nodes, such that the property does not hold for the network graph but all of the nodes accept.
- 6.
We consider only connected networks, since in disconnected networks one can never hope to carry out any computation involving more than one connected component. Also, it is fairly standard to assume an undirected graph topology, i.e., bidirectional communication links, although directed networks are also considered sometimes (for instance, in [BFO22]).
- 7.
For the centralized case, we denote \(\mathcal {P}(\textsf{crs},G,x)\) instead of \((\textsf{crs};G;x)\) as we have one entity that receives the entire input.
- 8.
A \(\textsf{RAM}\) machine M is given query access to an input x and an unbounded random-access memory array, and returns some output y. Each query to the input x or the memory is considered a unit-cost operation.
- 9.
This requires that \(G'\) not be connected, but that is not necessarily a problem for the prover, depending on the property \(\mathcal {L}\).
- 10.
- 11.
For simplicity we assume that nodes can query the communication infrastructure for a consistent order of their neighbors (e.g., by “port number”); thus the relative ordering \(I_{v\rightarrow u}\) does not count against v’s storage. This is a standard assumption in the area. In the general case, the port numbers themselves, which may stand for MAC addresses or similar, do not necessarily need to be consecutive numbers from \(1,\ldots ,\deg (v)\), but we can order v’s neighbors in order of increasing port number.
- 12.
We believe that this additional temporary storage requirement can be avoided using incrementally verifiable computation, but we have not gone through the details.
- 13.
As explained above, we actually require that this opening show that \(\textsf{h}\textsf{Read}_{r,i}\) and \(\textsf{h}\textsf{Read}_{r,i+1}\) only differ in the location d and \(\textsf{h}\textsf{Read}_{r,i+1}\) opens to m in that location.
References
Aiello, W., Bhatt, S.N., Ostrovsky, R., Rajagopalan, S.: Fast verification of any remote procedure call: short witness-indistinguishable one-round proofs for np. In: Proceedings of the 27th International Colloquium on Automata, Languages and Programming, pp. 463–474 (2000)
Aldema Tshuva, E., Oshman, R.: Brief announcement: on polynomial-time local decision. In: Proceedings of the 2022 ACM Symposium on Principles of Distributed Computing, pp. 48–50 (2022)
Awerbuch, B., Patt-Shamir, B., Varghese, G.: Self-stabilization by local checking and correction. In: Proceedings 32nd Annual Symposium of Foundations of Computer Science, pp. 268–277 (1991)
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In: Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, pp. 326–349 (2012)
Balliu, A., D’Angelo, G., Fraigniaud, P., Olivetti, D.: What can be verified locally? J. Comput. Syst. Sci. 97, 106–120 (2018)
Ben Shimon, Y., Fischer, O., Oshman, R.: Proof labeling schemes for reachability-related problems in directed graphs. In: Parter, M. (ed.) SIROCCO 2022. LNCS, vol. 13298, pp. 21–41. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-09993-9_2
Brakerski, Z., Holmgren, J., Kalai, Y.T.: Non-interactive delegation and batch np verification from standard computational assumptions. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, pp. 474–482 (2017)
Badrinarayanan, S., Kalai, Y.T., Khurana, D., Sahai, A., Wichs, D.: Succinct delegation for low-space non-deterministic computation. In: Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, pp. 709–721 (2018)
Bick, A., Kol, G., Oshman, R.: Distributed zero-knowledge proofs over networks. In: SODA, pp. 2426–2458. SIAM (2022)
Choudhuri, A.R., Garg, S., Jain, A., Jin, Z., Zhang, J.: Correlation intractability and SNARGs from sub-exponential DDH. Cryptology ePrint Archive (2022)
Choudhuri, A.R., Jain, A., Jin, Z.: Non-interactive batch arguments for NP from standard assumptions. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12828, pp. 394–423. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84259-8_14
Choudhuri, A.R., Jain, A., Jin, Z.: SNARGs for P from LWE. In: 62nd IEEE Annual Symposium on Foundations of Computer Science (FOCS), pp. 68–79 (2021)
Di Crescenzo, G., Lipmaa, H.: Succinct NP proofs from an extractability assumption. In: Beckmann, A., Dimitracopoulos, C., Löwe, B. (eds.) CiE 2008. LNCS, vol. 5028, pp. 175–185. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69407-6_21
Dwork, C., Langberg, M., Naor, M., Nissim, K., Reingold, O.: Succinct proofs for np and spooky interactions (2004). http://www.cs.bgu.ac.il/kobbi/papers/spooky_sub_crypto.pdf
Feuilloley, L., Bousquet, N., Pierron, T.: What can be certified compactly? compact local certification of MSO properties in tree-like graphs. In: PODC, pp. 131–140. ACM (2022)
Feuilloley, l.: Introduction to local certification. Disc. Math. Theor. Comput. Sci. 23(3) (2021)
Feuilloley, L., Fraigniaud, P., Hirvonen, J., Paz, A., Perry, M.: Redundancy in distributed proofs. Distrib. Comput. 34(2), 113–132 (2021)
Fraigniaud, P., Göös, M., Korman, A., Suomela, J.: What can be decided locally without identifiers? In: Proceedings of the 2013 ACM Symposium on Principles of Distributed Computing, pp. 157–165. ACM, New York (2013)
Fraigniaud, P., Halldórsson, M.M., Korman, A.: On the impact of identifiers on local decision. In: Baldoni, R., Flocchini, P., Binoy, R. (eds.) OPODIS 2012. LNCS, vol. 7702, pp. 224–238. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35476-2_16
Fraigniaud, P., Korman, A., Peleg, D.: Towards a complexity theory for local distributed computing. J. ACM (JACM) 60(5), 1–26 (2013)
Fraigniaud, P., Montealegre, P., Oshman, R., Rapaport, I., Todinca, I.: On distributed merlin-arthur decision protocols. In: Censor-Hillel, K., Flammini, M. (eds.) SIROCCO 2019. LNCS, vol. 11639, pp. 230–245. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-24922-9_16
Fraigniaud, P., Montealegre, P., Rapaport, I., Todinca, I.: A meta-theorem for distributed certification. In: Parter, M. (ed.) SIROCCO 2022. LNCS, vol. 13298, pp. 116–134. Springer, Heidelberg (2022). https://doi.org/10.1007/s00453-023-01185-1
Fraigniaud, P., Patt-Shamir, B., Perry, M.: Randomized proof-labeling schemes. Distrib. Comput. 32, 217–234 (2019)
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Göös, M., Suomela, J.: Locally checkable proofs in distributed computing. Theory Comput. 12(1), 1–33 (2016)
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing, pp. 99–108 (2011)
Holmgren, J., Rothblum, R.: Delegating computations with (almost) minimal time and space overhead. In: 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS), pp. 124–135. IEEE (2018)
Jawale, R., Kalai, Y.T., Khurana, D., Zhang, R.: SNARGs for bounded depth computations and PPAD hardness from sub-exponential LWE. In: Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, pp. 708–721 (2021)
Korman, A., Kutten, S., Peleg, D.: Proof labeling schemes. In: Proceedings of the Twenty-Fourth Annual ACM Symposium on Principles of Distributed Computing, pp. 9–18 (2005)
Kalai, Y., Lombardi, A., Vaikuntanathan, V., Wichs, D.: Boosting batch arguments and RAM delegation. In: Proceedings of the 55th Annual ACM Symposium on Theory of Computing (STOC), pp. 1545–1552 (2023)
Kol, G., Oshman, R., Saxena, R.R.: Interactive distributed proofs. In: Symposium on Principles of Distributed Computing (PODC), pp. 255–264 (2018)
Kutten, S., Peleg, D.: Fast distributed construction of small k-dominating sets and applications. J. Algor. 28, 27 (1998)
Kalai, Y., Paneth, O.: Delegating RAM computations. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 91–118. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_4
Kalai, Y.T., Paneth, O., Yang, L.: How to delegate computations publicly. In: Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, pp. 1115–1124 (2019)
Kalai, Y.T., Raz, R., Rothblum, R.D.: Delegation for bounded space. In Proceedings of the Forty-Fifth Annual ACM Symposium on Theory of Computing, pp. 565–574 (2013)
Kalai, Y.T., Raz, R., Rothblum, R.D.: How to delegate computations: the power of no-signaling proofs. In: Proceedings of the Forty-Sixth Annual ACM Symposium on Theory of Computing, pp. 485–494 (2014)
Lynch, N.A.: Distributed Algorithms. Morgan Kaufmann, Burlington (1996)
Merkle, R.C.: A certified digital signature. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 218–238. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_21
Micali, S.: Computationally sound proofs. SIAM J. Comput. 30(4), 1253–1298 (2000)
Naor, M., Parter, M., Yogev, E.: The power of distributed verifiers in interactive proofs. In: Chawla, S. (ed.) Symposium on Discrete Algorithms (SODA), pp. 1096–115 (2020)
Ostrovsky, R., Perry, M., Rosenbaum, W.: Space-time tradeoffs for distributed verification. In: Das, S., Tixeuil, S. (eds.) SIROCCO 2017. LNCS, vol. 10641, pp. 53–70. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72050-0_4
Peleg, D.: Distributed Computing: A Locality-Sensitive Approach. Society for Industrial and Applied Mathematics, Philadelphia (2000)
Patt-Shamir, B., Perry, M.: Proof-labeling schemes: broadcast, unicast and in between. In: Spirakis, P., Tsigas, P. (eds.) SSS 2017. LNCS, vol. 10616, pp. 1–17. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69084-1_1
Sarma, A.D., et al. Distributed verification and hardness of distributed approximation. SIAM J. Comput. (special issue of STOC 2011) (2012)
Waters, B., Wu, D.J.: Batch arguments for and more from standard bilinear group assumptions. In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022. LNCS, vol. 13508, pp. 433–463. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15979-4_15
Acknowledgments
We would like to thank Omer Paneth for fruitful and illuminating iscussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Aldema Tshuva, E., Boyle, E., Cohen, R., Moran, T., Oshman, R. (2023). Locally Verifiable Distributed SNARGs. In: Rothblum, G., Wee, H. (eds) Theory of Cryptography. TCC 2023. Lecture Notes in Computer Science, vol 14369. Springer, Cham. https://doi.org/10.1007/978-3-031-48615-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-48615-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48614-2
Online ISBN: 978-3-031-48615-9
eBook Packages: Computer ScienceComputer Science (R0)



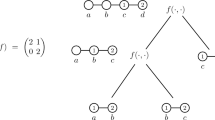

 s), a distributed analog of
s), a distributed analog of  s with a Global Prover
s with a Global Prover with a Distributed Prover
with a Distributed Prover
