Keywords

1 Introduction

To attain a specified speed in high speed machinery, they require to pass through critical speed. The maximum response of unbalanced rotating machinery can be affected by a modification in operating speed or rate of acceleration. The fatigue cracks among the various faults in rotor bearing systems is known as a grave threat to an uninterrupted operation of rotating machinery due to their potential to cause catastrophic failure. The dynamic response of a slant-cracked rotor passing through critical speed have been calculated by Prabhakar et al. using finite element method and the transient response of the cracked rotor for passing through critical speed has been analyzed for various crack depths, angular acceleration and torsional excitation for finding crack detection and monitoring techniques [1]. Since the vibration response during start up and shut down is important to detect cracks, a signal processing technique has been applied by Babu et al. to transient response of a cracked rotor [2]. The Hilbert Huang transform found to be better compared to fast Fourier transform and continuous wavelet transform. Chandra et al. utilized the rotor start up vibrations to perform fault identification using time frequency techniques using three signal processing tools namely short time Fourier transform, continuous wavelet transform and Hilbert Huang transform [3]. The computational time of Hilbert Huang transform is obtained very less in comparison to continuous wavelet transform however for noisy data continuous wavelet transform is preferred over Hilbert Huang transform.

Since the maximum response of rotating machinery can be affected by a modification in operating speed or rate of acceleration, to traverse a machine safely through the critical speed, it can be quickly accelerated to decrease the destructive influence of the presence of critical speeds [4,5,6,7,8,9]. Since during run down the deceleration rates are slower than acceleration rates in startup, many resonant problems occur on run down, resulting in machine damage which necessitates the study of this phenomenon and its effective parameters. Broad review of the state of the art in rotating machinery with particular regard to passing through critical speed is presented herein.

The overcritical induction motor under electromagnetic forces accelerated passing through the critical speed was studied by Pennacchi et al. [10]. A finite element model was developed and dependency of magnetic stiffness and damping on the rotational speed of the sleeve bearings is considered.

In this study the influences of support parameters on the cracked rotor response is investigated. A model consists of crack fault for passing through critical speed is analyzed. An in depth study on support parameters that are effective in the transient response of rotating machinery is presented.

2 Rotor System Model

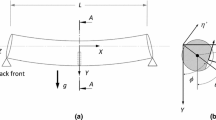
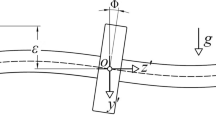
To perform a preliminary analysis of the rotor bearing system, a rotor mounted symmetrically on two bearings is indicated in Fig. 1. The generalized coordinates of the rotor system are considered as X, Y, Z, ϕ, θ and ψ.

Fig. 1.
figure 1

Representation of a rotor system.

Full size image

The equations of motion of the rotor system can be achieved using the Lagrangian approach. The Lagrange ‘s equations can be expressed as:

$$ \frac{{\text{d}}}{{{\text{dt}}}}\frac{\partial L}{{\partial \dot{q}}} + \frac{\partial R}{{\partial \dot{q}}} - \frac{\partial L}{{\partial q}} = 0 $$
(1)

In order to apply Lagrange’s equations, the kinetic energy T, including rotational and translational kinetic energy, and potential energy U∗, should be calculated:

$$ L = T - U^* $$
(2)

In order to derive the kinetic and potential energy see Refs. [11] and [14].

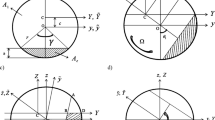
The crack is modeled according to Fig. 2. The dashed segment present the crack segment. The centroidal area moment of inertia of the cracked element about \(\overline{X }\)- and \(\overline{Y }\)-axis are \({I}_{\overline{X} }\) and \({I}_{\overline{Y} }\), respectively. According to [12], the time varying area moments of inertia \({I}_{\overline{X} }\) and \({I}_{\overline{Y} }\) and \({I}_{\overline{XY} }\) about \(\overline{X }\)- and \(\overline{Y }\)-axis during the shaft rotation are given as.

$$ I_{\overline{X}} (t) = \frac{{I_{\overline{x}} + I_{\overline{y}} }}{2} + \frac{{I_{\overline{x}} - I_{\overline{y}} }}{2}\cos (2\psi ) - I_{\overline{x}\overline{y}} \sin (2\psi ) $$
$$ I_{\overline{Y}} (t) = \frac{{I_{\overline{x}} + I_{\overline{y}} }}{2} - \frac{{I_{\overline{x}} - I_{\overline{y}} }}{2}\cos (2\psi ) + I_{\overline{x}\overline{y}} \sin (2\psi ) $$
(3)
$$ I_{\overline{X}\overline{Y}} (t) = \frac{{I_{\overline{x}} - I_{\overline{y}} }}{2}\sin (2\psi ) + I_{\overline{x}\overline{y}} \cos (2\psi ) $$

where \({I}_{\overline{x} }\) = Ix − Ace2, \({I}_{\overline{y} } = \)Iy and Ix and Iy are the area moments of inertia of the cracked element about the rotating x − and y − axis, Ac is the area of the cracked element and e is its centroid location on the y − axis. Since y is the axis of symmetry of the cracked element cross section area during rotation, \({I}_{\overline{xy} }\) = 0. Ac and e have been calculated in [13] as

$$ A = R^2 (\pi - \cos^{ - 1} (1 - \mu ) + (1 - \mu )\gamma ) $$
(4)
$$ e = \frac{2R^3 }{{3A_1 }}\gamma^3 $$
(5)

where \(\mu =h/R\) is the non-dimensional crack depth, h is the crack depth in the radial direction and \(\gamma =\sqrt{\mu (2-\mu )}\). The area moments of inertia Ix and Iy of the cracked element about x- and y-axis, respectively, have also been determined in Ref. [13] for \(0\le \mu \le 1\) as

$$ I_x = \frac{\pi R^4 }{4} + \frac{R^4 }{4}((1 - \mu )(2\mu^2 - 4\mu + 1)\gamma + \sin^{ - 1} (1 - \mu )) $$
(6)
$$ I_y = \frac{\pi R^4 }{4} - \frac{R^4 }{{12}}((1 - \mu )(2\mu^2 - 4\mu - 3)\gamma + 3\sin^{ - 1} (\gamma )) $$
(7)
Fig. 2.
figure 2

Representation of the cracked element cross section a) before rotation b) after rotation.

Full size image

Accordingly, the area moment of inertia and the transversal and polar moment of inertia,

i.e. Jt and JP, of the cracked element should be modified. Since the transversal and polar moment of inertia per length are Jt = \(\frac{1}{4}\) ρπR4 and JP = 2Jt of a rotor element without crack, the relations (Eq. 3) can be utilized to modify the transversal and polar moment of inertia of a cracked one.

Note that the moment of inertia is calculated for a rotating system, as a result it is not accurate to use Fourier series to model the breathing mechanism of the cracked element. Therefore, using Eq. (1) the governing equations of motion in matrix form for a rotor system in a rotor system can be obtained as:

$$ {\bf{M}}{\mkern 1mu} {\mkern 1mu} {\ddot{\bf{q}}} + \dot{\psi }{\bf{G}}{\mkern 1mu} {\mkern 1mu} {\dot{\bf{q}}} + {\bf{C}}{\mkern 1mu} {\mkern 1mu} {\dot{\bf{q}}} + {\bf{K}}{\mkern 1mu} {\mkern 1mu} {\bf{q}} = {\bf{F}} $$
(8)

where M, G, C, K and F are mass matrix, gyroscopic matrix, damping matrix, stiffness matrix and force vector, respectively and q is displacement vector.

To set up the dynamic model of the rotor system, the finite element method is utilized. In this method, the solution is subdivided into finite elements on which shape functions are defined to approximate the solution. The rotor shaft is modeled by the Euler-Bernoulli beam element and the cross-section of the shaft is assumed to be uniform in each element. The shaft is discretized into N finite elements with 6 degrees of freedom (DOFs), including three rotational and three translational DOFs at each node.

3 Results and Discussion

In this section, the results based on the proposed formulation are also presented and discussed. The six-degree-of-freedom rotor bearing models are used to demonstrate the influences of various parameters based on the FEM method using the Euler-Bernoulli beam element.

3.1 Validation of Results

The accuracy of the proposed formulation is evaluated herein. The dynamic response of a simple rotor system, according to Fig. 3, is investigated for comparison study. The rotor parameters are tabulated in Table 1.

The time response in x and y directions of node 1 and node 6 are achieved according to Fig. 4. It can be found that the results are coincident with Dyrobes ones. Dyrobes is a rotordynamics software which offers rotordynamic analysis, vibration analysis, bearing performance and balancing calculations based in Finite Element Analysis. The software combines an intuitive Windows-based interface with sophisticated modeling and analysis capabilities that can satisfy the most demanding industry requirements.

Fig. 3.
figure 3

Representation of a rotor system for comparison study.

Full size image

3.2 Support Parameter Study

The influences of support parameters on the dynamic behavior of the cracked rotor bearing system to pass through critical speed is conducted herein to choose the right ones. For this purpose, a rotor system with one shaft and two supports is considered. The distribution of residual shaft bow is assumed as the first order bending mode of shaft.

Fig. 4.
figure 4

Comparison study between Dyrobes and present study - Time response.

Full size image
Table 1. Definition of geometric and physical properties of a rotor bearing system.
Full size table

Additionally, the rotor parameters are considered according to Table 1 unless otherwise stated. In this section, δ parameter means the radial displacement of a node, i.e. \({\delta }_{6}=\sqrt{{U}_{6}^{2}+{V}_{6}^{2}}\), and node 6 is in the middle of the rotor.

The influences of support parameters including stiffness and damping are evaluated based on the aforementioned formulation and the results are described in Figs. 5 and 6. This analysis provides the design insights into select the rotor parameters and failure prevention for passing through critical speed.

As is shown in Figs. 5 and 6, the vibration amplitude and critical frequency of a rotor system are affected by the support parameters. Thus, it is suitable to tune support parameters by acting on the amount of damping and stiffness for specific purpose. As a result, by increasing damping, the vibration amplitude is diminished but stiffness affects in different way. According to Figs. 5a, b and c, for a rotor passing through critical speed, the increase in stiffness reduces the vibration amplitude but according to Figs. 5g, h and i, the rise of stiffness increases the vibration amplitude for a rotor which cannot pass through critical speed.

Fig. 5.
figure 5

The influences of stiffness parameters on angular velocity and transient response.

Full size image
Fig. 6.
figure 6

The influences of damping parameters on angular velocity and transient response.

Full size image

4 Conclusion

The main purpose of the present study was to examine the dynamic response of a cracked rotor system. The equations of motion for 6 degrees of freedom system were obtained using Lagrange’s equations and a FE model of the rotor system was developed. The Newmark-β integration scheme was utilized to calculate the model’s equations of motion and find the transient start up response. The influences of support parameters were studied and it was shown that the support parameters have significant effect in changing dynamic characteristics of the rotor system to assist the system to pass through critical speeds.