The influence of a transversal crack on rotor nonlinear transient response

Abstract

In the present study, the overshooting vibrational amplitude in transient response of a cracked rotor is calculated and experimentally validated. A Jeffcott rotor model that includes a nonlinear breathing mechanism is considered and to be validated by experimental data. Furthermore, a nonlinear stability analysis is performed via Lyapunov largest exponent to correlate the overshoot value and the observed rotor behavior. It is concluded that numerical results obtained from the enhanced Jeffcott rotor model that includes a nonlinear restoring force tend to describe well experimental data, and the system overshooting is sensitive to rotor cracks.

1 Introduction

Monitoring and diagnostics of a cracked rotor have been of an increasing importance in recent years because the propagating cracks have a serious detrimental effects on the reliability of turbomachinery specially the dynamic behavior of rotor-bearing systems with cracked shafts. Sekhar and Prabhu [1] were among the first to study the transient vibrational behavior on cracked rotors when passing through critical speed. They focused their attention on the oscillations developed near the critical speed and established that the phase between eccentricity and crack must be taken into account [2]. Furthermore, they found that the slant crack in the rotor can be detected by the transient response [3] and then they used continuous wavelet transform (CWT) to identify the subharmonic resonant peaks when the cracked rotor is passing through its critical speed, particularly for higher accelerations [4, 5]. By using CWT, Sekhar [6] focused his attention on studying the subcritical response peaks for detecting cracks even for low crack depths in a coast-down rotor and observed that the energy computed from the CWT analysis is sensitive to rotor cracks. Then, Zou et al. [7] introduced the wavelet time-frequency analysis algorithm to study the dynamic response of a cracked rotor when its frequency passed subcritical speeds. They concluded that the wavelet analysis algorithm could be useful for identification of cracked rotor dynamics.

Han and Chu [8, 9] found that under certain crack depth, the instability regions could vanish by the transverse crack. When the asymmetric angle is around $\uppi /2$, increasing the crack depth would enhance the instability regions. They also found that the instability of a rotor-bearing system with two breathing transverse cracks has some unique features that differ from that of the single cracked rotor system [10].

By using the Hilbert Huang transform for extracting the salient features from time response of the cracked rotor passing through its critical speed, Babu et al. [11] observed that this transform is particularly useful for identifying very small crack depths where the CWT fails to detect them. However, Sinou demonstrated that the CWT and the Power Spectral Density can detect the presence of open cracks in rotating machinery on the $2\times$ harmonic components when the notched rotor passes through transient signals [12]. By analyzing the dynamics of the transient signals, Wang [13] found that by separating transient vibration information in a varying rotational speed environment could improve the diagnostic capability in detecting rotor cracks. In fact, he used the adaptive natured time waveform reconstructed order tracking method, and the Vold-Kalman filter order tracking (VKF-OT) to obtain the dynamics response of cracked rotors by separating transient vibrations effects of the rotor changing rotational speed harmonics. Based on Wang findings, it is clear that the performance of a cracked rotor could be identified by using transient dynamics. In fact, there are evidence in the literature that transient signals of dynamical systems could predict undesirable effects that need to be overcome to have stable system response [14, 15]. Therefore, the aim of this paper focuses on using transient dynamics and the concept of overshooting to study both theoretically and experimentally, the dynamics of a cracked rotor and its stability behavior by using Lyapunov characteristic exponents.

Fig. 1

a Crack location on shaft and inertial reference system (X, Y, Z) are shown. b Inertial (Y, Z) and rotational ($\xi ,\eta$) coordinate systems

2 Mathematical model

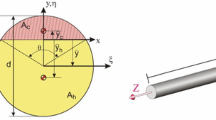
In this paper, an enhanced mathematical model that describes the dynamics of a cracked Jeffcott rotor that takes into account the cubic nonlinear effects of the restoring forces $F_Y$ and $F_Z$ is introduced. Figure 1 depicts the common definition of both rotating and stationary reference systems from which the restoring forces $F_Y$ and $F_Z$ can be expressed as a function of the rotor angular position $\theta$, as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_Y } \\ {F_Z } \\ \end{array} }} \right\} =\left[ {{\begin{array}{ll} {\cos \theta }&{} {-\sin \theta } \\ {\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left\{ {{\begin{array}{ll} {F_\xi } \\ {F_\eta } \\ \end{array} }} \right\} . \end{aligned}$$

(1)

Due to the crack, the restoring forces $F_\xi$ and $F_\eta$ are commonly defined in the directions of minimum and maximum stiffness, i.e., $\xi$ that describes the direction perpendicular to the crack front, and the coordinate $\eta$ to represent the direction parallel to the crack front, as illustrated in Fig. 1. Therefore, the system restoring forces are defined by the following expression:

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_\xi } \\ {F_\eta } \\ \end{array} }} \right\} =\left[ {{\begin{array}{ll} {k_\xi }&{} {k_{\xi \eta } } \\ {k_{\xi \eta } }&{} {k_\eta } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} \xi \\ \eta \\ \end{array} }} \right\} +\left[ {{\begin{array}{l} {\varepsilon \xi ^{3}} \\ 0 \\ \end{array} }} \right] . \end{aligned}$$

(2)

In Eq. (2), a nonlinear restoring force has been added to consider nonlinear effects of the rotor dynamics. Now, substituting Eq. (2) into Eq. (1) yields:

$$\begin{aligned} F_Y= & {} \left( {k_\xi \xi +k_{\xi \eta } \eta +\varepsilon \xi ^{3}} \right) \cos \theta \nonumber \\&-\left( {k_{\xi \eta } \xi +k_\eta \eta } \right) \sin \theta \end{aligned}$$

(3a)

$$\begin{aligned} F_Z= & {} \left( {k_\xi \xi +k_{\xi \eta } \eta +\varepsilon \xi ^{3}} \right) \sin \theta \nonumber \\&+\left( {k_{\xi \eta } \xi +k_\eta \eta } \right) \cos \theta . \end{aligned}$$

(3b)

Since the following relationship

$$\begin{aligned} \left\{ {{\begin{array}{l} \xi \\ \eta \\ \end{array} }} \right\} =\left[ {{\begin{array}{ll} {\cos \theta }&{} {\sin \theta } \\ {-\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left\{ {{\begin{array}{l} Y \\ Z \\ \end{array} }} \right\} \end{aligned}$$

(4)

must hold between the two coordinate systems, then Eq. (4) can be used to write Eq. (3) in terms of the coordinates $Y-Z$, as follows:

$$\begin{aligned} F_Y= & {} \frac{Y}{2}\left[ {\left( {k_\xi {+}k_\eta } \right) {+}\left( {k_\xi -k_\eta } \right) \cos 2\theta -2k_{\xi \eta } \sin 2\theta } \right] \nonumber \\&+\,\frac{Z}{2}\left[ {\left( {k_\xi -k_\eta } \right) \sin 2\theta +2k_{\xi \eta } \cos 2\theta } \right] \nonumber \\&+\,\varepsilon \left( {Y\cos \theta +Z\sin \theta } \right) ^{3}\cos \theta \end{aligned}$$

(5a)

$$\begin{aligned} F_Z= & {} \frac{Y}{2}\left[ {\left( {k_\xi -k_\eta } \right) \sin 2\theta +2k_{\xi \eta } \cos 2\theta } \right] \nonumber \\&+\,\frac{Z}{2}\left[ \left( {k_\xi +k_\eta } \right) +\left( {k_\eta -k_\xi } \right) \cos 2\theta \right. \nonumber \\&\left. +\,2k_{\xi \eta } \sin 2\theta \right] {+}\varepsilon \left( {Y\cos \theta {+}Z\sin \theta } \right) ^{3}\sin \theta \nonumber \\ \end{aligned}$$

(5b)

Fig. 2

Experimental setup, machine fault simulator adapted to perform as a cracked rotor

Next, the restoring forces given by Eq. (5) can be incorporated into the mathematical model described in [16] and references cited there in, to get:

$$\begin{aligned}&m{\ddot{Y}}+c{\dot{Y}}+(k_{\xi }+k_{\eta })\frac{Y}{2} +\varepsilon (Y\cos \theta +Z\sin \theta )^{3}\cos \theta \nonumber \\&\qquad +\,\frac{G}{2}\left\{ (k_{\xi }-k_{\eta })\cos 2\theta -2k_{\xi \eta }\sin 2\theta \right\} Y\nonumber \\&\qquad +\,\frac{G}{2}\left\{ (k_{\xi }-k_{\eta })\sin 2\theta +2k_{\xi \eta }\cos 2\theta \right\} Z\nonumber \\&\quad =m \, e\, \omega ^{2}\cos (\theta -\beta )-m\, g+m\, e\, \alpha \sin \theta \end{aligned}$$

(6a)

$$\begin{aligned}&m{\ddot{Z}}+c{\dot{Z}}+(k_{\xi }+k_{\eta })\frac{Z}{2} +\varepsilon (Y\cos \theta +Z\sin \theta )^{3}\sin \theta \nonumber \\&\qquad +\,\frac{G}{2}\left\{ (k_{\eta }-k_{\xi })\cos 2\theta -2k_{\xi \eta }\sin 2\theta \right\} Z\nonumber \\&\qquad +\,\frac{G}{2}\left\{ (k_{\xi }-k_{\eta })\sin 2\theta +2k_{\xi \eta }\cos 2\theta \right\} Y\nonumber \\&\quad =m\, e\, \omega ^{2}\sin (\theta -\beta )-m\, e\, \alpha \cos \theta \end{aligned}$$

(6b)

where m is the rotor mass, c represents the rotor viscous damping, $\varepsilon$ is the cubic nonlinear coefficient, Y and Z are the rotor vibration amplitudes at the midspan, G is the crack breathing function, $k_{i}$ is the shaft lateral stiffness either along the crack front ($\eta$), perpendicular to the crack front ($\xi$) and the cross-coupled stiffness ($\eta \xi$) generated by the cracked shaft, $\theta$ represents the crack angular position measured from an inertial coordinate system, e is the unbalance eccentricity, and $\beta$ is the angle between the crack and the rotor unbalance, as shown in Fig. 1.

2.1 Breathing function definition

The breathing function, G, used in the present investigation is a combination of Mayes and Davis equation (7) defined as [17]

$$\begin{aligned} G=\frac{1+\cos \psi }{2} \end{aligned}$$

(7)

and the Cheng function [18]

$$\begin{aligned} \cos \psi =\frac{Y\cos \theta +Z\sin \theta }{\sqrt{Y^{2}+Z^{2}}}. \end{aligned}$$

(8)

The breathing function given by Eq. (7) takes into account the dynamical response of the rotor by considering the crack angular position, $\psi$, relative to the rotational reference system ($\xi '\eta '$).

2.2 Overshooting

Overshoot arises when the system is undergoing free motion and is suddenly subjected to harmonic excitation with a near-resonant frequency, which leads to transient response during the transition to steady-state system behavior. The determination of this value is of practical interest in understanding the importance of time in controlling the dynamical behavior of oscillatory systems [14, 15], since this is estimated by considering the influence of the system parameters such as nonlinear and damping effects. In general, the system overshooting is defined as

$$\begin{aligned} \% \hbox { Overshooting}=100\left( {\frac{x_\mathrm{tran} -x_\mathrm{ss} }{x_\mathrm{ss} }} \right) \end{aligned}$$

(9)

where $x_{\mathrm{tran}}$ and $x_\mathrm{ss}$ represent the peak transient and steady-state amplitudes of the system, respectively. This concept will be used to study how a Jeffcot rotor dynamics is changing during the appearance of cracks.

2.3 Largest Lyapunov exponent

The concept of Lyapunov characteristic exponents (LCE), also known as Lyapunov spectrum, was introduced by Lyapunov [19] when studying the stability of nonstationary solutions of ordinary differential equations. This spectrum allows to characterize quantitatively the stochasticity properties of nonlinear systems and measures the sensitivity of the system to initial conditions. Lyapunov characteristic exponents also indicate the rate of divergence of nearby trajectories, a key component of chaotic dynamics. Lyapunov exponents can determine the rate of dependence of a system on the initial conditions considering the divergence or convergence of nearby orbits.

Fig. 3

Measurement ports and bolted joint to reproduce the cracked shaft

Fig. 4

Data acquisition block diagram. A Experimental cracked rotor, B electrical motor, C tachometer signal, D four proximity transducers signals, two for each measurement plane, E variable frequency drive, F signal conditioner, G data acquisition interface unit and ADRE® software, H National Instruments® acquisition system and LabView® software

Fig. 5

Overshoot evolution along different rotation velocities for different crack sizes. $L = 0.69\,\hbox {m}$, $E = 210\,\hbox {GPa}$, $r = 7.97\times 10^{-3}\,\hbox {m}$, $e= 19\,\upmu \hbox {m}$, $g = 9.81\, \hbox {m/s}^{2}$, $m = 2.79\,\hbox {kg}$, $c = 11.46\,\hbox {N}\,\hbox {s/m}$, $\alpha = 0\, \mathrm{rad}/s^{2}$, $\beta = 0{^{\circ }}$, $\varepsilon = 4x10^{10}\,\hbox {N/m}^{3}$, $k_\eta =\left( {1-{\Delta }k_\eta } \right) k_0$, $k_\xi =\left( {1-{\Delta }k_\xi } \right) k_0$, $k_{\xi \eta } =({\Delta }k_\xi /5)\,k_{0}$, ${\Delta }k_\eta =3.6353\times 10^{-1}\left( {\frac{a}{D}} \right) ^{3}-1.6278\times 10^{-2}\left( {\frac{a}{D}} \right) ^{2}+3.8189\times 10^{-3}\left( {\frac{a}{D}} \right) +6.9077\times 10^{-5}$, ${\Delta }k_\xi =1.4995\left( {\frac{a}{D}} \right) ^{3}+2.8640\times 10^{-2}\left( {\frac{a}{D}} \right) ^{2}+4.6384\times 10^{-2}\left( {\frac{a}{D}} \right) -4.9829\times 10^{-4}$

3 Experimental setup

The equipment employed to collect experimental data includes a rotor, eddy current displacement proximity probes, motor speed control, and a data acquisition module. The test workbench shown in Fig. 2 consists of two elastic shafts connected by means of a bolted joint in order to reproduce the cracked rotor, as illustrated in Fig. 3. The rotor’s shaft of 12.7 mm is simply supported at both ends, with 690 mm of supports span. The diameter and thickness of the disk rotor are 115 and 39.2 mm, respectively. The rotor system is driven by an electric motor incorporated with a shaft through a flexible coupling.

The data acquisition block diagram is shown in Fig. 4, describing the main components used in the experimental setup. (A) Experimental cracked rotor, (B) electrical motor, (C) tachometer signal, (D) four proximity transducers signals, two for each measurement plane, (E) variable frequency drive, (F) signal conditioner, (G) data acquisition interface unit and ADRE® software, (H) National Instruments® acquisition system and LabView® software. Two different acquisitions system were used to collect, record and analyze the data; therefore, it was possible to take information provided by both systems. The variable frequency driver is the Delta® VFD-B, and the proximity transducers used to measure the rotor vibrational behavior are Bently Nevada® 3300 5 mm probe.

Fig. 6

Overshoot evolution along different rotation velocities and its comparison with the system stability derived by means of the largest Lyapunov exponent (LLE), $a/D = 0.4$ all remaining parameters values are the same as in Fig. 5

Fig. 7

Orbital response and spectrogram of the velocity ratio of $\omega /\omega _{n} = 0.48$ (Point A in Fig. 6)

4 Experimental and numerical results

The obtained results are divide into two sections: first the numerical predictions are estimated at constant angular speed, while in the second part, the results come from experimental acquisition data and from numerical predictions by considering a shaft constant angular acceleration.

4.1 Analysis at constant angular speed

In order to solve the enhanced mathematical model, the algorithm based on the explicit Runge–Kutta (RK), which is included in the MATLAB computer symbolic package as the built-in function called ode45, has been used. This algorithm varies the step size, choosing the step size at each step in an attempt to achieve the desired accuracy. Initial conditions used to run the numerical simulation were $Y\left( 0\right) =30\,\upmu \hbox {m}$, $Z\left( 0 \right) =30\,\upmu \hbox {m}$, ${\dot{Y}}(0)=0$ and ${\dot{Z}}(0)=0$.

Fig. 8

Orbital response and spectrogram of the velocity ratio of $\omega /\omega _{n} = 0.62$ (Point B in Fig. 6)

By numerically integrating Eq. (6), it is possible to predict the evolution of the rotor overshooting through the velocity ratio interval, $\omega /\omega _{n}$, between 0.25 and 1.5, as shown in Fig. 5. As it can be seen from Fig. 5, even if the crack is very small, there is a significant change in the system overshooting behavior mainly near the local resonance of $1/3\,\omega /\omega _{n}$. Notice that when the rotor has no crack, the overshooting, at this particular speed, tends to decrease, when the rotor has a small crack ($a/D = 0.1$), the overshooting plots exhibit significant and sudden decreased values.

The stability of Eq. (1) has been evaluated from the largest Lyapunov exponent (LLE) theory, using the algorithm developed by Wolf et al. [20]. Figure 6 shows a comparison between the computed LLE of the system and the overshooting value. As it is seen from Fig. 6, a stable rotor behavior is exhibited in the majority of the velocity ratio interval $\omega / \omega _{n}$, shown. However, the rotor has unstable behavior at the angular velocity ratio of $\omega / \omega _{n} = 0.99$ at which the overshooting value tends to approach to the limit value of minus 100%. Furthermore, it is observed from Fig. 6 that there is a change in the overshooting value at the same point at which LLE has a local maximum peak, i. e., at the angular speed of $\omega /\omega _{n} = 0.62$. A slight change of about 10% in LLE is captured closed to the region at which the overshooting plots have a peak value (point B).

Figures 7 and 8 depict the orbital response and spectrogram of the cracked rotor dynamic response at the velocity ratios of $\omega /\omega _{n} = 0.48$, and 0.62, respectively. In both cases, the response contains an internal loop. Also, from the spectrogram of Fig. 8b, it is observed that transient response vanishes at about 1 s. The size of the inside loop shown in Figs. 7 and 8 is a clear indicator of the presence of an open transverse crack in rotating machinery, as discussed in [11].

Fig. 9

Overshoot evolution along different unbalance angular positions, $\beta$, and the corresponding rotor Lyapunov stability analysis by considering the system parameter values of: $a/D = 0.4$ and $\omega /\omega _{n} = 0.99$

Fig. 10

Orbital response and spectrogram at $\beta = 72.5{^{\circ }}$, point C in Fig 9

Figure 9 shows the overshoot and LLE evolution at the velocity ratio of $\omega /\omega _{n} = 0.99$. Here the unbalance orientation, $\beta$, with respect of the crack front varies from $0{^{\circ }}$ to $360{^{\circ }}$. Notice from Fig. 9, that $\beta$ influences the system stability [21], i.e., at the value of $=72.5^{\circ }$, the vibrational response of the cracked rotor is stable; therefore, it can be concluded from Fig. 9 that the rotor can be tuned to stable behavior if the unbalance angle is around $72.5{^{\circ }}$. The orbital response and the spectrogram at this unbalance angle is shown in Fig. 10.

Furthermore, the dynamic rotor response behavior observed in Figs. 6 and 9 can be described from the overshooting of the system, i.e., the overshooting curve can be used to analyze the stability of the rotor since its qualitative behavior corresponds to the stability predictions provided by the values of the largest Lyapunov exponents.

4.2 Comparison of experimental and numerical results when the rotor is subjected to constant angular acceleration

In this section results, comparisons between numerical and experimental results are performed by considering a Jeffcott rotor subjected to constant angular acceleration. Figure 11 shows two different cases: one with an imbalance orientation $\beta = 0{^{\circ }}$, and the other with $\beta = 180{^{\circ }}$. Figure 11a, b exhibits the collected experimental data and the numerical predictions for $\beta = 0{^{\circ }}$. It is observed that the enhanced numerical model tends to capture the transient response and internal resonances that are characteristic in highly nonlinear systems. Furthermore, at the resonant frequency ($t = 30\,\hbox {s}$) experimental evidence shows a right-sided bending that the modified model tends to capture because the system restoring forces are assumed to have nonlinear cubic behavior. In fact, from the spectrograms shown in Fig. 11, it is possible to distinguish the main harmonics provided by the collected data and from numerical simulations computed from Eq. (6). In this case, the spectrogram of the experimental data and the one obtained from numerical simulations agree well.

Fig. 11

Response and spectrogram from rotor run-up, $a/D = 0.15$, $\alpha = 6\,\hbox {rad/s}^{2}$, $c = 41.69\,\hbox {N}\,\hbox {s/m}$, $L =0.69\,\hbox {m}$, $E = 210\,\hbox {GPa}$, $r = 7.97\times 10^{-3}\hbox {m}$ and $\varepsilon = 4\times 10^{10}\,\hbox {N/m}^{3}$. For $\beta = 0{^{\circ }}$, $e = 22.86\,\upmu \hbox {m}$ and for $\beta = 180{^{\circ }}$, $e = 13.71\,\upmu \hbox {m}$. a Experimental: $\beta =0{^{\circ }}$, b Numerical: $\beta =0{^{\circ }}$, c Experimental: $\beta =180{^{\circ }}$, d Numerical: $\beta =180{^{\circ }}$

Fig. 12

Orbital evolution at different angular velocities, $a/D = 0.15$, $\beta = 0{^{\circ }}$, $\alpha =6 \,\hbox {rad/s}^{2}$, $c = 41.69\,\hbox {N} \,\hbox {s/m}$, $e = 22.86 \,\upmu \hbox {m}$, $L = 0.69\,\hbox {m}$, $E = 210\,\hbox {GPa}$, $r = 7.97\times 10^{-3}\,\hbox {m}$ and $\varepsilon = 4\times 10^{10}\,\hbox {N/m}^{3}$. a $\omega /\omega _n=0.33$, b $\omega /\omega _n=0.33$, c $\omega /\omega _n=0.50$, d $\omega /\omega _n=0.55$, e $\omega /\omega _n=0.66$, f $\omega /\omega _n=0.66$

Fig. 13

Orbital evolution at different angular velocities, $a/D = 0.15$, $\beta = 180{^{\circ }}$, $\alpha = 6\,\hbox {rad/s}^{2}$, $c = 41.69\,\hbox {N}\, \hbox {s/m}$, $e = 13.71\,\upmu \hbox {m}$, $L = 0.69\,\hbox {m}$, $E = 210\,\hbox {GPa}$, $r = 7.97\times 10^{-3}\,\hbox {m}$ and $\varepsilon = 4\times 10^{10}\,\hbox {N/m}^{3}$. a $\omega /\omega _n=0.33$, b $\omega /\omega _n=0.33$, c $\omega /\omega _n=0.50$, d $\omega /\omega _n=0.55$, e $\omega /\omega _n=0.66$, f $\omega /\omega _n=0.66$

The orbital response and its evolution as the angular speed increases is shown in Figs. 12 and 13 for the cases at which $\beta = 0{^{\circ }}$ and $\beta = 180{^{\circ }}$, respectively. Notice that the mathematical model given by Eq. (6), with its breathing model and cubic nonlinear terms is capturing the complex cracked rotor response. In fact, the internal loops at the frequency ratios of $\omega /\omega _{n} = 0.33$ and 0.5 are qualitatively and quantitatively described well.

Experimental and numerically computed overshoot system values are illustrated in Fig. 14. Here the cases of $a/D = 0.15$, and 0.30 with $\beta = 0{^{\circ }}$ and $180{^{\circ }}$ were considered. The overshooting value is plotted according to the amount of the rotor damage level. It can be observed from Fig. 14 that a monotonic increase behavior in the overshooting value takes place as the damage level increases. Furthermore, numerical predictions and experimental data tend to agree not only in the system qualitative behavior, but also in its quantitative response since the maximum relative error attained does not exceed the value of 51%. This is an improvement when compared to the results found in [22] in which peak responses between analytical and experimental data were considered.

It is important to mention that in Sect. 4.1, the overshooting value has been obtained considering the numerical integration results computed at constant angular speed. In this case, the maximum system overshooting is about 3000%; meanwhile in Sect. 4.2, the overshooting has been determined when the rotor is subjected to a constant angular acceleration which allow us to compare experimental and numerical results. In fact, Fig. 14 illustrates the corresponding overshooting plots obtained from experimental data and those computed numerically by using Eq. (6). Notice that when the nonlinear cubic term is considered, the numerical results tend to approach to the experimental overshooting values.

Fig. 14

Overshooting comparison between experimental amplitudes and model prediction

5 Conclusions

In the present study, the overshooting vibrational amplitude in transient response of a cracked rotor is calculated and experimentally measured. A Jeffcott rotor model that includes a nonlinear breathing mechanism that combines the Cheng function [18] with that introduced by Mayes and Davis [17], and nonlinear restoring force effects were considered. The corresponding equations of motion were numerically solved by using the Runge–Kutta fourth-order algorithm. Then, the overshooting concept was used in order to capture the amplitude peaks exhibited by the nonlinear system response behavior during transient vibrations in order to identify the appearance of small crack depths into the rotor. In fact, it has been found by plotting the system overshooting versus the frequency ratio, $\omega /\omega _{n}$, that the corresponding curve has relative minimum values at the points at which small crack depths (a/D) appears, as illustrated in Fig. 5. Furthermore, Lyapunov exponents were computed to determine under which parameter values the system becomes unstable. Surprisingly, the Lyapunov exponent curve has peak values at the same regions at which the overshooting curves reach their relative maximum values, as shown in Figs. 5 and 9. Based on these results, it is concluded that the overshooting curve plotted against the frequency ratio $\omega /\omega _{n}$ could be used not only to detect the appearance of small crack depth into the Jeffcott rotor, but also to examine the system dynamics behavior.

To further assess the applicability of the system overshooting in detecting small crack depths in the rotor system, experimental test was performed by considering a rotor with constant angular acceleration. It has been observed from Figs. 11, 12, 13 and 14 that the theoretical model tends to capture the transient response and internal resonances of the Jeffcott rotor system, i.e., numerical predictions and experimental data tend to agree with the system qualitative and quantitative dynamic behavior. Based on the above results, it is concluded that the usage of the system overshooting as well as of the Lyapunov exponents can have a significant impact in monitoring and diagnosing of a cracked Jeffcott rotor.