A Computational Investigation of the Characteristics of Velocity Slips and Convective Boundary Conditions in Maxwell Nanofluid Flow over a Permeable Stretching Surface with Activation Energy

Abstract

In this study, we analyze the effects of velocity slips and convective boundary conditions in the flow and heat transfer of Maxwell nanofluid across a stretching sheet considering magnetic field, thermal radiation, chemical reaction, and activation energy. The influence of Brownian diffusion and thermophoresis are considered using Buongiorno’s nanofluid model. By applying suitable similarity variables, the governing Maxwell nanofluid flow equations, which include the momentum, energy, and nanoparticle volume fraction are simplified to nonlinear differential equations. MATLAB’s bvp4c finite difference tool is used to solve the nondimensionalized differential equations. In order to illustrate the influence of physical factors on velocity, temperature, and nanoparticle volume fraction, the numerical solutions are shown graphically. In addition, the skin friction, rate of heat transmission, and mass transfer are all given physical interpretations. The current analysis demonstrates that the velocity slip and suction parameters significantly reduce the velocity. Increased thermal radiation and Biot number for temperature raise the temperature profile. Further, the activation energy and thermophoresis factors lead to a decrease in the mass transfer rate, while the Lewis number and Biot number due to concentration contribute to an increase.

Nomenclature
T	Temperature	$K_1$	Chemical reaction parameter
c	Velocity ratio parameter	$h_2$	Convective mass transfer coefficient
u, v, w	Velocity components	$k^2_r$	Chemical reaction coefficient
M	Magnetic parameter	$B_0$	Constant magnetic field
x, y, z	Space coordinates	$D_{T}$	Coefficient of thermal diffusion
K	Deborah number	$Bi_1$	Biot number for temperature
n	Fitted rate constant	$Bi_2$	Biot number for concentration
Le	Lewis number	$w_0$	Suction velocity
$u_{\text {w}}$, $v_{\text {w}}$	Stretching velocities	Greek Symbols
E	Dimensionless activation energy	$\alpha _1$	Velocity slip parameter
k	Thermal conductivity	$\mu$	Dynamic viscosity
$k^*$	Mean absorption coefficient	$\theta _{\text {w}}$	Temperature ratio parameter
$T_\infty ,C_\infty$	Ambient temperature and concentration	$\kappa$	Boltzmann constant
S	Suction parameter	$\rho$	Density
Rd	Thermal radiation parameter	$\theta$	Dimensionless temperature
Pr	Prandtl number	$\lambda$	Fluid relaxation time
$c_p$	Specific heat	$\alpha$	Thermal diffusivity
C	Concentration	$\nu$	Kinematic viscosity
Nt	Thermophoresis parameter	$\phi$	Dimensionless concentration
$T_{\text {w}}, C_{\text {w}}$	Surface temperature and concentration	$\sigma ^*$	Stefan-Boltzmann constant
Nb	Brownian motion parameter	$\beta$	Slip coefficient
$E_a$	Activation energy	$\sigma$	Electrical conductivity
$D_B$	Mass diffusivity	$\tau$	Ratio between effective heat capacity
$h_1$	Convective heat transfer coefficient		of nanoparticles and base fluid

1 Introduction

In the petroleum industry and engineering applications, non-Newtonian fluid flow coupled with heat and mass transfer is of significant interest. Desalination, refrigeration and air conditioning, compact heat exchangers, chemical processing equipment, solid matrix heat exchangers, solar power collectors, and other applications [1, 2] are examples. The Laplace and Hankel transforms were used to calculate the velocity field and shear stress field of a generalised Maxwell fluid that flows between two infinite coaxial circular cylinders [3]. By employing the multi-step differential transform approach, Keimanesh et al. [4] investigated third grade non-Newtonian fluid flow between two parallel plates. Nadeem et al. [5] presented a model of a two-dimensional Williamson fluid past a stretched sheet that they had developed. Seyedi et al. [6] investigated effect of natural convection on non-Newtonian fluid flow between two vertical plates using Galerkin interpolation scaling functions.

Thermal radiation effects on nanofluid flow and heat transfer are becoming increasingly popular because nanofluids have a variety of characteristics. In addition, the influence of radiative heat transfer has increased dramatically in the design of modern energy conversion systems [7], plasma studies, agriculture, and petroleum industries [8, 9]. Numerous research have been conducted in this area to investigate the impacts of heat radiation in various areas. A two-dimensional MHD mixed convection viscoelastic fluid flow across a porous wedge with heat radiation was investigated by Rashidi et al. [10], who sought an analytical solution. Daniel and Daniel [11] did research on the theoretical impact of buoyancy and heat radiation on MHD flow past a stretched porous sheet. Pal and Mandal [12] discussed the influence of thermal radiation, non-uniform heat source/sink and suction on MHD micropolar nanofluid flow across a stretched sheet. MHD viscous fluid was flowed over a horizontally rotating disc, and Shah et al. [13] explored the effect of non-linear thermal radiations on the unsteady flow of the fluid. Effect of thermal radiation on MHD stagnation-point flow over a nonlinearly moving sheet was described by Jamaludin et al. [14] with mathematical solutions. Tarakaramu et al. [15] investigated the impact of nonlinear thermal radiation and Joule heating on the flow of a three-dimensional viscoelastic nanofluid via a stretched surface.

In various physical scenarios involving suspensions, foams and polymer solutions [16], the assumption of slip flow boundary condition is necessary. The no-slip boundary condition is involved in the research listed above. With the Soret and Dufoue effect, Babu and Sandeep [17] investigated multiple slip effects on the magnetohydrodynamic Williamson fluid flow past a variable thickness stretching sheet. Using a non-isothermal radiate wedge submerged in ferrofluid, Rashad [18] analysed the impact of partial slip and thermal radiation on MHD boundary layer flow in his research. With entropy analysis, Ellahi et al. [19] looked at the combined impact of MHD and slip on a flat moving plate over a wide range of physical factors. Das et al. [20] examined multiple slips as well as nonlinearly changing thermal radiation on a 3D MHD nonlinear convective tangent hyperbolic nanofluid flow generated by a bidirectional stretching surface with Soret and Dufour impacts.

In the investigation of a number of physical phenomena, including engineering and oil storage, activation energy is often taken into consideration. A few theoretical studies that discuss the function of activation energy in fluid dynamics are currently available. Numerous uses of Arrhenius activation energy, as well as chemical reactions, have made fluid dynamics an appealing area for researchers. The least amount of energy required to stimulate the particles or molecules in which physical transit occurs is known as activation energy. This is due to the fact that different chemical processes need some amount of energy merely to begin. Other uses of activation energy include atomic processes, the discovery of compounds, and thermal lubricant recovery [21,22,23]. Fayyadh et al. [24] investigated the magneto-flow and heat transfer of the Carreau nanofluids model in the presence of Arrhenius activation energy and chemical reaction toward a stretching/shrinking surface. Akbar et al. [25] studied the effects of gyrotactic motile microorganisms and Arrhenius activation on the bioconvection peristaltic transport of nanofluid. They also considered variable viscosity, Brownian diffusion, porous medium, mixed convection, nonuniform heat absorption/generation, viscous dissipation, and thermophoresis diffusion. Shoaib et al. [26] examined the significance of activation energy during chemical reactions, temperature gradient, and thermal radiations of 3-D steady magnetite Casson nanofluid flow over an oscillating disk.

Convective heating is very common in engineering practises such as nuclear reactors, gas turbines and thermal energy storage [27, 28]. These activities generate a high temperature, which is transferred to the flow via the convective boundary condition. To better understand the impact of convective boundary conditions on the MHD flow of nanofluids near a stretching rotaing disc with partial slip effects, Mustafa and Khan [29] carried out a numerical study. On mixed convection MHD micropolar fluid with non-linear stretched sheet, Patel and Singh [30] investigated the impacts of convective heat boundary condition, viscous dissipation and Joule heating, among other things. MHD Casson fluid flow across an exponentially extending curved sheet was studied by Kumar et al. [31] and shown to be affected by convective heating, thermal radiation and Joule heating. Das et al. [32] explored effects of convective heating, velocity slips, and activation energy on unsteady MHD 3D Carreau nanofluid flow over a stretching sheet. Mandal et al. [33] examined the convective heat transfer and entropy generation of magnetohydrodynamic Maxwell nanofluid flow including gyrotactic microorganisms along a stretching cylinder with heat source and chemical reaction.

To the best of the authors’ knowledge, no studies have reported the impacts of velocity slip, activation energy, and convective heating on Maxwell nanofluid to this day. Hence, the purpose of this study is to investigate the effects of velocity slip, activation energy, and convective heating on MHD Maxwell nanofluid flow via a permeable stretching surface when thermal radiation is present. The problem of non Newtonian nanofluid flow across a stretched surface is extremely helpful in gas turbines, aerodynamic heating, food processes, biomedicines, polymer processing, and other fields. In order to convert the dimensional governing equations into their dimensionless counterparts, proper similarity transformations have been used. The bvp4c solver in MATLAB is applied to simulate reduced highly nonlinear ordinary differential equations. The effects of significant factors on the momentum, temperature, concentration, and skin friction coefficients, as well as the Nusselt and Sherwood numbers, are graphically depicted.

2 Mathematical Modelling

Fig. 1.

Geometry of the flow problem

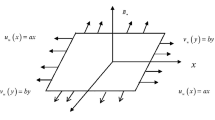
Consider a 3D Maxwell nanofluid flow across a stretched surface in the xy-plane, with the fluid at $z\ge 0$. In the x-direction, the sheet is stretched with a linear velocities of $u_{\text {w}}=ax$ and $v_{\text {w}}=by$ (a and b being positive constants). We’ll call these two values $T_{\text {w}}$ and $C_{\text {w}}$, the surface temperatures and concentrations. $T_\infty$ and $C_\infty$, on the other hand, represent the temperature and concentration far away from the surface, as illustrated in Fig. 1. The stretched surface is subjected to a magnetic force of strength $B_0$, which is applied normal to the surface. Thermal radiation and activation energy are considered to study the fluid flow. Another consideration is that the flow field does not have any polarization of charges since no external electric field is applied, which corresponds to the condition when no energy is injected or withdrawn from the fluid by electrical methods. Furthermore, a fluid with a low magnetic Reynolds number is thought to be a metallic liquid or partly ionized. So fluid motion’s effect on the induced magnetic field is minuscule in compared to the applied magnetic field. The governing equations may be reconstructed on the basis of the aforementioned flow assumptions [34, 35]:

$$\begin{aligned} \dfrac{\partial u}{\partial x}+\dfrac{\partial v}{\partial y}+\dfrac{\partial w}{\partial z}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\dfrac{\partial u}{\partial x}+v\dfrac{\partial u}{\partial y}+w\dfrac{\partial u}{\partial z}+\lambda \left( u^2\dfrac{\partial ^2 u}{\partial x^2}+v^2\dfrac{\partial ^2 u}{\partial y^2}+2uv\dfrac{\partial ^2 u}{\partial x \partial y}+2uw\dfrac{\partial ^2 u}{\partial x \partial z}+2vw\dfrac{\partial ^2 u}{\partial y \partial z}\right) \nonumber \\&\quad =\nu \dfrac{\partial ^2 u}{\partial z^2}-\dfrac{\sigma B^2_0}{\rho _f}\left( u+\lambda w\dfrac{\partial u}{\partial z}\right) , \end{aligned}$$

(2)

$$\begin{aligned}&u\dfrac{\partial v}{\partial x}+v\dfrac{\partial v}{\partial y}+w\dfrac{\partial v}{\partial z}+\lambda \left( u^2\dfrac{\partial ^2 v}{\partial x^2}+v^2\dfrac{\partial ^2 v}{\partial y^2}+2uv\dfrac{\partial ^2 v}{\partial x \partial y}+2vw\dfrac{\partial ^2 v}{\partial y \partial z}+2uw\dfrac{\partial ^2 v}{\partial x \partial z}\right) \nonumber \\&\quad =\nu \dfrac{\partial ^2 v}{\partial z^2}-\dfrac{\sigma B^2_0}{\rho _f}\left( v+\lambda w\dfrac{\partial v}{\partial z}\right) , \end{aligned}$$

(3)

$$\begin{aligned} \begin{aligned} u\dfrac{\partial T}{\partial x}+v\dfrac{\partial T}{\partial y}+w\dfrac{\partial T}{\partial z}=&\alpha \dfrac{\partial ^2\,T}{\partial z^2}+\tau \left\{ D_B\dfrac{\partial T}{\partial z}\dfrac{\partial C}{\partial z}+\dfrac{D_T}{T_\infty }\left( \dfrac{\partial T}{\partial z}\right) ^2\right\} -\dfrac{1}{(\rho c_p)_f}\dfrac{\partial q_r}{\partial z}, \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} u\dfrac{\partial C}{\partial x}+v\dfrac{\partial C}{\partial y}+w\dfrac{\partial C}{\partial z}=D_B\dfrac{\partial ^2\,C}{\partial z^2}+\dfrac{D_T}{T_\infty }\dfrac{\partial ^2\,T}{\partial z^2}-k^2_r\left( C-C_\infty \right) \left( \frac{T}{T_\infty }\right) ^{n} e^{\left( \frac{-E_a}{\kappa T}\right) }. \end{aligned} \end{aligned}$$

(5)

The following are the physical boundary conditions for the present problem [36,37,38]:

$$\begin{aligned} \left. {\begin{aligned}&u-ax+\lambda \left( u\dfrac{\partial u}{\partial x}-au\,{+}\,v\dfrac{\partial u}{\partial y}\,{+}\,w\dfrac{\partial u}{\partial z}\right) {=}\,\beta \dfrac{\partial u}{\partial z},\,v-by\,{+}\,\lambda \left( u\dfrac{\partial v}{\partial x}-bv\,{+}\,v\dfrac{\partial v}{\partial y}\,{+}\,w\dfrac{\partial v}{\partial z}\right) {=}\,\beta \dfrac{\partial v}{\partial z},\,w\,{=}\,w_0,\\ {}&-k\dfrac{\partial T}{\partial z}=h_1\left( T_{\text {w}}-T\right) ,~-D_B\dfrac{\partial C}{\partial z}=h_2\left( C_{\text {w}}-C\right) ,~\text {at}~ z=0, \\ {}&u\rightarrow 0,\quad v\rightarrow 0,\quad T\rightarrow T_\infty ,\quad C\rightarrow C_\infty \quad \text {as}\quad z\rightarrow \infty . \end{aligned}} ~\right\} \end{aligned}$$

(6)

The following Rosseland’s estimate for an optically thick fluid is used to approximate the radiative heat flux $q_r$ [39]:

$$\begin{aligned} q_r=-\dfrac{16\sigma ^*T^3}{3k^*}\dfrac{\partial T}{\partial z}. \end{aligned}$$

(7)

The energy equation has the following form when expression (7) is applied to Eq. (4):

$$\begin{aligned} \begin{aligned} u\dfrac{\partial T}{\partial x}+v\dfrac{\partial T}{\partial y}+w\dfrac{\partial T}{\partial z}=&\alpha \dfrac{\partial ^2\,T}{\partial z^2}+\tau \left\{ D_B\dfrac{\partial T}{\partial z}\dfrac{\partial C}{\partial z}+\dfrac{D_T}{T_\infty }\left( \dfrac{\partial T}{\partial z}\right) ^2\right\} +\dfrac{16\sigma ^*T^2}{\left( 3\rho c_p\right) _f k^{*}}\left\{ T\dfrac{\partial ^2\,T}{\partial Z^2}+3\left( \dfrac{\partial T}{\partial Z}\right) ^2\right\} . \end{aligned} \end{aligned}$$

(8)

The following similarity variables are included in order to achieve similar solutions for Eqs. (2), (3), (8), and (5), subject to the boundary constraints (6):

$$\begin{aligned} \begin{aligned}&u=axf^{\prime }(\eta ),\quad v=ayg(\eta ),\quad w=-\sqrt{a\nu }(f(\eta )+g(\eta )),\quad \theta (\eta )=\dfrac{T-T_\infty }{T_{\text {w}}-T_\infty },\quad \phi (\eta )=\dfrac{C-C_\infty }{C_{\text {w}}-C_\infty },\quad \eta =z\sqrt{\dfrac{a}{\nu }}. \end{aligned} \end{aligned}$$

(9)

The following ordinary differential equations result from substituting the aforementioned similarity variables in Eqs. (2), (3), (8), and (5):

$$\begin{aligned} \begin{aligned}&f^{\prime \prime \prime }-{f^{\prime }}^2+(MK+1)(f+g)f^{\prime \prime }+K(2f^{\prime }(f+g)f^{\prime \prime }-(f+g)^2f^{\prime \prime \prime })-Mf^{\prime }=0, \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned}&g^{\prime \prime \prime }-{g^{\prime }}^2+(MK+1)(f+g)g^{\prime \prime }+K(2g^{\prime }(f+g)g^{\prime \prime }-(f+g)^2g^{\prime \prime \prime })-Mg^{\prime }=0, \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned}&\theta ^{\prime \prime }+Pr(f+g)\theta ^{\prime }+PrNb\theta ^{\prime }\phi ^{\prime }+PrNt\left( \theta ^{\prime }\right) ^2+\dfrac{4}{3}Rd\left\{ 1+\theta \left( \theta _{\text {w}}-1\right) \right\} ^2\left[ 3\left( \theta ^{\prime }\right) ^2\left( \theta _{\text {w}}-1\right) \right. \nonumber \\&\quad \left. +\left\{ 1+\theta \left( \theta _{\text {w}}-1\right) \right\} \theta ^{\prime \prime }\right] =0, \end{aligned}$$

(12)

$$\begin{aligned} \begin{aligned}&\phi ^{\prime \prime }+PrLe(f+g)\phi ^{\prime }+\dfrac{Nt}{Nb}\theta ^{\prime \prime }-PrLeK_1(1+(\theta _{\text {w}}-1)\theta )^{n}e^{\left( -\frac{E}{1+(\theta _{\text {w}}-1)\theta }\right) }\phi =0. \end{aligned} \end{aligned}$$

(13)

The dimensionless boundary conditions are written as follows:

$$\begin{aligned} \left. \begin{aligned}&f^{\prime }(0)=1-K\left\{ {f^{\prime }}^2-f^{\prime }-(f+g)f^{\prime \prime }\right\} +\alpha _1f^{\prime \prime },\quad g^{\prime }(0)=c-K\left\{ {g^{\prime }}^2-cg^{\prime }-(f+g)g^{\prime \prime }\right\} +\alpha _1g^{\prime \prime },\\ {}&f(0)=S,\quad g(0)=0,\quad \theta ^{\prime }(0)=-Bi_1\left( 1-\theta (0)\right) ,\quad \phi ^{\prime }(0)=-Bi_2\left( 1-\phi (0)\right) ,\\ {}&f^{\prime }(\infty )\rightarrow 0,\quad g(\infty )\rightarrow 0,\quad \theta (\infty )\rightarrow 0,\quad \phi (\infty )\rightarrow 0. \end{aligned} ~~~\right\} \end{aligned}$$

(14)

where

$K=\lambda a$,   $Pr=\dfrac{\nu }{\alpha }$,   $M=\dfrac{\sigma B^2_0}{a\rho _f}$,   $Nb=\dfrac{\tau D_B\left( C_{\text {w}}-C_\infty \right) }{\nu }$,   $Nt=\dfrac{\tau D_T\left( T_{\text {w}}-T_\infty \right) }{\nu T_\infty }$, $\alpha _1=\beta \sqrt{\dfrac{a}{\nu }}$, $S=-\dfrac{w_0}{\sqrt{a\nu }}$, $K_1=\dfrac{k_r^2}{a}$,   $\theta _{\text {w}}=\dfrac{T_{\text {w}}}{T_\infty }$,   $E=\dfrac{E_a}{\kappa T_\infty }$,   $Bi_1=\dfrac{h_1}{k}\sqrt{\dfrac{\nu }{a}}$,   $Rd=\dfrac{4\sigma ^*T^3_\infty }{k^*k}$,   $c=\dfrac{b}{a}$,   $Le=\dfrac{\alpha }{D_B}$,   $Bi_2=\dfrac{h_2}{D_B}\sqrt{\dfrac{\nu }{a}}$.

3 Local Skin-Friction Coefficients, Nusselt Number and Sherwood Number

In this fluid flow problem, the local skin-friction coefficients ($C_{fx}$, $C_{fy}$), Nusselt number ($Nu_{x}$), and Sherwood number ($Sh_{x}$) are the relevant physical quantities, and their expressions are as follows:

$$\begin{aligned} C_{fx}=\dfrac{\nu }{u^2_{\text {w}}}{\left[ (1+K)\dfrac{\partial u}{\partial z}\right] _{z=0}}, \end{aligned}$$

(15)

$$\begin{aligned} C_{fy}=\dfrac{\nu }{v^2_{\text {w}}}{\left[ (1+K)\dfrac{\partial v}{\partial z}\right] _{z=0}}, \end{aligned}$$

(16)

$$\begin{aligned} Nu_{x}=-\dfrac{x}{k\left( T_{\text {w}}-T_\infty \right) }\left[ \left( k+\dfrac{16\sigma ^*T^3}{3k^*}\right) \dfrac{\partial T}{\partial z}\right] _{z=0}, \end{aligned}$$

(17)

$$\begin{aligned} Sh_{x}=-\dfrac{xD_B}{D_B\left( C_{\text {w}}-C_\infty \right) }\left( \dfrac{\partial C}{\partial z}\right) _{z=0}. \end{aligned}$$

(18)

Using the dimensionless variables provided in (9), the aforementioned physical quantities may be stated in non-dimensional form

$$\begin{aligned} C_{fx}\sqrt{Re_{x}}=(1+K)f^{\prime \prime }(0), \end{aligned}$$

(19)

$$\begin{aligned} C_{fy}\sqrt{Re_{y}}=(c)^{-\frac{3}{2}}(1+K)g^{\prime \prime }(0), \end{aligned}$$

(20)

$$\begin{aligned} \frac{Nu_{x}}{\sqrt{Re_x}}=-\left[ 1+\frac{4}{3}Rd\left\{ 1+\left( \theta _{\text {w}}-1\right) \theta (0)\right\} ^3\right] \theta ^{\prime }(0), \end{aligned}$$

(21)

$$\begin{aligned} \frac{Sh_x}{\sqrt{Re_x}}=-\phi '(0), \end{aligned}$$

(22)

where $Re_{x}=\dfrac{u_{\text {w}}x}{\nu }$ and $Re_{y}=\dfrac{v_{\text {w}}y}{\nu }$ are the local Reynolds numbers.

4 Implementation of Numerical Technique

4.1 Solution Procedure

MATLAB’s bvp4c code is used to solve the nonlinear ordinary differential equations (ODE) that govern flow Eqs. (10–13) with boundary conditions 14. Other researchers have extensively implemented this code to tackle the boundary value issue. The MATLAB routine is a representation of a finite difference algorithm that achieves fourth-order precision. For the solver to work, the equations need to be rewritten as a system of equivalent first-order differential equations.

Table 1. Comparison of $-f^{\prime \prime }(0)$’s numerical findings with previously published data

Table 2. Comparison of $-g^{\prime \prime }(0)$’s numerical findings with previously published data

4.2 Results Validation

To validate the employed technique, we got $-f^{\prime \prime }(0)$ and $-g^{\prime \prime }(0)$ values and compared them to earlier reported results by Hayat and Awais [40] and Kumar et al. [8] in Tables 1 and 2 where $M = K= \alpha _1 = S = 0.0$ for a variety of c values. It is recognized that the comparison is realistic, which provides assurance of the accuracy of the numerical results presented in this study.

5 Results and Discussion

Many important factors have been looked at in this section. They have an effect on velocities, temperature, concentration, skin friction, rate of heat transfer, and rate of mass transfer. To do the calculations, we chose $K=0.1$, $Pr=S=2.0$, $Nt=n=0.5$, $M=1$, $Rd=K_1=0.2$, $Nb=\alpha _1=0.4$, $Le=1$, $\theta _{\text {w}}=1.3$, $Bi_1=Bi_2=0.3$, $E=0.6$ and $c=0.7$.

Fig. 2.

Impact of M on $f^{\prime }(\eta )$

Fig. 3.

Impact of M on $g^{\prime }(\eta )$

Fig. 4.

Impact of $\alpha _1$ on $f^{\prime }(\eta )$

Fig. 5.

Impact of $\alpha _1$ on $g^{\prime }(\eta )$

Fig. 6.

Impact of S on $f^{\prime }(\eta )$

Fig. 7.

Impact of S on $g^{\prime }(\eta )$

Fig. 8.

Impact of Rd on $\theta (\eta )$

Fig. 9.

Impact of $Bi_1$ on $\theta (\eta )$

Figures 2 and 3 demonstrate the non-dimensional velocities $f'(\eta )$ and $g'(\eta )$ for different magnetic field parameter values M. The velocities $f'(\eta )$ and $g'(\eta )$ decrease as the magnetic parameter M increases. The physical explanation for this behavior is that increasing the magnetic parameter operating transverse to the flow enhances the Lorentz force, which tends to resist the fluid motion. The velocity slip parameter $\alpha _1$ has a significant impact on fluid flow, as seen in Figs. 4 and 5. By raising the velocity parameter $\alpha _1$, the velocities $f'(\eta )$ and $g'(\eta )$ decrease. The slip between the fluid and the sheet surface increases as the velocity slip parameters rise. As a result, a partial slip velocity is transferred to the flow-field that tends to minimize fluid velocities. Figures 6 and 7 express that enhanced values of S imply the decreasing nature of flow velocities. Suction is utilized to regulate the nanofluid flow physically, with the purpose of reducing velocities by minimizing drag on nanoparticles in an external flow.

Fig. 10.

Impact of Nb on $\theta (\eta )$

Fig. 11.

Impact of Nb on $\phi (\eta )$

Fig. 12.

Impact of Nt on $\theta (\eta )$

Fig. 13.

Impact of Nt on $\phi (\eta )$

Fig. 14.

Impact of $Bi_2$ on $\phi (\eta )$

Fig. 15.

Impact of Le on $\phi (\eta )$

Fig. 16.

Impact of $K_1$ on $\phi (\eta )$

Fig. 17.

Impact of E on $\phi (\eta )$

Fig. 18.

Impact of M and S on $-C_{fx}\sqrt{Re_{x}}$

Fig. 19.

Impact of $\alpha _1$ and S on $-C_{fx}\sqrt{Re_{x}}$

Fig. 20.

Impact of M and S on $-C_{fy}\sqrt{Re_{y}}$

Fig. 21.

Impact of $\alpha _1$ and S on $-C_{fy}\sqrt{Re_{y}}$

Figure 8 illustrates the effect of the thermal radiation parameter Rd on the temperature distribution. The graphic clearly shows that with increasing Rd values, $\theta (\eta )$ is upsurged. In general, increasing radiative characteristics promote molecular mobility within the system, resulting in frequent collisions between particles that convert to heat energy. As a result, the temperature has risen. The effect of Biot number for temeperature on the temperature field is explored in Fig. 9. The increase in $Bi_1$ indicates that conduction dominates convection heat transfer at the surface. Consequently, for higher $Bi_1$ values, temperature curves are accelerated. According to Figs. 10 and 11, an increase in Nb results in an increase in $\theta (\eta )$ and a decrease in $\phi (\eta )$ over the boundary layer area. When microscopic particles in the flow field come into contact with one other, they create thermal energy, raising the fluid temperature. As a result of Brownian diffusion, the volume fraction of nanoparticles in the boundary layer decreases as they recede from the sheet’s surface. It is clear from Figs. 12 and 13 that when Nt grows, $\theta (\eta )$ and $\phi (\eta )$ rise with it. When a nanoparticle in touch with a stretched sheet is heated by the sheet’s temperature, it exhibits a thermophoretic force that causes it to push back other nanoparticles in its vicinity. An increase in Nt raises the thermophoretic force, which drives the nanoparticles from a hot location to a cool one inside the boundary layer, increasing he temperature of the nanofluid and the volume fraction of the nanoparticles. Figure 14 shows the influence of $Bi_2$ on the dispersion of concentration. The graphic demonstrates that there is a direct relationship between $\phi (\eta )$ and $Bi_2$. As the Brownian diffusivity coefficient is inversely proportional to the $Bi_2$, this means the velocity-dependent diffusion of momentum is more powerful than the temperature-dependent diffusion. So, $\phi (\eta )$ is amplified. Figure 15 depicts the relationship between the Lewis number Le and the concentration profile. $\phi (\eta )$ decelerates as Le increases throughout the boundary layer area. The Lewis number is the ratio of heat diffusivity to mass diffusivity, according to its definition. Increasing the Lewis number means that there is more thermal diffusion and less mass diffusion, which makes the concentration boundary layer thinner. The influence of the chemical reaction parameter $K_1$ on species concentration is depicted in Fig. 16. We can observe from this graph that as $K_1$ increases, $\phi (\eta )$ falls. This is because there is more thermal energy available to obtain the activation energy required to compensate for the breakdown of atoms’ bonds. The activation energy parameter E has been displayed in Fig. 17 to show how it affects concentration distribution. This diagram clearly shows that $\phi (\eta )$ and E have a direct relationship. As E increases, the pace of a chemical reaction physically increases. Hence, $\phi (\eta )$ is heightened.

Fig. 22.

Impact of Rd and $Bi_1$ on $\frac{Nu_{x}}{\sqrt{Re_x}}$

Fig. 23.

Impact of Nt and Nb on $\frac{Nu_{x}}{\sqrt{Re_x}}$

Fig. 24.

Impact of Nt and Nb on $\frac{Sh_{x}}{\sqrt{Re_x}}$

Fig. 25.

Impact of Le and $Bi_2$ on $\frac{Sh_{x}}{\sqrt{Re_x}}$

The differences in the local surface drag coefficients $-C_{fx}\sqrt{Re_{x}}$ and $-C_{fy}\sqrt{Re_{y}}$ scatterings of Maxwell nanofluid as a function of M, $\alpha _1$, and S are depicted in Figs. 18, 19, 20 and 21. The figures demonstrate that $-C_{fx}\sqrt{Re_{x}}$ and $-C_{fy}\sqrt{Re_{y}}$ degrade with increasing $\alpha _1$ values, but M and S exhibit the opposite pattern. Figures 22 and 23 illustrate the effects of Rd, $Bi_1$, Nt and Nb on the local Nusselt number $\frac{Nu_{x}}{\sqrt{Re_x}}$. On the basis of the figures, it can be concluded that $\frac{Nu_{x}}{\sqrt{Re_x}}$ is directly proportional to Rd and $Bi_1$, however an inverse relationship can be noticed between Nt and Nb. The effects of Nt, Nb, Le, $Bi_2$, $K_1$, and E on local mass transfer rate $\frac{Sh_{x}}{\sqrt{Re_x}}$ scattering are displayed in Figs. 24, 25 and 26. Figures show that $\frac{Sh_{x}}{\sqrt{Re_x}}$ is heightened with increasing amounts of Nb, Le, $Bi_2$, and $K_1$, whereas an inverse association is noticed with Nt and E.

Fig. 26.

Impact of E and $K_1$ on $\frac{Sh_{x}}{\sqrt{Re_x}}$

6 Conclusions

The effects of velocity slip, activation energy, and convective heating on MHD Maxwell nanofluid flow across a permeable stretched surface heated by thermal radiation are examined computationally in this study using MATLAB’s bvp4c solver. The following conclusions are made from the findings:

• For increasing levels of the velocity slip and suction parameters, the velocity decreases in magnitude.

• Increasing the Biot number for temperature and thermal radiation can enhance temperature profiles.

• Concentration field increases with an elevation in the Biot number for concentration and the activation energy parameter.

• Increases in the magnetic field and suction parameter augment the shear stress function, whilst velocity slip lowers it.

• The combination of radiation absorption, thermal radiation, and convection heating can all help to boost the heat transmission rate.

• Activation energy can uplift mass transfer rate while chemical reaction slows it down.