Hall current and thermo-diffusion effects on magnetohydrodynamic convective flow near an oscillatory plate with ramped type thermal and solutal boundary conditions

Abstract

The present discussion deals with the study of time-dependent hydromagnetic free convection fluid flow with heat and mass transfer over an oscillating vertical plate which is placed in a porous medium with ramped wall temperature and wall concentration in the presence of Hall current, rotation, chemical reaction, thermal radiation, thermo-diffusion (Soret effect). The governing system of equations is non-dimensionalized by using suitable dimensionless variables and parameters. The non-dimensional equations are solved analytically using the Laplace transform technique. The influence of various pertinent flow parameters on velocity, temperature and concentration fields are analyzed and portrayed through figures, whereas the skin friction, Nusselt number and Sherwood number are described and shown in tabular form.

1 Introduction

Theoretical/experimental study of magnetohydrodynamic (MHD) natural convection flow of viscous, incompressible and electrically conducting fluids with heat and mass transfer past an oscillating vertical plate implanted in a porous medium received significant attention because of its various applications in industrial, astrophysical [1], geophysical processes. In view of this, a voluminous amount of research is done in the past few decades. Chen [2] investigated MHD natural convective flow with heat and mass transfer past a permeable inclined surface with power-law surface temperature and surface concentration. Makinde and Sibanda [3] illustrated heat and mass transfer of an MHD natural convective fluid flow past a moving vertical porous plate placed in a uniform permeable medium. Hamad et al. [4] studied combined heat and mass transfer with MHD slip past a moving plate in a permeable medium. Javaherdeh et al. [5] discussed 2-dimensional laminar MHD free convection flow with heat and mass transfer near a moving vertical plate in a permeable medium with power-law type surface temperature and surface concentration. Seth et al. [6] analyzed hydromagnetic free convective and rotating flow of second-grade fluid induced by an oscillating vertical plate embedded in a porous medium.

When the strength of the applied magnetic field is strong and/ or the fluid is ionized whose density is quite low, Hall current plays a significant role. In the case of ionized fluid, the electric current is usually carried by electrons which undergo continuous collisions with other neutral or charged particles. When the electric field is very strong, the conductivity parallel to the electric field is decreased, and a current is thereby produced in the direction perpendicular to both electric and magnetic fields. This phenomenon is termed as Hall effect, and the current itself is defined as Hall current. Many investigators examined the effect of Hall current on MHD natural convection flow because of its important applications in industry and engineering viz. Hall current accelerator, nuclear power reactors, energy storage system, magnetometers, hydromagnetic power generation, spacecraft population etc. Considering these facts, Kinyanjui et al. [7] analyzed time-dependent MHD free convective flow in a rotating frame of reference considering viscous dissipation and Hall current into account. Takhar et [8] studied MHD flow with moving free-stream over a vertical plate in a rotating medium considering Hall current. Siddiqa et al. [9] demonstrated the Hall phenomenon on free convection fluid flow with a strong transverse magnetic field. Furthermore, Seth et al. [10] discussed Hall current and rotation effects on MHD free convection flow with heat and mass transfer of a heat-absorbing fluid past an impulsively moving vertical plate with ramped temperature.

It is well known that the thermal radiation effect plays a vital role in space technology (aircraft, missiles, satellites, space vehicles) and manufacturing processes involving high temperature (nuclear power plants, gas turbines). Thermal radiation also helps in controlling the heat transfer process in the polymer processing industry. These applications encouraged many researchers to perform a voluminous amount of research work on fluid flow problems considering thermal radiation impact into account. Hossain and Takhar [11] studied the radiation effect on mixed convection flow near a vertical plate with constant wall temperature. Mbeledogu and Ogulu [12] presented a closed-form solution of the problem on time-dependent hydromagnetic free convection flow with heat and mass transfer of a rotating fluid past a vertical porous plate taking thermal radiation into account. Pal and Mondal [13] and Hayat et al. [14] analyzed radiation effect on mixed convection along a vertical flat plate embedded in a porous medium. Hussain et al. [15] deliberated thermal radiation impact on magneto-nanofluid flow generated by an accelerated moving plate with an inclined magnetic field.

Internal heat generation/absorption becomes important in several practical situations involving heat transfer processes, like fire and combustion modeling, fluids undergoing exothermic and/or endothermic chemical reaction, convection in Earth’s mantle, development of metal waste from spent nuclear fuel etc. Taking into consideration the significance of such applications, Chamkha [16] investigated MHD unsteady mixed convective heat and mass transfer flow past a vertical porous plate placed in a fluid-saturated porous medium considering heat absorption into account. Nandkeolyar and Das [17] illustrated heat absorption effect on the convective and time-dependent hydromagnetic flow of a dusty fluid along a flat surface with ramped type temperature at the surface. Noor and Abbasbandy [18] described the free convection and thermophoretic hydromagnetic flow over an isothermal inclined plate with heat source/sink and thermal radiation. Makinde [19] presented similarity solution for MHD mixed convective stagnation point flow with heat and mass transfer toward a vertical plate embedded in a highly porous medium with radiation and internal heat generation.

The study of heat and mass transfer with chemical reaction in moving fluid is significant in various physical phenomena, such as fluids undergoing an exothermic and endothermic chemical reaction, manufacturing of ceramic and glassware, smelting food processing [20] etc. It may be noted that, in many chemical engineering processes, chemical reactions take place between a foreign mass and the ambient fluid. Chemical reactions significantly affect buoyancy-driven flows and as a result, the interaction between chemical reaction and convection plays a decisive role in fluid flow characteristics. However, there are different orders of a chemical reaction. Among those, the first-order chemical reaction is the simplest one. In this case, the rate of reaction is directly proportional to the species concentration. Muthucumaraswamy et al. [21] investigated the effect of chemical reaction on MHD heat and mass transfer flow, which is past a moving vertical plate. Zeuco and Ahmed [22] illustrated mixed convection on hydromagnetic heat and mass transfer flow past an infinite vertical permeable plate in the presence of first-order chemical reaction. Das [23] analyzed the effect of the first-order chemical reaction and thermal radiation on MHD free convection heat and mass transfer rotating flow of a micropolar fluid past a semi-infinite porous plate with a constant heat source. Nandkeolyar et al. [24] investigated the unsteady hydromagnetic free convective heat and mass transfer of a viscous, incompressible and electrically conducting fluid past a flat plate with ramped wall temperature in the presence of thermal radiation and chemical reaction. Hussain et al. [25] described time-dependent MHD free convective heat and mass transfer flow past an accelerated moving vertical plate embedded in a porous medium in the presence of Hall current, heat absorption and chemical reaction with ramped type boundary conditions for surface temperature and concentration in a rotating system.

Mass flux due to a temperature gradient, popularly known as the Soret effect or thermo-diffusion or thermophoresis, becomes significant for isotope separation. This effect is often neglected in the mass transfer process under the assumption that it is of a small order of magnitude than the effect described by Fick’s law. But, it plays an important role when there is a difference of density in the flow regime which includes the areas such as petrology, hydrology, geosciences and to name a few. It is very useful in making a mixture of gases with very light molecular weights like H$_2$, He etc. and medium molecular weights like N$_2$, air etc. The importance of thermo-diffusion effect on convective transport phenomena in clear fluids is described nicely in the well-known book by Eckert and Drake [26]. Narayana et al. [27] discussed heat and mass transfer flow with free convection past a vertical plate in a thermally stratified porous medium filled with non-Newtonian liquid under the Soret effect. Jha et al. [28] presented a numerical solution of the problem of Soret driven unsteady MHD mixed-convection flow of a viscoelastic fluid over an infinite vertical plate in the presence of a heat source. Soret impact on time-dependent natural convective fluid flow past an accelerating vertical moving plate placed in a porous medium considering Hall current and heat absorption into account was deliberated by Seth et al. [29]. Hussanan et al. [30] analyzed the effect of thermo-diffusion on time-dependent MHD mixed convective flow past an oscillatory vertical plate placed in a porous medium considering the Newtonian heating condition. Kataria and Patel [31] investigated Soret and thermal radiation effects on hydromagnetic Casson fluid flow over plate moving periodically in porous medium taking heat generation and chemical reaction into account. The combined impact of Soret and Dufour on hydromagnetic free convective flow past an inclined stretching sheet placed in a non-Darcy medium considering heat absorption, chemical reaction and viscous dissipation aspects was examined by Seth et al. [32]. Later on, Kataria and Patel [33] described the Soret effect on the transient free convective magnetohydrodynamic flow of a second grade fluid past along infinite vertical plate situated in a porous medium with ramped surface temperature and ramped surface concentration. Arifuzzaman et al. [34] discussed unsteady natural convective MHD fluid flow past a vertical oscillating permeable plate with the effect of heat absorption, thermal radiation and higher-order chemical reaction. Soret effect on hydromagnetic natural convective flow toward a nonlinearly stretched surface in the presence of velocity slip and buoyancy forces was examined by Seth et al. [35]. Subsequently, Seth et al. [36] illustrated the thermo-diffusion effect on hydromagnetic Casson fluid flow past a vertical plate embedded in porous medium in the presence of Joule heating, chemical reaction, Newtonian heating and viscous dissipation.

Motivated by the above research studies, the main objective of the present investigation is to analyze the effect of Hall current and thermo-diffusion (Soret) on magnetohydrodynamic natural convection flow of an optically thick radiating fluid along an oscillatory moving vertical plate situated in a fluid-saturated uniform porous medium with ramped type thermal and solutal conditions at the surface in rotating frame. The impacts of heat generation/absorption and chemical reaction of the first order are also taken into account. As per the authors’ knowledge, no attempt has been made to analyze such a physical problem which may have strong bearings on various problems in astrophysics, geophysics and fluid engineering. Some of the applications are found in electromagnetic device design, plasma physics, extraction of petroleum products and gases, power and chemical engineering, cosmical flight, nuclear power reactors etc. The governing equations are converted into non-dimensional form with the help of suitable transformation and then solved analytically using Laplace transform. The influence of different physical parameters on fluid velocity, temperature and species concentration are discussed through figures and tables.

2 Mathematical formulation and solution

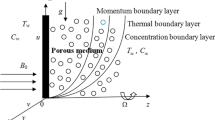
Consider the time-dependent MHD free convective and rotative flow with heat and mass transfer of a viscous, incompressible and electrically conducting fluid over an oscillating vertical plate embedded in a porous medium in the presence of Hall current. Further, the effects of thermal radiation, internal heat generation/absorption and chemical reaction are also considered. The Cartesian coordinate system is chosen in such a way that $x'$-axis is along the length of the plate in the upward direction and $y'$-axis is normal to the plane of the plate while $z'$-axis is measured along the width of the plate. A constant magnetic field of strength $B_0$ acting in $y'$-direction is applied. Both fluid and the plate rotate simultaneously about the $y'$-axis with constant angular velocity $\varOmega$. Initially, i.e., when $t'\le 0$, both fluid and the plate are kept at rest and maintained at a constant temperature $T_0$ and constant concentration $C_0$. When $t'>0$, the plate starts oscillating in its plane $(y'=0)$ with velocity $u'=u_0\cos (\omega ^* t')$. Temperature of the wall is quickly enhanced and /or reduced to $T_0+(T_w-T_0)t'/t_0$ when $t'\le t_0$ and $T_w$ when $t'>t_0$ and is thereafter maintained at uniform temperature $T_w$. Similarly, the species concentration is also quickly raised and/or reduced to $C_0+(C_w-C_0)t'/t_0$ for $t'\le t_0$ and $C_w$ for $t'>t_0$, respectively, and is kept at uniform concentration $C_w$ thereafter. It is considered that a homogeneous chemical reaction of order one with a constant rate $k'$ is supposed to live between the fluid and dispersing species. A physical sketch of the problem is shown in Fig. 1. The plate is assumed to be electrically non-conducting and of infinite extent in the directions of $x'$ and $z'$. So, all the physical quantities excluding the pressure are dependent on $y'$ and $t'$ only.

Fig. 1

Physical sketch of the problem

Further, it is also considered that no external electric field is applied into the flow field, so the effect of polarization of charges is negligible, which corresponds to the case where no energy is added or extracted from the fluid by electrical means. Moreover, it is assumed that the fluid is a metallic liquid or partially ionized, having a small magnetic Reynolds number. Therefore, the induced magnetic field generated by fluid motion is negligible in comparison to the applied one.

Based on the assumptions made above and under Boussinesq approximation, the momentum, energy and concentration equations for unsteady rotative MHD natural convective heat and mass transfer flow of an incompressible, electrically conducting, viscous and chemically reactive fluid along an oscillating vertical plate placed in a porous medium considering into account the impact of thermal radiation, Hall current and internal heat generation, are given by (Hussain et al. [25])

$$\begin{aligned}&\frac{\partial u'}{\partial t'}+2\varOmega w'=\nu \frac{\partial ^2 u'}{\partial y'^2}-\frac{\sigma B_{0}^2}{\rho }\left( \frac{u'+mw'}{1+m^2}\right) -\frac{\nu }{K'_{1}}u' \nonumber \\&\quad +\text {g}\beta (T-T_{0})+\text {g}\beta ^*(C-C_{0}), \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial w'}{\partial t'}-2\varOmega u'=\nu \frac{\partial ^2 w'}{\partial y'^2}+\frac{\sigma B_{0}^2 }{\rho }\left( \frac{mu'-w'}{1+m^2}\right) -\frac{\nu }{K'_{1}}w', \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial T}{\partial t'}=\frac{k}{\rho c_{p}}\frac{\partial ^2 T}{\partial y'^2}+\frac{Q_{0}}{\rho c_{p}}(T-T_{0})-\frac{1}{\rho c_{p}}\frac{\partial q_{r}}{\partial y'}, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial C}{\partial t'}=D\frac{\partial ^2 C}{\partial y'^2}+D_{T}\frac{\partial ^2 T}{\partial y'^2}-k'(C-C_{0}). \end{aligned}$$

(4)

Initial and boundary conditions associated with the current fluid flow problem are

$$\begin{aligned} \begin{aligned}&u'=0,\quad w'=0,\quad T=T_{0},\quad C=C_{0} \quad \text {when}\quad t'\le 0 \quad \text {and}\quad y'\ge 0,\\&u'=u_{0}\cos (\omega ^* t'),\quad w'=0 \quad \text {when }\quad t'> 0 \quad \text { and }\quad y'=0,\\&T=T_{0}+(T_{w}-T_{0})t'/t_{0},~ C=C_{0}+(C_{w}-C_{0})t'/t_{0} \quad\text {when}\quad 0<t'\le t_{0}\quad\text{and} \quad y'=0,\\&T=T_{w},\quad C=C_{w} \quad \text {when}\quad t'>t_{0} \quad \text {and}\quad y'=0,\\&u'\rightarrow 0,\quad w'\rightarrow 0,\quad T\rightarrow T_{0},\quad C\rightarrow C_{0} \quad \text {when} \quad t' > 0 \quad \text {and}\quad y'\rightarrow \infty . \end{aligned} \end{aligned}$$

(5)

Following dimensionless variables are introduced for the non-dimensionlization of Eqs. (1)–(4):

$$\begin{aligned} y&=\frac{u_{0}y'}{\nu },\quad t=\frac{u_{0}^2t'}{\nu },\quad U=\frac{u'}{u_{0}},\quad W=\frac{w'}{u_{0}}, \nonumber \\ \theta&=\frac{T-T_{0}}{T_{w}-T_{0}},\quad \phi =\frac{C-C_{0}}{C_{w}-C_{0}}. \end{aligned}$$

(6)

For an optically thick fluid, the radiative heat flux $q_r$ is approximated with the help of Rosseland approximation [14] and is expressed in the form

$$\begin{aligned} q_r=-\frac{4\sigma ^ *}{3k^*}\frac{\partial T^4}{\partial y'}, \end{aligned}$$

(7)

where $\sigma ^*$ is the Stefan–Boltzman constant and $k^*$ is mean absorption coefficient.

We assume that the difference between fluid temperature T and free-stream temperature $T_0$ is small enough so that $T^4$ can be expanded in Taylor’s series about $T_0$. This will lead to, after discarding the second and higher-order terms, linearize Eq. (7) and the following relations may be obtained:

$$\begin{aligned} T^4 \cong 4T_{0}^3 T-3T_{0}^4. \end{aligned}$$

(8)

With the help of the expressions defined in (6)–(8), Eqs. (1)–(4) reduce to following dimensionless form:

$$\begin{aligned}&\frac{\partial U}{\partial t}+2K_2^2W=\frac{\partial ^2 U}{\partial y^2}-M\left( \frac{U+mW}{1+m^2}\right) -\frac{U}{K_{1}}+{\mathrm{Gr}}\theta +{\mathrm{Gc}}\phi , \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial W}{\partial t}-2K_2^2U=\frac{\partial ^2 W}{\partial y^2}+M\left( \frac{mU-W}{1+m^2}\right) -\frac{W}{K_{1}}, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial \theta }{\partial t}=\left( \frac{1+R}{\mathrm{Pr}}\right) \frac{\partial ^2 \theta }{\partial y^2}+Q\theta , \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial \phi }{\partial t}=\frac{1}{\mathrm{Sc}}\frac{\partial ^2 \phi }{\partial y^2}+{\mathrm{Sr}}\frac{\partial ^2 \theta }{\partial y^2}-{\mathrm{Kr}}\phi , \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned}&{\mathrm{Gr}}=\frac{\nu \text {g}\beta \left( T_{w}-T_{0}\right) }{u_0^3},\quad {\mathrm{Gc}}=\frac{\nu \text {g}\beta ^*\left( C_{w}-C_{0}\right) }{u_0^3},\quad M=\frac{\sigma B_0^2\nu }{\rho u_0^2},\\&K_1=\frac{K'_1u_0^2}{\nu ^2},\quad K_2^2=\frac{\nu \varOmega }{u_0^2},\quad \alpha =\frac{k}{\rho c_p},\quad {\mathrm{Pr}}=\frac{\nu }{\alpha },\quad Q=\frac{\nu Q_0}{\rho c_p u_0^2},\\&R=\frac{16\sigma ^*T_w}{3kk^*}, \quad Sc=\frac{\nu }{D},\quad {\mathrm{Kr}}=\frac{\nu k'}{u_0^2},\quad Sr=\frac{D_T(T_w-T_0)}{\nu (C_w-C_0)}. \end{aligned} \end{aligned}$$

(13)

The corresponding dimensionless initial and boundary conditions are reduced to:

$$\begin{aligned} \begin{aligned}&U=0,\quad W=0,\quad \theta =0,\quad \phi =0 \quad \text {when}\quad t\le 0 \quad \text {and}\quad y\ge 0,\\&U=\cos (\omega t),\quad W=0 \quad \text {when}\quad t> 0\quad \text {and}\quad y=0 ,\\&\theta =t,\quad \phi =t \quad \text {when}\quad 0<t\le 1 \quad \text {and}\quad y=0,\\&\theta =1,\quad \phi =1 \quad \text {when}\quad t>1 \quad \text {and}\quad y=0,\\&U\rightarrow 0,~~ W\rightarrow 0,~~ \theta \rightarrow 0,~~ \phi \rightarrow 0 ~~ \text {when}~~ t>0 ~~ \text {and}~~ y\rightarrow \infty , \end{aligned} \end{aligned}$$

(14)

where $\displaystyle \omega =\dfrac{\omega ^*\nu }{u_0^2}$ and $t_0=\dfrac{\nu }{u_0^2}$.

The combined form of Eqs. (9) and (10) is:

$$\begin{aligned} \frac{\partial F}{\partial t}=\frac{\partial ^2 F}{\partial y^2}-\lambda F+{\mathrm{Gr}}\theta +{\mathrm{Gc}}\phi , \end{aligned}$$

(15)

where $\lambda =\frac{M(1-im)}{1+m^2}+\frac{1}{K_1}-2iK^2$ and $F=U+iW$.

The compact form of initial and boundary conditions of Eq. (14) can be written as:

$$\begin{aligned} \begin{aligned}&F=0,\quad \theta =0,\quad \phi =0 \quad \text {when}\quad t\le 0 \quad \text {and}\quad y\ge 0,\\&F=\cos (\omega t)\quad \text {when}\quad t>0 \quad \text {and}\quad y=0,\\&\theta =t,\quad \phi =t \quad \text {when}\quad 0<t\le 1 \quad \text {and}\quad y=0,\\&\theta =1,\quad \phi =1 \quad \text {when}\quad t>1 \quad \text {and}\quad y=0,\\&F\rightarrow 0,\quad \theta \rightarrow 0,\quad \phi \rightarrow 0 \quad \text {when}\quad t>0 \quad \text {and}\quad y\rightarrow \infty . \end{aligned} \end{aligned}$$

(16)

Using Laplace transform technique, we have solved Eqs. (11), (12) and (15) subject to the initial and boundary conditions as defined in (16), and obtained the exact solution for fluid velocity, fluid temperature and species concentration as presented below:

$$\begin{aligned} F(y,t)&= f_4(0,1,t,y,1,\lambda )-(i\omega /2)f_3(1,-i\omega ,t,y,1,\lambda ) \nonumber \\&+(i\omega /2)f_3(1,i\omega ,t,y,1,\lambda )\nonumber \\&+(\mathrm{Gr}/g)f_2(g,j,t,y,1,\lambda )+(\mathrm{Gc}/n)f_2(n,q,t,y,1,\lambda )\nonumber \\&+r_1f_3(d,c,t,y,1,\lambda )-r_1f_3(n,q,t,y,1,\lambda ) \nonumber \\&-r_2f_2(d,c,t,y,1,\lambda )\nonumber \\&+r_2f_2(n,q,t,y,1,\lambda )-r_3f_3(d,c,t,y,1,\lambda ) \nonumber \\&+r_3f_3(g,j,t,y,1,\lambda )\nonumber \\&+r_4f_2(d,c,t,y,1,\lambda )-r_4f_2(g,j,t,y,1,\lambda ) \nonumber \\&-({\mathrm{Gr}}/g)f_2(g,j,t,y,\beta _2,\beta _1)\nonumber \\&-r_1f_3(d,c,t,y,{\mathrm{Sc}},\beta _3)-({\mathrm{Gc}}/n)f_2(n,q,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_1f_3(n,q,t,y,{\mathrm{Sc}},\beta _3)-r_2f_2(n,q,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_2f_2(d,c,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_3f_3(d,c,t,y,\beta _2,\beta _1)-r_3f_3(g,j,t,y,\beta _2,\beta _1) \nonumber \\&-r_4f_2(d,c,t,y,\beta _2,\beta _1) \nonumber \\&+r_4f_2(g,j,t,y,\beta _2,\beta _1) \nonumber \\&-(Gr/g)H(t-1)f_2(g,j,t-1,y,1,\lambda ) \nonumber \\&-(Gc/n)H(t-1)f_2(n,q,t-1,y,1,\lambda ) \nonumber \\&-r_1H(t-1)f_3(d,c,t-1,y,1,\lambda ) \nonumber \\&+r_1H(t-1)f_3(n,q,t-1,y,1,\lambda ) \nonumber \\&+r_2H(t-1)f_2(d,c,t-1,y,1,\lambda ) \nonumber \\&-r_2H(t-1)f_2(n,q,t-1,y,1,\lambda ) \nonumber \\&+r_3H(t-1)f_3(d,c,t-1,y,1,\lambda ) \nonumber \\&-r_3H(t-1)f_3(g,j,t-1,y,1,\lambda ) \nonumber \\&-r_4H(t-1)f_2(d,c,t-1,y,1,\lambda ) \nonumber \\&+r_4H(t-1)f_2(g,j,t-1,y,1,\lambda ) \nonumber \\&+({\mathrm{Gr}}/g)H(t-1) f_2(g,j,t-1,y,\beta _2,\beta _1) \nonumber \\&+r_1H(t-1)f_3(d,c,t-1,y,{\mathrm{Sc}},\beta _3)\nonumber \\&+({\mathrm{Gc}}/n)H(t-1)f_2(n,q,t-1,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_3H(t-1)f_3(g,j,t-1,y,\beta _2,\beta _1) \nonumber \\&+r_2H(t-1)f_2(n,q,t-1,y,{\mathrm{Sc}},\beta _3) \nonumber \\&-r_2H(t-1)f_2(d,c,t-1,y,{\mathrm{Sc}},\beta _3) \nonumber \\&-r_3H(t-1)f_3(d,c,t-1,y,\beta _2,\beta _1) \nonumber \\&-r_1H(t-1)f_3(n,q,t-1,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_4H(t-1)f_2(d,c,t-1,y,\beta _2,\beta _1) \nonumber \\&-r_4H(t-1)f_2(g,j,t-1,y,\beta _2,\beta _1). \end{aligned}$$

(17)

$$\begin{aligned} \theta (y,t)&=f_1(t,\beta _2,y,\beta _1)-H(t-1)f_1(t-1,\beta _2,y,\beta _1). \end{aligned}$$

(18)

$$\begin{aligned} \phi (y,t)&=f_1(t,{\mathrm{Sc}},y,\beta _3)-f_3(b,c,t,y,\beta _2,\beta _1) \nonumber \\&+f_3(b,c,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&-(a/d)f_2(d,c,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+(a/d)f_2(d,c,t,y,\beta _2,\beta _1)\nonumber \\&-H(t-1)f_3(b,c,t-1,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+(a/d)H(t-1)f_2(d,c,t-1,y,{\mathrm{Sc}},\beta _3)\nonumber \\&-H(t-1)f_1(t-1,{\mathrm{Sc}},y,\beta _3) \nonumber \\&+H(t-1)f_3(b,c,t-1,y,\beta _2,\beta _1)\nonumber \\&-(a/d)H(t-1)f_2(d,c,t-1,y,\beta _2,\beta _1). \end{aligned}$$

(19)

To understand the influences of ramped surface temperature on the fluid flow, a comparison of present results with those of isothermal plate case is necessary. The expressions for fluid velocity, temperature and species concentration with isothermal temperature at the surface are presented in the following forms:

$$\begin{aligned} F(y,t)&=f_4(0,1,t,y,1,\lambda )-(i\omega /2)f_3(1,-i\omega ,t,y,1,\lambda ) \nonumber \\&+(i\omega /2)f_3(1,i\omega ,t,y,1,\lambda )\nonumber \\&-({\mathrm{Gr}}/g)f_3(g,j,t,y,1,\lambda )-({\mathrm{Gc}}/n)f_3(n,q,t,y,1,\lambda ) \nonumber \\&+r_2f_3(d,c,t,y,1,\lambda )\nonumber \\&-r_2f_3(n,q,t,y,1,\lambda )-r_1f_4(c,d,t,y,1,\lambda )\nonumber \\&+r_1f_4(q,n,t,y,1,\lambda )\nonumber \\&-r_4f_3(d,c,t,y,1,\lambda )+r_4f_3(g,j,t,y,1,\lambda ) \nonumber \\&+r_3f_4(c,d,t,y,1,\lambda )\nonumber \\&-r_3f_4(j,g,t,y,1,\lambda ) \nonumber \\&+({\mathrm{Gr}}/g)f_3(g,j,t,y,\beta _2,\beta _1)\nonumber \\&+({\mathrm{Gc}}/n)f_3(n,q,t,y,\beta _2,\beta _1) \nonumber \\&-r_2f_3(d,c,t,y,{\mathrm{Sc}},\beta _3)\nonumber \\&+r_2f_3(n,q,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&+r_1f_4(c,d,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&-r_1f_4(q,n,t,y,{\mathrm{Sc}},\beta _3)\nonumber \\&+r_4f_3(d,c,t,y,\beta _2,\beta _1) \nonumber \\&-r_4f_3(g,j,t,y,\beta _2,\beta _1) \nonumber \\&-r_3f_4(c,d,t,y,\beta _2,\beta _1)\nonumber \\&+r_3f_4(j,g,t,y,\beta _2,\beta _1). \end{aligned}$$

(20)

$$\begin{aligned} \theta (y,t)&=f_4(0,1,t,y,\beta _2,\beta _1). \end{aligned}$$

(21)

$$\begin{aligned} \phi (y,t)&=f_4(0,1,t,y,{\mathrm{Sc}},\beta _3) \nonumber \\&-(a/d)f_3(d,c,t,y,\beta _2,\beta _1) \nonumber \\&+(b/d)f_4(c,d,t,y,\beta _2,\beta _1)\nonumber \\&+(a/d)f_3(d,c,t,y,{\mathrm{Sc}},\beta _3)-(b/d)f_4(c,d,t,y,{\mathrm{Sc}},\beta _3), \end{aligned}$$

(22)

where $a={\mathrm{Sr}}{\mathrm{Sc}}\beta _1$,   $b={\mathrm{SrSc}}\beta _2$,   $c=\beta _3-\beta _1$,   $d={\mathrm{Sc}}-\beta _2$,   $g=\beta _2-1$,   $j=\beta _1-\lambda$,   $n={\mathrm{Sc}}-1$,   $q=\beta _3-\lambda$,   $\beta _1=-\frac{{\mathrm{PrQ}}}{1+R}$,   $\beta _2=\frac{{\mathrm{Pr}}}{1+R}$,   $\beta _3=ScK_2$, and $r_i$, $f_i$ $(i=1,2,3,4)$ are prescribed in “Appendix A”.

The expressions for the dimensionless shear stress components $\tau _x$ and $\tau _z$ at the plate in the primary and secondary flow directions, respectively, Nusselt number Nu and Sherwood number Sh for both ramped surface temperature and isothermal plate are expressed in the following compact forms:

For the ramped surface temperature :

$$\begin{aligned} \tau&=\tau _x+i\tau _z \nonumber \\&=-b_{14}f_5(\beta _1,\beta _2,0,1,t) \nonumber \\&-b_{15}f_5(\beta _1,\beta _2,c,d,t) \nonumber \\&-b_{16}f_6(\beta _1,\beta _2,d,c,t)\nonumber \\&-b_{17}f_5(\beta _1,\beta _2,j,g,t) \nonumber \\&-b_{18}f_6(\beta _1,\beta _2,g,j,t)\nonumber \\&+b_{25}f_5(\lambda ,1,0,1,t)\nonumber \\&+b_{21}f_5(\lambda ,1,c,d,t) \nonumber \\&-b_{22}f_6(\lambda ,1,d,c,t)\nonumber \\&+b_{17}f_5(\lambda ,1,j,g,t) \nonumber \\&+b_{18}f_6(\lambda ,1,g,j,t)\nonumber \\&-b_{23}f_5(\lambda ,1,q,n,t) \nonumber \\&+b_{24}f_6(\lambda ,1,n,q,t)\nonumber \\&-b_{19}f_5(\beta _3,{\mathrm{Sc}},0,1,t)\nonumber \\&-b_{20}f_5(\beta _3,\mathrm{Sc},c,d,t)\nonumber \\&+b_{23}f_5(\beta _3,\mathrm{Sc},q,n,t)\nonumber \\&+b_{26}f_6(\beta _3,\mathrm{Sc},d,c,t)\nonumber \\&-b_{24}f_6(\beta _3,\mathrm{Sc},n,q,t)\nonumber \\&-b_{12}f_5(\lambda ,1,i\omega ,1,t) \nonumber \\&-b_{12}f_5(\lambda ,1,-i\omega ,1,t)\nonumber \\&+b_{14}H(t-1)f_5(\beta _1,\beta _2,0,1,t-1)\nonumber \\&+b_{15}H(t-1)f_5 (\beta _1,\beta _2,c,d,t-1)\nonumber \\&+b_{16}H(t-1)f_6(\beta _1,\beta _2,d,c,t-1) \nonumber \\&+b_{17}H(t-1)f_5(\beta _1,\beta _2,j,g,t-1)\nonumber \\&+b_{18}H(t-1)f_6(\beta _1,\beta _2,g,j,t-1) \nonumber \\&-b_{25}H(t-1)f_5(\lambda ,1,0,1,t-1)\nonumber \\&-b_{21}H(t-1)f_5(\lambda ,1,c,d,t-1) \nonumber \\&-b_{18}H(t-1)f_6(\lambda ,1,g,j,t-1)\nonumber \\&+b_{23}H(t-1)f_5(\lambda ,1,q,n,t-1) \nonumber \\&-b_{24}H(t-1)f_6(\lambda ,1,n,q,t-1)\nonumber \\&+b_{22}H(t-1)f_6(\lambda ,1,d,c,t-1)\nonumber \\&-b_{17}H(t-1)f_5(\lambda ,1,j,g,t-1)\nonumber \\&+b_{19}H(t-1)f_5(\beta _3,\mathrm{Sc},0,1,t-1) \nonumber \\&+b_{20}H(t-1)f_5(\beta _3,\mathrm{Sc},c,d,t-1)\nonumber \\&-b_{23}H(t-1)f_5(\beta _3,\mathrm{Sc},q,n,t-1)\nonumber \\&-b_{26}H(t-1)f_6(\beta _3,\mathrm{Sc},d,c,t-1)\nonumber \\&+b_{24}H(t-1)f_6(\beta _3,\mathrm{Sc},n,q,t-1), \end{aligned}$$

(23)

$$\begin{aligned} \mathrm{Nu}&=-f_6(\beta _1,\beta _2,0,1,t)+H(t-1)f_6(\beta _1,\beta _2,0,1,t-1), \end{aligned}$$

(24)

$$\begin{aligned} \mathrm{Sh}&=b_3f_5(\beta _1,\beta _2,0,1,t) \nonumber \\&+b_4f_5(\beta _1,\beta _2,c,d,t) \nonumber \\&-b_2f_6(\beta _1,\beta _2,d,c,t)\nonumber \\&+f_6(\beta _3,\mathrm{Sc},0,1,t)-b_3f_5(\beta _3,\mathrm{Sc},0,1,t) \nonumber \\&-b_4f_5(\beta _3,\mathrm{Sc},c,d,t)\nonumber \\&+b_2f_6(\beta _3,\mathrm{Sc},d,c,t) \nonumber \\&-b_3H(t-1)f_5(\beta _1,\beta _2,0,1,t-1)\nonumber \\&-b_4H(t-1)f_5(\beta _1,\beta _2,c,d,t-1) \nonumber \\&+b_2H(t-1)f_6(\beta _1,\beta _2,d,c,t-1)\nonumber \\&+H(t-1)f_6(\beta _3,\mathrm{Sc},0,1,t-1) \nonumber \\&+b_3H(t-1)f_5(\beta _3,\mathrm{Sc},0,1,t-1)\nonumber \\&+b_4H(t-1)f_5(\beta _3,\mathrm{Sc},c,d,t-1) \nonumber \\&-b_2H(t-1)f_6(\beta _3,\mathrm{Sc},d,c,t-1). \end{aligned}$$

(25)

For the isothermal plate :

$$\begin{aligned} \tau&=\tau _x+i\tau _z \nonumber \\&=-b_5f_5(\beta _1,\beta _2,c,d,t) \nonumber \\&-b_6f_5(\beta _1,\beta _2,0,1,t)\nonumber \\&-b_7f_5(\beta _1,\beta _2,j,g,t)\nonumber \\&+b_{13}f_5(\lambda ,1,0,1,t)\nonumber \\&+b_{10}f_5(\lambda ,1,c,d,t)\nonumber \\&+b_7f_7(\lambda ,1,j,g,t)\nonumber \\&-b_9f_5(\lambda ,1,q,n,t)\nonumber \\&-b_8f_5(\beta _3,\mathrm{Sc},c,d,t)\nonumber \\&+b_9f_5(\beta _3,\mathrm{Sc},q,n,t)\nonumber \\&-b_{11}f_5(\beta _3,\mathrm{Sc},0,1,t)\nonumber \\&-b_{12}f_5(\lambda ,1,i\omega ,1,t)\nonumber \\&-b_{12}f_5(\lambda ,1,-i\omega ,1,t), \end{aligned}$$

(26)

$$\begin{aligned} \mathrm{Nu}&=f_5(\beta _1,\beta _2,0,1,t), \end{aligned}$$

(27)

$$\begin{aligned} \mathrm{Sh}&=b_1f_5(\beta _1,\beta _2,c,d,t)\nonumber \\&+b_2f_5(\beta _1,\beta _2,0,1,t) \nonumber \\&+(1-b_2)f_5(\beta _3,Sc,0,1,t)\nonumber \\&-b_1f_5(\beta _3,\mathrm{Sc},c,d,t), \end{aligned}$$

(28)

where $f_5$, $f_6$ and $b_i$’s are mentioned in “Appendix A”.

3 Results and discussion

3.1 Fluid flow analysis

The influence of various flow parameters such as Hall current parameter m, rotation parameter $K_2$, solutal Grashof number Gc, thermal Grashof number Gr, Soret number Sr, frequency of oscillation $\omega$ and time t on the fluid flow for ramped surface temperature as well as for isothermal plate has been investigated with the help of the solutions obtained in Eqs. (17) and (20), and presented in graphical form in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 for distinct values of the flow parameters considering magnetic parameter $M=5$, permeability parameter $K_1=0.4$, heat generation/absorption parameter $Q=3$ ($Q>0$ implies heat generation and $Q<0$ implies heat absorption), thermal radiation parameter $R=2$, Prandtl number $Pr=0.71$ (partially ionized air [37, 38]) and Schmidt number $Sc=0.22$.

Fig. 2

Variation of primary velocity profile with m

Fig. 3

Variation of secondary velocity profile with m

Fig. 4

Variation of primary velocity profile with $K_2$

Fig. 5

Variation of secondary velocity profile with $K_2$

Effect of Hall current on velocity field is shown in Figs. 2 and 3. From the figures, it is evident that both primary velocity (U) and secondary velocity (W) profiles increase with the enhancement of Hall current parameter for ramped surface temperature as well as for isothermal plate. This signifies that Hall current enhances both primary and secondary fluid velocities inside the boundary layer region. Physically, for escalating values of m, the effective thermal conductivity is decelerated. As a result, the impact of the magnetic damping force on U and W is declined. Hence, both the velocity profiles are hiked. The behavior of velocity distribution with varying rotation parameter is depicted in Figs. 4 and 5. It is found that primary fluid velocity reduces. In contrast, the secondary velocity of the fluid enhances on uprising values of $K_2$ everywhere in the boundary layer for ramped surface temperature as well as for isothermal plate. This indicates that rotation has retarding influence over primary fluid velocity, whereas it has an accelerating influence over secondary fluid velocity within the boundary layer. It is known that rotation induces fluid velocity in the secondary flow direction by inhibiting the flow in the primary direction. Its accelerating impact is much more dominant in the region near the plate because the Coriolis force is more prevalent near the axis of rotation.

Fig. 6

Variation of primary velocity profile with Gr

Fig. 7

Variation of secondary velocity profile with Gr

Fig. 8

Variation of primary velocity profile with Gc

Fig. 9

Variation of secondary velocity profile with Gc

Figures 6, 7, 8, 9 demonstrate the impact of thermal and solutal buoyancy forces on flow-field. It is observed that an increase in either thermal or solutal Grashof number leads to an increase in both the primary and secondary velocity profiles within the boundary layer in case of ramped surface temperature as well as the isothermal plate. Gr signifies the relative strength of thermal buoyancy force to viscous force, while Gc signifies the relative strength of solutal buoyancy force to viscous force. The convective flow is induced due to thermal and solutal buoyancy forces. Therefore, for growing values of Gr and Gc, the strength of thermal and solutal buoyancy forces increase. As a result, an enhancement in both primary and secondary flow velocities occur in the boundary layer region. The effect of Soret number or thermo-diffusion parameter on velocity field is displayed in Figs.  10, 11. It is elucidated from the figures that both primary and secondary velocity profiles increase with the increase of Soret number for ramped surface temperature as well as for isothermal plate. The Soret number measures the effect of the temperature gradients inducing mass diffusion. It is seen that an increase in the Soret number increases the velocity profiles.

Fig. 10

Variation of primary velocity profile with Sr

Fig. 11

Variation of secondary velocity profile with Sr

Fig. 12

Variation of primary velocity profile with $\omega$

Fig. 13

Variation of secondary velocity profile with $\omega$

Fig. 14

Variation of primary velocity profile with t

Fig. 15

Variation of secondary velocity profile with t

The impact of frequency of oscillation of the plate is presented in Figs. 12, 13. From the figures, it is perceived that both primary and secondary velocity profiles decrease upon uprising the value of the frequency parameter. The effect of time on flow-field is shown in Figs. 14, 15. It is evident from the figures that as time progresses, both the primary and secondary velocity profiles increase for ramped surface temperature as well as isothermal plate within the boundary layer.

Table 1 Value of primary shear stress ($\tau _x$) for different physical parameters

The variation of shear stresses (primary and secondary shear stresses $\tau _x$ and $\tau _z$ respectively) at the plate with respect to the flow parameters has been analyzed with the help of analytical expressions (23)–(26) and the numerical results are displayed in tabular form as shown in Tables 1 and 2 for different values of m, $K_2$, Gr, Gc, Sr, $\omega$ and t taking $M=5$, $K_1=0.4$, $Kr=0.2$, $Q=3$, $R=2$, Pr = 0.71 and Sc = 0.22. It is noticed from Tables 1 and 2 that $\tau _x$ increases on increasing $K_2$, whereas it decreases on increasing m, Gr, Gc, Sr, $\omega$ and t for ramped surface temperature as well as for isothermal plate. This means that the rotation parameter tends to boost primary shear stress. In contrast, Hall current, thermal and solutal buoyancy forces, thermo-diffusion, oscillation frequency and time tend to reduce the primary shear stress for both ramped surface temperature and isothermal plate. The secondary shear stress increases on increasing m, $K_2$, Gc, Gr, Sr and t and decreases on increasing $\omega$ for ramped surface temperature as well as for isothermal plate. This means that Hall current, rotation, thermal and solutal buoyancy forces, thermo-diffusion and time tend to enhance secondary shear stress, whereas the frequency of oscillation tends to reduce secondary shear stress for ramped surface temperature as well as with isothermal plate.

Table 2 Value of secondary shear stress ($\tau _z$) for different physical parameters

3.2 Heat transfer analysis

Variations in fluid temperature $\theta$ obtained from the analytical expressions (18) and (21) are displayed in graphical form versus boundary layer coordinate y in Figs. 16, 17, 18 for different values of heat generation/absorption parameter Q, radiation parameter R and time t considering Prandtl number $Pr=0.71$.

Fig. 16

Variation of temperature profile with Q

Fig. 17

Variation of temperature profile with R

Fig. 18

Variation of temperature profile with t

Fig. 19

Variation of concentration profile with Kr

It is illustrated from Figs. 16, 17, 18 that, for both ramped surface temperature and isothermal plate, fluid temperature increases on increasing either Q or R or time t everywhere in the boundary layer. This implies that, for both ramped surface temperature and isothermal plate, fluid temperature is enhanced with the enhancement of heat generation or radiation or time within the boundary layer region. Physically, additional heat is generated for rising values of Q in the boundary layer and therefore, fluid temperature is enhanced. For escalating values of R, thermal radiation provides an additional means to diffuse energy in the boundary layer and due to this fluid temperature is highlighted.

Table 3 Value of Nusselt number (Nu) for different physical parameters

The exact values of Nusselt number at the plate, obtained from Eqs. (24) and (27), are presented in tabular form and shown in Table 3 for different values of Q, R and t considering Pr = 0.71. Table 3 depicts that, for both ramped surface temperature and isothermal plate, Nu decreases with increasing Q and R. On uprising values of t, Nu is reduced for the isothermal plate, whereas it is enhanced for ramped surface temperature. This indicates that heat generation and thermal radiation tend to lower the Nusselt number for both ramped surface temperature and isothermal plate. For ramped surface temperature, the heat transfer rate at the plate is enhanced, whereas it is decreased with the progress of time for the isothermal plate.

3.3 Mass transfer analysis

The exact values of species concentration $\phi$, calculated by solving Eqs. (19) and (22) analytically, are displayed graphically in Figs. 19, 20, 21 for distinct values of chemical reaction parameter Kr, Soret number Sr and time t considering $Q=3$, $R=2$, Pr = 0.71 and Sc = 0.22.

It is perceived from Figs. 19, 20, 21 that, for both ramped surface temperature and isothermal plate, species concentration reduces on uprising values of Kr, whereas Sr and t have accelerating effects on species concentration everywhere in the boundary layer region. Thus, for both ramped surface temperature and isothermal plate, the chemical reaction has the tendency to lower species concentration while the opposite result is seen for mass diffusion. However, there is an enhancement in the species concentration with the increase of Soret number and time within the boundary layer region. Since the destructive chemical reaction rate is enhanced for uprising values of Kr, the concentration profile is declined. An observation toward Figs. 16, 17, 18, 19, 20, 21 leads that fluid temperature and species concentration both are maximum at the plate surface and after that decreases properly with respect to the y to reach the free stream temperature and concentration.

Fig. 20

Variation of concentration profile with Sr

Fig. 21

Variation of concentration profile with t

The numerical values of Sherwood number Sh at the surface have been calculated from the expressions (25) and (28) and are presented in tabular form as shown in Table 4 for different values of Kr, Sr and t. It is revealed from Table 4 that Sherwood number increases on increasing Kr and it decreases on increasing Sr for ramped surface temperature as well as for isothermal plate. On the other hand, with the progress of time t, the Sherwood number increases for the ramped surface temperature, whereas the opposite result is observed for the isothermal plate. This indicates that chemical reaction has the tendency to enhance the rate of mass transfer at the surface. In contrast, thermo-diffusion has an opposite behavior for ramped surface temperature as well as for isothermal plate. For ramped surface temperature, the rate of mass transfer at the surface is increased, whereas for the isothermal plate, the rate of mass transfer at the surface is decreased with the progress of time.

Table 4 Value of Sherwood number (Sh) for different physical parameters

4 Conclusions

The most important concluding remarks of the present problem are summarized below :

• Primary fluid velocity increases with the increase of m, Gr, Gc, Sr and t, whereas there is a reverse impact on it for $K_2$ and $\omega$.

• Secondary fluid velocity increases with the increase of m, Gr, Gc, Sr, $K_2$ and t, whereas opposite behavior is observed for $\omega$.

• Fluid temperature is enhanced with the enhancement of Q, R and t.

• Sr and t tend to enhance species concentration, whereas Kr has a reverse effect on it.

• An increase in m, Gr, Gc, $\omega$ and t lead to reduce primary skin friction and $K_2$ has an opposite impact on it for ramped surface temperature as well as for isothermal plate.

• Secondary skin friction enhances on uprising values of m, $K_2$, Gr, Gc, Sr and t, whereas opposite trend is observed for $\omega$.

• For both ramped surface temperature and isothermal plate, Nusselt number decreases with the increase of Q and R. However, for ramped surface temperature, the Nusselt number increases and for the isothermal plate, it decreases with the increase of t.

• For both ramped surface temperature and isothermal plate, the Sherwood number increases with an increase of Sr and Kr. However, the Sherwood number increases for ramped surface temperature, while for the isothermal plate, it decreases with the progress of t.

Appendix A

$b_1=\dfrac{b}{d}-\dfrac{a}{c}$,   $b_2=\dfrac{a}{c}$,   $b_3=\dfrac{b}{c}$,   $b_4=\dfrac{ad}{c^2}-\dfrac{b}{c}$,   $b_5=\dfrac{dr_4}{c}-r_3$,   $b_6=\dfrac{gr_4}{j}-\dfrac{dr_4}{c}-\dfrac{Gr}{j}$,   $b_7=r_3+\dfrac{Gr}{j}-\dfrac{gr_4}{j}$,   $b_8=r_1-\dfrac{dr_2}{c}$,   $b_9=r_1-\dfrac{Gc}{q}-\dfrac{nr_2}{q}$,   $b_{10}=b_5+b_8$,   $b_{11}=\dfrac{dr_2}{c}-\dfrac{Gc}{q}-\dfrac{nr_2}{q}$,   $b_{12}=\dfrac{1}{2}$,   $b_{13}=b_6+b_{11}$,   $b_{14}=\dfrac{gr_3}{j}-\dfrac{dr_3}{c}$,   $b_{15}=\dfrac{dr_3}{c}-\dfrac{d^2r_4}{c^2}$,   $b_{16}=\dfrac{dr_4}{c}$,   $b_{17}=\dfrac{g^2r_4}{j^2}-\dfrac{gr_3}{j}-\dfrac{gGr}{j^2}$,   $b_{18}=\dfrac{Gr}{j}-\dfrac{gr_4}{j}$,   $b_{19}=\dfrac{dr_1}{c}-\dfrac{nr_1}{q}$,   $b_{20}=\dfrac{d^2r_2}{c^2}-\dfrac{dr_1}{c}$,   $b_{21}=b_{15}+b_{20}$,   $b_{22}=\dfrac{dr_2}{c}-\dfrac{dr_4}{c}$,   $b_{23}=\dfrac{nGc}{q^2}+\dfrac{n^2r_2}{q^2}-\dfrac{nr_1}{q}$,   $b_{24}=\dfrac{Gc}{q}+\dfrac{nr_2}{q}$,   $b_{25}=b_{14}+b_{19}$,   $r_1=\dfrac{bGc}{dq-cn}$,   $r_2=\dfrac{aGc}{dq-cn}$,   $r_3=\dfrac{bGc}{dj-cg}$,   $r_4=\dfrac{aGc}{dj-cg}$,

$$\begin{aligned}&f_1(a_1,a_2,a_3,a_4)=\left( a_1+\frac{a_2a_3}{2\sqrt{a_4}}\right) e^{a_3\sqrt{a_4}}\text {erfc}\left( \frac{a_3\sqrt{a_2}}{2\sqrt{a_1}} +\frac{\sqrt{a_4a_1}}{\sqrt{a_2}}\right) \nonumber \\&\quad +\left( a_1-\frac{a_2a_3}{2\sqrt{a_4}}\right) e^{-a_3\sqrt{a_4}} \text {erfc}\left( \frac{a_3\sqrt{a_2}}{2\sqrt{a_1}} -\frac{\sqrt{a_4a_1}}{\sqrt{a_2}}\right) , \\&f_2(a_1,a_2,a_3,a_4,a_5,a_6)=\frac{a_1^2}{2a_2^2} \left[ e^{-\frac{a_2a_3}{a_1}}\left\{ e^{a_4\sqrt{a_5\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) }} \text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}} +\sqrt{\left( \frac{a_6}{a_5} -\frac{a_2}{a_1}\right) a_3}\right) \right. \right. \\&\quad +\left. \left. e^{-a_4\sqrt{a_5\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) }}\text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}-\sqrt{\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) a_3}\right) \right\} \right. \\&\quad +\left. \frac{a_2}{a_1}\left\{ e^{a_4\sqrt{a_6}}\text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}+\frac{\sqrt{a_6a_3}}{\sqrt{a_5}}\right) \left( a_3-\frac{a_1}{a_2}+\frac{a_4a_5}{2\sqrt{a_6}}\right) \right. \right. \\&\quad +\left. \left. e^{-a_4\sqrt{a_6}}\text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}-\frac{\sqrt{a_6a_3}}{\sqrt{a_5}}\right) \left( a_3-\frac{a_1}{a_2} -\frac{a_4a_5}{2\sqrt{a_6}}\right) \right\} \right] \\&f_3(a_1,a_2,a_3,a_4,a_5,a_6)=\frac{a_1}{2a_2} \left[ e^{-\frac{a_2a_3}{a_1}}\left\{ e^{a_4\sqrt{a_5\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) }} \text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}} +\sqrt{\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) a_3}\right) \right. \right. \\&\quad +\left. \left. e^{-a_4\sqrt{a_5\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) }}\text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}-\sqrt{\left( \frac{a_6}{a_5}-\frac{a_2}{a_1}\right) a_3}\right) \right\} .\right. \\&\quad -\left. \left\{ e^{a_4\sqrt{a_6}}\text {erfc} \left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}} +\frac{\sqrt{a_6a_3}}{\sqrt{a_5}}\right) \left( a_3-\frac{a_1}{a_2} +\frac{a_4a_5}{2\sqrt{a_6}}\right) \right. \right. \\&\quad +\left. \left. e^{-a_4\sqrt{a_6}}\text {erfc} \left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}} -\frac{\sqrt{a_6a_3}}{\sqrt{a_5}}\right) \left( a_3-\frac{a_1}{a_2} -\frac{a_4a_5}{2\sqrt{a_6}}\right) \right\} \right] \\&f_4(a_1,a_2,a_3,a_4,a_5,a_6)=\frac{1}{2}\left[ e^\frac{-a_1a_3}{a_2}\left\{ e^{a_4\sqrt{a_5\left( \frac{a_6}{a_5}-\frac{a_1}{a_2}\right) }} \text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}+\sqrt{\left( \frac{a_6}{a_5}-\frac{a_1}{a_2}\right) a_3}\right) \right. \right. \\&\quad +\left. \left. e^{-a_4\sqrt{a_5\left( \frac{a_6}{a_5} -\frac{a_1}{a_2}\right) }}\text {erfc}\left( \frac{a_4\sqrt{a_5}}{2\sqrt{a_3}}-\sqrt{\left( \frac{a_6}{a_5}-\frac{a_1}{a_2}\right) a_3}\right) \right\} \right] \\&f_5(a_1,a_2,a_3,a_4,a_5)=\frac{e^{-\frac{a_3a_5}{a_4}}}{2}\left[ \frac{2\sqrt{a_2}e^{-\left( \frac{a_1}{a_2}-\frac{a_3}{a_4}\right) a_5}}{\sqrt{\pi a_5}}+\sqrt{\left( a_1-\frac{a_2a_3}{a_4}\right) }\right. \\&\quad \times \left. \text {erfc}\left\{ -\sqrt{\left( \frac{a_1}{a_2}-\frac{a_3}{a_4}\right) a_5}\right\} -\sqrt{\left( a_1-\frac{a_2a_3}{a_4}\right) }\right. \\&\quad \times \left. \text {erfc}\left\{ \sqrt{\left( \frac{a_1}{a_2} -\frac{a_3}{a_4}\right) a_5}\right\} \right] \\&f_6(a_1,a_2,a_3,a_4,a_5)= \frac{1}{2}\left[ -\frac{2\sqrt{a_2}e^{-\frac{a_1a_5}{a_2}}\left( a_5-\frac{a_3}{a_4}\right) }{\sqrt{\pi a_5}}-\frac{a_2}{2\sqrt{a_1}}\text {erfc}\left( -\frac{\sqrt{a_1a_5}}{\sqrt{a_2}}\right) \right. \\&\quad -\left. \sqrt{a_1}\left( a_5-\frac{a_3}{a_4}\right) \text {erfc} \left( -\frac{\sqrt{a_1a_5}}{\sqrt{a_2}}\right) \right. \\&\quad +\left. \frac{a_2}{2\sqrt{a_1}}\text {erfc} \left( \frac{\sqrt{a_1a_5}}{\sqrt{a_2}}\right) +\sqrt{a_1} \left( a_5-\frac{a_3}{a_4}\right) \text {erfc} \left( \frac{\sqrt{a_1a_5}}{\sqrt{a_2}}\right) \right] \end{aligned}$$