A Computational Study of Local Fractional Helmholtz and Coupled Helmholtz Equations in Fractal Media

Abstract

In this manuscript, an approximate analytical solution of the Helmholtz and coupled Helmholtz equations of fractional order is obtained using local fractional Sumudu decomposition method (LFSDM). The Helmholtz equations play an important role in the study of various physical problems such as seismology, tsunamis, optics, acoustics, medical imaging, electrostatics and quantum mechanics. To validate the efficiency and reliability of the employed scheme, the Helmholtz and coupled Helmholtz equations are considered. The results obtained with this scheme are in a good agreement with previous works. Moreover, the graphical presentations for obtained solutions are also illustrated for distinct values of order of a partial derivative.

1 Introduction

In last decades, fractional calculus has been applied very frequently in the field of applied sciences and technology. Actually, the area of fractional calculus is concerned with integral and derivatives of real order and it significantly handles scientific and engineering problems by formulating them in the form of fractional differential equations such as the diffusion equations [1], the gas dynamic equation [2], telegraph equation [3], wave equation [4,5,6,7], Fokker-Planck equation [8, 9], Laplace equation [10], Klein-Gordon equations [11], Helmholtz equation [12], and Burger’s equations [13].

Various local fractional schemes have been used to solve the local fractional PDEs (LFPDEs) such as the local fractional decomposition method [13,14,15], local fractional variational iteration method [16,17,18,19,20,21,22], local fractional differential transform method [23, 24], local fractional series expansion method [25, 26], local fractional Sumudu decomposition method [27], local fractional reduce differential transform method [28], local fractional Laplace variational iteration method [29], local fractional Laplace decomposition method [30], and local fractional Laplace homotopy perturbation method [31, 32]. This paper presents the copulation of LFST and LFADM, which is called as LFSDM, to solve the local fractional Helmholtz and coupled Helmholtz equations.

The paper is arranged in the following way: The basic definitions for calculus and fractional integration are presented in Sect. 2, the method used are analyzed in Sect. 3, illustrative examples are given that explain the effectiveness of the method proposed in Sect. 4, the numerical results and discussion are described in the Sect. 5 and finally, the conclusion is provided in Sect. 6.

2 Mathematical Fundamentals

Definition 2.1.

The LF derivative of $\varphi \left( \mu \right)$ of order $\varepsilon$ at $\mu_{0}$ is [14,15,16]:

$$ \varphi^{\left( \varepsilon \right)} \left( {\mu_{0} } \right) = \mathop {\lim }\limits_{{\mu \to \mu_{0} }} \frac{{{\Gamma }\left( {1 + \varepsilon } \right)\left[ {\varphi \left( \mu \right) - \varphi \left( {\mu_{0} } \right)} \right]}}{{\left( {\mu - \mu_{0} } \right)^{\varepsilon } }}, \quad \,0 < \varepsilon \le 1 $$

(1)

Definition 2.2.

The Mittage-Leffler function is defined by [14]:

$$ E_{\varepsilon } \left( {\mu^{\varepsilon } } \right) = \sum\limits_{k = 0}^{\infty } {\frac{{\mu^{k\varepsilon } }}{{{\Gamma }\left( {1 + k\varepsilon } \right)}}} , \;\; \mu \in R, \quad \;0 < \varepsilon \le 1 $$

(2)

Definition 2.3.

The LFST of $\varphi \left( \mu \right)$ given by [26]

$$ ST_{\varepsilon } \left\{ {\varphi \left( \mu \right)} \right\} = \frac{1}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\int\limits_{0}^{\infty } {E_{\varepsilon } \left( { - w^{\varepsilon } \mu^{\varepsilon } } \right)\frac{\varphi \left( \mu \right)}{{w^{\varepsilon } }}\left( {d\mu } \right)^{\varepsilon } } . $$

(3)

Following (4), its inverse formula is defined by

$$ ST_{\varepsilon }^{ - 1} \left( {ST_{\varepsilon } \left\{ {\varphi \left( \mu \right)} \right\}} \right) = \varphi \left( \mu \right),\;\;\, 0 < \varepsilon \le 1. $$

(4)

The properties for LFST are:

• 1. $ST_{\varepsilon } \left\{ {\frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}} \right\} = w^{\varepsilon } .$

• 2. $ST_{\varepsilon } \left\{ {\frac{{\partial^{m\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \mu^{m\varepsilon } }}} \right\} = \frac{1}{{w^{m\varepsilon } }}\left[ {ST_{\varepsilon } \left\{ {\varphi \left( {\mu ,\tau } \right)} \right\} - \sum\nolimits_{k = 0}^{m - 1} {w^{k\varepsilon } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }}} } \right].$

3 Analysis of LFSDM

Let us consider the PDE with LFDOs:

$$ L_{\varepsilon } \varphi \left( {\mu ,\tau } \right) + R_{\varepsilon } \varphi \left( {\mu ,\tau } \right) = g\left( {\mu ,\tau } \right), \quad \quad \;\, 0 < \varepsilon \le 1 $$

(5)

where $L_{\varepsilon } \varphi \left( {\mu ,\tau } \right) = \frac{{\partial^{m\varepsilon } }}{{\partial \mu^{m\varepsilon } }}\varphi \left( {\mu ,\tau } \right)$, $R_{\varepsilon }$ denotes linear LFDO, and $g\left( {\mu ,\tau } \right)$ is the non-differentiable source term.

Applying the LFST on Eq. (5), and using the property of the LFST, we get

$$ ST_{\varepsilon } \left\{ {\varphi \left( {\mu ,\tau } \right)} \right\} = \sum\limits_{k = 0}^{m - 1} {w^{k\varepsilon } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }} + } w^{m\varepsilon } ST_{\varepsilon } \left\{ {g\left( {\mu ,\tau } \right)} \right\} - w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \varphi \left( {\mu ,\tau } \right)} \right\}. $$

(6)

Taking the inverse of LFST on Eq. (6), we have

$$ \begin{aligned} \varphi \left( {\mu ,\tau } \right) & = \sum\limits_{k = 0}^{m - 1} {w^{k\varepsilon } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }}\frac{{\mu^{k\varepsilon } }}{{{\Gamma }\left( {1 + k\varepsilon } \right)}}} + ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {g\left( {\mu ,\tau } \right)} \right\}} \right] \\ & \;\, - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \varphi \left( {\mu ,\tau } \right)} \right\}} \right]. \\ \end{aligned} $$

(7)

Now, procedure of ADM suggests the decomposition of the unknown function $\varphi \left( {\mu ,\tau } \right)$ as an infinite series in the following way

$$ \varphi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right). $$

(8)

By making use of the Eq. (8) in Eq. (7), it yields the following result:

$$ \begin{aligned} \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) & = \sum\limits_{k = 0}^{m - 1} {w^{k\varepsilon } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }}} \frac{{\mu^{k\varepsilon } }}{{{\Gamma }\left( {1 + k\varepsilon } \right)}} + ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {g\left( {\mu ,\tau } \right)} \right\}} \right] \\ & - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right)} \right\}} \right]. \\ \end{aligned} $$

(9)

Matching both sides of (9) provides

$$ \begin{aligned} & \varphi_{0} \left( {\mu ,\tau } \right) = \sum\limits_{k = 0}^{m - 1} {w^{k\varepsilon } } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }}\frac{{\mu^{k\varepsilon } }}{{{\Gamma }\left( {1 + k\varepsilon } \right)}} + ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {g\left( {\mu ,\tau } \right)} \right\}} \right] \\ & \varphi_{1} \left( {\mu ,\tau } \right) = - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \left[ { \varphi_{0} \left( {\mu ,\tau } \right)} \right]} \right\}} \right], \\ & \varphi_{2} \left( {\mu ,\tau } \right) = - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \left[ { \varphi_{1} \left( {\mu ,\tau } \right)} \right]} \right\}} \right], \\ & \varphi_{3} \left( {\mu ,\tau } \right) = - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \left[ { \varphi_{2} \left( {\mu ,\tau } \right)} \right]} \right\}} \right], \\ & \quad \quad \quad \;\; \vdots \\ \end{aligned} $$

(10)

The general form of above obtained local fractional recursive relations is

$$ \begin{array}{*{20}l} {\varphi_{0} \left( {\mu ,\tau } \right) = \sum\limits_{k = 0}^{m - 1} {w^{k\varepsilon } } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \tau^{k\varepsilon } }}\frac{{\mu^{k\varepsilon } }}{{{\Gamma }\left( {1 + k\varepsilon } \right)}} + ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {g\left( {\mu ,\tau } \right)} \right\}} \right], } \hfill \\ {\varphi_{n} \left( {\mu ,\tau } \right) = - ST_{\varepsilon }^{ - 1} \left[ {w^{m\varepsilon } ST_{\varepsilon } \left\{ {R_{\varepsilon } \left[ { \varphi_{n - 1} \left( {\mu ,\tau } \right)} \right]} \right\}} \right], \quad \; n \ge 1, 0 < \varepsilon \le 1 } \hfill \\ \end{array} $$

(11)

4 Application of LFSDM

Example 4.1.

Consider the Helmholtz equation with LFDO:

$$ \frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \mu^{2\varepsilon } }} + \frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }} + \varphi \left( {\mu ,\tau } \right) = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} , $$

(12)

with

$$ \varphi \left( {0,\tau } \right) = 0, \quad \, \varphi^{\left( \varepsilon \right)} \left( {0,\tau } \right) = \frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}. $$

(13)

Taking LFST of (12), we get

$$ \begin{aligned} ST_{\varepsilon } & \left\{ {\varphi \left( {\mu ,\tau } \right)} \right\} = \sum\limits_{k = 0}^{1} {w^{k\varepsilon } } \frac{{\partial^{k\varepsilon } \varphi \left( {0,\tau } \right)}}{{\partial \mu^{k\varepsilon } }} + w^{2\varepsilon } ST_{\varepsilon } \left\{ {\frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}} \right\} \\ & \quad \quad \quad \quad - w^{2\varepsilon } ST_{\varepsilon } \left\{ {\frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }} + \varphi \left( {\mu ,\tau } \right)} \right\} \\ & = w^{\varepsilon } \frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} + w^{3\varepsilon } \frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} - w^{2\varepsilon } ST_{\varepsilon } \left\{ {\frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }} + \varphi \left( {\mu ,\tau } \right)} \right\}. \\ \end{aligned} $$

The inversion of LFST implies that

$$ \begin{aligned} \varphi \left( {\mu ,\tau } \right) & = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} + \frac{{\mu^{3\varepsilon } }}{{{\Gamma }\left( {1 + 3\varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} \\ & \quad - ST_{\varepsilon }^{ - 1} \left[ {w^{2\varepsilon } ST_{\varepsilon } \left\{ {\frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }} + \varphi \left( {\mu ,\tau } \right)} \right\}} \right]. \\ \end{aligned} $$

(14)

Now, procedure of ADM suggests the decomposition of the unknown function $\varphi \left( {\mu ,\tau } \right)$ as an infinite series in the following way

$$ \varphi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right). $$

(15)

Substituting (15) in (14), it yields the following result:

$$ \begin{aligned} \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) & = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} + \frac{{\mu^{3\varepsilon } }}{{{\Gamma }\left( {1 + 3\varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}} \\ & \;\; - ST_{\varepsilon }^{ - 1} \left[ {w^{2\varepsilon } ST_{\varepsilon } \left\{ {\frac{{\partial^{2\varepsilon } }}{{\partial \tau^{2\varepsilon } }}\sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) + \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right)} \right\}} \right]. \\ \end{aligned} $$

(16)

On comparing both sides of (16), we have:

Therefore, the approximate solution $\varphi \left( {\mu ,\tau } \right)$ of Eq. (12) is expressed by

$$ \varphi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}\frac{{\tau^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}. $$

(17)

The result is the same as the one which is obtained by the LFLADM [12] and LFLHPM [31].

Example 4.2.

Now we examine the coupled Helmholtz equations with LFDOs:

$$ \begin{aligned} & \frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \mu^{2\varepsilon } }} + \frac{{\partial^{2\varepsilon } \psi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }} - \varphi \left( {\mu ,\tau } \right) = 0, \\ & \frac{{\partial^{2\delta } \psi \left( {\mu ,\tau } \right)}}{{\partial \mu^{2\delta } }} + \frac{{\partial^{2\delta } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\delta } }} - \psi \left( {\mu ,\tau } \right) = 0, \\ \end{aligned} $$

(18)

with

$$ \begin{aligned} & \varphi \left( {0,\tau } \right) = 0, \,\varphi^{\left( \varepsilon \right)} \left( {0,\tau } \right) = E_{\varepsilon } \left( {\tau^{\varepsilon } } \right), \\ & \psi \left( {0,\tau } \right) = 0, i\psi^{\left( \varepsilon \right)} \left( {0,\tau } \right) = E_{\varepsilon } \left( {\tau^{\varepsilon } } \right). \\ \end{aligned} $$

(19)

Taking LFLT of (18), we obtain

$$ \begin{aligned} & ST_{\varepsilon } \left\{ {\varphi \left( {\mu ,\tau } \right)} \right\} = w^{\varepsilon } E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) + w^{2\varepsilon } ST_{\varepsilon } \left\{ {\varphi \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } \psi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }}} \right\}, \\ & ST_{\varepsilon } \left\{ {\varPsi \left( {\mu ,\tau } \right)} \right\} = - w^{\varepsilon } E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) + w^{2\varepsilon } ST_{\varepsilon } \left\{ {\psi \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }}} \right\}, \\ \end{aligned} $$

(20)

The inversion of LFST implies that

$$ \begin{aligned} & \varphi \left( {\mu ,\tau } \right) = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) + ST_{\varepsilon }^{ - 1} \left[ {w^{2\varepsilon } ST_{\varepsilon } \left\{ {\varphi \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } \psi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }}} \right\}} \right], \\ & \psi \left( {\mu ,\tau } \right) = - \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) + ST_{\varepsilon }^{ - 1} \left[ {w^{2\varepsilon } ST_{\varepsilon } \left\{ {\psi \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } \varphi \left( {\mu ,\tau } \right)}}{{\partial \tau^{2\varepsilon } }}} \right\}} \right]. \\ \end{aligned} $$

(21)

Now, we compose the unknown functions $\varphi \left( {\mu ,\tau } \right)$ and $\psi \left( {\mu ,\tau } \right)$ in the form of infinite series as

$$ \begin{aligned} & \varphi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right), \\ & \psi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\psi_{n} } \left( {\mu ,\tau } \right). \\ \end{aligned} $$

(22)

On making use of (22) in (21), it yields the following result:

$$ \begin{aligned} & \quad \quad \;\sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) = \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) \\ & + ST_{\varepsilon }^{ - 1} \left[ {w^{2\delta } ST_{\varepsilon } \left\{ {\sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } }}{{\partial \tau^{2\varepsilon } }}\left( {\sum\limits_{n = 0}^{\infty } {\psi_{n} } \left( {\mu ,\tau } \right)} \right)} \right\}} \right], \\ & \quad \quad \;\sum\limits_{n = 0}^{\infty } {\psi_{n} } \left( {\mu ,\tau } \right) = - \frac{{\mu^{\varepsilon } }}{{{\Gamma }\left( {1 + \varepsilon } \right)}}E_{\varepsilon } \left( {\tau^{\varepsilon } } \right) \\ & + ST_{\varepsilon }^{ - 1} \left[ {w^{2\varepsilon } LT_{\varepsilon } \left\{ {\sum\limits_{n = 0}^{\infty } {\psi_{n} } \left( {\mu ,\tau } \right) - \frac{{\partial^{2\varepsilon } }}{{\partial \tau^{2\varepsilon } }}\left( {\sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right)} \right)} \right\}} \right]. \\ \end{aligned} $$

(23)

Now, comparison of both sides of (23) yields

Hence, the solutions are expressed as

$$ \begin{aligned} & \varphi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\varphi_{n} } \left( {\mu ,\tau } \right) = E_{\varepsilon } \left( {\tau^{\varepsilon } } \right)\frac{{sinh_{\varepsilon } \left( {\sqrt 2 \mu^{\varepsilon } } \right)}}{\sqrt 2 }. \\ & \psi \left( {\mu ,\tau } \right) = \sum\limits_{n = 0}^{\infty } {\psi_{n} } \left( {\mu ,\tau } \right) = - E_{\varepsilon } \left( {\tau^{\varepsilon } } \right)\frac{{sinh_{\varepsilon } \left( {\sqrt 2 \mu^{\varepsilon } } \right)}}{\sqrt 2 }. \\ \end{aligned} $$

(24)

The result (24) is the same as the one which is obtained by the LFADM [12] and LFHPM [31].

5 Numerical Results and Discussion

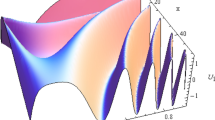
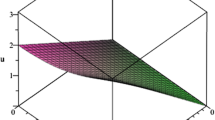
In this segment, the numerical simulations for solution of Helmholtz and coupled Helmholtz equations obtained via LFSDM are presented. The numerical investigation of Helmholtz and coupled Helmholtz equations considers different values of $\varepsilon = 1,\,\,\frac{\log 2}{{\log 3}}$. Here, the Matlab software is utilized to draw all the 3D plots. Figures 1 & 2 show the 3D surface plot for solution $\varphi (\mu ,\tau )$ for Example 1 for $\varepsilon = 1.0$ and $\varepsilon = \,\frac{\log 2}{{\log 3}}$, respectively. Figure 2 represents the variation of $\varphi (\mu ,\tau )$ in fractal dimension. Similarly, the 3D surface plots for solution $\varphi (\mu ,\tau )$ for Example 2 are depicted in Figs. 3 and 4 for $\varepsilon = 1.0$ and $\varepsilon = \,\frac{\log 2}{{\log 3}}$, respectively. Figures 5 & 6 represent the 3D variation for solution $\psi \left( {\mu ,\,\tau } \right)$ for Example 2 for $\varepsilon = 1,\,\,\frac{\log 2}{{\log 3}}$, respectively. Figure 6 represents the variation of $\varphi (\mu ,\tau )$ on Cantor set.

Fig. 1.

3D behaviour of $\varphi (\mu ,\tau )$ for Example 1 w.r.t. $\mu$ and $\tau$ for $\varepsilon = 1.0$

Fig. 2.

3D behaviour of $\varphi (\mu ,\tau )$ for Example 1 w.r.t. $\mu$ and $\tau$ for $\varepsilon = \frac{\log 2}{{\log 3}}$

Fig. 3.

3D variation of $\varphi (\mu ,\tau )$ for Example 2 w.r.t. $\mu$ and $\tau$ for $\varepsilon = 1.0$

Fig. 4.

3D variation of $\varphi (\mu ,\tau )$ for Example 2 w.r.t. $\mu$ and $\tau$ for $\varepsilon = \frac{\log 2}{{\log 3}}$

Fig. 5.

3D behaviour of $\psi \left( {\mu ,\,\tau } \right)$ for Example 2 w.r.t. $\mu$ and $\tau$ for $\varepsilon = 1.0$

Fig. 6.

3D behaviour of $\psi \left( {\mu ,\,\tau } \right)$ for Example 2 w.r.t. $\mu$ and $\tau$ for $\varepsilon = \frac{\log 2}{{\log 3}}$

6 Conclusions

In this work, the LFSDM is conveniently employed to obtain the approximate solution of Helmholtz and coupled Helmholtz equations within LFDOs. The proposed algorithm provides a solution in a series form that converges rapidly to an exact solution if it exists. From the obtained results, it is clear that the FSDM yields very accurate solutions using only a few iterates. The method is very powerful and efficient in finding semi-analytical solutions for wide classes of LFPDEs.