1 Introduction

The physical processes in many branches of engineering and nonlinear research, such as fibre optics, nonlinear plasma, geophysics, fuzzy mechanics, thermodynamics, laser physics, and so forth, are described by the nonlinear wave models (Iqbal et al. 2019; Islam et al. 2023; Seadawy et al. 2019; Islam et al. 2023; Akbar et al. 2023). Many scientists have investigated novel models in recent decades to explain fundamental physical meanings of real-world challenges (Seadawy and Iqbal 2021; Iqbal et al. 2022; Seadawy et al. 2021; Iqbal et al. 2023). In the contemporary scientific and technological period, numerous researchers are working to develop a variety of analytical techniques to precisely solve nonlinear wave models (Seadawy et al. 2022; Zahed et al. 2022; Uddin et al. 2021; Iqbal et al. 2022; Uddin et al. 2022). Fractional calculus is now a fundamental ingredient of many important applications in new physics and applied science. Particularly, the nonlinear fractional partial differential equations (NFPDEs) are capable of modeling a wide range of physical processes in applied science, such as chemical engineering, quantum mechanics, nonlinearity optical communications, solid-state physics, plasma physics and many others (Abdelrahman et al. 2021; Akter et al. 2023; Uddin et al. 2022, 2021). These equations play important roles in describing the underlying mechanics of numerous scientific phenomena. Furthermore, mathematical models containing a fractional order derivative provide a good representation of the features of the behavior of nonlinear systems in a variety of scientific and engineering fields (Abdelrahman and AlKhidhr 2020; Sarwar and Iqbal 2018; Foukrach 2018). In this sense, fractional order models perform better than integer order ones. In light of this, several approaches are put forth and created to solve various sorts of NFPDEs (Younis and Rizvi 2015; Hosseini et al. 2017; Khodadad et al. 2017; Iqbal et al. 2018, 2020).

An intriguing conformable fractional derivative was introduced by Khalil et al. (2014). This definition has received a lot of attention because of its simplicity and efficiency As a result, numerous powerful studies have been produced using this new definition (Rezazadeh et al. 2018; Zeliha 2019; Abdelwahed et al. 2022; Abdelrahman et al. 2022). The following is a description of fractional differentiation and some of its properties (Khalil et al. 2014):

Definition 1.1

(Khalil et al. 2014) Let \(\mathfrak {G}: (0, \infty ) \rightarrow {\mathbb {R}}\) be a function, then the \(\alpha\) order of the conformable derivative of \(\mathfrak {G}\) is

$$\begin{aligned} D_{t}^{\alpha }(\mathfrak {G}(t))=\lim \limits _{\varsigma \rightarrow 0} \frac{\mathfrak {G}(t+\varsigma t^{1-\alpha })-\mathfrak {G}(t)}{\varsigma }, \,\,\,t>0,\,\,1 \ge \alpha >0. \end{aligned}$$

This definition satisfies:

  1. (i)

    \(D_{t}^{\alpha }(C_{1}\,\mathfrak {G} +C_{2}\,\mathfrak {H})=C_{1} D_{t}^{\delta }(\mathfrak {G})+C_{2} D_{t}^{\alpha }(\mathfrak {H}), \,\,C_{1}; C_{2} \in {\mathbb {R}}\),

  2. (ii)

    \(D_{t}^{\alpha }(t^{\iota })=\iota t^{\iota -\alpha }, \,\,\iota \in {\mathbb {R}},\)

  3. (iii)

    \(D_{t}^{\alpha }(\mathfrak {G}\,\mathfrak {H}) =\mathfrak {H}\,D_{t}^{\alpha }(\mathfrak {G})+\mathfrak {G} \,D_{t}^{\delta }(\mathfrak {H}),\)

  4. (iv)

    \(D_{t}^{\alpha }(\frac{\mathfrak {G}}{\mathfrak {H}}) =\frac{\mathfrak {H}\,D_{t}^{\alpha }(\mathfrak {G}) -\mathfrak {G}\,D_{t}^{\alpha }(\mathfrak {H})}{\mathfrak {H}^2}.\)

Referring to Khalil et al. (2014) for further information regarding the benefits and characteristics of conformable fractional definition.

Since the behaviour of real-world applications is influenced by their past states, NFPDEs are recommended for understanding and analyzing real-world systems. Recently, the study of nonlinear Schrödinger equation even of integer or fractional order is quite fascinating (Seadawy et al. 2020; Islam et al. 2022, 2022, 2022; Yokuş et al. 2022; Hafez et al. 2019; Uddin and Hafez 2022). The fractional nonlinear Schrödinger equation (NLSE) is so crucial in fractional quantum mechanics (Laskin 2002, 2000a, b). Three NLSE models were proposed by Darvishi et al. (2018) as space-time fractional types, and he subsequently introduced optical soliton solutions for these models using the sine-cosine technique. Darvishi and Najaf (2020) then used the semi-inverse variational principle to provide some additional soliton solutions for these three models. Through this study we investigate the following space-time fractional NLSE (Darvishi et al. 2018):

$$\begin{aligned} i\, D_{t}^{\alpha }u+D_{x}^{2\gamma }u+2\delta \mid u\mid ^2 \,u=0\,,\,\,\,\, 1 \ge \alpha , \gamma > 0, \end{aligned}$$
(1.1)

\(\delta \in {\mathbb {R}}-\{0\}\), u(x, t) is a complex valued function.

In Abdelrahman and AlKhidhr (2020), we developed a robust solver technique based on the Jacobian elliptic function method (Dai and Zhang 2006; Wanga et al. 2005) to solve NFPDE. This approach explicitly provides the unified structure of solitary waves of various types of NFPDEs. It is also uncomplicated, reliable and effective. In this study, we employed this technique in order to generate some new solitary waves for Eq. (1.1). Namely, we produce in the form of hyperbolic, shocks, soliton, explosive form, superperiodic, and trigonometric structures. These waves are critical in describing vital complicated processes in fractional quantum mechanics (Laskin 2002, 2000a, b) and optical fiber communications (Abdelwahed et al. 2021; Abdelrahman et al. 2021). To the best of our knowledge, no previous scientific work has been done using this technique.

The remaining components of this study are as follows. Sect. 2 describes the unified solver. Sect. 3 provides new solitary waves to the space-time fractional NLSE (1.1). The physical investigation of the acquired results is described in Sect. 4. Section 5 introduces the effect of the fraction parameters on the obtained solutions properties. Finally, Sect. 6 provides a concluding remark on the obtained results.

2 Description of the method

Here, we provide a succinct overview of the unified solver. Consider the following NFPDEs:

$$\begin{aligned} F(u,D^{\alpha }_{t}u,D^{\gamma }_{x}u,D^{\alpha }_{t}D^{\gamma }_{x}u,...) =0,\,\,0 < \gamma ,\alpha \le 1. \end{aligned}$$
(2.1)

Utilizing the wave transformation:

$$\begin{aligned} u(x,t)=U(\eta ), \ \ \ \ \ \ \eta = k \,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha } \end{aligned}$$
(2.2)

converts Eq. (2.1) to the following ODE:

$$\begin{aligned} G(U,U',U'',U''',....) = 0. \end{aligned}$$
(2.3)

Several NFPDEs can be simplified in applied science to:

$$\begin{aligned} L\, U''+M\, U^3+N\,U =0, \end{aligned}$$
(2.4)

L, M and N are constants rely on the proposed equation’s constants and the wave transformations’ speed. Balancing \(U''\) and \(U^{3}\), gives the homogenous balance one. Thus, the solution of Eq. (2.4) takes the form Dai and Zhang (2006), Wang et al. (2005), Abdelrahman and AlKhidhr (2020):

$$\begin{aligned} U=A_{0}+A_{1} sn(\eta )+B_{1} cn(\eta ), \end{aligned}$$
(2.5)

where \(A_{0}\), \(A_{1}\) and \(B_{1}\) are constants to be calculated. Equation (2.5) gives

$$\begin{aligned} U'&=A_{1} cn(\eta )\, dn(\eta )-B_{1} sn(\eta )\,dn(\eta ), \end{aligned}$$
(2.6)
$$\begin{aligned} U''&=-{m}^{2} sn(\eta )\,A_{1}+2\,A_{1} sn^{3}(\eta ){m}^{2}+2 \,m^{2} sn^{2}(\eta )cn(\eta )\,B_{1}-A_{1} sn(\eta )-B_{1} cn(\eta ). \end{aligned}$$
(2.7)

Substituting Eqs. (2.5–2.7) into Eq. (2.4) and equating all coefficients of \(sn^{3}\), \(sn^{2} { cn}\), \(sn^{2}\), \(sn { cn}\), sn, cn, \(sn^{0}\) to zero, gives system of algebraic equations. Solving these equations, yields:

Case 1

$$\begin{aligned}&A_0=0,A_1=\pm \sqrt{\frac{-2L}{M}} m, B_1=0, N=L(1+m^2).\nonumber \\&U_{1}(x,t) = \pm \sqrt{\frac{-2L}{M}} m\, sn(\eta ). \end{aligned}$$
(2.8)

When \(m \rightarrow 1\), Eq. (2.8) becomes

$$\begin{aligned} U_{1}(x,t)= \pm \sqrt{\frac{-2L}{M}}\, tanh(\eta ). \end{aligned}$$
(2.9)

Case 2

$$\begin{aligned}&A_0=0,A_1=\pm \sqrt{\frac{-L}{2M}} m, B_1=-\sqrt{\frac{L}{2M}} m, N=\frac{1}{2}L(2-\,m^2).\nonumber \\&U_{2}(x,t) = \pm \sqrt{\frac{-L}{2M}} m\, sn(\eta ) -\sqrt{\frac{L}{2M}} m\, cn(\eta ). \end{aligned}$$
(2.10)

When \(m \rightarrow 1\), Eq. (2.10) becomes

$$\begin{aligned} U_{2}(x,t)= \pm \sqrt{\frac{-L}{2M}} \, tanh(\eta ) -\sqrt{\frac{L}{2M}} \, sech(\eta ). \end{aligned}$$
(2.11)

Case 3

$$\begin{aligned}&A_0=0,A_1=\pm \sqrt{\frac{-L}{2M}} m, B_1 =\sqrt{\frac{L}{2M}} m, N=\frac{1}{2}L(2-m^2).\nonumber \\&U_{3}(x,t)= \pm \sqrt{\frac{-L}{2M}} m\, sn(\eta ) +\sqrt{\frac{L}{2M}} m\, cn(\eta ). \end{aligned}$$
(2.12)

When \(m \rightarrow 1\), Eq. (2.12) becomes

$$\begin{aligned} U_{3}(x,t)= \pm \sqrt{\frac{-L}{2M}}\, tanh(\eta ) +\sqrt{\frac{L}{2M}} \, sech(\eta ). \end{aligned}$$
(2.13)

Case 4

$$\begin{aligned}&A_0=0,A_1=0, B_1=\pm \sqrt{\frac{2L}{M}}\,m, N=L(1-2m^2).\nonumber \\&U_{4}(x,t)= \pm \sqrt{\frac{2L}{M}}\,m\, cn(\eta ). \end{aligned}$$
(2.14)

When \(m \rightarrow 1\), Eq. (2.14) becomes

$$\begin{aligned} U_{4}(x,t)= \pm \sqrt{\frac{2L}{M}}\, sech(\eta ). \end{aligned}$$
(2.15)

3 The solutions of the fractional nonlinear Schrödinger equation

In this section, we present the application of the unified solver technique to the space-time fractional nonlinear Schrödinger equation. Using the wave transformation (Darvishi et al. 2018):

$$\begin{aligned} u(x,t)= e^{i \Theta }U(\eta ),\,\,\eta = k \,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }, \,\,\Theta = p\,\frac{x^{\gamma }}{\gamma }- c \,\frac{t^{\alpha }}{\alpha }. \end{aligned}$$
(3.1)

Substituting Eq. (3.1) into Eq. (1.1), yields \(v = 2 p k\) and

$$\begin{aligned} L\, U'' + M\, U^3 + N\, U=0, \end{aligned}$$
(3.2)

where \(L = k^2, M =2 \delta\) and \(N =c-p^2\). The solutions of Eq. (1.1) are:

Family I:

$$\begin{aligned} U_{1}(x,t)= \pm i\,\frac{k}{\sqrt{\delta }}\, m\, sn \left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.3)

As a result, the solutions of Eq. (1.1) are:

$$\begin{aligned} u_{1}(x,t)= \pm i\,\frac{k}{\sqrt{\delta }} \,e^{i \left( p\,\frac{x^{\gamma }}{\gamma } - c \,\frac{t^{\alpha }}{\alpha }\right) }\, m\, sn \left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.4)

Family II:

$$\begin{aligned} U_{2}(x,t)= \pm \,i\,\frac{k}{2\sqrt{\delta }} \, m\, sn\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) -\frac{k}{2\sqrt{\delta }} m\, cn \left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.5)

As a result, the solutions of Eq. (1.1) are:

$$\begin{aligned} u_{2}(x,t)= \left( \pm \,i\,\frac{k}{2\sqrt{\delta }} \, tanh\left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) - \frac{k}{2\sqrt{\delta }} \, sech\left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) \right) \,e^{i \left( p\,\frac{x^{\gamma }}{\gamma } -c \,\frac{t^{\alpha }}{\alpha }\right) }. \end{aligned}$$
(3.6)

Family III:

$$\begin{aligned} U_{3}(x,t)= \pm \,i\,\frac{k}{2\sqrt{\delta }} \, m\, sn\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) + \frac{k}{2\sqrt{\delta }} \, m \, cn\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.7)

As a result, the solutions of Eq. (1.1) are:

$$\begin{aligned} u_{3}(x,t)= \left( \pm \,i\,\frac{k}{2\sqrt{\delta }} \, m\, sn\left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) + \frac{k}{2\sqrt{\delta }} \, m\, cn \left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) \right) \,e^{i \left( p\,\frac{x^{\gamma }}{\gamma } -c \,\frac{t^{\alpha }}{\alpha }\right) }. \end{aligned}$$
(3.8)

Family IV:

$$\begin{aligned} U_{4}(x,t)= \pm \frac{k}{\sqrt{\delta }}\,m\, cn \left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.9)

As a result, the solutions of Eq. (1.1) are:

$$\begin{aligned} u_{4}(x,t)= \pm \frac{k}{\sqrt{\delta }} \, e^{i \left( p\,\frac{x^{\gamma }}{\gamma } -c \,\frac{t^{\alpha }}{\alpha }\right) }\,m\, cn\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(3.10)

4 Results and discussion

The fractional NLSE is very important in optical propagations and complex environmental media. Darvishi et al. (2018) introduced optical soliton solutions for this equation using the sine-cosine technique. Darvishi and Najaf (2020) presented only one family of the Jacobian-elliptic function utilizing the semi-inverse variational principle. In this paper, we implemented the solver technique to produce some vital solutions. The suggested method is creative, effective, and straightforward. The acquired fractional forms perform in solitary, shock rational, superperiodic, hyperbolic (trigonometric) structures. These solutions are so important in various fields of applied science. On the other hand, it would be more appropriate for us to investigate how the fractal parameters affect the characteristics, structures, and forms of nonlinear wave patterns.

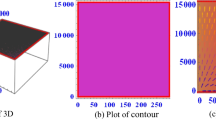
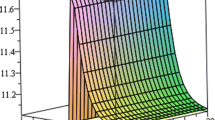
Consequently, we research how the fractional time and space parameter affects the solutions that are produced. Equation (3.4) describes the dissipative behaviour that depends on the values of the parameters affecting the system. This describes a shock and periodic super propagating behaviour as given in Figs. 1, 2, 3, 4. it was noted that shock and periodic super trajectories depends on \(\gamma\) and \(\alpha\) as depicted in Figs. 2 and 4. For example, when \(\gamma\) values are less than 0.5, the periodical wave begins to transform into the super shock wave, as shown in Figs. 1, 2. On the other hand, regarding the change in \(\alpha\) parameter in Figs. 3, 4, we find that the periodic wave begins to transform into a damped oscillatory periodic form for \(\alpha > 0.3\), for which the wave amplitude decreases while the width is gradually increases. It was noted that shock and periodic super trajectories depends on \(\gamma\) and \(\alpha\) as depicted in Figs. 2 and 4. Equations (3.6) and (3.8) are characterized by cnoidal, shocksolitons like, supershock like waves as in Figs. 5, 6, 7, 8. Figure 7 represents a physical geometrical profile that contains a mixture of cnoidal, periodic and shock formations. Equation (3.10) is a third family of solutions which also characterize three profiles namely cnoidal wave, sharp supersolitonic propagation and shocksolitons like waves as shown in Figs. 9, 10, 11.

On the other hand, when \(m \rightarrow 1\), the solutions (3.4), (3.6), (3.8) and (3.10), respectively become

$$\begin{aligned} \hat{u}_{1}(x,t)&= \pm i\,\frac{k}{\sqrt{\delta }}\,e^{i \left( p\,\frac{x^{\gamma }}{\gamma }- c \,\frac{t^{\alpha }}{\alpha }\right) } \, tanh\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(4.1)
$$\begin{aligned} \hat{u}_{2}(x,t)&= \left( \pm \,i\,\frac{k}{2\sqrt{\delta }} \, tanh\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) - \frac{k}{2\sqrt{\delta }} \, sech \left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) \right) \,e^{i \left( p\,\frac{x^{\gamma }}{\gamma } - c \,\frac{t^{\alpha }}{\alpha }\right) }. \end{aligned}$$
(4.2)
$$\begin{aligned} \hat{u}_{3}(x,t)&= \left( \pm \,i\,\frac{k}{2\sqrt{\delta }} \, tanh\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) + \frac{k}{2\sqrt{\delta }} \, sech \left( k\,\frac{x^{\gamma }}{\gamma }-v \,\frac{t^{\alpha }}{\alpha }\right) \right) \,e^{i \left( p\,\frac{x^{\gamma }}{\gamma } -c \,\frac{t^{\alpha }}{\alpha }\right) }. \end{aligned}$$
(4.3)
$$\begin{aligned} \hat{u}_{4}(x,t)&= \pm \frac{k}{\sqrt{\delta }} \, e^{i \left( p\,\frac{x^{\gamma }}{\gamma }- c \,\frac{t^{\alpha }}{\alpha }\right) } \,sech\left( k\,\frac{x^{\gamma }}{\gamma } -v \,\frac{t^{\alpha }}{\alpha }\right) . \end{aligned}$$
(4.4)

Finally, the fractional NLSE that described the waves propagations in complex fractal medium with fractal characteristics that may causing wave trapping or changing wave pictures such as width and amplitude via medium fractal parameters. This appears in the form of fractional order equation. This mathematical order modulates the Wave properties such as amplitude and width. For the importance of the superior solutions deduced in this work and due to their generality, it is possible to compare them to some previous research works which depends on the Jacobi elliptic functions modulus m and fractional parameters values, while providing the conditions and restrictions imposed on the equation see Darvishi et al. (2018), Darvishi and Najaf (2020).

Fig. 1
figure 1

Graph of \(u_{1}(x,t)\) with x & \(\gamma\) for \(k=1.5, p=1, \delta =1\)

Full size image
Fig. 2
figure 2

Graph of \(u_{1}(x,t)\) with x & \(\gamma\) for \(k=1.5, p=1, \delta =1\)

Full size image
Fig. 3
figure 3

Graph of \(u_{1}(x,t)\) with t & \(\alpha\) for \(k=1.5, p=1, \delta =1\)

Full size image
Fig. 4
figure 4

Graph of \(u_{1}(x,t)\) with t & \(\alpha\) for \(k=1.5, p=1, \delta =1\)

Full size image
Fig. 5
figure 5

Graph of \(u_{3}(x,t)\) with x & \(\gamma\) for \(k=1.7 p=1.1, \delta =2\)

Full size image
Fig. 6
figure 6

Graph of \(u_{3}(x,t)\) with x & \(\gamma\) for \(k=1.7 p=1.1, \delta =2\)

Full size image
Fig. 7
figure 7

Graph of \(u_{3}(x,t)\) with t & \(\alpha\) for \(k=1.7 p=1.1, \delta =2\)

Full size image
Fig. 8
figure 8

Graph of \(u_{3}(x,t)\) with t & \(\alpha\) for \(k=1.7 p=1.1, \delta =2\)

Full size image
Fig. 9
figure 9

Graph of \(u_{4}(x,t)\) with x & \(\gamma\) for \(k=1.9 p=1.3, \delta =2.2\)

Full size image
Fig. 10
figure 10

Graph of \(u_{4}(x,t)\) with x & \(\gamma\) for \(k=1.9 p=1.3, \delta =2.2\)

Full size image
Fig. 11
figure 11

Graph of \(u_{4}(x,t)\) with t & \(\alpha\) for \(k=1.9 p=1.3, \delta =2.2\)

Full size image
Fig. 12
figure 12

Graph of \(u_{1}(x,t)\) with t & \(\alpha\) for \(k=1.5, p=1, \delta =1\)

Full size image
Fig. 13
figure 13

Graph of \(u_{4}(x,t)\) with t & \(\alpha\)

Full size image
Fig. 14
figure 14

Graph of \(u_{4}(x,t)\) with t & \(\alpha\) for \(k=1.9 p=1.3, \delta =2.2\)

Full size image
Fig. 15
figure 15

Graph of \(u_{4}(x,t)\) with t & \(\alpha\) for \(k=1.9 p=1.3, \delta =2.2\)

Full size image

5 Fractional parameters effects

We investigate the effect of the fraction parameters on the obtained solutions properties. The change of both Eqs. (3.4) and (3.10) with x and \(\gamma\) is plotted in Figs. 12, 13. It was found that increasing the \(\gamma\) factor produces a change in phase and periodic time to periodic cnoidal wave of Eq. (3.4) and sharp supersoliton wave for Eq. (3.10). The imaginary part variation of Eq. (3.10) with t and \(\alpha\) is depicted in Fig. 14. It was considered that by increasing factor \(\alpha\) the wave is converted into superhuge solitonlike structure. Finally, increasing \(\alpha\) in Fig. 15, the sharp super soliton becomes highly frequency propagating super wave.

6 Conclusions

The fractional nonlinear Schrödinger equation has been studied using conformable fraction space-time derivatives. Using the offered strategy, numerous appealing solutions to the investigated equations are fruitfully generated, confirming great performance. The reported solutions are of great importance for serious applications, like optical communications, quantum models, new astrophysics studied and many others. The time-space fractional orders are affected the wave type, phase and frequencies which constrained the behaviour dynamics of generated solutions. Indeed, our results can be used in improving fluid models that describe the tidal lagoons which emerging promising model for new studies in tidal power generations. Finally, the proposed approach is efficient, simple, and innovative, and it is recommended for further study in order to obtain closed form analytic solutions to several nonlinear fractional model related to nonlinear sciences in future studies.