New Bounds and Constructions for Neighbor-Locating Colorings of Graphs

Abstract

A proper k-vertex-coloring of a graph G is a neighbor-locating k-coloring if for each pair of vertices in the same color class, the sets of colors found in their neighborhoods are different. The neighbor-locating chromatic number $\chi _{NL}(G)$ is the minimum k for which G admits a neighbor-locating k-coloring. A proper k-vertex-coloring of a graph G is a locating k-coloring if for each pair of vertices x and y in the same color-class, there exists a color class $S_i$ such that $d(x,S_i)\ne d(y,S_i)$. The locating chromatic number $\chi _{L}(G)$ is the minimum k for which G admits a locating k-coloring. It follows that $\chi (G)\le \chi _L(G)\le \chi _{NL}(G)$ for any graph G, where $\chi (G)$ is the usual chromatic number of G.

We show that for any three integers p, q, r with $2\le p\le q\le r$ (except when $2=p=q<r$), there exists a connected graph $G_{p,q,r}$ with $\chi (G_{p,q,r})=p$, $\chi _L(G_{p,q,r})=q$ and $\chi _{NL}(G_{p,q,r})=r$. We also show that the locating chromatic number (resp., neighbor-locating chromatic number) of an induced subgraph of a graph G can be arbitrarily larger than that of G.

Alcon et al. showed that the number n of vertices of G is bounded above by $k(2^{k-1}-1)$, where $\chi _{NL}(G)=k$ and G is connected (this bound is tight). When G has maximum degree $\varDelta$, they also showed that a smaller upper-bound on n of order $k^{\varDelta +1}$ holds. We generalize the latter by proving that if G has order n and at most $an+b$ edges, then n is upper-bounded by a bound of the order of $k^{2a+1}+2b$. Moreover, we describe constructions of such graphs which are close to reaching the bound.

1 Introduction

In the area of identification/location problems, one is given a discrete structure (such as a graph) and one wishes to identify its elements, that is, to be able to pairwise distinguish them from each other. This can be done by constructing, for example, dominating sets [15, 22] or colorings [2, 9, 13] of the graph. The identification process may be based on distances [9, 21] or on neighborhoods [2, 22], and we may wish to distinguish all vertex pairs [15, 21, 22], only adjacent ones [13], or those with the same color [2, 9]. This vast research area has many applications both in practical settings like fault-diagnosis in networks [15], biological testing [18], machine learning [11] and theoretical settings such as game analysis [12], isomorphism testing [4] or logical definability [16], to name a few.

Taking cues from the above research topics, recently, two variants of graph coloring were introduced, namely, locating coloring [9] and neighbor-locating coloring [2, 5]. While the former concept has been well-studied since 2002 [5,6,7,8,9,10, 19, 20, 23,24,25]), our focus of study is the latter, which was introduced in 2014 in [5] under the name of adjacency locating coloring, renamed in 2020 in [2] and studied in a few papers since then [1, 3, 14, 17].

Throughout this article, we will use the standard terminologies and notations used in “Introduction to Graph Theory” by West [26].

Given a graph G, a (proper) k-coloring is a function $f: V(G) \rightarrow C$, where C is a set of k colors, such that $f(u) \ne f(v)$ whenever u is adjacent to v. The value f(v) is called the color of v. The chromatic number of G, denoted by $\chi (G)$, is the minimum k for which G admits a k-coloring.

Given a k-coloring f of G, its $i^{th}$ color class is the collection $S_i$ of vertices that have received the color i. The distance between a vertex x and a set S of vertices is given by $d(x, S) = \min \{d(x, y) : y \in S\}$, where d(x, y) is the number of edges in a shortest path connecting x and y. Two vertices x and y are metric-distinguished with respect to f if either $f(x)\ne f(y)$ or $d(x,S_i)\ne d(y,S_i)$ for some color class $S_i$. A k-coloring f of G is a locating k-coloring if any two distinct vertices are metric-distinguished with respect to f. The locating chromatic number of G, denoted by $\chi _L(G)$, is the minimum k for which G admits a locating k-coloring.

Given a k-coloring f of G, suppose that a neighbor y of a vertex x belongs to the color class $S_i$. In such a scenario, we say that i is a color-neighbor of x (with respect to f). The set of all color-neighbors of x is denoted by $N_f(x)$. Two vertices x and y are neighbor-distinguished with respect to f if either $f(x) \ne f(y)$ or $N_f(x) \ne N_f(y)$. A k-coloring f is neighbor-locating k-coloring if each pair of distinct vertices are neighbor-distinguished. The neighbor-locating chromatic number of G, denoted by $\chi _{NL}(G)$, is the minimum k for which G admits a neighbor-locating k-coloring.

Observe that a neighbor-locating coloring is, in particular, a locating coloring. Thus, we have the following relation among the three parameters [2]:

$$\chi (G) \le \chi _{L}(G) \le \chi _{NL}(G).$$

Note that for complete graphs, all three parameters have the same value, that is, equality holds in the above relation. Nevertheless, the difference between the pairs of values of parameters $\chi , \chi _{NL}$ and $\chi _L, \chi _{NL}$, respectively, can be arbitrarily large. Moreover, it was proved that for any pair p, q of integers with $3\le p\le q$, there exists a connected graph $G_1$ with $\chi (G_1)=p$ and $\chi _{NL}(G_1)=q$ [2] and a connected graph $G_2$ with $\chi _{L}(G_2)=p$ and $\chi _{NL}(G_2)=q$ [17]. The latter of the two results positively settled a conjecture posed in [2]. We strengthen these results by showing that for any three integers p, q, r with $2\le p\le q\le r$, there exists a connected graph $G_{p,q,r}$ with $\chi (G_{p,q,r})=p$, $\chi _L(G_{p,q,r})=q$ and $\chi _{NL}(G_{p,q,r})=r$, except when $2=p=q<r$.

One fundamental difference between coloring and locating coloring (resp., neighbor-locating coloring) is that the restriction of a coloring of G to an (induced) subgraph H is necessarily a coloring, whereas the analogous property is not true for locating coloring (resp., neighbor-locating coloring). Interestingly, we show that the locating chromatic number (resp., neighbor-locating chromatic number) of an induced subgraph H of G can be arbitrarily larger than that of G.

Alcon et al. [2] showed that the number n of vertices of G is bounded above by $k(2^{k-1}-1)$, where $\chi _{NL}(G)=k$ and G has no isolated vertices, and this bound is tight. This exponential bound is reduced to a polynomial one when G has maximum degree $\varDelta$, indeed it was further shown in [2] that the upper-bound $n\le k\sum _{j=1}^{\varDelta }{k-1\atopwithdelims ()j}$ holds (for graphs with no isolated vertices and when $\varDelta \le k-1$). It was left open whether this bound is tight. The cycle rank c of a graph G, denoted by c(G), is defined as $c(G) = |E(G)| - n(G) + 1$. Alcon et al. [3] gave the upper bound $n\le \frac{1}{2}(k^3+k^2-2k)+2(c-1)$ for graphs of order n, neighbor-locating chromatic number k and cycle rank c. Further, they also obtained tight upper bounds on the order of trees and unicyclic graphs in terms of the neighbor-locating chromatic number [3], where a unicyclic graph is a connected graph having exactly one cycle.

As a connected graph with cycle rank c and order n has $n+c-1$ edges and a graph of order n and maximum degree $\varDelta$ has at most $\frac{\varDelta }{2}n$ edges, the two latter bounds can be seen as two approaches for studying the neighbor-locating coloring for sparse graphs. We generalize this approach by studying graphs with given average degree, or in other words, graphs of order n having at most $an+b$ edges for some constants a, b (such graphs have average degree $2a+2b/n$). For such graphs, we prove the upper bound $n\le 2b+k\sum \limits _{i=1}^{2a}(2a+1-i){k-1\atopwithdelims ()i}$. Furthermore, we show that this bound is asymptotically tight, by a construction of graphs with $an+b$ edges (where 2a is any positive integer and 2b any integer) and neighbor-locating chromatic number $\varTheta (k)$, whose order is $\varTheta (k^{2a+1})$. Moreover, when $b=0$, the graphs can be taken to have maximum degree 2a. This implies that our bound and the one from [2] are roughly tight.

In Sect. 2, we study the connected graphs with prescribed values of chromatic number, locating chromatic number and neighbor-locating chromatic number. We also study the relation between the locating chromatic number (resp., neighbor-locating chromatic number) of a graph and its induced subgraphs. Finally, in Sect. 3 we study the density of graphs having bounded neighbor-locating chromatic number.

2 Gaps Among $\chi (G), \chi _L(G)$ and $\chi _{NL}(G)$

  The first result we would like to prove involves three different parameters, namely, the chromatic number, the locating chromatic number, and the neighbor-locating chromatic number.

Theorem 1

For all $2 \le p \le q \le r$, except when $p=q=2$ and $r >2$, there exists a connected graph $G_{p,q,r}$ satisfying $\chi (G_{p,q,r}) = p$, $\chi _{L}(G_{p,q,r}) = q$, and $\chi _{NL}(G_{p,q,r}) = r$.

Proof

First of all, let us assume that $p=q=r$. In this case, for $G_{p,q,r} = K_p$, it is trivial to note that $\chi (G_{p,q,r})=\chi _L(G_{p,q,r})=\chi _{NL}(G_{p,q,r})=p$. This completes the case when $p=q=r$.

Second of all, let us handle the case when $p < q=r$. If $2 = p < q = r$, then take $G_{p,q,r}= K_{1,q-1}$. Therefore, we have $\chi (G_{p,q,r})=2$ as it is a bipartite graph, and it is known that $\chi _L(G_{p,q,r})=\chi _{NL}(G_{p,q,r})=q$ [2, 9].

If $3 \le p < q = r$, then we construct $G_{p,q,r}$ as follows: start with a complete graph $K_p$, on vertices $v_0, v_1, \cdots , v_{p-1}$, take $(q-1)$ new vertices $u_1, u_2, \cdots , u_{q-1}$, and make them adjacent to $v_0$. It is trivial to note that $\chi (G_{p,q,r})=p$ in this case. Moreover, note that we need to assign q distinct colors to $v_0, u_1, u_2, \cdots , u_{q-1}$ under any locating or neighbor-locating coloring. On the other hand, $f(v_i) = i$ and $f(u_j) = j$ is a valid locating q-coloring as well as neighbor locating q-coloring of $G_{p,q,r}$. Thus we are done with the cases when $p < q=r$.

Thirdly, we are going to consider the case when $p=q < r$. If $3 = p = q < r$, then let $G_{p,q,r} = C_n$ where $C_n$ is an odd cycle of suitable length, that is, a length which will imply $\chi _{NL}(C_n)=r$. It is known that such a cycle exists [1, 5]. As we know that $\chi (G_{p,q,r})=3$, $\chi _L(G_{p,q,r})=3$ [9], and $\chi _{NL}(G_{p,q,r})=r$ [1, 5], we are done.

If $4 \le p = q < r$, then we construct $G_{p,q,r}$ as follows: start with a complete graph $K_p$ on vertices $v_0, v_1, \cdots , v_{p-1}$, and an odd cycle $C_n$ on vertices $u_0, u_1, \cdots , u_{n-1}$, and identify the vertices $v_0$ and $u_0$. Moreover, we say that the length of the odd cycle $C_n$ is a suitable length, that is, it is of a length which ensures $\chi _{NL}(C_n)=r$ and under any neighbor-locating r-coloring of $C_n$, every color is used at least twice. It is known that such a cycle exists [1, 5]. Notice that $\chi (G_{p,q,r})=p$ and $\chi _L(G_{p,q,r})=q$. On the other hand, as the neighborhood of the vertices of the cycle $C_n$ (subgraph of $G_{p,q,r}$) doesnot change if we consider it as an induced subgraph except for the vertex $v_0 = u_0$. Thus, we will need at least r colors to color $C_n$ while it is contained inside $G_{p,q,r}$ as a subgraph. Hence $\chi _{NL}(G_{p,q,r})=r$. Thus, we are done in this case also.

Finally, we are into the case when $p< q < r$. If $p=2$, $q=3$ and $r>3$, then let $G_{p,q,r}=P_n$ where $P_n$ is a path of suitable length, that is, a length which ensures $\chi _{NL}(G_{p,q,r})=r$. It is known that such a path exists [3]. As we know that $\chi (G_{p,q,r})=2$, $\chi (G_{p,q,r})=3$ [9] and $\chi _{NL}(G_{p,q,r})=r$ [1, 5]. If $p=2$ and $3<q<r$, refer [17] for this case.

If $3 = p< q <r$, then we start with an odd cycle $C_n$ on vertices $v_0, v_1, \cdots , v_{n-1}$ of a suitable length, where suitable means, a length that ensures $\chi _{NL}(C_n)=r$ and under any neighbor-locating r-coloring of $C_n$, every vertex has two distinct color-neighbors. It is known that such a cycle exists [1, 5]. Take $q-1$ new vertices $u_1, u_2, \cdots , u_{q-1}$ and make all of them adjacent to $v_0$. This so obtained graph is $G_{p,q,r}$. It is trivial to note that $\chi (G_{p,q,r})=3$ in this case. Note that we need to assign q distinct colors to $v_0,u_1, u_2, \cdots , u_{q-1}$ under any locating or neighbor-locating coloring. One can show in a similar way like above that $\chi _L(G_{p,q,r})=q$ and $\chi _{NL}(G_{p,q,r})=r$.

If $4 \le p< q <r$, then we start with a path $P_n$ of a suitable length, that is, it is of a length which ensures $\chi _{NL}(P_n)=r$ and under any neighbor-locating r-coloring of $P_n$, every color is used at least twice. It is known that such a path exists [1, 5]. Let $P_n = u_0 u_1 \cdots u_{n-1}$. Now let us take a complete graph on p vertices $v_0, v_1, \cdots , v_{p-1}$. Identify the two graphs at $u_0$ and $v_0$ to obtain a new graph. Furthermore, take $(q-2)$ independent vertices $w_1, w_2, \cdots , w_{q-2}$ and make them adjacent to $u_{n-2}$. This so obtained graph is $G_{p,q,r}$. One can show in a similar way like above that we have $\chi (G_{p,q,r})=p, \chi _{L}(G_{p,q,r})=q$, and $\chi _{NL}(G_{p,q,r})=r$.    $\square$

Furthermore, we show that, unlike the case of chromatic number, an induced subgraph can have an arbitrarily higher locating chromatic number (resp., neighbor-locating chromatic number) than that of the graph.

Theorem 2

For every $k \ge 0$, there exists a graph $G_k$ having an induced subgraph $H_k$ such that $\chi _L(H_k) - \chi _L(G_k) = k$ and $\chi _{NL}(H_k) - \chi _{NL}(G_k) = k$.

Proof

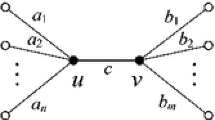
The graph $G_k$ is constructed as follows. We start with 2k independent vertices $a_1, a_2, \cdots , a_{2k}$ and k disjoint edges $b_1b'_1, b_2b'_2, \cdots , b_kb'_k$. After that we make all the above mentioned vertices adjacent to a special vertex v to obtain our graph $G_k$. Notice that v and the $a_i$s must all receive distinct colors under any locating coloring or neighbor-locating coloring. On the other hand, the coloring f given by $f(v) = 0$, $f(a_i) = i$, $f(b_i) = 2i-1$, and $f(b'_i) = 2i$ is indeed a locating coloring as well as a neighbor-locating coloring of $G_k$. Hence we have $\chi _L(G_k) = \chi _{NL}(G_k) = (2k+1)$.

Now take $H_k$ as the subgraph induced by v, $a_i$s and $b_i$s. It is the graph $K_{1,3k}$, and we know that all vertices must get distinct colors under any locating coloring or neighbor-locating coloring. Hence we have $\chi _L(H_k) = \chi _{NL}(H_k) = (3k+1)$.

This completes the proof.    $\square$

3 Bounds and Constructions for Sparse Graphs

  In this section, we study the density of graphs having bounded neighbor-locating chromatic number.

3.1 Bounds

The first among those results provides an upper bound on the number of vertices of a graph in terms of its neighbor-locating chromatic number. This, in particular shows that the number of vertices of a graph G is bounded above by a polynomial function of $\chi _{NL}(G)$.

Theorem 3

Let G be a connected graph on n vertices and m edges such that $m\le an+b$, where 2a is a positive integer and 2b is an integer. If $\chi _{NL}(G)=k$, then

$$n \le 2b+k \sum _{i=1}^{2a}(2a+1-i){k-1 \atopwithdelims ()i}.$$

In particular, any graph whose order attains the upper bound must be of maximum degree $2a+1$ and with exactly $k{k-1 \atopwithdelims ()i}$ number of vertices of degree i.

Proof

Let $D_i$ and $d_i$ denote the set and the number of vertices in G having degree equal to i, respectively, and let $D_i^+$ and $d_i^{+}$ denote the set and the number of vertices in G having degree at least i, for all $i \ge 1$. Using the handshaking lemma, we know that

$$\sum _{v \in V(G)} deg(v) = 2|E(G)| = 2m \le 2(an+b).$$

Notice that, as G is connected, and hence does not have any vertex of degree 0, it is possible to write

$$\sum _{v \in V(G)} deg(v) = \sum _{i=1}^{2a} i \cdot d_i + \sum _{v \in D_{2a+1}^+} deg(v).$$

Moreover, the number of vertices of G can be expressed as

$$n = (d_1 + d_2 + \cdots + d_{2a}) + d_{2a+1}^+ = d_{2a+1}^+ + \sum _{i=1}^{2a} d_{i}.$$

Therefore, combining the above equations and inequalities, we have

$$\begin{aligned} \sum _{i=1}^{2a} i \cdot d_i + \sum _{v \in D_{2a+1}^+} deg(v) \le 2b + 2a \left( d_{2a+1}^+ + \sum _{i=1}^{2a} d_{i}\right) \end{aligned}$$

which implies

$$\begin{aligned} d_{2a+1}^+ \le \sum _{v \in D_{2a+1}^+} \left( deg(v) - 2a \right) \le \left( \sum _{v \in D_{2a+1}^+} deg(v)\right) - 2a d_{2a+1}^+ \le 2b + \sum _{i=1}^{2a} (2a-i)d_{i} \end{aligned}$$

since there are exactly $d_{2a+1}^+$ terms in the summation $\sum _{v \in D_{2a+1}^+} \left( deg(v) - 2a \right)$ where each term is greater than or equal to 1, as $deg(v) \ge 2a +1$ for all $v \in D_{2a+1}^+$.

Let f be any neighbor-locating k-coloring of G. Consider an ordered pair $(f(u), N_f(u))$, where u is a vertex having degree at most s. Thus, u may receive one of the k available colors, while its color neighborhood may consist of at most s of the remaining $(k-1)$ colors. Thus, there are at most $k \sum _{i=1}^{s} {k-1 \atopwithdelims ()i}$ choices for the ordered pair $(f(u), N_f(u))$. As for any two vertices u, v of degree at most s, the following ordered pairs $(f(u), N_f(u))$ and $(f(v), N_f(v))$ must be distinct, we have

$$\sum _{i=1}^s d_i \le k \sum _{i=1}^{s} {k-1 \atopwithdelims ()i}.$$

Using the above relation, we can show that

$$\sum _{i=1}^{2a} (2a+1-i)d_i = \sum _{s=1}^{2a} \left( \sum _{i=1}^s d_i \right) \le \sum _{s=1}^{2a} \left( k \sum _{i=1}^{s} {k-1 \atopwithdelims ()i} \right) = k \sum _{i=1}^{2a} (2a+1-i) {k-1 \atopwithdelims ()i}.$$

As

$$\sum _{i=1}^{2a} (2a+1-i)d_i = \sum _{i=1}^{2a}d_i + \sum _{i=1}^{2a} (2a-i)d_i \text { and } d_{2a+1}^+ \le 2b + \sum _{i=1}^{2a} (2a-i)d_{i},$$

we have

$$n = d_{2a+1}^+ + \sum _{i=1}^{2a} d_{i} \le 2b + k \sum _{i=1}^{2a} (2a+1-i) {k-1 \atopwithdelims ()i}.$$

This completes the first part of the proof.

For the proof of the second part of the Theorem, we notice that if the order of a graph $G^*$ attains the upper bound, then equality holds in all of the above inequations. In particular, we must have $d_{2a+1}^+ = \sum _{v \in D_{2a+1}^+} (deg(v)-2a)$ which implies that $G^*$ cannot have a vertex of degree more than $2a+1$. Moreover, we also have the following equality.

$$\sum _{i=1}^s d_i = k \sum _{i=1}^{s} {k-1 \atopwithdelims ()i} \text { for}\, s=1, 2, \ldots , 2a+1.$$

This proves that $G^*$ has exactly $k{k-1 \atopwithdelims ()i}$ vertices of degree i.    $\square$

Next we are going to present some immediate corollaries of Theorem 3. A cactus is a connected graph in which no two cycles share a common edge.

Corollary 1

Let G be a cactus on n vertices and m edges. If $\chi _{NL}(G)=k$, then

$$n \le \frac{k^4+11k^2-12k-6}{6}.$$

Moreover, if the cactus has exactly t cycles, then we have

$$n \le 2(t-1)+\frac{k^3+k^2-2k}{2}.$$

Proof

Observe that G has at most $\frac{3(n-1)}{2}$ edges. So, by substituting $a=\frac{3}{2}$ and $b=-\frac{3}{2}$ in the bound for n established in Theorem 3, we have

$$\begin{aligned} n \le 2b + k \sum _{i=1}^{2a} (2a+1-i) {k-1 \atopwithdelims ()i}&= -3 + k\sum _{i=1}^{3} (4-i) {k-1 \atopwithdelims ()i} \\&= -3 + 3k {k-1 \atopwithdelims ()1} + 2k {k-1 \atopwithdelims ()2} + k {k-1 \atopwithdelims ()3}\\&= \frac{k^4+11k^2-12k-6}{6}. \end{aligned}$$

Note that, if the cactus G has exactly t cycles, then G has exactly $(n+t-1)$ edges. Hence, replacing $a=1$ and $b = (t-1)$ in the bound for n established in Theorem 3, we obtain the required bound for the cactus.    $\square$

A graph is t-degenerate if its every subgraph has a vertex of degree at most t.

Corollary 2

Let G be a t-degenerate graph on n vertices and m edges. If $\chi _{NL}(G)=k$, then

$$n\le k\sum _{i=1}^{2t}(2t+1-i){k-1\atopwithdelims ()i}-t(t+1).$$

Proof

Observe that the number of edges in a t-degenerate graph is $m\le tn-\frac{t(t+1)}{2}$. Substituting $a=t$ and $b=-\frac{t(t+1)}{2}$ in the bound for n established in Theorem 3, we obtain the required bound.    $\square$

A planar graph is 5-degenerate, thus using the above corollary, we know that for a planar graph G one can obtain an upper bound of |V(G)|. However, since $|E(G)| \le 3|V(G)|-6$, we are able to obtain a better bound.

Corollary 3

Let G be a planar graph on n vertices and m edges. If $\chi _{NL}(G)=k$, then

$$n\le k\sum _{i=1}^{6}(7-i){k-1\atopwithdelims ()i}-12.$$

Proof

Note that the number of edges in a planar graph is at most $3n-6$. Substituting $a=3$ and $b=-6$ in the bound for n established in Theorem 3, we get the required bound.    $\square$

3.2 Tightness

Next we show the asymptotic tightness of Theorem 3. To that end, we will prove the following result.

Theorem 4

Let 2a be a positive integer and let 2b be an integer. Then, there exists a graph G on n vertices and m edges satisfying $m \le an+b$ such that $n = \varTheta (k^{2a+1})$ and $\chi _{NL}(G)=\varTheta (k)$. Moreover, when $b=0$, G can be taken to be of maximum degree 2a.

The proof of this theorem is contained within a number of observations and lemmas. Also, the proof is constructive, and the constructions depend on particular partial colorings. Therefore, we are going to present a series of graph constructions, their particular colorings, and their structural properties. We are also going to present the supporting observations and lemmas in the following.

Lemma 1

Let us consider a $(p \times q)$ matrix whose $ij^{th}$ entry is $m_{i,j}$, where $p < q$. Let M be a complete graph whose vertices are the entries of the matrix. Then there exists a matching of M satisfying the following conditions:

• (i) The endpoints of an edge of the matching are from different columns.

• (ii) Let $e_1$ and $e_2$ be two edges of the matching. If one endpoint of $e_1$ and $e_2$ are from the $i^{th}$ columns, then the other endpoints of them must belong to distinct columns.

• (iii) The matching saturates all but at most one vertex of M per column.

Proof

Consider the permutation $\sigma = (1\ 2\ \cdots q)$. The matching consists of edges of the type $m_{(2i-1),j}m_{2i,\sigma ^i(j)}$ for all $i \in \{1, 2, \cdots , \lfloor \frac{p}{2} \rfloor \}$ and $j \in \{1, 2, \cdots , q\}$. We will show that this matching satisfies all listed conditions.

Observe that, a typical edge of the matching is of the form $m_{(2i-1),j}m_{2i,\sigma ^i(j)}$. As the second co-ordinates of the subscript of the endpoints of the said edge is different, condition (i) from the statement is verified.

Suppose that there are two edges of the type $m_{(2i-1),j}m_{2i,\sigma ^i(j)}$ and $m_{(2i'-1),j'} m_{2i',\sigma ^{i'}(j')}$. If $m_{(2i-1),j}$ and $m_{(2i'-1),j'}$ are from the same column, that is, $j = j'$, then we must have $i \ne i'$ as they are different vertices. Thus $\sigma ^i(j) \ne \sigma ^{i'}(j) = \sigma ^{i'}(j')$ as $i \ne i'$. If $m_{(2i-1),j}$ and $m_{2i',\sigma ^{i'}(j')}$ are from the same column, then we have $j = \sigma ^{i'}(j')$. Moreover, if we have $j' = \sigma ^{i}(j)$, then it will imply that

$$j = \sigma ^{i'}(\sigma ^{i}(j)) = \sigma ^{i+i'}(j).$$

This is only possible if $q | (i+i')$, which is not possible as $i, i' \in \{1, 2, \cdots , \lfloor \frac{p}{2} \rfloor \}$. Therefore, we have verified condition (ii) of the statement.

Notice that, the matching saturates all the vertices of M when p is even, whereas it saturates all except the vertices in the $p^{th}$ row of the matrix when p is odd. This verifies condition (iii) of the statement.    $\square$

Corollary 4

  Let G be a graph with an independent set M of size $(p \times q)$, where $M = \{m_{ij}: 1 \le i \le p, 1 \le j \le q\}$ and $p < q$. Moreover, let $\phi$ be a $(k'+q)$-coloring of G satisfying the following conditions:

• 1. $k'+1 \le \phi (x) \le k'+ q$ if and only if $x \in M$,

• 2. x and y are neighbor-distinguished unless both belong to M,

• 3. $\phi (m_{ij}) = k'+j$.

Then it is possible to find spanning supergraph $G'$ of G by adding a matching between the vertices of M which will make $\phi$ a neighbor-locating $(k'+q)$-coloring of $G'$.

Proof

First of all build a matrix whose $ij^{th}$ entry is the vertex $m_{ij}$. After that, build a complete graph whose vertices are entries of this matrix. Now using Lemma 1, we can find a matching of this complete graph that satisfies the three conditions mentioned in the statement of Lemma 1. We construct $G'$ by including exactly the edges corresponding to the edges of the matching, between the vertices of M. We want to show that after adding these edges and obtaining $G'$, indeed $\phi$ is a neighbor-locating $(k'+q)$-coloring of $G'$.

Notice that by the definition of $\phi$, $(k'+q)$ colors are used. So it is enough to show that the vertices of $G'$ are neighbor-distinguished with respect to $\phi$. To be exact, it is enough to show that two vertices x, y from M are neighbor-distinguished with respect to $\phi$ in $G'$. If $\phi (x) = \phi (y)$, then they must have different color-neighborhood inside M according to the conditions of the matching. This is enough to make x, y neighbor-distinguished.    $\square$

Now we are ready to present our iterative construction. However, given the involved nature of it, we need some specific nomenclatures to describe it. For convenience, we will list down some points to describe the whole construction.

• (i) An i-triplet is a 3-tuple of the type $(G_i, \phi _i, X_i)$ where $G_i$ is a graph, $\phi _i$ is a neighbor-locating (ik)-coloring of $G_i$, $X_i$ is a set of $(i+1)$-tuples of vertices of $G_i$, each having non-repeating elements. Also, two $(i+1)$-tuples from $X_i$ do not have any entries in common.

• (ii) Let us describe the 1-triplet $(G_1, \phi _1, X_1)$ explicitly. Here $G_1$ is the path $P_t = v_1v_2\cdots v_t$ on t vertices where $t = 4\left\lfloor \frac{k(k-1)(k-2)+4}{8}\right\rfloor$. As

  $$\frac{(k-1)^2(k-2)}{2} < 4\left\lfloor \frac{k(k-1)(k-2)+4}{8}\right\rfloor \le \frac{k^2(k-1)}{2},$$

  we must have $\chi _{NL}(P_t) = k$ (see [2]). Let $\phi _1$ be any neighbor-locating k-coloring of $G_1$ and

  $$X_1 = \{(v_{i-1}, v_{i+1}) : i\equiv 2,3 \pmod 4 \}.$$

• (iii) Suppose an i-triplet $(G_i, \phi _i, X_i)$ is given. We will (partially) describe a way to construct an $(i+1)$-triplet from it. To do so, first we will construct an intermediate graph $G'_{i+1}$ as follows: for each $(i+1)$-tuple $(x_1, x_2, \cdots , x_{i+1}) \in X_i$ we will add a new vertex $x_{i+2}$ adjacent to each vertex from the $(i+1)$-tuple. Moreover, $(x_1, x_2, \cdots , x_{i+1}, x_{i+2})$ is designated as an $(i+2)$-tuple in $G'_{i+1}$. After that, we will take k copies of $G'_{i+1}$ and call this so-obtained graph as $G''_{i+1}$. Furthermore, we will extend $\phi _i$ to a function $\phi _{i+1}$ by assigning the color $(ik+j)$ to the new vertices from the $j^{th}$ copy of $G'_{i+1}$. The copies of the $(i+2)$-tuples are the $(i+2)$-tuples of $G''_{i+1}$.

• (iv) Consider the $(i+1)$-triplet $(G''_{i+1}, \phi _{i+1}, X''_{i+1})$ where $X''_{i+1}$ denotes the set of all $(i+2)$-tuples of $G''_{i+1}$. The color of an $(i+2)$-tuple $(x_1, x_2, \cdots , x_{i+2})$ is the set

  $$C((x_1, x_2, \cdots , x_{i+2}))= \{\phi _i(x_1), \phi _i(x_2), \cdots , \phi _i(x_{i+2})\}.$$

  Let us partition the set of new vertices based on the colors used on the elements (all but the last one) of the $(i+2)$-tuple of which it is (uniquely) part of. To be explicit, the last elements of two $(i+2)$-tuples are in the same partition if and only if they have the same color. Let this partition be denoted by $X_{i1}, X_{i2}, \cdots , X_{is_i}$, for some integer $s_i$.

• (v) First fix a partition $X_{ir}$ of $X_i$. Next construct a matrix with its $\ell ^{th}$ column having vertices from $X_{ir}$ as its entries if they are also from the $\ell ^{th}$ copy of $G'_{i+1}$ in $G''_{i+1}$. Thus the matrix is a $(p \times q)$ matrix where $p = |X_{ir}|$ and $q = k$. We are going to show that, $p < q$. However, for convenience, we will defer it to a later part (Lemma 2).

• (vi) Let us delete all the new vertices from $G''_{i+1}$ except for the ones in $X_{ir}$. This graph has the exact same properties of the graph G from Corollary 4 where $X_{ir}$ plays the role of the independent set M. Thus it is possible to add a matching and extend the coloring (like in Corollary 4). We do that for each value of r and add the corresponding matching to our graph $G''_{i+1}$. After adding all such matchings, the graph we obtain is $G_{i+1}$.

Lemma 2

  We have $|X_{ir}| < k$, where $X_{ir}$ is as in Item(v) of the above list.

Proof

It is easy to calculate that the set of 2-tuples having the same color in $G_1$ is strictly less than k. After that we are done by induction.    $\square$

Lemma 3

The function $\phi _{i+1}$ is a neighbor-locating coloring of $G_{i+1}$.

Proof

The function $\phi _{i+1}$ is constructed from $\phi _i$, alongside constructing the triplet $G_{i+1}$ from $G_i$. While constructing, we use the same steps from that of Corollary 4. Thus, the newly colored vertices become neighbor-distinguished in $G_{i+1}$ under $\phi _{i+1}$.    $\square$

The above two lemmas validate the correctness of the iterative construction of $G_i$s. However, it remains showing how $G_i$s help us prove our result. To do so, let us prove certain properties of $G_i$s.

Lemma 4

The graph $G_i$ is not regular and has maximum degree $(i+1)$.

Proof

As we have started with a path, our $G_1$ has maximum degree 2 and is not regular. In the iteration step for constructing the graph $G_{i+1}$ from $G_i$, the degree of an old vertex (or its copy) can increase at most by 1, while a new vertex of $G_{i+1}$ is adjacent to exactly $(i+1)$ old vertices and at most one new vertex. Hence, a new vertex in $G_{i+1}$ can have degree at most $(i+2)$. Therefore, the proof is done by induction.    $\square$

Finally, we are ready to prove Theorem 4.

Proof of Theorem 4. Given a and b, to build the example that will prove the theorem, one can consider $G = G_{2a+1}$.    $\square$