Local Neighbor-Distinguishing Index of Graphs

Abstract

Suppose that G is a graph and $\phi$ is a proper edge-coloring of G. For a vertex $v\in V(G)$, let $C_{\phi }(v)$ denote the set of colors assigned to the edges incident with v. The graph G is local neighbor-distinguishing with respect to the coloring $\phi$ if for any two adjacent vertices x and y of degree at least two, it holds that $C_{\phi }(x)\not \subseteq C_{\phi }(y)$ and $C_{\phi }(y)\not \subseteq C_{\phi }(x)$. The local neighbor-distinguishing index, denoted $\chi '_\textrm{lnd}(G)$, of G is defined as the minimum number of colors in a local neighbor-distinguishing edge-coloring of G. For $n\ge 2$, let $H_n$ denote the graph obtained from the bipartite graph $K_{2,n}$ by inserting a 2-vertex into one edge. In this paper, we show the following results: (1) For any graph G, $\chi '_\textrm{lnd}(G)\le 3\Delta -1$; (2) suppose that G is a planar graph. Then $\chi '_\textrm{lnd}(G)\le \lceil 2.8\Delta \rceil +4$; and moreover $\chi '_\textrm{lnd}(G)\le 2\Delta +10$ if G contains no 4-cycles; $\chi '_\textrm{lnd}(G)\le \Delta +23$ if G is 3-connected; and $\chi '_\textrm{lnd}(G)\le \Delta +6$ if G is Hamiltonian.

1 Introduction

Only simple graphs are considered in this paper. Let G be a graph with vertex set V(G), edge set E(G), minimum degree $\delta (G)$ and maximum degree $\Delta (G)$ (for short, $\Delta$). For a vertex $v\in V(G)$, let $d_G(v)$ denote the degree of v in G. Set $|G|=|V(G)|$ and $||G||=|E(G)|$. A k-vertex, $k^-$-vertex, and $k^+$-vertex of G are a vertex with degree k, at most k, and at least k, respectively. A graph G is normal if it contains no isolated edges, and formal if it contains no leaves. A graph G is called planar if it can be embedded in the plane such that all edges intersect in their end-vertices. A plane graph is a particular drawing of a planar graph in the plane. For two nonnegative integers p, q with $p<q$, we use [p, q] to denote the set of all integers between p and q (including p and q).

An edge-k-coloring of a graph G is a mapping $\phi$ from the edge set E(G) to the color set $\{1,2,\ldots ,k\}$ such that no two adjacent edges get same color. Here two edges are said to be adjacent if they share at least one common end vertex. The chromatic index $\chi '(G)$ of the graph G is defined as the smallest integer k such that G admits an edge-coloring using k colors. Given an edge-k-coloring $\phi$ of G and for a vertex $v\in V(G)$, we use $C_{\phi }(v)$ to denote the set of colors assigned to the edges incident with v. Suppose that x, y are any pair of adjacent vertices in G. We say that $\phi$ is neighbor-distinguishing if $C_{\phi }(x)\ne C_{\phi }(y)$, strict neighbor-distinguishing if $C_{\phi }(x)\not \subseteq C_{\phi }(y)$ and $C_{\phi }(y)\not \subseteq C_{\phi }(x)$, and local neighbor-distinguishing if $C_{\phi }(x)\not \subseteq C_{\phi }(y)$ and $C_{\phi }(y)\not \subseteq C_{\phi }(x)$ whenever $d_G(x),d_G(y)\ge 2$. The neighbor-distinguishing index $\chi '_\textrm{a}(G)$ (strict neighbor-distinguishing index $\chi '_\textrm{snd}(G)$, local neighbor-distinguishing index $\chi '_\textrm{lnd}(G)$, respectively) of G is the smallest k such that G has a neighbor-distinguishing edge-k-coloring (a strict neighbor-distinguishing edge-k-coloring, a local neighbor-distinguishing edge-k-coloring, respectively).

As an easy observation, a graph G has a neighbor-distinguishing edge-coloring if and only if G is normal, and G has a strict neighbor-distinguishing edge-coloring if and only if G is formal. But the local neighbor-distinguishing edge-coloring is well defined for any graph G.

It is evident that $\chi '_\textrm{snd}(G)\ge \chi '_\textrm{a}(G)\ge \Delta$ for any formal graph G. Moreover, the following propositions hold obviously.

Proposition 1

If G is a graph with $\delta (G)\ge 2$, then $\chi '_\textrm{lnd}(G)=\chi '_\textrm{snd}(G)$.

Proposition 2

If G is an $r~(\ge 2)$-regular graph, then $\chi '_\textrm{lnd}(G)=\chi '_\textrm{snd}(G)=\chi '_\textrm{a}(G)$.

Zhang et al. [23] introduced the neighbor-distinguishing edge-coloring of graphs and proposed the following challenging conjecture.

Conjecture 1

Every normal graph G, other than a 5-cycle, has $\chi '_\textrm{a}(G)\le \Delta +2$.

Akbari et al. [1] proved that every normal graph G satisfies $\chi '_\textrm{a}(G)\le 3\Delta$. This result was gradually improved to $\chi '_\textrm{a}(G)\le 2.5\Delta$ by Wang et al. [21], and to $\chi '_\textrm{a}(G)\le 2\Delta +2$ by Vučković [17]. In 2005, using probabilistic analysis, Hatami [10] showed that every normal graph G with $\Delta > 10^{20}$ has $\chi '_\textrm{a}(G)\le \Delta +300$. Recently, this result was improved, by Joret and Lochet [13], to that $\chi '_\textrm{a}(G)\le \Delta +19$ for a normal graph with sufficiently large $\Delta$. Suppose that G is a normal planar graph. It was shown in [11] that if $\Delta \ge 12$ then $\chi '_\textrm{a}(G)\le \Delta +2$. Moreover, Wang and Huang [20] showed that if $\Delta \ge 16$, then $\Delta \le \chi '_\textrm{a}(G)\le \Delta +1$, and $\chi '_\textrm{a}(G)=\Delta +1$ if and only if G contains adjacent $\Delta$-vertices. This result was improved in [19] to that if $\Delta \ge 14$, then $\Delta \le \chi '_\textrm{a}(G)\le \Delta +1$, and $\chi '_\textrm{a}(G)=\Delta +1$ if and only if G contains adjacent $\Delta$-vertices.

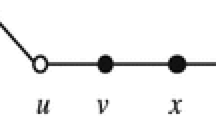
The strict neighbor-distinguishing edge-coloring of graphs was studied in [24] (named there the Smarandachely adjacent vertex edge coloring). Let $H_n$ ($n\ge 2$) denote the graph obtained from the bipartite graph $K_{2,n}$ by inserting a 2-vertex into one edge. It is easy to show that $\chi '_\textrm{snd}(H_n)=2n+1=2\Delta (H_n)+1$. Based on this fact, Gu et al. [8] raised the following conjecture.

Conjecture 2

Every connected formal graph G, different from $H_{\Delta }$, has $\chi '_\textrm{snd}(G)\le 2\Delta$.

Because $\chi '_\textrm{snd}(K_{2,n})=2n=2\Delta (K_{2,n})$, the upper bound $2\Delta$ in Conjecture 2 is sharp. Conjecture 2 remains open, but it was confirmed for graphs with $\Delta \le 3$ in [8] and $K_4$-minor-free graphs in [9].

In this paper, we continue to study the strict neighbor-distinguishing edge-coloring of graphs, in particular, for the class of planar graphs. As a helpful tool, we consider its relaxed form, i.e., local neighbor-distinguishing edge-coloring of graphs. Our main results in this paper are stated as follows:

• $\chi '_\textrm{lnd}(G)\le 3\Delta -1$ for any simple graph G;

• $\chi '_\textrm{lnd}(G)\le \lceil 2.8\Delta \rceil +4$ for a planar graph G;

• $\chi '_\textrm{lnd}(G)\le 2\Delta +10$ for a planar graph G without 4-cycles;

• $\chi '_\textrm{lnd}(G)\le \Delta +23$ for a 3-connected planar graph G;

• $\chi '_\textrm{lnd}(G)\le \Delta +6$ for a Hamiltonian planar graph G.

2 An Upper Bound

Let G be a graph and $\phi$ be a local neighbor-distinguishing edge-k-coloring of G. For the sake of briefness, $\phi$ is called a k-LNDE-coloring of G. Two adjacent vertices u and v are exclusive in $\phi$ if $C_{\phi }(u)\not \subseteq C_{\phi }(v)$ and $C_{\phi }(v)\not \subseteq C_{\phi }(u)$. To give an upper bound of the local neighbor-distinguishing index of a graph, we need to use the following result:

Lemma 2.1

([23]) For a cycle $C_n$ with $n\ge 3$,

$$\begin{aligned} \chi '_\textrm{a}(C_n)=\left\{ \begin{array}{ll} 3, &{} {\textrm{if}}\, n=3;\\ 5, &{} {\textrm{if}}\, n=5;\\ 4, &{} {\textrm{if}}\, n\ne 3,5. \end{array}\right. \end{aligned}$$

Theorem 2.2

Every graph with $\Delta \ge 2$ has $\chi '_\textrm{lnd}(G)\le 3\Delta -1$.

Proof

The proof is by induction on the edge number ||G||. If $||G||\le 3\Delta -1$, then the result holds trivially since we can color the edges of G with distinct colors. Let G be a graph with $||G||\ge 3\Delta \ge 6$. Without loss of generality, assume that G is connected. So, it follows that $\Delta \ge 2$ and $\delta (G)\ge 1$. In the following, we write simply $K=3\Delta -1$ and let $C=[1,K]$ denote the set of K colors.

First assume that $\delta (G)=1$. Let v be a vertex adjacent to leaves $x_1,\ldots ,x_l$ and $2^+$-vertices $y_1,\ldots ,y_k$, where $l\ge 1$ and $k\ge 0$. Let $H=G-x_1$. Then H is a graph with $||H||<||G||$ and $\Delta (H)\le \Delta$. By the induction hypothesis, H admits a K-LNDE-coloring $\phi$ using the color set C. For $i\in [1,k]$, since v and $y_i$ are exclusive in $\phi$, there exists a color $r_i\in C_{\phi }(y_i){\setminus } C_{\phi }(v)$. Set $R(v)=\{r_1,\ldots ,r_k\}$, which is called the second-level forbidden set of vertex v. Obviously, $|R(v)|\le k$. Based on $\phi$, we color $vx_1$ with a color $a\in C{\setminus } (C_{\phi }(v)\cup R(v))$. Since $|C{\setminus } (C_{\phi }(v)\cup R(v))|\ge 3\Delta -1- |C_{\phi }(v)|-k\ge 3\Delta -1-(\Delta -1)-(\Delta -1) = \Delta +1\ge 3$, a exists and so the coloring is available. It is easy to check that the resultant coloring is a K-LNDE-coloring of G.

Next assume that $\delta (G)\ge 2$. If $\Delta =2$, then G is a cycle. By Lemma 2.1 and Proposition 2, $\chi '_\textrm{lnd}(G)=\chi '_\textrm{a}(G)\le 5=3\Delta -1$. So assume that $\Delta \ge 3$. The proof is split into two cases as follows, depending on the size of $\delta (G)$.

Case I.$\delta (G)=2$.

Let v be a 2-vertex with neighbors $v_1,v_2$ such that $d_G(v_1)\le d_G(v_2)$. Without loss of generality, we may suppose that $d_G(v_2)\ge 3$ by the assumption that $\Delta \ge 3$. The proof is split into two subcases as follows.

• $d_G(v_1)=2$. Let $u_1$ be the neighbor of $v_1$ other than v. If $u_1=v_2$, then $H=G-vv_1$ is a graph with $||H||<||G||$ and $\Delta (H)=\Delta$. By the induction hypothesis, H admits a K-LNDE-coloring $\phi$ using the color set C. Based in $\phi$, it suffices to color $vv_1$ with some color in $C\setminus C_{\phi }(v_2)$. If $u_1\ne v_2$, then let $H=G-v$, which has a K-LNDE-coloring $\phi$ using the color set C by the induction hypothesis. We first color $vv_2$ with $a\in C{\setminus } (C_{\phi }(v_2)\cup R(v_2)\cup \{\phi (v_1u_1)\})$, where $R(v_2)$ is the second-level forbidden set of vertex $v_2$, as defined before. Then we color $vv_1$ with $b\in C{\setminus } (C_{\phi }(u_1)\cup C_{\phi }(v_2)\cup \{a\})$. For short, we write $C^+_{\phi }(v_2)=C_{\phi }(v_2)\cup R(v_2)$ in the following discussion. Since $|C{\setminus } (C^+_{\phi }(v_2)\cup \{\phi (v_1u_1)\})|\ge 3\Delta -1-2(d_G(v_2)-1)-1\ge \Delta \ge 2$ and $|C{\setminus } (C_{\phi }(u_1)\cup C_{\phi }(v_2)\cup \{a\})|\ge 3\Delta -1-2\Delta \ge \Delta -1\ge 1$, both a and b exist and hence $\phi$ is extended to G.

• $d_G(v_1)\ge 3$. Let $H=G-v$, which admits a K-LNDE-coloring $\phi$ using C. Based on $\phi$, we color $vv_1$ with $a\in C\setminus (C^+_{\phi }(v_1)\cup C_{\phi }(v_2))$, and $vv_2$ with $b\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{a\})$. Since $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2))|\ge 3\Delta -1-2(\Delta -1)-(\Delta -1)\ge 2$ and $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{a\})|\ge 3\Delta -1-2(\Delta -1)-(\Delta -1)-1\ge 1$, a, b exist and $\phi$ is extended to G.

Case II. $\delta (G)\ge 3$.

Take a vertex $v\in V(G)$ with $d_G(v)=\delta (G)\ge 3$. Let $v_0, \ldots ,v_{k-1}$ be the neighbors of v in G, where $k=d_G(v)$. Let $H=G-v$. Then H is a graph with $\delta (H)\ge 2$, $\Delta (H)\le \Delta$, and $||H||<||G||$. By the induction hypothesis, H admits a K-LNDE-coloring $\phi$ using C. Let $x_1, \ldots ,x_m$ be the neighbors of $v_0$ in H, where $m=d_G(v_0)-1\ge 2$. For $i\in [1,m]$, there exists a color $r_i\in C_{\phi }(x_i){\setminus } C_{\phi }(v_0)$ since $v_0$ and $x_i$ are exclusive in $\phi$. Let $R(v_0)=\{r_1, \ldots ,r_m\}$. Similarly, we can define $R(v_1), \ldots ,R(v_{k-1})$. Let $U_i=C^+_{\phi }(v_i)$ for $i\in [0,k-1]$. Then $|U_i|=|C_{\phi }(v_i)\cup R(v_i)|\le |C_{\phi }(v_i)|+|R(v_i)|\le (\Delta -1)+(\Delta -1)=2\Delta -2$.

To extend $\phi$ to G, we design a coloring procedure as following.

Step 0. Color $vv_0$ with a color $c_0\in C{\setminus } (U_0\cup C_{\phi }(v_1))$, and then set $B_0=\{c_0\}$.

Step 1. For $i\in [1,k-1]$, we do the following operation, where all indices are taken modulo k:

• If $B_{i-1}\subseteq C_{\phi }(v_{i+1})$, then we color $vv_i$ with a color $c_i\in C\setminus (U_i\cup C_{\phi }(v_{i+1}))$; otherwise, we color $vv_i$ with a color $c_i\in C{\setminus } (U_i\cup B_{i-1})$.

• Set $B_i=B_{i-1}\cup \{c_i\}$.

Step 2. If $i=k-1$, stop. Otherwise, set $i=i+1$, then go to Step 1.

Let $\pi$ denote the resultant edge-coloring of G after the above iterative process is ended. Let $B=B_{k-1}$. Then $B=C_{\pi }(v)$. We will show that $\pi$ is a K-LNDE-coloring of G.

Claim 1. $\pi$ is a proper edge-K-coloring of G.

Proof

We first prove the existence of the color $c_i$ for $i\in [0,k-1]$. In fact, since $|C{\setminus } (U_0\cup C_{\phi }(v_1))|\ge |C|-|U_0|-|C_{\phi }(v_1)|\ge (3\Delta -1)-(2\Delta -2)-(\Delta -1) =2$, $c_0$ exists. Assume that $1\le i\le k-1$. If $B_{i-1}\subseteq C_{\phi }(v_{i+1})$, then $c_i\in C\setminus (U_i\cup C_{\phi }(v_{i+1}))$ by Step 1. Since $|C{\setminus } (U_i\cup C_{\phi }(v_{i+1}))|\ge (3\Delta -1)-(2\Delta -2)-(\Delta -1)=2$, $c_i$ exists. Otherwise, $B_{i-1}\not \subseteq C_{\phi }(v_{i+1})$. By Step 1, $c_i\in C{\setminus } (U_i\cup B_{i-1})$. Since $|B_{i-1}|\le i\le k-1=d_G(v)-1=\delta (G)-1\le \Delta -2$, it follows that $|C{\setminus } (U_i\cup B_{i-1})|\le (3\Delta -1)-(2\Delta -2)-(\Delta -2)=3$; thus, $c_i$ exists. Next, we need to show that $c_0,c_1,\ldots ,c_{k-1}$ are mutually distinct. Actually, this is true from the definition of $B_i$’s. Hence, $\pi$ is a proper edge-K-coloring of G.$\square$

Claim 2. $\pi$ is local neighbor-distinguishing.

Proof

It suffices to show that for any edge $xy\in E(G)$, we have

$$\begin{aligned} C_{\pi }(x)\not \subseteq C_{\pi }(y)\ \textrm{and} \ C_{\pi }(y)\not \subseteq C_{\pi }(x)(*) \end{aligned}$$

By symmetry, we consider the following three possibilities.

Case 1. $x,y\notin \{v,v_0,\ldots ,v_{k-1}\}$.

Note that $\pi (e)=\phi (e)$ for each edge e incident with x or y in G. This implies that $C_{\pi }(x)=C_{\phi }(x)$ and $C_{\pi }(y)=C_{\phi }(y)$. Since $C_{\phi }(x)\not \subseteq C_{\phi }(y)$ and $C_{\phi }(y)\not \subseteq C_{\phi }(x)$, $(*)$ holds.

Case 2. $y\notin \{v,v_0, \ldots ,v_{k-1}\}$ and $x=v_i$ for some $i\in [0,k-1]$.

By symmetry, suppose that $i=0$, i.e., $x=v_0$. Then $C_{\pi }(y)=C_{\phi }(y)$ and $C_{\pi }(v_0)=C_{\phi }(v_0)\cup \{c_0\}$. Since $C_{\phi }(v_0)\not \subseteq C_{\phi }(y)$, it is immediate to derive that $C_{\pi }(v_0)= C_{\phi }(v_0)\cup \{c_0\} \not \subseteq C_{\phi }(y) = C_{\pi }(y)$. Conversely, there is a color $b\in R(v_0)$ such that $b\in C_{\phi }(y){\setminus } C_{\phi }(v_0)$ and $c_0\ne b$. This implies that $C_{\pi }(y) \not \subseteq C_{\pi }(v_0)$. Hence, $(*)$ holds.

Case 3. $x=v$ and $y=v_i$ for some $i\in [0,k-1]$.

Then $C_{\pi }(v)=B$ and $C_{\pi }(v_i)=C_{\phi }(v_i)\cup \{c_i\}$. Let $i\in [0,k-1]$. Since $d_G(v)=k=\delta (G)\le d_G(v_i)$, it is easy to derive that $C_{\pi }(v_i)\not \subset C_{\pi }(v)=B$. Conversely, suppose that $B\subset C_{\pi }(v_i)$. We discuss three possibilities to get a contradiction.

• $i=0.$ Since $B_{k-2}=\{c_0, \ldots ,c_{k-2}\} \subset B \subset C_{\pi }(v_0)$, it follows that $c_{k-1}\in C{\setminus } (U_{k-1}\cup C_{\phi }(v_0))$ by Step 1. This implies that $c_{k-1}\notin C_{\phi }(v_0)$, which contradicts the assumption that $c_{k-1}\in B_{k-1}=B\subset C_{\pi }(v_0)$.

• $i=1.$ Step 0 implies that $c_0\in C{\setminus } (U_0\cup C_{\phi }(v_1))$. Thus, $c_0\notin C_{\pi }(v_1)$. Since $c_0\in B$, it follows that $B\not \subset C_{\pi }(v_1)$, which is a contradiction.

• $i\in [2,k-1].$ Note that $B_{i-2}=\{c_0, \ldots ,c_{i-2}\}\subset B\subset C_{\pi }(v_{i})$. By Step 1, $c_{i-1}\in C\setminus (U_{i-1}\cup C_{\phi }(v_i))$, implying $c_{i-1}\notin C_{\phi }(v_i)$, which contradicts the assumption that $c_{i-1}\in B_{i-1}\subset B\subset C_{\pi }(v_i)$.

By Claims 1 and 2, $\pi$ is a K-LNDE-coloring of G. $\square$

Theorem 2.3 follows immediately from Theorem 2.2 and Proposition 1:

Theorem 2.3

Every formal graph G has $\chi '_\textrm{snd}(G)\le 3\Delta -1$.

3 General Planar Graphs

Assume that G is a plane graph. A cycle $C^*$ of G is called a separating cycle if there exist at least one vertex in the interior and exterior of $C^*$, respectively.

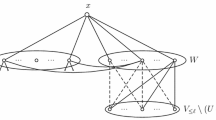
A bunch B(x, y; m) of length $m\ge 3$ with x and y as poles is defined as m paths $Q_1, Q_2,\ldots ,Q_m$ having the following properties, as shown in 1:

• (a) Each $Q_i$ has length 1 or 2 and joins x and y;

• (b) For each $i\in [1,m-1]$, the cycle formed by $Q_i$ and $Q_{i+1}$ is not separating;

• (c) This sequence of paths is maximal, that is, there does not exist a path $Q_0$ (or $Q_{m+1}$) that can be added to B(x, y; m) with conditions (a) and (b) preserved.

Fig. 1

a B(x, y; m) with $xy\notin E(G)$; b B(x, y; m) with $xy\in E(G)$

If the length of $Q_i$ is 2, say $P_i=xz_iy$, then $z_i$ is called a brother. If $Q_i=xy$, then xy is called a parental edge. Assume that $z_i$ exists. We further say that $z_i$ is an external brother if $i\in \{1,m\}$, an internal brother if $i\in [2,m-1]$, and a strictly internal brother if $i\in [3,m-2]$. It is easy to see that each internal brother is of degree 2, 3, or 4 and adjacent only to the poses and possibly to one or two of brothers.

Borodin et al. [4] introduced the concept of the bunch in a plane graph and established a structural theorem on plane graphs. For our purposes, we only give the following simplified version of their theorem.

Lemma 3.1

([4]) Every plane graph G with $\delta (G)\ge 2$ contains one of the following configurations:

• (A1) a k-vertex v, $k\in [2,5]$, with neighbors $v_1, \ldots ,v_{k}$ such that $d_G(v_i)\le 25$ for all $i\in [1,k-1]$, and $d_G(v_1)+ \cdots +d_G(v_{k-1})\le 38$;

• (A2) a bunch B(x, y; m) with $d_G(x)\ge 26$ and $m\ge 0.2d_G(x)$.

Using Lemma 3.1, we can obtain an upper bound of the local neighbor-distinguishing index of planar graphs.

Theorem 3.2

If G is a planar graph, then $\chi '_\textrm{lnd}(G)\le \lceil 2.8\Delta \rceil +4$.

Proof

The proof proceeds by induction on ||G||. If $||G||\le \lceil 2.8\Delta \rceil +4$, then the result holds trivially. Let G be a planar graph with $||G||\ge \lceil 2.8\Delta \rceil +5\ge 5$. Without loss of generality, suppose that G is connected and embedded in the plane. If $\Delta \le 29$, then $\chi '_\textrm{lnd}(G)\le 3\Delta -1\le \lceil 2.8\Delta \rceil +4$ by Theorem 2.2. So suppose that $\Delta \ge 30$, which implies that $||G||\ge \lceil 2.8\Delta \rceil +4\ge 88$. In what follows, let $C=[1,K]$, where $K=\lceil 2.8\Delta \rceil +4$, be the set of K colors.

If G contains a 1-vertex v, then the graph $G-v$ admits a K-LNDE-coloring $\phi$ using the color set C by the induction hypothesis. Similarly to the proof of Theorem 2.2, $\phi$ can be extended to G.

So suppose that $\delta (G)\ge 2$. By Lemma 3.1, G contains the configurations (A1) or (A2). Our proof is split into the following cases.

Case 1. G contains a k-vertex v, $k\in [2,5]$, with neighbors $v_1,\ldots ,v_{k}$ such that $d_G(v_i)\le 25$ for all $i\in [1,k-1]$, and $d_G(v_1)+\cdots +d_G(v_{k-1})\le 38$.

Without loss of generality, assume that $d_G(v_1)\le \cdots \le d_G(v_k)$. Depending on the size of k, we have some subcases to be considered below.

Case 1.1. $k=2$.

Note that $d_G(v_1)\le 25$. Let $H=G-v$, which admits a K-LNDE-coloring $\phi$ using C. Based on $\phi$, we color $vv_2$ with a color $a\in C\setminus (C^+_{\phi }(v_2)\cup C_{\phi }(v_1))$, where $C^+_{\phi }(v_2)=C_{\phi }(v_2)\cup R(v_2)$ as defined in 2, and $vv_1$ with a color $b\in C{\setminus } (C^+_{\phi }(v_1) \cup C_{\phi }(v_2)\cup \{a\})$. Since $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1))|\ge \lceil 2.8\Delta \rceil +4 -2(d_G(v_2)-1)-(d_G(v_1)-1)\ge 2.8\Delta +7-2\Delta -25=0.8\Delta -18 \ge 6$ and $|C{\setminus } (C^+_{\phi }(v_1) \cup C_{\phi }(v_2)\cup \{a\})|\ge \lceil 2.8\Delta \rceil +4 - 2(25-1)-(\Delta -1)-1\ge 1.8\Delta -44\ge 10$, both a and b exist and hence $\phi$ is extended to G.

By Case 1.1, we may assume that $d_G(v_i)\ge 3$ for all $i\in [1,k]$ in the subsequent discussion.

Case 1.2. $k=3$.

Note that $d_G(v_2)\le 25$, and since $d_G(v_1)+d_G(v_2)\le 38$, we derive that $d_G(v_1)\le 19$. Let $H=G-\{vv_1, vv_2\}$, which has a K-LNDE-coloring $\phi$ using C. Suppose that $\phi (vv_3)=1$. We color $vv_2$ with $a\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{1\})$ and $vv_1$ with $b\in C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup \{a\})$. It is easy to calculate that $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{1\})|\ge \lceil 2.8\Delta \rceil +4-2(\Delta -1)-(d_G(v_1)-1)-1 \ge 0.8\Delta +6-d_G(v_1)\ge 0.8\Delta +6-19\ge 11$ and $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup \{a\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(v_1)-1)-(d_G(v_2)-1)-\Delta -1\ge 1.8\Delta +6-(d_G(v_1)+d_G(v_2))-d_G(v_1) \ge 1.8\Delta +6-38-19\ge 3$. Hence, both a and b exist. Let $\phi '$ denote the resultant coloring after $vv_1$ and $vv_2$ are colored. Obviously, $\phi '$ is a proper edge-K-coloring of G. Note that $C_{\phi '}(v)=\{1,a,b\}$, $a\notin C_{\phi '}(v_1)$, $b\notin C_{\phi '}(v_2)$, and $a,b\notin C_{\phi '}(v_3)$. Since $d_G(v_i)\ge 3$ for $i\in [1,3]$, v is exclusive with each of its neighbors. Consequently, $\phi '$ is a K-LNDE-coloring of G.

Case 1.3. $k=4$.

Since $d_G(v_1)+d_G(v_2)+d_G(v_3)\le 38$ and $d_G(v_i)\ge 3$ for $i\in [1,4]$, it follows that $d_G(v_1)\le 12$, $d_G(v_2)\le 17$, and $d_G(v_3)\le 25$. Let $H=G-\{vv_1, vv_2,vv_3\}$, which has a K-LNDE-coloring $\phi$ using C and with $\phi (vv_4)=1$. We color $vv_3$ with $a\in C{\setminus } (C^+_{\phi }(v_3)\cup C_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{1\})$, $vv_2$ with $b\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a\})$, and $vv_1$ with $c\in C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a,b\})$. It is easy to check that $|C{\setminus } (C^+_{\phi }(v_3)\cup C_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{1\})|\ge 88-2(d_G(v_3)-1)-(d_G(v_2)-1)-(d_G(v_1)-1)-1= 91-d_G(v_3)-(d_G(v_1)+d_G(v_2)+d(v_3))\ge 91-25-38=28$, $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(v_2)-1)-(d_G(v_1)-1)-(d_G(v_3)-1)-\Delta -1\ge 1.8\Delta +7-d_G(v_2)-(d_G(v_1)+d_G(v_2)+d_G(v_3))\ge 1.8\Delta +7-17-38\ge 6$, and $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a,b\})|\ge \lceil 2.8\Delta \rceil +4- 2(d_G(v_1)-1)-(d_G(v_2)-1)-(d_G(v_3)-1)-\Delta -2\ge 1.8\Delta +6-d_G(v_1)-(d_G(v_1)+d_G(v_2)+d_G(v_3))\ge 1.8\Delta +6-12-38\ge 10$. Hence, $vv_1,vv_2,vv_3$ can be colored properly. Let $\phi '$ denote the resultant coloring of G. It is easy to observe that $C_{\phi '}(v)=\{1,a,b,c\}$, and $b,c\notin C_{\phi '}(v_4)$, $b,c\notin C_{\phi '}(v_3)$, $a,c\notin C_{\phi '}(v_2)$, and $a,b\notin C_{\phi '}(v_1)$. Since $d_G(v_i)\ge 3$ for $i\in [1,4]$, v is exclusive with each of its neighbors in $\phi '$. Consequently, $\phi '$ is a K-LNDE-coloring of G.

Case 1.4. $k=5$.

Since $d_G(v_1)+ \cdots +d_G(v_4)\le 38$ and $d_G(v_i)\ge 3$ for $i\in [1,5]$, it is immediate to deduce that $d_G(v_1)\le 9$, $d_G(v_2)\le 11$, $d_G(v_3)\le 16$, and $d_G(v_4)\le 25$. Let $H=G-\{vv_1, vv_2,vv_3,vv_4\}$, which has a K-LNDE-coloring $\phi$ using C such that $\phi (vv_5)=1$. Define the sets $M_4=\bigcup \limits _{i=1}^{4} C_{\phi }(v_i)$ and $M_5=M_4\cup C_{\phi }(v_5)$. We have to consider two possibilities as follows.

Case 1.4.1. $d_G(v_5)\ge 4$.

We color $vv_4$ with $a\in C{\setminus } (M_4\cup R(v_4)\cup \{1\})$, $vv_3$ with $b\in C{\setminus } ( M_4\cup R(v_3) \cup \{1,a\})$, $vv_2$ with $c\in C\setminus (M_5\cup R(v_2)\cup \{a,b\})$ and $vv_1$ with $d\in C\setminus (M_5\cup R(v_1) \cup \{a,b,c\})$. It is easy to calculate that $|C{\setminus } (M_4\cup R(v_4)\cup \{1\})|\ge 88-2(d_G(v_4)-1)-(d_G(v_1)-1)-(d_G(v_2)-1)-(d_G(v_3)-1)-1=92-d_G(v_4)-(d_G(v_1)+d_G(v_2)+d_G(v_3)+d_G(v_4))\ge 92-25-38=29$, $|C{\setminus } ( M_4\cup R(v_3) \cup \{1,a\})|\ge 88-2(d_G(v_3)-1)-(d_G(v_1)-1)- (d_G(v_2)-1)-(d_G(v_4)-1)-2=91-d_G(v_3)-(d_G(v_1)+d_G(v_2)+d_G(v_3)+d_G(v_4))\ge 91-16-38=37$, $|C{\setminus } (M_5\cup R(v_2)\cup \{a,b\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(v_2)-1)-(d_G(v_1)-1)-(d_G(v_3)-1)-(d_G(v_4)-1)-d_G(v_5)-2 \ge 1.8\Delta + 7-d_G(v_2)-(d_G(v_1)+d_G(v_2)+d_G(v_3)+d_G(v_4))\ge 1.8\Delta +7-11-38\ge 12$, and $|C{\setminus } (M_5\cup R(v_1) \cup \{a,b,c\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(v_1)-1)-(d_G(v_2)-1)-(d_G(v_3)-1)-(d_G(v_4)-1)-d_G(v_5)-3 \ge 1.8\Delta + 6-d_G(v_1)-(d_G(v_1)+d_G(v_2)+d_G(v_3) +d_G(v_4))\ge 1.8\Delta +6-9-38\ge 13$. Thus, the resultant coloring, denoted $\phi '$, is a proper edge-K-coloring of G. Observe that $C_{\phi '}(v)=\{1,a,b,c,d\}$, $c,d\notin C_{\phi '}(v_5)$, $c,b,d\notin C_{\phi '}(v_4)$, $a,c,d\notin C_{\phi '}(v_3)$, $a,b,d\notin C_{\phi '}(v_2)$, and $a,b,c\notin C_{\phi '}(v_1)$. Since $d_G(v_5)\ge 4$ and $d_G(v_i)\ge 3$ for $i\in [1,4]$, v is exclusive with each of its neighbors in $\phi '$. Hence, $\phi '$ is a K-LNDE-coloring of G.

Case 1.4.2. $d_G(v_5)=3$.

It follows that $d_G(v_i)=3$ for all $i\in [1,4]$. It is evident that $|M_5|\le 2\times 4+3=11$. We color $vv_4$ with $a\in C{\setminus } (M_5\cup R(v_4))$, $vv_3$ with $b\in C{\setminus } (M_5\cup R(v_3)\cup \{a\})$, $vv_2$ with $c\in C{\setminus } (M_5\cup R(v_2)\cup \{a,b\})$, and $vv_1$ with $d\in C{\setminus } (M_5\cup R(v_1)\cup \{a,b,c\})$. Then $|C{\setminus } (M_5\cup R(v_4))|\ge 88-11-2=75$, $|C{\setminus } (M_5\cup R(v_3)\cup \{a\})|\ge 88-11-2-1=74$, $|C{\setminus } (M_5\cup R(v_2)\cup \{a,b\})|\ge 88-11-2-2 =73$, $|C{\setminus } (M_5\cup R(v_1)\cup \{a,b,c\})|\ge 88-11-2-3=72$. It is easy to check that the extended coloring is a K-LNDE-coloring of G.

Case 2. G contains a bunch B(x, y; m) with $d_G(x)\ge 26$ and $m\ge 0.2d_G(x)$.

Here we use directly the notation in the definition of B(x, y; m), as shown in 1. Since $d_G(x)\ge 26$, it follows that $m\ge 6$. We need to deal with the following two subcases.

Case 2.1. There exist two adjacent vertices u and w such that $3\le d_G(u)\le d_G(w)\le 4$.

Case 2.1.1. $d_G(u)=3$.

Let s, t be the neighbors of u other than w. In view of the proof of Case 1.1, we may assume that $d_G(s),d_G(t)\ge 3$. Let $H=G-\{uw,us\}$, which has a K-LNDE-coloring $\phi$ using C such that $\phi (ut)=1$. We color us with $a\in C{\setminus } (C^+_{\phi }(s)\cup C_{\phi }(w)\cup \{1\})$ and uw with $b\in C{\setminus } (C^+_{\phi }(w)\cup C_{\phi }(s)\cup C_{\phi }(t)\cup \{a\})$. It is easy to check that $|C{\setminus } (C^+_{\phi }(s)\cup C_{\phi }(w)\cup \{1\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(s)-1)-(d_G(w)-1)-1\ge 0.8 \Delta + 6 -d_G(w)\ge 0.8\Delta +6-4=26$ and $|C{\setminus } (C^+_{\phi }(w)\cup C_{\phi }(s)\cup C_{\phi }(t)\cup \{a\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(w)-1)-(d_G(s)-1)-d_G(t)-1\ge 0.8\Delta +6-2\times 4\ge 22$. Hence, the resultant coloring $\phi '$ is a proper edge-K-coloring of G. Since $C_{\phi '}(u)=\{1,a,b\}$, $a\notin C_{\phi '}(w)$, and $b\notin C_{\phi '}(s)\cup C_{\phi '}(t)$, u is exclusive with each of its neighbors in $\phi$. Thus, $\phi$ is extended to G.

Case 2.1.2. $d_G(u)=d_G(w)=4$.

Let s, t, z be the neighbors of u other than w. By Case 2.1.1, assume that $d_G(s),d_G(t),d_G(z)\ge 4$. Let $H=G-\{uw,us\}$, which has a K-LNDE-coloring $\phi$ using C such that $\phi (ut)=1$ and $\phi (uz)=2$. Since $d_H(u)=2$, we see that $1\notin C_{\phi }(z)$ and $2\notin C_{\phi }(t)$. We color us with $a\in C{\setminus } (C^+_{\phi }(s)\cup C_{\phi }(w)\cup \{1,2\})$ and uw with $b\in C{\setminus } (C^+_{\phi }(w)\cup C_{\phi }(s) \cup \{1,2,a\})$. Since $|C{\setminus } (C^+_{\phi }(s)\cup C_{\phi }(w)\cup \{1,2\})|\ge \lceil 2.8\Delta \rceil +4-2(d_G(s)-1)- (d_G(w)-1)- 2\ge 0.8\Delta +5-d_G(w)=0.8\Delta +5-4\ge 25$ and $|C{\setminus } (C^+_{\phi }(w)\cup C_{\phi }(s) \cup \{1,2,a\})|\ge \lceil 2.8\Delta \rceil +4 -2(d_G(w)-1)- (d_G(s)-1)-3 \ge 1.8\Delta +4-2\times 4\ge 50$, uw and us can be colored properly. Denote by $\phi '$ the resultant coloring. Noting that $C_{\phi '}(u)=\{1,2,a,b\}$, $1\notin C_{\phi '}(z)$, $2\notin C_{\phi '}(t)$, $a\notin C_{\phi '}(w)$, and $b\notin C_{\phi '}(s)$, we obtain a K-LNDE-coloring of G.

Case 2.2. All strictly internal brothers are of degree 2 in G.

Let S denote the set of brothers $z_i$’s with $d_G(z_i)=2$ in B(x, y; m). Obviously, S contains all strictly internal brothers of B(x, y; m). Since $d_G(x)\ge 26$ and $m\ge 0.2d_G(x)>5$, B(x, y; m) has at least one strictly internal brother. Thus, $s:=|S|\ge m-5\ge 1$. Let $H=G-S$, which has a K-LNDE-coloring $\phi$ using C. Let $E_x=\{wx\,|\,w\in S\}$ and $E_y=\{wy\,|\,w\in S\}$. For each edge $e_x\in E_x$ and each edge $e_y\in E_y$, we define a list assignment L as follows:

$L(e_x)=C\setminus (C^+_{\phi }(x)\cup C_{\phi }(y))$, $L(e_y)=C\setminus (C^+_{\phi }(y)\cup C_{\phi }(x))$.

First suppose that $xy\notin E(G)$. Then $s\ge m-4\ge 2$. It is easy to compute that $|L(e_y)|\ge \lceil 2.8\Delta \rceil +4- 2(d_G(y)-s)-(d_G(x)-s)\ge 2.8\Delta +4 +3\,s-2d_G(y)-d_G(x)\ge 0.8\Delta +4+s+2\,s-d_G(x)\ge 0.8\Delta +4+s+2(m-4)-d_G(x)\ge 0.8\Delta -4+s+2\times (0.2d_G(x))-d_G(x) =0.8\Delta -4+s-0.6d_G(x)\ge 0.2\Delta -4+s\ge s+2$, and $|L(e_x)|\ge \lceil 2.8\Delta \rceil +4- 2(d_G(x)-s)-(d_G(y)-s)\ge 1.8\Delta +4 +2\,s +s-2d_G(x)\ge 1.8\Delta +4+2\,s+(m-4)-2d_G(x)= 1.8\Delta +2\,s+m-2d_G(x)\ge 1.8\Delta +2\,s+0.2d_G(x)-2d_G(x)\ge 2\,s$.

Next suppose that $xy\in E(G)$. In this case, $s\ge m-5\ge 1$. Because $xy\in E(G)$, we have $\phi (xy)\in C_{\phi }(x)\cap C_{\phi }(y)$ and hence $|C_{\phi }(x)\cap C_{\phi }(y)|\ge 1$. So, $|L(e_y)|\ge \lceil 2.8\Delta \rceil +4- 2(d_G(y)-s)-(d_G(x)-s)+1\ge 2.8\Delta +5 +3\,s-2d_G(y)-d_G(x)\ge 0.8\Delta +5+s+2\,s-d_G(x)\ge 0.8\Delta +5+s+2(m-5)-d_G(x)\ge 0.8\Delta -5+s+2\times (0.2d_G(x))-d_G(x) =0.8\Delta -5+s-0.6d_G(x)\ge 0.2\Delta -5+s\ge s+1$, and $|L(e_x)|\ge \lceil 2.8\Delta \rceil +4- 2(d_G(x)-s)-(d_G(y)-s)+1\ge 1.8\Delta +5 +2\,s +s-2d_G(x)\ge 1.8\Delta +5+2\,s+(m-5)-2d_G(x)= 1.8\Delta +2\,s+m-2d_G(x)\ge 1.8\Delta +2\,s+0.2d_G(x)-2d_G(x)\ge 2\,s$.

In each of the above two cases, we first color the edges in $E_y$ with distinct colors in $L(e_y)$ and then use $C_y$ to denote the set of colors assigned to the edges in $E_y$. Then we color the edges in $E_x$ with distinct colors in $L(e_x)\setminus C_y$. It is easy to check that the resultant coloring is a K-LNDE-coloring of G. $\square$

By Proposition 1, we have the following:

Theorem 3.3

If G is a formal planar graph, then $\chi '_\textrm{snd}(G)\le \lceil 2.8\Delta \rceil +4$.

4 Planar Graphs Without 4-Cycles

For the class of planar graphs without 4-cycles, we can show that Conjecture is almost true (away from a constant). To achieve this goal, we need to apply the following structural lemma.

Lemma 4.1

([18]) Let G be a planar graph with $\delta (G)\ge 2$ and without 4-cycles. Then G contains a k-vertex v, $k\in [2,4]$, whose neighbors $v_1,\ldots ,v_k$ satisfy one of the following conditions, assuming $d_G(v_1)\le \cdots \le d_G(v_k):$

• (1) $k=2$ and $d_G(v_1)\le 11$;

• (2) $k=3$ and $d_G(v_1)+d_G(v_2)\le 14$;

• (3) $k=4$ and $d_G(v_1)+d_G(v_2)+d_G(v_3)\le 15$.

Theorem 4.2

If G is a planar graph without 4-cycles, then $\chi '_\textrm{lnd}(G)\le 2\Delta +10$.

Proof

The proof proceeds by induction on ||G||. If $||G||\le 2\Delta +10$, then the result holds trivially. Let G be a connected planar graph with $||G||\ge 2\Delta +11\ge 11$. If $\Delta \le 11$, then $\chi '_\textrm{lnd}(G)\le 3\Delta -1\le 2\Delta +10$ by Theorem 2.2. So suppose that $\Delta \ge 12$. Again, let $K=2\Delta +10$ and $C=[1,K]$ denote a set of K colors. Hence, $|C|=K=2\Delta +10\ge 34$.

First assume that $\delta (G)=1$. Let u be a 1-vertex adjacent to a vertex v. Then $d_G(v)\ge 2$ by the assumption. Let $H=G-u$, which has a K-LNDE-coloring $\phi$ using C. We color uv with a color $a\in C{\setminus } C^+_{\phi }(v)$. Since $|C{\setminus } C^+_{\phi }(v)|\ge 2\Delta +10-2(d_G(v)-1)\ge 2\Delta +10-2(\Delta -1)=12$, $\phi$ is extended to G.

Next assume that $\delta (G)\ge 2$. By Lemma 4.1, G contains a k-vertex v, $k\in [2,4]$, whose neighbors $v_1, \ldots ,v_k$ satisfy one of the conditions (1) to (3), where $d_G(v_1)\le \cdots \le d_G(v_k)$. By the above proof, we may assume that $d_G(v_i)\ge 2$ for all $i\in [1,k]$.

Case 1. $k=2$ and $d_G(v_1)\le 11$.

Let $H=G-v$, which admits a K-LNDE-coloring $\phi$ using C. We have to discuss two possibilities.

• $d_G(v_1)=2$. Let y be the neighbor of $v_1$ other than v. We color $vv_2$ with $a\in C{\setminus } (C^+_{\phi }(v_2)\cup \{\phi (yv_1)\})$ and $vv_1$ with $b\in C{\setminus } (C_{\phi }(y)\cup C_{\phi }(v_2)\cup \{a\})$. Since $|C{\setminus } (C^+_{\phi }(v_2)\cup \{\phi (v_1y)\})|\ge 2\Delta +10-2(d_G(v_2)-1)-1\ge 11$ and $|C{\setminus } (C_{\phi }(y)\cup C_{\phi }(v_2)\cup \{a\})|\ge 2\Delta +10-\Delta -(\Delta -1)-1=10$, $\phi$ is extended to G.

• $d_G(v_1)\ge 3$. We color $vv_2$ with $a\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1))$ and $vv_1$ with $b\in C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{a\})$. Since $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1))|\ge 2\Delta +10-2(\Delta -1)-10 \ge 2$ and $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{a\})|\ge 2\Delta +10-2(d_G(v_1)-1)-\Delta \ge \Delta +10-2\times 10\ge 2$, $\phi$ is extended to G.

Now, by Case 1, we may assume that $d_G(v_i)\ge 3$ for all $i\in [1,k]$ in the following two situations.

Case 2. $k=3$ and $d_G(v_1)+d_G(v_2)\le 14$.

It follows that $d_G(v_1)\le 7$ and $d_G(v_2)\le 11$. Let $H=G-\{vv_1, vv_2\}$, which has a K-LNDE-coloring $\phi$ using C such that $\phi (vv_3)=1$. We color $vv_2$ with $a\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{1\})$ and $vv_1$ with $b\in C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup \{a\})$. Since $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup \{1\})|\ge 2\Delta +10-2(\Delta -1)-(d_G(v_1)-1)-1 \ge 12-(7-1)-1=5$ and $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup \{a\})|\ge 2\Delta +10-2(d_G(v_1)-1)-(d_G(v_2)-1)-\Delta -1\ge \Delta +12-d_G(v_1)- (d_G(v_1)+d_G(v_2)) \ge 24-7-14=3$, both a and b exist. Let $\phi '$ denote the resultant coloring. Then $C_{\phi '}(v)=\{1,a,b\}$, $a\notin C_{\phi '}(v_1)$, and $b\notin C_{\phi '}(v_2)\cup C_{\phi '}(v_3)$. Thus, v is exclusive with each of its neighbors and hence $\phi$ is extended to G.

Case 3. $k=4$ and $d_G(v_1)+d_G(v_2)+d_G(v_3)\le 15$.

Then $d_G(v_1)\le 5$, $d_G(v_2)\le 6$, and $d_G(v_3)\le 9$. Let $H=G-\{vv_1, vv_2,vv_3\}$, which has a K-LNDE-coloring $\phi$ using C such that $\phi (vv_4)=1$. We color $vv_3$ with $a\in C{\setminus } (C^+_{\phi }(v_3)\cup C_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{1\})$, $vv_2$ with $b\in C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a\})$, and $vv_1$ with $c\in C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a,b\})$. Noting that $|C{\setminus } (C^+_{\phi }(v_3)\cup C_{\phi }(v_1)\cup C_{\phi }(v_2)\cup \{a\})|\ge 34-2(d_G(v_3)-1)-(d_G(v_2)-1)-(d_G(v_1)-1)-1= 37-d_G(v_3)-(d_G(v_1)+d_G(v_2)+d_G(v_3))\ge 37-9-15=13$, $|C{\setminus } (C^+_{\phi }(v_2)\cup C_{\phi }(v_1)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a\})|\ge 2\Delta +10-2(d_G(v_2)-1)-(d_G(v_1)-1)-(d_G(v_3)-1)-\Delta -1\ge \Delta +13-d_G(v_2)-(d_G(v_1)+d_G(v_2)+d_G(v_3))\ge \Delta +13-6-15\ge 4$, and $|C{\setminus } (C^+_{\phi }(v_1)\cup C_{\phi }(v_2)\cup C_{\phi }(v_3)\cup C_{\phi }(v_4)\cup \{a,b\})|\ge 2\Delta +10- 2(d_G(v_1)-1)-(d_G(v_2)-1)-(d_G(v_3)-1)-\Delta -2\ge \Delta +12-d_G(v_1)-(d_G(v_1)+d_G(v_2)+d_G(v_3))\ge \Delta +12-5-15\ge 4$, $vv_1,vv_2,vv_3$ can be properly colored. Let $\phi '$ denote the resultant coloring. Since $C_{\phi '}(v)=\{1,a,b,c\}$, $a,b\notin C_{\phi '}(v_1)$, $a,c\notin C_{\phi '}(v_2)$, $c,b\notin C_{\phi '}(v_3)$, and $b,c\notin C_{\phi '}(v_4)$, $\phi '$ is a K-LNDE-coloring of G.

By Proposition 1, the following theorem holds automatically.

Theorem 4.3

If G is a formal planar graph without 4-cycles, then $\chi '_\textrm{snd}(G)\le 2\Delta +10$.

5 Planar Graphs with [2, k]-Factors

For two positive integers $k_1,k_2$ with $k_2\ge k_1$, a spanning subgraph F of a graph G is called an $[k_1,k_2]$-factor if $k_1\le d_F(v)\le k_2$ for all $v\in V(G)$. Tutte [15] showed that every 4-connected planar graph is Hamiltonian, i.e., it has a 2-connected [2, 2]-factor. By relaxing the 4-connected condition, Gao [7] showed that every 3-connected planar graph has a 2-connected [2, 6]-factor. Enomoto et al. [5] extended this result by showing that every 3-connected planar graph G with $\delta (G)\ge 4$ has a 2-connected [2, 3]-factor. Both numbers 6 and 3 in these two results are best possible with respect to the required conditions.

The core $G_{\Delta }$ of a graph G is the subgraph of G induced by $\Delta$-vertices.

Lemma 5.1

Let $k\ge 3$. If a connected graph G has a connected [2, k]-factor, then G contains a connected [2, k]-factor F whose core is acyclic.

Proof

Let F be a connected [2, k]-factor of G with the least number of edges. We claim that the core of F is acyclic. Suppose to the contrary that $F_{\Delta }$ contains a cycle C. Let $e=xy\in E(C)$ be an arbitrary edge, and set $F'=F-e$. Obviously, $F'$ is a connected spanning subgraph of G. If $v\in V(G){\setminus } \{x,y\}$, then $d_{F'}(v)=d_F(v)$. If $v\in \{x,y\}$, then $d_{F'}(v)=d_F(v)-1\ge k-1\ge 2$. It follows that $F'$ is a connected [2, k]-factor of G with $||F'||<||F||$, which contradicts the choice of F. $\square$

The following result can be derived from Lemma 5.1 and the results in [5] and [7].

Corollary 5.2

Let G be a planar graph.

• (1) If G is 3-connected, then G contains a connected [2, 6]-factor F whose core is acyclic.

• (2) If G is 3-connected and $\delta (G)\ge 4$, then G contains a connected [2, 3]-factor F whose core is acyclic.

The celebrated Vizing’s Theorem gives a tight upper bound for the chromatic index of a simple graph.

Theorem 5.3

([16]) Every simple graph G has $\Delta \le \chi '(G)\le \Delta +1$.

A simple graph G is said to be Class 1 if $\chi '(G)=\Delta$ and Class 2 if $\chi '(G)=\Delta +1$.

Theorem 5.4

([6]) If the core of a simple graph G is a forest, then G is Class 1.

Theorem 5.5

([14]) If G is a planar graph with $\Delta \ge 7$, then G is Class 1.

An edge-partition of a graph G is a decomposition of G into subgraphs $G_1, \ldots ,G_m$ such that $E(G)=E(G_1)\cup \cdots \cup E(G_m)$ and $E(G_i)\cap E(G_j)=\emptyset$ for $i\ne j$.

Suppose that H is a subgraph of a graph G. A restricted-strong edge-k-coloring of H on G is an edge-coloring $\phi : E(H)\rightarrow [1,k]$ such that any two edges $e_1,e_2\in E(H)$ having distance at most two in G get distinct colors. The restricted-strong chromatic index of H on G, denoted $\chi '_\textrm{s}(H|_G)$, is the smallest integer k such that H has a restricted-strong edge-k-coloring on G.

Since all planar graphs G considered in Theorems 5.6 to 5.11 contain a [2, k]-factor, it follows that $\delta (G)\ge 2$, which implies that $\chi '_\textrm{lnd}(G)=\chi '_\textrm{snd}(G)$ by Proposition 1.

Theorem 5.6

Suppose that a connected graph G can be edge-partitioned into two graphs F and H such that F is a connected [2, k]-factor of G with $k\ge 2$. Then $\chi '_\textrm{snd}(G)\le \chi '(H)+\chi '_\textrm{s}(F|_G).$

Proof

Note that $2\le \delta (F)\le \Delta (F)\le k$ and $\Delta (H)\le \Delta (G)-\delta (F)\le \Delta (G)-2$. Let $\chi '(H)=l$ and $\chi '_\textrm{s}(F|_G)=m$. Let $\phi$ be an edge-l-coloring of H using the color set $C_1=[1,l]$ and $\pi$ be a restricted-strong-edge-coloring of F on G using the color set $C_2=[l+1,l+m]$. We define an edge-coloring f of G as follows: $f(e)=\phi (e)$ for $e\in E(H)$, and $f(e)=\pi (e)$ for $e\in E(F)$. Obviously, f is a proper edge-$(l+m)$-coloring of G using the color set $C_1\cup C_2$. If we can show that f is strict neighbor-distinguishing, then it holds naturally that $\chi '_\textrm{snd}(G)\le l+m=\chi '(H)+\chi '_\textrm{s}(F|_G)$. In fact, for any edge $e=xy\in E(G)$, since $d_F(x),d_F(y)\ge 2$, there exist an edge $e_x\in E(F)\setminus \{e\}$ incident with x and an edge $e_y\in E(F)\setminus \{e\}$ incident with y. Since $e_x$ and $e_y$ have the distance 2 in G, it follows that $\pi (e_x)\notin C_{\pi }(y)$ and $\pi (e_y)\notin C_{\pi }(x)$. Because $C_1\cap C_2=\emptyset$, we have that $\pi (e_x)\notin C_{f}(y)$ and $\pi (e_y)\notin C_{f}(x)$, and so x and y are exclusive. $\square$

A family of graphs $\mathcal G$ is called minor-closure if it is closed under deleting vertices, deleting edges, or contracting edges. Let $\chi (G)$ denote the chromatic number of a graph G, which is defined as the smallest integer k for which the vertices of G can be colored using k colors such that no two adjacent vertices get same color. For a family of minor-closure graphs $\mathcal{G}$, we define $\chi (\mathcal{G})=\max \{\chi (G)\,|\,G\in \mathcal{G}\}$. It is easily seen that the family of planar graphs, denoted $\mathcal{P}$, is minor-closure and $\chi (\mathcal{P})\le 4$ by the Four-Color Theorem [2].

Lemma 5.7

([22]) If F is a subgraph of a planar graph G, then $\chi '(F|_G)\le 4\chi '(F)$.

Combining Theorem 5.6 and Lemma 5.7, the following theorem holds automatically.

Theorem 5.8

Let G be a connected planar graph with a connected [2, k]-factor F, and $H=G-E(F)$. Then $\chi '_\textrm{snd}(G)\le \chi '(H)+4\chi '(F)$.

Theorem 5.9

Let G be a planar graph. Then the following statements (1) and (2) hold.

(1) If G is 3-connected, then $\chi '_\textrm{snd}(G)\le \Delta +23$.

(2) If G is 3-connected and $\delta (G)\ge 4$, then $\chi '_\textrm{snd}(G)\le \Delta +11$.

Proof

(1) Since G is 3-connected, it follows from Corollary 5.2(1) that G has a connected [2, 6]-factor F whose core is acyclic. Let $H=G-E(F)$. Then G is edge-partitioned into two subgraphs F and H. If $\Delta (F)\le 5$, then $\chi '(F)\le 5+1=6$ by Theorem 5.3. If $\Delta (F)=6$, then $\chi '(F)=6$ by Theorem 5.4. Hence, it always holds that $\chi '(F)\le 6$. On the other hand, since $\Delta (H)\le \Delta (G)-2$, we have $\chi '(H)\le \Delta (G)-2+1=\Delta -1$ by Theorem 5.3. So, by Theorem 5.8, $\chi '_\textrm{snd}(G)\le \chi '(H)+4\chi '(F)\le \Delta (H)+4\times 6\le \Delta -1+24=\Delta +23$. (2) By Corollary 5.2(2), G has a connected [2, 3]-factor F whose core is acyclic. Let $H=G-E(F)$. Then G is edge-partitioned into two subgraphs F and H. If $\Delta (F)=2$, then $\chi '(F)\le 2+1=3$ by Theorem 5.3. If $\Delta (F)=3$, then $\chi '(F)=3$ by Theorem 5.4. Hence, we always have that $\chi '(F)\le 3$. By Theorem 5.3, $\chi '(H)\le \Delta (H)+1\le \Delta (G)-2+1=\Delta -1$. By Theorem 5.8, $\chi '_\textrm{snd}(G)\le \chi '(H)+4\chi '(F)\le \Delta -1+4\times 3=\Delta +11$. $\square$

Theorem 5.10

If a planar graph G is Hamiltonian, then $\chi '_\textrm{snd}(G)\le \Delta +6$.

Proof

Let $C=v_0v_1\cdots v_{n-1}v_0$ be a Hamiltonian cycle of G, where $n=|V(G)|$. Let $H=G-E(C)$. Then $H\cup C$ is an edge-partition of G with $\Delta (H)\le \Delta -2$. Let $\chi '(H)=k$. First we give an edge-k-coloring of H using the color set $B_1=[1,k]$. Then we define an edge-7-coloring $\pi$ of C using the color set $B_2=[k+1,k+7]$ in two ways below:

• Assume that n is even. Set $M=\{v_0v_1,v_2v_3,\ldots ,v_{n-2}v_{n-1}\}$, and give a restricted-strong edge-4-coloring of M on G using the colors in $[k+1,k+4]$. Afterward, if $n\equiv 0$ (mod 4), then we color alternatively $v_1v_2,v_3v_4,\ldots ,v_{n-1}v_0$ with $k+5$ and $k+6$. If $n\equiv 2$ (mod 4), then we color $v_1v_2$ with $k+7$, and then color alternatively $v_3v_4,v_5v_6,\ldots ,v_{n-1}v_0$ with $k+5$ and $k+6$.

• Assume that n is odd. Set $M=\{v_0v_1,v_2v_3,\ldots ,v_{n-3}v_{n-2}\}$, and give a restricted-strong edge-4-coloring of M on G using $[k+1,k+4]$. Then we color $v_{n-1}v_0$ with $k+7$ and then color alternatively $v_1v_2,v_3v_4,\ldots ,v_{n-2}v_{n-1}$ with $k+5$ and $k+6$.

Let f denote the resultant edge-$(k+7)$-coloring of G formed by combining $\phi$ and $\pi$, using the color set $B_1\cup B_2$. It is easy to inspect that f is proper, i.e., any two adjacent edges having distinct colors. It remains to show that f is strict neighbor-distinguishing. Let $e=xy$ be an arbitrary edge of G. By the definition of M, at most one of x and y is not incident with any edge in M.

First assume that each of x and y is incident with an edge in M, respectively. Since M is a matching of G, there exist the unique $e_x\in M$ incident with x and the unique $e_y\in M$ incident with y. We have two possibilities as follows.

• $e_x=e_y$, that is, $e=e_x=e_y\in M$, say $e=v_iv_{i+1}$, where indices are taken modulo n. Then $v_{i-1}v_i,v_{i+1}v_{i+2}\in E(C)\setminus M$. By the definition of $\pi$, $\pi (v_{i-1}v_i),\pi (v_{i+1}v_{i+2})\in [k+5,k+7]$ and $\pi (v_{i-1}v_i)\ne \pi (v_{i+1}v_{i+2})$. Noting that $\pi (v_{i-1}v_i)\notin C_{f}(v_{i+1})$ and $\pi (v_{i+1}v_{i+2})\notin C_{f}(v_{i})$, $v_i$ and $v_{i+1}$ are exclusive in f.

• $e_x\ne e_y$. Since $e_x$ and $e_y$ have distance 2 in G, the definition of $\pi$ implies that $\pi (e_x)\ne \pi (e_y)$ and $\pi (e_x),\pi (e_y)\in [k+1,k+4]$. So, $\pi (e_x)\notin C_f(y)$ and $\pi (e_y)\notin C_f(x)$, and henceforth x and y are exclusive. Next assume that x is not incident with any edge in M. Then $x=v_{n-1}$. There are two subcases to be considered.

• $y\in \{v_0,v_{n-2}\}$, say $y=v_0$. Because $v_0v_1\in M$ satisfies $\pi (v_0v_1)\in [k+1,k+4]$, and $v_{n-2}v_{n-1}\in E(C){\setminus } M$ satisfies $\phi (v_{n-2}v_{n-1})\in [k+5,k+7]$, it follows that $\pi (v_0v_1)\notin C_f(v_{n-1})$ and $\pi (v_{n-2}v_{n-1})\notin C_f(v_0)$, and therefore, x and y are exclusive.

• $y\in \{v_1,\ldots ,v_{n-2}\}$, say $y=v_i$ for some $i\in [1,n-2]$. Then exactly one of $v_{i-1}v_i$ and $v_iv_{i+1}$ belongs to M, whose color is $a\in [k+1,k+4]$. Moreover, assuming that $\pi (v_{n-1}v_0)=b$ and $\pi (v_{n-2}v_{n-1})=c$, then $b,c\in [k+5,k+7]$. Since $a\notin C_f(v_{n-1})$ and at least one of b and c does not belong to $C_f(v_i)$, x and y are exclusive.

The above analysis and Theorem 5.3 show that $\chi '_\textrm{snd}(G)\le k+ 4+3\le \Delta -1+7=\Delta +6.$ $\square$

By Theorem 5.5 and the proof of Theorem 5.10, we can obtain the following better result.

Theorem 5.11

If G is a Hamiltonian planar graph with $|G|\equiv 0\,\mathrm{(mod \ 4)}$ and $\Delta \ge 9$, then $\chi '_\textrm{snd}(G)\le \Delta +4$.

A Halin graph is a plane graph $G=T\cup C$, where T is a plane tree with no vertex of degree two and at least one vertex of degree three or more, and C is a cycle connecting the pendant vertices of T in the cyclic order determined by the drawing of T.

Halin graphs are 3-connected, but any of their proper subgraphs is not. Bondy and Lovász [3] showed that Halin graphs are almost pancyclic with the possible exception of an even cycle. In particular, Halin graphs are Hamiltonian.

By Theorem 5.10, we have the following:

Corollary 5.12

If G is a Halin graph, then $\chi '_\textrm{snd}(G)\le \Delta +6$.

6 Concluding Remarks

In this section, we are going to provide some open problems on the local neighbor-distinguishing edge-coloring of graphs. In contrast to Conjecture 2, we first put forward the following conjecture:

Conjecture 3

Every connected graph G, different from $H_{\Delta }$, has $\chi '_\textrm{lnd}(G)\le 2\Delta$. Observing the local neighbor-distinguishing index of $K_{2,n}$, we see that the upper bound $2\Delta$ in Conjecture 3 is tight if it were true.

Problem 1. Does every planar graph satisfy Conjecture $3\,?$

Problem 2. Is it true that there exists a constant c such that every planar graph G without 4-cycles has $\chi '_\textrm{lnd}(G)\le \Delta +c\,?$