FDGATII: Fast Dynamic Graph Attention with Initial Residual and Identity

Abstract

Despite their recent popularity, deep and efficient Graph Neural Networks remain a major challenge due to (a) over-smoothing, (b) noisy neighbours (heterophily), and (c) the suspended animation problem. Inspired by the attention mechanism’s ability to focus on selective information, and prior work on feature preserving mechanisms, we propose FDGATII, a dynamic deep-capable model that addresses all these challenges simultaneously and efficiently. Specifically, by combining Initial Residuals and Identity with the more expressive dynamic self-attention, FDGATII effectively handles noise in heterophilic graphs and is capable of depths over 32 with no over-smoothing, overcoming two main limitations of many prior GNN techniques. By using edge-lists, FDGTII avoids computationally intensive matrix operations, is parallelizable and does not require knowing the graph structure upfront. Experiments on 7 standard datasets show that FDGATII outperforms the GAT and GCN based benchmarks in accuracy and performance on fully supervised tasks. We obtain State-of-the-art (SOTA) on the highly heterophilic Chameleon and Cornell datasets with 1 layer, and come only 0.1% short of Cora SOTA with zero graph pre processing. https://github.com/gayanku/FDGATII

1 Introduction

Recently, research on graphs has been receiving increased attention due to the great expressive power and pervasiveness of graph structured data [29]. Many interesting irregular domain tasks such as 3D meshes, social networks, telecommunication networks and biological networks involve data that are not representable in grid-like structures [25]. As a unique non-Euclidean data structure for machine learning, graphs can be used to represent diverse feature rich domains.

A Graph Neural Network (GNN) generalizes deep neural networks (DNNs) from regular structures to irregular graph data. GNNs perform neighbourhood structure aggregation and node feature transformation to map nodes to low dimensional embeddings [15, 17], mostly differing in how aggregation and combination is performed [4]: Graph Convolutional Network (GCN) [13] uses convolution [16]; Graph Attention Network (GAT) [25] uses attention; GraphSage [8] uses max pooling. Downstream tasks such as node classification, clustering, and link prediction [8, 22] use these aggregated low dimensional vectors [28].

Most graphs require the interaction between nodes that are not directly connected, i.e., higher-order information which is achieved by stacking GNN layers [2]. However, stacking layers degrades the performance [5, 20] due to over-smoothing: node representations become indistinguishable with increasing number of layers [6, 13, 26]. Further, GNNs in general are not able to handle long-range information due to over-squashing: information from the exponentially growing receptive field being compressed into fixed-length node vectors [2] due to its unfocused aggregation mechanism. Finally, deeper models stop responding to training due to the suspended animation problem [26], i.e. depth is a problem [6].

To avoid these problems, several works combine deep propagation with shallow neural networks; SGC [26] used the K-th power of the adjacency matrix to capture higher-order information; H2GCN [29] aggregates higher-order information at each round. However, this form of linear combination of neighbour features at each layer looses the powerful expression ability of deep nonlinear architectures, essentially making them shallow models [5].

In another attempt to address the problem and incorporate deeper layers, JKNet [27] used dense skip connections, DropEdge [23] randomly removed graph edges and GCNII [5] added a portion of Initial residual and Identity. GCNII showed remarkable results for up to 64 layers and is the SOTA (Table 2) in Cora, a homophilic benchmark dataset. However, all these are spectral approaches based on the Laplacian eigenbasis and requires the whole graph structure [25]. The normalization used is computationally expensive and not scalable.

Furthermore, due to naive uniform aggregation of the neighbourhood, most of these models, including GCNII, are more suitable for homophilic datasets, where nodes linked to each other are more likely to belong in the same class, i.e., neighbourhoods with low noise. In practice, real-world graphs are also often noisy with connections between unrelated nodes [12], resulting in poor performance in current GNNs. As many popular GNN models implicitly assume homophily, results may be biased, unfair or erroneous [19]. This can result in a ‘filter bubble’ phenomenon in a recommendation system (reinforcing existing beliefs/views, and downplaying the opposite ones), or making minority groups less visible in social networks [29]. As a result, despite GCNIIs SOTA in homophilic datasets (Cora), its accuracy in heterophilic datasets (Texas, Wisconsin) is relatively poor [29].

On the other hand, [24] showed that self-attention is sufficient for achieving SOTA performance. GAT [25] generalizes attention for graphs using attention-based neighbourhood aggregation. Importantly, GAT improves on simple averaging [13] and max pooling [8] by allowing every node to compute a weighted average of its neighbours [4], which is a form of selective aggregation. The generalization ability of the attention mechanism helps GNNs generalize to larger and more noisy graphs [14]. By determining individual attention on each neighbour, GAT ignores irrelevant neighbours and focuses on those that are relevant [2].

Surprisingly, yet, GATs heterophilic performance is poor (Table 2).

A refinement, GATv2 [4], uses a more expressive dynamic attention, where the ranking of attended nodes is better conditioned on the query node by replacing the supposedly monotonic GAT attention function with a universal approximator attention function that is strictly more expressive. However, GAT or GATv2 alone, in its current form cannot handle heterophilic data due to the still present essentially local aggregation operation [17].

In Table 2, under heterophily, only H2GCN outperforms a Multilayer Perceptron (MLP) of 1 layer which uses only node features and no structural information. Furthermore, most GNN models use simple graph convolution based aggregation schemes [8, 13], leading to filter incompleteness. While this can be solved by using a more complex graph kernel [1], currently, even attention-based models perform poorly given heterophilic data, despite the ability to focus on the most “relevant" content.

Thus, it remains an open problem to design efficient GNN models that effectively handle (a) over-smoothing, (b) suspended animation and (c) heterophily/noise simultaneously. As observed by [5], it is even unclear whether the network depth is a resource or a burden when designing new GNNs. Motivated by these limitations, we propose a generalizable, efficient, and parallelizable attention based deep-capable model that addresses aforementioned challenges simultaneously. Our main contributions are:

• We introduce a novel deep-capable GNN model, FDGATII, successfully combining strengths of GCN and GAT worlds by using dynamic attention supplemented with Initial residual and Identity, capable of handling the major graph challenges: over-smoothing, noisy neighbours (heterophily) and suspended animation simultaneously. To the best of our knowledge, this is the first time a graph attentional model has demonstrated depths of up to 32, a limitation of many prior GNN techniques, attention based or otherwise, and show that dynamic attention is better suited for heterophilic datasets, if used with modifications.

• FDGATII is computationally efficient. It does not require an adjacency matrix as input nor its subsequent, expensive matrix operations or normalizations. Further, its attention layers can be parallelized across edges while feature computation can be parallelized across all nodes.

• FDGATII has the same complexity as SOTA GCN models, but uses significantly fewer layers to achieve comparable or better results, yielding a superior efficiency-to-accuracy ratio across homophilic and heterophilic datasets.

Extensive experiments on 7 benchmarks show that FDGATII outperforms GAT and GCN based benchmarks in accuracy as well as on accuracy vs efficiency, on fully supervised tasks. FDGATII achieves SOTA accuracy results on Chameleon and Cornell datasets, beating H2GCN, a model specifically designed for heterophily. There is zero graph pre processing. FDGATII consumes over a magnitude less computational resources and is only –0.1% below SOTA for Cora, placing a close second. By not assuming homophily, FDGATII minimises its potential negative effects: bias, unfairness and potential for filter bubbles. FDGATII is also capable of inductive learning. Table 1 has a full feature comparison.

Table 1. Feature comparison: GAT, GCN, GCNII and FDGATII. *Cham & Cornell

2 Related Work

2.1 Notation

$G = (V,E)$ is an undirected graph with n nodes $v_j \in V$ and m edges $(v_i,v_j) \in E$. $\bar{G} = (V,\bar{E})$ is its self-looped graph. A is the adjacency matrix, D the degree matrix of G. Adjacency matrix and degree matrix of $\bar{G}$ is $\bar{A} = A+I$ and $\bar{D} = D+I$. The symmetric positive semi definite normalized graph Laplacian matrix is given by $L = I_{n}- D^{-1/2}AD^{-1/2}$ with eigen-decomposition $U\varLambda U^T$. $\varLambda$ is its diagonal eigenvalue matrix, $U \in R^{n \times n}$ is the unitary eigenvector matrix.

2.2 Convolution and GCN

Given signal x and filter $g_{\gamma }(\varLambda ) = diag(\gamma )$ the graph convolution operation is $g_\gamma (L)*x = U g_\gamma (\varLambda )U^Tx$ where $\gamma \in R^n$ is the vector of spectral filter coefficients. $g_\gamma (\varLambda )$ can be approximated by a truncated expansion of a K^th order Chebyshev polynomial [9], where $\theta \in \textbf{R}^{K+1}$ corresponds to a vector of polynomial coefficients:

$$\begin{aligned} \textbf{U}g_{\theta }\left( \varLambda \right) \textbf{U}^{T}\textbf{x}\approx \textbf{U}\left( \sum _{l = 0}^{K}\theta _l\mathbf {\varLambda }^l\right) \textbf{U}^T\textbf{x} =\left( \sum _{l = 0}^{K}\theta _l\textbf{L}^l\right) \textbf{x} \end{aligned}$$

(1)

GCN [13] simplifies graph convolution by fixing $K=1,\theta _0=2\theta$ and $\theta _1=-\theta$ to get $g_{\theta }*x =\theta (I+D^{-1/2}AD^{-1/2})x$ and uses a normalized adjacency matrix, $\bar{P} = \bar{D}^{-1/2}\bar{A}\bar{D}^{-1/2}=(D+I_n)^{-1/2}(A+I_n)(D+I_n)^{-1/2}$. Each GCN layer (Eq. 2) contains a nonlinear activation function $\sigma$, typically ReLU.

$$\begin{aligned} \textbf{H}^{l+1} = \sigma \left( \bar{\textbf{P}}\textbf{H}^l\textbf{W}^l\right) \end{aligned}$$

(2)

However, node embeddings are aggregated recursively layer by layer. Embeddings in the final layer requires all previous embeddings, resulting in high memory cost. GCN gradient update in the full-batch training scheme needs storing all intermediate embeddings, limiting scalability. As the learned filters depend on the Laplacian eigenbasis, which depends on the entire graph structure, a model trained on a graph cannot be directly applied to a different graph structure [25].

2.3 GCNII

GCNII [5] extends the fixed coefficient GCN to a deep model by expressing the K order polynomial filter as arbitrary coefficients using Initial residual and Identity (II). Essentially, GCNII 1) combines the preprocessed (normalized) representation $\bar{\textbf{P}}\textbf{H}^l$ with an initial residual connection from the first layer $\textbf{H}^0$; and 2) adds an identity $\textbf{I}_{n}$ to the l-th weight matrix $\textbf{W}^l$. By using a connection to the initial residual $\textbf{H}^0$, GCNII ensures that the final representation of each node retains at least a $\alpha _l$ fraction from the input layer.

However, as GCNII combines neighbour embeddings by uniformly averaging, its heterophilic performance is relatively poor. GCNs preserve structure over features, regardless of the graph’s heterophilic nature, resulting in original node features being destroyed [11]. Further, [20] showed that GCNs tend to fail when graphs are dense and do not always improve with more layers. Alternatively, a selective aggregation of the neighbourhood allows focusing on relevant nodes [29].

2.4 Attention Mechanism and GAT

The DP (dot-product) attention mechanism (Equation 3) [18, 24] has been widely used in GNNs [12, 28]. Different from DP, GAT [25] uses concatenation followed by a 1-layer feed-forward network parameterized by $\textbf{a}$ (Eq. 4).

$$\begin{aligned} e\left( \textbf{h}_{i},\textbf{h}_{j}\right) =\text {LeakyReLU}( {(\textbf{W}\textbf{h}_{i})}^T \cdot \textbf{W}\textbf{h}_{j} ) \end{aligned}$$

(3)

$$\begin{aligned} e\left( \textbf{h}_{i},\textbf{h}_{j}\right) = \text {LeakyReLU} \left( \textbf{a}^{T} \cdot \left[ \textbf{W}\textbf{h}_{i}\parallel \textbf{W}\textbf{h}_{j}\right] \right) \end{aligned}$$

(4)

In contrast to GCN, which weighs all neighbours $j\in \mathcal {N}_i$ with equal importance, GAT computes a learned weighted average of the representations of $\mathcal {N}_i$ using attention. Compared to GCN, assigning different weights for neighbours can mitigate noise and achieve better results [28] while being more robust in the presence of noisy “irrelevant" neighbours [2].

Fig. 1.

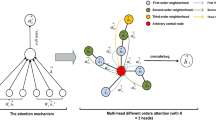
FDGATII uses dynamic attention to combine relevant neighbours via edge-lists, an $\alpha \%$ of initial representation $h^0$ projected via $fc_{0}$ and a $\beta \%$ of Identity $I_{n}$ at each layer. Attention module concatenates source (row) and destination (column) features of each edge, projects via $W_{H}^{n}$, applies a non-linearity (leaky-relu) and an exp() to obtain the edgewise attentions before reshaping to a matrix suitable for softmax with the query. After multiple layers, an $fc_{1}$ projection and log softmax provides the node classification.

3 Proposed Architecture

Our proposed design (Fig. 1) is built upon a local embedding step that extracts local node embeddings from feature vectors using GATv2. To extend GATv2 to handle heterophilic and noisy data, we borrow two techniques from GCNII [5] and H2GCN [29] with modifications, namely residual connection and identity.

However, the theoretical foundation of our model, which is grounded in the spatial domain, is completely different from GCNII which is spectral. We do not require edge values; only the presence or absence of an edge: i.e. a simple list of edges. Using only the edge-list as [25], with self-loops as [10, 13], we avoid computationally intensive matrix operations such as inversions or eigen-decompositions and the need to know the graph structure upfront. Experiments show our design is efficient, robust and generalizes well to homophilic and heterophilic datasets alike.

Typically, GNN models follow an iterative learning approach:

$$\begin{aligned} \begin{aligned} \textbf{h}_i^{1+1}=\text {COMBINE}\Big (\textbf{h}_i^l, \text {AGG}(\{\textbf{h}_j^l : j \in N_i\})\Big ), \\ \textbf{h}_i^0=\textbf{X}_i, \text {and } y_i=\text {arg max}\{\text {softmax}(\textbf{h}_i^K)\textbf{W}\} \end{aligned} \end{aligned}$$

where, $\text {AGG}$ is a permutation invariant aggregation operator and $\text {COMBINE}$ is a learnable function. By adding self-nodes, we amalgamate COMBINE and AGG to simplify the process and apply a more expressive attention operator ATTN to both tasks simultaneously, defined by:

$$\begin{aligned} \begin{aligned} \textbf{h}_i^{1+1}=\text {ATTN}(\{\textbf{h}_j^l : j \in N_i \cup i\}) \end{aligned} \end{aligned}$$

3.1 Initial Residual and Identity (II)

We incorporate initial representation $\textbf{H}^{0}$ and identity $\textbf{I}_{n}$, in $\alpha _l$ and $\beta _l$ fractions, with edge-list $\bar{\textbf{E}}$ to formally define the $(l+1)$-th layer of FDGATII as:

$$\begin{aligned} \textbf{H}^{l+1}=\sigma \left[ \left( \left( 1-\alpha _l\right) \text {ATTN}({\bar{\textbf{E}}},\textbf{H}^l)+\alpha _l\textbf{H}^{0}\right) \right. \left. \cdot \left( \left( 1-\beta _l\right) \textbf{I}_{n} +\beta _l\textbf{W}^l\right) \right] \end{aligned}$$

(5)

According to [10], identity mapping of the form $\textbf{H}^{l+1}=\textbf{H}^l(\textbf{W}^l+\textbf{I}_{n})$, as in Eq. 5, satisfies the following properties: 1) the optimal weight matrices $\textbf{W}^l$ have small norms; 2) the only critical point is the global minimum. The first property allows us to put strong regularization on $\textbf{W}^l$ to avoid over-fitting, while the latter is desirable in semi-supervised tasks where training data is limited.

Next, it is theoretically proven [20] that a K-layer GNN’s convergence rate depends on $s^K$, where s is the maximum singular value of the weight matrices $\textbf{W}^l,l = 0,\ldots ,K-1$. By replacing $\textbf{W}^l$ with $(1-\beta _l)\textbf{I}_{n}+\beta _l\textbf{W}^l$ and regularizing $\textbf{W}^l$, resulting singular values of $(1-\beta _l)\textbf{I}_{n}+\beta _l\textbf{W}^l$ stay closer to 1, which implies that $s^{K}$ is large, and the information loss is relieved.

3.2 Selection of Proper Attention

It has been shown that GAT is better at learning label-agreement between a target node and its neighbors than DP attention [12]. Variance of GAT depends only on the norm of features, while the DP variance depends on the variance of the input’s dot-product and the expectation of the square of the input’s dot-product. As a result, with more layers, more features of i and j correlating resulting in a larger dot-product and the subsequent softmax normalization which increases the larger values further, DP is only able to attend to a small set of neighbours.

3.3 Dynamic Attention (GATv2)

According to [4], the main problem in the standard GAT scoring function (Eq. 4) is that the learned layers $\textbf{W}$ and $\textbf{a}$ are applied consecutively, and thus can be collapsed into a single linear layer. GATv2 replaces the linear approximator with a universal approximator (Eq. 6) and has been shown to perform better on noisy data [4]. Further, theoretically, DP is strictly weaker than GATv2. We use this form of dynamic attention for our aggregation function.

Specifically, a scoring function $e:R^{d}\times R^{d}\rightarrow R$ computes a score for every edge (j, i), which indicates the importance of the features of the neighbour j to the node i:

$$\begin{aligned} \small e\left( \textbf{h}_{i},\textbf{h}_{j}\right) =\textbf{a}^T \cdot \text {LeakyReLU}\left( \textbf{W}\left[ \textbf{h}_{i}\parallel \textbf{h}_{j}\right] \right) , \end{aligned}$$

(6)

where attention scores $\textbf{a}\in R^{2d^{'}}$ and weights $\textbf{W}\in R^{d^{'}\times d}$ are learned. $\parallel$ denotes vector concatenation. We capture the graph structure using edges, computing $e_{i,j}$ for all $j \in N_i$ neighbourhood of node i. Attention scores are normalized across all connected sparse neighbours $j\in \mathcal {N}_i$ using softmax.

$$\begin{aligned} \alpha _{ij} = softmax_{j}\left( e\left( \textbf{h}_{i},\textbf{h}_{j}\right) \right) =\frac{exp\left( e\left( \textbf{h}_{i},\textbf{h}_{j}\right) \right) }{\sum _{j^{'}\in \mathcal {N}_{i}}^{} exp\left( e\left( \textbf{h}_{i},\textbf{h}_{j^{'}}\right) \right) } \end{aligned}$$

(7)

Finally, we compute the weighted average of the transformed features of the neighbour nodes (followed by a nonlinearity $\sigma$) as the new representation of i, using the normalized attention coefficients:

$$\begin{aligned} \text {ATTN}_{i}^{'} = \sigma \left( \sum _{j\in \mathcal {N}_{i}}^{}\alpha _{ij}\textbf{W}\textbf{h}_{j}\right) \end{aligned}$$

(8)

In addition to Eq. 5, following [5], we also propose FDGATII* with dual weight matrices for smoother representation, defined as:

$$\begin{aligned} \begin{aligned} \textbf{H}^{l+1}&= \sigma \left[ (1-\alpha _l) \text {ATTN}({\bar{\textbf{E}}},\textbf{H}^l) \left( (1-\beta _l) \textbf{I}_n + \beta _l \textbf{W}_1^l \right) \right. \\&\quad \left. + \alpha _l\textbf{H}^{0} \left( (1-\beta _l) \textbf{I}_n + \beta _l \textbf{W}_2^l\right) \right] \end{aligned} \end{aligned}$$

(9)

GCNII [5] uses $\beta _l$ is to ensure the decay of the weight matrix adaptively increases with more layers. While FDGATII typically achieves best accuracy early with a few layers, we still adopt the same mechanism, $\beta _l = log\left( \frac{\lambda }{l}+1\right) \approx \frac{\lambda }{l}$, where $\lambda$ is a hyperparameter, for robustness at high depth. Following [27], we add skip connections in the form of initial representations $H^0$ as in [5].

FDGATII differs from existing models with respect to its use of a modified attention mechanism. Notably, we demonstrate competitive performance of GATv2+II with only a few layers in non-homophilous networks. Using edge-lists avoids computationally intensive matrix operations. Table 1 summarizes how FDGATII accumulates all benefits from GCN and GAT worlds with none of the drawbacks.

3.4 Datasets and Experiments

Homophily is the fraction of edges which connect two nodes of the same label [17]. A higher value (1) indicates strong homophily; a lower value (0) indicates strong heterophily.

We evaluate FDGATII against SOTA GNNs on benchmark graph datasets for fully supervised classification. Following [5, 21], we use 7 datasets (Table 5). Cora, Citeseer and Pubmed are homophilic citation networks where nodes correspond to documents, and edges correspond to citations. The remaining four are heterophilic datasets of web networks, where nodes and edges represent web pages and hyperlinks, respectively. Node feature vectors are bag-of-word representations of the document. Following [5, 21] we use the same data splits, 60:20:20 nodes for training:validation:testing, learning rate = 0.01, hidden units = 64 and measure the average performance on the 10 splits for each dataset.

We choose GCNII [5] as our performance and accuracy benchmark as it is (a) more current; (b) most similar to our work in the use of initial representation and identity; (c) actively attempts to solve over smoothing (d) is the SOTA in Cora (a prominent dataset for GNN model comparison) and most importantly (d) it is a deep-capable model. We also compare with H2GCN [29] which is the SOTA for Cornel, Texas and Wisconsin; highly heterophelic datasets, but note that H2GCN is a shallow model.

For training and inference time measurements we perform GPU warm-up and synchronization prior to measurements. We take the average time for 1000 inferences to lower any possibility of errors and to be more reflective of real-world use of models. We ignore pre processing times, but point out, unlike the benchmarks, FDGATII has no expensive full graph eigen operations or normalizations.

Table 2. Mean classification accuracy of full-supervised node classification. (a) reported by [5], (b) reported by [29], (c) best results running GCNII (official author implementation) and H2GCN (public pytorch repo: github.com/GitEventhandler/H2GCN-PyTorch) on data splits of [5], (d): our FDGATII, with same splits. Best is bold and second underlined. # of layers in parenthesis.

Table 3. Inductive learning - F1 (micro) on PPI. (1): Results from [5]. (2): Our results with identical settings and Eq. 5. Note, we do not require any data pre processing

Fig. 2.

Accuracy, epochs, training and inference time comparison. For variants, we use the lowest average time taken to run all 10 standard splits. $\textrm{Efficiency} = 1/time$. Original GCNII is in pytorch. Original H2GCN is in TF. A public pytorch H2GCN is used to eliminate any framework effects. Tested on Google colab with GPU.

Table 4. Ablation study w/0 II and w/0 dynamic attention. * Eq. 5, ** Eq. 9. Hyperparameter settings from [5]. L1 and L2 are 1 and 2 layers, respectively.

4 Results and Discussion

4.1 Fully Supervised Node Classification

Table 2 reports the mean classification accuracy. We reuse the metrics already reported by [5] and [29]. We observe that FDGATII demonstrates SOTA results on heterophilic datasets while still being competitive on the homophilic datasets. Further, FDGATII exhibits significant accuracy increases over its attention based predecessor, GAT. This result suggests that dynamic attention with initial residuals and identity improves the predictive power whilst keeping the layer count (and hence the model parameters and computational requirements) low.

4.2 Inductive Learning

We use the PPI dataset and follow [8] using 20:2:2 graphs for train:validation:test. For settings, we follow [5]: 2048 hidden units, learning rate 0.001. Similar to [5, 25], we add a skip connection from layer l to $l+1$. Table 3 reports the F1 (micro) scores. Results show that FDGATII is capable of competitive inductive learning.

4.3 Ablation Study

In this section, along with Table 4, we consider the effect of various design strategies. Our 1 or 2-layer models, without Initial residual and Identity (II), is theoretically equivalent to GAT(static attention)/GATv2(dynamic attention). The ablation study indicates that the addition of II together with dynamic attention results in improvements on the heterophilic dataset performance. This result suggests that both II and dynamic attention techniques are needed to solve the problem of over-smoothing and data heterophily. Figure 4 also confirms GAT/GATv2 cannot handle heterophily or depth unaided, while FDGATII shows significant and consistently better results.

Fig. 3.

Efficiency vs accuracy, on GPU with warm-up. left: average inference time for 1000 iterations. right: average training efficiency for 10 iterations. $\textrm{Efficiency} = log(1/ time)$. Top-right is better.

4.4 Performance and Efficiency

Figure 3 summarizes the high accuracy-to-computational-time-efficiency ratio of FDGATII clearly indicating its superior performance mix. The proposed architecture performs consistently better across noisy and diverse datasets with comparable or better accuracy (Table 2) while exhibiting superiority in training and inference times, specifically 12x faster training speeds and up to 9x faster inference speeds over our chosen deep-capable SOTA benchmark, GCNII [5]. FDGATII is 3x faster than H2GCN [29] on Citeseer. Our dynamic attention achieves higher expressive power with fewer layers paying selective attention to nodes, while the II supplements self-node features in highly heterophilic datasets.

By using edge-lists, FDGATII avoids computationally intensive eigen decompositions and matrix operations as well as the need to know the graph structure upfront. Also, output feature computation can be parallelized across nodes while the attention computation can be parallelized across all edges. While FDGATII has the same time complexity of GCNII, by using significantly fewer layers (Table 2 and Table 5), it achieves comparable or better results with superior efficiency-to-accuracy ratios. Note, in Fig. 2, the graph pre processing (inversion, normalization) times for benchmarks were not taken into account due to focus on model training and inference. FDGATII has zero graph pre processing.

4.5 Suspended Animation and Over Smoothing

Responding to training indicates absence of suspended animation [26], while effectively handling higher receptive fields indicates robustness to over-smoothing [6]. Figure 4 shows FDGATII’s performance for 3 selected datasets under increasing layer depth. There is no evidence of performance degradation from suspended animation or over smoothing even at depth of 32. Accuracy is achieved early and sustained over higher depths. In Cora, the drop is 0.1 for 32 layers. H2GCN reported OOM for depths over 8.

Fig. 4.

Accuracy vs layer depth (on Goole Colab with GPU). FDGATII is consistent. H2GCN OOM after 8 layers. Depth and heterophily degrades GAT/GATv2 accuracy.

Table 5. Final model hyperparameters.

4.6 Broader Issues Related to Heterophily

Many popular GNN models implicitly assume homophily, producing results that may be biased, unfair or erroneous [29]. This can result in the so-called ‘filter bubble’ phenomenon in a recommendation system (reinforcing existing beliefs/views, and downplaying the opposite ones), or make minority groups less visible in social networks, creating ethical implications [7]. FDGATII’s novel self-attention mechanism, where dynamic attention supplemented with II for feature preservation, reduces the filter bubble phenomenon and its potential negative consequences, ensuring fairness and less bias.

This offers new possibilities for future research into data where ‘opposites attract’, in which the majority of linked nodes are different, such as social and dating networks (the majority of persons of one gender connect with the opposite gender), chemistry and biology (amino acids bond with dissimilar types in protein structures), e-commerce (sellers with promoters and influencers), and dark web and other cybercrime related activities [29]. In a typical dark web social network, fraudsters are more likely to connect to intermediaries and prospective victims than to other fraudsters. Illicit actors will form ties with other actors who play different roles [3], resulting in heterophilic characteristics.

5 Conclusion

We propose FDGATII, a novel efficient dynamic attention-based model that combines attentional aggregation with dual feature preserving mechanisms based on Initial residual and Identity. FDGATII successfully combines strengths of both GCN and GAT worlds with none of the drawbacks, is inductive, able to handle noise in graphs and achieves depths of upto 32; a first for any attentional model and a limitation of many prior GNN techniques. Extensive experiments on a wide spectrum of benchmark datasets show that FDGATII achieves SOTA or second-best accuracy on benchmark fully supervised tasks. FDGATII has exceptional accuracy and efficiency whilst simultaneously addressing over-smoothing, suspended animation and heterophily prevalent in real world datasets.