Pattern Analysis of Substantia Nigra in Parkinson Disease by Fifth-Order Tensor Decomposition and Multi-sequence MRI

Abstract

This work proposes a new feature extraction method to analyse patterns of the substantia nigra in Parkinson disease. Recent imaging techniques such that neuromelanin-sensitive MRI enable us to recognise the region of the substantia nigra and capture early Parkinson-disease-related changes. However, automated feature extraction of Parkinson-disease-related changes and their geometrical interpretation are still challenging. To tackle these challenges, we introduce a fifth-order tensor expression of multi-sequence MRI data such as T1-weighted, T2-weighted, and neuromelanin images and its tensor decomposition. Reconstruction from the selected components of the decomposition visualises the discriminative patterns of the substantia nigra between normal and Parkinson-disease patients. We collected multi-sequence MRI data from 155 patients for experiments. Using the collected data, we validate the proposed method and analyse discriminative patterns in the substantia nigra. Experimental results show that the geometrical interpretation of selected features coincides with neuropathological characteristics.

1 Introduction

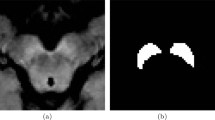
Parkinson disease is the second most common progressive neurodegenerative disorder, with approximately 8.5 million people who had been affected worldwide in 2017 [1]. The characteristic of Parkinson disease is a progressive loss of dopaminergic neurons in the substantia nigra pars compacta [2]. Currently, the diagnosis of Parkinson disease depends on the clinical features acquired from patient history and neurological examination [3]. A traditional role of MRI for Parkinson disease is supporting clinical diagnosis by enabling the exclusion of other disease processes [4]. However, several advanced imaging markers have emerged as tools for the visualisation of neuro-anatomic and functional processes in Parkinson disease. As one of them, neuromelanin-sensitive MRI uses high-spatial-resolution T1-weighted imaging with fast spin-echo sequences at 3-Tesla MRI [5, 6]. This new imaging technique provides a neuromelanin image (NMI) with neuromelanin-sensitive contrast, and T1 high-signal-intensity areas in the midbrain represent neuromelanin-rich areas. Since neuromelanin exists only in dopaminergic neurons of the substantia nigra pars compacta and noradrenergic neurons of locus coeruleus, NMI is useful for analysing the substantia nigra by capturing early Parkinson-disease-related changes. Figure 1 shows the examples of slice images of T1-weighted image (T1WI), T2-weighted image (T2WI), and NMI with annotation labels of the substantia nigra.

Fig. 1.

Slices of volumetric images of three-type sequences. (a) T1WI. (b) T2WI. (c) NMI. (a)–(c) show the same region including substantia nigra of a normal patient. (d) G.T. for the region of the substantia nigra. By manual normalisation of intensities shown in (c), an expert neurologist can recognise the regions of the substantia nigra.

We propose a new feature-extraction method to analyse patterns of substantia nigra in Parkinson disease. For the analysis, we use T1WI, T2WI, and NMI. Even though only NMI is the valid imaging for recognising the region of the substantia nigra among these three, T1WI and T2WI help obtain anatomical information. In addition to anatomical information, a simple division of intensities of T1WI by ones of T2WI yields a new quantitative contrast, T1w/T2w ratio, with sensitivity to neurodegenerative changes [7]. A combination of different imaging sequences can offer more useful information for the analysis. Therefore, we use these multi sequences for our analysis. In developing a new feature extraction method, we set a triplet of volumetric images: T1WI, T2WI, and NMI to be a multi-sequence volumetric image for each patient. As the extension of a higher-order tensor expression of a set of volumetric images [8], we express a set of multi-sequence volumetric images by a fifth-order tensor expression shown in Fig. 2(a). Inspired by tensor-based analytical methods [9,10,11], we decompose this fifth-order tensor into a linear combination of fifth-order rank-1 tensors. By re-ordering the elements of this decomposition result, as shown in Fig. 2(b), we obtain the decomposition of each multi-sequence volume image. This decomposition is a linear combination of fourth-order rank-1 tensors and their weights. Since this decomposition is based on the identical fourth-order rank-1 tensors, a set of weights expresses the characteristics of a multi-sequence volumetric image. Therefore, by selecting discriminative weights as feature vectors for normal and Parkinson disease, we achieve a feature extraction for analysing patterns of the substantia nigra between normal- and Parkinson-disease patients.

Fig. 2.

Tensor expression and decomposition of multi-sequence volumetric images. (a) Fifth-order expression of a set of sampled multi-sequence volumetric images. (b) Decomposition of multi-sequence volumetric image.

2 Mathematical Preliminary

2.1 Matrix Operations

We introduce two products of matrices since these are necessary for the CP-decomposition. Setting the Kronecker product of vectors $\boldsymbol{a}=(a_i) \in \mathbb {R}^I$ and $\boldsymbol{b}=(b_j) \in \mathbb {R}^J$ as $\boldsymbol{a} \otimes \boldsymbol{b} = [a_1 b_1, a_1 b_2, \dots , a_1 b_J, \dots , a_{I-1}b_J, a_I b_1,\dots , a_I b_J ]^{\top }$, we have Khatori-Rao product between two matrices $\mathcal {A} \in \mathbb {R}^{I \times K}$ and $\mathcal {B} \in \mathbb {R}^{J \times K}$ by

$$\begin{aligned} \boldsymbol{A} \odot \boldsymbol{B} = [\boldsymbol{a}_1 \otimes \boldsymbol{b_1}, \boldsymbol{a}_2 \otimes \boldsymbol{b_2}, \dots , \boldsymbol{a}_K \otimes \boldsymbol{b_K} ], \end{aligned}$$

(1)

where $\boldsymbol{a}_i$ and $\boldsymbol{b}_i$ are i-th column vectors of $\boldsymbol{A}$ and $\boldsymbol{B}$, respectively. For the same-sized matrices $\boldsymbol{A}=(a_{ij}), \boldsymbol{B}=(b_{ij}) \in \mathbb {R}^{I \times J}$, Hadamard product is the elementwise matrix product

$$\begin{aligned} \boldsymbol{A} *\boldsymbol{B} = \begin{bmatrix} a_{11}b_{11} &{} a_{12}b_{12} &{} \dots &{} a_{1J}b_{1j} \\ a_{21}b_{21} &{} a_{22}b_{22} &{} \dots &{} a_{2J}b_{2j} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ a_{I1}b_{I1} &{} a_{I2}b_{I2} &{} \dots &{} a_{IJ}b_{Ij} \end{bmatrix}. \end{aligned}$$

(2)

These products are used in Algorithm 1.

2.2 Tensor Expresstion and Operations

We briefly introduce essentials of tensor algebra for the CP-decomposition-based feature extraction. In tensor algebra, the number of dimensions is refered as order of a tensor. We set a fifth-order tensor $\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times I_4 \times I_5}$. An element $(i_1, i_2 ,i_3, i_4, i_5)$ of $\mathcal {A}$ is denoted by $a_{i_1 i_2 i_3 i_4 i_5}$. The index of a tensor is refered as mode of a tensor. For examples, $i_3$ is the index for mode 3. A fifth-order tensor $\mathcal {A}$ is a rank one if it can be expressed by the ourter products of five vectors $\boldsymbol{u}^{(j)} \in \mathbb {R}^{I_j}$, $j=1,2, 3, 4, 5$, that is

$$\begin{aligned} \mathcal {A} = \boldsymbol{u}^{(1)} \circ \boldsymbol{u}^{(2)} \circ \boldsymbol{u}^{(3)} \circ \boldsymbol{u}^{(4)} \circ \boldsymbol{u}^{(5)}, \end{aligned}$$

(3)

where $\circ$ expresses the outer product of two vectors. Furthermore, a cubical tensor $\mathcal {C} \in \mathbb {R}^{I \times I \times I \times I \times I}$ is diagonal if $a_{i_1 i_2 i_3 i_4 i_5} \ne 0$ only if $i_1 = i_2 = i_3 = i_4 = i_5$. We use $\underline{\boldsymbol{I}}$ to denote the cubical identity tensor with ones of the superdiagonal and zeros elsewhere.

For two tensors $\mathcal {A}, \mathcal {B} \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times I_4 \times I_5}$, we have the inner product

$$\begin{aligned} \left\langle \mathcal {A}, \mathcal {B} \right\rangle = \sum _{i_1=1}^{I_1} \sum _{i_2=1}^{I_2} \sum _{i_3=1}^{I_3} \sum _{i_4=1}^{I_4} \sum _{i_5=1}^{I_5} a_{i_1 i_2 i_3 i_4 i_5} b_{i_1 i_2 i_3 i_4 i_5}, \end{aligned}$$

(4)

where $a_{i_1 i_2 i_3 i_4 i_5}$ and $b_{i_1 i_2 i_3 i_4 i_5}$ expresses elements of $\mathcal {A}$ and $\mathcal {B}$, respectively. This inner norm derives a norm of tensor

$$\begin{aligned} \Vert \mathcal {A} \Vert = \sqrt{\left\langle \mathcal {A}, \mathcal {A} \right\rangle } = \sqrt{ \sum _{i_1=1}^{I_1} \sum _{i_2=1}^{I_2} \sum _{i_3=1}^{I_3} \sum _{i_4=1}^{I_4} \sum _{i_5=1}^{I_5} a_{i_1 i_2 i_3 i_4 i_5}^2 }. \end{aligned}$$

(5)

Unfolding of a tensor $\mathcal {A}$ is reshaping $\mathcal {A}$ by fixing one mode $\alpha$. The $\alpha$-mode unfolding gives a matrix $\mathcal {A}_{(\alpha )} \in \mathbb {R}^{I_{\alpha } \times (I_{\beta }I_{\gamma }I_{\delta }I_{\epsilon })}$ for $\{ \alpha , \beta , \gamma , \delta , \epsilon \} = \{1,2,3,4,5 \}$. For a tensor and its unfoding, we have the bijection $\mathfrak {F}_{(n)}$ such that

$$\begin{aligned} \mathfrak {F}_{(n)} \mathcal {A} = \mathcal {A}_{(n)}, \ \ \ \mathcal {A} = \mathfrak {F}_{(n)}^{-1} \mathcal {A}_{(n)}. \end{aligned}$$

(6)

This n-mode unfolding derives n-mode product with a matrix $\boldsymbol{U}^{(n)} \in \mathbb {R}^{J \times I_{n}}$

$$\begin{aligned} \mathcal {A} \times _{n} \boldsymbol{U}^{(n)} = \mathfrak {F}_{(n)}^{-1} (\boldsymbol{U}^{(n)}\mathcal {A}_{(n)}). \end{aligned}$$

(7)

For elements $u^{(n)}_{ji_{n}}$ with $j=1,2,\dots ,J$ and $i_{n}= 1,2, \dots , I_{n}$ of $\boldsymbol{U}^{(n)}$, we have

$$\begin{aligned} (\mathcal {A} \times _{n} \boldsymbol{U}^{(n)})_{i_1 \dots i_{n-1} j i_{n+1} \dots i_5 } = \sum ^{I_{n}}_{i_{n}=1} a_{i_1i_2 \dots i_5} u^{(n)}_{ji_{n}}. \end{aligned}$$

(8)

3 Feature Extraction for Multi-sequence Volumetric Data

We propose a new feature extraction method to analyse the difference of multi-sequence volumetric images between two categories. Setting $\mathcal {Y}_{i,1} \in \mathbb {R}^{I_1 \times I_2 \times I_3}$ for $j=1, 2, \dots , I_4$ to be volumetric images measured by different $I_4$ sequences for i-th sample, we have multi-sequence volumetric images as a fourth-order tensor $\mathcal {X}_{i} = [\mathcal {Y}_{i,1}, \mathcal {Y}_{i,2}, \dots ,\mathcal {Y}_{i,I_4}] \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times I_4}$. We express multi-sequence volumetric data of $I_5$ samples by a fifth-order tensor $\mathcal {T} = [\mathcal {X}_1, \mathcal {X}_2, \dots , \mathcal {X}_{I_5} ] \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times I_4 \times I_5}$ as shown in Fig. 2(a) . In this expression, we assume that regions of interest are extracted with cropping and registration as the same-sized volumetric data via preprocessing. For $\mathcal {T}$, we compute CP decomposition [11, 12]

$$\begin{aligned} \mathcal {T} = \sum _{r=1}^R \boldsymbol{u}_r^{(1)} \circ \boldsymbol{u}_r^{(2)} \circ \boldsymbol{u}_r^{(3)} \circ \boldsymbol{u}_r^{(4)} \circ \boldsymbol{u}_r^{(5)} + \mathcal {E} \end{aligned}$$

(9)

by minimising the norm $\Vert \mathcal {E} \Vert$ of a reconstruction error $\mathcal {E}$. In Eq. (9), a tensor is decomposed to R rank-1 tensors. Therefore, R is refered to as a CP rank. Algorithm 1 summarises the alternative reast square method [13, 14] for CP decomposition.

From the result of Eq. (9), setting $u^{(n)}_{kr}$ is the k-th element of $\boldsymbol{u}^{(n)}_r$, we have reconstructed volumetric and multi-sequencel volumetric images by

$$\begin{aligned} \check{\mathcal {Y}}_{ji}= & {} \sum _{r=1}^R u_{jr}^{(4)} u_{ir}^{(5)} (\boldsymbol{u}_r^{(1)} \circ \boldsymbol{u}_r^{(2)} \circ \boldsymbol{u}_r^{(3)} ), \end{aligned}$$

(10)

$$\begin{aligned} \check{\mathcal {X}}_i= & {} \sum _{r=1}^R u_{ir}^{(5)} (\boldsymbol{u}_r^{(1)} \circ \boldsymbol{u}_r^{(2)} \circ \boldsymbol{u}_r^{(3)} \circ \boldsymbol{u}_r^{(4)}), \end{aligned}$$

(11)

respectively. Figure 2(b) illustrates the visual interpretation of Eqs. (10) and (11). In these equations, rank-1 tensors $\boldsymbol{u}_r^{(1)} \circ \boldsymbol{u}_r^{(2)} \circ \boldsymbol{u}_r^{(3)}, r=1,2, \dots , R$ express parts of patterns among all volumetric images in three-dimensional space. In Eq. (11), rank-1 tensors $(\boldsymbol{u}_r^{(1)} \circ \boldsymbol{u}_r^{(2)} \circ \boldsymbol{u}_r^{(3)} \circ \boldsymbol{u}_r^{(4)}), r=1,2, \dots , R$ expresses parts of patterns among multi-sequence volumetric images. In Eq. (11), $u_{ri}^{(5)}$ indicates the importance of a part of patterns among multi-sequence data for i-th sample. Therefore, a set $u_{i11}^{(5)}, u_{i2}^{(5)}, \dots , u_{iR}^{(5)}$ express features of multi-sequence pattern of i-th sample.

We select discriminative feature from the results of CP decomposition to analyse the difference between two categories. Setting $C_1$ and $C_2$ to be sets of indices of images for two categories, we have the means and variances of $u_{ir}^{(5)}$ by

$$\begin{aligned} \mu _r = \mathbb {E}(u_{ir}^{(5)}) \quad&\textrm{and}&\quad \sigma _r^2 = \mathbb {E} ((u_{ir}^{(5)} - \mu _r)^2 ), \end{aligned}$$

(12)

$$\begin{aligned} \mu _{1r} = \mathbb {E}(u_{ir}^{(5)}| i \in C_1 ) \quad&\textrm{and}&\quad \sigma _{1r}^2 = \mathbb {E} ((u_{ir}^{(5)} - \mu _{1r})^2 | i \in C_1 ), \end{aligned}$$

(13)

$$\begin{aligned} \mu _{2r} = \mathbb {E}(u_{ir}^{(5)}| i \in C_2 ) \quad&\textrm{and}&\quad \sigma _{2r}^2 = \mathbb {E} ((u_{ir}^{(5)} - \mu _{2r})^2 | i \in C_2 ), \end{aligned}$$

(14)

for all indices of i, $C_1$ and $C_2$, respectively. We set intra-class and inter-class variance by

$$\begin{aligned} \sigma _{\textrm{B}r}^2= & {} \frac{N_1}{N} (\mu _{1r} - \mu _r)^2 + \frac{N_2}{N}(\mu _{2r} - \mu _r)^2, \end{aligned}$$

(15)

$$\begin{aligned} \sigma _{\textrm{W}r}^2= & {} \frac{N_1}{N} \sigma _{1r}^2 + \frac{N_2}{N} \sigma _{2r}^2, \end{aligned}$$

(16)

respectively. Using Eqs. (15) and (16), we have seperability [16, 17] as

$$\begin{aligned} s_r = \frac{\sigma ^2_{\textrm{B}r}}{\sigma ^2_{\textrm{W}r}} = \frac{\sigma ^2_{\textrm{B}r}}{\sigma ^2_{r} - \sigma ^2_{\textrm{B}r}}. \end{aligned}$$

(17)

Sorting $s_1, s_2, dots, S_R$ in desending order, we have a sorted index $\tilde{r}_1, \tilde{r}_2, \dots , \tilde{r}_R$ satisfying $s_{\tilde{r}_1} \ge s_{\tilde{r}_2} \ge \dots \ge s_{\tilde{r}_R}$ and $\{ \tilde{r}_1, \tilde{r}_2, \dots , \tilde{r}_R \} = \{1, 2, \dots , R \}$. We select L elements from $\boldsymbol{u^{(5)}_r }, r=1, 2, \dots , R$ as $\boldsymbol{f}_{i} = [ u^{(5)}_{i \tilde{r}_1}, u^{(5)}_{i \tilde{r}_2}, \dots , u^{(5)}_{i \tilde{r}_L }]^{\top } \in \mathbb {R}^{L}$ for multi-sequence volumetric images of i-th sample. Since these L elements have large seperabilities among R features, these elements indicate discriminative patterns in multi-sequence volumetric images between two categories.

4 Experiments

To analyse patterns of the substantia nigra between normal and Parkinson-disease patients in multi-sequence volumetric images: T1WI, T2WI, and NMI, we collected 155 multi-sequence volumetric images of 73 normal and 82 Parkinson-disease patients in a single hospital. In each multi-sequence volumetric image, T2WI and NMI are manually registered to the coordinate system of T1WI. Furthermore, a board-certified radiologist with ten years of experience specialising in Neuroradiology annotated regions of substantia nigra in NMIs. Therefore, each multi-sequence image has a pixel-wise annotation of the substantia nigra.

As the preprocessing of feature extraction, we cropped the regions of interest (ROI) of the substantia nigra from T1WI, T2WI, and NMI by using the annotations. The size of T1WI and T2WI is $224\times 300\times 320$ voxels of the resolution of $0.8\,\text {mm}\times 0.8\,\text {mm}\times 0.8\,\text {mm}$. The size of NMI is $512 \times 512 \times 14$ voxels of the resolution of $0.43\,\text {mm}\times 0.43\,\text {mm}\times 3.00\,\text {mm}$. We registered NMI to the space of T1WI for the cropping of ROIs. Setting the centre of an ROI to be the centre of gravity in a substantia nigra’s region, we expressed an ROI of each sequence as third-order tensors of $64\times 64\times 64$.

In each third-order tensor, after setting elements of the outer region of substantia nigra to be zero, we normalised all the elements of a third-order tensor in the range of [0, 1].

We expressed these third-order tensors of three sequences for 155 patients by a fifth-order tensor $\mathcal {T} \in \mathbb {R}^{64 \times 64 \times 64 \times 3 \times 155}$ and decomposed it by Algorithm 1 for $R=64, 155, 300,$ 1000, 2000, 4000, 6000. For the computation, we used Python with CPU of Intel Xeon Gold 6134 3.20 GHz and main memory 192 GB. Figure 3(a) shows the computational time of the decompositions. Figure 3(b) shows the mean reconstruction error ${\mathbb {E}}\left[ \Vert \mathcal {Y}_{ij} - \check{\mathcal {Y}}_{ij} \Vert / \Vert \mathcal {Y}_{ij} \Vert \right]$ for each sequence. Figure 4 summarises examples of the reconstructed volumetric images. From each of the seven decomposition results, we extracted 100-dimensional feature vectors.

We checked each distributions of feature vectors for the seven sets of the extracted features. In feature extraction, we set $C_1$ and $C_2$ to be sets of indices for normal and Parkinson-disease categories, respectively. For the checking, setting $(\cdot , \cdot )$ and $\Vert \cdot \Vert _2$ to be the inner product of vectors and $L_2$ norm, we computed a cosine similarity $(\boldsymbol{f}, \boldsymbol{\mu }) / (\Vert \boldsymbol{f}\Vert _2 \Vert \boldsymbol{\mu } \Vert _2)$ between a feature vector $\boldsymbol{f} \in \{ \boldsymbol{f}_i \}_{i=1}^{155}$ and the mean vector $\boldsymbol{\mu }= \mathbb {E}( \boldsymbol{f}_i | i \in C_1)$. The left column of Fig. 5 shows the distributions of the consine similarities. Furthermore, we mapped feature vectors from 100-dimensional space onto two-dimensional space by t-SNE [18], which approximately preserves the local topology among feature vectors in the original space. The right column of Fig. 5 shows the mapped feature vectors in a two-dimensional space.

Fig. 3.

Computational time and reconstruction error in CP decomposition. (a) Computational time against a CP rank. (b) Mean reconstruction errors of volumetric images against a CP rank. The mean reconstruction errors are computed for sequences: T1WI, T2WI, and NMI.

Fig. 4.

Example slices of reconstructed and original multi-sequence volumetric images. The images express axial slices of reconstructed images for T1WI, T2WI, and NMI. R expresses a CP rank used in a CP decomposition.

Finally, we explored the geometrical interpretation of selected features. As shown in Fig. 6, some selected features have large magnitudes. We thought these large-magnitude features express important patterns for an image. Therefore, we multiplied these large magnitudes (approximately 10 to 20 of 100 features) by 0.7 as feature suppression and reconstructed images for CP decomposition of $R=6000$. By comparing these reconstructed multi-sequence volumetric images, we can observe important patterns corresponding to the suppressed features as not-reconstructed patterns. Figure 7 compares reconstructed multi-sequence volumetric images before and after the suppression of selected features.

Fig. 5.

Distribution of extracted feature vectors. Left column: Distribution of cosine similarities between a feature vector $\boldsymbol{f} \in \{ \boldsymbol{f}_i \}_{i=1}^{155}$ and the mean vector $\boldsymbol{\mu }= \mathbb {E}(\boldsymbol{f}_i | i \in C_1)$. Right column: Visualisation of distribution of feature vectors. We map 100-dimensional feature vectors onto a two-dimensional space. In the top, middle, and bottom rows, we extracted 100-dimensional feature vectors from CP decompositions of $R=1000, 4000$, and 6000, respectively.

5 Disucussion

In Fig. 3(b), the curves of mean reconstruction errors for T1WI and NMI are almost coincident, whilst the one of T2WI is different from these two. These results imply that intensity distributions on the substantia nigra between T1WI and NMI have similar structures. Even though the intensity distribution of T2WI has the common structure for T1WI and NMI, T2WI has different characteristics from these two. These characteristics are visualised in Fig. 4. Three images express shapes of substantia nigra, but the intensity distribution of T2WI are different from T1WI and NMI. Furthermore, Fig. 6(b)–(d) also indicate the same characteristics. In Fig. 6(b) and (d), the selected features for T1WI and NMI have similar distributions of elements, even though the one of T2WI has a different distribution.

Fig. 6.

Examples of extracted features. (a) Extracted 100-dimensional feature vector $[ u^{(5)}_{i \tilde{r}_1}, u^{(5)}_{i \tilde{r}_2}, \dots , u^{(5)}_{i \tilde{r}_{100} }]^{\top }$. (b)–(d) Scaled extracted feature vectors $[ u^{(4)}_{j1} u^{(5)}_{i \tilde{r}_1}, u^{(4)}_{j2} u^{(5)}_{i \tilde{r}_2}, \dots , u^{(4)}_{j100} u^{(5)}_{i \tilde{r}_{100} }]^{\top }$, where we set $j=1,2,3$ for T1WI, T2WI, and NMI, respectively. In (a)–(d), horizontal and vertical axes express an index of an element and value of element, respectively.

Fig. 7.

Reconstruction with and without selected features. The top row shows the axial slices of the original multi-sequence volumetric images. In the top row, red dashed circles indicate the discriminative regions in multi-sequence volumetric images between normal and Parkinson disease. The middle row shows the axial slice of the reconstructed images from a CP decomposition of $R=6000$. The bottom row shows the axial slices of reconstructed images for a CP decomposition of $R=6000$, where we multiply the large feature values in selected 100 features by 0.7. (Color figure online)

In Fig. 4, the reconstruction of detail intensity distributions of multi-sequence volumetric images needs large R, while the blurred shape of the substantia nigra is captured even in small R such as 64, 300 and 1000. Since Algorithm 1 searches for rank-1 tensors to minimise reconstruction error by solving the least squares problems for each mode, the CP decomposition firstly captures common patterns among sequences and patients with a small number of rank-1 tensors. To obtain rank-1 tensors expressing non-common patterns among the images, we have to increase the number of rank-1 tensors in the CP decomposition.

In Fig. 5(a), for normal and Parkinson disease, two distributions of cosine similarities almost overlap. This result shows that the selected features from the CP decomposition of $R=1000$ are indiscriminative for two categories. As R increases in Fig. 5 (c) and (e), the overlap of the distributions between the two categories decreases. Figure 5(b), (d), and (f) also show the same characteristics as Fig. 5(a), (c), and (e). These results and the results in Fig. 4 imply that discriminative features between the two categories exist in non-common patterns with detailed local intensity distributions among multi-sequence volumetric images.

Figure 7 depicts the reconstructed images’ missing regions after the suppression of selected features. Comparing the middle and bottom rows of Fig. 7, we observed the missing regions in specific parts of the substantia nigra. In the top row of Fig. 7, missing regions are marked on the original images by a red dashed circle. The marked regions include the regions of severe loss of neurons in Parkinson disease. The pars compacta of the substantia nigra is divided into ventral and dorsal tiers, and each tier is further subdivided into medial to lateral regions. In Parkinson disease, the ventrolateral tier of substantia nigra loses first, and then the ventromedial tier also loses. Typically the cells of 70–90% in the ventrolateral tier have been lost by the time a Parkinson-disease patient dies [19]. Since the missing regions include the ventrolateral tiers, we coluded that the proposed method achieved neuropathologically correct feature extraction.

6 Conclusions

We proposed a new feature extraction method to analyse patterns of the substantia nigra in Parkinson disease. For the feature extraction, we expressed multi-sequence volumetric images as a fifth-order tensor and decomposed it. The proposed method selects discriminative features from the tensor decomposition result. A series of experiments show the validity of the proposed method and important patterns in multi-sequence volumetric images for discrimination of Parkinson disease. Especially, our geometrical interpretation of the selected features in the visualisation clarified the discriminative region of the substantial nigra between normal and Parkinson-disease patients. Based on the suggested tensor-based pattern expression, we will explore an optimal feature-extraction method as a topic for future work.