Introduction

Parkinson disease (PD) is a common progressive neurodegenerative disorder in our ageing society. Approximately 8.5 million people have been affected worldwide in 2017 [1]. The diagnosis of PD depends on the clinical features acquired from the patient’s history and neurological examination [2]. Available treatments for PD are still only for symptomatic relief and fail to stop the neurodegeneration progress. Early-stage PD biomarkers are desired for timely clinical intervention and understanding of pathophysiology [3]. Several advanced imaging markers have emerged as tools for visualising neuro-anatomic and functional processes in PD. As one of them, neuromelanin-sensitive MRI uses high-spatial-resolution T1-weighted imaging with fast spin-echo sequences at 3-Tesla MRI [4, 5]. This imaging provides a neuromelanin image with neuromelanin-sensitive contrast, and T1 high-signal-intensity areas in the midbrain represent neuromelanin-rich areas. One characteristic of PD is progressive loss of dopaminergic neurons in the substantia nigra pars compacta [6]. Furthermore, neuromelanin exists only in dopaminergic neurons of the substantia nigra pars compacta and noradrenergic neurons of locus coeruleus. Therefore, a neuromelanin image is useful for analysing the substantia nigra by capturing early PD-related changes. Figure 1 shows examples of a neuromelanin image and its annotation label indicating the substantia nigra.

To analyse the substantia nigra as volumetric data, which enables us to analyse shape and texture information simultaneously, our group tackled the automated volumetric segmentation by deep learning models [7, 8] and the statistical analysis by higher-order tensor decomposition [9]. For the segmentation, by using neuromelanin images, we achieved a more accurate segmentation [8] than T2-weighted images [7]. In the statistical analysis [9], we found that T1-weighted and neuromelanin images share similar three-dimensional patterns in a fifth-order tensor decomposition of multisequence of T1-weighted, T2-weighted and neuromelanin images. Furthermore, in the decomposition, we found that three-dimensional patterns of the substantia nigra in neuromelanin images are more compressible than T1- and T2-weighted images. These previous results indicate that we can obtain the small number of informative features of the substantia nigra from neuromelanin images. In related works, even though a deep learning model with an large dataset of T1-weighted images of the whole brain has been reported [10], the analysis of the substantia nigra on a neuromelanin image has been reported only for a small dataset of 55 patients [11]. Furthermore, this analysis manually selected a rectangular region around the substantia nigra on the axial slices of and input to a two-dimensional convolutional neural network. A volumetric data analysis for the substantia nigra is still an open problem.

We propose a new feature-extraction method to analyse PD-related patterns in neuromelanin images of the substantia nigra. Exploring discriminative features for classifying the substantia nigra between PD and non-PD is essential for finding PD biomarkers. As a higher-order tensor expression of volumetric images [12], we express a set of volumetric images of the extracted substantia nigra as a fourth-order tensor. Inspired by tensor-based analytical methods [13,14,15], we decompose this into a linear combination of fourth-order rank-1 tensors. By re-ordering the elements of this decomposition result, we obtain each decomposed volumetric image by identical third-order rank-1 tensors. Since decompositions of each image are based on the identical third-order rank-1 tensors, a set of weights expresses the characteristics of a volumetric image. Therefore, by selecting discriminative weights for classifying PD and non-PD as a feature vector, we achieve a feature extraction for analysing patterns of the substantia nigra. Our tensorial feature extraction offers the visualisation of discriminative patterns by reconstructing an volumetric image from selected features.

Fig. 1
figure 1

Neuromelanin imaging and substanita nigra.a Captured image. b Annotated region of the substantia nigra

Full size image

Methods

Tensor expression

In tensor algebra, the number of dimensions is referred to as the order of a tensor. We set an M-th-order tensor \(\mathcal {A} \in \mathbb {R}^{I_1 \times I_2 \times \dots \times I_M}\). An element with indices \((i_1, i_2,i_3, \dots , i_M)\) in \(\mathcal {A}\) is denoted by \(a_{i_1 i_2 \dots i_M}\). The index of a tensor is referred to as the mode of a tensor. For example, \(i_3\) is the index for mode 3.

Fig. 2
figure 2

Tensorial expression by decomposing a volumetric image for feature extraction, selection and visualisation

Full size image

An M-th-order tensor \(\mathcal {A}\) is a rank one if it can be expressed by M vectors by

$$\begin{aligned} \mathcal {A} = \varvec{u}^{(1)} \circ \varvec{u}^{(2)} \circ \dots \circ \varvec{u}^{(M)}, \end{aligned}$$
(1)

where \(\circ \) expresses the outer product. Furthermore, we have a norm of a tensor as

$$\begin{aligned} \Vert \mathcal {A} \Vert = \sqrt{ \sum _{i_1=1}^{I_1} \sum _{i_2=1}^{I_2} \dots \sum _{i_M=1}^{I_M} a_{i_1 i_2 \dots i_M }^2 }. \end{aligned}$$
(2)

Expressing data as a tensor, we can decompose it into a linear combination of rank-1 tensors and evaluate its reconstruction error with the norm.

Tensorial feature extraction

We propose a feature extraction method for classifying volumetric images between two categories. This work assumes that three-dimensional patterns of volumetric images can be decomposed into common three-dimensional patterns if volumes of interest (VOIs) are extracted and pre-registered to an appropriate coordinate system for their analysis. Setting a volumetric image to a third-order tensor \(\mathcal {X} \in \mathcal {R}^{I_1 \times I_2 \times I_3}\), we have a linear combination of R patterns such that

$$\begin{aligned} \mathcal {X} \approx \sum _{r=1}^R f_{r} \mathcal {Y}_r = \sum _{r=1}^R f_{r} (\varvec{u}_r^{(1)} \circ \varvec{u}_r^{(2)} \circ \varvec{u}_r^{(3)}), \end{aligned}$$
(3)

where a rank-1 third-order tensor \(\mathcal {Y}_r \) and scalar \(f_r\) express a decomposed three-dimensional pattern and its coefficient, respectively. Figure 2 illustrates our tensor expression of volumetric images. Since \(f_r\) indicates the importance of the r-th decomposed three-dimensional pattern \(\mathcal {Y}_r\), we can express the three-dimensional pattern of \(\mathcal {X}\) by a feature vector

$$\begin{aligned} \varvec{f} = [f_1, f_2, \dots , f_R]^{\top }. \end{aligned}$$
(4)

For the practical computation of the above feature extraction, we introduce nonnegative tensor factorisation, an extension of canonical polyadic (CP) decomposition.

Canonical polyadic decomposition

Setting \(\mathcal {X}_{j} \in \mathbb {R}^{I_1 \times I_2 \times I_3}\) for \(j=1, 2, \dots , J\) to be volumetric images in a training dataset, we express these J volumetric images as the fourth-order tensor \(\mathcal {T} \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times I_4 }\), where we set \(I_4 = J\). For \(\mathcal {T}\), we have a CP decompositionFootnote 1 [14,15,16]

$$\begin{aligned} \mathcal {T} = \sum _{r=1}^R \varvec{u}_r^{(1)} \circ \varvec{u}_r^{(2)} \circ \varvec{u}_r^{(3)} \circ \varvec{u}_r^{(4)} + \mathcal {E} \end{aligned}$$
(5)

by minimising a reconstruction error \(\Vert \mathcal {E} \Vert \). The number of rank-1 tensors in tensor decomposition is referred to as the CP rank of a tensor. Note that there is no orthogonal constraint for \(\varvec{u}_r^{(n)}, r=1,2,\dots , R\) for an alternative-least square solution [16,17,18] in a CP decomposition. Since a reconstructed volume image is given by

$$\begin{aligned} \mathcal {X}_j \approx \sum _{r=1}^{R} u_{jr}^{(4)} (\varvec{u}_r^{(1)} \circ \varvec{u}_r^{(2)} \circ \varvec{u}_r^{(3)} ), \end{aligned}$$
(6)

where \(u_{jr}^{(4)}\) is the j-th element of \(\varvec{u}_{r}^{(4)}\), we have a feature vector

$$\begin{aligned} \varvec{f}_j = [u_{j1}^{(4)}, u_{j2}^{(4)}, \dots , u_{jR}^{(4)}]^{\top } \end{aligned}$$
(7)

of an image \(\mathcal {X}_j\) in a training set.

Furthermore, setting \(\check{\mathcal {X}}_{k} \in \mathbb {R}^{I_1 \times I_2 \times I_3}\) for \(k=1, 2, \dots , K\) to volumetric images in a testing dataset, we express these K volumetric images as a fourth-order tensor \(\mathcal {Q} \in \mathbb {R}^{I_1 \times I_2 \times I_3 \times \check{I}_4}\), where we set \(\check{I}_4 = K\). By computing only \(\check{\varvec{U}}^{(4)} = [\check{\varvec{u}}^{(4)}_1, \check{\varvec{u}}^{(4)}_2, \dots , \check{\varvec{u}}^{(4)}_R ]\) with the obtained matrices \(\{ \varvec{U}^{(n)} = [\varvec{u}^{(n)}_1, \varvec{u}^{(n)}_2,\) \(\dots , \varvec{u}^{(n)}_R ] \}_{n=1}^3\) in Eq. (5), we can decompose volumetric images of a testing dataset with the three-dimensional patterns in a training dataset. As a result, we have a feature vector

$$\begin{aligned} \check{\varvec{f}}_k = [\check{u}_{k1}^{(4)}, \check{u}_{k2}^{(4)}, \dots , \check{u}_{kR}^{(4)}]^{\top } \end{aligned}$$
(8)

of an image \(\check{\mathcal {X}_k}\) in a testing set.

Nonnegative tensor factorisation

We introduce nonnegative tensor factorisation (NTF) [13, 15, 16] into feature extraction. NTF is a simple extension of CP decomposition. We add nonnegative constraint \(\varvec{U}^{(n)} = [\varvec{u}^{(n)}_1, \varvec{u}^{(n)}_2, \dots , \varvec{u}^{(n)}_R ] \in \mathbb {R}_{+}^{I_n \times R}\) for \(n=1,2,3,4\), where \(\mathbb {R}_{+}\) is a set of nonnegative real values, into a decomposition in Eq. (5). In the practical computation of NTF, we iteratively update each element with a gradient-based method from initial random nonnegative values. For a decomposition of a testing dataset, we add a nonnegative constraint \(\check{U}^{(4)} \in \mathbb {R}_{+}^{\check{I}_4 \times R}\). Using the Khatori-Rao product \(\odot \), Hadamard product \(*\) and Hadamard division \(\oslash \) [15, 16, 19], Algorithms 1 and 2 summarise NTF for training and test datasets, respectively. From the results of Algorithms 1 and 2, we have \(\{ \varvec{f}_j \}_{j=1}^J\) and \(\{ \check{\varvec{f}}_k \}_{k=1}^K\).

Feature selection

We integrate the feature-selection process [20] into our method to capture discriminative features for two-category classification. For a set of extracted features \(\{ \varvec{f}_j \}_{j=1}^{J}\) of a training dataset with the condition \(R < J\), we assume each feature belongs to either the category \(\mathcal {C}_1\) or \(\mathcal {C}_2\). Therefore, features are divided into two sets, \(\{ \varvec{f}_{1i} \}_{i=1}^{N_1}\) and \(\{ \varvec{f}_{2i}^{} \}_{i=1}^{N_2}\), where \(N_1\) and \(N_2\) represent the number of images in the first and second categories, respectively. Setting \(\varvec{F}_l = [\varvec{f}_{l1}, \varvec{f}_{l2}, \dots , \varvec{f}_{l N_l} ]\) for \(l=1,2\), we have autocorrelation matrices \(\varvec{A}_1 = \frac{1}{N_1} \varvec{F}_1 \varvec{F}_1^{\top }\) and \(\varvec{A}_2 = \frac{1}{N_2} \varvec{F}_2\varvec{F}_2^{\top }\). These two matrices introduce an autocorrelation matrix of all the features by

$$\begin{aligned} \varvec{A}= P(\mathcal {C}_1) \varvec{A}_1 + P(\mathcal {C}_2)\varvec{A}_2, \end{aligned}$$
(9)

where we set \(P(\mathcal {C})_1= \frac{N_1}{N_1+N_2}\) and \({P(\mathcal {C}_2)} = \frac{N_2}{N_1+N_2}\). For \(\varvec{A}\), we have the eigendecomposition \(\varvec{A} = \varvec{V}\varvec{\Xi }\varvec{V}^{\top }\), where \(\varvec{\Xi }= \textrm{diag}(\xi _1,\xi _2,\dots ,\xi _R)\) consists of eigenvalues \(\xi _i\) for \(i=1,2, \dots , R\) with the condition \(\xi _1\ge \xi _2 \ge \dots \ge \xi _{R} > 0\). This eigendecomposition derives a whitening matrix \(\varvec{W} = \varvec{\Xi }^{-\frac{1}{2}}\varvec{V}^{\top }\).

figure a
figure b

From the whitening matrix \(\varvec{W}\) and Eq. (9), we have

$$\begin{aligned} \varvec{WAW}^{\top }= & {} \varvec{W}P(\mathcal {C}_1) \varvec{A}_1 \varvec{W}^{\top } + \varvec{W}P(\mathcal {C}_2) \varvec{A}_2\varvec{W}^{\top }\nonumber \\= & {} \tilde{\varvec{A}}_1 + \tilde{\varvec{A}}_2 = \varvec{I}, \end{aligned}$$
(10)

where \(\varvec{I}\) is an identity matrix. The solutions of the eigenvalue problems \( \tilde{\varvec{A}}_l \varvec{\phi }_{l,i} = \lambda _{l,i} \varvec{\phi }_{l,i}\) and Eq. (10) derive relations \(\tilde{\varvec{A}}_2 \varvec{\phi }_{2,i} = ( \varvec{I} - \tilde{\varvec{A}}_1 ) \varvec{\phi }_{2,i}\) and \(\tilde{\varvec{A}_1} \varvec{\phi }_{2,i} =(1 - \lambda _{2,i} ) \varvec{\phi }_{2,i} \) for \(l =1,2\). These lead to

$$\begin{aligned} \varvec{\phi }_{2,i} = \varvec{\phi }_{1, R-i+1} \end{aligned}$$
(11)

and

$$\begin{aligned} \lambda _{2, i} = 1- \lambda _{1, R-i+1} \end{aligned}$$
(12)

for \(i=1,2, \dots , R\) and \(l =1,2\). These relations imply that the eigenvectors corresponding to the large eigenvalues of \(\tilde{\varvec{A}}_1\) contribute to expressing \(\mathcal {C}_1\), although they make a minor contribution to expressing \(\mathcal {C}_2\).

In this work, setting \(\varvec{\Phi } = [\varvec{\phi }_{1,1}, \varvec{\phi }_{1,2}, \dots , \varvec{\phi }_{1,d}]\), we project extracted feature vectors by

$$\begin{aligned} \varvec{g}_j = \varvec{\Phi }^{\top }\varvec{f}_j, \ \ \ j=1, 2, \dots , J, \end{aligned}$$
(13)
$$\begin{aligned} \check{\varvec{g}}_k = \varvec{\Phi }^{\top }\check{\varvec{f}}_k, \ \ \ k=1, 2, \dots , K, \end{aligned}$$
(14)

to select \(\mathcal {C}_1\)-related features.

Classification and its visual interpretation

We classify a feature-selected vector and reconstruct its three-dimensional pattern for visual interpretation. For the classification of \(\varvec{g} \in \{ \varvec{g}_j \}_{j=1}^J \cup \{ \check{\varvec{g}}_k \}_{k=1}^K\), we have a discriminant function

$$\begin{aligned} h(\varvec{g}) = \varvec{w}^{\top } \varvec{g} + w_0, \end{aligned}$$
(15)

where \(\varvec{w}=[w_1, w_2, \dots , w_d]^{\top }\) and \(w_0\) are a weight vector and thresholding criterion, respectively. We compute \(\varvec{w}\) by Fisher’s linear discriminant analysis (LDA) [21] from the feature-selected vectors of a training dataset. Setting means \(\mu _1\) and \(\mu _2\) of projected feature vectors in \(\mathcal {C}_1\) and \(\mathcal {C}_2\), respectively, in a projected space given by \(\varvec{w}\), we define \(w_0 = \lambda \mu _1 + (1 - \lambda ) \mu _2 \) with a hyperparameter \(\lambda \in [0, 1]\). Using Eq. (15), we classify \(\varvec{g}\) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} h(\varvec{g}) > 0, &{} \varvec{g} \in \mathcal {C}_1, \\ \textrm{otherwise}, &{} \varvec{g} \in \mathcal {C}_2. \end{array}\right. } \end{aligned}$$
(16)

We set \(\tilde{g}_p\) with an index \(p=1, 2, \dots , d\) to the pth element of \( \tilde{\varvec{g}}=\varvec{w} \odot \varvec{g}\). Since positive elements of \(\tilde{\varvec{g}}\) show the selected features’ relevance to \(\mathcal {C}_1\), we have \(\varvec{g}^{+} = (g^{+}_p)\) by filtering

$$\begin{aligned} g^{+}_p = {\left\{ \begin{array}{ll} g_p, &{} \tilde{g}_p > 0, \\ 0, &{} \textrm{otherwise}. \end{array}\right. } \end{aligned}$$
(17)

Using an element \(f_r^{+}\) of \(\varvec{f}^{+}=\varvec{\Phi }\varvec{g}^{+}\), we can reconstruct \(\mathcal {C}_1\)-related three-dimensional patterns in \(\mathcal {X} \in \{ \mathcal {X}_j \}_{j=1}^J \cup \{ \check{\mathcal {X}}_k \}_{k=1}^K\) from its feature-selected vector \(\varvec{g}\) by

$$\begin{aligned} \mathcal {X}^{+} = \textrm{ReLU} \left( \sum _{r=1}^{R} f^{+}_r (\varvec{u}^{(1)}_r \circ \varvec{u}^{(2)}_r \circ \varvec{u}^{(3)}_r ) \right) , \end{aligned}$$
(18)

where ReLU replaces negative values in an input tensor with zero.

Experiments

Datasets

Patients diagnosed with PD based on the UK PD Society Brain Bank clinical criteria and healthy subjects without any neurological diseases [22], who visited Juntendo Hospital between 2019 and 2022, were recruited with IRB approval. Using a 3T scanner (MAGNETOM Prisma, Siemens Healthcare), we collected neuromelanin images of 263 patients: 124 PD and 139 non-PD patients with additional spectral presaturation inversion-recovery pulses [2]. General scan parameters were as follows: 600/12 ms repetition time/echo time; echo train length of 14; 2.5 mm slice thickness; 0.5 mm slice gap; 3.0 mm spacing between slices; 512 \(\times \) 359 acquisition matrix; 220 \(\times \) 220 mm field of view (0.43 \(\times \)0.43 mm pixel size); 175 Hz/pixel bandwidth, three-averages; 7:15 min of total scan time.

In this collection, first, we obtained T1-weighted images by setting AC-PC lines to be parallel against axial slices in each patient. The size of a T1-weighted image is \(224 \times 300 \times 320\) voxels, each of which is 0.80 mm \(\times \) 0.80 mm \(\times \) 0.80 mm. Second, we obtained neuromelanin images for all the patients. The size of a neuromelanin image is \(512 \times 512 \times 14\) voxels, each of which is 0.43 mm \(\times \) 0.43 mm \(\times \) 3.00 mm. Third, for each patient, we registered a neuromelanin image to a T1-weighted image by rigid transform, where we used the FMRIB software library’s linear registration tool [23].

For these neuromelanin images, a board-certified radiologist with ten years of experience specialising in neuroradiology annotated regions of the substantia nigra by using MRIcron [24]. Based on the annotations, we cropped the VOIs of the substantia nigra from the neuromelanin images. Setting the centre of a VOI to be the centre of gravity in a region of the substantia nigra, we expressed a VOI of each sequence as third-order tensors of \(64 \times 64 \times 64\) voxels. In each third-order tensor, after setting elements of the outer region of substantia nigra to be zero, we normalised all the elements of each third-order tensor in the range of [0, 1]. We randomly divided these images into training and testing datasets, as summarised in Table 1. Figure 3 summarises the age distributions in our datasets.

Table 1 Details of training and testing datasets
Full size table
Fig. 3
figure 3

Age distribution of our datasets. The range of patients’ ages is 45–87. The averages of ages in training, testing and all datasets are 68.5, 70.5 and 69.3, respectively. The ratios of males and females in training, testing and all datasets are 1.00:0.90, 1.00:1.25 and 1.00:1.03, respectively

Full size image
Fig. 4
figure 4

Characteristics of NTF and eigendecomposition. Mean reconstruction errors in NTF. We set \(R=64, \!155, 250, 500, 1000, 2000, 4000\) b Eigenvalues of normalised autocorrelation matrix of 64-dimensional feature vectors for PD’s training dataset. Characteristics of NTF and eigendecomposition

Full size image
Fig. 5
figure 5

ROC curves of substantia nigra classification. a Training dataset. b Testing dataset. In a and b, we set \(R=64, \!155, 250, 500, 1000, 2000, 4000\) and \(\lambda =\)0.00, 0.05, 0.10, \(\dots \), 1.00

Full size image

Evaluation of substantia nigra classification

To evaluate the proposed feature-extraction method, we classify extracted feature vectors by a linear function \(g(\varvec{f}) = \varvec{w}^{\top }\varvec{f} +w_0\), where \(\varvec{f} \in \{ \varvec{f}_j \}_{j=1}^J \cup \{ \check{\varvec{f}}_k \}_{k=1}^K\). We extract feature vectors from training and testing datasets by Algorithms 1 and 2, respectively, for \(R=64, 155, 250, 500, 1000,2000, 4000\). Figure 4a shows CP-rank and mean relative reconstruction error \(\mathbb {E}(\Vert \mathcal {X} - \sum _{r=1}^R f_r \mathcal {Y}_r \Vert / \Vert \mathcal {X} \Vert )\) for each CP rank. Using extracted features for the training dataset, we computed \(\varvec{w}\) and \(w_0\) in the same manner described in Sect. Methods. As the evaluation metric of classification accuracy, we set sensitivity and specificity to the ratios of correctly classified images in PD and non-PD categories, respectively. Figure 5 summarises classification accuracy for training and testing datasets for different \(\lambda \).

Fig. 6
figure 6

Classification accuracy after feature selections. a \(d=7\). b \(d=15\). c \(d=18\)

Full size image

To evaluate the validity of our feature selection, we computed classification accuracy for the selected features with the procedure described in Sect. Methods. Figure 6 shows the classification accuracy with feature selection for \(R=64\) and \(d=7, 15, 18\). Figure 5b illustrates the eigenvalue distribution of the normalised autocorrelation matrix for the PD category. Figure 7 presents examples of reconstructed volumetric images before and after feature selection. For the reconstruction from selected features, we used Eq. (18).

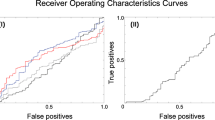
For a comparative evaluation, we computed the classification accuracy of a support vector machine (SVM) [25]. We trained a linear SVM model using the extracted feature vectors of the training dataset without the feature selection. For training a linear SVM model, we set the weight of the regularisation to one and used the balanced weight \((N_1+N_2)/2N_l\) for the lth category. To enable SVM to output estimated probability for each category, we adopted Platt’s likelihood [26]. If an SVM’s output probability for the PD category exceeds a criterion, we classify input as \(\mathcal {C}_1\). Using the criterion from 0.00 to 1.00 with the step size of 0.05, we plotted the ROC curves of training and testing datasets for the linear-SVM model. For the computation of SVM, we used scikit-learn. Figure 8 summarises the comparative evaluation between LDA with feature selection (ours) and SVM without feature selection.

Fig. 7
figure 7

Qualitative evaluation of reconstructed images. The top, middle and bottom rows show slices of the original, reconstruction from NTF and reconstruction from selected features for \(R=64\). PD4 is selected from the testing dataset, and the others are selected from the training dataset

Full size image
Fig. 8
figure 8

Comparison with support vector machine

Full size image
Fig. 9
figure 9

Results of fivefold cross-validation for LDA with the feature selection. a-e show classification accuracy for the testing datasets in folds from 1 to 5. For each fold, we set \(d=8, 12, 16, 20, 24, 28, 32, 48, 64\) and \(\lambda =0.00, 0.05, 0.10, \dots , 1.00\)

Full size image

To further explore our approach, we performed fivefold cross-validation by splitting all the data into training and testing datasets. In training steps in each fold, we selected features and computed \(\varvec{w}\) for \(d=\)8, 12, 16, 20, 24, 28, 32, 48, 64. Figure 9 shows the results of the fivefold cross-validation.

Discussion

Figure 5 indicates that increasing the CP rank results in the extraction of indiscriminative features for unseen images in the substantia nigra classification, even though Fig. 4a shows that increasing the CP rank contributes to decreasing the reconstruction error. For the given 155 images in the training dataset, Fig. 5 shows that CP ranks from 64 to 500 are acceptable for the classification. For these CP ranks, Fig. 5b shows insufficient sensitivities and specificities of approximately 0.60. NTF was originally designed only for analysis, not for classification. Therefore, these results imply the necessity of feature selection to capture category-specific discriminative features.

Figure 4b shows that fewer than 18 eigenvectors express essential patterns for the PD category. As shown in Fig. 6, our feature selection using the appropriate eigenvectors improved the sensitivity and specificity of the testing dataset. Figure 8 illustrates the higher generalisation ability of our approach than the linear SVM. Even though there is a gap in classification accuracy between training and testing datasets for the linear SVM, our proposed method achieved the small one. The proposed method achieved a sensitivity of 0.72 and a specificity of 0.64 for training and testing datasets.

We also presented the reconstruction of the selected features in Fig. 7. Generally, the pars compacta of the substantia nigra is divided into ventral and dorsal tiers, and each tier is further subdivided into medial to lateral regions. In PD, the ventrolateral tier of the substantia nigra loses first, and then the ventromedial tier also loses. Typically, the cells of 70–90% in the ventrolateral tier have been lost by the time a PD patient dies [27]. In Fig. 7, our feature selection captures three-dimensional patterns related to the ventrolateral tiers.

In Fig. 9, the three of fivefold show the feature selection’s improvement of sensitivity and specificity. These indicate the validity of the proposed method. However, the optimal number of the feature selection for those folds differs. Furthermore, for the other folds, the feature selection does not work. These results imply that more data collection is needed. In the case of a sufficiently large dataset, after randomly removing 10–25% of the dataset, we can have approximately the same distribution shape as the original dataset. If we randomly remove 10–25% of a small dataset, we might have a different distribution shape from the original dataset. To achieve expert-level precise classification [28, 29] of the substantia nigra between PD and non-PD, we are required to capture more discriminative features from a large dataset.

Conclusions

This paper proposed a tensorial feature-extraction method for substantia nigra analysis towards PD diagnosis. Since category-specific features should be discriminative, we evaluated the accuracy of classifying the substantia nigra between PD and non-PD cases. The experimental evaluations demonstrated the method’s validity, where the classification accuracy is acceptable as a preliminary study. Unlike deep learning approaches, our proposed method directly reconstructs important patterns to interpret classification results visually.