Approximate Bayesian Algorithm for Tensor Robust Principal Component Analysis

Abstract

Recently proposed Tensor Robust Principal Component Analysis (TRPCA) (Lu et al. in Tensor robust principal component analysis: exact recovery of corrupted low-rank tensors via convex optimization, 2019 [14]) aims to exactly recover the low-rank and sparse components from their sum, extending the Low-Rank Tensor Completion model of Mu et al. (Lower bounds and improved relaxations for tensor recovery, 2013 [17]). We construct a Bayesian approximate inference algorithm for TRPCA, based on regression adjustment methods suggested in the literature to correct for high-dimensional nature of the problem (Blum in J Am Stat Assoc 105(491), 2010 [3]; Blum and François in Stat Comput 20(1):63–73, 2010 [4]). Our results are compared to previous studies using variational Bayes inference for tensor completion (Hawkins and Zhang in Conference: IEEE international conference on data mining, 2018 [11]). In a short application, we study spatiotemporal traffic data imputation using nine-week spatiotemporal traffic speed data set of Guangzhou, China.

1 Introduction: Tensor Robust Principal Component Analysis and Its Extensions

Classical Principal Component Analysis (PCA) is the most widely used statistical tool for data analysis and dimensionality reduction. It is computationally efficient and powerful for the data which are mildly corrupted by small noises. However, a major issue of PCA is that it is brittle to grossly corrupted observations or presence of outliers, which are ubiquitous in real world data. To date, a number of robust versions of PCA were proposed. But many of them suffer from the high computational cost. The recently proposed Robust PCA [7] is the first polynomial-time algorithm with strong performance guarantees. Suppose we are given a data matrix $X \in \mathbb {R}^{n_{1} \times n_{2}}$ which can be decomposed as $X = L_{0} + E_{0}$ where $L_{0}$ is low-rank and $E_{0}$ is sparse. It is shown in Candès et al. [7] that if the singular vectors of $L_{0}$ satisfy some incoherent conditions, $L_{0}$ is low-rank and $E_{0}$ is sufficiently sparse, then $L_{0}$ and $E_{0}$ can be recovered with high probability by solving the following convex optimization problem:

$$\begin{aligned} \min _{L,E}\left\| L \right\| _{*} + \lambda \left\| E \right\| _{1},\quad s.t. \ X = L + E \end{aligned}$$

(1)

where $\left\| L \right\| _{*}$ denotes the nuclear norm (sum of the singular values of $L$), $\left\| E \right\| _{1}$ denotes the $\ell$1-norm (sum of the absolute values of all the entries in $E$) and

$$\begin{aligned} \lambda = 1/\sqrt{\max {(n_{1},n_{2})}} \end{aligned}$$

(2)

To use RPCA, one has to first restructure/transform the multi-way data into a matrix. Such a preprocessing usually leads to the information loss and would cause performance degradation. To alleviate this issue, a common approach is to manipulate the tensor data by taking the advantage of its multi-dimensional structure. In this work, we study the Tensor Robust Principal Component (TRPCA) which aims to exactly recover a low-rank tensor corrupted by sparse errors.

Tensors are mathematical objects that can be used to describe physical properties, just like scalars and vectors. They are a generalisation of scalars and vectors; a scalar is a zero rank tensor, and a vector is a first rank tensor. The rank (or order) of a tensor is defined by the number of directions (i.e. dimensionality of the array) required to describe it.

The tensor multi rank of $\mathcal {A} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ is a vector $r \in \mathbb {R}^{n_{3}}$ with its $i$-th entry as the rank of the $i$-th frontal slice of $\overline{\mathcal {A}}$, i.e., $r_{i} = rank({\overline{A}}^{\left( i \right) })$. The tensor tubal rank, denoted as $\text {rank}_{t}(\mathcal {A})$, is defined as the number of nonzero singular tubes of $\mathcal {S}$, where $\mathcal {S}$ is from the t-SVD of $\mathcal {A} = \mathcal {U} * \mathcal {S} * \mathcal {V}^{*}$. That is

$$\begin{aligned} \text {rank}_{t}\left( \mathcal {A} \right) = \#\{ i:\ \mathcal {S}(i,i,:) \ne 0\} = \max _{i}r_{i} \end{aligned}$$

(3)

The tensor nuclear norm of a tensor $\mathcal {A} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$, denoted as $\left\| \mathcal {A} \right\| _{*}$, is defined as the average of the nuclear norm of all the frontal slices of $\overline{\mathcal {A}}$, i.e., $\left\| \mathcal {A} \right\| _{*} = \frac{1}{n_{3}}\sum \nolimits _{i = 1}^{n_{3}}\left\| {\overline{A}}^{\left( i \right) } \right\| _{*}$.

Tensor Robust PCA (TRPCA) [14] aims to exactly recover a low-rank tensor corrupted by sparse errors. It aims to recover the low tubal rank component $\mathcal {L}_{0}$ and sparse component $\mathcal {E}_{0}$ from $\mathcal {X} = \mathcal {L}_{0} + \mathcal {E}_{0} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ by convex optimization

$$\begin{aligned} \min _{\mathcal {L}, \mathcal {E}}\left\| \mathcal {L} \right\| _{*} + \lambda \left\| \mathcal {E} \right\| _{1},\ s.t.\mathcal {X} = \mathcal {L} + \mathcal {E} \end{aligned}$$

(4)

We firstly define few necessary concepts. An orthogonal tensor is a tensor $Q \in \mathbb {R}^{n \times n \times n_{3}}$ if it satisfies:

$$\begin{aligned} Q^{*}*Q = Q*Q^{*} = I \end{aligned}$$

(5)

where I is the identity tensor.

f-diagonal tensor is a tensor if each of its frontal slices is a diagonal matrix.

The Tensor Singular Value Decomposition (T-SVD) for third order tensors was proposed by Kilmer and Martin [13] and has been applied successfully in many fields, such as computed tomography, facial recognition, and video completion. Kilmer and Martin presented the concept of a tensor-tensor product with suitable algebraic structure such that classical matrix-like factorizations are possible. In particular, they gave the definition of the Tensor SVD (T-SVD) over this new product, and showed that truncating that expansion does give a compressed result that is optimal in the Frobenius norm.

Theorem 1

(Tensor Singular Value Decomposition (T-SVD) [13, 14]) Let $\mathcal {A} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$. Then it can be factored as:

$$\begin{aligned} \mathcal {A} = \mathcal {U}*\mathcal {S}*\mathcal {V}^{*} \end{aligned}$$

(6)

where $\mathcal {U} \in \mathbb {R}^{n_{1} \times n_{1} \times n_{3}}$, $\mathcal {V} \in \mathbb {R}^{n_{2} \times n_{2} \times n_{3}}$ are orthogonal, and $\mathcal {S} \in \mathbb {R}^{n_{1} \times n_{2} \times n_{3}}$ is an f-diagonal tensor.

Alternative tensor factorization is CANDECOMP/PARAFAC (CP) and expresses a $N$-way tensor $\mathcal {A}$ as the sum of multiple rank-1 tensors:

$$\begin{aligned} \mathcal {A} = \sum _{r = 1}^{R}{s_{r}a_{r}^{(1)}{^\circ }...{^\circ }a_{r}^{(N)},\ \ \ \ with\ a_{r}^{(k)} \in \mathbb {R}^{I_{k}}} \end{aligned}$$

(7)

Our Bayesian approach is based on likelihood representation of the problem in (4) following variational Bayes perspective of Hawkins and Zhang [11]. Variational perspectives have been earlier adopted as solutions to intractable likelihood problems in matrix and tensor completion [1, 21, 22]. In general, likelihood free perspective is applied to matrix and tensor completion problems as computational complexity is significantly higher for high-dimensional data than that of other methods, and convergence is generally hard to assess [1, 5]. In order to address problems of high-dimensionality in approximate Bayesian inference regression adjustment is often recommended [2,3,4,5, 18] and we use it also in our analysis.

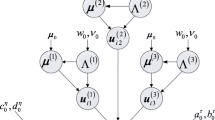
We assume that each tensor slice can be fit by $\mathcal {X}_{k} = {\widetilde{\mathcal {X}}}_{k} + \mathcal {S}_{k} + \mathcal {E}_{k}$, where ${\widetilde{\mathcal {X}}}_{k}$ is low-rank, $\mathcal {S}_{k}$ contains sparse outliers and $\mathcal {E}_{k}$ denotes dense noise with small magnitudes. We will denote with $\mathcal {Y}_{\Omega ,k}$ the observation of current slice and by $\mathcal {S}_{\Omega ,k}$ its outliers. For the likelihood function representation let $\tau$ specify the noise precision, ${\widehat{a}}_{i_{n}}^{\left( n \right) }$ the $i_{n}$-th row of $A^{\left( n \right) }$, $\lambda$ controls the rank of factorization and $\{\gamma _{i_{1},\ldots , i_{N}}\}$ controls the sparsity of $\mathcal {S}_{\Omega }$.

We define the likelihood function and used priors for the transformed problem in (4) using Gaussian and Gamma priors as:

$$\begin{aligned} \left( \mathcal {Y}_{\Omega }\left| \left\{ A^{\left( n \right) } \right\} _{n = 1}^{N + 1}\right. ,\mathcal {S}_{\Omega },\tau \right) = \prod _{(i_{1},\ldots ,i_{n}) \in \Omega }^{}\mathcal {N}(\mathcal {Y}_{i_{1}\ldots i_{N}}\left| \left\langle {\widehat{a}}_{i_{1}}^{\left( 1 \right) },\ldots ,{\widehat{a}}_{i_{N}}^{\left( N \right) }\right\rangle + \mathcal {S}_{i_{1}\ldots i_{N}},\tau ^{- 1} \right) \end{aligned}$$

(8)

$$\begin{aligned}&\left( \Theta \left| \mathcal {Y}_{\Omega } \right) \right. \nonumber \\&= \frac{p\left( \mathcal {Y}_{\Omega }\left| \left\{ A^{\left( n \right) } \right\} _{n = 1}^{N + 1}\right. ,\mathcal {S}_{\Omega },\tau \right) \left\{ \prod _{n = 1}^{\left( N + 1 \right) }{p\left( A^{\left( n \right) }|\lambda \right) } \right\} p\left( \lambda \right) p\left( \mathcal {S}_{\Omega }|\gamma \right) p\left( \gamma \right) p(\tau )}{p(\mathcal {Y}_{\Omega })} \end{aligned}$$

(9)

$$\begin{aligned} p\left( A^{\left( n \right) }\left| \lambda \right) =\right. \prod _{i_{n} = 1}^{I_{n}}\mathcal {N}({\widehat{a}}_{i_{n}}^{\left( n \right) }\left| 0,\Lambda ^{- 1} \right) , \quad \forall n \in [1,N + 1]\end{aligned}$$

(10)

$$\begin{aligned} p\left( \mathcal {S}_{\Omega }\left| \right. \gamma \right) = \prod _{(i_{1},\ldots ,i_{N}) \in \Omega }^{}\mathcal {N}(\mathcal {S}_{i_{1}\ldots i_{N}}\left| 0,\gamma _{i_{1}\ldots i_{N}}^{- 1}\right) \end{aligned}$$

(11)

$$\begin{aligned} p\left( \tau \right) = Ga\left( \tau |a_{0}^{\tau },b_{0}^{\tau }\right) , \quad p\left( \lambda \right) = \prod _{r = 1}^{R}{\textit{Ga}\left( \lambda _{r}|c_{0},d_{0}\right) } \end{aligned}$$

(12)

$$\begin{aligned} p(\gamma ) = \prod _{(i_{1},\ldots ,i_{N})\in \Omega }^{}{Ga(}\gamma _{i_{1}\ldots i_{N}}\left| a_{0}^{\gamma },b_{0}^{\gamma }\right) \end{aligned}$$

(13)

2 Scheme of the Approximate Bayesian Algorithm

Modern statistical applications increasingly require the fitting of complex statistical models. Often these models are “intractable” in the sense that it is impossible to evaluate the likelihood function. This prohibits standard implementation of likelihood-based methods, such as maximum likelihood estimation or a Bayesian analysis. To overcome this problem there has been substantial interest in “likelihood-free” or simulation-based methods. Examples of such likelihood-free methods include simulated methods of moments [10], indirect inference (Gourièroux and Ronchetti 1993) [12], synthetic likelihood [9] and approximate Bayesian computation [19]. Of these, approximate Bayesian computation (ABC) methods are arguably the most common methods for performing Bayesian inference [15, 19]. For a number of years, ABC methods have been popular in population genetics (e.g. Cornuet et al. [8]) and systems biology (e.g. Toni et al. [20]); more recently they have seen increased use in other application areas, such as econometrics [6] and epidemiology [9].

In our ABC algorithm for TRPCA we amend the variational Bayes perspective of Hawkins and Zhang [11] who use it on a temporally defined problem. We use regression adjustment based ABC using as a summary statistic array of tensor first and second moment defined as $k$-statistics [16] and tensor tubal rank as defined above.

Scheme of the algorithm:

• Step 1. Simulate $\theta ^{(i)},i = 1,\ldots ,n$ according to the prior structure defined above.

• Step 2. Simulate $s^{(i)} = \text {array}(\mathcal {A})^{(i)}$ using the generative model $p(s^{\left( i \right) }|\theta ^{\left( i \right) })$.

• Step 3. Associate with each pair $(\theta ^{\left( i \right) },s^{\left( i \right) })$ a weight $w^{\left( i \right) } \propto K_{h}(\left\| s^{\left( i \right) } - s_{\text {obs}} \right\| )$, where $K_{h}$ is a kernel function and || || the multidimensional Euclidean distance.

• Step 4. Fit a regression model where the response is $\theta$ and the predictive variables are the summary statistics $s$. Use a regression model to adjust the $\theta ^{\left( i \right) }$ in order to produce a weighted sample of adjusted values. We use heteroskedastic adjustment, following Blum (2017), as follows:

  $$\begin{aligned} \theta _{c'}^{(i)} = \widehat{m}(s_{\text {obs}}) + \frac{\widehat{\sigma }(s_{\text {obs}})}{\widehat{\sigma }(s^{(i)})}(\theta ^{(i)} - \widehat{m}(s^{(i)})) \end{aligned}$$

  (14)

  where $\widehat{m}$ and $\widehat{\sigma }$ are the standard estimators of the conditional mean and of the conditional standard deviation.

3 Numerical Experiments and Application

With the development of intelligent transportation systems, large quantities of urban traffic data are collected on a continuous basis from various sources. These data sets capture the underlying states and dynamics of transportation networks and the whole system. In general, traffic data register full spatial and temporal features, together with some other site-specific attributes. Usually, we can organize the spatiotemporal traffic data into a multi-dimensional structure. Combined with information from other links in a city, the overall spatiotemporal data can be structured as a multi-dimensional array, which is often referred to as a tensor. A common drawback that undermines the use of such spatiotemporal data is the “missingness” problem, which may result from various factors such as hardware/software failure, network communication problems, and zero/limited reports from floating/crowdsourcing systems.

To demonstrate the performance of this model, in this section we conduct numerical experiments based on a large-scale traffic speed data set collected in Guangzhou, China. The data set is generated by a widely-used navigation app on smart phones. The data set contains travel speed observations from 214 road segments in two months (61 days from August 1, 2016 to September 30, 2016) at 10-min interval (144 time intervals in a day). The speed data can be organized as a third-order tensor (road segment $\times$ day $\times$ time interval). Among the 1.88 million elements, about 1.29% are not observed or provided in the raw data.

In Tables 1 and 2 we compare performance of different models applied to several scenarios. We compare: Bayesian Gaussian CANDECOMP/PARAFAC (BGCP) tensor decomposition model, high accuracy low-rank tensor completion (HaLRTC) (Liu et al. 2013), which is used in Ran et al. (2016), SVD-combined tensor decomposition (STD) (Chen et al. 2018), DA (daily average) fills the missing value with an average of observed data (over different days) for the same road segment and the same time window (Li et al. 2013). kNN is another baseline method where the neighbors refer to road segments. Finally, TRPCA-VAR and TRPCA-ABC refer to tensor robust PCA specification in variational Bayes and approximate Bayesian computation algorithm form. The mean absolute percentage error (MAPE) and root mean square error (RMSE) are used to evaluate model performance. Our first experiment examines the performance of different models and different representations in the random missing scenario. In the second experiment, we present a more realistic temporally correlated missing scenario. From the original data set we create five novel datasets with different missing rates ranging from 10 to 50%. We use two data representations: matrix representation (A) and third-order tensor representation (B).

Table 1 The imputation performance of BGCP, HaLRTC, STD, DA (daily average), kNN, TRPCA-VAR and TRPCA-ABC for two data representations in the first scenario (best models are highlighted in bold)

As can be seen from the tables (the best models are marked in bold), for the random missing scenario, frequently the Variational Bayes specification performs best. On the other hand, our ABC approach performs very well in the second, temporally correlated missing scenario.

Table 2 The imputation performance of BGCP, HaLRTC, STD, DA, kNN, TRPCA-VAR and TRPCA-ABC for two data representations in the second scenario (best models are highlighted in bold)

4 Conclusion

Our article provides an initial step in the development of ABC algorithms for tensor completion and tensor principal component analysis. We upgrade the tensor robust PCA approach of Lu and coauthors using approximate Bayesian perspective which provides ground for further research in the area of Bayesian approaches in matrix and tensor completion. Also, our article provides additional information on approximate Bayesian approaches to high-dimensional problems in statistics.

Few possible extensions of our work and pathways for future work seem apparent:

• Other possibilities of the ABC algorithms (such as SMC, HMC, other regression and marginal adjustment approaches) integrated nested Laplace approximation, including additional upgrades of the variational approach of Hawkins and Zhang should lead to more evidence on methodological possibilities to approach matrix and tensor completion from a Bayesian computational perspective.

• Different loss and divergence measures (for example Bregman type divergence measures) could be tested and asymptotics of the approach developed.

• Extension to different type of tensor measures and different specifications of the tensor robust PCA (the specification we use is only one of the possible ones) as well as extensions to any type and size of a tensor.