Abstract
This paper studies the existence of finite, ground-complete axiomatisations of CSP-like parallel composition operators, and the restriction operator from CCS, modulo bisimilarity. More specifically, we build on Moller’s result to the effect that bisimilarity does not have a finite, ground-complete equational axiomatisation over a minimal fragment of CCS, and we use a reduction technique by Aceto et al. to lift it to various extensions of BCCSP with CSP-like parallel operators, and to the recursion and relabelling free fragment of CCS.
This work has been partially supported by the project “Open Problems in the Equational Logic of Processes” (OPEL) of the Icelandic Research Fund (grant No. 196050-051). E. Anastasiadi has been supported by the project “Runtime and Equational Verification Of Concurrent Programs” (REVOCOP) of the Reykjavik University Research Fund (grant No. 222021-051). V. Castiglioni has been supported by the project “Programs in the wild: Uncertainties, adaptabiLiTy and veRificatiON” (ULTRON) of the Icelandic Research Fund (grant No. 228376-051).
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Some of Frits Vaandrager’s early seminal contributions were firmly rooted in the theory and applications of process algebras and their semantics. Having been brought up in the tradition of Bergstra and Klop’s Algebra of Communicating Processes (ACP) [14, 16, 17], Frits Vaandrager studied semantic models of algebraic process description languages [25, 26], equational axiomatisations of process equivalences [15] and their application in verification (see, for instance, [24, 39]). Moreover, together with Aceto and Bloom, in [3] he initiated the study of methods for generating finite, ground-complete, equational axiomatisations of bisimilarity [32, 36] from operational specifications given in the GSOS format [18]. The techniques proposed in [3] can be used to synthesise auxiliary operators, such as Bergstra and Klop’s left- and communication-merge operators, that make finite axiomatisations possible and paved the way to several further studies in the literature—see, for instance, the developments presented in [10, 21, 27, 31].
The use of auxiliary operators to obtain finite, equational, ground-complete axiomatisations of bisimilarity, even for very inexpressive process algebras, was justified by Moller in [33,34,35], where he showed that bisimilarity has no finite axiomatisation over minimal fragments of Milner’s Calculus of Communicating Systems (CCS) [32] and Bergstra and Klop’s ACP. (Henceforth, we will consider the recursion, relabelling and restriction free fragment of CCS, which, for simplicity, we still denote as CCS.) Moller’s above-mentioned, path-breaking, negative results have been followed by a wealth of research on non-finitely-based fragments of process algebras—see, for instance, [1, 2, 4,5,6,7,8, 12, 20].
Our Contribution. In this paper, we celebrate Frits Vaandrager’s early contributions to the study of algebraic process description languages by answering the two questions that Rob van GlabbeekFootnote 1 asked the first author after his invited talk at LICS 2021Footnote 2:
Would Moller’s non-finite axiomatisability result for CCS remain true if we replaced CCS parallel composition with the parallel operators from Hoare’s Communicating Sequential Processes (CSP) [29]? And what if we added the restriction operator to CCS instead?
Our first contributions concern the existence of finite, ground-complete axiomatisations of bisimilarity over process algebras that extend the language BCCSP [22, 28, 32] with parallel operators from CSP. (BCCSP is a common fragment of Milner’s CCS and Hoare’s CSP suitable for describing finite process behaviour.)
For each set of actions A, the CSP parallel operator \(\,|_A\,\) behaves like interleaving parallel composition for all actions that are not contained in A, but requires transitions of its operands that are labelled with some action \(a \in A\) to synchronise. The result of such a synchronisation is an a-labelled transition of the composite parallel process, which can itself synchronise further with a-labelled steps from its environment. Therefore, unlike CCS parallel composition that is based on hand-shaking communication, the parallel operators from CSP support multi-way synchronisation and span the whole spectrum from pure interleaving parallel composition (the operator \(\,|_\emptyset \)) to synchronous composition (the operator \(\,|_{\textrm{Act}}\), where Act is the whole collection of actions that processes may perform).
We start our investigations by considering the languages \(\text {BCCSP}_{\!A}^{\texttt{p}}\), which extend BCCSP with the parallel operator \(\,|_A\,\) for some subset A of the whole set of actions \(\textrm{Act}\), and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), which contains the parallel operator \(\,|_A\,\) for each \(A \subseteq \textrm{Act}\), and the \(\tau \)-prefixing operator for a distinguished action \(\tau \not \in \textrm{Act}\). We show that Moller’s non-finite axiomatisability result for bisimilarity still holds over \(\text {BCCSP}_{\!A}^{\texttt{p}}\), when A is a strict subset of \(\textrm{Act}\), and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\). On the other hand, bisimilarity affords a finite, ground-complete axiomatisation over \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\).
The proofs of the above-mentioned negative results for \(\text {BCCSP}_{\!A}^{\texttt{p}}\), when A is a strict subset of \(\textrm{Act}\), and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) employ a reduction-based technique proposed in [11] for showing new, non-finite axiomatisability results over process algebras from already-established ones. In our setting, such reductions are translations from terms in the languages \(\text {BCCSP}_{\!A}^{\texttt{p}}\) (\(A \subset Act\)) and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) to those in the fragment of CCS studied by Moller that
-
preserve sound equations and equational provability over the source language, and
-
reflect an infinite family of equations responsible for the non-finite axiomatisability of the target language.
No reduction from \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) to CCS satisfying the former property modulo bisimilarity reflects Moller’s family of equations witnessing his negative result over CCS. Therefore, the reduction technique cannot be applied to \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\). Indeed, we present a finite, ground-complete axiomatisation of bisimilarity over \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\).
We also show that, if we consider the language \(\text {BCCSP}^{\texttt{p}}\), namely BCCSP with a parallel operator \(|_A\) for each \(A \subseteq \textrm{Act}\), then no reduction that is structural, i.e. that does not introduce new variables and it is defined compositionally over terms, can reflect Moller’s family of equations. However, we conjecture that bisimilarity does not admit a finite, ground-complete axiomatisation over \(\text {BCCSP}^{\texttt{p}}\).
For our final contribution, we consider the language \(\text {CCS}^\texttt{r}\), namely CCS enriched with restriction operators of the form \(\cdot \backslash R\). Informally, \(R \subseteq \textrm{Act}\) is a set of actions that are restricted, meaning that the execution of a-labelled transitions (and of their “complementary actions”) is prevented in \(t \backslash R\) for all \(a \in R\). By exploiting the reduction technique described above, we show that Moller’s negative result can be lifted to \(\text {CCS}^\texttt{r}\), giving thus that bisimilarity admits no finite, ground-complete axiomatisation over CCS with restriction.
Our contributions can then be summarised as follows:
-
1.
We consider \(\text {BCCSP}_{\!A}^{\texttt{p}}\), i.e., BCCSP enriched with one CSP-style parallel composition operator \(\,|_A\), with \(A \subset \textrm{Act}\), and we show that, over that language, bisimilarity admits no finite, ground-complete axiomatisation (Theorem 4).
-
2.
We consider \(\text {BCCSP}^{\texttt{p}}\), i.e., BCCSP enriched with all CSP-style parallel composition operators \(\,|_A\), and we show that there is no structural reduction from \(\text {BCCSP}^{\texttt{p}}\) to CCS that can reflect the family of equations used by Moller to prove the negative result for bisimilarity over CCS (Theorem 5).
-
3.
We consider \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), i.e., \(\text {BCCSP}^{\texttt{p}}\) enriched with the \(\tau \)-prefixing, and we show that this algebra admits no finite, ground-complete axiomatisation modulo bisimilarity (Theorem 6).
-
4.
We consider \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\), i.e., BCCSP enriched with the CSP-style parallel composition operator \(\,|_{\textrm{Act}}\), and we present a finite, ground-complete axiomatisation for it, modulo bisimilarity (Theorem 7).
-
5.
We consider \(\text {CCS}^\texttt{r}\), i.e., CCS with the restriction operator, and we show that bisimilarity has no finite, ground-complete axiomatisation over it (Theorem 8).
Organisation of Contents. In Sect. 2 we review basic notions on process semantics, behavioural equivalences, and equational logic. We also briefly recap Moller’s negative result for bisimilarity over CCS. In Sect. 3 we give a bird’s-eye view of the reduction technique from [11]. In Sect. 4, we present the lifting of Moller’s negative result to \(\text {BCCSP}_{\!A}^{\texttt{p}}\) (for \(A \subset \textrm{Act}\)) and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), we study the case of \(\text {BCCSP}^{\texttt{p}}\), and then we discuss the collapse of the negative result in the case of \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\). In Sect. 5, we use the reduction technique to prove the non-finite axiomatisability result for \(\text {CCS}^\texttt{r}\). We conclude by discussing some directions for future work in Sect. 6.
2 Preliminaries
In this section we present some background notions on process algebras and equational logic. To make our contribution self-contained, we also briefly recap Moller’s work on the nonexistence of finite axiomatisations modulo bisimilarity over the recursion, relabelling, and restriction free fragment of CCS (henceforth simply referred to as CCS).
Labelled Transition Systems and Bisimilarity. As semantic model for the algebraic process description languages that we will study, we consider classic Labelled Transition Systems [30].
Definition 1
(Labelled Transition System). A labelled transition system (LTS) is a triple \((\mathcal {P},\textrm{Act},\xrightarrow {\, {} \, })\), where \(\mathcal {P}\) is a set of processes (or states), \(\textrm{Act}\) is a set of actions (or labels), and \({\xrightarrow {\, {} \, }} \subseteq \mathcal {P}\times \textrm{Act}\times \mathcal {P}\) is a (labelled) transition relation.
In what follows, we assume that the set of actions \(\textrm{Act}\) is finite and non-empty. We let \(p,q,\dots \) range over \(\mathcal {P}\), and \(a,b,\dots \) over \(\textrm{Act}\). Moreover, as usual, we use \(p \xrightarrow {\, {a} \, } p'\) in lieu of \((p,a,p') \in {\xrightarrow {\, {} \, }}\). For each \(p \in \mathcal {P}\) and \(a \in \textrm{Act}\), we write \(p \xrightarrow {\, {a} \, }\) if \(p \xrightarrow {\, {a} \, } p'\) holds for some \(p'\), and
 otherwise. For a sequence of actions \(\rho = a_1 \cdots a_n\) (\(n \ge 0\)), and processes \(p,p'\), we write \(p \xrightarrow {\, {\rho } \, } p'\) if and only if there exists a sequence of transitions \(p = p_0 \xrightarrow {\, {a_1} \, } p_1 \xrightarrow {\, {a_2} \, } \cdots \xrightarrow {\, {a_n} \, } p_n = p'\). If \(p \xrightarrow {\, {\rho } \, } p'\) holds for some process \(p'\), then \(\rho \) is a trace of p. All the LTSs we will consider in this paper are finite and loop-free. The depth of a process p in such an LTS, denoted by \(\textrm{depth}(p)\), is then defined as the length of a longest trace of p.
otherwise. For a sequence of actions \(\rho = a_1 \cdots a_n\) (\(n \ge 0\)), and processes \(p,p'\), we write \(p \xrightarrow {\, {\rho } \, } p'\) if and only if there exists a sequence of transitions \(p = p_0 \xrightarrow {\, {a_1} \, } p_1 \xrightarrow {\, {a_2} \, } \cdots \xrightarrow {\, {a_n} \, } p_n = p'\). If \(p \xrightarrow {\, {\rho } \, } p'\) holds for some process \(p'\), then \(\rho \) is a trace of p. All the LTSs we will consider in this paper are finite and loop-free. The depth of a process p in such an LTS, denoted by \(\textrm{depth}(p)\), is then defined as the length of a longest trace of p.
Behavioural equivalences have been introduced as a tool to establish whether the behaviours of two processes are indistinguishable for their observers. In the literature we can find several notions of behavioural equivalence based on the observations that an external observer can make on a process. In this paper we consider the classic notion of bisimilarity [32, Chapter 4, Definition 1].
Definition 2
(Bisimilarity). Let \((\mathcal {P},\textrm{Act},\xrightarrow {\, {} \, })\) be a LTS. A binary symmetric relation \(\,{\mathcal R}\,\subseteq \mathcal {P}\times \mathcal {P}\) is a bisimulation if, and only if, whenever \((p,q) \in \,{\mathcal R}\,\) and \(p \xrightarrow {\, {a} \, } p'\) then there exists a process \(q'\) such that \(q \xrightarrow {\, {a} \, } q'\) and \((p',q') \in \,{\mathcal R}\,\). We say that p and q are bisimilar if there is a bisimulation relation \(\,{\mathcal R}\,\) such that \((p,q) \in \,{\mathcal R}\,\).
The union of all the bisimulation relations is called bisimilarity, and denoted by \(\sim \).
It is well known that \(\sim \) is an equivalence relation over \(\mathcal {P}\), and it is the largest bisimulation relation [32, Chapter 4, Proposition 2].
Remark 1
Bisimilarity preserves the depth of processes, i.e., whenever \(p \sim q\), then \(\textrm{depth}(p) = \textrm{depth}(q)\).
The Language BCCSP. In this paper we will consider several algebraic process description languages, each characterised by the presence of a particular operator, or sets of operators. As all those languages are extensions of BCCSP [28], consisting of the basic operators from CCS [32] and CSP [29], in this section we use that language to introduce some general notions and notations on term algebras that will be useful throughout the remainder of the paper.
BCCSP terms are defined by the following grammar:
where x is drawn from a countably infinite set of variables \(\textrm{Var}\), a is an action from \(\textrm{Act}\), \(a.(\cdot )\) is the prefixing operator, defined for each \(a \in \textrm{Act}\), and \(\cdot + \cdot \) is the nondeterministic choice operator. We shall use the meta-variables \(t,u,\dots \) to range over process terms, and write \(\textrm{var}(t)\) for the collection of variables occurring in the term t. The size of a term t, denoted by \(\textrm{size}(t)\), is the number of operator symbols in t. A term is closed if it does not contain any variables. Closed terms, or processes, will be denoted by \(p,q,\dots \). In particular, we denote the set of all BCCSP terms by \(\mathbb {T}(\text {BCCSP})\), and the set of closed BCCSP terms (or BCCSP processes) by \(\mathcal {P}(\text {BCCSP})\). This notation can be directly extended to all the languages that we will consider. Moreover, we omit trailing \(\textbf{0}\)’s from terms and we use a summation \(\sum _{i = 1}^{k}t_i\) to denote the term \(t= t_1+\cdots +t_k\), where the empty sum represents \(\textbf{0}\). Henceforth, for each action \(a \in \textrm{Act}\) and natural number \(m \ge 0\), we let \(a^0\) denote \(\textbf{0}\) and \(a^{m+1}\) denote \(a.(a^m)\).
We use the Structural Operational Semantics (SOS) framework [37] to equip processes with an operational semantics. The SOS rules (also called inference rules, or deduction rules) for the BCCSP operators given above are reported in Table 1. A (closed) substitution \(\sigma \) is a mapping from process variables to (closed) terms. Substitutions are extended from variables to terms, transitions, and rules in the usual way. Note that \(\sigma (t)\) is closed, if so is \(\sigma \). The inference rules in Table 1 allow us to derive valid transitions between closed BCCSP terms. The operational semantics for BCCSP is then modelled by the LTS whose processes are the closed terms in \(\mathcal {P}(\text {BCCSP})\), and whose labelled transitions are those that are provable from the SOS rules. The same approach will be applied to all the extensions of BCCSP that we will consider. The SOS rules of each language will be presented in the respective sections.
We call an equivalence relation a congruence over a language if it is compositional with respect to the operators of the language, i.e., the replacement of a component with an equivalent one does not affect the overall behaviour. Formally, the congruence property for bisimilarity over BCCSP, and its extensions, consists in verifying whether, given any n-ary operator f,
Since all the operators considered in this paper are defined by inference rules in the de Simone format [38], by [23, Theorem 4] we have that bisimilarity is a congruence over BCCSP and over all the languages that we will study.
Equational Logic. An equational axiomatisation (or axiom system) over a language L is a collection E of equations \(t \approx u\), which are referred to as axioms, over the terms in L. We write \(E \vdash t \approx u\) if the equation \(t \approx u\) is derivable from the axioms in E using the rules of equational logic, presented in Table 2, that express, respectively, reflexivity, symmetry, transitivity, substitution, and closure under L contexts. Without loss of generality, we assume that substitution can be used only when \((t \approx u) \in E\). In this case, \(\sigma (t) \approx \sigma (u)\) is called a substitution instance of an axiom in E.
We are interested in equations that are valid modulo some congruence relation \(\,{\mathcal R}\,\) over the closed terms in the language L. An equation \(t \approx u\) is sound modulo \(\,{\mathcal R}\,\), written \(t \,{\mathcal R}\,u\), when \(\sigma (t) \,{\mathcal R}\,\sigma (u)\) for all closed substitutions \(\sigma \). An axiomatisation E is sound modulo \(\,{\mathcal R}\,\) over L if for all terms t, u in \(\mathbb {T}(L)\), we have that whenever \(E \vdash t \approx u\), then \(t \,{\mathcal R}\,u\). E is (ground-)complete modulo \(\,{\mathcal R}\,\) if \(t \,{\mathcal R}\,u\) implies \( E \vdash t \approx u\), for all (closed) L terms t and u. A congruence \(\,{\mathcal R}\,\) is said to be finitely based if there exists a finite axiomatisation E that is sound and complete modulo \(\,{\mathcal R}\,\).
A classic question is whether an algebra modulo the chosen notion of behavioural congruence (in this work, bisimilarity) affords a finite equational axiomatisation. For example, as shown by Hennessy and Milner in [28], the equations in Table 3 are a finite axiomatisation of bisimilarity over BCCSP. We denote by \(\mathcal {E}_0\) the axiom system consisting of the equations in Table 3. Later on, we will extend this set of axioms to present our positive result for \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\).
Moller’s Result over CCS. In his thesis [33], Moller gave a celebrated non-finite axiomatisability result in the field of process algebra, namely:
Theorem 1
Bisimilarity admits no finite, ground-complete axiomatisation over CCS.
Specifically, Moller considered the language \(\text {CCS}_a\) with interleaving parallel composition, defined over \(\textrm{Act}= \{a\}\) by the following syntax:

where \(x \in \textrm{Var}\), and \(\mathbin {\Vert }\) denotes the interleaving parallel composition operator. The SOS rules for \(\text {CCS}_a\) operators are given by the rules in Table 1, plus the rules for the interleaving parallel operator presented in Table 4.
In detail, for his result, Moller applied the following proof strategy, later referred to as the proof-theoretic approach to negative results [9]. He considered the infinite family of equations \(\varPhi \) with
and he proved that whenever n is larger than the size of any term occurring in the equations in a finite, sound axiom system E, then equation \(\varphi _n\) cannot be derived from E. Hence, Theorem 1 specialised to the following result, which will play a fundamental role in the technical development of our contributions:
Theorem 2
(Moller’s negative result [33, Theorem 5.2.12]). No finite axiom system that is sound modulo bisimilarity over \(\text {CCS}_a\) can prove the whole family of equations \(\varPhi \). Thus no finite, ground-complete axiom system can exist for \(\text {CCS}_a\) modulo bisimilarity.
3 The Proof Strategy: Reduction Mappings
The non-finite axiomatisability results that we will present in this paper are all obtained by means of a proof technique, proposed in [11], that allows for transferring this kind of negative results across process languages. Even though we only apply that technique out-of-the-box towards establishing new results, we decided to give, in this section, an overview of the terminology and results presented in [11], to improve the readability of our paper. As our studies are focused on the axiomatisability of bisimilarity, we consider only this behavioural congruence in the presentation below.
We consider two processes description languages defined over the same set of variables: \(L_{\textrm{neg}}\) and \(L_{\textrm{new}}\). \(L_{\textrm{neg}}\) is known to be non-finitely axiomatisable modulo bisimilarity, whereas \(L_{\textrm{new}}\) is the language for which we want to prove this negative result. The aim of the proof technique proposed in [11] is to establish whether it is possible to lift the known result for \(L_{\textrm{neg}}\) to \(L_{\textrm{new}}\). This approach is based on a variation of the classic idea of reduction mappings that, in this setting, are translations from \(\mathbb {T}(L_{\textrm{new}})\) to \(\mathbb {T}(L_{\textrm{neg}})\) that preserve soundness and provability.
Given a translation mapping \(\,\widehat{\,\cdot \,}\,:\mathbb {T}(L_{\textrm{new}}) \rightarrow \mathbb {T}(L_{\textrm{neg}})\) and a collection E of equations over \(L_{\textrm{new}}\) terms, we let \(\widehat{E} = \{\widehat{t} \approx \widehat{u} \mid t \approx u \in E\}\). The notion of reduction is then formalised as follows:
Definition 3
(Reduction). A mapping \(\,\widehat{\,\cdot \,} :\mathbb {T}(L_{\textrm{new}}) \rightarrow \mathbb {T}(L_{\textrm{neg}})\) is a reduction from \(\mathbb {T}(L_{\textrm{new}})\) to \(\mathbb {T}(L_{\textrm{neg}})\), when for all \(t,u \in \mathbb {T}(L_{\textrm{new}})\):
-
1.
\(t \sim u \implies \widehat{t} \sim \widehat{u}\), i.e., \(\,\widehat{\,\cdot \,}\,\) preserves sound equations, and
-
2.
\(E \vdash t \approx u \implies \widehat{E} \vdash \widehat{t} \approx \widehat{u}\), for each axiom system E over \(L_{\textrm{new}}\), i.e., \(\,\widehat{\,\cdot \,}\,\) preserves provability.
Interestingly, in [11, Theorem 2] it is proved that if a mapping is structural, then it automatically satisfies Definition 3.2. Hence, the notion of structural mapping will be crucial in the development of our results, as it allows for a significant simplification of the technical proofs.
Definition 4
(Structural mapping). A mapping \(\,\widehat{\,\cdot \,} :\mathbb {T}(L_{\textrm{new}}) \rightarrow \mathbb {T}(L_{\textrm{neg}})\) is structural if:
-
It is the identity function over variables, i.e., \(\widehat{x} = x\) for each variable x.
-
It does not introduce new variables, i.e., the set of variables occurring in the term \(\widehat{f(x_1, \ldots , x_n)}\) is included in \(\{x_1, \ldots , x_n\}\), for each operator f in \(L_{\textrm{new}}\) and sequence of distinct variables \(x_1, \ldots , x_n\).
-
It is defined compositionally, i.e. \(\widehat{f(t_1,\dots , t_n)} = \widehat{f(x_1,\dots , x_n)}[\widehat{t_1}/x_1, \dots ,\widehat{t_n}/x_n]\) for each operator f in \(L_{\textrm{new}}\), sequence of distinct variables \(x_1, \ldots , x_n\) and sequence of terms \(t_1, \ldots , t_n\). (Here \([\widehat{t_1}/x_1, \ldots ,\widehat{t_n}/x_n]\) stands for the substitution mapping each variable \(x_i\) to \(\widehat{t_i}\) (\(1\le i \le n\)), and acting like the identity function on all the other variables.)
Given a substitution \(\sigma :\textrm{Var}\rightarrow \mathbb {T}(L_{\textrm{new}})\), we let \(\widehat{\sigma } :\textrm{Var}\rightarrow \mathbb {T}(L_{\textrm{neg}})\) denote the substitution that maps each variable x to \(\widehat{\sigma (x)}\).
Proposition 1
Assume that \(\,\widehat{\,\cdot \,} :\mathbb {T}(L_{\textrm{new}}) \rightarrow \mathbb {T}(L_{\textrm{neg}})\) is a structural mapping. Then
-
\(\widehat{\sigma (t)} = \widehat{\sigma }(\widehat{t})\), for each term \(t \in \mathbb {T}(L_{\textrm{new}})\), and for each substitution \(\sigma :\textrm{Var}\rightarrow \mathbb {T}(L_{\textrm{new}})\).
Assume now that we have an infinite collection E of equations that are sound modulo bisimilarity, but that are not derivable from any finite, sound axiom system over \(L_{\textrm{neg}}\). The idea in [11] is then that if a structural mapping \(\,\widehat{\,\cdot \,}\,\) is a reduction from \(\mathbb {T}(L_{\textrm{new}})\) to \(\mathbb {T}(L_{\textrm{neg}})\) that contains all the equations in E in its range, then the “malicious” collection of equations that map to those in E cannot be derivable from any finite, sound axiom system over \(L_{\textrm{new}}\). In fact, if those derivations were possible, then the equational properties of \(\,\widehat{\,\cdot \,}\,\) would allow us to write derivations (obtained via the translations of the equational proofs) of the equations in E from a finite, sound axiom system over \(L_{\textrm{neg}}\). As this contradicts the established negative result over \(L_{\textrm{neg}}\), the non-finite axiomatisability result over \(L_{\textrm{new}}\) follows.
The intuitions above are formalised in the following definition and theorem.
Definition 5
(E-reflection). Let E be a collection of equations over \(L_{\textrm{neg}}\). A reduction \(\,\widehat{\,\cdot \,}\,\) is E-reflecting, when for each \(t \approx u \in E\), there are terms \(t',u' \in \mathbb {T}(L_{\textrm{new}})\) such that the equation \(t' \approx u'\) is sound modulo \(\sim \), \(\widehat{t'} = t\) and \(\widehat{u'} = u\). A reduction is ground E-reflecting, if the conditions above are satisfied over closed equations.
Theorem 3
(The lifting theorem). Assume that there is a collection of (closed) equations E over \(L_{\textrm{neg}}\) that is sound modulo \(\sim \) and that is not derivable from any finite sound axiom system over \(L_{\textrm{neg}}\). If there exists a (ground) E-reflecting reduction from \(L_{\textrm{new}}\) to \(L_{\textrm{neg}}\), then there is no sound and (ground-)complete finite axiom system for \(\sim \) over \(L_{\textrm{new}}\).
We remark that the notion of (ground) E-reflecting reduction requires that only the equations in E are reflected. This means that to establish the negative result over \(L_{\textrm{neg}}\) it is enough to identify a particular family of equations that is reflected, disregarding the effects of the reduction on other sound equations. For our purposes, it will be enough to consider the family of equations \(\varPhi \) used by Moller to prove Theorem 2. Hence, our target language will always be \(\text {CCS}_a\), for some action a, and we will use the lifting technique presented in this section to prove negative results for the languages \(\text {BCCSP}_{\!A}^{\texttt{p}}\) (Sect. 4.2), \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) (Sect. 4.3), and \(\text {CCS}^\texttt{r}\) (Sect. 5).
4 Axiomatisability Results for CSP Parallel Composition
In this section we investigate the existence of finite, ground-complete axiomatisations of bisimilarity over the process description languages \(\text {BCCSP}_{\!A}^{\texttt{p}}\) (for all \(A \subset \textrm{Act}\)), \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\), \(\text {BCCSP}^{\texttt{p}}\) and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\). In detail, we apply the reduction technique presented in Sect. 3 to lift Moller’s negative result to \(\text {BCCSP}_{\!A}^{\texttt{p}}\), for each \(A \subset \textrm{Act}\), and to \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) (Theorem 4 and Theorem 6, respectively). In between, we show that the reduction technique cannot be applied to \(\text {BCCSP}^{\texttt{p}}\) (Theorem 5). Conversely, we establish a positive result for \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\), providing a finite, ground-complete axiomatisation for bisimilarity over this language (Theorem 7).
4.1 The Languages \(\text {BCCSP}_{\!A}^{\texttt{p}}\), \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\), \(\text {BCCSP}^{\texttt{p}}\) and \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\)
The languages that we consider in this section are obtained by extending BCCSP with instances of the CSP-like parallel composition operator \(|_A\), where \(A \subseteq \textrm{Act}\) is the set of actions that must be performed synchronously by the parallel components. For this reason, we shall henceforth refer to A in \(|_A\) as to the synchronisation set. The operator then behaves like interleaving parallel composition on the complement of A.
In detail, the languages are defined by the following grammar
with \(x \in \textrm{Var}\) and \(a \in \textrm{Act}\), and they differ in the choice of the synchronisation set(s) \(A \subseteq \textrm{Act}\) as follows:
-
\(\textbf{BCCSP}_{\!\!A}^{\texttt{p}}\) The parallel operator \(|_A\) is defined only over the fixed set \(A \subset \textrm{Act}\) (notice that the inclusion is strict).
-
\(\textbf{BCCSP}_{\!\!\textrm{Act}}^{\texttt{p}}\) The only synchronisation set is the entire set of actions \(\textrm{Act}\).
-
\(\textbf{BCCSP}^{\texttt{p}}\) There are no restrictions on the choice of synchronisation sets, i.e. the signature of the language contains the operator \(|_{A}\) for all \(A \subseteq \textrm{Act}\).
-
\(\textbf{BCCSP}_{\!\tau }^{\texttt{p}}\) This is like \(\text {BCCSP}^{\texttt{p}}\) with the additional property that the prefixing operator is of the form \(\mu .t\), with \(\mu \in \textrm{Act}\cup \{\tau \}\) for a special action label \(\tau \not \in \textrm{Act}\) (see Sect. 4.3 for further details).
The SOS rules for the CSP-like parallel composition operator \(|_A\) are given in Table 5. The operational semantics of each of the above-mentioned languages is then given by the rules in Table 1 and those in Table 5, in which A is instantiated according to the considered language.
Let \(L \in \{\text {BCCSP}_{\!A}^{\texttt{p}},\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}},\text {BCCSP}^{\texttt{p}},\text {BCCSP}_{\!\tau }^{\texttt{p}}\}\). Since in the technical results to follow we will need to distinguish between transitions over L processes and transitions over \(\text {CCS}_a\) processes, to avoid possible confusion we will denote the transition relation over \(\mathcal {P}(L)\) induced by the rules in Tables 1 and 5 by \(\xrightarrow {\, {} \, }_{\texttt{p}}\). Similarly, we can properly instantiate the definition of bisimilarity over L processes:
Definition 6
(Bisimilarity over \(\textbf{BCCSP}_{\!\!A}^{\texttt{p}}\), \(\textbf{BCCSP}_{\!\!\textrm{Act}}^{\texttt{p}}\), \(\textbf{BCCSP}^{\texttt{p}}\) and \(\textbf{BCCSP}_{\!\tau }^{\texttt{p}}\)). Let L be any of \(\text {BCCSP}_{\!A}^{\texttt{p}},\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}},\text {BCCSP}^{\texttt{p}},\text {BCCSP}_{\!\tau }^{\texttt{p}}\). Bisimulation relations over L processes are defined by applying Definition 2 to the LTS \((\mathcal {P}(L),\textrm{Act},\xrightarrow {\, {} \, }_{\texttt{p}})\) induced by the SOS rules in Tables 1 and 5. We use the symbol \(\sim _\texttt{p}\) to denote bisimilarity over L processes.
It is worth noticing that, as briefly outlined above, when the parallel components t, u in \(t \;|_A\; u\) contain only actions that are not in A, then the semantics of \(|_A\) coincides with the semantics of CCS interleaving parallel composition. On the other hand, when t and u contain only actions in A, then \(\,|_A\,\) behaves like “synchronous” parallel composition. The following example highlights these observations.
Example 1
Let \(A \subseteq \textrm{Act}\) and \(b \in A\). It is not difficult to see that
and therefore
In particular, we have that the axiom
is sound modulo \(\sim _{\texttt{p}}\) over the languages considered in this section.
Conversely, if we pick an action \(a \not \in A\), then we have
and thus
\(\blacktriangleleft \)
Notice that, for \(a \not \in A\), if we let
then the family of equations \(\varPhi _A = \{\varphi _A^n \,\mid \, n \in \mathbb {N}\}\) can be thought of as the counterpart in \(\text {BCCSP}_{\!A}^{\texttt{p}}\) of the family \(\varPhi \) used by Moller to prove Theorem 2. As we will see, this correspondence will be instrumental in applying the reduction technique to those languages.
4.2 The Negative Result for \(\text {BCCSP}_{\!A}^{\texttt{p}}\)
We start our investigations with \(\text {BCCSP}_{\!A}^{\texttt{p}}\), for a given set \(A \subset \textrm{Act}\). In particular, by applying the proof methodology discussed in Sect. 3, we prove that:
Theorem 4
\(\text {BCCSP}_{\!A}^{\texttt{p}}\) does not have a finite, ground-complete axiomatisation modulo bisimilarity.
Our first step consists in defining a mapping allowing us to rewrite \(\text {BCCSP}_{\!A}^{\texttt{p}}\) terms into \(\text {CCS}_a\) terms. As the target language is built over a specific action, it is natural to have a definition of our mapping that is parametric in that action. Hence, choose an action \(a \in \textrm{Act}\setminus A\). Notice that the requirement that the inclusion \(A \subset \textrm{Act}\) be strict guarantees that such an action a exists.
Definition 7
(The mapping \(\texttt{p}^A_a\)). The mapping \(\texttt{p}^A_a:\mathbb {T}(\text {BCCSP}_{\!A}^{\texttt{p}}) \rightarrow \mathbb {T}(\text {CCS}_a)\) is defined inductively over the structure of terms as follows:
By Definition 7, for each \(t \in \mathbb {T}(\text {BCCSP}_{\!A}^{\texttt{p}})\), the only action occurring in \(\texttt{p}^A_a(t)\) is a.
In order to lift the negative result in Theorem 2 to \(\text {BCCSP}_{\!A}^{\texttt{p}}\), we need to prove that the proposed mapping \(\texttt{p}^A_a\) is a ground \(\varPhi \)-reflecting reduction. Let us first focus on showing that \(\texttt{p}^A_a\) is a reduction, i.e., we need to show that it satisfies the two constraints in Definition 3.
Remark 2
For simplicity, we shall sometimes extend the mapping notation from terms to equations. For instance, if \(e: t \approx u\) is an equation over \(\text {BCCSP}_{\!A}^{\texttt{p}}\) terms, we shall write \(\texttt{p}^A_a(e)\) to denote the equation over \(\text {CCS}_a\) terms \(\texttt{p}^A_a(t) \approx \texttt{p}^A_a(u)\).
The following lemma is immediate from Definition 7.
Lemma 1
The mapping \(\texttt{p}^A_a\) is structural.
Hence, in light of Proposition 1, the mapping \(\texttt{p}^A_a\) satisfies Definition 3.2. Our order of business will now be to show that \(\texttt{p}^A_a\) preserves sound equations.
Lemma 2
For all \(p \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\) and \(q \in \mathcal {P}(\text {CCS}_a)\), if \(\texttt{p}^A_a(p) \xrightarrow {\, {a} \, } q\), then there exists a \(\text {BCCSP}_{\!A}^{\texttt{p}}\) process \(p'\) such that \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p'\) and \(\texttt{p}^A_a(p') = q\).
Proof
We proceed by structural induction over p.
-
Case \(p = \textbf{0}\). This is vacuous, since \(\texttt{p}^A_a(p)\) has no outgoing transition.
-
Case \(p=b.p_0\). By Definition 7 and the assumption that \(\texttt{p}^A_a(p) \xrightarrow {\, {a} \, } q\), we have that \(b = a \not \in A\) and \(\texttt{p}^A_a(p_0) = q\). As \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p_0\), the claim follows.
-
Case \(p = p_1 \;|_A\; p_2\). By Definition 7, we have that \(\texttt{p}^A_a(p) = \texttt{p}^A_a(p_1) \mathbin {\Vert } \texttt{p}^A_a(p_2)\). Moreover, by the proviso of the lemma, \(\texttt{p}^A_a(p_1) \mathbin {\Vert } \texttt{p}^A_a(p_2) \xrightarrow {\, {a} \, } q\), for some \(\text {CCS}_a\) process q. This follows by an application of either rule (lPar) or rule (rPar) from Table 4. We can assume, without loss of generality, that rule (lPar) was applied. (The case of an application of rule (rPar) follows from a similar reasoning.) Hence \(\texttt{p}^A_a(p_1) \xrightarrow {\, {a} \, } q'\) for some \(\text {CCS}_a\) process \(q'\) such that \(q' \mathbin {\Vert } \texttt{p}^A_a(p_2) = q\). By the induction hypothesis, we obtain that \(p_1 \xrightarrow {\, {a} \, }_{\texttt{p}} p_1'\) for some \(p_1' \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\) such that \(\texttt{p}^A_a(p_1') = q'\). Hence, as \(p_1 \xrightarrow {\, {a} \, }_{\texttt{p}} p_1'\) and \(a \not \in A\), we can apply rule (lParA) from Table 5 and obtain that \(p = p_1 \;|_A\; p_2 \xrightarrow {\, {a} \, }_{\texttt{p}} p_1' \;|_A\; p_2\). Since \(\texttt{p}^A_a(p_1' \;|_A\; p_2) = \texttt{p}^A_a(p_1') \mathbin {\Vert } \texttt{p}^A_a(p_2) = q' \mathbin {\Vert } \texttt{p}^A_a(p_2) = q\), the claim follows.
-
Case \(p = p_1 + p_2\). This case is similar to the case of parallel composition discussed above. The only difference is that rules (lSum) and (rSum) from Table 1 are applied in place of rules (lParA) and (rParA), respectively. \(\square \)
Lemma 3
For all \(p,p' \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\), if \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p'\) then \(\texttt{p}^A_a(p) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p')\).
Proof
We proceed by induction on the size of the proof for the transition \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p'\). We distinguish three cases, according to the last inference rule from Tables 1 and 5 that is applied in the proof. (Notice that the analysis of symmetric rules is omitted.) We remark that since \(a \not \in A\), rule (syncA) cannot be applied as the last rule in the proof for \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p'\).
-
Rule (act). In this case, we have that \(p=a.p'\) and \(p \xrightarrow {\, {a} \, }_{\texttt{p}} p'\). By Definition 7, we have that \(\texttt{p}^A_a(a.p') = a.\texttt{p}^A_a(p')\), and, thus, we can apply rule (act) and obtain that \(\texttt{p}^A_a(p) = \texttt{p}^A_a(a.p') = a.\texttt{p}^A_a(p') \xrightarrow {\, {a} \, } \texttt{p}^A_a(p')\). Hence the claim follows in this case.
-
Rule (lSum). In this case, we have that \(p = p_0 +p_1\), \(p_0 \xrightarrow {\, {a} \, }_{\texttt{p}} p'\), and \(\texttt{p}^A_a(p) = \texttt{p}^A_a(p_0) + \texttt{p}^A_a(p_1)\). By the inductive hypothesis we get that \(\texttt{p}^A_a(p_0) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p')\). By applying now rule (lSum), we conclude that \(\texttt{p}^A_a(p) = \texttt{p}^A_a(p_0) + \texttt{p}^A_a(p_1) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p')\).
-
Rule (lParA). In this case, as \(a \not \in A\), we have that \(p = p_0\;|_A\; p_1\), \(p_0 \xrightarrow {\, {a} \, }_{\texttt{p}} p_0'\) for some \(p_0' \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\), and \(p' = p_0' \;|_A\; p_1\). By induction, we obtain that \(\texttt{p}^A_a(p_0) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p_0')\). Hence, by applying rule (lPar) from Table 4 to \(\texttt{p}^A_a(p)\), we get that \(\texttt{p}^A_a(p) = \texttt{p}^A_a(p_0) \mathbin {\Vert } \texttt{p}^A_a(p_1) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p'_0) \mathbin {\Vert } \texttt{p}^A_a(p_1) = \texttt{p}^A_a(p_0' \;|_A\; p_1) = \texttt{p}^A_a(p')\). \(\square \)
We can now proceed to prove that \(\texttt{p}^A_a\) satisfies Definition 3.1 as well. Moreover, we show that it is also ground \(\varPhi \)-reflecting.
Proposition 2
The mapping \(\texttt{p}^A_a\) satisfies the following properties:
-
1.
For all \(t,u \in \mathbb {T}(\text {BCCSP}_{\!A}^{\texttt{p}})\), if \(t \sim _{\texttt{p}} u\) then \(\texttt{p}^A_a(t) \sim \texttt{p}^A_a(u)\).
-
2.
The mapping \(\texttt{p}^A_a\) is ground \(\varPhi \)-reflecting.
Proof
We prove the two items separately.
-
1.
First, observe that for every (closed) term t in \(\text {CCS}_a\) there is a (closed) term \(t_a^{\texttt{p},A}\) in \(\text {BCCSP}_{\!A}^{\texttt{p}}\) such that \(\texttt{p}^A_a(t_a^{\texttt{p},A}) = t\). The term \(t_a^{\texttt{p},A}\) is defined as follows:
$$\begin{aligned}&\quad \textbf{0}_a^{\texttt{p},A} = \textbf{0}\qquad \qquad x_a^{\texttt{p},A} = x \qquad \qquad (a.t)_a^{\texttt{p},A} = a.t_a^{\texttt{p},A} \\&(t + u)_a^{\texttt{p},A} = t_a^{\texttt{p},A} + u_a^{\texttt{p},A} \qquad \qquad (t \mathbin {\Vert } u)_a^{\texttt{p},A} = t_a^{\texttt{p},A} \;|_A\; u_a^{\texttt{p},A}. \end{aligned}$$Given a \(\text {CCS}_a\) substitution \(\sigma \), we define \(\sigma _a^{\texttt{p},A}\) to be the \(\text {BCCSP}_{\!A}^{\texttt{p}}\) substitution given by \(\sigma _a^{\texttt{p},A}(x) = (\sigma (x))_a^{\texttt{p},A}\). By Proposition 1 and since the mapping \(\texttt{p}^A_a\) is structural (Lemma 1), we have that
$$ \texttt{p}^A_a(\sigma _a^{\texttt{p},A}(t)) = \texttt{p}^A_a(\sigma _a^{\texttt{p},A})(\texttt{p}^A_a(t)) = \sigma (\texttt{p}^A_a(t)), $$for all \(t \in \mathbb {T}(\text {BCCSP}_{\!A}^{\texttt{p}})\).
To prove the claim, it is then enough to show that the following relation
$$ \mathcal {R} = \{ (\sigma (\texttt{p}^A_a(t)), \sigma (\texttt{p}^A_a(u))) \mid t \sim _{\texttt{p}} u \text { and } \sigma :\textrm{Var}\rightarrow \mathcal {P}(\text {CCS}_a)\} $$is a bisimulation relation over \(\text {CCS}_a\) processes.
Notice, first of all, that since \(\sim _{\texttt{p}}\) is symmetric, then so is \(\,{\mathcal R}\,\). Assume now that \(\sigma (\texttt{p}^A_a(t)) \,{\mathcal R}\,\sigma (\texttt{p}^A_a(u))\), where \(t,u \in \mathbb {T}(\text {BCCSP}_{\!A}^{\texttt{p}})\) and \(\sigma \) is a closed \(\text {CCS}_a\) substitution. By the definition of \(\,{\mathcal R}\,\), we have that \(t \sim _{\texttt{p}} u\). Assume now that \(\sigma (\texttt{p}^A_a(t)) \xrightarrow {\, {a} \, } q\) for some \(q \in \mathcal {P}(\text {CCS}_a)\). By the observation above, this means that \(\texttt{p}^A_a(\sigma _a^{\texttt{p},A}(t)) \xrightarrow {\, {a} \, } q\). By Lemma 2, we get that \(\sigma _a^{\texttt{p},A}(t) \xrightarrow {\, {a} \, }_{\texttt{p}} p'\) for some \(p' \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\) such that \(\texttt{p}^A_a(p') = q\). As \(t \sim _{\texttt{p}} u\) implies that \(\sigma _a^{\texttt{p},A}(t) \sim _{\texttt{p}} \sigma _a^{\texttt{p},A}(u)\), we have that \(\sigma _a^{\texttt{p},A}(u) \xrightarrow {\, {a} \, }_{\texttt{p}} p''\), for some \(p'' \in \mathcal {P}(\text {BCCSP}_{\!A}^{\texttt{p}})\) such that \(p' \sim _{\texttt{p}} p''\). Additionally, by Lemma 3 we have that \(\sigma (\texttt{p}^A_a(u)) = \texttt{p}^A_a(\sigma _a^{\texttt{p},A}(u)) \xrightarrow {\, {a} \, } \texttt{p}^A_a(p'')\). We can then conclude by noticing that, since \(p' \sim _{\texttt{p}} p''\), by definition of \(\,{\mathcal R}\,\) it holds that \(q = \texttt{p}^A_a(p') \,{\mathcal R}\,\texttt{p}^A_a(p'')\), i.e., \(\,{\mathcal R}\,\) is a bisimulation relation over \(\text {CCS}_a\) processes.
-
2.
In order to show that \(\texttt{p}^A_a\) is ground \(\varPhi \)-reflecting, it is enough to argue that the family \(\varPhi _A\) consisting of the closed equations \(\varphi _A^n\) defined in Eq. 1 is mapped exactly onto \(\varPhi \). Since \(a \not \in A\) we have that \(\texttt{p}^A_a\) simply replaces all the occurrences of \(\,|_A\,\) in each equation \(\varphi _A^n\) with \(\mathbin {\Vert }\). Hence, we have that \(\texttt{p}^A_a(\varphi _A^n) = \varphi _n\), for each \(n \ge 0\). \(\square \)
From Lemma 1 and Proposition 2, we can infer that \(\texttt{p}^A_a\) is a well-defined reduction as in Definition 3, and it is also ground \(\varPhi \)-reflecting. Theorem 4 then follows by Theorem 2 and Theorem 3.
4.3 The Case of \(\text {BCCSP}^{\texttt{p}}\) and the Negative Result for \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\)
Given the negative result over \(\text {BCCSP}_{\!A}^{\texttt{p}}\), it is natural to wonder what happens when we extend that language to \(\text {BCCSP}^{\texttt{p}}\), namely BCCSP enriched with an operator \(\,|_A\,\), for each \(A \subseteq \textrm{Act}\).
One might expect that bisimilarity does not have a finite, ground-complete axiomatisation over \(\text {BCCSP}^{\texttt{p}}\) and indeed we conjecture that such a results holds. However, the reduction method cannot be applied to prove such a claim. Specifically, consider the language \(\text {BCCSP}^{\texttt{p}}\) over \(\textrm{Act}= \{a\}\). We can prove the following result:
Theorem 5
There is no structural reduction from \(\text {BCCSP}^{\texttt{p}}\) to \(\text {CCS}_a\) that is ground \(\varPhi \)-reflecting.
Proof
To simplify notation, let us use \(\,|_a\,\) in place of \(\,|_{\{a\}}\).
Assume that \(\widehat{\,\cdot \,}\) is a structural reduction from \(\text {BCCSP}^{\texttt{p}}\) to \(\text {CCS}_a\). Our aim is to prove that \(\widehat{\,\cdot \,}\) is not ground \(\varPhi \)-reflecting.
To this end, we start by recalling that, since \(\widehat{\,\cdot \,}\) is structural (Definition 4), then:
Moreover, as \(\widehat{\,\cdot \,}\) preserves sound equations (Definition 3), we have that:
Assume now that
for some \(t \in \mathbb {T}(\text {CCS}_a)\) with \(\textrm{var}(t) \subseteq \{x_1,x_2\}\) (as \(\widehat{\,\cdot \,}\) is structural).
We can distinguish two cases, according to whether t is a closed term or not. In both cases, we shall show that \(\widehat{\,\cdot \,}\) is not ground \(\varPhi \)-reflecting.
-
Case 1: t is a closed \(\text {CCS}_a\) term. In this case, for each \(n \ge 0\), we have that
$$\begin{aligned} t \sim \widehat{a^n} \sim \textbf{0}. \end{aligned}$$(9)Indeed,
$$\begin{aligned} \widehat{a^n} \sim {}&\widehat{a^n \,|_a\, a^n}&\text {(by 5)} \\ \sim {}&t[\widehat{a^n}/x_1, \widehat{a^n}/x_2]&\text {(by 3 and 8)} \\ \sim {}&t[\widehat{\textbf{0}}/x_1, \widehat{\textbf{0}}/x_2]&\text {(since }t\text { is closed)} \\ \sim {}&\widehat{\textbf{0}}&\text {(by 3 and 5 with }n = 0\text {)}. \end{aligned}$$We now claim that
Claim 1:
For each \(p \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\), it holds that \(\widehat{p} \sim \widehat{\textbf{0}}\).
Before proving Claim 1 above, we observe that by using it we can immediately show that the mapping \(\widehat{\,\cdot \,}\) is not ground \(\varPhi \)-reflecting. Indeed, since
by Claim 1 there cannot be two processes \(p,q \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\) such that \(\widehat{p} = a \mathbin {\Vert } a\) and \(\widehat{q} = a \mathbin {\Vert } (a + a^2)\). Let us now prove Claim 1.
Proof of Claim 1:
We proceed by induction on the structure of process p.
-
The case \(p = \textbf{0}\) is trivial.
-
Case \(p = aq\). We have
$$\begin{aligned} \widehat{p} ={}&\widehat{ax}[\widehat{q}/x]&\text {(by 2)} \\ \sim {}&\widehat{ax}[\widehat{\textbf{0}}/x]&\text {(by induction and }\sim \text { is a congruence)} \\ \sim {}&\widehat{a\textbf{0}}&\text {(by 2)} \\ \sim {}&\hat{\textbf{0}}&\text {(by 9)}. \end{aligned}$$ -
Case \(p = p_1 \odot p_2\) for some binary operator \(\odot \in \{+,|_\emptyset ,|_a\}\). In this case,
$$\begin{aligned} \widehat{p} ={}&\widehat{x_1 \odot x_2}[\widehat{p_1}/x_1, \widehat{p_2}/x_2]&\text {(by 3)} \\ \sim {}&\widehat{x_1 \odot x_2}[\widehat{\textbf{0}}/x_1, \widehat{\textbf{0}}/x_2]&\text {(by induction and }\sim \text { is a congruence)} \\ \sim {}&\widehat{\textbf{0}\odot \textbf{0}}&\text {(by 3)} \\ \sim {}&\widehat{\textbf{0}}&\text {(by 5}{-}\text {7 according to the form of }{\odot }\text {).} \end{aligned}$$This concludes the Proof of Claim 1.
The proof of Case 1 is now complete.
-
Case 2: t is an open \(\text {CCS}_a\) term. Assume, without loss of generality, that t contains at least an occurrence of \(x_1\). (The cases of \(x_2 \in \textrm{var}(t)\) and \(x_1,x_2 \in \textrm{var}(t)\) can be treated in a similar fashion and are therefore omitted.) Firstly, we observe that for each \(p \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\)
$$\begin{aligned} \widehat{\textbf{0}} \sim {}&\widehat{ap \,|_a\, \textbf{0}}&\text {(by 4)} \\ ={}&t[\widehat{ap}/x_1, \widehat{\textbf{0}}/x_2]&\text {(by 3 and 8)}. \end{aligned}$$Moreover, we recall that for every \(u \in \text {CCS}_a\) and \(y \in \textrm{Var}\), it holds that whenever \(y \in \textrm{var}(u)\) then \(\textrm{depth}(\sigma (y)) \le \textrm{depth}(\sigma (u))\) for every closed substitution \(\sigma \). Hence, since \(t \in \mathbb {T}(\text {CCS}_a)\) and \(x_1 \in \textrm{var}(t)\), we have that
$$\begin{aligned} \textrm{depth}(\widehat{ap}) \le \textrm{depth}(\widehat{ap \,|_a\, \textbf{0}}) = \textrm{depth}(\widehat{\textbf{0}}). \end{aligned}$$(10)We claim that
Claim 2:
For each \(n \ge 0\) and processes \(p_1,\dots ,p_n \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\), it holds that \(\textrm{depth}(\widehat{\sum _{i=1}^n ap_i}) \le \textrm{depth}(\widehat{\textbf{0}})\).
Proof of Claim 2:
We proceed by induction on \(n \ge 0\).
-
The case \(n=0\) is trivial.
-
For the inductive step, we have that:
$$\begin{aligned}&\textrm{depth}(\widehat{\sum _{i=1}^{n+1} ap_i}) \\ ={}&\textrm{depth}(\widehat{\sum _{i=1}^n ap_i + ap_{n+1}}) \\ ={}&\textrm{depth}(\widehat{x_1+x_2}[\widehat{\sum _{i=1}^n ap_i}/x_1, \widehat{ap_{n+1}}/x_2])&\text {(by 3)} \\ \le {}&\textrm{depth}(\widehat{x_1+x_2}[\widehat{\textbf{0}}/x_1, \widehat{\textbf{0}}/x_2])&\text {(by induction and 10)} \\ ={}&\textrm{depth}(\widehat{\textbf{0}+ \textbf{0}})&\text {(by 3)} \\ ={}&\textrm{depth}(\widehat{\textbf{0}})&\text {(by 6 and Remark 1}). \end{aligned}$$
This concludes the Proof of Claim 2.
Claim 3:
For each \(p \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\) it holds that \(\textrm{depth}(\widehat{p}) \le \widehat{(}\textbf{0})\).
Proof of Claim 3:
First of all, we notice that each \(\text {BCCSP}^{\texttt{p}}\) process can be rewritten into head normal form up to bisimilarity. This means that, given any \(p \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\), we have that \(p \sim \sum _{i = 1}^n ap_i\) for some \(n \ge 0\) and \(p_1,\dots ,p_n \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\).
Since \(\widehat{\,\cdot \,}\) preserves sound equations, we have
Hence, by Claim 2 above, it follows that
This concludes the Proof of Claim 3.
We can now proceed to show that \(\widehat{\,\cdot \,}\) is not ground \(\varPhi \)-reflecting. Let \(k = \textrm{depth}(\widehat{\textbf{0}})\). We have that equation \(\varphi _{k} \in \varPhi \) is of the form:
In particular, the depth of \(a \mathbin {\Vert } (\sum _{i=1}^k a^i)\) is \(k+1\). Therefore, by 11, there is no \(p \in \mathcal {P}(\text {BCCSP}^{\texttt{p}})\) such that \(\widehat{p} = a \mathbin {\Vert } (\sum _{i=1}^k a^i)\).
The proof of Case 2 is now concluded.
This completes the proof of the Theorem 5. \(\square \)
Although we proved Theorem 5 in the simplified setting of \(\textrm{Act}=\{a\}\), it is not difficult to see that the proof can be extended to the general case \(\{a\} \subset \textrm{Act}\) in a straightforward manner.
Since the reduction method cannot be applied, one might show the non-existence of a finite, ground-complete axiomatisation of bisimilarity over \(\text {BCCSP}^{\texttt{p}}\) by adapting the strategy employed by Moller in his proof of Theorem 2. However, since that proof would require several pages of technical results, we leave it as an avenue for future research, and we deal with the presence of all the operators \(\,|_A\,\) in a simplified setting.
The basic idea behind the reduction defined for \(\text {BCCSP}_{\!A}^{\texttt{p}}\) is that we can always identify an action \(a \in \textrm{Act}\setminus A\) such that the parallel operator \(\,|_A\,\) always allows for interleaving of a-moves of its arguments. Clearly, if we add an operator \(\,|_A\,\) for each \(A \subseteq \textrm{Act}\) to the language, it is no longer possible to identify such an action. There is, however, a special action that is not used to build syntactically CSP terms, but it is however necessary to express their semantics: the silent action \(\tau \not \in \textrm{Act}\). CSP terms are defined over \(\textrm{Act}\), which means that the language does not offer a \(\tau \)-prefixing operator; however, in order to properly define the operational semantics of the internal choice operator, the set of action labels in the LTS is \(\textrm{Act}\cup \{\tau \}\). In particular, as explained in [19], the operational semantics of the parallel operators always allow for the interleaving of \(\tau \)-moves of their arguments.
Hence, we now consider \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), i.e., the extension of \(\text {BCCSP}^{\texttt{p}}\) that includes the \(\tau \)-prefixing operator, and we prove the following result:
Theorem 6
\(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) modulo bisimilarity does not afford a finite, ground-complete axiomatisation.
To this end, we apply the same proof technique that we used in Sect. 4.2 for \(\text {BCCSP}_{\!A}^{\texttt{p}}\). The reduction mapping for \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) is almost identical to the mapping \(\texttt{p}^A_a\) defined for \(\text {BCCSP}_{\!A}^{\texttt{p}}\), the only difference being that now we consider the language \(\text {CCS}_\tau \) as target language, i.e., \(\text {CCS}_a\) with \(a = \tau \).
Remark 3
Theorem 2 remains true over \(\text {CCS}_\tau \). In fact, as we are considering strong bisimilarity, there is no difference between \(\tau \) and any other observable action \(a \in \textrm{Act}\). Specifically, if we let \(\varPhi _\tau \) be the family of equations in \(\varPhi \) in which each occurrence of a is replaced by \(\tau \), then we can repeat Moller’s arguments in a step-by-step fashion to obtain that no finite axiom system, that is sound modulo bisimilarity, can prove the whole family of equations \(\varPhi _\tau \).
Definition 8
(The mapping \(\texttt{p}_\tau \)). The mapping \(\texttt{p}_\tau :\mathbb {T}(\text {BCCSP}_{\!\tau }^{\texttt{p}}) \rightarrow \mathbb {T}(\text {CCS}_\tau )\) is defined inductively over the structure of \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) terms as follows:
Intuitively, we use the mapping \(\texttt{p}_\tau \) to eliminate any action \(b \ne \tau \) from terms, so that a process \(\texttt{p}_\tau (p \;|_A\; q)\) can perform a transition \(\texttt{p}_\tau (p \;|_A\; q) \xrightarrow {\, {\tau } \, } p'\), for some \(\text {CCS}_a\) process \(p'\), if and only if \(b = \tau \). (Recall that, by construction \(\tau \not \in A\) for each \(A\subseteq \textrm{Act}\).)
First, we note that this mapping is a structural mapping.
Lemma 4
The mapping \(\texttt{p}_\tau \) is structural.
We now state the corresponding results over \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) to Lemma 2 and Lemma 3.
Lemma 5
For all \(p \in \mathcal {P}(\text {BCCSP}_{\!\tau }^{\texttt{p}})\) and \(q \in \mathcal {P}(\text {CCS}_\tau )\), if \(\texttt{p}_\tau (p) \xrightarrow {\, {\tau } \, } q\), then there exists a \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) process \(p'\), such that \(p \xrightarrow {\, {\tau } \, }_{\texttt{p}} p'\) and \(\texttt{p}_\tau (p') = q\).
Proof
The proof is by structural induction over p. We omit it since it is similar to that of Lemma 2. \(\square \)
Lemma 6
For all \(p,p' \in \mathcal {P}(\text {BCCSP}_{\!\tau }^{\texttt{p}})\), if \(p \xrightarrow {\, {\tau } \, }_{\texttt{p}} p'\) then \(\texttt{p}_\tau (p) \xrightarrow {\, {\tau } \, } \texttt{p}_\tau (p')\).
Proof
The proof proceeds by induction over the size of the proof for \(p \xrightarrow {\, {\tau } \, }_{\texttt{p}} p'\). It is analogous to the proof of Lemma 3, and it is therefore omitted. \(\square \)
The following result, which extends Proposition 2 to \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), allows us to prove that \(\texttt{p}_\tau \) is a well-defined reduction mapping that is also ground \(\varPhi _\tau \)-reflecting.
Proposition 3
The following properties hold for the mapping \(\texttt{p}_\tau \):
-
1.
For all \(t,u \in \mathbb {T}(\text {BCCSP}_{\!\tau }^{\texttt{p}})\), if \(t \sim _{\texttt{p}} u\), then \(\texttt{p}_\tau (t) \sim \texttt{p}_\tau (u)\).
-
2.
The mapping \(\texttt{p}_\tau \) is ground \(\varPhi _\tau \)-reflecting.
Proof
-
1.
We start by observing that for every (closed) term t in \(\text {CCS}_\tau \) there is a (closed) term \(t_\tau ^{\texttt{p}}\) in \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) such that \(\texttt{p}_\tau (t_\tau ^{\texttt{p}}) = t\). The term \(t_\tau ^{\texttt{p}}\) is defined as follows:
$$\begin{aligned}&\textbf{0}_\tau ^{\texttt{p}} = \textbf{0}\qquad \qquad x_\tau ^{\texttt{p}} = x \qquad \qquad (\tau .t)_\tau ^{\texttt{p}} = \tau .t_\tau ^{\texttt{p}} \\&(t + u)_\tau ^{\texttt{p}} = t_\tau ^{\texttt{p}} + u_\tau ^{\texttt{p}} \qquad \qquad (t \mathbin {\Vert } u)_\tau ^{\texttt{p}} = t_\tau ^{\texttt{p}} \;|_\emptyset \; u_\tau ^{\texttt{p}}. \end{aligned}$$Then, given a \(\text {CCS}_\tau \) substitution \(\sigma \), we define the \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\) substitution \(\sigma _\tau ^{\texttt{p}}\) by \(\sigma _\tau ^{\texttt{p}}(x) = (\sigma (x))_\tau ^{\texttt{p}}\). By Lemma 4 and Proposition 1, we have that \(\texttt{p}_\tau (\sigma _\tau ^{\texttt{p}}(t)) = \texttt{p}_\tau (\sigma _\tau ^{\texttt{p}})(\texttt{p}_\tau (t)) = \sigma (\texttt{p}_\tau (t))\) for all \(t \in \mathbb {T}(\text {BCCSP}_{\!\tau }^{\texttt{p}})\).
The proof of this statement then proceeds as that of the corresponding statement in Proposition 2, and it is therefore omitted.
-
2.
Consider the family of equations \(\varPhi _{\tau ,\emptyset } = \{\varphi _{\tau ,\emptyset }^n \,\mid \, n \in \mathbb {N}\}\), where the closed equations \(\varphi _{\tau ,\emptyset }^n\) are defined as in Eq. 1, using the set \(\emptyset \) as synchronisation set, and replacing each occurrence of a with \(\tau \). It is straightforward to prove that \(\texttt{p}_\tau (\varphi _{\tau ,\emptyset }^n) = \varphi _{\tau ,n}\) for each \(n \in \mathbb {N}\). Hence, \(\texttt{p}_\tau \) is ground \(\varPhi _\tau \)-reflecting. \(\square \)
Theorem 6 is then obtained as a direct consequence of Lemma 4, Proposition 3, Theorem 3, and Theorem 2.
4.4 The Case of \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\)
We now argue that the requirement that the inclusion \(A \subset \textrm{Act}\) be strict, used in Sect. 4.2, is indeed necessary for Theorem 4 to hold. We also notice that a similar requirement is not explicitly expressed for the validity of Theorem 6, proved in Sect. 4.3, because having \(\,|_A\,\) defined for all \(A \subseteq \textrm{Act}\) automatically guaranteed the existence of at least one synchronisation set A such that \(a \not \in A\) for some action \(a \in \textrm{Act}\), namely the synchronisation set \(A = \emptyset \). Moreover, as discussed in Example 1, given a synchronisation set A, the requirement \(a \not \in A\) is crucial to guarantee the soundness modulo bisimilarity of equation \(\varphi _A^n\), for any \(n \in \mathbb {N}\) (see Eq. 1).
In this section, we handle the border case of the language \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\), which includes only the parallel operator \(\,|_\textrm{Act}\), and we show that for this special case a positive result holds: we provide a finite, ground-complete axiomatisation of bisimilarity over this language. Let us consider the axiom system \(\mathcal {E}_{\texttt{p}} = \mathcal {E}_0 \cup \{\text {P1},\text {P2},\text {P3},\text {P4},\text {P5}\}\), where \(\mathcal {E}_0\) consists of the axioms in Table 3, and axioms P1–P5 are reported in Table 6. Notice that the axiom schemata P4 and P5 generate only finitely many axioms. More precisely, P4 generates \(|\textrm{Act}|\) axioms, and P5 generates \(|\textrm{Act}|\times (|\textrm{Act}|-1)\) axioms. We will now prove the following result:
Theorem 7
\(\mathcal {E}_{\texttt{p}}\) is a finite, ground-complete axiomatisation of \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) modulo bisimilarity.
The idea behind the proof of Theorem 7 is that the axioms in Table 6 allow us to eliminate all occurrences of the parallel operator \(\,|_{\textrm{Act}}\,\) from \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) processes. Hence, every \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) process can be proven equal to a BCCSP process using \(\mathcal {E}_{\texttt{p}}\). The ground-completeness of \(\mathcal {E}_{\texttt{p}}\) then follows from that of \(\mathcal {E}_0\) proven in [28]. To that end, we first show:
Lemma 7
For all closed BCCSP terms p and q, there exists a closed BCCSP term r such that \(\mathcal {E}_{\texttt{p}} \vdash p \;|_{\textrm{Act}}\; q \approx r\).
Proof
The proof is by induction on \(\textrm{size}(p \;|_{\textrm{Act}}\; q)\). First of all we notice that, given any closed BCCSP term p, we can assume, without loss of generality, that \(p = \sum _{i \in I} a_i p_i\) for some finite index set I, actions \(a_i \in \textrm{Act}\), and closed BCCSP terms \(p_i\), for \(i \in I\). In fact, in case p is not already in this shape, then by applying axioms A2 and A4 in Table 3 we can remove superfluous occurrences of \(\textbf{0}\) summands. In particular, we remark that this transformation does not increase the number of operator symbols occurring in p. Thus we proceed under the assumption that
We proceed by a case analysis on the cardinality of the sets of indexes I and J.
-
If either \(I = \emptyset \) or \(J=\emptyset \), then \(p=\textbf{0}\) or \(q=\textbf{0}\). In light of P1, without loss of generality, we can assume that \(q = \textbf{0}\) and we have that \(p \;|_{\textrm{Act}}\; q = p \;|_{\textrm{Act}}\; \textbf{0}\). Thus by applying axiom P3, we get \(\mathcal {E}_{\texttt{p}} \vdash p \;|_{\textrm{Act}}\; q \approx \textbf{0}\) and we are done.
-
If both I and J are singletons, then we have that \(p = a.p'\) and \(q = b.q'\), for some \(a,b \in \textrm{Act}\) and BCCSP processes \(p'\) and \(q'\).
If \(a=b\), then we use axiom P4 to get \(\mathcal {E}_{\texttt{p}}\vdash a.p' \;|_{\textrm{Act}}\; a.q' \approx a.(p' \;|_{\textrm{Act}}\; q')\). Since the size of \(p' \;|_{\textrm{Act}}\; q'\) is smaller than that of \(p \;|_{\textrm{Act}}\; q\), by the induction hypothesis, there exists a BCCSP process \(r'\) such that \(\mathcal {E}_{\texttt{p}} \vdash p' \;|_{\textrm{Act}}\; q' \approx r'\). Thus we have \(\mathcal {E}_{\texttt{p}} \vdash a.p' \;|_{\textrm{Act}}\; a.q' \approx a.r'\), which is a BCCSP process.
In the case that \(a \ne b\), then we can use axiom P5, to infer \(\mathcal {E}_{\texttt{p}}\vdash a.p' \;|_{\textrm{Act}}\; b.q' \approx \textbf{0}\) and we are done.
-
We can now assume, without loss of generality, that \(|I| > 1\) and \(|J| \ge 1\). This means that we can express p as the summation of two summands of smaller size that are different from \(\textbf{0}\), i.e. \(p = p_1+ p_2\), for some BCCSP processes \(p_1\) and \(p_2\). Then, we use axiom P2 to get \(\mathcal {E}_{\texttt{p}}\vdash (p_1 + p_2) \;|_{\textrm{Act}}\; q \approx (p_1 \;|_{\textrm{Act}}\; q) + (p_2 \;|_{\textrm{Act}}\; q)\). Since both \(p_1 \;|_{\textrm{Act}}\; q\) and \(p_2 \;|_{\textrm{Act}}\; q\) have size less than that of \(p \;|_{\textrm{Act}}\; q\), by the induction hypothesis, we have that there exist BCCSP processes \(r'\) and \(r''\) such that \(\mathcal {E}_{\texttt{p}}\vdash p_1 \;|_{\textrm{Act}}\; q \approx r'\) and \(\mathcal {E}_{\texttt{p}}\vdash p_2 \;|_{\textrm{Act}}\; q \approx r''\). We thus have that \(\mathcal {E}_{\texttt{p}}\vdash p \;|_{\textrm{Act}}\; q \approx r' +r''\), which is a BCCSP process, and we are done. \(\square \)
The above lemma is the key step in the elimination of \(|_{\textrm{Act}}\) from closed terms. Namely:
Proposition 4
For every closed \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) process p there exists a closed BCCSP process q such that \(\mathcal {E}_{\texttt{p}}\vdash p \approx q\).
Proof
The proof is straightforward by structural induction on p and using Lemma 7 in the case that p is of the form \(p_1 \,|_{\textrm{Act}}\, p_2\), for some \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) processes \(p_1,p_2\). \(\square \)
The ground-completeness of \(\mathcal {E}_{\texttt{p}}\) over \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) follows from Proposition 4 and the ground-completeness of \(\mathcal {E}_0\) over BCCSP [28].
5 The Case of Restriction
In this section we apply the reduction technique described in Sect. 3 to show that bisimilarity does not have a finite, ground-complete equational axiomatisation over the recursion and relabelling free fragment of CCS. In detail, we assume a finite set of action names \(\textrm{Act}\), and we let \(\overline{\textrm{Act}}\) denote the set of action co-names, i.e., \(\overline{\textrm{Act}}=\{\overline{a} \mid a \in \textrm{Act}\}\). As usual, we postulate that \(\overline{\overline{a}}=a\) and \(a \ne \overline{a}\) for all \(a \in \textrm{Act}\). Then, we let \(\textrm{Act}_\tau = \textrm{Act}\cup \overline{\textrm{Act}} \cup \{\tau \}\), where \(\tau \not \in \textrm{Act}\cup \overline{\textrm{Act}}\). Henceforth, we let \(\mu ,\nu ,\dots \) range over actions in \(\textrm{Act}_\tau \), \(\alpha ,\beta ,\dots \) range over actions in \(\textrm{Act}\cup \overline{\textrm{Act}}\), and \(a,b,\dots \) range over actions in \(\textrm{Act}\).
We denote by \(\text {CCS}^\texttt{r}\) the recursion and relabelling free fragment of CCS with the full merge operator (denoted by \(~|~\)) generated by the following grammar:

where \(x \in \textrm{Var}\), \(\mu \in \textrm{Act}_\tau \) and \(R \subseteq \textrm{Act}\cup \overline{\textrm{Act}}\).
Following [32], the action symbol \(\tau \) will result from the synchronised occurrence of the complementary actions \(\alpha \) and \(\overline{\alpha }\), as described by the inference rules in Table 7.
We recall that the restriction operator \(t \backslash R\) prevents t (and its derivatives) from performing any \(\alpha \)-transition, for all \(\alpha \in R\).
The operational semantics of \(\text {CCS}^\texttt{r}\) is obtained by adding the inference rules for the full merge and the restriction operator given in Table 7 to the rules for BCCSP operators given in Table 1. In the technical results that follow, we will need to distinguish between transitions over \(\text {CCS}^\texttt{r}\) processes, and transitions over \(\text {CCS}_a\) processes. Hence, to avoid possible confusion and favour thus readability, we adopt the same strategy we used in Sect. 4, and use special symbols to distinguish them: we denote the transition relation induced by the rules in Tables 1 and 7 by \(\xrightarrow {\, {} \, }_{\texttt{r}}\), and bisimilarity over \(\mathcal {P}(\text {CCS}^\texttt{r})\) by \(\sim _{\texttt{r}}\).
Definition 9
(Bisimulation over \(\textbf{CCS}^\texttt{r}\)). Bisimulation relations over \(\text {CCS}^\texttt{r}\) processes are defined by applying Definition 2 to the LTS \((\mathcal {P}(\text {CCS}^\texttt{r}),\textrm{Act}_\tau ,\xrightarrow {\, {} \, }_{\texttt{r}})\) induced by the SOS rules in Table 7. We use the symbol \(\sim _\texttt{r}\) to denote bisimilarity over \(\text {CCS}^\texttt{r}\) processes.
5.1 The Negative Result
Our main goal in this section is to prove the following theorem:
Theorem 8
Bisimilarity has no finite, ground-complete axiomatisation over \(\text {CCS}^\texttt{r}\).
To this end, as already done in Sects. 4.2 and 4.3, we exploit the reduction technique from [11] and Moller’s non-finite axiomatisability result from \(\text {CCS}_a\) (Theorem 2). In detail:
-
We select a particular action \(a \in \textrm{Act}\).
-
We consider the language \(\text {CCS}_a\) and the instantiation of the equations \(\varphi _n\) in the family \(\varPhi \) over processes defined using only that action.
-
We provide a translation mapping from \(\text {CCS}^\texttt{r}\) to \(\text {CCS}_a\), denoted by \(\texttt{r}_a\), whose definition will be parametric in the chosen action a, that will allow us to eliminate all \(\text {CCS}^\texttt{r}\) terms in which the execution of a is restricted, while ensuring the possibility to perform any a-transition that is unrestricted.
It will be then enough to show that the mapping \(\texttt{r}_a\) is structural, it preserves the soundness of equations from \(\text {CCS}^\texttt{r}\) to \(\text {CCS}_a\), and it is ground \(\varPhi \)-reflecting, to obtain the validity of the lifting of the negative result in Theorem 2 to \(\text {CCS}^\texttt{r}\), proving thus Theorem 8.
5.2 The Reduction
Choose an action a from the action set \(\textrm{Act}\). Then we define a mapping \(\texttt{r}_a:\mathbb {T}(\text {CCS}^\texttt{r}) \rightarrow \mathbb {T}(\text {CCS}_a)\) allowing us to rewrite any \(\text {CCS}^\texttt{r}\) term into a \(\text {CCS}_a\) term.
Definition 10
(The mapping \(\texttt{r}_a\)). The mapping \(\texttt{r}_a:\mathbb {T}(\text {CCS}^\texttt{r}) \rightarrow \mathbb {T}(\text {CCS}_a)\) is defined inductively as follows:
Notice that a is the only action that may possibly occur in \(\texttt{r}_a(t)\), for each \(t \in \mathbb {T}(\text {CCS}^\texttt{r})\).
We now proceed to show that the mapping \(\texttt{r}_a\) is a well-defined reduction, according to Definition 3. As a first step, we notice that \(\texttt{r}_a\) is structural by definition.
Lemma 8
The mapping \(\texttt{r}_a\) is structural.
We now proceed to prove two technical lemmas, that will be useful to prove that \(\texttt{r}_a\) is a reduction.
Lemma 9
For all \(p \in \mathcal {P}(\text {CCS}^\texttt{r})\), and \(q \in \mathcal {P}(\text {CCS}_a)\), if \(\texttt{r}_a(p) \xrightarrow {\, {a} \, } q\), then there exists some \(p' \in \mathcal {P}(\text {CCS}^\texttt{r})\) such that \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p'\) and \(\texttt{r}_a(p') = q\).
Proof
The proof proceeds by structural induction over the \(\mathcal {P}(\text {CCS}^\texttt{r})\) process p. As for prefixing, nondeterministic choice, and parallel composition the proof is analogous to that of the corresponding steps in Lemma 2, we limit ourselves to present only the inductive step related to the restriction operator.
Let \(p = p_1 \backslash R\). We can distinguish two cases, according to whether \(a \in R\) or \(\overline{a}\in R\), or not (see Definition 10):
-
Assume that \(a \in R\) or \(\overline{a} \in R\). Then \(\texttt{r}_a(p) = \textbf{0}\), and this case becomes vacuous as
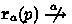 .
. -
Assume now that \(a,\overline{a} \not \in R\). Then \(\texttt{r}_a(p) = \texttt{r}_a(p_1)\) and \(\texttt{r}_a(p_1) \xrightarrow {\, {a} \, } q\). By induction over \(p_1\), there is some \(p_1' \in \mathcal {P}(\text {CCS}^\texttt{r})\) such that \(p_1 \xrightarrow {\, {a} \, }_{\texttt{r}} p_1'\) and \(\texttt{r}_a(p_1') = q\). Since \(a,\overline{a} \not \in R\), by an application of rule (r4) from Table 7 we obtain that \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p_1' \backslash R\). Finally, by Definition 10, since \(a,\overline{a} \not \in R\) it follows that \(\texttt{r}_a(p_1' \backslash R) = \texttt{r}_a(p_1') = q\) as required. \(\square \)
Lemma 10
For all \(p,p' \in \mathcal {P}(\text {CCS}^\texttt{r})\), if \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p'\), then \(\texttt{r}_a(p) \xrightarrow {\, {a} \, } \texttt{r}_a(p')\).
Proof
The proof proceeds by induction over the size of the proof for the transition \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p'\). Also in this case, given the similarities with the proofs of the corresponding cases in Lemma 3, we limit ourselves to analyse only the case in which the last inference rule from Table 7 that is applied in the proof for \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p'\) is rule (r4), i.e., the rule for restriction. (In particular, we remark that since \(a \ne \tau \), rules (r3) and (r5) cannot be applied as the last rules in the proof for \(p \xrightarrow {\, {a} \, }_{\texttt{r}} p'\).)
Let (r4) be the last rule applied in the proof. In this case, \(p = p_1 \backslash R\), \(p_1 \xrightarrow {\, {a} \, }_{\texttt{r}} p_1'\), and \(p' = p_1' \backslash R\). In particular, the application of rule (r4) guarantees that \(a,\overline{a} \not \in R\), so that \(\texttt{r}_a(p) = \texttt{r}_a(p_1)\), by Definition 10. By induction we obtain that \(\texttt{r}_a(p_1) \xrightarrow {\, {a} \, } \texttt{r}_a(p_1')\). Clearly, this directly gives \(\texttt{r}_a(p) \xrightarrow {\, {a} \, } \texttt{r}_a(p_1')\). Since, moreover, \(a,\overline{a} \not \in R\), by Definition 10 we also get that \(\texttt{r}_a(p') = \texttt{r}_a(p_1' \backslash R) = \texttt{r}_a(p_1')\). We can then conclude that \(\texttt{r}_a(p) \xrightarrow {\, {a} \, } \texttt{r}_a(p')\). \(\square \)
We now have all the ingredients necessary to prove that the mapping \(\texttt{r}_a\) is a well-defined ground \(\varPhi \)-reflecting reduction.
Proposition 5
The mapping \(\texttt{r}_a\) satisfies the following properties:
-
1.
For each \(t,u \in \mathbb {T}(\text {CCS}^\texttt{r})\), \(t \sim _\texttt{r} u\) implies \(\texttt{r}_a(t) \sim \texttt{r}_a(u)\).
-
2.
The mapping \(\texttt{r}_a\) is ground \(\varPhi \)-reflecting.
Proof
We prove the two statements separately.
-
1.
First of all, for each \(t \in \mathbb {T}(\text {CCS}_a)\) we define \(t_a^{\texttt{r}} \in \mathbb {T}(\text {CCS}^\texttt{r})\) as follows:
$$\begin{aligned}&\textbf{0}_a^{\texttt{r}} = \textbf{0}\qquad \qquad x_a^{\texttt{r}} = a \qquad \qquad (a.t)_a^{\texttt{r}} = a.t_a^{\texttt{r}} \\&(t+u)_a^{\texttt{r}} = t_a^{\texttt{r}} + u_a^{\texttt{r}} \qquad \qquad (t \mathbin {\Vert } u)_a^{\texttt{r}} = t_a^{\texttt{r}} ~|~u_a^{\texttt{r}}. \end{aligned}$$It is then immediate to check that for each \(t \in \mathbb {T}(\text {CCS}_a)\) we have that \(\texttt{r}_a(t_a^{\texttt{r}}) = t\). Then, given any \(\text {CCS}_a\) substitution \(\sigma \), we define \(\sigma _a^{\texttt{r}}\) as the \(\text {CCS}^\texttt{r}\) substitution such that \(\sigma _a^{\texttt{r}}(x) = (\sigma (x))_a^{\texttt{r}}\). The claim then follows by applying the same reasoning used in the proof of Proposition 2.
-
2.
Consider the family of equations \(\varPhi _{\texttt{r}}\) defined as follows:
$$\begin{aligned}&\varphi _\texttt{r}^n : a ~|~\sum _{i = 1}^n a^i \approx a.\sum _{i=1}^n a^i + \sum _{j=1}^n a^{j+1}&(n \ge 0) \\&\varPhi _{\texttt{r}} = \{\varphi _{\texttt{r}}^n \mid n \ge 0\}. \end{aligned}$$It is straightforward to prove that \(\texttt{r}_a(\varphi _{\texttt{r}}^n) = \varphi _n\) for each \(n \in \mathbb {N}\), and thus that \(\texttt{r}_a\) is ground \(\varPhi \)-reflecting. \(\square \)
Theorem 8 is then a immediate consequence of Lemma 8, Proposition 5, Theorem 3, and Theorem 2.
6 Concluding Remarks
In this paper, we have exploited the reduction technique from [11], for the lifting of negative results across process algebras, to prove the non-finite axiomatisability of various extensions of BCCSP modulo bisimilarity. In detail, we have proved that bisimilarity does not admit a finite, ground-complete axiomatisation 1. over \(\text {BCCSP}_{\!A}^{\texttt{p}}\), i.e., BCCSP enriched with a CSP-like parallel operator \(\,|_A\), with \(A \subset \textrm{Act}\), 2. over \(\text {BCCSP}_{\!\tau }^{\texttt{p}}\), i.e., BCCSP enriched with \(\tau \)-prefixing, \(\tau \not \in \textrm{Act}\), and CSP-like parallel operators with any possible synchronisation set, and 3. over \(\text {CCS}^\texttt{r}\), i.e., the recursion and relabelling free fragment of CCS. Interestingly, among all these negative results, we found a positive one: if we consider only the CSP-like parallel operator \(\,|_\textrm{Act}\), forcing all the actions in the parallel components to be synchronised, then a finite, ground-complete axiomatisation of bisimilarity over \(\text {BCCSP}_{\!\textrm{Act}}^{\texttt{p}}\) exists. Moreover, we have proved that the reduction technique from [11] cannot be applied in the case of \(\text {BCCSP}^{\texttt{p}}\), i.e., BCCSP enriched with all parallel operators \(\,|_A\,\) for \(A \subseteq \textrm{Act}\).
As a natural step for future work, we will provide a direct proof of the fact that bisimilarity does not admit a finite, ground-complete axiomatisation over \(\text {BCCSP}^{\texttt{p}}\).
Moreover, we plan to investigate how far the lifting technique of [11] can be pushed. In particular, we are interested in studying whether (some variations of) it can be used to lift known results for strong behavioural equivalences to their weak counterparts or to potentially extend results over weak behavioural congruences (such as Theorem 10 presented in [1]) to new settings.
Another possible direction for future work, would be to focus on full recursion free CCS. Aceto, Ingólfsdóttir, Luttik and van Tilburg gave an equational axiomatisation of bisimilarity over recursion-free CCS with interleaving parallel composition and the left-merge operator in [13]. That result crucially depends on the fact that restriction and relabelling distribute over interleaving parallel composition. On the other hand, neither restriction nor relabelling distribute over parallel composition in the presence of synchronisation. Obtaining a complete axiomatisation of full recursion free CCS modulo bisimilarity, with restriction, relabelling and parallel composition that allows for synchronisation is a natural, and very challenging, avenue for future research.
Notes
- 1.
Rob van Glabbeek was one of Frits Vaandrager’s early collaborators and fellow doctoral student at CWI.
- 2.
See https://www.youtube.com/watch?v=2PxM3f0QWDM for a recording of that talk.
References
Aceto, L., Anastasiadi, E., Castiglioni, V., Ingólfsdóttir, A., Luttik, B.: In search of lost time: axiomatising parallel composition in process algebras. In: Proceedings of LICS 2021, pp. 1–14. IEEE (2021). https://doi.org/10.1109/LICS52264.2021.9470526
Aceto, L., Anastasiadi, E., Castiglioni, V., Ingólfsdóttir, A., Luttik, B., Pedersen, M.R.: On the axiomatisability of priority III: priority strikes again. Theor. Comput. Sci. 837, 223–246 (2020). https://doi.org/10.1016/j.tcs.2020.07.044
Aceto, L., Bloom, B., Vaandrager, F.W.: Turning SOS rules into equations. Inf. Comput. 111(1), 1–52 (1994). https://doi.org/10.1006/inco.1994.1040
Aceto, L., Castiglioni, V., Fokkink, W., Ingólfsdóttir, A., Luttik, B.: Are two binary operators necessary to finitely axiomatise parallel composition? In: Proceedings of CSL 2021. LIPIcs, vol. 183, pp. 8:1–8:17 (2021). https://doi.org/10.4230/LIPIcs.CSL.2021.8
Aceto, L., Castiglioni, V., Ingólfsdóttir, A., Luttik, B., Pedersen, M.R.: On the axiomatisability of parallel composition: a journey in the spectrum. In: Proceedings of CONCUR 2020. LIPIcs, vol. 171, pp. 18:1–18:22 (2020). https://doi.org/10.4230/LIPIcs.CONCUR.2020.18
Aceto, L., Fokkink, W., van Glabbeek, R.J., Ingólfsdóttir, A.: Nested semantics over finite trees are equationally hard. Inf. Comput. 191(2), 203–232 (2004). https://doi.org/10.1016/j.ic.2004.02.001
Aceto, L., Fokkink, W., Ingólfsdóttir, A.: A menagerie of non finitely based process semantics over BPA* - from ready simulation to completed traces. Math. Struct. Comput. Sci. 8(3), 193–230 (1998). http://journals.cambridge.org/action/displayAbstract?aid=44743
Aceto, L., Fokkink, W., Ingólfsdóttir, A., Luttik, B.: CCS with Hennessy’s merge has no finite-equational axiomatization. Theor. Comput. Sci. 330(3), 377–405 (2005). https://doi.org/10.1016/j.tcs.2004.10.003
Aceto, L., Fokkink, W., Ingolfsdottir, A., Luttik, B.: Finite equational bases in process algebra: results and open questions. In: Middeldorp, A., van Oostrom, V., van Raamsdonk, F., de Vrijer, R. (eds.) Processes, Terms and Cycles: Steps on the Road to Infinity. LNCS, vol. 3838, pp. 338–367. Springer, Heidelberg (2005). https://doi.org/10.1007/11601548_18
Aceto, L., Fokkink, W., Ingólfsdóttir, A., Luttik, B.: A finite equational base for CCS with left merge and communication merge. ACM Trans. Comput. Log. 10(1), 6:1–6:26 (2009). https://doi.org/10.1145/1459010.1459016
Aceto, L., Fokkink, W., Ingólfsdóttir, A., Mousavi, M.R.: Lifting non-finite axiomatizability results to extensions of process algebras. Acta Inf. 47(3), 147–177 (2010). https://doi.org/10.1007/s00236-010-0114-7
Aceto, L., Fokkink, W., Ingólfsdóttir, A., Nain, S.: Bisimilarity is not finitely based over BPA with interrupt. Theor. Comput. Sci. 366(1–2), 60–81 (2006). https://doi.org/10.1016/j.tcs.2006.07.003
Aceto, L., Ingólfsdóttir, A., Luttik, B., van Tilburg, P.: Finite equational bases for fragments of CCS with restriction and relabelling. In: Ausiello, G., Karhumäki, J., Mauri, G., Ong, L. (eds.) TCS 2008. IIFIP, vol. 273, pp. 317–332. Springer, Boston, MA (2008). https://doi.org/10.1007/978-0-387-09680-3_22
Baeten, J.C.M., Basten, T., Reniers, M.: Process Algebra: Equational Theories of Communicating Processes. Cambridge Tracts in Theoretical Computer Science, Cambridge University Press (2009). https://doi.org/10.1017/CBO9781139195003
Baeten, J.C.M., Vaandrager, F.W.: An algebra for process creation. Acta Informatica 29(4), 303–334 (1992). https://doi.org/10.1007/BF01178776
Bergstra, J.A., Klop, J.W.: Process algebra for synchronous communication. Inf. Control 60(1–3), 109–137 (1984). https://doi.org/10.1016/S0019-9958(84)80025-X
Bergstra, J.A., Klop, J.W.: Algebra of communicating processes with abstraction. Theor. Comput. Sci. 37, 77–121 (1985). https://doi.org/10.1016/0304-3975(85)90088-X
Bloom, B., Istrail, S., Meyer, A.R.: Bisimulation can’t be traced. J. ACM 42(1), 232–268 (1995). https://doi.org/10.1145/200836.200876
Brookes, S.D., Roscoe, A.W., Walker, D.J.: An operational semantics for CSP. Report, University of Oxford (1986)
Chen, T., Fokkink, W., van Glabbeek, R.J.: On the axiomatizability of impossible futures. Log. Methods Comput. Sci. 11(3) (2015). https://doi.org/10.2168/LMCS-11(3:17)2015
Fokkink, W.J., Luttik, S.P.: An \(\upomega \)-complete equational specification of interleaving. In: Montanari, U., Rolim, J.D.P., Welzl, E. (eds.) ICALP 2000. LNCS, vol. 1853, pp. 729–743. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45022-X_61
Glabbeek, R.J.: The linear time - branching time spectrum. In: Baeten, J.C.M., Klop, J.W. (eds.) CONCUR 1990. LNCS, vol. 458, pp. 278–297. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0039066
van Glabbeek, R.J.: Full abstraction in structural operational semantics (extended abstract). In: Proceedings of AMAST 1993, pp. 75–82. Workshops in Computing (1993)
van Glabbeek, R., Vaandrager, F.: Modular specifications in process algebra. In: Wirsing, M., Bergstra, J.A. (eds.) Algebraic Methods 1987. LNCS, vol. 394, pp. 465–506. Springer, Heidelberg (1989). https://doi.org/10.1007/BFb0015049
van Glabbeek, R., Vaandrager, F.: Petri net models for algebraic theories of concurrency. In: de Bakker, J.W., Nijman, A.J., Treleaven, P.C. (eds.) PARLE 1987. LNCS, vol. 259, pp. 224–242. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-17945-3_13
Groote, J.F., Vaandrager, F.W.: Structured operational semantics and bisimulation as a congruence. Inf. Comput. 100(2), 202–260 (1992). https://doi.org/10.1016/0890-5401(92)90013-6
Groote, J.F., de Vink, E.P.: An axiomatization of strong distribution bisimulation for a language with a parallel operator and probabilistic choice. In: ter Beek, M.H., Fantechi, A., Semini, L. (eds.) From Software Engineering to Formal Methods and Tools, and Back. LNCS, vol. 11865, pp. 449–463. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30985-5_26
Hennessy, M., Milner, R.: Algebraic laws for nondeterminism and concurrency. J. ACM 32(1), 137–161 (1985). https://doi.org/10.1145/2455.2460
Hoare, C.A.R.: Communicating Sequential Processes. Prentice-Hall (1985)
Keller, R.M.: Formal verification of parallel programs. Commun. ACM 19(7), 371–384 (1976). https://doi.org/10.1145/360248.360251
Middelburg, C.A.: Probabilistic process algebra and strategic interleaving. Sci. Ann. Comput. Sci. 30(2), 205–243 (2020). https://doi.org/10.7561/SACS.2020.2.205
Milner, R.: Communication and Concurrency. PHI Series in Computer Science. Prentice Hall (1989)
Moller, F.: Axioms for Concurrency. Ph.D. thesis, Department of Computer Science, University of Edinburgh, July 1989. https://era.ed.ac.uk/bitstream/handle/1842/11182/Moller1989.pdf, report CST-59-89. Also published as ECS-LFCS-89-84
Moller, F.: The importance of the left merge operator in process algebras. In: Paterson, M.S. (ed.) ICALP 1990. LNCS, vol. 443, pp. 752–764. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0032072
Moller, F.: The nonexistence of finite axiomatisations for CCS congruences. In: Proceedings of LICS 1990, pp. 142–153 (1990). https://doi.org/10.1109/LICS.1990.113741
Park, D.: Concurrency and automata on infinite sequences. In: Deussen, P. (ed.) GI-TCS 1981. LNCS, vol. 104, pp. 167–183. Springer, Heidelberg (1981). https://doi.org/10.1007/BFb0017309
Plotkin, G.D.: A structural approach to operational semantics. Report DAIMI FN-19, Computer Science Department, Aarhus University (1981)
de Simone, R.: Higher-level synchronising devices in Meije-SCCS. Theor. Comput. Sci. 37, 245–267 (1985). https://doi.org/10.1016/0304-3975(85)90093-3
Vaandrager, F.W.: Algebraic techniques for concurrency and their application. Ph.D. thesis, University of Amsterdam, February 1990
Acknowledgements
The first author thanks Frits Vaandrager for the joint work they did about thirty years ago and Rob van Glabbeek for asking the questions that led to the research presented in this article.
We thank the reviewers for their valuable comments on our paper. In particular, we are very grateful to the reviewer who spotted a technical error in the original manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Aceto, L., Anastasiadi, E., Castiglioni, V., Ingólfsdóttir, A. (2022). Non-finite Axiomatisability Results via Reductions: CSP Parallel Composition and CCS Restriction. In: Jansen, N., Stoelinga, M., van den Bos, P. (eds) A Journey from Process Algebra via Timed Automata to Model Learning . Lecture Notes in Computer Science, vol 13560. Springer, Cham. https://doi.org/10.1007/978-3-031-15629-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-15629-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-15628-1
Online ISBN: 978-3-031-15629-8
eBook Packages: Computer ScienceComputer Science (R0)





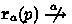 .
.