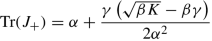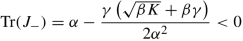1 Introduction

A minimal models of vertebrae formation were studied in [8] concerning periodic structures formation. The authors proposed two kinds of reaction-diffusion models, from which one is of clock-and-wavefront type and the other one is of Turing type. Our goal is to show that in case of the Turing type model the kinetic system as well the reaction-diffusion system exhibit oscillating solutions. The chapter is organised as follows. In the next section we introduce the model. In the section that follows we examine the existence and stability of some equilibria. In the third section we show the occurence of Hopf bifurcation in the kinetic system as well as in the parabolic system.

2 The Model

The model proposed by Annie Lemarchand and Bogdan Nowakowski (cf. [8]), which describes vertebrae formation is governed by

$$\displaystyle \begin{aligned} \left. \begin{array}{lll} \partial_tA & = & d_A\Delta_{\mathbf{r}}A+f_A(A,B),\\\\ \partial_tB & = & d_B\Delta_{\mathbf{r}}B+f_B(A,B) \end{array} \right\} \end{aligned} $$
(1)

on \(\overline {\Omega }\times \mathbb {R}_0^+\) where Ω is a bounded, connected spatial domain with piecewise smooth boundary ∂ Ω, d A, d B > 0 represent the diffusion coefficients, A(r, t) and B(r, t) are the concentrations of the species at time t ∈ [0, +∞) and place \(\mathbf {r}\in \overline {\Omega }\). The kinetic part of the model (1)

$$\displaystyle \begin{aligned} \left. \begin{array}{lllll} \dot{A} & = & f_A(A,B) & := & -\alpha A+\beta A^2B,\\\\ \dot{B} & = & f_B(A,B) & := & \gamma -\delta B-\beta A^2B \end{array} \right\} \end{aligned} $$
(2)

(α, β, γ, δ > 0) was inspired from the Schnakenberg model (cf. [9])

$$\displaystyle \begin{aligned} \dot{A}=A^2B-A,\qquad \dot{B}=-A^2B+k_{Sch} \end{aligned} $$
(3)

and the Gray-Schott model (cf. [4])

$$\displaystyle \begin{aligned} \dot{A}=-AB^2-k_{GS}^1 A+k_{GS}^2,\qquad \dot{B}=AB^2-k_{GS}^3 B-k_{GS}^4. \end{aligned} $$
(4)

We are interested in solutions \(\boldsymbol {\Phi }:\overline {\Omega } \times \mathbb {R}^+_0\rightarrow \mathbb {R}^2\) of (2) that satisfy the no-flux boundary conditions

$$\displaystyle \begin{aligned} \quad \left(\mathbf{n}\cdot\nabla_{\mathbf{r}}\right) \mathbf{S}\left(\mathbf{r},t\right)=\mathbf{0}\quad \left(\left(\mathbf{r},t\right)\in\partial \Omega\times\mathbb{R}_0^+\right), \end{aligned} $$
(5)

resp. non-negative initial conditions

$$\displaystyle \begin{aligned} \mathbf{S}\left(\mathbf{r},0\right)= {\mathbf{S}}_{0}\left(\mathbf{r}\right)\ge\mathbf{0}\quad \left(\left(\mathbf{r},t\right)\in \overline{\Omega}\times\{0\}\right) \end{aligned} $$
(6)

where S := (A, B), and n denotes the outer unit normal to ∂ Ω.

3 The Kinetic System

It was mentioned in the original paper [8] that parameters α, β, γ, δ are chosen such that the system possesses three steady states. It is easy to see that this is the case when

$$\displaystyle \begin{aligned} K:=\beta\gamma^2-4\alpha^2\delta>0 \end{aligned} $$
(7)

holds. In this case the kinetic system (2) exhibits three equilibria in the first quadrant of the phase space, namely one on the boundary: E b := (0, γ∕δ) and two interior equilibria (cf. Fig. 1.): E ± := (A ∓, B ±) where

$$\displaystyle \begin{aligned}A_\pm:=\frac{\beta\gamma\pm\sqrt{\beta K}}{2\alpha\beta}\qquad \mathrm{and}\qquad B_\pm:=\frac{\alpha}{\delta}\cdot A_\pm. \end{aligned}$$
Fig. 1
figure 1

A phase portrait of system (2) for K < 0, resp. K > 0

Full size image

In what follows we study the stability of possible equilibria \(\overline {\mathbf {S}}:=(\overline {S}_1,\overline {S}_2)\) of the kinetic system (2) and the possibility of Hopf bifurcations. The coefficient matrix of the system linearized at \(\overline {\mathbf {S}}\) is

$$\displaystyle \begin{aligned}\mathfrak{A}:=J_{(f_A,f_B)}(\overline{S}_1,\overline{S}_2)=\left[\begin{array}{cc} -\alpha+2\beta \overline{S}_1\overline{S}_2 & \beta \overline{S}_1^2 \\ -2\beta \overline{S}_1\overline{S}_2 & -\delta-\beta \overline{S}_1^2 \end{array} \right] \end{aligned}$$

with trace

and determinant

$$\displaystyle \begin{aligned}\det(J_{(f_A,f_B)}(\overline{S}_1,\overline{S}_2))=\alpha\delta+\alpha\beta \overline{S}_1^2-2\beta\delta \overline{S}_1\overline{S}_2. \end{aligned}$$

A simple linear stability analysis shows that E b is always locally asymptotically stable, because the Jacobian of system (2) at these equilibrium point takes the form

$$\displaystyle \begin{aligned}J_b:=J_{(f_A,f_B)}(0,\gamma/\delta)=\left[\begin{array}{cc} -\alpha & 0 \\ 0 & -\delta \end{array} \right]. \end{aligned}$$

The Jacobians evaluated at E ± have the form

$$\displaystyle \begin{aligned}J_+:=J_{(f_A,f_B)}(E_+)=\left[\begin{array}{cc} \alpha & \frac{\left(\sqrt{\beta K}-\beta\gamma\right)^2}{4\alpha^2\beta}\\ -2\alpha & \frac{\gamma\left(\sqrt{\beta K}-\beta\gamma\right)}{2\alpha^2} \end{array}\right] \end{aligned}$$

and

$$\displaystyle \begin{aligned}J_-:=J_{(f_A,f_B)}(E_-)=\left[\begin{array}{cc} \alpha & \frac{\left(\sqrt{\beta K}+\beta\gamma\right)^2}{4\alpha^2\beta} \\ -2\alpha & -\frac{\gamma\left(\sqrt{\beta K}+\beta\gamma\right)}{2\alpha^2} \end{array}\right]. \end{aligned}$$

Based on the form of the characteristic polynomial

it is easy to determine the stability of the equilibrium points. It is clear that

  • the matrix J + is unstable, because

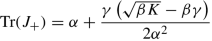
    and

    $$\displaystyle \begin{aligned}\det(J_+)=\frac{K-\gamma\sqrt{\beta K}}{2\alpha}, \end{aligned}$$

    furthermore \(\det (J_+)\) is negative due to K < βγ 2;

  • the matrix J − is stable if and only if

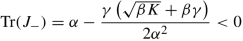
    hold, because

    $$\displaystyle \begin{aligned}\det(J_-)=\frac{K+\gamma\sqrt{\beta K}}{2\alpha}>0. \end{aligned}$$

Since the determinant of J − stays positive, then Hopf bifurcation can occur only if the trace is changing its sign. It is easy to calculate that if α > δ then if and only if

$$\displaystyle \begin{aligned}\beta=\frac{\alpha^4}{\gamma^2(\alpha-\delta)} \end{aligned}$$

holds. Thus, by fixed α, γ, δ, the parameter β will play the role of the bifurcating parameter.

Theorem 3.1

Suppose that

$$\displaystyle \begin{aligned} \alpha>\delta\qquad \mathrm{and}\qquad \alpha\neq2\delta \end{aligned} $$
(8)

hold, then at

$$\displaystyle \begin{aligned} \beta^*:=\frac{\alpha^4}{\gamma^2(\alpha-\delta)} \end{aligned} $$
(9)

the equilibrium E −(β) of (2) undergoes a Poincaré-Andronov-Hopf bifurcation: E −(β) loses its stability at β ∗ and system (2) has a branch of periodic solutions bifurcating from E −(β) near β = β ∗ (cf. Fig. 2 .).

Fig. 2
figure 2

A phase portrait of system (2) when (7), (8) and (9) hold

Full size image

Proof

The characteristic polynomial of the matrix \(\mathfrak {A}\) at E −(β) has the form

where

Clearly,

$$\displaystyle \begin{aligned}\det(\beta^*)=\alpha(\alpha-\delta)>0, \end{aligned}$$

resp. from (8)

follows, which proves the statements of the theorem (cf. [5, 7]). □

4 The Parabolic System

In what follows we consider system (1) with homogeneous Neumann boundary conditions (5) and nonnegative initial conditions (6). Clearly, a spatially constant solution Φ(⋅) = ( Φ1(⋅), Φ2(⋅)) of system (1) satisfies boundary conditions (5) and system (2). The equilibria of system (2) are constant solutions of (1), (5) at the same time. In order to investigate the local dynamical behavior of system (1) near the equilibria E b and E ± of (2) we linearize (1) at these equilibria. The linearized system at the equilibrium point

$$\displaystyle \begin{aligned}\mathbf{S}=(S_1,S_2)\in\left\{E_b,E_\pm\right\} \end{aligned}$$

with the same initial and boundary conditions has the form

$$\displaystyle \begin{aligned} \frac{\partial\mathbf{Z}}{\partial t}=D\cdot\Delta_{\mathbf{r}}\mathbf{Z}+\mathfrak{A}\mathbf{Z} \quad \mathrm{in}\quad \Omega\times\mathbb{R}_0^+ \end{aligned} $$
(10)
$$\displaystyle \begin{aligned} \left(\mathbf{n}\cdot\nabla_{\mathbf{r}}\right)\mathbf{Z}=\mathbf{0}\quad \mathrm{in} \quad \partial\Omega\times\mathbb{R}_0^+ \end{aligned} $$
(11)
$$\displaystyle \begin{aligned} \mathbf{Z}\left(\mathbf{r},0\right)={\mathbf{Z}}_0\left(\mathbf{r}\right)\quad \mathrm{on} \qquad \overline{\Omega}\times\left\{0\right\} \end{aligned} $$
(12)

where

$$\displaystyle \begin{aligned}\mathfrak{A}:=J_{(f_A,f_B)}(\mathbf{S})=:\left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]. \end{aligned}$$

Using the method of eigenfunction expansions for the spatial domain Ω the solutions of problem (10) and (11) have the form

$$\displaystyle \begin{aligned}\boldsymbol{\Psi}(\mathbf{r},t)=\sum_{n=0}^\infty\psi_n(\mathbf{r})\exp\left(\mathfrak{A}_nt\right)\boldsymbol{\Psi}_{0_n} \qquad ((\mathbf{r},t)\in\overline{\Omega}\times\mathbb{R}^+_0) \end{aligned}$$

(cf. [6]), where for \(n\in \mathbb {N}_0\)

$$\displaystyle \begin{aligned} \mathfrak{A}_n:=\mathfrak{A}-\lambda_nD,\qquad \boldsymbol{\Psi}_{0_n}:=\int_\Omega{\mathbf{Z}}_0\left(\mathbf{r}\right)\psi_n(\mathbf{r})\,\mathrm{d}\mathbf{r} \end{aligned}$$

and λ n is the nth eigenvalue of the minus Laplacian on Ω subject to homogeneous Neumann boundary conditions, resp. ψ n is the corresponding normalized eigenfunction, i.e. λ n and ψ n are solutions of

$$\displaystyle \begin{aligned}\Delta\psi=-\lambda\psi,\qquad \left.\frac{\partial\psi}{\partial\mathbf{n}}\right|{}_{\partial\Omega}=0. \end{aligned}$$

It is well known (cf. [3]) that

$$\displaystyle \begin{aligned}0=\lambda_0\leq\lambda_1\leq\lambda_2\leq\ldots\leq\lambda_n\longrightarrow+\infty\qquad (n\rightarrow\infty) \end{aligned}$$

and the eigenfunctions to different eigenvalues are orthogonal to each other.

According to [1, 2] the equilibrium S of (1), (5) is asymptotically stable if for all \(n\in \mathbb {N}_0\) the matrix \(\mathfrak {A}_n\) is stable, i.e. both eigenvalues of \(\mathfrak {A}_n\) have negative real parts; furthermore S is unstable if for some index \(n\in \mathbb {N}_0\) there exists an eigenvalue of \(\mathfrak {A}_n\) with positive real part. The characteristic polynomial of the matrix \(\mathfrak {A}_n\) have the form

$$\displaystyle \begin{aligned} \Delta_{\mathfrak{A}_n}(z):= z^2-\mathfrak{T}_nz+\mathfrak{D}_n\qquad (z\in\mathbb{C}) \end{aligned} $$
(13)

where

and

$$\displaystyle \begin{aligned}\mathfrak{D}_n:=\det(\mathfrak{A}_n)=\lambda_n^2\det(D)-\lambda_n\left(d_Aa_{22}+d_Ba_{11}\right)+\det(\mathfrak{A}). \end{aligned}$$

Thus, if S = (S 1, S 2) = E − then for all β > 0 the characteristic equation of \(\mathfrak {A}_n\) has the form

$$\displaystyle \begin{aligned}\Delta_{\mathfrak{A}_n}(z,\beta)= z^2-\mathfrak{T}_n(\beta)z+\mathfrak{D}_n(\beta)=0\qquad (z\in\mathbb{C},\;n\in\mathbb{N}_0) \end{aligned}$$

where

$$\displaystyle \begin{aligned}\mathfrak{T}_n(\beta):=\alpha-\frac{\gamma\left(\beta\gamma+\sqrt{\beta K}\right)}{2\alpha^2}-\lambda_n(d_A+d_B) \end{aligned}$$

and

$$\displaystyle \begin{aligned}\mathfrak{D}_n(\beta):=\lambda_n^2d_Ad_B+\left(\frac{d_A\gamma(\sqrt{\beta K}+\beta\gamma)}{2\alpha^2}-d_B\alpha\right)\lambda_n+ \frac{K+\gamma\sqrt{\beta K}}{2\alpha}. \end{aligned}$$

In order to have Hopf bifurcation one has to show that a pair of complex conjugate roots

$$\displaystyle \begin{aligned}\mu(\beta)\pm\imath\nu(\beta) \end{aligned}$$

crosses the imaginary axis with non-zero velocity, that is for a β ∗ > 0

$$\displaystyle \begin{aligned}\mu(\beta_*)=0,\qquad \nu(\beta_*)\neq0\qquad \mathrm{and}\qquad \mu'(\beta_*)\neq0 \end{aligned}$$

hold. This is fulfilled (cf. [5]) if exists \(n\in \mathbb {N}_0\) and β ∗ > 0 such that

$$\displaystyle \begin{aligned} \mathfrak{T}_n(\beta_*)=0,\qquad \frac{\partial}{\partial\beta}\mathfrak{T}_n(\beta_*)\neq0,\qquad \mathfrak{D}_n(\beta_*)>0 \end{aligned} $$
(14)

and

$$\displaystyle \begin{aligned} \mathfrak{T}_m(\beta_*)\neq0,\quad \mathfrak{D}_m(\beta_*)\neq0\qquad (n\neq m\in\mathbb{N}_0). \end{aligned} $$
(15)

We have to remark that β ∗ in (9) is always a Hopf bifurcation value, since

$$\displaystyle \begin{aligned}\mathfrak{T}_0(\beta^*)=0\qquad \mathrm{and}\qquad \mathfrak{T}_n(\beta^*)=-\lambda_n(d_A+d_B)<0\quad (n\in\mathbb{N}), \end{aligned}$$

resp.

$$\displaystyle \begin{aligned}\mathfrak{D}_n(\beta^*)=\lambda_n^2d_Ad_B+\alpha\left(d_A-d_B\right)\lambda_n+\alpha(\alpha-\delta)>0\qquad (n\in\mathbb{N}_0) \end{aligned}$$

if

$$\displaystyle \begin{aligned} d_A>d_B\qquad \mathrm{an}d\qquad \alpha>\delta \end{aligned} $$
(16)

hold. This corresponds to the Hopf bifurcation of spatially homogeneous periodic orbits which have been known from Theorem 3.1. Apparently β ∗ is also the unique value for β for the Hopf bifurcation of spatially homogeneous periodic orbits (cf. Fig. 3.).

Fig. 3
figure 3

Solution of system (1) when (9) and (16) hold

Full size image

In what follows, we shall search for spatially non-homogeneous Hopf bifurcation value in case of \(n\in \mathbb {N}\). For \(0\leq \beta \in \mathbb {R}\) let define

$$\displaystyle \begin{aligned}E(\beta):=\alpha-\frac{\gamma\left(\beta\gamma+\sqrt{\beta K}\right)}{2\alpha^2}= \alpha-\frac{\gamma\left(\beta\gamma+\sqrt{\beta(\beta\gamma^2-4\alpha^2\delta)}\right)}{2\alpha^2} \end{aligned}$$

then

$$\displaystyle \begin{aligned}E(0)=\alpha>0\qquad \mathrm{and}\qquad \lim\limits_{\beta\rightarrow+\infty}E(\beta)=-\infty \end{aligned}$$

and it follows from (7) that

$$\displaystyle \begin{aligned}E'(\beta)=-\frac{\gamma\left(\gamma+\frac{\beta\gamma^2-2\alpha^2\delta}{\sqrt{\beta(\beta\gamma^2-4\alpha^2\delta)}}\right)}{2\alpha^2}<0\qquad (\beta>0). \end{aligned}$$

This means that E is stricktly decreasing and in case of

$$\displaystyle \begin{aligned} \alpha>2\delta+\lambda_n(d_A+d_B) \end{aligned} $$
(17)

there is a unique solution β = β n > 0 of the equation

$$\displaystyle \begin{aligned}E(\beta)=\lambda_n(d_A+d_B),\qquad \mathrm{resp.}\qquad \mathfrak{T}_n(\beta)=0. \end{aligned}$$

Direct calculation shows that the unique positive solution has the form

$$\displaystyle \begin{aligned}\beta_n:=\frac{\alpha^2\left(\alpha-\lambda_n(d_A+d_B)\right)^2}{\gamma^2\left(\alpha-\delta-\lambda_n(d_A+d_B)\right)} \end{aligned}$$

holds.

Theorem 4.1

The transversality condition, i.e.

$$\displaystyle \begin{aligned} \mu'(\beta_n)<0\qquad (n\in\mathbb{N}_0) \end{aligned} $$
(18)

is satisfied.

Proof

It is easy to see that

$$\displaystyle \begin{aligned}\mu'(\beta_n)=\frac{1}{2}\cdot\frac{\partial}{\partial\beta}\mathfrak{T}_n(\beta_n)= \frac{1}{2}\cdot E'(\beta_n)<0\qquad (n\in\mathbb{N}_0) \end{aligned}$$

which proves the statement of the theorem. □

It is also clear that for all \(n\in \mathbb {N}\)

$$\displaystyle \begin{aligned}\mathfrak{T}_n(\beta_n)=0\qquad \mathrm{and}\qquad \mathfrak{T}_m(\beta_n)\neq0\quad (n\neq m\in\mathbb{N}) \end{aligned}$$

hold.

Next we will investigate whether

$$\displaystyle \begin{aligned}\mathfrak{D}_m(\beta_n)\neq0\qquad (m\in\mathbb{N}_0),\end{aligned}$$

and in particular, \(\mathfrak {D}_n(\beta _n)>0\). It is easy to see that

$$\displaystyle \begin{aligned}\mathfrak{D}_m(\beta_n)=\lambda_m^2d_Ad_B+\left(\frac{d_A\gamma(\sqrt{\beta_n K}+\beta_n\gamma)}{2\alpha^2}-d_B\alpha\right)\lambda_m+ \frac{K+\gamma\sqrt{\beta K}}{2\alpha}. \end{aligned}$$

Because

$$\displaystyle \begin{aligned}\frac{d_A\gamma(\sqrt{\beta_n K}+\beta_n\gamma)}{2\alpha^2}-d_B\alpha=\frac{\gamma d_A}{2\alpha^2}\cdot(E+F)-d_B\alpha \end{aligned}$$

where

$$\displaystyle \begin{aligned}E:=\frac{\alpha^2\left(\alpha-\lambda_n(d_A+d_B)\right)^2}{\gamma\left(\alpha-\delta-\lambda_n(d_A + d_B)\right)}, \end{aligned}$$

and

$$\displaystyle \begin{aligned}F:=\sqrt{\frac{\alpha^4(\alpha-\lambda_n(d_A+d_B))^2(\alpha-2\delta-\lambda_n(d_A+d_B))^2}{\gamma^2(\alpha-\delta-\lambda_n(d_A + d_B))^2}} \end{aligned}$$

we obtain the following result.

Theorem 4.2

If an \(n\in \mathbb {N}_0\) is chosen such that assumptions (17) and

$$\displaystyle \begin{aligned} d_B<d_A\cdot\frac{\alpha-\lambda_nd_A}{\alpha+\lambda_nd_A} \end{aligned} $$
(19)

hold, then in system (1) Poincaré-Andronov-Hopf bifurcation takes place: E −(β) loses its stability at β n and system (1) has a branch of periodic solutions bifurcating from E −(β) near β = β n.

Proof

Obviously, if (17) holds then

$$\displaystyle \begin{aligned}F=\frac{\alpha^2(\alpha-\lambda_n(d_A+d_B))(\alpha-2\delta-\lambda_n(d_A+d_B))}{\gamma\left(\alpha-\delta-\lambda_n(d_A + d_B)\right)}. \end{aligned}$$

Thus,

$$\displaystyle \begin{aligned}\begin{array}{lll} \displaystyle \frac{\gamma d_A}{2\alpha^2}\cdot(E+F)& = & \displaystyle d_A\cdot\left\{\frac{\left(\alpha-\lambda_n(d_A+d_B)\right)^2}{\alpha-\delta-\lambda_n(d_A + d_B)}\right.\\\\ & & \displaystyle\left.+\frac{(\alpha-\lambda_n(d_A+d_B))(\alpha-2\delta-\lambda_n(d_A+d_B))}{\alpha-\delta-\lambda_n(d_A + d_B)}\right\}\\\\ & = & \displaystyle\frac{d_A(\alpha-\lambda_n(d_A+d_B))\left[2\alpha-2\delta-2\lambda_n(d_A+d_B)\right]}{2\left(\alpha-\delta-\lambda_n(d_A + d_B)\right)}\\\\ & = & \displaystyle d_A(\alpha-\lambda_n(d_A+d_B)). \end{array} \end{aligned}$$

Hence, if condition (19) holds then

$$\displaystyle \begin{aligned}\frac{\gamma d_A}{2\alpha^2}\cdot(E+F)-d_B\alpha=-d_B(\alpha+\lambda_nd_A)+d_A(\alpha-\lambda_n d_A)>0. \end{aligned}$$

This means that \(\mathfrak {D}_m(\beta _n)>0\). This with the transversality condition (18) together proves Hopf bifurcation. □