1 Introduction

Morphogenesis is a general concept in biology including all the processes which generate shapes and cellular organizations in a living organism referring to “birth of forms”. Many models have been proposed for the morphogenesis in embryonic or adult animals (Allard et al. 2007; Bidhendi and Korhonen 2012; Bownes 1975; Brodland et al. 2010; Conte et al. 2007; Wang and Devarajan 2005; Davidson et al. 1999; Dawes-Hoang et al. 2005; Faure et al. 2007), like the gastrulation, taking into account all the factors responsible of the tissue genesis, for example those built by P. Tracqui and his coworkers (cf. obituary in Annex) and the general tendency since ten years is to offer a hybrid approach of the modelling having a discrete part (e.g., at cell proliferation, cytoskeleton organisation and genetic regulation levels) (Forest and Demongeot 2008; Forgacs and Newman 2005; Fouard et al. 2012) and a continuous part (e.g., at morphogen diffusion, enzymatic kinetics and cell migration levels) (Galle et al. 2005).

A very important stage of morphogenesis in animals is the gastrulation we will study in Sect. 2. The early embryo performs rapid cell divisions until the formation of the blastula, a geometrically simple closed elongated sphere or “pill-shaped” structure that consists of a single cell layer enclosing the hollow blastocœle (Forest and Demongeot 2008). Gastrulation includes mass movements of cells to form complex structures (e.g., tissues) from a simple initial shape (blastula). There are a number of inner cell structures that affect the cell movement and behaviour: (1) the cytoskeleton plays an important part in cellular motion and shape. It consists of three kinds of protein filaments: actin filaments, intermediate filaments and microtubules (Gumbiner 2005; Hardin and Keller 1988; Karr and Alberts 1986; Leptin 1999; Leptin and Grunewald 1990; Maniotis et al. 1997; Martin et al. 2008, 2010; Miyoshi and Takai 2008; Nesme et al. 2005; Oda and Tsukita 2000; Cui et al. 2005; Royou et al. 2004), (2) the Adherens Junctions (AJs) contain complexes of the transmembrane adhesion molecule E-cadherin and the adaptors α-catenin and ß-catenin (Galle et al. 2005; Maniotis et al. 1997). They are formed in the lateral surfaces of the cells and they offer strong links between neighbouring cells (Martin et al. 2008, 2010; Miyoshi and Takai 2008; Nesme et al. 2005), and (3) the myosin fibres are thin filaments found in the cytoskeleton of cells. They are flexible, versatile and relatively strong and they serve as tensile platforms for muscle contraction. One of the most important cell movements during gastrulation is the invagination of the ventral cells (also called primitive streak formation), which initiates the creation of the ventral furrow (Oda and Tsukita 2000; Cui et al. 2005; Royou et al. 2004; Schejter and Wieschaus 1993). The process starts after the flattening of the cells on the ventral midline (Stephanou and Tracqui 2002). The myosin of the most ventrally located cells becomes concentrated at their apical sides (Davidson et al. 1999; Karr and Alberts 1986). This excess of myosin causes the constriction of their apical surface and a simultaneous apico-basal elongation. At this point, these cells move inwards and initiate the creation of the streak. A lot of research and bibliography have been dedicated to modelling the ventral furrow invagination. A very popular organism which has served as reference for these models is the Drosophila melanogaster (Conte et al. 2007; Faure et al. 2007; Stephanou and Tracqui 2002).

The main contribution of this work focuses on the study of the relationship between the apical constriction of the ventral cells and the invagination. We will analyze in Sect. 2.1 the effect of a factor that, to our knowledge, has not yet been extensively studied: the geometry of the embryo. For this purpose, we have created two 3D biomechanical models, one for the embryo of the Drosophila melanogaster (“pill-shaped”) and one for the embryo of the Xenopus lævis (spherical), incorporating the previous mentioned factors: (1) cell elasticity due to the cytoskeleton, (2) strong bonds between cells due to AJs, and (3) contraction of the apical face due to myosin fibers. The in vivo phenomenon and the dynamic numerical simulations are compared to analyze the impact of the embryo’s geometry on the invagination process. The comparison between the Drosophila melanogaster and the Xenopus lævis models will be done in Sect. 3. providing a better understanding of this impact.

2 Gastrulation

2.1 The Embryo Geometry

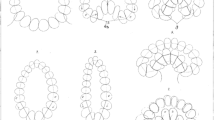
To ensure the specific shape of the Drosophila melanogaster’s embryo (Bownes 1975; Leptin 1999), we built a 3D biomechanical model composed by an elongated sphere (or “pill-shaped” mesh, symmetric along the antero-posterior and the dorso-ventral axis (cf. Fig. 1a–c), consisting of 2268 nodes forming 756 mono-layered hexahedra modelling the cells. The total length of the mesh is 460 µm and the diameter of its cross-section is 280 µm. The spherical mesh modeling the Xenopus Laevis embryo (Gumbiner 2005) consists of 904 nodes forming 450 mono-layered hexahedra (Fig. 1d). The diameter of its cross-section is 280 µm, same as the Drosophila melanogaster’s model. Each hexahedron is approximately 20 µm × 20 µm × 40 µm, resulting to an average volume of around 160 µm3. Cells on the ventral midline area of the embryo (see outlined cells in Fig. 1a) are of particular interest in the invagination process. We distinguish two sub-areas of the ventral midline: the ventral medial layer (VML) and the ventral curved extremities (VCE), as described in Fig. 1c. The equivalence between the biological and in silico cells is presented in Table 1.

Fig. 1
figure 1

The model of the Drosophila melanogaster embryo seen from an antero-ventral point of view (a). In b a cross-section of the model is presented showing the apical and basal faces of the cells. The dashed area highlights the ventral hexahedra, i.e., the hexahedra of the ventral area of the embryo submitted to an apical constriction. We distinguish two important areas in the model (c): the ventral medial layer (VML) and the ventral curved extremities (VCE). The spherical model of the Xenopus Laevis is presented in (d)

Full size image
Table 1 Cell modelling
Full size table

The behaviour of cells, defined as cellular objects in the simulation is controlled by three general principles: elasticity, contractility and incompressibility. Elasticity and contractility are considered as forces applied on each particle corresponding to each of the 4 active nodes of the apical surface of the cell hexahedron, these nodes modelling the focal points on which are exerted these elasticity and contractility forces produced by the neighbouring cells and denoted F e and F c respectively. Incompressibility is considered as a constraint that acts directly on the particles’ positions.

2.2 Cell Elasticity

The general principle is that elasticity is based on a shape memory force applied to each particle depending on its connected particles (neighbours) and on the so called rest shape attractor, i.e., a reference cell state corresponding to the cell without deformation. The particles are modelling the focal points of application of the forces produced by neighbouring cells. Each particle is defined by a position, a mass, and a list of elastic properties. Let P(t + 1) be the current position of a given particle at time t + 1 and P i (t), i ∈ {1, …, n} the positions of its n neighbouring particles at time t. The idea is to express the position P(t + 1) as a function f of the positions P i (t) and of the position P* of the particle in the rest shape attractor, with v i (t) denoting the vector P(t)P i (t). f computes the position of a particle at time (t + 1) based on the configuration of its neighbouring particles at time t and some scalars defined at rest shape, i.e., when the cell is not deformed. A single spring is used to generate an elastic force F e that brings the particle towards its position in the rest shape attractor. The model is then similar to the spring model with preload described in Wang and Devarajan (2005): for a general spring connecting the considered particle to its ith neighbour particle, let denote by P i * the preload position of the considered node on the spring i, and by U i the length of the ith spring when the mass-spring model is in its natural rest state. Consequently, the force F ei exerted by the ith neighbouring particle is a function of the current position of the particle and the position of its preload attractor:

$$ F_{ei} \left( t \right) = - \left( {P_{i}^{*} + k_{e} \left( {||v_{i} \left( t \right)|| - U_{i} } \right)v_{i} \left( t \right)/||v_{i} \left( t \right)||} \right), $$

where the Hooke’s constant k e is here defined as a simple scalar uniformly distributed along the particles.

2.3 Apical Constriction

The main characteristics of contractility taken into account in our model are: application particles, mechanical and electrical properties and, mainly, fibres generating contractility between particles. The principle used here is again a force created by an preload attractor due to the presence of a neighbouring particle located in the direction of the fibre. An internal contractile force F c is then generated by the ith fibre and given by:

$$ F_{ci} \left( t \right) = - \left( {P_{i}^{*} + k_{c} \left( {||v_{i} \left( t \right)|| - U_{i} } \right)v_{i} \left( t \right)/||v_{i} \left( t \right)||} \right), $$

where k c is the contractility coefficient. It can vary during the simulation. A positive coefficient yields to an active contraction. When k c is decreasing to zero, the contractile force is nullified and the cell returns to its original configuration, due to the elasticity property.

Each cell hexahedron can then be considered as an elastic element in a finite elements model (FEM) on which we apply the discrete Newton equation for getting the displacement of the considered particle using the balance of the forces F ei (t) and F ci (t) exerted on it (Wang and Devarajan 2005). All the cells are supposed to have the same properties and comparably equal initial volumes, regardless of their position in the structure, as well as the same elasticity constant: for the stress strain equation, we use a simple linear elasticity constitutive law with the same rather small Young modulus equal to 1000 Pa (Davidson et al. 1999). Concerning the Poisson ratio (of transverse contraction strain to longitudinal extension strain in the direction of stretching elastic force), we have chosen a conventionally used value in the bibliography of cell and soft tissue modelling close to 0.5 (Bidhendi and Korhonen 2012; Conte et al. 2007; Galle et al. 2005; Maniotis et al. 1997).

The domain of the flattened ventral zone where the invagination will occur is 70 %–80 % of the egg length (Sweeton et al. 1991). In order to simulate the apical constriction of the cells, contraction forces are generated between the nodes of the apical surface of each cell using discrete springs (Fig. 2). It should be noted that, to our knowledge, there is little experimental data regarding the value of the active forces that cells can generate at this stage of the morphogenesis. Brodland et al. (2010) aims to provide such data, but the direction of the forces in 3D is not specified. Consequently, the intensity of the contraction forces was optimized in order to conform to observed changes in shape (Oda and Tsukita 2000): it was chosen in order to induce a 30 % decrease of the apical surface of the cell located in the VML. The same value is applied to all the cells of the ventral area of the embryo (outlined row of cells in Fig. 1a) in order to ensure an equal initial distribution of forces along the antero-posterior axis of the structure.

Fig. 2
figure 2

a All the cells are modelled as easily deformable hexahedra. They are defined by 8 nodes located at the vertices of the hexahedra. For VML hexahedra, contraction forces are applied on the apical nodes (red arrows) to induce the apical constriction. The shape of the hexahedron changes, from an initial regular hexahedral shape (left) to a prismatic shape (right). b The most ventrally located cells of the model where contraction forces are added to their apical faces are highlighted (pink colour with black cross). The number of rows of hexahedra receiving this force can vary (in this case three rows are contractile representing a total area of 4 × 14 × 3 = 168 μm2). (Color figure online)

Full size image

2.4 Cell-to-Cell Bonds (AJs)

Adherens junctions (AJs) are binding neighbouring cells. They are formed in the lateral surfaces of the cells (Martin et al. 2008; Nesme et al. 2005; Sweeton et al. 1991). In our model, we have considered AJs to be located on the vertices of the cells (hexahedra) and to offer an unbreakable binding (Martin et al. 2010; Nesme et al. 2005). This is achieved by the mesh connectivity, which also allows a faster propagation of the forces during the simulation.

2.5 Incompressibility

In this section, we present the principle of the method implemented to control the volume of the cells. Consider the surface of an object in 3D represented by a mesh of triangles with n vertices. Let P 1, …, P n be the positions of these vertices in a local referential defined by the sides of the triangle, and X the vector of size 3n composed by the positions of all these vertices: X = (P 1, … , P n ) is the vector describing the state of the polyhedron. Let V(X(t)) be the volume function of the mesh at time t with V 0 the initial volume. The technique implemented is as follows: suppose a deformation of the triangular mesh represented by the vector X(t). The method implemented allows us to find a vector X(t + Δt) from X(t), whose volume is equal to V 0 (the initial volume). Consequently, what we need to do is to determine the displacement of each vertex, solving the following system:

$$ X\left( {t + \Delta t} \right) = X\left( t \right) + \lambda \nabla V\left( {X\left( t \right)} \right),\,{\text{with}}\,V\left( {X(t + \Delta t)} \right) = V_{0} , $$

where ∇V is the gradient of the volume V and λ is a scalar to be calculated (cf. Eq. 2). In the case of the Drosophila embryo, the system can be written as:

$$ X_{i} \left( {t + \Delta t} \right) = X_{i} \left( t \right) + \lambda \nabla V\left( {X_{i} \left( t \right)} \right),\forall i \in \left\{ {1, \ldots ,n} \right\},\,{\text{with}}\,\sum_{i} V(X_{i} (t + \Delta t)) = V_{0} , $$
(1)

where ∇V(X i (t)) is the gradient of the ith component of the volume function. More precisely, if we denote \( \overline{ij} (t) \) the vector between the vertices i and j at time t, then, if i 1, …, i 6 are the 6 neighbours of i, then:

$$ V\left( {X_{i} \left( t \right)} \right) = \langle X_{i} \left( t \right),A_{i} \left( t \right) \rangle,\,{\text{where}}\,A_{i} \left( t \right) = \left[ {\sum_{k = 1,6} \overline{ii}_{k} \left( t \right) \wedge \overline{ii}_{k + 1} \left( t \right)} \right]/6 $$

In a triangular mesh, it is possible to prove that: ∇V(X i (t)) = A i (t) and that the system (1) can be reduced thanks to the Newton equation to a 3rd degree equation in λ:

$$ \lambda^{3} \sum_{i} a_{i} + \lambda^{2} \sum_{i} b_{i} + \lambda \sum_{i} c_{i} + \sum_{i} d_{i} - V_{0} = \, 0. $$
(2)

The parameter λ is space and volume dependent, hence for example the V 0 variability influences the cell deformation. In further studies, this influence will be studied on the displacement ΔX i (t) = λ ∇V(X(t)) of the vertex i of the mesh applied according to the λ value equal to the unique real root of Eq. (2) (Allard et al. 2007; Bidhendi and Korhonen 2012; Dawes-Hoang et al. 2005; Forgacs and Newman 2005; Miyoshi and Takai 2008). This equation is calculated after the Newton equation resulting from the balance of the forces F ei and F ci applied at each vertex i for controlling incompressibility to avoid a too important change of cell volume.

2.6 Cell Division

The term “mesh cutting” refers to modifying an existing mesh by moving nodes to a cutting entity and modifying the connectivity of the mesh so that the original mesh fits a new geometry. “Mesh segmentation” is the process of partitioning a mesh into more visually simple and meaningful components. Generally, users cut a meaningful component from its underlying mesh by specifying which parts of the mesh belong to the “foreground” (part to be cut out) and the rest to the background. Although it is quite easy for a human to specify foreground and background by saying something like “cut out the ears from the bunny model” to another human, the computer is still a long way from the sort of cognitive object understanding required to do this work unassisted. The major issues that a mesh cutting method needs to address are: (1) definition of the cut path, (2) element removal and re-meshing, (3) number of new elements created when re-meshing is performed and (4) representation of the cutting tool (Fig. 3).

Fig. 3
figure 3

Z-slices of cell membranes revealed with Spider-GFP showing the apical constriction of ventral cells followed by invagination (Martin et al. 2010). a, b Describe the first steps of the contraction along a longitudinal line, i.e., a generator of the embryo cylinder. With the red arrows. In c, we point out that the cells located in the extremities of the embryo are the first to invaginate and as they move towards the interior of the embryo, they disappear from the image. In d, the cells closer to the centre of the embryo move towards the interior as well, showing a propagation of the invagination from the extremities to the ventral medial layer. In e, the successive ventral profiles of the mesh are showing the progressive invagination going from the extremities to the centre of the embryo. (Color figure online)

Full size image

In general, we can say that the mitotic procedure of an individual eucaryotic cell follows the following path:

  • The mother cell arrives at a dividing state (either triggered by a mitogen, i.e., a chemical substance that encourages a cell to commence mitosis, or receiving an electrical signal (Blackiston et al. 2009) or by growing over a certain level).

  • The mother cell is split into two daughter cells (for our simulation, we are going to assume that the two offsprings have the same size).

  • The two new cells are temporary linked and share a common surface.

  • The daughter cells inherit their mother’s properties.

  • The life of a cell ends with apoptosis (this aspect is of no interest for our model).

The main challenges of the hexahedral division that we had to address when dividing an hexahedral element corresponding to a cell and participating in the topology of a finite element mesh are (Fig. 4):

  • To determine the direction of the division (cut)

  • To make sure that the two new elements are well defined and placed in the topology

  • To make sure that they are close/linked to each other (share a facet or nodes of the mesh)

  • To make sure that they will “try” to acquire the same size and shape that their mother originally had (rest shape).

Fig. 4
figure 4

Instances of an individual hexahedral division in a simple 3-hexahedron mesh. a The hexahedrons in their initial state. b The points that define the position of the cut in the mesh are positioned. c The mother middle hexahedron is removed. d The two daughter hexahedrons are placed in the mesh. e Daughter hexahedrons start to inflate for acquiring the original form of their mother. f Hexahedrons have acquired the same form as their mother, signalling the end of the process

Full size image

The process of the division of a single hexahedron is shown in Fig. 4. We choose to divide the middle hexahedron in a very simple hexahedral mesh comprised of 3 hexahedrons. A linear constitutive law defines the elasticity of the mesh with a rather small Young modulus of E = 1000 Pa and a commonly used Poisson ratio close to v = 0.5. The values of the Young Modulus and the Poisson ratio are not essential in this particular example, they were chosen because we use the same values in the model of the Drosophila melanogaster embryo. The only existing forces are the elasticity forces of the finite element method; there are no external forces (gravity, superimposed forces from the user…). The direction of the division plane is vertical to the main axis of the mesh.

The comparison of the invagination process is given on Fig. 5, with (b) and without (c) cell division. Notice that the distance (green line) between the 2 nodes positioned higher than all others in the 2 meshes is smaller in (b) than in (c). Figure 6 shows an evidence of the existence of proliferation at the end of the invagination (Oda and Tsukita 2000).

Fig. 5
figure 5

a Configuration of forces for the embryo after the cell division. Daughter cells will try to expand their apical facet in order to acquire the initial parallelepiped shape of their mother. This would be done with elastic forces (green arrows) which, as a side-effect (notably due to the incompressibility), would cause the forces shown in red arrows to appear, driving ventral closure. b, c Show the result of the daughter cells expansion at the end of the process with cell division (b) and without cell division (c). (Color figure online)

Full size image
Fig. 6
figure 6

Evidence of a proliferation activity shown by using Brdu incorporation imaging (Oda and Tsukita 2000) (left) on the extremities of the ventral furrow at the end of the invagination process (right)

Full size image

2.7 Implementation

The simulation of the 3D biomechanical model of the embryo is performed by SOFA (an Open-Source Simulation Open Framework Architecture) (Allard et al. 2007; Dawes-Hoang et al. 2005) using CamiTK/MML2, an open-source framework, in order to compare and evaluate biomechanical simulations (Forgacs and Newman 2005). The hexahedral elements are implemented following the method described in Miyoshi and Takai (2008): the deformation of each element is decomposed into a rigid motion, a pure deformation, and a fast implicit dynamic integration without assembling a global stiffness matrix.

The contractile forces are generated by an explicit 3D mass-spring network linking the nodes of the apical surface of each cell of the ventral area. Each spring uses a Kelvin–Voigt material, where a spring and a damper are acting in parallel. The linear system is solved dynamically using a conjugate gradient iterative algorithm. We define a state of equilibrium for our model when all nodal displacements are lower than 0.2 µm/s (at that point the simulation stops automatically). The resulting behaviour of combined soft elasticity and apical constriction is illustrated in Fig. 7 (see also Supplementary material). Thanks to MML, a set of values are monitored during the dynamic simulation that includes displacements and surfaces, in order to extract details concerning cell behaviour and motion.

Fig. 7
figure 7

Simulation of the ventral furrow invagination process on the “pill-shaped” embryo of Drosophila melanogaster. Instances of the geometry from an antero-ventral (top) and a ventral point of view (bottom). Notice the apical constriction of the ventral hexahedra which triggers the invagination

Full size image

3 Comparison Between Drosophila melanogaster and Xenopus lævis Models

3.1 Invagination of the Drosophila melanogaster Embryo

The nodes of the apical face of the ventral hexahedra (Fig. 1b) are submitted to attractive forces of equal intensity (red arrows in Fig. 5). Figure 7 demonstrates four instances of the phenomenon from an antero-ventral and a ventral point of view. We notice that the invagination of the ventral hexahedra starts right after the initiation of their apical constriction. In addition, as they start to move inwards, they also pull the neighbouring hexahedra, thus increasing the invagination (Fig. 7). The observed total depth of the streak is 28.89 µm, consistent with in vivo studies of the phenomenon (Cui et al. 2005). Figure 8a demonstrates the comparison of the velocities of two hexahedra located at the VML and the VCE of the geometry respectively. The velocity of a hexahedron is measured by computing at each time-step of the simulation the displacement of its barycentre. Let v m be the velocity of the hexahedron in the VML and v c be the velocity of the hexahedron in the VCE. We notice that for the first 15 min the hexahedron in the VCE moves faster than the one in the VML (v c  > v m ). After 30 s, the difference between the velocities of the two hexahedra reaches its maximum value (approximately v c  = 3.65v m ). The model reaches a state of equilibrium after 15 min (Figs. 9, 10) when the stopping criterion of the simulation has been reached.

Fig. 8
figure 8

The velocities of the barycentres of two cells located at the two areas of interest in the model of the Drosophila melanogaster (a) and in the model of the Xenopus lævis (b). Notice in a the faster movement of the barycentre in the VCE (blue) in the beginning and the equalization of the velocities after approximately t = 15 min. In b, the two barycentres have almost equal velocities throughout the simulation. (Color figure online)

Full size image
Fig. 9
figure 9

Coloured cross-section of the Drosophila melanogaster model after t = 15 min. The colour scale corresponds to the intensity of the nodes displacements. (Color figure online)

Full size image
Fig. 10
figure 10

Series of coloured top views of the Drosophila melanogaster model after t = 5, 10, 15, 20 min. The colour scale corresponds to the intensity of the nodes displacements. Cells that move the most intensely at the beginning are the cells located at the ends of the embryo. Then the invagination spreads throughout the blastula like in the experiments of the Fig. 3. (Color figure online)

Full size image

3.2 Invagination of the Xenopus laevis Embryo

Figure 11 demonstrates four instances of the simulation from an antero-ventral and a ventral point of view. The observed total depth of the streak is 27.44 µm. Figure 8b demonstrates the comparison of the velocities of two cells, one located at the middle of the ventral midline (corresponding to the VML) and one located at the curved part (corresponding to the VCE). The velocities of the two barycentres are almost equal throughout the simulation, which means that the formation of the inner streak happens simultaneously along the spherical geometry. After 30 s, the difference of the velocities of the two hexahedra reaches its maximum value (approximately v c  = 1.23 v m ).

Fig. 11
figure 11

Simulation of the invagination process on the spherical embryo Xenopus laevis. Instances of the geometry from an antero-ventral (top) and a ventral point of view (bottom)

Full size image

3.3 External Constraints

The environment of the embryo is mainly composed by the vitelline layer (VL), the chorion and the yolk, that impact the cell movements. We model VL as a rigid external shell that surrounds the embryo and blocks outwards trajectories of the elements. In an other work (Conte et al. 2007), the yolk is modelled as a fluid which hinders the invagination, but there is not sufficient scientific data concerning its effect on the process. Thus, the yolk is not taken into account in our model.

4 Discussion

In Martin et al. (2010), the in vivo monitoring of the invagination in the Drosophila melanogaster shows that the area where the apical constriction starts and the area where the invagination starts differ (Fig. 3). In fact, the actin-myosin contractions occur first in the ventral medial layer (VML), while the invagination starts from the ventral curved extremities (VCE) and then propagates to the VML. So the question remains: ‘What makes the invagination start from the curved extremities?’ In this work, we attempt to answer this question from a mechanical point of view only. First, we assume that the diffusion of myosin along the ventral area is so fast that all the cells start to constrict simultaneously. Nevertheless, we have shown that a centre node in the VCE displaces faster than a centre node in the VML (Fig. 8). The node displacements of the embryo after t = 15 s of simulation are represented by a colour scale in Figs. 9 and 10. The difference between the VCE and the VML is clearly visible: the displacement of the nodes in the VCE are in the (13–17) µm range while the displacements of the nodes in the VML are in the (7–10) µm range. We can conclude that despite the uniform initial distribution of forces along the ventral area of the model, the invagination is non-uniform following the process suggested in Martin et al. (2010).

In order to explain this observation, we need to take into consideration the geometry of the embryo. The asymmetry of the geometry in the VCE creates an imbalance of forces directed inwards generating an inward displacement of the node. The contracting forces applied on a node located at the VML do not generate any imbalance and therefore no displacement. The first nodes to move inwards are the nodes in the VCE. Their inward displacement later pulls the neighbouring cell nodes, causing the invagination to propagate towards the VML. This is confirmed by the simulation of the Xenopus laevis embryo where the formation of the inner streak is happening almost simultaneously along the spherical geometry (Fig. 8b).

Finally, the proliferation provides a way, experimentally proved, to complete the process of invagination. Figure 5 shows the existence of a force (represented by red arrows) exerted by the cells located on both sides of the gastrulation streak, reducing its diameter (Fig. 5b) if the proliferation takes place at bottom of the streak, with respect to the observed diameter in the absence of mitosis (Fig. 5c). Consideration should be given to a repeat of the proliferation to the upper border of the streak (as suggested by the experimental data in Fig. 6) so that these borders sufficiently closed permit the establishment of intercellular gap junctions corresponding to the closure of the gastric tube (Tepass and Hartenstein 1994). A non mechanical effect may also play a role, such as the genetic control of growth of filipodia leading to cell contacts at the top of the tube in formation (Mammoto and Ingber 2010), adhesive interactions between these filopodia causing the appearence of tethers ensuring the dorsal closure (Millard and Martin 2008).

The model is interesting in that it postulates a minima only the mechanical stress (mainly related to the elasticity and contractility of the concerned cells) to account for the early stages of formation of the streak during the gastrulation. Its shortcomings come from the insufficient consideration of the cell proliferation process and of the growth mechanisms of filipodia closing the roof of the gastric streak. Future work is undertaken from this perspective, taking into account the recent experimental works on the genetic control of the cytoskeleton of cells involved during gastrulation (Gjorevski and Nelson 2010; Navis and Bagnat 2015).

5 Conclusion

The ventral furrow invagination propagates from the ventral curved extremities to the ventral medial layer (cf. Fig. 11; Martin et al. 2010). The comparison of the simulations of the invagination process in the embryos of the Drosophila melanogaster and the Xenopus lævis shows that the geometry of the embryo plays an important role. From a biomechanical point of view, we suggest that the “pill-shaped” geometry of the embryo of the Drosophila melanogaster as well as the mechanical stress exerted on this shape mainly by elastic and contractile cellular forces are responsible for the sequence experimentally observed of the invagination propagation.