Keywords

1 Introduction

Roger Penrose, Reinhard Henzel, Andrea Ghez are the laureates of the 2020 Nobel Prize in Physics. Using the general theory of relativity, Penrose theoretically predicted the gravitational collapse of massive stars, space–time singularities, and the birth of black holes [1, 2]. Genzel and Ghez discovered and described a supermassive black hole in the center of our Milky Way galaxy [3, 4]. Earlier Thorne [5] showed that a star can collapse under the influence of its own gravity: the space around it becomes curved, the star disappears and a black hole appears. It has been experimentally established, that the merger of two black holes [6], two neutron stars [7] is accompanied by the emission of gravitational waves. In [8, 9], a description of the parameters of gravitational waves, relict photons and their relations with the parameters of the Higgs boson was carried out in the framework of the Dicke superradiance model. In this case, supernonradiative states of gravitational fields are possible [10, 11]. However, the mechanisms of transitions from black holes with light masses (of the order of \(29 - 32\;M_{s}\) [6, 7], where \(M_{s}\) is the mass of the Sun) to supermassive (of the order of \(4 - 5 \times 10^{6} \;M_{s}\) [3, 4]) and relativistic (of the order \(10^{11} \;M_{s}\)) black holes have not yet been described. The creation of such theoretical models requires taking into account stochastic processes, the mass distribution functions of black holes in the Universe, the effect of ordering operators and the presence of qubit states [12, 13] for binary black holes and neutron stars. It also becomes necessary to describe the ejections of matter (relativistic jets) from a supermassive black hole [14]. The use of experimental methods with high angular resolution [15] makes it possible to study the nature of the Higgs field by the example of the behavior of solar active regions (coronal holes). The parameters of active objects are determined by the connections with the Higgs boson and with the different nature of the Higgs field. In [16], experimental evidence was obtained for the decay of the Higgs boson into a lepton pair and a photon, which indicates to the presence of an asymmetry of matter and antimatter [16, 17]. Experimentally in [18] the processes of formation and decay of tetraquarks were investigated. The authors believe that the structure of the new tetraquark contains charmed diquark and antidiquark, which are coupled by gluon interaction. In [19], a target made of gaseous deuterium was irradiated with a proton beam and the cross section for reactions with the formation of a helium isotope was measured. The authors estimated the baryon density for the early Universe during the process of primordial nucleosynthesis. However, the contributions of nonzero rest mass antineutrinos to Higgs fields have not been described.

The aim of this work is to describe the parameters of black holes, relativistic jets, active microobjects, their connections with the Higgs boson and the Higgs field of various nature (taking into account antineutrinos with nonzero rest mass) within the framework of a number of fractal cosmology models.

2 Models for Describing Black Hole Masses

In [8, 9] the Dicke superradiance model was used to describe gravitational waves and relict photons from binary black holes and neutron stars. For the ratio of the radiation intensities (maximum \(I_{m}\) to initial \(I(0)\)) was obtained

$$ \begin{aligned} & I_{m} /I(0) = (a_{0} + a_{m} )(a_{0} - a_{m} + 1);\quad a_{0}^{2} = a_{m}^{2} + z^{\prime}_{\mu } (z^{\prime}_{\mu } + 2)/4; \\ & a_{m}^{2} = z^{\prime}_{A2} ;\quad N_{ra} = z^{\prime}_{A2} + z^{\prime}_{\mu } . \\ \end{aligned} $$
(1)

Here \(z^{\prime}_{A2} = 1034.109294\) and \(z^{\prime}_{\mu } = 7.18418108\) are the usual and cosmological redshifts; the number of relic photons \(N_{ra} = 1041.293475\); intensity ratio \(I_{m} /I(0) = 81.06580421\). Supernonradiative states (of which the radiation intensity is equal to zero) were considered within the framework of the models \({\text{A}}_{0}\), \({\text{A}}_{1}\) [8, 9]. In the model \({\text{A}}_{0}\), the characteristic value of the number of bosons in the equilibrium state \(N_{0A} = 3.557716045 \times 10^{5}\) was obtained. This made it possible to determine the characteristic energy \(E_{0A} = N_{0A} E_{G} = 4.311073329\;{\text{eV}}\), where the rest energy of the graviton \(E_{G} = 12.11753067\;\upmu {\text{eV}}\). In the model \({\text{A}}_{1}\), a characteristic distribution density function \(n^{\prime}_{zg} = 0.114317037\) is obtained, where \(n^{\prime}_{zg} + |n_{zg} | = 1\) for Fermi-type particles. This function allows us to determine the characteristic frequencies \(\nu^{\prime}_{zg}\), \(\nu_{zg}^{ * }\), \(\nu_{D0}\)

$$ \begin{aligned} & \nu^{\prime}_{zg} = n^{\prime}_{zg} \nu_{G0} ;\quad \nu_{zg}^{ * } = \nu^{\prime}_{zg} /\psi_{01} ; \\ & \psi_{01} = \varepsilon_{01} /E_{H0} ;\quad \nu_{G0} = N_{0A} \cdot \nu_{D0} . \\ \end{aligned} $$
(2)

Here \(E_{H0} = 125.03238\,{\text{GeV}}\) and \(\varepsilon_{01} = 126.9414849\,{\text{GeV}}\) are Higgs boson energies obtained without and taking into account the Higgs field; frequency \(\nu_{G0} = 2.9304515\;{\text{GHz}}\), \(\psi_{01} = 1.015268884\) [8, 9]. Based on (2), we find the numerical values \(\nu^{\prime}_{zg} = 335.0005326\,{\text{MHz}}\), \(\nu_{zg}^{ * } = 329.9623754\,{\text{MHz}}\), \(\nu_{D0} = 8.236889799\;{\text{kHz}}\). Our calculated frequency \(\nu_{zg}^{ * }\) practically coincides with the frequency of 330 MHz, at which dark matter dominates from observations of radio filaments [20].

Model \({\mathbf{B}}_{{\mathbf{0}}}\). Black holes with light masses \(M_{bh}\) are described on the basis of spectra for occupation numbers \(n_{Ax} = n_{A0} S^{\prime}_{0x}\) and \(n_{Ax}^{ * } = n_{A0} S_{xu}\) (\(x = 1,2,3,4\); spectral parameters \(S^{\prime}_{0x}\) and \(S_{xu}\) are determined in [8, 9]) within the framework of the anisotropic model, where the main parameter \(n_{A0} = 58.04663887\) is determined based on the expressions

$$ \begin{aligned} & n_{A0} = (z^{\prime}_{\mu \lambda } )^{2} - 1 = (z^{\prime}_{\mu } + 3/2)(z^{\prime}_{\mu } - 1/2);\quad z^{\prime}_{\mu \lambda } = z^{\prime}_{\mu } + 1/2; \\ & 1/z^{\prime}_{\mu \lambda } = \sin \varphi^{\prime}_{\mu \lambda } ;\quad n^{\prime}_{A0} = (z^{\prime}_{\mu \lambda } )^{2} ;\quad n^{\prime}_{A0} - n_{A0} = 1; \\ & \varphi^{\prime}_{\mu \lambda } = \varphi_{a} Q_{H2} ;\quad (n_{h1} + n_{h2} ) - 2n_{A4} = n_{{{\kern 1pt} G}} . \\ \end{aligned} $$
(3)

Using the example of binary black holes in [8, 9] and expressions (3), the quanta number of the second black hole \(n_{h2} = M_{h2} /M_{s} = n_{A0} /2 = 29.02331944\), the first black hole \(n_{h1} = M_{h1} {\kern 1pt} /M_{s} = 35.98093926\) before their merger was obtained. After the merger, a black hole is formed with a number of quanta \(2n_{A4} = M_{bh} /M_{s} = 62.0042587\) and a number of quanta \(n_{G} = 1/Q_{H2} = 3\) are carried away by gravitational waves. In the general case, the number of quanta \(n_{A0}\), \(n_{G}\) and the cosmological redshift \(z^{\prime}_{\mu }\) determine the number of quanta of the gluon field \(n_{g} = 2n_{G} /[z^{\prime}_{\mu } (z^{\prime}_{\mu } + 1) - n_{A0} ]\). At \(n_{G} = 3\), constant parameters \(z^{\prime}_{\mu }\) from (1), \(n_{A0}\) from (3) we obtain \(n_{g} = 8\). If \(n_{G}\), \(z^{\prime}_{\mu }\), \(n_{A0}\) are variables, then the number of quanta of the gluon field \(n_{g}\) becomes a function of these three arguments, that is typical for bulk fractal structures of the Universe.

Model \({\mathbf{B}}_{1}\). To estimate the masses of supermassive black holes, we write down the basic relations for the energies

$$ \begin{aligned} & E_{H0} /E_{G} = \nu_{H0}^{ * } /\nu_{G0} = N_{HG} ;\quad E_{G} /\nu_{G0} = E_{H0} /\nu_{H0}^{ * } = 2\pi \hbar ; \\ & E_{H0} /E_{0A} = N_{0n} ;\quad E_{H0} /\varepsilon_{0n} = N_{0n}^{ * } ;\quad N_{0n}^{ * } = (1 + n^{\prime}_{zg} )N_{0n} . \\ \end{aligned} $$
(4)

Here \(\hbar\) is Planck's constant. Taking into account (4), we find the parameters \(N_{HG} = 1.031830522 \times 10^{16}\), \(N_{0n} = 2.900261036 \times 10^{10}\), \(N_{0n}^{ * } = 3.231810284 \times 10^{10}\), energy \(\varepsilon_{0n} = 3.86880321\,{\text{eV}}\). The parameter \(N_{HG}^{{}}\) is a function of the main parameters \(N_{ra}\), \(N_{0A}\), \(N_{0n}\)

$$ \begin{aligned} & N_{HG} = N_{ra} N_{c\nu } = N_{0A} N_{0n} = N_{D\nu } n_{ra} = N_{ra} N_{0A} n_{ra} ; \\ & N_{c\nu } = N_{0A} n_{ra} ;\quad N_{0n} = N_{ra} n_{ra} ;\quad N_{D\nu }^{{}} = N_{ra} N_{0A} , \\ \end{aligned} $$
(5)

where parameters \(n_{ra} = 2.785248449 \times 10^{7}\), \(N_{D\nu } = 3.704626502 \times 10^{8}\), \(N_{c\nu } = 9.909123093 \times 10^{12}\) are additional. For bulk fractal structures of the Universe, the main and additional parameters from (5) can be operators. In the general case, these operators do not commute; when describing light and supermassive black holes, the appearance of stochastic properties is possible. We introduce the distribution density functions in the ground \(f_{ra}\) and excited \(f^{\prime}_{ra}\) states for relic photons

$$ \begin{aligned} & f^{\prime}_{ra} - f_{ra} = 1;\quad f^{\prime}_{ra} = \left\langle {\hat{c}_{ra} \;\hat{c}_{ra}^{ + } } \right\rangle = N_{ra} /(N_{ra} - z^{\prime}_{\mu } ); \\ & f_{ra} = \left\langle {\hat{c}_{ra}^{ + } \;\hat{c}_{ra} } \right\rangle = z^{\prime}_{\mu } /(N_{ra} - z^{\prime}_{\mu } ) \\ \end{aligned} $$
(6)

where \(\hat{c}_{ra}^{ + } ,\,\,\hat{c}_{ra} {\kern 1pt}\) are creation and annihilation operators of relic photons; 〈… 〉 is averaging symbol. Based on (6), (1), we find the numerical values \(f_{ra} = 0.006947216\), \(f^{\prime}_{ra} = 1.006947216\). Expressions (1)–(6) make it possible to estimate the masses \(M_{0B}\), \(M_{b0}\), \(M^{\prime}_{b0}\) black holes by the formulas

$$ \begin{aligned} & M_{0B} = f^{\prime}_{ra} M_{b0} ;\quad M_{b0} /M_{s} = n_{g} (1 + n^{\prime}_{zg} )n_{ra} /n_{A0} ; \\ & M^{\prime}_{b0} = M_{0B} - M_{b0} = f_{ra} M_{b0} . \\ \end{aligned} $$
(7)

The numerical values are equal: \(M_{0B} /M_{s} = 4.307173111 \times 10^{6}\), \(M_{b0} /M_{s} = 4.277456693 \times 10^{6}\), \(M^{\prime}_{b0} /M_{s} = 0.029716418 \times 10^{6}\). Our estimate of the mass \(M_{0B} /M_{s}\) practically coincides with the mass of the central body \(4.31 \times 10^{6}\) of a supermassive black hole in the center of the Milky Way galaxy [3, 4]. The value \(2M^{\prime}_{b0} /M_{s} = 0.059432836 \times 10^{6}\) determines the error \(0.06 \times 10^{6}\), associated with the error in measuring the parameters of the orbit of the S2 star, rotating around the central body [3, 4].

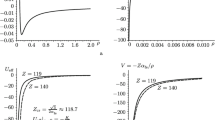
Model \({\mathbf{B}}_{2}\). The fractal structure of the Universe is characterized by the distribution of masses of black holes, which are found in the center of various galaxies. So for a supermassive black hole in the core of the galaxy M87, using the Event Horizon Telescope [21, 22], a shadow image in the radio range was obtained. Using four Chandra X-ray observations [14] for the MAXI J1820 + 070 binary black hole relativistic jets were detected. To estimate the upper mass limit \(M_{J0} = N_{0A} M_{b0}\), we will represent the central body of a supermassive black hole as a Bose condensate of black holes with masses \(M_{b0}\). In this case, for the parameter \(N_{0A} {\kern 1pt} = \psi_{1A} N_{GE}^{ * }\), representation is acceptable, where \(\psi_{1A}^{2} = 1 + \Omega_{m}^{ * }\), \(N_{GE}^{ * } = M_{s} /M_{E} = R_{Gs} /R_{GE}\). Here \(M_{E}\) is mass of the Earth; \(R_{Gs}\) and \(R_{GE}\) are Schwarzschild gravitational radii of the Sun and Earth; \(N_{GE}^{ * } = 3.32958 \times 10^{5}\). In this model, the density of matter near supermassive black holes \(\Omega_{m}^{ * } = 0.141730642\) is close to our calculated value \(\Omega_{m} = 0.141145722\) from [23, 24] and the value of 0.141 obtained by the Planck observatory, based on the new Hubble constant \(H_{0}^{ * }\) for the attenuation of γ-rays against the intergalactic background. As a result, we find \(M_{J0} /M_{s} = 15.21797631 \times 10^{11}\). For experimentally search of supermassive black holes near the upper mass boundary, brightness distributions, changes in stellar radiation intensity when photographing galaxies with high resolution, adaptive optical spectroscopy to compensate for fluctuations in the atmosphere, and speckle spectroscopy are used [4]. For the maximum radiation intensity \(I_{m}\) from (1) near the upper mass boundary, the representation is acceptable

$$ \begin{aligned} & I_{m} = I_{1}^{ * } + I_{2}^{ * } ;\quad I_{1}^{ * } = n^{\prime}_{zg} I_{m} = {\text{v}}_{1J}^{2} I_{m} \sin^{2} (\theta_{W}^{ * } ); \\ & I_{2}^{ * } = n_{zg} I_{m} = ({\text{u}}_{1J}^{2} + {\text{v}}_{1J}^{2} cos^{2} (\theta_{W}^{ * } ))I_{m} ; \\ & {\text{v}}_{1J}^{2} = k_{1J}^{2} = 0.5(1 - I(0)/I_{m} );\quad {\text{u}}_{1J}^{2} = (k^{\prime}_{1J} )^{2} = 0.5(1 + I(0)/I_{m} ); \\ & {\text{u}}_{1J}^{2} + {\text{v}}_{1J}^{2} = 1;\quad I_{1}^{ * } /I_{m} = k_{1J}^{2} {\text{sn}}^{2} (u_{1W} ;k_{1J} ) = n^{\prime}_{zg} ;\quad I_{2}^{ * } /I_{m} = {\text{dn}}^{2} (u_{1W} ;k_{1J} ) = n_{zg} \\ \end{aligned} $$
(8)

Here \(k_{1J}\), \(k^{\prime}_{1J}\) and \(u_{1W}\) are modulli and effective displacement for elliptic functions \({\text{sn}}(u_{1W} ;k_{1J} )\), \({\text{cn}}(u_{1W} ;k_{1J} )\), \({\text{dn}}(u_{1W} ;k_{1J} )\); the angle \(\theta_{W}^{ * }\) acts as the effective Cabibo angle for supermassive black holes; parameters \({\text{u}}_{1J}\), \({\text{v}}_{1J}\) depend on the initial and maximum radiation intensity and are analogous to the N. N. Bogolyubov's transformation parameters in the theory of superconductivity. Numerical values are equal: \(k_{1J}^{2} = 0.493832171\), \((k^{\prime}_{1J} )^{2} = 0.506167829\), \(\sin^{2} (\theta_{W}^{ * } ) = 0.231489651\), \(\cos^{2} (\theta_{W}^{ * } ) = 0.768510349\), intensity distribution density functions \(f_{J1} = I_{1}^{ * } /I_{2}^{ * } = 0.129072187\), \(f^{\prime}_{J1} = I_{m} /I_{2}^{ * } = 1.129072187\). Expressions (8) allow us to estimate the masses of black holes \(M^{\prime}_{J1}\), \(M_{J1}\) near the upper mass boundary by the formulas

$$ M^{\prime}_{J1} - M_{J1} = M_{J0} ;\quad M^{\prime}_{J1} = f^{\prime}_{J1} M_{J0} ;\quad M_{J1} = f_{J1} M_{J0} ;\quad f^{\prime}_{J1} - f_{J1} = 1 $$
(9)

Based on (9), we obtain a numerical value \(M_{J1} /M_{s} = 1.964217483 \times 10^{11}\), that is close to the experimental value \(1.96 \times 10^{11} M_{s}\) for the supermassive black hole SDSS J140821.67 + 025,733.2. For intermediate masses of black holes, the maximum radiation intensity \(I_{m}^{ * }\) can change over a segment \(I(0) \le I_{m}^{ * } \le I_{m}\). These changes are described by a variable number of quanta \(n_{m}^{ * }\) and an inversion parameter \(B_{Jm}\)

$$ \begin{aligned} & n_{m}^{ * } = I_{m}^{ * } /I_{m} = {\text{u}}_{1J}^{2} + {\text{v}}_{1J}^{2} B_{Jm} ;\quad B_{1}^{ * } = B_{Jm} (n^{\prime}_{zg} ) = - {\text{u}}_{1J}^{2} /{\text{v}}_{1J}^{2} + \sin^{2} (\theta_{W}^{ * } ); \\ & - 1 \le B_{Jm} \le 1;\quad B_{2}^{ * } = B_{Jm} (n_{zg} ) = \cos^{2} (\theta_{W}^{ * } );\quad n_{1J} = {\text{v}}_{1J}^{2} + n^{\prime}_{zg} ; \\ & n^{\prime}_{1J} = {\text{u}}_{1J}^{2} - n^{\prime}_{zg} ;\quad n_{1J} + n^{\prime}_{zg} = 1. \\ \end{aligned} $$
(10)

From (10) it follows, that a black hole with an intermediate mass can be in different states, which are determined by a pair of parameters \(n_{m}^{ * }\) and \(B_{Jm}\). Let's introduce these states: ground \(J1\) (\(n_{m}^{ * } = 1\), \(B_{Jm} = 1\)), supernonradiative \(J2\) (\(n_{m}^{ * } = {\text{u}}_{1J}^{2}\), \(B_{Jm} = 0\)), fully inverse state \(J3\)(\(n_{m}^{ * } = {\text{u}}_{1J}^{2} - {\text{v}}_{1J}^{2}\), \(B_{Jm} = - 1\)), partially inverse state \(J4\) (\(n_{m}^{ * } = n^{\prime}_{zg}\), \(B_{Jm} = B_{1}^{ * }\)), deviated from the ground \(J5\) (\(n_{m}^{ * } = n_{zg}\), \(B_{Jm} = B_{2}^{ * }\)). The parameters \(B_{1}^{ * } = - 0.793489803\), \(1 + B_{1}^{ * } = 0.206510197\), \(B_{2}^{ * }\), \(n_{1J} = 0.391850792\), \(n^{\prime}_{1J} = 0.608149208\) carry information about the characteristic parameters (velocities, energies) of a relativistic jet (ejection of matter from a supermassive black hole) [14].

3 Relativistic Jets

To describe the parameters of a relativistic jet, we will use the basic model equations

$$ Q_{H2} R_{AB} /2R_{AH} = n^{\prime}_{F} + 0.5;\quad \Omega_{0\nu } = (n^{\prime}_{F} )^{2} ;\quad \Omega_{\tau L} E_{W0} = \Omega_{\tau L}^{ * } E_{Z0} . $$
(11)

Here the parameter \(Q_{H2} = 1/3\) is determined by the expression from (3) and is related to the angles \(\varphi^{\prime}_{\mu \lambda }\), \(\varphi_{a} = 22.43261135^{ \circ }\), cosmological redshift \(z^{\prime}_{\mu }\) from our anisotropic model [8] of the expanding Universe; the number of quanta \(n^{\prime}_{F} = 0.054219932\) determines the Fermi level and the neutrino density \(\Omega_{0\nu } = 0.002939801\); the lepton quantum number \(\Omega_{\tau L} = 0.002402187\) is related to the quantum number \(\Omega_{\tau L}^{ * } = 0.002116741\) through the rest energies \(E_{W0} = 80.35235464\;{\text{GeV}}\) and \(E_{Z0} = 91.188\;{\text{GeV}}\) for \(W0\) and \(Z0\) bosons, respectively; Hubble radius \(R_{AH} = 13.75 \times 10^{9} \cdot L_{c0}\). From (11) we find the characteristic radius (horizon of matter particles) \(R_{AB} = 45.72314437 \times 10^{9} \cdot L_{c0}\). Note, that parameters are: \(L_{c0} = {\text{light year}} = c_{0} \tau_{c0} = {\kern 1pt} N_{c0} L_{ES} = 0.306597989\,{\text{pc}}\); limiting speed of light in vacuum \(c_{0} = 2.99792458 \times 10^{5} \;{\text{km}}\;{\text{s}}^{ - 1}\), \(N_{c0} = 6.324043414 \times 10^{4}\), \(\tau_{c0} = 365.2503353\,{\text{day}} = {3}{\text{.155762897}} \times {10}^{7} \;{\text{s}}\), \(L_{ES} = 1{\text{au = 1}}{.495995288} \times 10^{8} \;{\text{km}}\). Based on (11), we introduce the refractive index \(n_{AB}\) of the medium of matter particles

$$ n_{AB} = Q_{AB}^{2} ;\quad Q_{AB} = R_{AB} /R_{AH} = 2(n^{\prime}_{F} + 0.5)/Q_{H2} . $$
(12)

Numerical values are \(n_{AB} = 11.05775038\); \(Q_{AB} = 3.325319591\). Next, we find the particle velocities \(\upsilon_{AH}\), \(\upsilon_{0\xi }\), \(\upsilon_{AW}\) and velocities ratios \(\xi_{AH}\), \(\xi_{0J}\), \(\xi_{AW}\)

$$ \upsilon_{AH}^{2} = c_{0}^{2} /n_{AB} ;\quad \upsilon_{AH} S_{1u}^{2} = \upsilon_{0\xi } S_{2u}^{2} = \upsilon_{AW} ;\quad \xi_{AH} = \upsilon_{AH} \;c_{0} ;\quad \xi_{0J} = \upsilon_{0\xi } /c_{0} . $$
(13)

Values are: \(\upsilon_{AH} = 9.015447983 \times 10^{4} \;{\text{km}}\;{\text{s}}^{ - 1}\), \(\upsilon_{0\xi } = 1.803089597 \times 10^{5} {\text{km}}\;{\text{s}}^{ - 1}\), \(\upsilon_{AW} = 196.9672387\;{\text{km}}\;{\text{s}}^{ - 1}\); \(\xi_{AH} = 0.300722975\), \(\xi_{0J} = 0.60144595\), \(\xi_{AW} = \upsilon_{AW} /c_{0} = 657.0119876 \times 10^{ - 6}\).

From our model \({\mathbf{B}}_{2}\) it follows, that the density of matter near supermassive black holes \(\Omega_{m}^{ * } > \Omega_{m}\). This leads to a change in the refractive index of the medium \(n_{AB}\), the radius \(R_{AB}\) from (12), the neutrino density \(\Omega_{0\nu }\) from (11), and the particle velocities from (13). Accounting for these changes near supermassive black holes is described by new parameters

$$ \begin{aligned} & \overline{n}_{AB} = \overline{Q}_{AB}^{2} ;\quad \overline{Q}_{AB} = \overline{R}_{AB} /R_{AH} = 2(\overline{n}_{0\nu } + 0.5)/Q_{H2} ; \\ & \overline{\Omega }_{0\nu } = (\overline{n}_{0\nu } )^{2} ;\quad 2\overline{n}_{0\nu } = \Omega_{m}^{ * } - S_{2u} ;\quad \overline{\upsilon }_{AH} = c_{0} /\overline{Q}_{AB} ; \\ & \overline{\upsilon }_{AH} S_{1u}^{2} = \overline{\upsilon }_{0\xi } S_{2u}^{2} = \overline{\upsilon }_{AW} . \\ \end{aligned} $$
(14)

Numerical values are equal: medium refractive index \(\overline{n}_{AB} = 11.06252927\), radius \(\overline{R}_{AB} = 45.73302352 \times 10^{9} \cdot L_{c0}\), parameters \(\overline{Q}_{AB} = 3.326038074\), \(\overline{n}_{0\nu } = 0.054339679\), density of the relativistic neutrino \(\overline{\Omega }_{0\nu } = 0.002952801\); velocities \(\overline{\upsilon }_{AH} = 9.013500487 \times 10^{4} \;{\text{km}}\;{\text{s}}^{ - 1}\), \(\overline{\upsilon }_{0\xi } = 1.802700097 \times 10^{5} \;{\text{km}}\;{\text{s}}^{ - 1}\), \(\overline{\upsilon }_{AW} = 196.9246903\;{\text{km}}\;{\text{s}}^{ - 1}\); velocities ratios \(\overline{\xi }_{AH} = 1/\overline{Q}_{AB} = 0.300658013\), \(\overline{\xi }_{0J} = 2\overline{\xi }_{AH} = 0.601316027\), \(\overline{\xi }_{AW} = \overline{\upsilon }_{AW} /c_{0} = 656.8700603 \times 10^{ - 6}\).

Further, taking into account (1), (2), (8), we find the energies of the jet particles \(E_{0J}\) and \(E_{1J}\), \(E_{2J}\) in the absence and presence of the Higgs field, respectively, by the formulas

$$ E_{0J} /E_{H0} = I_{m} /I(0) = I_{1}^{ * } /I(0) + I_{2}^{ * } /I(0);\quad E_{1J} = \psi_{01} E_{0J} ;\quad E_{2J} = \psi_{02} E_{0J} . $$
(15)

Numerical values of energies are equal \(E_{0J} = 10.13585044\,{\text{TeV}}\), \(E_{1J} = 10.29061357\;{\text{TeV}}\), \(E_{2J} = 9.978687329\;{\text{TeV}}\), where \(\psi_{02} = 0.984494334\).

The effective Cabibo angle \(\theta_{W}^{ * }\) allows us to estimate the angular width \(\varphi_{W}^{ * }\) of the jet based on the angular parameters \(\varphi_{n0}\), \(\varphi_{En}\), \(\varphi_{E0}\) by the formulas

$$ \varphi_{W}^{ * } = \varphi_{n0} /\sin^{2} (\theta_{W}^{ * } );\quad \varphi_{n0} = 2n_{G} \,\varphi_{En} /n_{g} ;\quad \varphi_{En} = m_{n} \,\varphi_{E0} /m_{p} (1 + S_{1u} ), $$
(16)

where the parameters \(n_{G} ,\,\,n_{g}\) are determined in the model \({\mathbf{B}}_{0}\) by expressions (3);\(m_{n} /m_{p} = 1.008985047\) is the ratio of the neutron mass (\(m_{n}\)) to the proton mass (\(m_{p}\)). Based on (16), we find estimates of the angular parameters \(\varphi_{W}^{ * } = 2.592779092^{\prime\prime}\), \(\varphi_{n0} = 0.600201527^{\prime\prime}\), \(\varphi_{En} = 0.800268702^{\prime\prime}\), where the parameter \(\varphi_{E0} = 0.830215001^{\prime\prime}\) describes the behavior of photons near supermassive bodies in Einstein's theory [5]. The obtained estimates of the parameters \(\xi_{0J}\), \(E_{0J}\), \(\varphi_{W}^{ * }\) do not contradict the experimental data [14] for a velocity ratio of 0.6, an energy of 10TeV, and an angular width \(2.5928^{\prime\prime}\) of jet particles. Based on the effective radii \(R_{AB}\) from (12), \(\overline{R}_{AB}\) from (14), we obtain estimates of the distance \(R_{0}\) from the Sun to the supermassive black hole in the center of our Milky Way galaxy and the errors \(\delta R_{0}\) by the formulas

$$ \begin{aligned} & R_{0} = \overline{\delta }_{AB} /n_{R0} ;\quad \delta R_{0} = \overline{\delta }_{AB} /N_{R0} ;\quad \overline{\delta }_{AB} = (1 + \delta_{Q} )\delta_{AB} ; \\ & \delta_{AB} = \overline{R}_{AB} - R_{AB} ;\quad N_{R0} = n_{g} (N_{ra} + 0.5I_{m} /I(0)); \\ & n_{R0} = Q_{H2} (N_{ra} + n_{A0} - n_{g} - \overline{\xi }_{0J} ). \\ \end{aligned} $$
(17)

The numerical values of the parameters are equal: \(N_{R0} = 8654.611017\), \(n_{R0} = 363.5795993\), \(\delta_{AB} = 9.87915 \times 10^{6} \cdot L_{c0}\), \(\overline{\delta }_{AB} = 9.879150543 \times 10^{6} \cdot L_{c0}\). Based on (17), we find estimates of the distance \(R_{0} = 8.330851608\;{\text{kpc}}\) and error \(\delta R_{0} = 0.349978489\;{\text{kpc}}\).

Based on the distribution density function \(f^{\prime}_{J1}\) from (9), the number of quanta \(\overline{n}_{0\nu }\) from (14), we find the radius \(r_{JB}\) of the central body by the formulas

$$ \begin{aligned} & N_{G0} \;r_{JB} = \delta^{\prime}_{JB} + l_{AB} ;\quad \delta^{\prime}_{JB} = \overline{\delta }_{AB} \;f^{\prime}_{J1} ;\quad l_{AB} = \overline{\delta }_{AB} \sin (\theta_{0\nu } ); \\ & N_{G0} = N_{a} /N_{HG} ;\quad N_{G0} E_{H0} = N_{a} E_{G} ;\quad \sin (\theta_{0\nu } ) = \overline{n}_{0\nu } (1 - \overline{n}_{0\nu } ) = \overline{n}_{0\nu } - \overline{\Omega }_{0\nu } . \\ \end{aligned} $$
(18)

Values of the parameters are equal: \(N_{G0} = 5.839561703 \times 10^{7}\), \(\theta_{0\nu } = 2.945548561^{ \circ }\), \(\sin (\theta_{0\nu } ) = 0.051386878\), \(l_{AB} = 5.076587037 \times 10^{5} \cdot L_{c0}\), \(\delta^{\prime}_{JB} = 11.15427411 \times 10^{6} \cdot L_{c0}\). From (18) we obtain \(r_{JB} = 0.199705618 \cdot L_{c0} = 1.262947001 \times 10^{4} {\text{au}}\).

Next, we find estimates for the semi-axes \(x_{0S}\), \(y_{0S}\) the elliptical orbit of the star S2, rotating around the central body by the formulas

$$ \begin{aligned} & y_{0S} = r_{JB} /\overline{n}_{AB} (1 + \Omega_{m}^{ * } );\quad x_{0S}^{2} /y_{0S}^{2} = S_{1u}^{2} \sin (\varphi_{0g} )/S_{2u}^{2} ; \\ & \sin^{2} (\varphi_{0g} ) = (n_{A0} - n_{g} )(E_{e} + E_{eh} )/E_{0g} ;\quad E_{0g} = n_{g} E_{H0} . \\ \end{aligned} $$
(19)

Here the rest energies of the gluon \(E_{0g} = 1.00025904\;{\text{TeV}}\), electron \(E_{e}\) and electron hole \(E_{eh}\) are assumed to be equal \(E_{e} = E_{eh} = 0.51099907\;{\text{MeV}}\); \(\sin (\varphi_{0g} ) = 0.007150827\), the angle of polarization of the radiation \(\varphi_{0g} = 0.409715696^{ \circ }\); semi-axes \(y_{0S} = 999.9241011\;{\text{au}}\), \(x_{0S} = 119.5804463\;{\text{au}}\). Our estimates of the parameters \(R_{0}\), \(\delta R_{0}\), \(r_{JB}\), \(x_{0S}\), \(y_{0S}\) agree with the experimental data [3, 4] for the distance \(8.33\,{\text{kpc}}\) from the Sun to the supermassive black hole in the center of the Milky Way galaxy, the error \(0.35\,{\text{kpc}}\), the radius of the central body \(0.2 \cdot L_{c0}\), for the semi-axes \(120\,{\text{au}}\), \(1000\,{\text{au}}\) the elliptical orbit of the S2 star, rotating around the central body, respectively.

4 Asymmetry of Matter, Antimatter and the Higgs Field

The presence of a Higgs field of various nature (gluon, lepton, neutrino, hadronic based on the parameter \(\Omega_{\tau L}^{ * }\) from (11), gravitational, etc.) leads to changes in the rest energy of the Higgs boson \(E_{H0}\) in (18); energies of holes (antiparticles) \(E_{eh}\) in (19), \(E_{\mu h}\), \(E_{\tau h}\) for \(e\), \(\mu\), \(\tau\)-leptons, respectively; the appearance of asymmetry of matter and antimatter. We introduce the energy \(E_{0L}\) based on the total energy \(\varepsilon_{0L}\) of paired leptons, the number of quanta of gluons \(n_{g}\)

$$ E_{0L} = n_{g} \varepsilon_{0L} ;\quad \varepsilon_{0L} = (E_{e} + E_{eh} ) + (E_{\mu } + E_{\mu h} ) + (E_{\tau } + E_{\tau h} ). $$
(20)

Here \(E_{\mu } = E_{\mu h} = 105.658389\;{\text{MeV}}\), \(E_{\tau } = E_{\tau h} = 1777.00\;{\text{MeV}}\) are rest energies for \(\mu\), \(\tau\)-leptons, respectively. From (20) we find the energies \(\varepsilon_{0L} = 3.766338776\;{\text{GeV}}\), \(E_{0L} = 30.13071021\;{\text{GeV}}\) (close to the data from [16]).

Next, we introduce the distribution density functions of the Bose type \(f_{gA}\) (ground state), \(f^{\prime}_{gA}\) (excited state) based on the number of quanta of black holes (\(n_{A0}\)), gluons (\(n_{g}\)). Based on \(E_{H0}\) we find the energy \(E_{gA}\), \(E^{\prime}_{gA}\)

$$ \begin{aligned} & f^{\prime}_{gA} - f_{gA} = 1;\quad f_{gA} = n_{g} /(n_{A0} - n_{g} );\quad f^{\prime}_{gA} = n_{A0} /(n_{A0} - n_{g} ); \\ & E_{gA} = E_{H0} \,f_{gA} /2;\quad E^{\prime}_{gA} = E_{H0} f^{\prime}_{gA} /2;\quad E^{\prime}_{gA} - E_{gA} = E_{H0} /2. \\ \end{aligned} $$
(21)

The numerical values are equal: \(f_{gA} = 0.159850895\), \(E_{gA} = 9.993268924\,{\text{GeV}}\), \(E^{\prime}_{gA} = 72.50945893\,{\text{GeV}}\). Taking into account the energy \(E_{gA}\) from (21), the expressions for the rest energies of leptons have the form

$$ E_{e} = E_{gA} \sin^{2} (\varphi_{eg} );\quad E_{\mu } = E_{gA} \sin^{2} (\varphi_{\mu g} );\quad E_{\tau } = E_{gA} \sin^{2} (\varphi_{\tau g} ). $$
(22)

Here angles are equal: \(\varphi_{eg} = \varphi_{0g}\), \(\varphi_{\mu g} = 5.901862921^{ \circ } ,\) \(\varphi_{\tau g} = 24.94112323^{ \circ } .\) To describe the interaction of \(\mu\) and \(e\)-leptons, we find the energies \(E^{\prime}_{\mu }\), \(E_{\mu }^{ * }\) from the expressions

$$ \begin{aligned} & E^{\prime}_{\mu } = E_{gA} \sin^{2} (\varphi_{\mu g} + \varphi_{eg} ) = (E_{\mu }^{2} + 4\Delta_{\mu }^{2} )^{1/2} ;\quad 2\Delta_{\mu } = n_{A0} E_{ex} ; \\ & E_{ex} = E_{e} + E^{\prime}_{h} ;\quad E_{\mu }^{ * } = E_{gA} \sin^{2} (\varphi_{\mu g} - \varphi_{eg} ) = (E_{\mu }^{2} - 4(\Delta_{\mu }^{ * } )^{2} )^{1/2} ; \\ & 2\Delta_{\mu }^{ * } = n_{A0} E_{ex}^{ * } ;\quad E_{ex}^{ * } = E_{e} + E_{h}^{ * } ;\quad E_{e} /E_{ex} = 0.5 + \sin (\varphi_{ex} ); \\ & E^{\prime}_{h} /E_{ex} = 0.5 - \sin (\varphi_{ex} );\quad E_{e} /E_{ex}^{ * } = 0.5 + \sin (\varphi_{ex}^{ * } ). \\ \end{aligned} $$
(23)

For variant I (sum of angles), the parameter values are:\(\varphi_{\mu g} + \varphi_{eg} = 6.311578617^{ \circ }\), \(E^{\prime}_{\mu } = 120.7760733\,{\text{MeV}}\), \(E^{\prime}_{\mu } - E_{\mu } = 15.11768432\,{\text{MeV}}\), energy gap \(\Delta_{\mu } = 29.25390878\;{\text{MeV}}\), energy \(E_{ex} = 1.007944968\;{\text{MeV}}\), hole energy \(E^{\prime}_{h} = 0.496945898\;{\text{MeV}}\), \(\sin (\varphi_{ex} ) = 0.0069712\), characteristic angle \(\varphi_{ex} = \,0.399423573^{ \circ }\). For variant II (angle difference), the parameter values are: \(\varphi_{\mu g} - \varphi_{eg} = 5.492147225^{ \circ }\), \(E_{\mu }^{ * } = 91.54109182\;{\text{MeV}}\), energy gap \(\Delta_{\mu }^{ * } = 26.38145028\;{\text{MeV}}\), energy \(E_{ex}^{ * } = 0.908974259\,{\text{MeV}}\), hole energy \(E_{h}^{ * } = 0.397975189\;{\text{MeV}}\), \(\sin (\varphi_{ex}^{ * } ) = 0.062171112\), characteristic angle \(\varphi_{ex}^{ * } = 3.564441086^{ \circ }\), \(E_{h}^{ * } /E_{ex}^{ * } = \,0.5 - \sin (\varphi_{ex}^{ * } )\). Note, that the values of the angle differences \((\varphi_{eg} - \varphi_{ex} )/2 = 18.52582072^{\prime\prime},\) \((\varphi_{eg} - \varphi_{ex} )/4 = 9.26291036^{\prime\prime}\) are characteristic of the angular widths of coronal holes on the Sun [15]. From (23) we find expressions easy for analyzing the asymmetry of individual contributions from \(E_{e}\), \(E_{\mu }\), different angles, in energy \(E^{\prime}_{\mu }\), \(E_{\mu }^{ * }\) in the form

$$ \begin{aligned} & (E^{\prime}_{\mu } + E_{\mu }^{ * } )/2 = E_{e} \cos^{2} (\varphi_{\mu g} ) + E_{\mu } \cos^{2} (\varphi_{eg} ); \\ & E^{\prime}_{\mu } - E_{\mu }^{ * } = E_{gA} \sin (2\varphi_{\mu g} )\sin (2\varphi_{eg} ). \\ \end{aligned} $$
(24)

Based on the energy \(E_{0L}\) from (20) we found characteristic energies \(\varepsilon_{dL}\), \(\varepsilon_{d0}\), \(\varepsilon^{\prime}_{dz}\) and the Higgs boson energies \(E_{Hd}\), \(E^{\prime}_{Hd}\), \(E_{Hg}\), \(E^{\prime}_{Hg}\), \(E_{HL}\), \(E^{\prime}_{HL}\)

$$ \begin{aligned} & E_{0L} = n_{g} \varepsilon_{0L} = n_{G} \varepsilon_{dL} ;\quad \varepsilon_{d0} = n_{A0} \varepsilon_{dL} ;\quad \varepsilon^{\prime}_{dz} = z^{\prime}_{\mu } (z^{\prime}_{\mu } + 1)\varepsilon_{dL} ; \\ & \varepsilon^{\prime}_{dz} = \varepsilon_{d0} + 2\varepsilon_{0L} ;\quad E_{Hd}^{2} = E_{H0}^{2} + \varepsilon_{dL}^{2} ;\quad (E^{\prime}_{Hd} )^{2} = E_{H0}^{2} - \varepsilon_{dL}^{2} ; \\ & E_{Hg}^{2} = E_{H0}^{2} + E_{gA}^{2} ;\quad (E^{\prime}_{Hg} )^{2} = E_{H0}^{2} - E_{gA}^{2} ; \\ & E_{HL}^{2} = E_{H0}^{2} + \varepsilon_{0L}^{2} ;\quad (E^{\prime}_{HL} )^{2} = E_{H0}^{2} - \varepsilon_{0L}^{2} . \\ \end{aligned} $$
(25)

Characteristic energies are \(\varepsilon_{dL} = 10.04357007\,{\text{GeV}}\) (close to the energy for dark matter from [20]), \(\varepsilon_{d0} = 582.9954848\;{\text{GeV}}\), \(\varepsilon^{\prime}_{dz} = 590.5281624\;{\text{GeV}}\). Energies \(\varepsilon_{dL}\), \(E_{gA}\), \(\varepsilon_{0L}\) describe the different nature of the Higgs field. The presence of the Higgs field leads to the appearance of active particles with energies \(E_{Hd} = 125.4351201\;{\text{GeV}}\), \(E^{\prime}_{Hd} = 124.6283385\;{\text{GeV}}\), \(E_{Hg} = 125.4311025\;{\text{GeV}}\), \(E^{\prime}_{Hg} = 124.6323819\;{\text{GeV}}\), \(E_{HL} = 125.0890937\;{\text{GeV}}\) (corresponds to the peak for the Higgs boson decay process from [16]), \(E^{\prime}_{HL} = 124.9756406\;{\text{GeV}}\). Energy differences \(\delta E_{Hg} = E_{Hd} - E_{Hg} = 4.0176\;{\text{MeV}}\), \(\delta E^{\prime}_{Hg} = E^{\prime}_{Hg} - E^{\prime}_{Hd} = 4.04343\,{\text{MeV}}\) describe the line width in the energy spectrum for the Higgs boson [16].

5 Active Microobjects

Based on the energies \(\varepsilon_{dL}\), \(E_{gA}\), \(\varepsilon_{0L}\) from (25) we find the radii \(R_{dL}\), \(R_{gA}\), \(R_{0L}\) of active microobjects associated with the different nature of the Higgs field

$$ \begin{aligned} & R_{dL} = A_{G} \,\varepsilon_{dL} ;\quad R_{gA} = A_{G} E_{gA} ;\quad R_{GL} = n_{G} R_{dL} = n_{g} R_{0L} ; \\ & R^{\prime}_{dz} = z^{\prime}_{\mu } (z^{\prime}_{\mu } + 1)R_{dL} ;\quad R_{d0} = n_{A0} R_{dL} ;\quad R^{\prime}_{dz} - R_{d0} = 2R_{0L} . \\ \end{aligned} $$
(26)

Here \(A_{G} = 0.960836162\;{\text{fm}}(eV)^{ - 1}\) is the constant from [23, 24]. The gravitational radii are: \(R_{dL} = 9.6502253\,{\mu m}\), \(R_{gA} = \,9.6018942\,{\mu m}\), \(R_{0L} = 3.6188345\,{\mu m}\). For characteristic radii we obtain: \(R_{d0} = 560.1631441\,{\mu m}\) (coupled to the number of quanta of the black hole \(n_{A0}\)); \(R^{\prime}_{dz} = 567.4008131\,{\mu m}\) (coupled to cosmological redshift \(z^{\prime}_{\mu }\)); \(R_{GL} = \,28.95067596\,{\mu m}\) (coupled with the number of quanta of the gravitational field in an excited state \(n_{G}\), or with the number of quanta of the gluon field \(n_{g}\)). Next, we find the characteristic lengths \(l_{d0}\), \(l^{\prime}_{dz}\), \(l_{0L}\) of active objects

$$ \begin{aligned} & l_{d0} /R_{d0} = l^{\prime}_{dz} /R^{\prime}_{dz} = l_{0L} /2R_{0L} = E_{\alpha u} /E_{H0} = S_{12u} ; \\ & S_{12u} = S_{1u} - S_{2u} ;\quad E_{\alpha u} - E_{\alpha S} = E_{c} ; \\ & E_{\alpha S} = S_{012} E_{H0} = \xi_{gS} E_{0g} ;\quad S_{012} = S^{\prime}_{01} - S^{\prime}_{02} ;\quad \xi_{gS} = S_{012} /n_{g} . \\ \end{aligned} $$
(27)

Here the parameters are: \(S_{12u} = 0.013690291\), \(S_{012} = 0.005451282\), \(\xi_{gS} = \,0.00068141\); the rest energy \(E_{c} = 1.030142904\,{\text{GeV}}\), c-quark gravitational radius \(R_{c} = A_{G} E_{c} = 0.989798554\,{\mu m}\); energy \(E_{\alpha S} = 0.681586763\,{\text{GeV}}\) is determined either through the rest energy of the Higgs boson, or through the energy of the gluon, energy \(E_{\alpha u} = 1.711729667\;{\text{GeV}}\); gravitational radii \(R_{\alpha S} = A_{G} E_{\alpha S} = 654.8932091\,{\text{nm}}\), \(R_{\alpha u} = A_{G} E_{\alpha u} = 1.644691763\;{\mu m}\). From (27) we obtain values of characteristic lengths \(l_{d0} = 7.6687965\,{\mu m}\), \(l^{\prime}_{dz} = 7.7678822\,{\mu m}\), \(l_{0L} = 99.085795\,{\text{nm}}\). From (27) it follows that it is possible to describe particles and antiparticles, compound particles (hadrons), which are experimentally observed at the LHC [16], on the basis of energies \(E_{\alpha u}\), \(E_{\alpha S}\), \(E_{c}\). As an example, consider the possibility of describing the energies \(E_{TQ}\), \(E^{\prime}_{TQ}\) of a tetraquark, a hadron by

$$ \begin{aligned} & E_{TQ} = 2E_{c} + 2\overline{E}_{c} ;\quad \overline{E}_{c} = E_{c} + E_{\alpha S} + \Delta_{\mu }^{ * } = E_{c} + \xi_{gS} E_{0g} + \Delta_{\mu }^{ * } = E_{\alpha u} + \Delta_{\mu }^{ * } ; \\ & E_{TQ} - E^{\prime}_{TQ} = 2(E_{\mu } + E^{\prime}_{\mu } );\quad E_{T1} = E_{TQ} - 2E^{\prime}_{\mu } - \Delta_{\mu };\\ & E_{T2} = E_{TQ} - 2E_{\mu }^{ * } + \Delta_{\mu }^{ * } . \\ \end{aligned} $$
(28)

Here \(\overline{E}_{c} = 1.738111117\;{\text{GeV}}\), \(E_{\mu } + E^{\prime}_{\mu } = 226.4344623\;{\text{MeV}}\) are the c-antiquark, muon pair energies, respectively. Energies \(E_{T1} = 6628.875515\;{\text{MeV}}\), \(E_{T2} = 6742.980837\,{\text{MeV}}\) determine the features of the type of local maximum, minimum on the experimental dependence of the number of events on the state of the tetraquark [18]. The base narrow peak corresponds to the tetraquark energy \(E_{TQ} = 6899.681571\;{\text{MeV}}\), and the broadened peak corresponds to the hadron energy \(E^{\prime}_{TQ} = 6446.812646\;{\text{MeV}}\). Note, that the energy difference \(E_{c} - E_{\mu }^{ * } = 938.6018122\;{\text{MeV}}\) (for the c-quark and antimuon) is close to the sum of the energies \(E_{p} + E_{e} = 938.7833217\;{\text{MeV}}\) (for the proton and the electron). This indicates us to the need and possibility of describing additional contributions from the neutrinos, hadron Higgs fields to the energies of active objects.

The classical decay of a neutron into a pair of proton-electron and antineutrino is described by the expressions

$$ \begin{aligned} & E_{n} = (E_{p} + E_{e} ) + n_{ra} \;\varepsilon_{\nu n} ;\quad \varepsilon_{\nu n} = (\varepsilon_{HG}^{2} + \Delta_{\nu n}^{2} )^{1/2} ;\quad \Delta_{\nu n}^{2} = z_{\nu n} (z_{\nu n} + 2)\varepsilon_{HG}^{2} ; \\ & \varepsilon_{\nu n} = \varepsilon_{HG} + z_{\nu n} \;\varepsilon_{HG} = \psi_{\nu n} \,\varepsilon_{HG} ;\quad \psi_{\nu n} = 1 + z_{\nu n} . \\ \end{aligned} $$
(29)

Here the rest energies are for neutrino \(\varepsilon_{HG} = 280.0460475\,{\text{MeV}}\) [23, 24], neutron \(E_{n} = 946.7027435\,{\text{MeV}}\), proton \(E_{p} = 938.2723226\,{\text{MeV}}\). From (29) we find the antineutrino energy \(\varepsilon_{\nu n} = 284.3344848\,{\text{meV}}\), energy gap \(\Delta_{\nu n} = 49.1966514\,{\text{meV}}\), parameters of the neutrino field \(z_{\nu n} = 0.015313329\), \(\psi_{\nu n} = 1.015313329\).

We take into account the contribution from the hadronic Higgs field by replacing the energy of the pair \((E_{p} + E_{e} )\) in (29) with the energy of the difference \(E_{c} - E_{\mu }^{ * }\) for the c-quark and antimuon. In this case, the antineutrino energy \(\varepsilon_{\nu n}\) is replaced by the renormalized antineutrino energy \(\overline{\varepsilon }_{\nu n}\) and is determined from the expressions

$$ \begin{aligned} & E_{n} = (E_{c} - E_{\mu }^{ * } ) + n_{ra} \overline{\varepsilon }_{\nu n} ;\quad \overline{\varepsilon }_{\nu n} = (\varepsilon_{HG}^{2} + \overline{\Delta }_{\nu n}^{2} )^{1/2} ;\quad \overline{\Delta }_{\nu n}^{2} = \overline{z}_{\nu n} (\overline{z}_{\nu n} + 2)\varepsilon_{HG}^{2} \\ & \overline{\varepsilon }_{\nu n} = \varepsilon_{HG} + \overline{z}_{\nu n} \,\varepsilon_{HG} = \overline{\psi }_{\nu n} \,\varepsilon_{HG} ;\quad \overline{\psi }_{\nu n} = 1 + \overline{z}_{\nu n} = \psi_{\nu n}^{ * } + 0.5\;n_{\nu n}; \\ &n_{\nu n}^{2} = \Omega_{\tau L}^{ * }\; \overline{\varepsilon }_{\nu n} = \varepsilon_{h\,\nu } + \varepsilon_{\nu n}^{ * } ;\quad \varepsilon_{h\nu } = 0.5n_{\nu n} \,\varepsilon_{HG} ;\\ & \varepsilon_{\nu n}^{ * } = (\varepsilon_{HG}^{2} + (\Delta_{\nu n}^{ * } )^{2} )^{1/2} = \psi_{\nu n}^{ * } \,\varepsilon_{HG} . \\ \end{aligned} $$
(30)

Here, the parameter \(n_{\nu n} = 0.046008054\) from (11) describes the contribution from the hadron Higgs field to the energy \(\varepsilon_{h\,\nu } = 6.442186838\;{\text{meV}}{.}\) Based on (30), we find the renormalized antineutrino energy \(\overline{\varepsilon }_{\nu n} = 290.8512992\;{\text{meV}}\), energy gap \(\overline{\Delta }_{\nu n} = 78.54100538\,{\text{meV}}\), parameters \(\overline{z}_{\nu n} = 0.038583839\), \(\overline{\psi }_{\nu n} = 1.038583839\). The energy \(\varepsilon_{\nu n}^{ * } = 284.4091123\,{\text{meV}}\), energy gap \(\Delta_{\nu n}^{ * } = 49.62614656\;{\text{meV}}\), field parameters \(z_{\nu n}^{ * } = \overline{z}_{\nu n} - 0.5n_{\nu n} = 0.015579812\), \(\psi_{\nu n}^{ * } = 1 + z_{\nu n}^{ * }\) describe a different state of the antineutrino, compared to the state from (29).

Taking into account (29), we find the baryon densities of the Universe \(\Omega_{b1}\) (ground state of matter), \(\Omega_{b2}\) (hole state of matter) from the expressions

$$ \Omega_{b1} = (0.5 - z_{\nu n} )\;n_{\nu n} ;\quad \Omega_{b2} = (0.5 + z_{\nu n} )n_{\nu n} ;\quad \Omega_{b1} + \Omega_{b2} = n_{\nu n} . $$
(31)

Numerical values are equal: \(\Omega_{b1} = 0.022299491\), \(\Omega_{b2} = 0.023708563\). At the same time \(\Omega_{b1} < \Omega_{b2}\), that confirms the presence of two states of baryonic matter due to the presence of the Higgs antineutrino field \(z_{\nu n}\). Replacing in (31) \(z_{\nu n}\) by \(z_{\nu n}^{ * }\) from (30) leads to other values of the baryon density \(\Omega_{b1}^{ * } = 0.02228723\), \(\Omega_{b2}^{ * } = 0.023720824\). Hence it follows, that the baryon density of the Universe depends on the states of the antineutrino field. On the other hand, within the framework of our anisotropic model (taking into account the polarization of the CMB), the base parameter \(n_{\nu n}\) can be independently determined from

$$ \begin{aligned} & n_{\nu n} = |\chi_{ef} |\sin(\varphi_{0g} ) + \psi_{rc} + 2\Omega_{0G} ; \\ & \Omega_{b1} = 0.5n_{\nu n} - 2n_{\tau L} \sin (\varphi_{0g} );\quad n_{\tau L}^{2} = \Omega_{\tau L} . \\ \end{aligned} $$
(32)

Here \(|\chi_{ef} | = 0.2504252\), \(\psi_{rc} = 0.04420725\), \(\Omega_{0G} = 4.99501253 \times 10^{ - 6}\) from [23, 24]. The values \(\Omega_{b1}\) from (32) and (31) coincide and agree with the baryon density of the Universe 0.0223 from the experimental data [19]. Note, that expressions (31) allow us to describe the inverse (at \(z_{\nu n} < 0\)) states, states with shifts \(\Omega^{\prime}_{b1}\), \(\Omega^{\prime}_{b2}\) or \(\overline{\Omega }_{b1}\), \(\overline{\Omega }_{b2}\) of the baryon density of the Universe

$$ \begin{aligned} & \Omega^{\prime}_{b1} = \Omega_{b1} - \Omega_{\tau L}^{ * } ;\quad \Omega^{\prime}_{b2} = \Omega_{b2} + \Omega_{\tau L}^{ * } ; \\ & \overline{\Omega }_{b1} = \Omega_{b1} + \Omega_{\tau L}^{ * } ;\quad \overline{\Omega }_{b2} = \Omega_{b2} - \Omega_{\tau L}^{ * } . \\ \end{aligned} $$
(33)

due to the presence of a contribution from \(\Omega_{\tau L}^{ * }\) while preserving the quantum number \(n_{\nu n}\). Numerical values are equal: \(\Omega^{\prime}_{b1} = 0.02018275\), \(\overline{\Omega }_{b1} = 0.024416232\). Expressions (31)–(33) can be used to describe the effective susceptibilities \(\chi_{\nu x}\) of active regions (\(x = A,B,C,D,E\)) of coronal holes on the Sun. In [15] the parameters \(N_{2x}\), \(N_{1x}\) for these regions were measured. Based on the formulas

$$ \begin{aligned} & \chi_{\nu x} = N_{2x} /N_{1x} ;\quad \chi_{bx} = \chi_{\nu x} + \Omega^{\prime}_{b1} ;\quad z_{bx} = (1 + \chi_{bx}^{2} )^{1/2} - 1 = 1 - (1 - \overline{\chi }_{bx}^{2} )^{1/2} ; \\ & \chi_{NA}^{2} = |\chi_{21} \cdot \chi_{12} | + 2\Omega_{0G} ;\quad \varepsilon_{bA} = (\varepsilon_{HG}^{2} + \Delta_{bA}^{2} )^{1/2} ;\quad \overline{\varepsilon }_{bA} = (\varepsilon_{HG}^{2} + \overline{\Delta }_{bA}^{2} )^{1/2} \\ \end{aligned} $$
(34)

estimates for each of the regions can be obtained: \(\chi_{\nu A} = 0.1721131\), \(\chi_{\nu B} = 0.1689743\), \(\chi_{\nu C} = 0.1744639\), \(\chi_{\nu D} = 0.1789925\), \(\chi_{\nu E} = 0.1608336\). From (34) independently (based on the susceptibility components \(\chi_{21}\), \(\chi_{12}\), constants \(a_{T}\), \(a_{\lambda }\) from our anisotropic model [23, 24]), we find \(\chi_{NA}\) exactly coinciding with \(\chi_{\nu A}\). For the susceptibility with a shift, we find: \(\chi_{bA} = 0.1922958\), \(z_{bA} = \,0.0183210\), \(\overline{\chi }_{bA} = \,0.1905423\). These susceptibilities determine the gaps \(\Delta_{bA} = \chi_{bA} \varepsilon_{HG} = 53.851680\;{\text{meV}}\), \(\overline{\Delta }_{bA} = \overline{\chi }_{bA} \,\varepsilon_{HG} = 53.360611\;{\text{meV}}\) (which correspond to the effective temperatures \(T_{bA} = a_{T} \Delta_{bA} = 39.489369\;^{ \circ } {\text{C}}\), \(\overline{T}_{bA} = a_{T} \overline{\Delta }_{bA} = 36.6398\;^{ \circ } {\text{C}}\)), energies \(\varepsilon_{bA} = 285.17677\,{\text{meV}}\), \(\overline{\varepsilon }_{bA} = 285.08445\,{\text{meV}}\) (which correspond to the wavelengths \(\lambda_{bA} = a_{\lambda } /2\varepsilon_{bA} = 2.1734659\,{\mu m}\), \(\overline{\lambda }_{bA} = a_{\lambda } /2\overline{\varepsilon }_{bA} = 2.1741698\,{\mu m}\)) in the spectra of neutrinos with nonzero rest mass.

These active microobjects can be part of the solar and intergalactic winds and affect to various physical, chemical, biological processes on Earth and in Universe.

6 Conclusions

The relationships between the base parameters of the Higgs boson and the parameters of black holes are established. Based on the distribution density functions of the number of quanta in the ground and excited states for relic photons, a lower mass estimate for a supermassive black hole is obtained. Based on the density distribution functions of the radiation intensity, an estimate of the mass near the upper boundary is obtained. The description of the central region of a supermassive black hole is made in terms of Bose condensate from black holes. Various states for a black hole with intermediate mass are introduced. Estimates for the mass and radius of the central body, the distance from the Sun to the supermassive black hole in the center of the Milky Way galaxy, the semi-axes of the elliptical orbit of S2 (rotating around the central body) are obtained.

The model equations are used to describe the base parameters of a relativistic jet: velocities, energy, angular width of jet particles.

It is shown, that the presence of a Higgs field of different nature leads to changes in the rest energy of the Higgs boson and the energies of holes (antiparticles) for paired leptons; the appearance of active microobjects with different energies and sizes; the appearance of asymmetry of matter and antimatter. A model for the classical decay of a neutron into a proton-electron pair and an antineutrino with a nonzero rest mass is proposed. The possibility of using this model to describe tetraquarks, the baryon density of the Universe, which depends on the states of antineutrinos, is shown.

Parameter estimates are consistent with experimental data.