Gravitational Waves, Relic Photons and Higgs Boson in a Fractal Models of the Universe

Abstract

Models for describing separate large-scale fractal structures of the Universe are proposed. The relationships between the parameters of gravitational waves, relic photons and the Higgs boson are established. Estimates of these parameters are given on examples of: merging two black holes, binary neutron stars; “Cold relict spot” (supervoid). The behavior of deformation fields on the fractal index for a number of quantum model systems with variable parameters is investigated. It is shown that the presence of nonlinear oscillations is characteristic for a fractal layer without a quantum dot. Stochastic behavior for the boundaries of the quantum dots cores is observed, an anisotropy effect is possible.

1 Introduction

The hypothesis of the presence of dark matter, dark energy in the Universe can be examined on the basis of direct gravitational effects, waves [1]. Electromagnetic radiation (photons) does not carry this direct information. For the creation of a gravitational wave detector and experimental proof of their existence, R. Weiss, K. Thorne and B. Barrish were awarded the Nobel Prize in Physics in 2017. A binary black hole merger with the energy release in the form of gravitational waves (GW) was recorded by the LIGO interferometers in Livingston and Hanford [2]. These signals represent the gravitational wave amplitude dependencies on time, and was recorded by the detectors LD (Livingston Detector) and HD (Hanford Detector). The appearance of GW from a binary neutron stars was recorded on August 17, 2017 [3]. These achievements in cosmology give impulse to the development of new theoretical models of the fractal structures of the Universe: Galaxies, superclusters of Galaxies, walls, filaments, voids [4], supervoid or the CMB Cold Spot [5], black holes, neutron stars [6]. The hypothesis of the hierarchical structure of the Universe makes it possible to use models of fractal dislocations, quantum dots with variable parameters to describe individual elements of the fractal structures of the Universe [7].

When describing various nonlinear physical models, singular points (attractors), lines, surfaces, special volumetric structures (strange attractors) arise. Many physical properties near the above features are stochastic in nature, it becomes necessary to model stochastic processes [8]. In [9,10,11,12] attractors and deformation field, mutual influence of attractors and stochastic processes in the coupled fractal multilayer nanosystems were investigated. In [11] the fractal oscillator model based on the theory of fractional calculus was proposed. In [12] transient processes in a multilayer fractal nanosystem with a nonlinear fractal oscillator were investigated. In the presence of variable parameters, features arise in the behavior of such fractal nanosystems.

The aim of the paper is to describe anisotropy, transient signals from binary objects (black holes, neutron stars); modelling of the deformation field of an individual layer in a multilayer fractal nanosystem (with variable parameters), investigation of the influence of a fractal index.

2 Anisotropic Model for Binary Black Holes

For the split energy branches $2 \varepsilon_{ 02}$, $2 \varepsilon_{ 01}$ in [7, 13, 14] there were expressions obtained, relating the rest energy of the Higgs boson $E_{H0} = 125.03238\,{\text{GeV}}$ and the order parameter for the Higgs field $\Delta^{\prime}_{ 0} = 21.93272771\,{\text{GeV}}$

$$ \begin{aligned} & \varepsilon_{02} = \left[ {E_{H0}^{2} - (\Delta^{\prime}_{0} )^{2} } \right]^{1/2} ; \varepsilon_{01} = \left[ {E_{H0}^{2} + (\Delta^{\prime}_{0} )^{2} } \right]^{1/2} ; \\ & \Delta^{\prime}_{0} = \psi^{\prime}_{0} E_{H0} ; \psi^{\prime}_{ 0} = \delta N^{\prime}_{0} / N^{\prime}_{0} ; (\xi^{\prime}_{ 0} )^{2} = N^{\prime}_{01} /N^{\prime}_{02} ; \\ & N^{\prime}_{02} = \left[ {(N^{\prime}_{0} )^{2} - (\delta N^{\prime}_{0} )^{2} } \right]^{1/2} ; N^{\prime}_{01} = \left[ {(N^{\prime}_{0} )^{2} + (\delta N^{\prime}_{0} )^{2} } \right]^{1/2} . \\ \end{aligned} $$

(1)

Parameters describing the presence of a Bose condensate taking into account the Higgs field are: $N^{\prime}_{0} = 3.7384680 \times 10^{5}$, $N^{\prime}_{01} = 3.7955502 \times 10^{5}$, $N^{\prime}_{02} = 3.6805005 \times 10^{5}$, $(\xi^{\prime}_{ 0} )^{2} = 1.031259246$, $\psi^{\prime}_{ 0} = 0.175416382$; energies $2\varepsilon_{01} = 253.8829698\,{\text{GeV}}$, $2\varepsilon_{ 02} = 246.1873393\,{\text{GeV}}$. Next, a quasi-one-dimensional lattice with two atoms in a unit cell (such as an effective atom and a Higgs boson with rest masses $m_{H}$ and $M_{H0}$) was introduced. The basic relations between parameter $\left| {\xi_{0H} } \right|^{2}$ with the rest masses $m_{H}$ and $M_{H0}$ are following

$$ \begin{aligned} & \left| {\xi_{0H} } \right|^{2} = m_{H} /M_{H0} = M_{H} /m_{H0} = E_{H} /E_{H0} = R_{H} /R_{H0} ; M_{Ha} = N_{a} M_{H} ; \\ & M^{\prime}_{H0} = N_{a} m_{H0} ; R_{H} = 2GM_{Ha} /c_{0}^{2} ; R_{H0} = 2GM^{\prime}_{H0} /c_{0}^{2} . \\ \end{aligned} $$

(2)

Here $M_{H} = N_{a} m_{H} = 24.41158758\,{\text{g}}$ and $m_{H0} = N_{a} M_{H0} = 134.2770693\,{\text{g}}$ are molar masses of the effective atom and the Higgs boson; $E_{H} = 22.73090194\,{\text{GeV}}$ is rest energy of an effective atom; $R_{H} = 21.84067257\,{{\upmu \text{m}}}$, $R_{H0} = 120.1356321\,{{\upmu \text{m}}}$ allow us the interpretation of Schwarzschild radii of black holes with masses $M_{Ha}$, $M^{\prime}_{H0}$; $G = 6.672 \times 10^{ - 8} \, {\text{cm}}^{3} \, {\text{g}}^{ - 1} \, {\text{s}}^{ - 2}$ is Newton’s gravitational constant; Avogadro number is $N_{a} = 6.025438 \times 10^{23}$; $c_{0}$ is the speed of light in a vacuum. Taking into account the value $\left| {\xi_{0H} } \right|^{2} = 0.181800122$, the main parameters of the theory $\left| {S^{\prime}_{01} } \right| = 0.039541282$, $S^{\prime}_{02} = 0.03409$, $S^{\prime}_{03} = 0.460458718$, $S^{\prime}_{04} = 0.53409$ were obtained. On the basis of energies $2 \varepsilon_{ 01}$, $2 \varepsilon_{ 02}$ from (1) and parameters $S^{\prime}_{0x} \, (x = 1,2,3,4)$ we obtain energy spectra $\varepsilon_{sx} = 2\varepsilon_{01} S^{\prime}_{0x}$, $\varepsilon^{\prime}_{sx} = 2\varepsilon_{02} S^{\prime}_{0x}$. These spectra make it possible (taking into account the Higgs field) to obtain the energy values $\varepsilon_{s3} + \varepsilon^{\prime}_{s2} = 125.2951532\,{\text{GeV}}$ and $\varepsilon_{s3} + \varepsilon^{\prime}_{s1} = 126.6371898\,{\text{GeV}}$ for the Higgs boson, which agree with the values of the energies 125.3 and 126.5 GeV, obtained at the LHC [15]. Based on the parameters $(\xi^{\prime}_{ 0} )^{2}$, $\left| {\xi_{0H} } \right|^{2}$ and the molar mass $M_{H}$, we introduce the susceptibility components

$$ \begin{aligned} & \chi_{11} = \left| {\xi_{0H} } \right|^{2} ; \chi_{21} = \chi_{02} = [(\xi^{\prime}_{ 0} )^{2} - 1]/\chi_{11} ; \chi_{31} = - \chi_{01} ;n_{F} + n^{\prime}_{F} = 1; \\ & n_{F} = M_{02} /M_{H} = \chi_{02} /\chi_{11} ; n^{\prime}_{F} = M_{01} /M_{H} = - \chi_{01} /\chi_{11} . \\ \end{aligned} $$

(3)

Taking into account (3), we find numerical values: $\chi_{11} = 0.181800122$, $\chi_{02} = 0.171942932$, $\chi_{01} = - 0.00985719$, $n_{F} = 0.945780069$, $n^{\prime}_{F} = 0.054219931$, $M_{01} = 1.323594585\,{\text{g}}$, $M_{02} = 23.087993\,{\text{g}}$.

On the basis of (3) and $E_{H0}$ we find the characteristic energies

$$ \begin{aligned} E_{1\nu } & = - \chi_{01} E_{H0} = n^{\prime}_{F} E_{H} ; E_{2\nu } = \chi_{02} E_{H0} = n_{F} E_{H} ; E_{H} = \chi_{11} E_{H0} . \\ E_{1\nu } & = M_{01} c_{0}^{2} = 1.232467935\,{\text{GeV}}; E_{2\nu } = M_{02} c_{0}^{2} = 21.49843401\,{\text{GeV}}. \\ \end{aligned} $$

(4)

Next, we introduce a row-vector $\hat{\chi }_{1} = (\chi_{11} ,\chi_{21} ,\chi_{31} )$ and a column-vector $\hat{\chi }_{1}^{ + }$. We find the effective susceptibility $| \chi_{ef} |$, molar mass $M_{ef}$ from the conditions

$$ \begin{aligned} \hat{\chi }_{1} \hat{\chi }_{1}^{ + } & = \left| { \chi_{ef} } \right|^{2} = \left| { \chi_{01} } \right|^{2} + \left| { \chi_{02} } \right|^{2} + \left| {\xi_{0H} } \right|^{4} = M_{ef}^{2} m_{H0}^{ - 2} ; \\ M_{ef}^{2} & = M_{01}^{2} + M_{02}^{2} + M_{H}^{2} . \end{aligned} $$

(5)

The numerical values are $\left| { \chi_{ef} } \right| = 0.250425279$, $M_{ef} = 33.62637256\,{\text{g}}$.

To take into account the nonlinear dependences of the effective displacements $u_{\mu } = {\text{F}}(\varphi_{\mu } ; k_{\mu } )$ (F is the incomplete elliptic integral of the first kind) on the angle $\varphi_{\mu }$, the modulus $k_{\mu }$ of elliptic functions, we use the fractal oscillator model [11, 12]. In this model, a matrix $\hat{T}_{ef}$ with elements $t_{ij}$ is introduced

$$ \begin{aligned} & t_{11} = k^{\prime}_{\mu } ; t_{12} = - k_{\mu } ; \; t_{21} = k_{\mu } {\text{cn}}(u_{\mu } ;k_{\mu } ); \; t_{22} = k^{\prime}_{\mu } {\text{cn}}(u_{\mu } ; k_{\mu } ); \\ & t_{23} = - {\text{sn}}(u_{\mu } ; k_{\mu } ); t_{13} = 0; \; t_{31} = k_{\mu } {\text{sn}}(u_{\mu } ;k_{\mu } ); \\ & t_{32} = k^{\prime}_{\mu } {\text{sn}}(u_{\mu } ;k_{\mu } ); \; t_{33} = {\text{cn}}(u_{\mu } ;k_{\mu } ); \quad i,j = 1,2,3. \end{aligned} $$

(6)

The action $\hat{T}_{ef}$ on $\left| {\chi_{ef} } \right|$ leads to a matrix $\left| {\hat{\chi }_{ef} } \right| = \hat{T}_{ef} \left| {\chi_{ef} } \right|$ with elements $\chi_{ij}$

$$ \begin{aligned} \chi_{11} & = k^{\prime}_{\mu } \left| {\chi_{ef} } \right|; \chi_{21} = k_{\mu } \left| { \chi_{ef} } \right|{\text{cn}}(u_{\mu } ;k_{\mu } ); \;\chi_{31} = k_{\mu } \left| {\chi_{ef} } \right|{\text{sn}}(u_{\mu } ;k_{\mu } ); \\ \chi_{12} & = - k_{\mu } \left| {\chi_{ef} } \right|; \;\chi_{22} = \chi_{11} \cos \varphi_{\mu } ; \; \chi_{32} = \chi_{11} \sin \varphi_{\mu } ;\chi_{23} = - \left| {\chi_{ef} } \right|\sin \varphi_{\mu } ; \\ \chi_{13} & = 0; \; \chi_{33} = \left| {\chi_{ef} } \right|\cos \varphi_{\mu } ; \; k^{\prime}_{\mu } = \chi_{11} /\left| {\chi_{ef} } \right|; \; (k^{\prime}_{\mu } )^{2} + k_{\mu }^{2} = 1. \\ \end{aligned} $$

(7)

The numerical values are $\chi_{12} = - 0.172225247$, $\chi_{22} = 0.181502111$, $\chi_{32} = 0.010405201$, $\chi_{23} = - 0.014332913$, $\chi_{33} = 0.250014775$, $k^{\prime}_{\mu } = 0.725965539$, $\sin \varphi_{\mu } = 0.057234291$. The characteristic angles $\varphi_{\mu } = 3.2810763^{ \circ }$, $\varphi_{\mu }^{ * } = \uppi / 2 + 2\varphi_{\mu }$, $\varphi^{\prime}_{\mu } = \uppi / 2 - \varphi_{\mu } = 86.7189237^{ \circ }$ can be determined from the presence of peaks in X-ray structural spectra. From (1) at $\psi^{\prime}_{ 0} = 0$ we obtain the order parameter $\Delta^{\prime}_{ 0} = 0$ and the equality of the energies $2\varepsilon_{ 02} = 2\varepsilon_{ 01} = 2E_{H0}$ of the branches of the spectrum. Then from (3) follows $(\xi^{\prime}_{ 0} )^{2} = 1$, $\chi_{21} = 0$, and from (7) we obtain the condition $k_{\mu } \left| { \chi_{ef} } \right| {\text{cn}}(u_{\mu } ;k_{\mu } ) = 0$. This condition can be fulfilled either at $k_{\mu } = 0$ or at ${\text{cn}}(u_{\mu } ;k_{\mu } ) = 0$. Then $\chi_{ij}$ will take numerical values different from those given above. If the parameter $\Delta^{\prime}_{ 0} \ne 0$, then from (7) follows the need to analyze other row-vectors $\hat{\chi }_{2} = (\chi_{12} ,\chi_{22} ,\chi_{32} )$, $\hat{\chi }_{3} = (\chi_{13} ,\chi_{23} ,\chi_{33} )$ and the column-vectors $\hat{\chi }_{2}^{ + }$, $\hat{\chi }_{3}^{ + }$ the susceptibility tensor $\hat{\chi }_{ef}$.

On the basis $Q_{H6} = 1.537746366$ from [13] and the susceptibility components $\chi_{ij}$, we write for the black hole spin tensor $\hat{n}_{hs}$ the elements in the form $n_{ij} = 2 / (2Q_{H6} - z_{ij} )$, where $z_{ij} = \chi_{ij} / 2$. For diagonal elements we find $n_{11} = 0.6701082$, $n_{22} = 0.6700747$, $n_{33} = 0.6778548$. After the binary black holes (BBH) merger in [2] the final value of the black hole spin of 0.67 and the value of the red shift $z_{s} = 0.09$ are determined. Our calculated values $n_{22}$ and $z_{22} = 0.090751056$ are close to these data. This indicates the tensor nature of the source of the black hole spin $\hat{n}_{hs}$ and redshift $z_{ij}$, which are related to the susceptibility $\chi_{ij}$. The main parameter $n_{A0}$ determines the spectrum for the occupation numbers $n_{Ax} = n_{A0} S^{\prime}_{0x}$ of black holes. The number of quanta $n_{h1} = M_{h1} / M_{s}$, $n_{h2} = M_{h2} / M_{s}$ BBH before merger, and the number of black hole quanta $2n_{A4} = M_{A4} /M_{s}$ after merger are determined through the cosmological redshift $z^{\prime}_{\mu }$, the parameter $Q_{H2}$ and $n_{A0}$ from expressions

$$ \begin{aligned} & \sin^{2} \varphi^{\prime}_{\mu \uplambda } = 2z_{Q} / (3z_{Q} + 1); \; \cos^{2} \varphi^{\prime}_{\mu \uplambda } = (z_{Q} + 1) / (3z_{Q} + 1); \; z_{Q} = 1 / (2n_{A0} - 1); \\ & n_{A0} = (z^{\prime}_{\mu \uplambda } )^{2} - 1 = (z^{\prime}_{\mu } + 3/2)(z^{\prime}_{\mu } - 1/2); \; z^{\prime}_{\mu \uplambda } = z^{\prime}_{\mu } + 1/2; \; 1/z^{\prime}_{\mu \uplambda } = \sin \varphi^{\prime}_{\mu \uplambda } ; \\ & n^{\prime}_{A0} = (z^{\prime}_{\mu \uplambda } )^{2} ; \; n^{\prime}_{A0} - n_{A0} = 1; \; z^{\prime}_{ Q} - z_{ Q} = 1; \; \varphi^{\prime}_{\mu \uplambda } = \varphi_{a} Q_{H2} . \\ \end{aligned} $$

(8)

Here $M_{h1}$, $M_{h2}$ are masses of first, second black holes before merger; $M_{A4}$ is black hole mass after merger; $M_{s}$ is mass of the Sun. Using the values of parameters $Q_{H2} = 1 / 3$, $z^{\prime}_{\mu } = 7.184181$ [13, 14], we find $\sin \varphi^{\prime}_{\mu \uplambda } = 0.130137486$, $n_{A0} = 58.04663887$. The angle $\varphi_{a} = 22.43261159^{ \circ }$ can be determined from the peak position on an amorphous substrate in the X-ray structural spectrum. Based on the spectrum $n_{Ax}$, we find the number of black hole quanta $2n_{A4} = 62.0042587$ that formed after the merger of two black holes. Number of quanta of the second black hole before merger is $n_{h2} = n_{A0} / 2 = n_{A4} - n_{A2} = n_{A3} + n_{A1} = 29.02331944$. As a result of the merger of these BBH, the number of quanta $n_{G} = 1 / Q_{H2} = 3$ is carried away by gravitational waves. The number of quanta of the first black hole before merger $n_{ h1} = 35.98093926$ we obtain from equation $(n_{h1} + n_{h2} ) - 2n_{A4} = n_{ G}$.

In [13, 14], by describing the anisotropy of the CMB, connections temperatures $T_{A} = T_{r} / N_{ra} = 2.61739852\,{\text{mK}}$, $T^{\prime}_{A} = T_{r} / z^{\prime}_{A2} = 2.635582153\,{\text{mK}}$ with the relict radiation temperature $T_{r} = 2.72548\,{\text{K}}$ were obtained, where $z^{\prime}_{A2} = 1034.109294$ is the usual redshift, $N_{ra} = z^{\prime}_{A2} + z^{\prime}_{\mu } = 1041.293475$. The temperature deviation $\delta T_{A} = T^{\prime}_{A} - T_{A} = 18.183633\,{{\upmu \text{K}}}$ agrees with the experimental average value $18\,{{\upmu \text{K}}}$ of temperature fluctuations in the relict background in the fractal model of the Universe. On the other hand, in our model the supervoid is determined by the temperature $T_{A}^{ * }$, the number of quanta $N_{ra}^{ * }$, the parameter $z_{\mu }^{ * }$

$$ T_{A}^{ * } = T_{r} / N_{ra}^{ * } ;\quad N_{ra}^{ * } = z^{\prime}_{A2} + z_{\mu }^{ * } ;\quad z_{\mu }^{ * } = 2n_{A4} + (n_{A1} - n_{A2} ). $$

(9)

The parameter $z_{\mu }^{ * } = 62.3206873$ allow us an interpretation as the effective cosmological shift at the early stages of the formation of the structure of the Universe after the Big Bang, and is related with numbers of black hole quanta $2n_{A4}$, $n_{A1}$, $n_{A2}$. Numerical values are $N_{ra}^{ * } = 1096.429981$, $T_{A}^{ * } = 2.4857766\,{\text{mK}}$. The temperature deviation $\delta T_{A}^{ * } = T_{A}^{ * } - T^{\prime}_{A} = - 149.8055448\,{{\upmu \text{K}}}$ agrees with the deviation $( - 150\,{{\upmu \text{K})}}$ from [5]. The sign “−” indicates that the area of the supervoid is colder than the neighboring areas.

3 Description of Transient Signals from Binary Objects

Busts of supernovae of type la, processes of BBH, binary neutron stars (BNS) merger can be considered as separate impulse sources in the Universe. In this case, transient gravitational-wave signals, relict radiation of photons arise. To describe the characteristic parameters and transient signals of the GW radiation from the BBH or BNS merger, we use the semiclassical superradiance model Dicke [16] and the quantum statistical theory of superradiance [17, 18]. For the radiation intensity J we have [16]

$$ J = J_{0} [(a_{0}^{2} - a_{m}^{2} ) + (a_{0} + a_{m} )] = J_{0} (a_{0} + a_{m} )[(a_{0} - a_{m} ) + 1]. $$

(10)

Here $J_{0}$ is the initial radiation intensity; parameters $a_{0}$, $a_{m}$ generally depend on the time, frequency and amplitude of the GW, the characteristics of the BBH or BNS. If $J = J_{m}$, where $J_{m}$ is the maximum radiation intensity, then from (10) we obtain expressions for the critical density $\rho_{c}$ ratio of the GW signal amplitude to the noise amplitude

$$ \rho_{c}^{2} = (z^{\prime}_{A2} - 1)/2 + J_{m} / (2J_{0} ); \; \; a_{0}^{2} = a_{m}^{2} + z^{\prime}_{\mu } (z^{\prime}_{\mu } + 2) / 4; \; \; a_{m} = (z^{\prime}_{A2} )^{1/2} . $$

(11)

The numerical values of the parameters are $a_{m} = 32.1575698$, $a_{0} = 32.4130298$, $J_{m} / J_{0} = 81.0658042$. The value $\rho_{c} = 23.602701$ is close to the critical value of 23.6 for BBH from [2]. The parameter $a_{0}$ is close to the ratio of the signal amplitude to the noise amplitude of 32.4 for BNS [3].

On the basis of model I from [13, 14] we write the expressions for the Hubble constant $H_{0}$, velocity $\upsilon_{ 0}$ in the model of a flat cosmology

$$ H_{0} = H_{01} /{\Omega}_{tH} = \upsilon_{ 0} / L_{ 0} ; \; \; \upsilon_{ 0} = \upsilon_{ 01} / {\Omega}_{tH} ; \;\; {\Omega}_{tH} = Q_{H0} + \left| {S^{\prime}_{ 01} } \right|. $$

(12)

Taking into account the values of Hubble constant $H_{01} = 73.2\,{\text{km}} \, {\text{s}}^{ - 1} \, {\text{Mpc}}^{ - 1}$, the velocity $\upsilon_{ 01} = 7.32 \times 10^{6} \, {\text{cm}} \, {\text{s}}^{ - 1}$ (which describe the accelerated expansion of the Universe), $Q_{H0} = 1.039541282$, $L_{0} = 0.30857 \times 10^{25} \, {\text{cm}}$ [12, 13], from (12) we obtain $H_{0} = 67.83540245\,{\text{km}} \, {\text{s}}^{ - 1} \, {\text{Mpc}}^{ - 1}$, $\upsilon_{ 0} = 6.783540245 \times 10^{6} \, {\text{cm}} \, {\text{s}}^{- 1}$.

In [13, 14], the values for the maximum $\nu_{r1} = 160.3988698\,{\text{GHz}}$ and shifted $\nu_{r2} = 142.8161605\,{\text{GHz}}$ frequencies of relict radiation photons were obtained. According to the relict radiation, taking into account $\xi_{q} = \nu_{r1} - \nu_{r2}$, in [7] the value of the gap $2 |\uplambda | N^{ 1/2} = 8.396945157\,{\text{GHz}}$ in the spectrum and density of cold dark matter ${\Omega}^{\prime}_{c1} = 4 |\uplambda |^{2} N / |\xi_{q} |^{2} = 0.228071512$ are obtained.

To calculate the wavelength $\uplambda_{{{{\upgamma }}b}}$ from the source for BNS, we use the energy spectra $\varepsilon_{\mu x} = 2\varepsilon^{\prime}_{01} S^{\prime}_{0x}$, $\varepsilon^{\prime}_{\mu x} = 2\varepsilon^{\prime}_{02} S^{\prime}_{0x}$, which are written in analogy with (1) on the basis of the energy of the Higgs boson and the order parameter $\delta_{\mu }$

$$ \begin{aligned} & 2\varepsilon^{\prime}_{ 01} = 2[E_{H0}^{2} + (\delta_{\mu } )^{2} ]^{ 1/2} ; \;\; 2\varepsilon^{\prime}_{ 02} = 2[E_{H0}^{2} - (\delta_{\mu } )^{2} ]^{ 1/2} ; \\ & \delta_{\mu } = E_{H0} \sin \varphi_{\mu } / Q_{H6} ; \;\; \uplambda_{{{{\upgamma }}b}} = R_{H0} \left| { \chi_{ef} } \right|(\varepsilon_{\mu 4} + \varepsilon_{\mu 2} )/(2E_{H0} ). \\ \end{aligned} $$

(13)

We note that the order parameter $\delta_{\mu }$ (describes the Bose-condensate) depends on the angle $\varphi_{\mu }$, parameter $Q_{H6}$, as follows from (7) and (8). The numerical values are $\delta_{\mu } = 4.6536541\,{\text{GeV}}$, $2\varepsilon^{\prime}_{01} = 250.2379072\,{\text{GeV}}$, $2\varepsilon^{\prime}_{02} = 249.8914929\,{\text{GeV}}$, $\uplambda_{{{{\upgamma }}b}} = 17081.85081\,{\text{nm}}$. Based on the calculated wavelength $\uplambda_{{{{\upgamma }}b}}$ from the source for BNS, we find the characteristic parameters

$$ \nu_{{{\upgamma}b}} = \upsilon_{ 0} / \uplambda_{{{{\upgamma }}b}} ; {\Omega}^{\prime}_{c2} = \nu_{{{{\upgamma }}b}}^{2} / (4|\uplambda |^{2} N); \upsilon_{{{{\upgamma}}b}}^{2} = \upsilon_{0}^{2} / {\Omega}^{\prime}_{c2} ; {\Omega}_{01} = \upsilon_{01}^{2} / \upsilon_{{{{\upgamma }}b}}^{2} . $$

(14)

Here $\nu_{{{{\upgamma }}b}} = 3.974973236\,{\text{GHz}}$ is frequency, ${\Omega}^{\prime}_{c2} = 0.224091707$ is density of cold dark matter, $\upsilon_{{{{\upgamma }}b}} = 14.34353643 \times 10^{6} \,{\text{cm}} \, {\text{s}}^{ - 1}$ is the effective Fermi-velocity associated with neutron stars; ${\Omega}_{01} = 0.260441196$. Taking into account (3), relations $n^{\prime}_{F\nu } = (n^{\prime}_{F} )^{2}$, $n_{F\nu } = n_{F} (1 + n^{\prime}_{F} )$ we find estimates of the densities of neutrinos ${\Omega}_{0 \nu } = n^{\prime}_{F \nu } = 0.0029398$, cold dark matter ${\Omega}_{c1} = {\Omega}^{\prime}_{c2} + {\Omega}_{0\nu } = 0.2270315$ (close to the estimate of the density of cold dark matter 0.227, obtained by other authors [1]). The wavelength $\uplambda_{{{{\upgamma }}h}}$ associated with the source from black holes is determined by expressions

$$ \uplambda_{{{{\upgamma }}h}} = \uplambda_{{{{\upgamma }}b}} /\eta_{bh} ; \;\; \eta_{bh} = (1 + {\Omega}_{01} /2)[1 + (n^{\prime}_{F} )^{2} /2]. $$

(15)

Parameter is $\eta_{bh} = 1.13188191$ and wavelength is $\uplambda_{{{{\upgamma }}h}} = 15091.54856\,{\text{nm}}$. The calculated values $\uplambda_{{{{\upgamma }}h}}$, $\uplambda_{{{{\upgamma }}b}}$ are close to the values of wavelengths 15091.4, 17081.7 nm for the sources from the BBH [2], BNS [3], respectively. From (1), (13) and (15) the relationships between Bose-condensates for black holes and neutron stars through energy $E_{H0}$ follow. The value $z_{ Q} = 0.008688605$ from (8) is close to the redshift of 0.009 of the source for BNS [3].

We find the spectrum for the occupation numbers $n_{cx}$ (based on $n_{ch}$) and the total number of quanta $n_{ tot}$ after the BNS merger from the expressions

$$ \begin{aligned} n_{cx} & = n_{ch} S^{\prime}_{ 0x} = M_{cx} / M_{s} ; \; n_{ch} = 1 / (\psi_{ch} - 1); \; \psi_{ch}^{*} = z^{\prime}_{ Q} \psi_{ch} ; \; \psi_{ch} = 1 + S^{\prime}_{ 02} / \chi_{11} ; \\ n_{tot} & = M_{tot} / M_{s} = 2n_{ c4} - n_{1c} = 2n_{ 3c} + (2n_{ 2c} + n_{ 1c} ); \; n^{\prime}_{ tot} = 2n_{ c4} - 2(n_{ c1} - n_{ c2} ) . \\ \end{aligned} $$

(16)

Numerical values are $n_{ch} = 5.332945778$; $\psi_{ch} = M_{ch} / M_{s} = 1.187513626$; $\psi_{ch}^{ * } = M_{ch}^{ * } / M_{s} = 1.197831463$; $M_{cx}$ and $M_{tot}$ are effective molar masses before and after merger. The calculated values $\psi_{ch}$ and $\psi_{ch}^{ * }$ are close to 1.188 and 1.1977 for effective molar masses $M_{ch}$ and $M_{ch}^{ * }$ within the GW detector from the BNS source [3]; $n_{ tot} = 2.742837254$ and $n^{\prime}_{ tot} = 2.81920162$ are close to 2.74 and 2.82 (low-spin and high-spin approximation) [3].

For the characteristic frequency $\nu_{GW}$ of the gravitational wave, we have

$$ \begin{aligned} & \nu_{GW} = 4\nu_{\uplambda 0} = N_{ra} \nu_{{{{\upgamma }}0}} ; \; \nu_{\uplambda 0} = 1 / (N^{\prime}_{0} - N^{\prime}_{02} )\tau_{s0} ; \; \tau_{s0} = 2(| {S^{\prime}_{01} } | + S^{\prime}_{02} )/\left| {\uplambda_{ \nu 0} } \right|; \\ & \tau_{s0} = \tau_{\uplambda 2} / N^{\prime}_{02} = \tau^{\prime}_{\uplambda 2} / N^{\prime}_{0} ; \; \tau^{\prime}_{\uplambda 2} - \tau_{\uplambda 2} = \tau_{\uplambda 0} = 1 / \nu_{\uplambda 0} ; \; \nu_{0} = 2z^{\prime}_{\mu } \nu_{\uplambda 0} / (2z^{\prime}_{\mu } + 1). \\ \end{aligned} $$

(17)

The parameter $\left| {\uplambda_{ \nu 0} } \right| = 130.5593846\,{\text{kHz}}$ is related to parameter $\delta_{\mu }$ from (13), describing the presence of a Bose-condensate for neutron stars. At $\left| {\uplambda_{ \nu 0} } \right| = 0$ from (17) follows, that the frequencies of the soft modes are $\nu_{\uplambda 0} = 0$ and $\nu_{GW} = 0$. Further from (17), we find $\tau_{s0} = 1.127935494\,{{\upmu \text{s}}}$, $\nu_{\uplambda 0} = 152.9437161\,{\text{Hz}}$, $\nu_{GW} = 611.7748643\,{\text{Hz}}$, $\nu_{0} = 142.9918607\,{\text{Hz}}$, $\tau_{\uplambda 0} = 6.538352972\,{\text{ms}}$, $\tau_{\uplambda 2} = 0.415136712\,{\text{s}}$, $\tau^{\prime}_{\uplambda 2} = 0.421675065\,{\text{s}}$.

The time of appearance of ${{\upgamma }}$-radiation after the merger of neutron stars $\tau_{{{{\upgamma }}0}}$ is determined by the difference in the coalescence times $\tau^{\prime}_{c0}$, $\tau_{c0}$

$$ \begin{aligned} & \tau_{{{{\upgamma }}0}} = \tau^{\prime}_{c0} - \tau_{c0} = 1 / \nu_{{{{\upgamma }}0}} ; \; \tau^{\prime}_{c0} = \tau_{{{{\upgamma }}0}} n^{\prime}_{A0} ; \; \tau_{c0} = 1/\nu_{c0} = \tau_{{{{\upgamma }}0}} n_{A0} ; \\ & \tau_{0} = 1 / \nu_{0} = \tau_{\uplambda 0} (1 + 1 / 2z^{\prime}_{\mu } ); \; \nu_{{{{\upgamma }}0}} = \nu_{c0} n_{A0} = \nu^{\prime}_{c0} n^{\prime}_{A0} ; \; \nu^{\prime}_{c0} = 1 / \tau^{\prime}_{c0} . \\ \end{aligned} $$

(18)

Numerical values are $\tau_{{{{\upgamma }}0}} = 1.7020861\,{\text{s}}$, $\tau_{c0} = 98.800376\,{\text{s}}$, $\tau^{\prime}_{c0} = 100.502462\,{\text{s}}$, $\nu_{{{{\upgamma }}0}} = 0.5875144\,{\text{Hz}}$, $\nu_{c0} = 0.0101214\,{\text{Hz}}$, $\nu^{\prime}_{c0} = 0.00995\,{\text{Hz}}$. The delay time GW between the detectors LD and HD $\tau_{0} = 6.993405\,{\text{ms}}$ from (18) is determined through the time $\tau_{\uplambda 0}$ from (17) and the cosmological redshift $z^{\prime}_{\mu }$.

We write the spectra $\nu_{rx} = 2\nu_{ra} S^{\prime}_{0x}$ and $\nu^{\prime}_{zx} = 2\nu^{\prime}_{z\mu } S^{\prime}_{0x}$ on basis $\nu_{ra}$ and $\nu^{\prime}_{z\mu }$

$$ \begin{aligned} & \nu_{ra} = {\Omega}_{ra} \nu_{\uplambda 0} = {\Omega}_{ra} \nu_{GW} / 4; \; \nu^{\prime}_{z\mu } = \nu_{ra} z^{\prime}_{\mu } ; \; {\Omega}_{ra} = N_{ra} {\Omega}^{\prime}_{c1} / z^{\prime}_{A2} ; \\ & \nu_{ra} = \nu_{r3} + \nu_{r1} = \nu_{r4} - \nu_{r2} ; \; \nu^{\prime}_{z\mu } = \nu^{\prime}_{z3} + \nu^{\prime}_{z1} = \nu^{\prime}_{z4} - \nu^{\prime}_{z2} ; \\ & \nu_{z\mu }^{ * } = \nu^{\prime}_{z3} + \nu^{\prime}_{z2} = \nu^{\prime}_{z4} - \nu^{\prime}_{z1} . \end{aligned} $$

(19)

Numerical values are ${\Omega}_{ra} = 0.229656$, $\nu_{ra} = 35.124438\,{\text{Hz}}$, $\nu^{\prime}_{z\mu } = 252.340321\,{\text{Hz}}$, $\nu_{z\mu }^{ * } = 249.589164\,{\text{Hz}}$. If $z^{\prime}_{\mu } = 1$, then from (19) follows, that the spectrum $\nu^{\prime}_{z\mu }$ goes to spectrum $\nu_{ra}$. When the black holes merger, the LD and HD detectors recorded the signals as a series of pulses, the frequency of which increased from 35 to 250 Hz. At the same time, the amplitude of the signals increased to the maximum value, and then dropped sharply to the noise level. Our calculated frequencies $\nu_{ra}$, $\nu^{\prime}_{z\mu }$, $\nu_{z\mu }^{ * }$ agree with the data on the detection of GW during of the BBH merger [2].

Next, we write the spectrum $\nu_{Wx} = \nu_{GW} S^{\prime}_{ 0x}$ on the basis of frequency $\nu_{GW}$. The value of the frequency $\nu_{W1} = 24.190362\,{\text{Hz}}$ is consistent with the value of the frequency $24\,{\text{Hz}}$, that the LD detector starts detecting in the GW detection experiment during BNS merger [3].

Let $h_{ mL}$, $h_{ mH}$ be maximum values of amplitudes of signals GW, registered by detectors LD, HD; $h_{\xi L}$, $h_{\xi H}$ are noise level after passing the GW. The GW signal on the HD detector appears later on a delay time $\tau_{0}$, than on the LD detector. Taking into account (10) and (11), we write the relations for the amplitudes of the signals GW arising from the black holes merger

$$ \begin{aligned} & 2h_{ mH} / h_{ mL} = (1 + a_{m} / a_{ 0} )[1 + (a_{ 0} - a_{m} )]; \; h_{ mH} h_{\xi L} = h_{ mL} h_{\xi H} ; \\ & 2h_{\xi H} /(2h_{ mH} + h_{\xi H} ) = 2h_{\xi L} / (2h_{ mL} + h_{\xi L} ) = |\xi_{ 0H} |^{2} . \\ \end{aligned} $$

(20)

On the basis of (20), we obtain the numerical values $h_{ mL} = 0.9168936 \times 10^{ - 21}$, $h_{ mH} = 1.146587 \times 10^{ - 21}$, $h_{\xi L} = 0.1833588 \times 10^{ - 21}$, $h_{\xi H} = 0.2292923 \times 10^{ - 21}$.

The maximum amplitude $h^{\prime}_{ mL}$ of the GW signal, the noise level GW before and after the neutron stars merger $h_{\xi L}^{ * }$ and $h^{\prime}_{ \xi L}$ (recorded by the LD detector) are determined by the formulas

$$ \begin{aligned} h^{\prime}_{ mL} & = 2a_{ 0} / n_{{ {\Omega} 2}} = 2a_{ 0} h_{ mH} ; \; h_{\xi L}^{ * } = 2a_{ m} / n_{J0} = 2a_{ m} h_{\xi H} ; \; 1/ n_{J0} = h_{\xi H} ; \\ h^{\prime}_{ \xi L} & = 2h^{\prime}_{ mL} \left| { \xi_{ 0H} } \right|^{2} / (2 - \left| {\xi_{ 0H} } \right|^{2} ); \; 1/ n_{{ {\Omega} 2}} = h_{ mH} = | \xi_{ q} |^{2} E_{G} /(4\left| \uplambda \right|^{2} N_{ra} E_{H0} N^{\prime}_{02} ). \\ \end{aligned} $$

(21)

Values are $h^{\prime}_{ mL} = 7.4328715 \times 10^{ - 20}$, $h_{\xi L}^{ * } = 1.4746969 \times 10^{ - 20}$, $h^{\prime}_{ \xi L} = 1.4864119 \times 10^{ - 20}$, $E_{G} = 12.11753067\,{\upmu} {\text{eV}}$, $h^{\prime}_{ mL} / h_{\xi L}^{ * } = 5.0402707$. The obtained estimates from (20) and (21) agree with the data from [2, 3].

4 Description of an Individual Layer with Variable Parameters

The hypothesis of the hierarchical structure of the Universe allows us to use models of fractal nanosystems (dislocations, quantum dots) to describe separate elements of large-scale fractal structures. When modelling the nonlinear effective displacements $u_{\mu } = {\text{F}}(\varphi_{\mu } ;k_{\mu } )$ from (6), the main parameter is $b_{ 0} = 1 - 2{\text{sn}}^{2} (u_{\mu } ;k_{\mu } )$. Expressions for the four branches of effective displacements $u_{\mu i} \, (i = 1,2,3,4 )$ have the form [12]

$$ 2u_{\mu 1} (z,\alpha ) = g_{1} - g_{2} + g_{4}; \; \; 2u_{\mu 2} (z,\alpha ) = g_{1} - g_{2} - g_{4} ; $$

(22)

$$ 2u_{\mu 3} (z,\alpha ) = - g_{1} - g_{2} + g_{5} ; \; \; 2u_{\mu 4} (z,\alpha ) = - g_{1} - g_{2} - g_{5} . $$

(23)

The functions $g_{1},g_{2},g_{3} ,g_{4} ,g_{5}$ depend on the coordinate z, the fractal index $\alpha$ along the axis Oz, and are modelled by expressions

$$ g_{2} (z,\alpha ) = g_{20} \left| {z - z_{c} } \right|^{ - \alpha } ; \; \; g_{3} (z,\alpha ) = g_{30} \left| {z - z_{c} } \right|^{ - 2\alpha } ; $$

(24)

$$ g_{20} (\alpha ) = 2^{ - 2\alpha } 3^{3\alpha - 1/2} {\Gamma} (\alpha + 1/3) {\Gamma} (\alpha + 2/3)/\sqrt \pi \, {\Gamma} (\alpha + 1/2); $$

(25)

$$ g_{30} (\alpha ) = 2 \cdot 3^{3\alpha - 1/2} \, {\Gamma} (\alpha + 1/3) {\Gamma} (\alpha + 2/3)/\pi ; \; \; g^{\prime}_{30} (\alpha ) = 1/g_{30} (\alpha ); $$

(26)

$$ g_{4} (z,\alpha ) = \left[ {(g_{1} + g_{2} )^{2} - g_{3} } \right]^{1/2} ; \; \; g_{5} (z,\alpha ) = \left[ {( - g_{1} + g_{2} )^{2} - g_{3} } \right]^{1/2} . $$

(27)

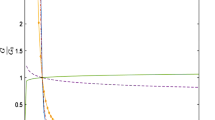
Here ${\Gamma}$ is the gamma function; $g_{20}$, $g_{30}$, $g^{\prime}_{30}$ are nonlinear discontinuous functions of the fractal index $\alpha$ (Fig. 1). The functions $g_{2}$, $g_{3}$ from (24) also become nonlinear on the background of power dependencies.

Fig. 1.

Behavior of functions $g_{20}$, $g_{30}$, $g^{\prime}_{30}$ on $\alpha$

The function $g_{20} (\alpha )$ has zeros at $\alpha = - (n_{\alpha } + 1 / 2)$, where $n_{\alpha } = 0,1,2 \ldots$. The function $g^{\prime}_{30} (\alpha )$ has zeros at $\alpha = - (n_{\alpha } + 1 / 3)$, $\alpha = - (n_{\alpha } + 2 / 3)$. The nonlinear function $g_{1}$ depends on $u_{\mu }$, $\alpha$ and indices n, m, j lattice nodes

$$ g_{1} (u_{\mu } ,\alpha ;n,m,j) = k_{\alpha }^{2} (1 - 2\text{sn}^{2} (u_{\mu } - u_{ 0} ;k_{\mu } )); \; \; k_{\alpha }^{2} = (1 - \alpha )/Q; $$

(28)

$$ Q = p_{0\alpha } - b_{1} (n - n_{0})^{2} / n_{c}^{2} - b_{2} (m - m_{0})^{2} / m_{c}^{2} ;\; \; p_{0\alpha } = p_{0} - b_{3} (j - j_{0})^{2} / j_{c}^{2} . $$

(29)

Here $u_{0}$ is constant displacement; $p_{0}$, $b_{1}$, $b_{2}$, $b_{3}$, $n_{0}$, $n_{c}$, $m_{0}$, $m_{c}$, $j_{0}$, $j_{c}$ are characteristic parameters. The function $k_{\alpha }$ depends on $\alpha$, indices n, m, j lattice nodes $N_{1} \times N_{2} \times N_{3}$. In our model, this function determines the behavior of the module $k_{\mu } = {\text{sn}}(u_{0\alpha } ,k_{\alpha } )$, where $u_{0\alpha } = {\text{F}}(\varphi_{0\alpha } ,k_{\alpha } )$; $\varphi_{0\alpha }$ is the polar angle. As a result $k_{\mu }$ (implicitly depends on n, m, j) and four branches $u_{\mu i}$ from (22) and (23) become random functions. In numerical simulation, for forward $z = z_{1}$ and backward $z = z_{2}$ waves it was assumed that $z_{1} = 0.053 + h_{z} (j_{z} + 33)$; $z_{2} = 6.653 - h_{z} (j_{z} + 33)$, $h_{z} = 0.1$; $j_{z} = 5$; $n = \overline{1,30}$; $m = \overline{1,40}$; $u_{0} = 29.537$; $u_{0\alpha } = \pi / 5.2$; $p_{0} = 1.0123$. The solution of Eqs. (22) and (23) for branches $u = u_{\mu i}$ is carried out by the iteration method on the variable m.

Consider the state of a layer without quantum dot ($b_{1} = b_{2} = b_{3} = 0$, $Q = p_{0}$). The behavior branches of the displacement function of the backward wave on $\alpha$ is given in Fig. 2.

Fig. 2.

Dependencies of the projections u on the plane $mOu$ for the backward wave on m for various $\alpha$: 1—$u_{\mu 1}$, 2—$u_{\mu 2}$, 3—$u_{\mu 3}$, 4—$u_{\mu 4}$

For the backward wave (Fig. 2a), in addition to the regular behavior of the 1, 2, 3 branches, the stochastic behavior of the 4 branch is observed, the 3 branch is characterized by the presence of the second harmonic. At $\alpha = - 1.5$ (Fig. 2b) oscillations with increased amplitudes are observed for branches 1 and 4, and damped oscillations with amplitudes of order for branches 3 and 2 are observed. At $\alpha = - 2.5$ (Fig. 2c), singularities appear in comparison with Fig. 2b: for branch 1 is change in shape, amplitude of oscillations; for branch 4 is doubling of the period of oscillations; for branches 3 and 2 are damped oscillations with reduced amplitudes of order $\pm 2 \times 10^{ - 10}$. At $\alpha = - 3.5$ (Fig. 2d) branches 3 and 2 demonstrate nonlinear oscillations: on separate peaks of 3 branches there are features such as a local minimum between two humps; branches 1, 4 take zero values. With a further change $\alpha$, the character of the behavior of all four branches practically does not change (similar to the behavior of Fig. 2b with the order of the branches 3, 1, 4, 2), which indicates the presence of a critical value $\alpha \approx \alpha_{c} = - 4.5$. This is due to the nonlinear behavior of discontinuous functions $g_{20}$, $g_{30}$ from (25) and (26) on $\alpha$. With a change $\alpha$ the behavior of the forward wave branches qualitatively coincides with that for the backward wave.

Next, we consider the state of the layer with a quantum dot (Fig. 3). Main parameters are $b_{1} = b_{2} = b_{3} = 1$; $n_{0} = 14.3267$; $n_{c} = 9.4793$; $m_{0} = 19.1471$; $m_{c} = 14.7295$; $j_{0} = 31.5279$; $j_{c} = 11.8247$. From (29) at $p_{0\alpha } = - 3.457 \, \times \, 10^{ - 11}$ we find the averaged values for the layer number j: $j_{1} = 19.63070035$, $j_{2} = 43.42509965$. At iterations it was accepted $j = j_{1}$. In this case, the module $k_{\mu }$ implicitly depends on n, m, and becomes a random function.

Fig. 3.

Dependencies u on n, m at $\alpha = - 0.5$ for different branches of the forward (a, b, c) and the backward (d, e, f) waves

The behavior of the displacement functions of all four branches for the forward (Fig. 3a–c) and the backward (Fig. 3d–f) waves is different. The 1 branch of the forward (Fig. 3a) and the backward (Fig. 3d) have peaks with large amplitudes, that confirms the state of the layer with the quantum dot. The behavior of the core of such quantum dot differs from the behavior of the cores of quantum dots from [14]. Instead of regular wave behavior [14], the cores boundaries become stochastic. Inside the cores, there are features of the type of islands, jumpers, narrowings, wells. For the 2 branch of the forward wave, the core has a convex form (Fig. 3b), and for the backward wave the core approaches to a flat form (Fig. 3e). For the 3 branch of the forward wave, the core has a concave form of the well type (Fig. 3c), and for the backward wave (Fig. 3f) the core has a flat bottom. At the boundaries of these cores there are peaks with small amplitudes (features such as additional wells, saddles, valleys are formed). These features of the deformation field behavior indicate the appearance of an effective multi-well potential in a layer with a quantum dot.

A further change $\alpha$ leads to a change in the stochastic behavior of the core boundaries (Fig. 4). For the 2 branch of the backward wave, at $\alpha = - 2.5$ (Fig. 4a), a stochastic peak down is observed on a stochastic background with a practically constant amplitude. At $\alpha = - 4.5$ the stochastic peak disappears, and the stochastic background remains (Fig. 4b). At $\alpha = - 8.5$ (Fig. 4c), in the stochastic background the formation of a failure near $m = m_{0}$ is observed.

Fig. 4.

Dependencies of the projections $u = u_{\mu 2}$ on the plane $mOu$ for backward wave on m for different $\alpha$

When the values of the semi-axes $n_{c}$, $m_{c}$ (Fig. 5) of quantum dot are changing, the behavior of the deformation field of the core and its boundary changes. For the first branch $u_{\mu 1}$ the effect of pronounced anisotropy is observed. A periodic fine structure appears on the boundaries for the forward wave (Fig. 5a), and for the backward wave there is a structure with fine wells (Fig. 5c).

Fig. 5.

Cross-sections $u_{\mu 1} \in [0;1.5]$ (top view) for forward (a, b) and backward (c) waves for different semi-axes, $n_{c}$, $m_{c}$ at $\alpha = - 0.5$

5 Conclusions

An anisotropic model is proposed for describing the main parameters of the BBH, BNS, the nature of the spin source of which has a tensor character. Taking into account the Higgs field, estimates are made of the energies of the Higgs boson, relict photons, and the temperature deviation of the relict background. It is shown that the nature of the supervoid or the “Cold relict spot” is associated with the presence of a black hole and its influence on relict photons. To describe the transition signals (gravitational waves, relict radiation), it is proposed to use the superradiance model R. H. Dicke and the quantum statistical theory of superradiance.

Based on the hypothesis of the hierarchical structure of the Universe, modelling of the deformation field of separate structures it is proposed to use of quantum model systems with variable parameters. It is shown that for a layer without a quantum dot, the presence of nonlinear oscillations is characteristic, which depend on the fractal index $\alpha$. The structure of the quantum dots cores in the layer has a convex, concave, and flat form with a stochastic boundary. The formation of stochastic peak and the appearance of failure on stochastic background is possible. The change in the semi-axes of the quantum dot leads to the anisotropy effect.